Introduction

In Computer Vision, most approaches rely on RGB images1,2. However, several studies have demonstrated that incorporating a fourth channel, the depth channel, yields significant improvements3,4,5 by integrating and making explicit additional information that was previously implicit in the captured image. Utilizing depth information, however, requires access to depth maps, which can be obtained through specialized hardware using an active sensing approach. Sensors such as LiDAR or certain types of cameras acquire depth by emitting a physical signal into the environment and measuring the time taken for its return. Depth plays an essential role in several practical applications. In robotics, it enhances autonomous navigation and obstacle avoidance6, while in autonomous driving, it provides a precise understanding of the surrounding environment7. Additionally, in virtual reality, depth data contributes to more realistic and immersive experiences, improving user engagement8. Despite its advantages, actively acquiring depth through sensors presents several challenges. First, depth maps generated by these devices are often sparse, providing depth values only at specific points rather than offering a dense and comprehensive representation of the scene. Moreover, integrating dedicated hardware imposes additional constraints on the system, increasing weight and power consumption, which can be critical for resource-limited applications.

These challenges can be mitigated through passive depth-sensing techniques, which shift the computational complexity from hardware to software. Unlike active sensing, passive approaches estimate scene depth without directly perturbing the environment, eliminating the need for specialized depth sensors. One prominent example of passive depth estimation is Monocular Depth Estimation (MDE)9, which infers depth information from a single RGB image. This complex, dense task allows for a more global view of the scene’s depth and minimises the reliance on specific hardware. In this context, Deep learning models are essential for obtaining accurate and reliable depth estimates. In particular, transformer architectures succeed in approaching this task with impressive results. Due to their ability to capture global features via the attention mechanism10, the transformer models specific to vision tasks, namely Vision Transformers (ViTs)11, can predict accurate and precise depth maps12,13,14. A major limitation of the ViT architecture is the computational cost of its attention module, which scales quadratically with the number of tokens being processed. While this module is essential for achieving high performance, it significantly impacts processing speed and memory usage, making dense prediction tasks such as MDE highly resource-intensive. This challenge is particularly critical in onboard or real-time applications, where the device’s processor is also responsible for tasks beyond network inference. In this context, the device is in a dynamic environment and it should generalize real and new data15,16,17,18 in a reliable and fast way. This fact, combined with the constrained computational resources of certain hardware platforms, creates a challenging environment for deploying ViT-based MDE models efficiently. To address this issue, our research focuses on integrating efficient attention mechanisms into state-of-the-art ViT architectures for MDE, aiming to achieve an optimal trade-off between performance and inference speed.

This paper provides a comprehensive analysis of the impact of efficient attention modules on various ViT architectures for MDE that achieve state-of-the-art performance. Specifically, optimizations are applied not only to the entire network but also independently to the encoder and decoder, enabling a more granular study of how attention modifications influence different network components. This approach helps identify the most effective optimizations, ultimately guiding the development of a model that balances inference speed with fidelity to baseline performance. The architectures under investigation include PixelFormer (PXF)12 and Neural Window Fully-connected CRFs (NeWCRFs)13, both of which are computationally intensive models that incorporate attention mechanisms in both the encoder and decoder. Additionally, we analyse METER14, a lightweight hybrid architecture that combines transformer-based processing with convolutional layers. By comparing the effects of optimizations on these models, we aim to understand how fully attention-based networks, such as PXF and NeWCRFs, perform relative to hybrid architectures like METER. The optimizations explored in this study introduce structural modifications to the attention mechanism. Specifically, MetaFormer (Meta)19 replaces the attention module with a token mixer of linear complexity, significantly reducing computational overhead. Meanwhile, Pyramid Vision Transformers (Pyra)20 adjust the computational granularity of the attention module by reducing the size of its processing elements, thereby altering its overall complexity. Through this analysis, we seek to determine the effectiveness of these optimizations in enhancing inference efficiency while maintaining high-quality depth predictions. Finally, the Mixture-of-Head (MoH) method21 introduces a routing mechanism to dynamically select the most effective attention heads, further enhancing computational efficiency. The choice of these types of efficient attention modules is based on the fact that they have been tested on various computer vision tasks, but not yet to MDE. In all cases considered, these attention modifications have led to promising results, making it interesting to evaluate their performance on a dense and complex task such as MDE. Moreover, each optimisation affects the attention modification differently: Meta simplifies the architecture, Pyra compresses the inputs, while MoH changes the routing of multi-head attention.

Given the structural modifications introduced by these optimizations, it is essential to employ an objective evaluation framework to assess their impact. To achieve this, our research leverages the Pareto Frontier, a systematic and analytical tool for identifying optimal solutions in multi-objective problems. In our context, each candidate model represents a potential solution, and only the Pareto-optimal models, those that are not outperformed across all objective criteria, are selected. A model is considered dominant if no other model surpasses it in both prediction quality and inference speed simultaneously. The resulting Pareto-optimal models define the frontier, representing the best trade-offs between these competing objectives. This approach provides a rigorous evaluation framework, allowing us to systematically compare optimised models against their respective baselines. While Pareto analysis has been applied in deep learning evaluations22 and in multi-modal object tracking23, it has not yet been explored specifically for MDE.

Our experiments are conducted on two benchmark datasets widely used for MDE: NYU Depth V224, which consists of indoor scenes, and KITTI25, which focuses on outdoor driving scenarios. By evaluating optimised networks across these datasets, we aim to assess their performance in diverse real-world conditions, ensuring the models generalize well to practical applications.

To provide a clear overview, our work can be summarized as follows:

  • We conduct an in-depth study on the impact of efficient attention modules on the qualitative and temporal performance of ViT models for the MDE task.

  • We analyse the impact of the efficient attention modules separately on the full network, encoder, and decoder, obtaining a descriptive evaluation of the optimisation’s contribution.

  • We introduce the Pareto Frontier as a systematic method to identify the optimised models that achieve the optimal trade-off between result quality and inference speed.

The rest of the article is organized as follows: In “Related works” section presents an overview of MDE, describing ViT architectures for this task and suitable optimizations for their attention modules. In “Methods” section exposes networks and efficient attention modules used in the experiments. “Results” section presents a detailed analysis of the experiments carried out. Finally, “Conclusions” section indicates conclusions and potential future research directions.

Related works

Monocular depth estimation

Depth estimation, in its most general form, concerns determining the distance between an object and the imaging sensor. From an application perspective, this process is crucial in various real-world domains, including robotics6, autonomous driving7 and augmented reality8. The depth measurement can be performed actively, by sensing the depth through dedicated hardware. That approach perceives the scene’s depth by perturbing the environment with a physical medium, such as LiDAR or Time-of-Flight. Another possible solution is to retrieve the depth passively, not by measuring but by estimating the value through software solutions. Our application context focuses on MDE, which is categorised as a passive method. This approach estimates image depth from a single RGB image on a per-pixel basis9. Among software-based solutions related to this task, several Deep Learning methods leverage neural networks to predict depth maps12,13,14. These techniques often achieve accurate results that are in part attributed to10 attention mechanisms, which enable the extraction of global information from the input image. However, despite their potential, these models are often constrained by a slow inference speed, primarily due to the weight of the network and the computational cost of some of their modules. This situation leads to challenges in scenarios where both precision and real-time performance are necessary.

Our research aims to identify solutions that can mitigate the complexity of MDE models while maintaining performance and improving inference speed.

Vision transformers for monocular depth estimation

Deep Learning-based solutions are widely used in the MDE task. Early approaches involved using Convolutional Neural Networks (CNN)26 to estimate the depth from a single input image. A representative work that introduces this type of model is the study by Eigen et al.27. Their approach captures the image context and then reconstructs the depth map by refining the local details of the obtained representation.

With the advent of Transformers and the attention mechanism10, these architectures have been extended to the field of imaging, through the introduction of ViTs11. These models process input images by tokenizing them into smaller patches. Due to their ability to capture long-range dependencies and model global spatial relationships, they have been widely adopted in Computer Vision28 tasks, including MDE. Several networks have exploited the ViT architecture with specific techniques to improve the quality of the predicted depth map. An example is the PixelFormer network12, which after extracting the image representation with a Swin Transformer backbone29, improves the quality of the predicted depth map by merging encoder and decoder features with an attention-based approach. Similarly, the NeWCRFs network13 exploits a decoder module that introduces Conditional Random Fields (CRF) integrated with attention mechanisms. In this framework, each CRF captures observable image features, such as textures and object positions, to define an energy function, which is then optimised to retrieve the depth estimation. In contrast to these networks, some recent solutions integrate CNNs with the capabilities of ViTs, developing hybrid approaches. For instance, METER14 is a lightweight model, combining a transformer-based encoder with a fully convolutional decoder. This architecture is suitable for experiments were conducted on devices with limited hardware resources and achieves a reasonable balance between efficiency and performance.

Despite the strong performance of the presented networks for the MDE task, they share common problems with ViT architectures. Transformer models are often characterized by a high number of parameters and floating point operations per second (FLOPs), resulting in memory-intensive networks and often slow inference. This issue is mitigated in lightweight transformer architectures, which achieve reasonable performance while maintaining lower computational demands. However, another challenge that affects all Transformers is the quadratic problem of the attention module10. This module has a quadratic computational cost concerning the input tokens, leading to a significant speed issue in MDE, as high-resolution inputs require processing a substantial number of tokens to predict a dense depth map. Recent research on MDE has introduced efficient attention mechanisms in networks addressing this task30,31; however, the trade-off between performance and speed remains insufficiently analysed.

This work addresses the optimisation of networks for MDE, which perform well but are limited by the computational cost of the attention module. Furthermore, this work focuses on achieving a trade-off between performance and speed through a structured and quantitative evaluation of the modified networks compared with their original models.

Efficient attention modules

Although in different ways, all the architectures presented use the attention mechanism. This module, in most cases, determines the model’s performance. However, attention presents a computational problem due to its quadratic complexity relative to the input tokens10. In ViT-based networks, where images are divided into a large number of patches11, this results in significant computational overhead. This situation poses challenges in time-critical applications such as autonomous driving or rescue robotics9.

To address this issue, several studies32 have explored techniques to optimise the attention modules. In particular, these methods aim to reduce the quadratic complexity of the mechanism, proposing new approaches to speed up the calculation and maintain performance. These methods are specifically designed to modify attention, in contrast to the promising optimisation present in the current literature33,34, or more general solutions such as quantisation35, pruning36 and knowledge distillation37 which reduce computational overhead by optimising the entire network. Regardless of the applied optimisation, modified models will experience a trade-off between performance and inference speed32,38. There are cases, however, where performance may even improve once the optimisation is introduced. A consistent example is MoH21, which modifies the entire multi-head attention mechanism. Since not all attention heads contribute equally to the final prediction39, the proposed optimisation employs a specialised routing mechanism to efficiently select the most relevant heads. This method has been used in computer vision tasks such as classification or image generation, but its application in MDE has not yet been proven.

Unlike MoH, some optimisations, such as Meta19 and Pyra20 focus more specifically on token processing within the attention module. Meta advances the idea that in ViT architectures, the quality of results depends primarily on the overall structure of the network, rather than on the attention module. This part of the network is intended as a token mixer and, given the initial assumption, is replaced with a much simpler module which performs the token mixing operation in a computationally lighter manner. Pyra optimisation, in particular, introduces spatially reduced attention, progressively decreasing the input size of the attention mechanism. This method allows for the better application of transformation architectures to dense tasks, dealing with less expensive computational elements. Both methods introduced have already been tested in the MDE task38, bringing encouraging results from the point of view of maintaining the performance and speed of the optimised models. However, a precise analytical definition of the trade-off between prediction quality and speed of inference remains unclear. The Efficient Error Rate introduces a possible approach in32, but this metric is based on values primarily influenced by network-wide optimisations, which substantially alter the number of parameters and the model’s memory weight. Another attempt to measure the trade-off between different objectives of a neural network was introduced by the work22, in which through the Pareto Frontier a systematic and precise way is proposed that comes directly from optimisation theory. To the best of our knowledge, the application of this method is limited in the context of Deep Learning and unexplored in the analysis of optimised models for MDE.

Building on these concepts, we aim to optimise ViT architectures for the MDE task. More specifically, techniques that modify the complexity of the attention modules have been adopted. The impact of these modifications will be evaluated in a general and systematic manner, independent of specific network values, focusing solely trade-off between quality and speed objectives.

Methods

Optimization framework

In this section of the article, the general approach proposed to modify and analyse the networks considered for the study is presented. As highlighted in the current literature, the issue associated with Transformer models, related to the quadratic cost of their attention module, has emerged10,38. Consequently, the need to optimize this part of the network arises, applying targeted modifications to mitigate the complexity of attention. However, to have a clear comparison between the modified networks and the baselines, a standardized process that can be applied to the networks and optimizations under study is essential.

Fig. 1
figure 1

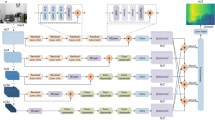
The general framework used to compare the different network-optimization configurations. The module Network architecture instantiates the network to be analysed, while the submodule Efficient Attention Module integrates the attention mechanism used by the encoder, decoder, or the entire network. On the left side a comparison is shown to illustrate how each optimization modifies the original module. The left module depicts the optimised attention, while the right one shows its standard version.

Full size image

This need leads to setting the proposed analysis through a specific framework. This approach takes advantage of the architectural similarities of the elements involved, allowing the various network-optimization combinations to be easily applied and immediately capture the results relevant to the research. The idea is shown in Fig. 1. The approach considers each component as a container, capable of integrating the different elements. In this way, a generic framework is obtained, with different instances depending on the dataset, network and optimization used.

More specifically, the framework includes a module related to the network architectures to be tested. This component itself contains two sub-structures: one for the encoder and the other for the decoder. These two elements are fundamental in the framework because they will integrate the different types of efficient attention modules and the classical one for the baseline. Thus, by instantiating these containers, it is possible to obtain the network configurations in a clear and precise manner.

This approach realises a consistent experimental framework that facilitates the reproducibility and the evaluation of the different modified models. Each network and optimization that realizes a configuration has its characteristics that determine the behaviour of the modified network. Details on these different elements are discussed in the following sections.

Network architectures

METER

METER14 is a hybrid and lightweight ViT network. It achieves strong performance, even in scenarios with limited hardware resources.

This network uses an encoder that extracts useful features for depth prediction from the input image. This module comprises different layers, including convolutions with small kernels to maintain fast data processing and transformer blocks. In particular, this is the only part of the network that has attention modules. This module is available in three sizes: XXS, XS, and S. Each increment increases the parameters and the network capabilities. The METER decoder is purely convolutional and is responsible for reconstructing the predicted depth map from the features extracted by the encoder.

Beyond the architecture, this work introduces a composite loss specific to the MDE task. This approach integrates different values tailored for depth estimation, considering the pixel-per-pixel difference, cosine similarity between prediction and ground truth, and penalty factors to enhance detail reconstruction. In addition, a dedicated data augmentation pipeline enhances the robustness of the network. The latter proposes a change in the colour and brightness of the input RGB image, called C Shift, to simulate different data acquisition conditions. Furthermore, virtual data augmentation is also applied to the depth maps, with the D Shift, which randomly shifts the depth map corresponding to the ground truth to reduce the risk of overfitting on specific depth values.

PixelFormer

PixelFormer12 approaches the MDE task in a particular form. For each image, the network adaptively predicts multiple intervals that divide the continuous depth value into a discrete range. Each pixel of the depth map to be estimated will be associated with a vector of weights, with several elements equal to the number of intervals estimated. The final depth of each pixel is calculated as a linear combination of the centres of the intervals predicted for the image, weighted by the values of the probability vector associated with that pixel.

The encoder, a Swin Transformer29, was presented in the original paper as a general backbone for computer vision tasks. Its feature extraction function is based on a hierarchical organisation to model information at different resolutions and on non-overlapping windows that, in their context, apply attention computation to the local context of an input patch. As in the previous model, the network is available in three configurations: tiny, base and large, each with increasing parameters. PixelFormer’s decoder, on the other hand, introduces the SAM mechanism that merges features from the encoder with those of the decoder through an attention mechanism to maximise information extraction from the encoder’s general and decoder-specific features.

NeWCRFs

The NeWCRFs13 network approaches the MDE task based on so-called CRFs. These elements are probabilistic models that capture spatial relationships in structured data. In MDE, these elements allow dependencies between pixels to be modelled so that the estimated depth is consistent with that of its neighbours. This approach applies CRFs on local windows to capture global information while limiting the computational impact to limited connections between neighbouring pixels.

The network applies this methodology through its decoder, supported by an attention mechanism to precisely and accurately model the connections between the different local windows related to the CRFs. The encoder module consists of a Swin Transformer29 that processes the input images, extracting global and hierarchical features while capturing long-range dependencies between pixels.

Fig. 2
figure 2

On one side, the classical attention module (a) is compared with the token mixer module of Meta (b) implemented by the pooling operation, and with the Pyra (c) approach in which key and values are spatially reduced. On the other side, MoH (e) approach modifies the routing system in the multi-head attention (d), addressing only some specific heads, and then aggregating them using a weighted sum.

Full size image

Efficient attention module

Meta-optimised modules

As shown, MetaFormer generalises the concept of ViTs by maintaining the overall architecture while allowing the use of different token mixers to replace the attention module. In particular, the work demonstrates that using a simple operator, such as pooling, instead of attention supports the hypothesis that the general ViT architecture is a key factor in model performance.

Taking the original formula of the attention, the difference between this and the one proposed in19 is very marked. Considering the classical formulation of the attention

$$\begin{aligned} \text {Attention}(Q, K, V) = \text {Softmax}\left( \frac{QK^\top }{\sqrt{d_h}}\right) V \end{aligned}$$
(1)

where Q are the queries, K the keys, V the values, \(d_h\) the size of the attention head and \(\text {Softmax}\) an activation function10, the Meta approach proposes the following modification

$$\begin{aligned} \text {MetaAttention}(x) = \text {Pooling}_k\left( x\right) \end{aligned}$$
(2)

where, in this case, x is directly the input given to the transformer, and the operator Pooling operates as suggested by its name, exploiting a kernel of dimension k that aggregates the elements of the input by averaging them among those that fall in its receptive field.

Using pooling as a token mixer allows for a module with linear computational complexity concerning the number of input tokens. In addition, it does not introduce trainable parameters that could burden the network’s structure.

Pyra-optimised modules

The Pyramid PVT approach is one of the proposed variants designed to mitigate the drawback associated with the quadratic complexity of the attention module, particularly in transformer-based networks for dense tasks, such as MDE. In this case, the number of tokens present is exceptionally high, exposing the network to the adverse effects of having a quadratic complexity dependent on this factor.

The concept presented in20 combines the advantages of convolutional neural networks26 and transformers10. It introduces a pyramid approach that progressively reduces the input’s resolution, maintaining a high-resolution representation in the first levels for greater accuracy in dense predictions. Although the attention equation closely resembles the original version shown in Eq. 1, a critical detail represents the core idea of the proposed method.

$$\begin{aligned} \text {PyraAttention}(Q, K, V) = \text {Softmax}\left( \frac{Q SR(K)^\top }{\sqrt{d_h}}\right) SR(V) \end{aligned}$$
(3)

The spatial reduction operator SR manipulates both K and Q keys, defined as follows

$$\begin{aligned} \text {SR}(x) = \text {Norm}\left( \text {Reshape}\left( x,R\right) W\right) \end{aligned}$$
(4)

This operation is applied to the input x, which, in our case, are the keys or values. The reduction ratio R applies a reshape operation to the input. The output is then subjected to a linear projection and normalisation. These steps reduce the computational cost of the attention operation by as much as \(R^2\) compared to its original form, allowing even considerable inputs to be better handled.

MoH-optimised modules

The concept presented by MoH does not modify the attention module itself but rather optimises the routing mechanism among multiple heads, as is depicted in Fig. 2. Attention remains so at the equation shown in Eq.  1. In its original form, multi-head attention is formulated as follows:

$$\begin{aligned} & \text {MultiHead}(Q, K, V) = \text {Concat}\left( H^1,H^2,\dots ,H^h\right) W_O \end{aligned}$$
(5)
$$\begin{aligned} & \text {H}^i = \text {Attention}(Q^i, K^i, V^i) \end{aligned}$$
(6)

It represents a linear concatenation of the various attention heads, with the matrix \(W_O\) as the final step. This form can be seen from another perspective.

$$\begin{aligned} \text {MultiHead}(Q, K, V) = \sum _{i=1}^{h}H^iW_O^i \end{aligned}$$
(7)

This is expressed by decomposing the linear projection matrix \(W_O\) row by row and describing the multi-head attention formula as a sum. This point serves as the foundation of the MoH technique. The multi-head attention set as in21 is defined as follows.

$$\begin{aligned} \text {MoH}(Q, K, V) = \sum _{i=1}^{h}g_iH^iW_O^i \end{aligned}$$
(8)

In this configuration, the routing score \(g_i\) acts as a router to select the best k heads of attention. This \(g_i\) value is non-zero if and only if the \(i_{th}\) attention head should be activated.

This attention mechanism categorises two types of heads: shared heads, which are always active and capture useful standard information in different contexts, and routed heads, which may or may not be active and do not share information between various contexts. The number of each type of head is a design decision to be made by those implementing the MoH mechanism.

Given this concept, the two-stage routing of the MoH approach is realised by the routing score \(g_i\), which is as follows.

$$\begin{aligned} & g_i = {\left\{ \begin{array}{ll} \alpha _1 \, \text {Softmax}\left( W_s x\right) _i, & \text {if } 1 \le i \le h_s, \\ \alpha _2 \, \text {Softmax}\left( W_r x\right) _i, & \text {if } \left( W_r x_t\right) _i \in \text {Top-K}\left( \left\{ \left( W_r x\right) _i \mid h_s + 1 \le i \le h\right\} \right) , \\ 0, & \text {otherwise.} \end{array}\right. } \end{aligned}$$
(9)
$$\begin{aligned} & {[}\alpha _1,\alpha _2] = \text {Softmax}\left( W_h x_t\right) \end{aligned}$$
(10)

x indicates the input token and \(h_s\) the number of shared heads. \(W_s\) and \(W_r\) are the projection matrices that combine the score of each head type, thus implementing the routing mechanism. The coefficients \(\alpha _1\) and \(\alpha _2\) are learned through the trainable matrix \(W_h\) to balance the overall contribution of the two kinds of heads. Learnable elements of the presented routing system are taken into account during training via an additional loss term specific to the task specific for the task that the network is performing21. This approach enables the dynamic selection of the most appropriate attention heads for each token, enhancing inference efficiency and accuracy.

Implementation details

Benchmark datasets

The datasets used in the subsequent experiments to analyse the impact of the chosen architectures are NYU Depth V224 and KITTI25. These two datasets are benchmarks for the MDE task.

The NYU dataset contains a collection of indoor scenes, with RGB images having a resolution of \(640 \times 480,\) and their associated depth maps, which have a maximum depth of 10 metres. There are 120K training samples, while there are 654 samples for the test phase.

As far as the KITTI dataset is concerned, it is conceptually opposed to the previous one; in fact, it is a collection of outdoor images with a resolution of \(1241 \times 376,\) and their respective depth maps, which, in this case, reaches up to 80 metres. The split of the dataset is such that there are 23K training samples and 697 test samples.

Evaluation metrics

The metrics used to evaluate the experimental results are standard qualitative measures used in MDE27: Root Mean Square Error (\(\text {RMSE},\) in metres [m]), Absolute Relative error (\(Abs_{Rel}\)), and the accuracy measures \(\delta _1,\) \(\delta _2,\) and \(\delta _3.\) Those metrics are presented in the following equations.

$$\begin{aligned} & \text {RMSE} = \sqrt{\frac{1}{N} \sum _{i=1}^{N} \left( y_i - \hat{y}_i\right) ^2} \end{aligned}$$
(11)
$$\begin{aligned} & Abs_{Rel} = \frac{1}{N} \sum _{i=1}^{N} \frac{|\hat{y}_i - y_i|}{y_i} \end{aligned}$$
(12)
$$\begin{aligned} & \delta _j = \frac{1}{N} \sum _{i=1}^{N} \max \left( \frac{y_i}{\hat{y}_i},\frac{\hat{y}_i}{y_i}\right) < 1.25^j \hspace{0.3cm} \text {for} \ j = 1,2,3 \end{aligned}$$
(13)

In this expressions, \(y_i\) is the depth ground truth for the \(i_{th}\) pixel, \(\hat{y}_i\) is the estimated depth for the \(i-th\) pixel, and N is the total number of pixels of the image.

For the inference speed test, inference time is measured as the duration in seconds [s] required for the network to perform the forward pass over the entire test set.

Experimental setup

The training configurations of the models follow the specifications reported in their respective papers12,13,14, with training conducted on multiple NVIDIA RTX5000 GPUs. In particular, PixelFormer and NeWCRFs were trained for 20 epochs, using Adam40 optimiser with parameters \(\beta = (0.9,0.999)\) and weight decay of \(10^{-2},\) a batch size of 8 samples, and an initial learning rate of \(4\times 10^{-5}\) reduced linearly to \(4\times 10^{-6}\). METER was trained for 60 epochs under different configurations, introducing the AdamW optimiser41 with parameters \(\beta = (0.9,0.999)\) and weight decay of \(10^{-1},\) a batch size of 128 samples, and an initial learning rate of \(10^{-3}\) reduced by a factor of 0.1 every 20 epochs. All the models were implemented through the PyTorch framework42. Unlike the other networks in this research, METER operates on smaller image sizes compared to the original samples of both datasets under consideration. However, depth maps predicted by METER can be compared by upscaling, with the downside of a lower resolution. Furthermore, the METER article indicates that the KITTI version should be trained using samples with filled-in depth maps. To ensure a fair comparison between the models in our study, METER was trained on the KITTI raw dataset, which contains sparse depth maps.

With regard to the application of the optimisations, an attempt was made to keep the parameters unchanged from the respective references19,20,21. However, for Meta and Pyra, some modifications, obtained through a trial-and-error process, were necessary to adapt the pooling and the spatial reduction operator to the embedding sizes of the respective networks.

The experiments in our work were performed on three different CPUs: Intel Core i9-7920X (I9X79), Intel Core i9-10900X (I9X10), and Intel Xeon Gold 6338 (XG38). Testing the inference on a CPU aims to isolate the impact of optimisations, to prevent parallelization from mitigating their contribution. Moreover, this scenario reflects real-world applications where networks operate directly on embedded devices. In this context, a hardware accelerator, such as a GPU, is not always available. In such cases, the processor must manage both network calculation and other device functionalities. For this reason, all tests were performed on a CPU limited to a single core. The experiments evaluate the models using standard metrics (RMSE, \(Abs_{Rel},\) \(\delta _1,\) \(\delta _2,\) \(\delta _3\)) and measure the inference speed for both baseline and optimised networks. The reported metrics describe the mean performance, and inference speed is defined as the time each network takes to perform a forward pass, one sample at a time, over the entire test set.

Results

Experiments

The experiments were conducted by applying optimisations to the network’s attention modules. In particular, each technique was observed on different parts of the models, analysing the impact on evaluation metrics and inference speed when the modification is applied to the whole network, to the encoder only, or to the decoder only. This approach enables the identification of the network parts most affected by the optimisation, highlighting which region yields the greatest improvements or experiences the most significant performance degradation. From this perspective, this analysis can identify models that achieve a meaningful trade-off between result quality and inference speed. To formalise this approach, the notation follows the network structure, where the encoder always precedes the decoder. More precisely:

  • Optimisation Network: the optimisation was applied to all the attention modules in the architecture;

  • Optimisation-Base Network: the optimisation was applied only to the attention modules present in the encoder of the architecture, while the decoder remained as it was in the non-optimised baseline model;

  • Base-Optimisation Network: the optimisation was only applied to the attention modules in the decoder of the architecture, while the encoder remained as it was in the non-optimised baseline model;

Table 1 Experimental results on the tiny (a), base (b), and large (c) models with the NYU Depth V2 dataset. Values in bold represent the best results between the baseline and the optimisations applied for that model. The lines highlighted in italic show the best trade-offs between RMSE and inference time considering all models. These points are those values that compose the Pareto frontier.
Full size table
Table 2 Experimental results on the tiny (a), base (b), and large (c) models with the KITTI dataset. Values in bold represent the best results between the baseline and the optimisations applied for that model. The lines highlighted in italic show the best trade-offs between RMSE and inference time considering all models. These points are those values that compose the Pareto frontier.
Full size table

The notation partially applies to METER: it only presents attention to its encoder, and the optimisation will be referred to as if applied to the entire network. Based on that, Tables 1 and 2 present the result of baseline models and their optimised versions, grouped by dataset to evaluate their performance on indoor and outdoor samples. Each test will have three tables, one for each network size: tiny, base and large. Each of these formats increases the number of parameters of the encoder, resulting in a more computationally demanding network.

Fig. 3
figure 3

Visual results for the large versions of the networks. For each model and dataset, we show the input RGB image (Input), the depth ground truth (GT), the prediction of the baseline model (Base), the prediction of the best-performing optimised model (Opt) and the qualitative and quantitative difference, indicated by the RMSE, between these two predictions (Diff).

Full size image

Some details become evident from the tests on the NYU Depth V2 dataset. For METER, we observe how the optimisations, except MoH, have a minimal impact on degrading qualitative metrics while also reducing inference times. Analysing the different model sizes, we observe that, in general, the Meta and Pyra optimisations enhance network performance in some cases, with Meta consistently achieving the best inference speed. However, in the large version of METER, this trend is observed only in inference speed, where the baseline outperforms the optimised versions. For the deeper architectures, PixelFormer and NeWCRFs, decoder-level optimisations yield performance comparable to, and in some cases better than, their respective baselines. Other optimisation applications tend to degrade performance metrics, although they result in reduced inference times. In particular, it can be seen that, in all dimensions of these networks, Meta is always the fastest when applied to the entire architecture. This behaviour is attributed to the simplicity of pooling, which replaces the computationally intensive attention. In indoor scenarios, optimisations generally improve network speed, occasionally at the cost of performance. However, in some cases, such as with optimised decoders, they maintain competitive evaluation metrics.

When analysing the results obtained on the outdoor samples of the KITTI dataset, METER exhibits difficulties in generalising depth maps different from those it was originally developed to work with. Regarding performance metrics, the optimisations do not replicate the improvements observed with indoor samples. They tend to improve the delta metrics for the tiny and base sizes while improving the RMSE and \(Abs_{Rel}\) errors in larger versions. However, the application of efficient attention also increases the network’s speed, resulting in better times in all the case studies. In deep architectures, we find similar behaviours in the optimisations, with Meta always presenting the best inference times and the decoder optimisations managing to keep performance equivalent to the baselines. Again, PixelFormer favours Meta and Pyra, while NeWCRFs work better with MoH. More specifically, as the size increases, the latter optimisation improves the performance of NeWCRFs.

Overall, the behaviour of the optimisations across the analysed networks follows identifiable trends. For instance, Meta primarily aims to accelerate inference, but often compromises prediction quality. Pyra is a good compromise between accuracy and speed. Conversely, MoH tends to enhance performance while yielding a comparatively smaller gain in speed. Each network, however, prefers certain optimisations over others regarding quality and speed. METER often works better with Pyra, PixelFormer performs well with the decoder modified with Pyra and NeWCRFs, and MoH is preferred over the decoder.

For the large versions, comparing the depth maps predicted by the baseline and the best-optimised model is insightful. As shown in Fig. 3, the predictions of the optimised models closely match those of the baseline across the analysed networks. In particular, the best-optimised versions of PixelFormer and NeWCRFs present predictions similar to those of their respective baselines. This is noticeable both in qualitative terms, observing the disparity maps between the two predictions, and in quantitative terms, with the RMSE between these two predictions. This behaviour is also understandable because of the similar evaluation metrics between the baseline and the best-optimised version. METER, however, is more affected by the optimisations, exhibiting a more pronounced difference between baseline and optimised predictions.

Fig. 4
figure 4

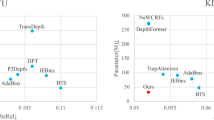
Pareto Frontiers built considering the RMSE and the mean of the three inference times of the models. The networks in these plots refer to the NYU dataset and are grouped by dataset and size: tiny (a), base (b), and large (c) models. The models in bold represent the optimal trade-offs, lying on the Pareto Frontier.

Full size image
Fig. 5
figure 5

Pareto Frontiers built considering the RMSE and the mean of the three inference times of the models. The networks in these plots refer to the KITTI dataset and are grouped by dataset and size: tiny (a), base (b), and large (c) models. The models in bold represent the optimal trade-offs, lying on the Pareto Frontier.

Full size image
Fig. 6
figure 6

Pareto Frontiers built considering the \(Abs_{rel}\) and the mean of the three inference times of the models. The networks in these plots refer to the NYU dataset and are grouped by dataset and size: tiny (a), base (b), and large (c) models. The models in bold represent the optimal trade-offs, lying on the Pareto Frontier.

Full size image

Trade-off performance-inference speed

The experimental setup yielded a comprehensive set of results, extensively illustrating how each type of optimisation impacts the network and its different modules. However, identifying the optimal trade-off between the obtained models solely from the tabular results is challenging. For this reason, the results were organised using the Pareto Frontier. This tool represents the set of optimised solutions where improving one objective would worsen at least one other. More specifically, all solutions are initially assumed to be optimal. Subsequently, each of them is compared with the others. Suppose one of the two chosen values is less than or equal to the other, with at least one of the two inequalities being strict. In that case, the first solution dominates the other, which is eliminated from the optimal solutions describing the best trade-offs. After this comparison, the remaining solutions will form the frontier.

In our case study, the two objectives are the RMSE, chosen as a quantitative index of model performance, and the average of the three CPU times, reporting the best trade-offs for these measures only. The choice of the RMSE as the indicator of network performance is given by the fact that this metric plays a key role in assessing the quality of the predicted depth, as it provides an indication of the overall consistency between prediction and ground truth9.

From these concepts, Pareto Frontiers were constructed by grouping the results by dataset and size of the networks under analysis, as illustrated in Figs. 4 and 5. Analytically, this approach identifies the optimal trade-offs between the two selected objectives. Graphically, this corresponds to a frontier where models closest to it are valuable compromises, while those farther away are sub-optimal solutions. The elements of each Pareto frontier, optimal solutions between quality and speed, are highlighted in Tables 1 and 2 with a italic line.

The Pareto Frontier provides a summary of the model distributions across different sizes and datasets. Each point represents a model. A point further to the left indicates a better RMSE, while a point lower on the graph indicates a faster inference time. As can be seen, in addition to the best models, there are several elements on the Pareto frontier which, from an analysis of the tables alone, could have turned out to be sub-optimal solutions. For example, in the case of the PixelFormer tiny architectures on NYU, the best optimisation turned out to be Meta on the decoder. However, employing the analytical method of the Pareto frontier, we find that all Meta and Pyra optimisations on the decoder turn out to be the optimal solutions with the best trade-off between performance and speed of inference. Looking at the graphs, we can see specific trends that the optimisations tend to present in each case study. Considering Meta optimisation, the models where it is applied generally exhibit reduced performance but improved inference speed, except when applied only to the decoder, where it sacrifices speed but achieves better performance.

In most cases, Pyra often finds itself in better performance zones than Meta, but in worse zones in terms of time. This phenomenon is amplified with MoH, which seems to prevail in performance over inference time. Meta is the optimisation most frequently appearing on the Pareto frontier, while Pyra and MoH occasionally approach or reach it. Sometimes, we also find baselines within this set.

So far, all results discussed have been based on the RMSE metric, as indicated at the beginning of this subsection. The RMSE provides an overall view of prediction quality, but has certain limitations. In particular, it tends to heavily penalise larger errors, without accurately representing the relative consistency between predicted depths, as it only measures absolute stability with respect to ground truth9.

To address this limitation, we have also represented the Pareto Frontier plots using the \(Abs_{rel}\) metric as a quality indicator. This index normalises the error with respect to the true depth, making it particularly suitable in scenarios with varying scales. Furthermore, \(Abs_{rel}\) proves to be more robust for assessing relative depth estimation quality9.

Analysing the impact of this change on the Pareto Frontier plots in Fig. 6, it can be seen that the overall situation remains substantially unchanged. Again, the most effective optimisations in terms of trade-off between quality and computational costs are those applied exclusively to the decoder. Among these, the Meta optimisation is frequently found on the optimal frontier, reinforcing what has emerged in previous experiments. It represents a particularly good choice for achieving a good balance between performance and speed of inference.

A further observation concerns the size of the frontiers. Compared to the graphs based on the RMSE metric, the frontiers obtained with \(Abs_{rel}\) tend to include a smaller number of models, thus being more contained. This suggests that the new metric applies a stricter criterion, favouring models that maintain better proportional accuracy across varying depth ranges.

Embedding entropy analysis

The various experiments conducted showed promising results for the optimised architectures, confirming the validity of the structural changes made to the attention modules, especially from an application perspective.

However, focusing on the PixelFormer and NeWCRFs models, the only ones to have undergone optimisations on both the encoder and decoder sides, an interesting result emerges. Among all the combinations tested, the architectures in which only the decoder has been optimised tend to perform best, particularly in terms of accuracy and also with respect to the trade-off between prediction quality and inference speed. This phenomenon is clearly observable in the results reported in Tables 1 and 2. In both datasets, models with an optimised decoder often exceed the baseline, or at least equal it, while maintaining acceptable computational efficiency.

Although not always the fastest in terms of inference time, these models show a more stable and robust balance compared to the fully optimised ones. This behaviour is further confirmed by the analysis of the Pareto Frontier, constructed using both the RMSE and the \(Abs_{rel}\) metric, as most of the models that lie on the optimal frontier are precisely those with decoder optimisation.

Fig. 7
figure 7

Embedding dispersion is measured using entropy values, specifically differential Gaussian entropy (left plot) and Kozachenko-Leonenko entropy (right plot), where a lower value indicates a better encoder embedding distribution compactness. Results for each network on the NYU Depth V2 dataset are grouped by model size: tiny (a), base (b), and large (c).

Full size image
Fig. 8
figure 8

Embedding dispersion is measured using entropy values, specifically differential Gaussian entropy (left plot) and Kozachenko-Leonenko entropy (right plot), where a lower value indicates a better encoder embedding distribution compactness. Results for each network on the KITTI dataset are grouped by model size: tiny (a), base (b), and large (c).

Full size image

At this point, in the light of such evident results, it is relevant to question the causes that justify the advantage obtained by the architectures with optimised decoders, and at the same time to understand the reasons why performance worsens when optimisations are applied to the encoder module, especially in the PixelFormer and NeWCRFs models.

The analysis of the results in Tables 1 and 2 lead to the idea that optimised encoders tend to generate embeddings that are less effective in guiding the depth map reconstruction process. Indeed, the quality metrics show a greater difficulty in producing consistent predictions faithful to ground truth. This leads us to formulate the hypothesis that such encoders, once modified, generate degraded latent representations.

Dispersed or unstructured embedding distribution in latent space makes the decoder reconstruction task more complex, as it struggles to predict accurate depth maps. And this is exactly what we observe in our experiments. Optimised decoders seem to work effectively when they receive sufficiently rich and coherent embeddings as input, which does not always seem to be the case when the encoder is modified.

In order to quantify how dispersed the embedding distribution actually is, it is necessary to use a precise metric established in the literature. The objective is to find a measure that indicates how much the embeddings produced by the encoder are representative of a compact and well-defined distribution.

Based on this idea, we leverage the theoretical framework of Variational Autoencoders (VAEs), because in its loss the regularisation term quantifies the trade-off between embedding compactness and informativeness43. This term corresponds to the Kullback-Leibler divergence between the distribution learned by the encoder and a standard Gaussian distribution (H). It includes, among other components, the differential entropy of the learned distribution, which quantifies the dispersion of the latent encoding, a value that is useful to gather information needed to verify our hypothesis.

Differential entropy measures, in nats (units of information based on the natural logarithm44), the continuous volume occupied by the embeddings. A lower, i.e. more negative, value indicates that the embeddings are more concentrated, so the latent distribution is more compact and less uncertain. While lower, intended as more negative, differential entropy does not necessarily imply higher informativeness with respect to the input, it does ensure a less dispersed embedding distribution, which generally makes the decoder’s reconstruction task easier43.

This metric assumes that the distribution that the distribution of embeddings follows a standard Gaussian. This concept may be too restrictive, since embeddings may present multimodal structures or heavy tails, not captured by a simple covariance matrix. For this reason, it is also useful to analyse information dispersion through non-parametric methods, such as the Kozachenko-Leonenko entropy estimator (\(H\_KL\)), due to its robustness to non-standard distributions45.

Again, a lower, more negative, value of the entropy estimated with the Kozachenko-Leonenko estimator, indicates more compact embeddings with less dispersion, while higher values reflect a greater dispersion of the point distribution and a possible loss of structure.

To perform the analysis with the tools described above, the embeddings produced as output by the encoder were considered. This approach was applied to all versions of the PixelFormer and NeWCRFs models, on NYU Depth V2 and KITTI datasets. The METER network was not included in the analysis, as it does not present the problem that is the subject of this study. In fact, the optimisations were only applied to the encoder, which is the only one containing attention modules14.

It is important to emphasise that the embeddings analysed come from all the architectural combinations considered (baseline, encoder-optimised, decoder-optimised, full-optimised). It might appear that by optimising only the decoder, the encoder remains unchanged compared to the non-optimised version. However, during training, the parameters of each module are updated differently according to the chosen optimisation. Consequently, the encoder of a decoder-only version never exactly coincides with that of the baseline, but also incorporates the changes resulting from the overall optimisation.

On the theoretical basis set out above, the implementation of the tools discussed supports the hypothesis formulated. In all the cases analysed, as shown in Figs. 7 and 8, any modification made to the encoder structure leads to a deterioration in the compactness of the embeddings it produces. A greater dispersion of the embeddings may compromises the decoder’s ability to effectively reconstruct the input, with a negative impact on the final quality metrics. This behaviour is consistent for both entropy indices considered, with stronger evidence in the case of the Kozachenko-Leonenko entropy estimator, whose non-parametric nature makes it more robust in non-standard contexts.

General optimisation comparison

Following the results obtained, it can be observed that optimisations aimed exclusively at the attention module confirm their effectiveness19,32. However, at this point in the analysis, it is interesting to compare these optimisations with more generic and widely used techniques. For this reason, the three neural networks analysed in this work were subjected to unstructured pruning and dynamic quantization techniques, both applied in post-training contexts.

The choice fell on these approaches because they were the most suitable for an unbiased comparison, given the fact that no modification to the network is required. to the network is required to fit them. These techniques allow a significant reduction in occupied memory and, in specific contexts, may improve inference times without requiring model retraining. Both techniques were implemented using the native functionality offered by the PyTorch42 framework.

Focusing on the general optimisations applied, a global unstructured approach was chosen for pruning, based on the L1 norm, i.e. the absolute value of the weights36. In this application, \(70\%\) of the smallest weights were pruned, selected globally from all convolutional and linear layers in the model. The choice of such a high pruning percentage was motivated by the aim to clearly observe the impact of this optimisation on the behaviour of the model.

As for the quantisation method, a dynamic approach was chosen, limited to the linear layers only. In this case, the weights were converted from \(32\text {-}bit\) floating-point representation to \(8\text {-}bit\) integer35.

Table 3 Performance and inference speed of the pruned (P) and quantized (Q) models with respect to the baselines. Results are reported for the tiny (a), base (b), and large (c) variants on the NYU Depth V2 (left) and KITTI (right) datasets.
Full size table

From the results shown in Table 3, it is clear tha the application of these techniques leads to a worsening of the metrics analysed. In particular, a decrease in prediction quality metrics was to be expected, since the optimisations considered have a strong structural impact on the model, modifying its topology35,36. In contrast, the optimisations applied to the attention module alone keep the structure of the architecture almost unchanged19,20,21.

The negative effects on the speed of inference can be explained in the way these optimisation are applied. In the first case, the unstructured pruning introduces sparse matrices to remove the network connections. Even if that approach reduces the number of effective active weights, those matrices may not be well supported on generic hardware, leading to the possibility of a less efficient computation36. For the dynamic quantization, the concept is similar. The post training quantization may not be completely supported or optimised for a general-purpose hardware, providing no guarantee of computational speed-up35.

Optimisations memory footprint

In addition to assessing the impact of optimisations on the performance and speed of neural networks, it is equally crucial to analyse how the structural characteristics of the models change as a result of a modification to the attention modules. In the context of efficient models, metrics such as the number of parameters and memory occupancy are commonly used to describe the memory footprint of the networks32.

Table 4 Number of network parameters and memory footprint relative to the tiny (a), base (b), and large (c) size. Values in bold represent the best values between the baseline and the optimisations applied for that model.
Full size table

Although the modifications discussed in this research focus exclusively on lowering the computation complexity of the attention modules and don’t primarily focus on memory reduction, observing how they affect the overall network structure can provide useful insights useful insights into the applicability of the modified models in real-world usage scenarios.

Significant observations emerge from Table 4, where the information about the different networks is collected. In particular, it can be seen that Meta optimisation consistently shows the best results in terms of parameters and memory weight among all the techniques analysed. This behaviour is consistent across all the application networks and combinations considered. The advantage of Meta is most likely linked to the way it is implemented19. In fact, by entirely replacing the structure of the attention module, including all the linear projection layers, with simple pooling, leads to a substantial reduction in memory and parameters associated with the network.

In contrast, the other optimisations considered show a different pattern regarding their impact on memory footprint. In particular, Pyra optimisation is the technique that leads to the largest increase in the analysed values. This is due to the spatial reduction modules that introduce new layers20 to consider in the overall network structure. For what concern MoH optimisation, however, the modified multi-head attention routing system21 does not introduce more overhead, maintaining almost unchanged the network parameters and memory weight.

Table 5 Inference times in seconds from the experiments on Jetson Orin Nano using the tiny versions of the networks.
Full size table

These results, however, do not significantly impact in the applicability of the modified models. The number of parameters and memory fluctuations remain bounded in a value near the baseline values. At the same time, often this increase is accompanied by an increment in quality of predictions. For this reason, optimisations aimed at the attention modules represent an effective strategy, offering a favourable trade-off between portability, efficiency and prediction quality, even if at the cost of a slight increase in certain computational metrics.

Resource-constrained device experiments

After analysing various aspects of modified models, in order to go into the applicative details of this study, experiments were conducted using limited hardware resources devices. In particular, the Jetson Orin Nano board was considered, a device frequently used in real-world scenarios for tasks involving Deep Learning models. Its low computational resources, compared to an ordinary device, make it an ideal context for evaluating the behaviour of optimised models under conditions closer to real-world conditions.

The experiments conducted on this hardware focused on analysing inference times, with the aim of highlighting the effectiveness of the proposed optimisations. The tests were carried out maintaining the same configuration used in the previous evaluations. In fact, inference was performed sample by sample on the entire test set of datasets used in this research. In this context, to adapt to the applicative scenario, we used only the tiny versions of the networks, which are more suitable for this application.

A detailed analysis of the Table 5 shows how the optimised models perform in the context considered. In particular, it is observed that Meta optimisation systematically leads to faster models than the baseline, confirming that its modification to the attention module is often the most efficient choice. Models optimised with Pyra also show an improvement in inference times, particularly when the optimisation is applied to only one module of the network, although performance is generally lower than in the Meta case. MoH optimisation, on the other hand, is the least suitable in this context, probably due to the overhead introduced by the routing mechanism, which may not fit well with resource-limited devices.

This behaviour is also confirmed in the case of the METER model, where once again MoH optimisation is the one with the worst performance, whereas Meta and Pyra allow significantly shorter inference times46,47.

Conclusions

This work analyses the impact of optimisations on ViT-based architectures for MDE by conducting experiments on indoor and outdoor scenario. In particular, the focus of the research was the application of efficient attention modules. To better understand the impact of these optimisations have been applied at different levels within each network, targeting the entire architecture, the encoder and the decoder. A detailed analysis was conducted to assess how these optimisations, applied to one of the most computationally intensive components of the models, influenced network performance in terms of quality and speed. Given the importance of a precise balance between these two objectives, the Pareto Frontier was important in analysing the trade-offs and analytically obtaining the optimal ones.

Some modifications led to optimised models with improved inference speed but a significant loss in performance, as seen in fully modified NeWCRFs with Meta or the application of MoH on METER. On the other hand, some results showed noteworthy cases where the optimised models have reported promising results, sometimes even surpassing the respective baseline, together with a consistent improvement in inference time. This is the case of the models optimised only on the decoder part, where the Pyra and Meta optimisations for PixelFormer and MoH for NeWCRFs have introduced promising models from the point of view of performance and speed.

These findings suggest new potential research directions based on the provided results. In particular, future works could investigate how broader optimisation techniques, such as quantisation, knowledge distillation, and pruning, behave when applied to the whole network and then to specific components. In addition, it may be worth investigating how the optimisations presented in this work behave on particularly complex dense tasks, such as optical flow estimation, where the balance between performance and speed is crucial in practical applications. In all of these cases, the application of the Pareto Frontier could serve as a valuable tool for objectively analysing trade-offs in Deep Learning tasks.