Introduction

Remaining a critical component of the global economy, oil serves as a primary energy source and raw material. It fuels diverse industries and underpins the production of chemicals, plastics, medicines, and many other goods1,2,3. Oil-rich nations, particularly those with vast production capabilities, harness their petroleum wealth as a primary engine for prosperity. The substantial financial returns from exporting oil provide these countries with the means to bolster their foundational infrastructure, stimulate industrial expansion, and foster innovation through technological uptake, thereby fast-tracking their overall economic and social evolution4,5,6. For companies, the industry represents a major revenue stream through activities such as extraction, refining, and distribution7,8. As a result, the accurate prediction and optimal management of oil production are essential for both oil-producing countries and the companies operating within the sector9,10,11.

Accurately predicting the future output of oil wells—that is, the quantity of crude extracted over a specific period—is an absolutely vital strategic endeavor for both oil and gas corporations and national economic strategist12,13. Reliable forecasts allow for efficient resource management, cost optimization in extraction, and the fulfillment of domestic and global energy demands14,15,16. Furthermore, these accurate predictions are instrumental in shaping key operational decisions, from determining where to drill new wells and when to schedule essential maintenance, to implementing effective long-term resource management strategies. Production forecasting holds immense importance for both corporate strategies and macroeconomic planning17. However, due to the complexities of oil reservoirs and the various factors influencing production including geological conditions, reservoir pressure, and oil characteristics, accurate forecasting remains a significant challenge in the oil industry18,19.

Since the early twentieth century, petroleum engineers have continuously worked on forecasting oil well production rates. This has involved developing and employing various models to simulate reservoir oil flow and refine production predictions for over a hundred years20. Such efforts have led to the development of empirical equations which are derived from experimental data and rely on parameters pertaining to reservoir and well characteristics21. Among these, the Gilbert equation is a well-known approach often cited for its simplicity and cost-efficiency. These equations can provide reasonable predictions for well production under specific conditions resembling their development data. However, their reliability diminishes when applied to new or diverse scenarios22,23.

One of the primary limitations of empirical equations is their lack of comprehensiveness. These equations are typically derived from experimental data specific to a particular reservoir or set of conditions that may not generalize well to different wells or environments24,25,26. Geological differences, as well as variations in reservoir pressure, temperature, and oil properties, can lead to inaccurate predictions when these equations are applied outside their original context27. Consequently, in intricate scenarios, their effectiveness plummets, frequently leading to erroneous forecasts and suboptimal strategic choices28,29.

Moving beyond the deficiencies of empirical equations, the advent of physical modeling and simulation methods has established a more resilient framework for forecasting oil production rates30,31,32. Leveraging specialized software, these simulation-driven approaches develop models of oil well and reservoir conditions. This is accomplished by weaving in diverse data, including geological structures, reservoir characteristics, and crucial physical parameters like pressure and temperature28,33. While these models offer potential for higher accuracy, their effectiveness is often hindered by uncertainties in the input data and the complexity of the models themselves24,28,34. Additionally, the challenges in collecting precise and extensive datasets, together with the sophistication of simulations, can result in low-accuracy or unreliable predictions, especially in cases involving highly complex reservoirs35,36.

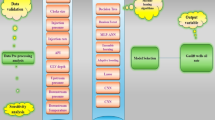
This study addresses the vital need for accurate predictions of choke flow performance to enhance crude oil production efficiency. Using a robust dataset from a Middle Eastern oil production site, the workflow begins with detailed data preprocessing to ensure reliability, including outlier detection via the MCOD algorithm. Key parameters, such as choke size, THP, GOR, BS&W, and oil API, were analyzed for statistical metrics and correlations. GBM models were developed and optimized using advanced algorithms like SADE and ES, with K-fold cross-validation employed to ensure model generalization. Performance evaluation, using metrics such as R2, MSE, and AARE%, shows SADE’s superior predictive accuracy. SHAP analysis further interprets the model, revealing choke size and THP as the most influential factors. Finally, visualizations including raincloud plots, cross-plots, and SHAP diagrams illustrate the robustness and interpretability of the developed framework. Figure 1 is the schematic workflow implemented in this research.

Fig. 1
figure 1

Schematic of the implemented methodology.

Full size image

Our research offers several key contributions to choke flow rate prediction in sub-critical oil wells. First, we present a cost-effective methodology that accurately predicts flow rates using only readily available wellhead data, removing the need for expensive downhole sensors or complex fluid characterization. Second, we provide a comprehensive comparative analysis of advanced metaheuristic-optimized machine learning algorithms (SADE, ES, PI, BBO), identifying the most robust and accurate model for this specific application. Third, we emphasize enhanced generalization and reliability, rigorously evaluating models on unseen data to ensure high predictive accuracy for real-world deployment. Finally, our developed tool offers practical industry applicability as a low-computational-cost solution that integrates seamlessly into existing field monitoring systems, advancing cost-effective production optimization and well management.

Methodology

Collected data analysis

This study developed and rigorously assessed its models using meticulously gathered field data from a Middle Eastern production unit. Table 1 offers a comprehensive statistical overview of this dataset, detailing key input data like wellhead pressure, choke size, gas-to-oil ratio, basic sediment and water content, and oil API, as well as the crucial production flowrate (our output variable). For each, Table 1 presents metrics like the maximum, minimum, mean, mode, kurtosis, skewness, and standard deviation. Our data-driven machine learning models were built upon a dataset of 198 distinct data points. A substantial 90% of these points were dedicated to the training and validation phases, employing a robust fivefold cross-validation strategy, while the remaining 10% was carefully set aside for an unbiased evaluation of the models’ performance.

Table 1 Statistic-based information relevant to studied data.
Full size table

This study aims to accurately estimate choke flow performance, defined as the oil production rate through wellhead chokes, and considers it the primary output variable in the model. The estimation is derived from a series of input factors. To enhance the understanding of the distribution, variability, and relationships between these input factors and choke flow performance, scatter matrix diagrams have been constructed and presented in Fig. 2. These diagrams offer a comprehensive visualization of the dataset, highlighting trends, correlations, and potential outliers, which are crucial for analyzing the data’s underlying structure and facilitating the development of a reliable predictive model. Furthermore, Fig. 3 displays raincloud plots for each variable, offering additional insights into their distribution and characteristics.

Fig. 2
figure 2

Scatter matrix diagram: Relationships between variables.

Full size image
Fig. 3
figure 3

Raincloud plots of all the input variables for choke flow performance modeling.

Full size image

Gradient boosting machine algorithm

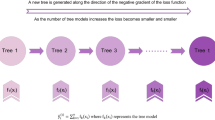
Introduced by Jerome Friedman in 1999, GBM are a powerful supervised ensemble learning approach. They construct a highly accurate predictive model by incrementally combining numerous decision trees. This iterative methodology specifically aims to correct the shortcomings of previous trees and minimize a predefined loss function, thereby significantly boosting predictive accuracy across both classification and regression problems37,38. GBM excels at managing complex, non-linear relationships and offers valuable insights into feature importance, aiding feature selection. However, its computational demands and the necessity for precise hyperparameter tuning (e.g., learning rate, tree depth) to mitigate overfitting and underfitting present notable challenges.

GBM employs an iterative, stage-by-stage methodology. It begins by fitting a simple model, such as a decision tree, to the dataset. The fundamental aim is to optimize the loss function, L(y,f(x)), where y represents the true value, f(x) the model’s output, and L the chosen loss metric. With each iteration, the model undergoes incremental updates designed to progressively reduce existing errors and sharpen its predictions39,40.

The first stage, which makes the first iteration is as below

$$F_{0} (x) = \mathop {\arg \min }\limits_{c} \sum\limits_{i = 1}^{n} {L(y_{i} ,C)}$$

where F0(x) is the initial constant prediction; L(yi,C) is the Loss function; y is the true target value; C is the weight or contribution of the weak learner.

The second step, for each iteration m, is as follows: For each data point i, determine the "pseudo-residuals" by taking the negative gradient of the loss function with respect to the model’s current predictions. This effectively quantifies the error direction for that specific observation.

$$r_{im} = - \left[ {\frac{{\partial L(y_{i} ,F(x_{i} ))}}{{\partial F(x_{i} )}}} \right]_{{F(x) = F_{m - 1} (x)}}$$
(1)

where Fm-1(x) is the current model prediction; rim is the pseudo-residuals of data poin i at the iteration step of m.

Next, a base learner is fitted to these residuals:

$$h_{m} (x) = \mathop {\arg \min }\limits_{h} \sum\limits_{i = 1}^{n} {(r_{im} - h(x_{i} ))^{2} }$$
(2)

In the fourth stage, the model is refined:

$$F_{m} (x) = F_{m - 1} (x) + \upsilon .h_{m} (x)$$
(3)

The learning rate (υ) in the GBM algorithm dictates how much each successively added decision tree contributes to the overall model’s correction. Iteratively, the algorithm introduces a new decision tree with the explicit purpose of mitigating the inaccuracies inherited from the combined output of all previous trees. GBM’s inherent flexibility is underscored by its capacity to customize the loss function (L), enabling it to align perfectly with specific problem goals and thus proving to be a highly versatile method. To improve the model’s generalization capabilities and prevent it from simply memorizing the training data, regularization techniques—specifically adjusting the learning rate (υ) and limiting tree depth—are applied. The culmination of this process is a final classifier that represents a weighted sum of predictions from its constituent trees, allowing it to gradually uncover deeper, more complex relationships within the data41,42,43. A schematic representation of the GBM manner is provided in Fig. 4.

Fig. 4
figure 4

Gradient Boosting Machine algorithm flowchart.

Full size image

Optimizations algorithms

Self-adaptive differential evolution (SADE)

SADE represents a significant enhancement over the conventional Differential Evolution (DE) algorithm. Unlike standard DE, SADE employs an adaptive mechanism that dynamically adjusts its control parameters throughout the optimization process. This adaptive approach has proven particularly effective for solving continuous optimization problems, demonstrating notable success in addressing complex, multimodal, and high-dimensional scenarios44,45. Key parameters, including the scaling factor (F) and crossover rate (CR), are automatically modified by SADE, eliminating the need for manual parameter tuning and enhancing the algorithm’s robustness and efficacy46.

The central concept of SADE lies in its ability to evolve a population of candidate solutions over successive generations while simultaneously self-adjusting control parameters based on their historical performance. This self-adaptive mechanism enables the algorithm to effectively balance exploration and exploitation within the search space, thereby improving convergence properties and yielding higher-quality solutions47,48.

Population initialization: The optimization begins with the creation of a population containing NP candidate solutions, denoted as X = [x1, x2, …, xNP], where each xi represents an individual solution within the search space. Each solution is structured as a D-dimensional vector, where D corresponds to the number of variables in the optimization problem. The initial population is typically generated randomly, ensuring that each solution adheres to the predefined boundaries of the search space.

Mutation: generating mutant vectors: For each individual solution xi in the population, a mutant vector vi is generated using a designated mutation strategy. A commonly used strategy is the “DE/rand/1” method, defined as:

$${\text{v}}_{{\text{i}}} = {\text{x}}_{{{\text{r1}}}} + {\text{F}}_{{\text{i}}} \cdot ({\text{x}}_{{{\text{r2}}}} - {\text{x}}_{{{\text{r3}}}} )$$
(4)

Here, xr1, xr2 and xr3 are three distinct, randomly selected individuals from the current population, while Fi  is the scaling factor associated with xi. The scaling factor Fi determines the magnitude of the differential variation and is crucial for balancing exploration and exploitation of the search space.

Crossover: After creating the mutant vector vi, a trial vector ui is then formed. This is done by combining elements from both the mutant vector vi and the target vector xi​ using a crossover operation. The crossover is defined as:

$$u_{ij} = \left\{ {\begin{array}{*{20}l} {v_{ij} } \hfill & {if\;rand(0,1) \le CR_{i} \;{\text{or}}\;j = j_{rand} } \hfill \\ {x_{ij} } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(5)

Here, j represents the dimension index (j = 1, 2, …, D), rand(0,1) is a random number from a uniform distribution between 0 and 1, and CRi is the crossover rate associated with the target vector xi. The index jrand is a randomly selected dimension index, ensuring that at least one element in the trial vector ui is directly inherited from the mutant vector vi.

Selection: The next step involves determining whether the trial vector ui or the target vector xi​ will advance to the next generation. This decision is based on the values of the objective function F(0) and follows this rule49:

$$x_{i}^{new} = \left\{ {\begin{array}{*{20}l} {u_{i} } \hfill & {{\text{if}}\;f(u_{i} ) \le f(x_{i} )} \hfill \\ {x_{i} } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(6)

By comparing the fitness of ui and xi, the vector with the better performance is selected for the subsequent generation.

Parameter adaptation: During the optimization process, the scaling factor Fi and crossover rate CRi are dynamically updated to enhance algorithm performance. After each generation, these parameters are adjusted based on the success of trial vectors. Specifically, when a trial vector ui is selected f(ui) ≤ f(xi), the corresponding Fi and CRi values are deemed successful and recorded in sets SF and SCR, respectively. At the end of a generation, new parameter values are calculated as:

$$F_{i}^{new} = \left\{ {\begin{array}{*{20}l} {randc(\mu F,0.1)} \hfill & {if\;S_{F} \ne 0} \hfill \\ {F_{i} } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(7)
$$CR_{i}^{new} = \left\{ {\begin{array}{*{20}l} {randn\left( {\mu_{CR} ,0.1} \right)} \hfill & {{\text{if}}\;S_{CR} \ne 0} \hfill \\ {CR_{i} } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(8)

Here, μF and μCR represent the mean values of the successful parameters stored within SF and SCR sets, respectively. The functions randc and randn generate random numbers from Cauchy and normal distributions, respectively, introducing variability into the parameter values. If SF or SCR are empty, parameters will not be update50,51,52.

Evolutionary strategies (ES)

ES is an optimization algorithm that mimics biological evolution to solve continuous problems. It iteratively develops a group of candidate solutions using mutation, recombination, and selection over successive generations. Each solution is represented by (x,σ), where x is the solution itself and σ dictates the magnitude of mutation for each component of x.53.

Initialization: The ES process begins by initializing a population of μ individuals. The solution vectors (x) are typically sampled randomly within the defined search bounds of the optimization problem, while the strategy parameters (σ) are initialized with small, positive values. For instance, the solution and strategy parameters can be initialized as follows:

$$x_{i} \sim Uniform(x_{i}^{\min } ,x_{i}^{\max } ),\;\;\sigma_{i} \sim {\text{Uniform(}}\sigma^{\min } {,}\sigma^{\max } {)}$$
(9)

Here, ximin and ximax define the valid range for the solution vector, while σmin and σmax establish the range for the strategy parameters.

Mutation and offspring generation: In each generation, λ offspring are created through the mutation process. Mutation operates by modifying both the solution vector x and its associated strategy parameters σ. Updated strategy parameters (denoted as σ′) are computed using a predefined mutation rule, which introduces variability into the mutation scale. This adaptive mechanism allows the algorithm to navigate complex search landscapes effectively. The mutation process ensures robust exploration while maintaining the ability to refine promising solutions over successive generations.

$$\mathop \sigma \limits^{\prime }_{i} = \sigma_{i} \times {\text{exp}}\left( {\tau \times N\left( {0.1} \right) + \mathop \tau \limits^{\prime } \times N_{i} \left( {0.1} \right)} \right)$$
(9)

In this context, N(0,1) represents a random variable drawn from a standard normal distribution, while Ni(0,1) denotes an independent random variable sampled separately for each dimension. The parameters τ and τ′ are learning rates, often chosen based on the dimensionality of the problem54:

$$\mathop x\limits^{\prime }_{i} = x_{i} + \mathop \sigma \limits^{\prime }_{i} N_{i} \left( {0.1} \right)$$
(10)

Recombination, when utilized, integrates information from multiple parent solutions to produce offspring. In the case of intermediate recombination, the offspring (x′,σ′) is generated as a weighted average of the μ parent solutions. The process can be mathematically expressed as:

$$\mathop x\limits^{\prime }_{i} = \frac{1}{\mu }\mathop \sum \limits_{j = 1}^{\mu } x_{i.j}$$
(11)
$$\mathop \sigma \limits^{\prime }_{i} = \frac{1}{\mu }\mathop \sum \limits_{j = 1}^{\mu } \sigma_{i.j}$$
(12)

Selection phase: Following the generation of offspring, the selection phase determines the individuals that will proceed to the next iteration. In the (μ + λ)-ES strategy, the top μ individuals are selected from the combined pool of μ parents and λ offspring. Alternatively, in the (μ,λ)-ES strategy, the selection occurs exclusively among the λ offspring, with λ ≥ μ. This approach ensures that the population evolves progressively toward better solutions with each generation.

One of the key strengths of Evolution Strategies (ES) lies in its self-adaptive mechanism, which enables the dynamic adjustment of strategy parameters (σ) throughout the optimization process. This self-adaptation effectively balances exploration (broad search of the solution space) with exploitation (refining optimal regions), making the method particularly effective for solving complex and high-dimensional optimization problems. Additionally, ES can be further enhanced with advanced techniques, such as Covariance Matrix Adaptation (CMA-ES), which improves the optimization process by adapting the covariance matrix of the search distribution55,56,57.

In summary, Evolution Strategies evolve a population of candidate solutions by iteratively applying mutation, recombination, and selection. The dynamic adjustment of strategy parameters enhances the robustness and versatility of the algorithm for continuous optimization problems58,59. The general procedure involves the following steps: initialization of the population, offspring generation through mutation and recombination, fitness evaluation, selection of the best individuals, and iteration until a termination criterion is met. The best solution obtained during this iterative process is presented as the final result60.

Bayesian probability improvement (BPI)

Bayesian Probability Improvement (BPI) represents a specialized optimization technique commonly employed within the Bayesian optimization framework. Bayesian optimization is a global optimization strategy designed for expensive black-box functions, offering particular advantages when evaluating the objective function is computationally costly, as it aims to identify the optimum with minimal function evaluations. Within this framework, BPI serves as an acquisition function that guides the optimization process by effectively balancing exploration of uncertain regions with exploitation of known promising areas61,62,63.

The fundamental objective of BPI is to maximize the probability that a newly selected candidate point will yield an improved objective function value compared to the current best observation. Unlike alternative acquisition functions like Expected Improvement (EI) or Upper Confidence Bound (UCB), BPI adopts a distinctly probabilistic perspective by directly quantifying the probability of improvement. This approach proves especially valuable in scenarios where increasing the likelihood of discovering a better solution takes precedence over maximizing the expected magnitude of improvement64.

At its core, BPI calculates the probability that the objective function amount at a new point x will surpass the current best-observed value, denoted as f(x +). This calculation utilizes the posterior distribution provided by a Gaussian Process (GP) model, which is widely employed in Bayesian optimization frameworks. The GP model provides a predicted mean μ(x) and variance σ2(x) for any location x in the search space. The probability of improvement is then derived from the cumulative distribution function (CDF) of the normal distribution65.

The BPI is mathematically formulated as:

$$BPI\left(x\right)=\varnothing \left(\frac{\mu \left(x\right)-f({x}^{+})}{\sigma (x)}\right)$$
(13)

where, Φ represents the cumulative distribution function of the standard normal distribution, μ(x) denotes the predicted mean of the GP at point x, σ(x) represents the predicted standard deviation of the GP at point x, f(x+) refers to the best objective function value observed thus far.

The BPI acquisition function is optimized to determine the next point for evaluation. Higher BPI values indicate a greater probability that the new point will improve upon the current best solution. This approach is particularly efficient when the primary goal is to ensure consistent progress with each evaluation, as it focuses on the likelihood of improvement rather than the potential magnitude of improvement66,67.

In conclusion, BPI represents a probabilistic acquisition function that leverages the predictive uncertainty quantified by a Gaussian Process to guide the search for optimal solutions. By prioritizing the probability of improvement, BPI provides a valuable tool within the Bayesian optimization framework, particularly when function evaluations are computationally expensive and the objective is to maximize the chances of finding superior solutions68.

Batch bayesian optimization (BBO)

BBO extends the traditional Bayesian optimization framework to enable the simultaneous evaluation of multiple points, referred to as a “batch,” rather than evaluating points sequentially. This adaptation is particularly advantageous in environments where parallel computing resources, such as high-performance computing clusters or distributed systems, are available. By leveraging parallelism, BBO seeks to significantly reduce the total optimization time while preserving the ability of Bayesian optimization to efficiently identify the global optimum69,70.

The primary innovation in BBO is the selection of a group of points for simultaneous evaluation instead of iteratively selecting individual points. This requires modifying the acquisition function to account for the interdependencies and correlations among points within the batch, as the evaluation of one point may provide information that affects the value of others in the group.

BBO commonly uses acquisition functions that balance exploring uncertain regions with exploiting promising areas within a batch. A popular method is Parallel Expected Improvement (q-EI), which extends the standard Expected Improvement (EI) function to evaluate multiple points at once. The q-EI function calculates the expected improvement beyond the current best value for a batch of q points, factoring in their correlations as predicted by the Gaussian Process (GP). The formula for q-EI is71:

$$q-EI\left(x\right)=E[maxf\left(x\right)-f\left({x}^{+}\right).0]$$
(14)

where, X = [x1,x2,…,xq] represents the batch of q points selected for evaluation, f(X) denotes the objective function values at the batch points, f(x +) is the current best-observed value of the objective function, E denotes the expectation taken over the joint posterior distribution of the GP at the batch points.

By explicitly considering the joint distribution over the batch, q-EI ensures that the selected points maximize the expected improvement collectively rather than in isolation72.

BBO) enhances the efficiency of traditional Bayesian optimization by enabling simultaneous evaluation of multiple points, thus reducing the total optimization time. The use of specially adapted acquisition functions, such as q-EI and Thompson Sampling, ensures that the optimization process continues to balance exploration and exploitation effectively. BBO is especially beneficial in scenarios where parallel computational resources are available, as it accelerates the optimization process while maintaining the high performance of Bayesian optimization in locating the global optimum73.

Models evaluation

A prevalent and powerful strategy for assessing the generalization capability of machine learning models is K-fold cross-validation. This method meticulously divides the complete dataset into K discrete and uniformly sized partitions, known as folds. In each iteration of the process, the model is trained on K-1 folds while the remaining fold is used to evaluate its performance. This approach is renowned for its straightforward implementation and ability to produce consistent, reliable results, making it a preferred choice among various cross-validation techniques. Its simplicity and balanced approach ensure its applicability across a broad range of machine learning tasks55,56,57.

To grasp the mechanics of K-fold cross-validation, let’s consider a scenario where K = 5 (as visually depicted in Fig. 5). The entire dataset is systematically segmented into five equally sized partitions, with each segment designated as a "fold." The validation process then unfolds iteratively: In the initial round, four of these folds collectively serve as the training data for the model, while the first fold is reserved exclusively for testing its performance. This pattern continues: in the subsequent iteration, the second fold becomes the dedicated test set, with the remaining four constituting the training material. This meticulous rotational scheme ensures that every one of the five folds functions precisely once as the test set, leading to a more robust and unbiased assessment of the model’s generalization capabilities74,75.

Fig. 5
figure 5

K-fold cross-validation Algorithm schematic.

Full size image

To assess the accuracy and effectiveness of each model, several key performance indicators were calculated, including RE%, AARE%, MSE, and R2. Detailed explanations of each metric are presented in the following sections15,76,77,78:

$$RE\% = \left( {\frac{{V^{pred} - V^{\exp } }}{{V^{\exp } }}} \right) \times 100$$
(10)
$$AARE\% = \frac{100}{N}\sum\limits_{i = 1}^{N} {\left( {\left| {\frac{{V_{i}^{pred} - V_{i}^{\exp } }}{{V_{i}^{\exp } }}} \right|} \right)}$$
(11)
$$MSE = \frac{{\sum\limits_{i = 1}^{N} {\left( {V_{i}^{pred} - V_{i}^{\exp } } \right)^{2} } }}{N}$$
(12)
$$R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{N} {\left( {V_{i}^{pred} - V_{i}^{\exp } } \right)^{2} } }}{{\sum\limits_{i = 1}^{N} {\left( {V_{i}^{\exp } - \overline{V} } \right)^{2} } }}$$
(13)

Within these equations, the subscript i serves to identify a unique data point from our entire dataset. For any given i, ‘pred’ signifies the value projected by our model, while ‘exp’ refers to the corresponding actual or experimentally observed value. Furthermore, N consistently represents the grand total data points.

Results and discussion

Comprehensive data characterization

Prior to developing machine learning models for predicting choke flow performance, ensuring data reliability through outlier management is paramount. This research implemented the Monte Carlo Outlier Detection (MCOD) algorithm, a robust technique for identifying outliers in large datasets using random sampling and density-based approaches. MCOD assesses local data density to pinpoint data points that deviate significantly from their neighbors. By employing Monte Carlo sampling to estimate data subsets, the algorithm reduces computational burden. Its effectiveness and scalability render it suitable for high-dimensional datasets and real-time applications. There’s a natural give-and-take between how accurate the MCOD method is and how fast it can compute results. This balance is influenced by the sample size and the number of nearest neighbors (k) you choose. Even with this trade-off, MCOD is incredibly useful for initial data exploration and finding anomalies, especially when you don’t need perfect precision or when you’re working with limited computing power. Its ability to balance accuracy and efficiency makes it a great tool for spotting outliers in complicated datasets.

A boxplot in Fig. 6 illustrates our dataset’s distribution and acceptable range, with most data points falling within this range, indicating high data quality. To maximize the models’ ability to generalize, the complete collected dataset was used for training. This comprehensive approach allows the models to discern underlying patterns effectively, resulting in more reliable and accurate predictions on unseen data.

Fig. 6
figure 6

(A) Detection of outliers using the MCOD algorithm and (B) Boxplot depicting the distribution of the dataset.

Full size image

Models’ optimization

This section focuses on how we applied various optimization algorithms to improve the Gradient Boosting Machine (GBM). Our goal was to fine-tune GBM’s performance by optimizing its hyperparameters, which we did both by directly applying optimization techniques and by using them with k-fold cross-validation. The specific hyperparameters we worked on were maximum depth, the number of estimators, minimum samples and maximum features needed for splitting, the learning rate, subsample size, and minimum samples required for leaves. Table 2 provides a complete overview of the parameter ranges we have explored and the best values identified by each optimization algorithm.

Table 2 Evaluating optimal gradient boosting hyperparameters using four optimization techniques within a specified parameter range.
Full size table

Figure 7 visualizes the Mean Squared Error (MSE) progression for each optimization algorithm over 200 iterations, identifying the best hyperparameter configurations (also in Table 2). Figure 8 then compares their computational times, which were measured on a machine with Intel Core i7-6700 CPU (3.40 GHz) and 16 GB RAM. The SADE method was the slowest at roughly 4200 s, whereas the ES algorithm was the fastest.

Fig. 7
figure 7

Iteration-wise MSE for different optimization methods.

Full size image
Fig. 8
figure 8

Runtime comparison of optimization algorithms integrated with GBM.

Full size image

Figure 8 clearly shows a stark difference in optimization progression: the SADE algorithm reached its peak performance—the lowest MSE—quite rapidly in the initial generations. Conversely, BPI, ES, and BBO algorithms demonstrated a more deliberate and gradual enhancement in their performance as the iterations continued.

Table 3 provides a comprehensive comparison of hybrid optimization approaches using the GBM estimator and Fig. 9 displays these metrics for testing stage per all models. The evaluation utilizes key metrics, including R2, MSE, and AARE%, across training, testing, and total data sets. The optimization algorithms considered are SADE, ES, PI, and BBO, with a specific focus on test-phase metrics as the primary indicators of model performance.

Table 3 Efficacy benchmarking of optimization algorithms on train, test, and all datasets.
Full size table
Fig. 9
figure 9

Testing performance of optimization algorithms: R2, AARE%, and MSE.

Full size image

From Table 3, it is evident that SADE exhibits the highest testing-phase accuracy among all algorithms. SADE achieves a testing R2 value of 0.5935, indicating moderate explanatory power in predicting choke performance compared to other methods. Furthermore, SADE demonstrates superior error minimization, evident in its lowest testing MSE. This substantial reduction in error reflects the algorithm’s enhanced ability to fit the data during testing. Additionally, the testing-phase AARE% for SADE is 22.59%, which, while not the lowest observed, still aligns closely with the algorithm’s robust prediction performance. The consistency between training and test performance for SADE highlights its reliability for modeling.

Despite its high accuracy, SADE comes with a trade-off in computational runtime, as its complex optimization structure results in additional computational overhead. Comparatively, while ES achieves a higher training R2 (0.8385) and a total R2 of 0.7985, its testing R2 is lower at 0.5794. This drop suggests a less stable generalization capability when applied to unseen data. ES also yields a testing MSE higher than SADE, which points to reduced prediction precision. Furthermore, its testing-phase AARE% of 28.62% is notably higher, indicating greater absolute errors in prediction during testing. Overall, ES demonstrates acceptable but weaker performance compared to SADE, particularly in testing metrics.

PI and BBO offer comparable results, both achieving higher testing-phase R2 values compared to SADE, with PI slightly outperforming BBO (0.5628 vs. 0.5717). However, an examination of testing MSE reveals clear deficiencies in these algorithms compared to SADE, with PI and BBO recording testing MSE values. These errors are significantly larger than SADE’s testing MSE, underscoring SADE’s superior capacity to minimize prediction errors. Additionally, both PI and BBO yield high AARE% values during testing (30.60% and 30.78%, respectively), which further highlight their reduced accuracy compared to SADE. While these algorithms perform well in training (PI with the highest training R2 of 0.8714), their weaker generalization capabilities during testing limit their overall utility.

While the SADE algorithm demands the highest computational cost (∼ 4200 s), it delivers superior predictive performance, achieving the lowest testing MSE and the highest R2 (0.5935) among all methods. In contrast, faster algorithms like ES sacrifice accuracy for efficiency, exhibiting gradual error reduction but failing to match SADE’s explanatory power or error minimization. This trade-off underscores SADE’s value in applications where precision is critical, despite its resource intensity, whereas ES or BBO may suffice for scenarios prioritizing rapid, approximate solutions. The 22.59% AARE% further confirms SADE’s reliability, justifying its computational overhead when model robustness is paramount.

Figure 10 compellingly illustrates the enhanced precision of our proposed models, with the SADE algorithm distinctly outperforming others. Its cross-plots reveal a significantly tighter clustering of data points around the unit slope line, a clear indicator of superior accuracy. This heightened performance is further underscored by the fitted line equations in the SADE plots, which lie remarkably close to the bisector line.

Fig. 10
figure 10

Visualizing discrepancies between modeled and real data for all optimizers during train and test.

Full size image

Figure 11 effectively visualizes the distribution of relative deviations for each of our hybrid models. A tighter clustering of data points around the y = 0 line indicates greater accuracy from the estimator. Based on this, the GBM estimator tuned by SADE stands out as the most efficient predictive tool among all evaluated methods. Complementing this, Fig. 12 offers a direct comparison between the estimated and real data points across all four algorithms.

Fig. 11
figure 11

RE% distribution against actual data for all optimizers (training & testing).

Full size image
Fig. 12
figure 12

Comparative plots of predicted vs. real data for all algorithms.

Full size image

Figure 13 provides a powerful look into our predictive model’s decision-making process through SHAP (SHapley Additive exPlanations) analysis. This visualization clearly highlights which individual features are most crucial in shaping the model’s output. By ranking input variables—including choke size, tubing head pressure (THP), gas-oil ratio (GOR), basic sediment and water (BS&W), and API—based on their average absolute SHAP values, we can quantify each feature’s contribution to the magnitude of the model’s predictions. The analysis strikingly reveals that choke size and THP have the highest mean SHAP values, solidifying their role as the primary drivers of the model’s predictions and overall performance.

Fig. 13
figure 13

SHAP feature importance.

Full size image

Figure 14 further investigates the SHAP analysis results for a choke flow performance model by demonstrating the impact of various input parameters on the model outputs. The plot visually represents how individual features affect choke flow predictions, where positive SHAP values correlate with an increase in choke flow and negative SHAP values indicate a decrease. The red points correspond to higher values for each feature. For instance, larger choke sizes are associated with elevated choke flow rates, while higher THP promotes greater oil production through the choke. Conversely, higher values of GOR and BS&W are linked to reductions in oil production or choke performance. These findings align with theoretical and practical observations from the literature.

Fig. 14
figure 14

SHAP feature conditions.

Full size image

Specifically, the SHAP results align with established principles associated with reservoir and well performance. Larger choke sizes reduce flow resistance79,80, enabling higher production rates. Similarly, increased THP reflects stronger reservoir pressure81,82, which facilitates greater oil production and higher flow rates. On the other hand, higher BS&W values signify poor reservoir quality, leading to increased pressure drops across the well and reduced production rates83,84. Excessively high GOR values not only result in increased oil flashing at the surface but also negatively impact total production rate (TPR) due to the adverse effects on oil well performance, such as reduced tubing pressure and efficiency85. These insights confirm the predictive relevance and practical validity of the SHAP analysis results in capturing the dynamics of choke flow performance.

The developed tools can be easily used to predict choke oil flow rate based on wellhead data. In addition, the same workflow can be applied in other fields so as to develop cost-effective, fast, reliable and accurate models.

Limitations and future work

The performance of any data-driven optimization approach is inherently tied to the quality and representativeness of the dataset. We acknowledge potential limitations stemming from data collection biases, the completeness and noise within the dataset, and whether the dataset size and diversity fully capture the problem’s complexity, which could affect the generalizability of our findings. We also recognize the risk of overfitting our optimization methods to the training data. While we employed strategies like cross-validation and regularization to mitigate this, some residual risk may remain, impacting performance on unseen data. Further validation on independent or larger datasets will be crucial.

Our current optimization framework operates under specific assumptions. We critically examine model simplifications (e.g., assumed linearity), the representativeness of parameter space boundaries, and any potential limitations or biases in the objective function design that might not fully align with real-world outcomes. These identified limitations serve as a foundation for clear and impactful future research directions. These include, but are not limited to, exploring advanced validation techniques, investigating hybrid optimization approaches, addressing data sparsity or imbalance, incorporating real-time or dynamic optimization, integrating multi-objective optimization, and conducting deployment and real-world impact studies to assess the practical implementation and evaluation of our optimized solutions.

Conclusions

This study demonstrates the successful application of machine learning to predict choke flow performance, utilizing a high-quality dataset from a crude oil production site. Preprocessing techniques, including the MCOD algorithm, were instrumental in ensuring reliable data for model development. The SADE algorithm was the top performer among the optimization methods used, achieving both the lowest MSE and the highest R2 value during the testing phase. The models developed in this study exhibited strong predictive accuracy, with SHAP analysis providing valuable insights into the relative importance of the input parameters. Specifically, choke size and THP emerged as the dominant factors influencing choke flow performance. These findings align with known physical principles, validating the models’ practical relevance. This research provides a robust framework for applying data-driven approaches to production optimization, with the potential for broader applications in the oil and gas industry. Our comparative analysis demonstrates that the SADE algorithm consistently delivers the highest accuracy in predicting choke flow rate during the crucial testing phase. SADE achieved a testing R2 of 0.5935, indicating superior explanatory power compared to other methods. Crucially, SADE exhibited the lowest testing MSE, reflecting its enhanced ability to minimize prediction errors and fit unseen data accurately. While its testing-phase AARE% of 22.59% was not the absolute lowest, it aligns well with its robust predictive performance and the overall consistency observed between its training and test results, highlighting its reliability for modeling. In comparison, other algorithms demonstrated weaker generalization capabilities. For instance, ES, despite a higher training R2 of 0.8385, showed a noticeable drop in testing R2 to 0.5794, along with a higher testing MSE and an AARE% of 28.62%, indicating reduced prediction precision for unseen data. Similarly, PI and BBO, while achieving training R2 values as high as 0.8714 (PI), recorded testing R2 values of 0.5628 and 0.5717 respectively, which are comparable to SADE’s R2 but come with significantly higher testing MSE values and high AARE% values of 30.60% (PI) and 30.78% (BBO). These metrics underscore their reduced accuracy and generalization when confronted with new data, limiting their overall utility compared to SADE.