Enhanced PCB defect detection via HSA-RTDETR on RT-DETR

Abstract

Common PCB (Printed Circuit Board) defects include missing holes, shorts, spurs, etc., which may lead to product performance degradation, malfunction or safety hazards. Within the framework of Smart Manufacturing and Industry 4.0, industry strives to achieve automated and intelligent PCB defect inspection by using advanced machine vision systems and artificial intelligence algorithms. However, PCB defect detection faces challenges such as high density and miniaturization, complex background interference, and multiscale targets. For this reason, this paper proposes a new method for PCB defect detection according to a hierarchical scale-aware attention (HSA) mechanism based on RT-DETR (Real-Time Detection Transformer), and thus the method is coded as HSA-RTDETR. The core of the new method resides in the enhancement of feature information of small target defects in a feature fusion network. Firstly, a new backbone network, R18-Faster-EMA, is designed to make the overall model more efficient; Secondly, the AIFI (Attention-based Intra-scale Feature Interaction) module is redesigned to replace the original multihead self-attention mechanism with cascaded group attention to highlight important features. Thirdly, a hierarchical scale-aware pyramid attention network (HS-PAN) is designed to realize multi-scale feature fusion and learn more comprehensive feature arrays. Finally, to improve the efficiency of the model, a new loss function is designed to speed up convergence and prioritize small target defects. Experiments show that the HSA-RTDETR method achieves a mean average precision of 96.9% for six defects in a PCB dataset, which outperforms other existing models in terms of precision and recall. Compared with the original RT-DETR algorithm, the proposed method improves precision, recall, and mAP50 by 5.8%, 7.9% and 5.4%, respectively, In addition, the inference speed reaches 66.2 frames per second (FPS), which is deemed effective for the detection of small target defects in PCBs.

Introduction

Printed circuit boards (PCBs), as one of the core components of electronic devices, have been playing a crucial role in modern industry. Due to the complexity and precision issues of manufacturing processes, PCBs often exhibit various defects, such as missing holes, mouse bites, open circuits, short circuits, spurs, and spurious copper¹. This issue is becoming increasingly pressing with the miniaturization of electronic devices. These defects can lead to abnormal circuit functions, interruptions in signal transmission, or even equipment failures, significantly impacting the reliability and performance of electronic devices. Since electronic devices are the backbone of smart manufacturing and Industry 4.0, fast and efficient detection of PCB defects can prevent the defective PCBs from being used in electronics and dramatically mitigate the undesired consequences.

Due to the increasingly smaller size of PCB defects, traditional manual inspection may fail to capture all important defects. This not only makes it difficult to meet the demand for large-scale automated defect detection, but also affects the quality of electronic products. AI (Artificial Intelligence)-based techniques have made significant progress in the field of surface defect detection, and the existing target detection algorithms can be divided into two main categories: Algorithms based on traditional deep convolutional neural networks (CNNs), and algorithms based on the transformer architecture. The former category based on CNN architectures can be further divided into two groups, namely, two-stage methods such as Fast R-CNN (region-based CNN)² and Faster R-CNN³, and one-stage methods such as YOLO (You Only Look Once) variants^{4,5,6,7,8,9,10} and SSD (Single Shot Detector)¹¹. Two-stage detection methods have high accuracy in the tasks of small feature detection. For example, Hu et al.¹² proposed a Faster R-CNN method of PCB defect detection using GARPN to predict more accurate anchor points and merge the residual units of ShuffleNetV2, but it requires layer-by-layer training and inference, resulting in high complexity. Yang et al.¹³ proposed a Faster R-CNN based ROI extraction algorithm for weld seams, incorporating FPN and CBAM into the feature extraction module and using K-means clustering to modify the setting of the prior frame to improve the detection accuracy of the model. For example, Zhang et al.¹⁴ proposed a lightweight DsPAN (Detail-sensitive PAN) module combining feature transformation and attention embedding for multi-scale small target defect detection with good detection results on multiple datasets;

However, the improved network has more layers increasing the number of convolutions computed. Xiao et al.¹⁵ proposed a CDI-YOLO-based PCB defect detection algorithm that introduces the Coordinate Attention mechanism (CA) to improve the backbone and neck network of YOLOv7-tiny and enhance the feature extraction capability.

Compared with traditional CNN-based methods, target detection algorithms based on the transformer architecture have obvious advantages in global perception, detail capture and sequence modeling. Benefiting from the mechanism of global perception makes a transformer able to analyze the whole image in detail at different scales and levels, which is conducive to accurately locating and identifying target objects. Detection Transformer (DETR) is an end-to-end target detector for transformers¹⁶, widely used in computer vision to detect image objects in a single step without explicitly defining or extracting features beforehand.

DETR transforms the target detection task into a sequence-to-sequence problem, eliminating the need to design complex manual feature extractors and candidate frame generators as a step in traditional methods, resulting in a more concise model. The general structure of DETR is shown in Fig. 1, and its working principle is mainly based on the transformer architecture, which consists of an encoder and a decoder that can effectively capture the long-range dependencies between input sequences. In DETR, the input image is passed through an encoder to generate a set of feature vectors, and then the decoder decodes these feature vectors into a set of bounding boxes of objects and corresponding categories. Compared to traditional methods, DETR does not need to use candidate frames or perform NMS operations, but directly outputs the bounding boxes and categories of all targets in the whole image, which is designed to allow the model to have a fixed computational cost in inference while avoiding the performance loss caused by NMS.

Fig. 1

Structure of DETR network.

Although DETR simplifies the detection process and alleviates performance bottlenecks caused by network management systems, it still suffers from two major problems: Slow training convergence and difficulty in optimizing queries. Many research teams have proposed DETR variants to address these issues. Specifically, Deformable-DETR¹⁷ introduces the mechanism of variable attention, which effectively improves the model’s ability to perceive targets at different scales. In addition, Deformable-DETR makes the model more flexible to capture target information at different scales by dynamically adjusting the focus of the attention, thus accelerating the convergence speed of training. Conditional DETR¹⁸ and Anchor DETR¹⁹ reduce the optimization difficulty of the query. DAB-DETR²⁰ introduces a 4D reference point and improves the performance of target detection by iteratively optimizing the prediction frame layer by layer. DN-DETR²¹ accelerates the training convergence process by identifying and removing noise in a way that allows the model to generate quality queries more accurately. Group-DETR²² accelerates the training process by introducing one-to-many assignments of groups. RT-DETR²³ improves the model’s ability to perceive multi-scale targets and accelerates the convergence of training by designing a hybrid encoder to extract multi-scale features and introducing IoU-aware queries to improve the initialization of object queries. The DETR method also has many applications in practical defect detection, such as Dang et al.²⁴ proposed a novel DETR-based approach for sewer defect localization and severity analysis using the transformer’s self-attention weights for severity analysis of localized defects. Zhu et al.²⁵ applied the Dilated Re-param Block to the Expanded Residual Module and introduced the Gather-and-Distribution mechanism for RT-DETR-based UAV (Unmanned Aerial Vehicle) detection, which greatly improved the feature extraction and multi-scale feature fusion capabilities and further improved the detection performance. Although the model based on target detection reduces the manual experience reliance while achieving high detection accuracy, there are still several key challenges in PCB defect detection due to the complexities of industrial production, as follows:

• The diversity of PCB defect sizes and the interference of complex backgrounds pose significant challenges to the target detection capability of existing models;

• Most of the existing methods are not suitable to extract multi-scale features, leading to deficiencies in mining deep semantic information and accurately locating targets;

• Targeting based on the Coordinate Attention mechanism improves the performance of the model by focusing on the relationship between different locations in the input data, but may lead to situations where the target boundary is not clear enough.

• Due to the complexity and diversity of PCB defects, there are often multiple defective regions that overlap each other or are occluded by other elements, which can lead to difficulties in accurately identifying and localizing each defect in traditional models.

To address the above challenges, this paper proposes a new method for PCB defect detection using a hierarchical scale-aware attention mechanism based on RT-DETR. The highlights of the proposed methods and the main contributions of this paper are as follows:

• A new backbone network R18-Faster-EMA is designed to advance the backbone network combined with the attention mechanism, so that the network obtains richer small-size information than Resnet18 used in the original RT-DETR. This makes the overall model is simpler, more efficient and lighter, with better expressibility.

• An AIFI module is designed to replace the original multiple self-attention mechanism with cascading group attention for selective feature attention and highlighting important features.

• A Hierarchical Scale-aware Pyramidal Attention Network (HS-PAN) is designed to realize multi-scale feature fusion, which allows the model to learn a more comprehensive array of PCB defect features.

• A new MPDIoU + NWD Loss is designed to improve the convergence speed of the model, and the regression results are more accurate and sensitive to PCB small target defects.

• The proposed method can achieve state-of-the-art performance on the PCB dataset compared to the benchmark model, and can efficiently and accurately perform PCB defect detection.

The remainder of the paper is organized as follows. The design of HSA-RTDETR method is described in Section “Proposed methodology”. Sections “Experiment” and “Results and discussion” describe the experiments in detail and analyze the results. Conclusions are drawn in Section “Conclusions”.

Proposed methodology

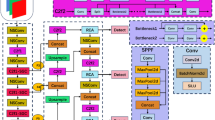
Based on deep learning object detection algorithms, RT-DETR improves on the architecture of DETR and Transformer with a series of innovations that increase the performance of the model. Although the RT-DETR algorithm has great advantages in detection accuracy and speed, the original network is easy to ignore small target features, and its direct application to PCB defect detection has encountered many issues. Therefore, in this paper, RT-DETR serves as a benchmark model for enhancing the module and structure. This improvement focuses on the backbone network, feature extraction, transformer structure, loss function, etc., to enhance feature representation, target detection performance, and model inference speed, thereby improving the model’s detection capability. As a result, a hierarchical scale-aware attention (HSA) mechanism based on RT-DETR is developed for PCB defect detection. The HSA-RTDETR model consists of a backbone network, an efficient hybrid encoder and a transformer decoder with an auxiliary prediction header, and its network structure is shown in Fig. 2. The output features of the last three stages (S3, S4, S5) of the backbone are used as inputs to the encoder. The hybrid encoder converts the multi-scale features into a series of image features through intra-scale interaction and cross-scale fusion. Subsequently, IoU-aware query selection is used to select a fixed number of image features from the encoder output sequence as the initial object query for the decoder. Finally, the decoder with an auxiliary prediction header iteratively optimizes the object query to generate boxes and confidence scores.

Fig. 2

Schematic of the proposed HSA-RTDETR network structure.

R18-faster-EMA network

The selection of an appropriate backbone network is particularly important in the study of RT-DETR-based PCB defect detection. The initial RT-DETR algorithm uses ResNet-l²⁶ and ResNet101²⁷ as backbone feature extraction networks. As the two have a larger model volume, they require higher inference time and resource consumption, which leads to structural redundancy and slow detection of the model in practical applications. The ResNet18 network²⁸ has lower computational complexity and wider applicability, consisting of a 7 × 7 convolutional layer, a maximum pooling layer, 4 blocks and a fully connected layer. However, ResNet 18 has a shallow structure and relatively weak representational capability, and it may not be able to adequately learn and represent highly abstract features in the dataset. Therefore, we design a more efficient and more capable representation of R18-Faster-EMA as the backbone in this paper, as shown in Fig. 3. Since the Basicblock is the core component of Resnet, which solves the problem of gradient vanishing during training through residual connections, and since the residual block has a relatively simple structure that contains the main convolutional and jump-connection parts compared to the other parts, it is easier to make improvements and experiments. Wu et al.²⁶ found through their research that under the condition of limiting the model complexity, increasing the base and capacity of the network model as much as possible can effectively improve the accuracy. At the same time, the improvement of the four basicblock can maintain the consistency of the network structure and avoid the introduction of unnecessary complexity and instability. Therefore, we have redesigned and optimized four of the Basicblocks, named the Faster-EMA Block, using ResNet18 as the benchmark network.

Fig. 3

R18-faster-EMA network.

Specifically, we employ a technique called Simplified Partial Convolution (PConv) in our design to reduce computational redundancy and memory accesses, thereby improving computational efficiency and saving memory. PConv performs spatial feature extraction by applying regular convolution on some of the input channels while keeping the other channels unchanged. To achieve contiguous or regular memory accesses, we compute the first or last contiguous group of channels as if they were representative of the entire feature map. Thus, the FLOP of PConv can be expressed as follows:

$$\begin{array}{*{20}c} {FLOP_{PConv} = h \times w \times k^{2} \times c_{p}^{2} } \\ \end{array}$$

(1)

where h is the vertical dimension of the input feature map, w is the horizontal dimension of the input feature map, k (kernel size) represents the size of the convolutional kernel, $c_{p}$ refers to the number of channels in the partial feature map that are not masked in the Partial Convolution (PConv). In the case where $r = \frac{{c_{p} }}{c} = \frac{1}{4}$, the FLOP of PConv is only 1/16th that of a regular Conv. Additionally, PConv has reduced memory accesses, which can be approximated as:

$$\begin{array}{*{20}c} {Memory\,Access_{PConv} \approx h \times w \times 2c_{p} + k^{2} \times c_{p}^{2} } \\ \end{array}$$

(2)

For $r=\frac{1}{4}$, PConv has only 1/4 the memory access of a normal convolution.

In order to fully and effectively utilize the information from all channels, this paper also adds two 1 × 1 convolutional layers behind PConv. This block adopts the characteristic of 1 × 1 convolution, which reduces the number of parameters, accelerates the training speed, and improves the nonlinear fitting ability of the model. However, the sensory field of 1 × 1 convolution is relatively small and lacks global feature acquisition. Then, we further add an Efficient Multi-Scale Attention (EMA)²⁹ module. As shown in Fig. 4, the structure of the EMA network is illustrated, which is more aggregated with multi-scale spatial structural information by placing 3 × 3 kernels with 1 × 1 branches in parallel for fast response. Compared to traditional convolutional neural networks (CNN), EMA combines local features from multiple input sources to enhance the performance of the model through parallel processing and self-attention mechanisms. This parallel convolution allows for faster training of the model when dealing with large-scale data and improves accuracy by allowing features to be processed in parallel at different scales.

Fig. 4

Efficient multi-scale attention network structure.

In addition to the above operators, normalization and activation layers are essential for high-performance neural networks. However, many previous studies have overused these layers, which can limit feature diversity, thus affecting performance and also slowing down the overall computation. In contrast, we only place normalization and activation layers in the middle of each Conv to maintain feature diversity and achieve lower latency. In addition, we use batch normalization (BN) instead of other alternatives, which can be merged with adjacent convolutional layers to speed up inference. In order to verify the effect of BN value selection on model performance, we conducted ablation experiments to compare the effects of different BN values on model accuracy and inference speed. In Table 1, the experimental results show that the model achieves the best accuracy and inference speed on the PCB dataset when the BN value is set to 0.1.

Table 1 Effect of different BN values on model performance.

In general, the R18-Faster-EMA as the backbone network focuses on the balance of high efficiency and representation capability. The PConv technique reduces computational redundancy and memory access, while the additional 1 × 1 convolutional layer and the EMA module enhance the global feature perception, providing higher efficiency and accuracy in PCB defect detection tasks.

Cascaded group attention mechanism

Multi-Head Self-Attention (MHSA) based Attention-based Intra-scale Feature Interaction (AIFI) is an important component of Efficient Hybrid Encoder. The core idea of MHSA during defect detection network training is to decompose a linear transformation into multiple heads, each performing a self-attention operation, and then stitching the outputs of all the heads together as the final representation. However, attention head redundancy is a serious problem in MHSA, which leads to computational inefficiency. To solve this problem, we redesigned the AIFI network structure to provide the attention head by different segmentation of the full features through the Cascaded Group Attention Mechanism (CGA), which saves the computational overhead and improved the diversity of the attention. Formally, CGA can be formulated as follows:

$$\begin{array}{*{20}c} {\tilde{X}_{ij} = AttnX_{ij} W_{ij}^{Q} ,X_{ij} W_{ij}^{K} ,X_{ij} W_{ij}^{V} } \\ \end{array}$$

(3)

$$\begin{array}{*{20}c} {\tilde{X}_{i + 1} = Concat\left[ {\tilde{X}_{ij} } \right]_{j} = {}_{i:h}^{ } W_{i}^{P} } \\ \end{array}$$

(4)

where h is the total number of heads, $W_{ij}^{Q}$, $W_{ij}^{K}$ and $W_{ij}^{V}$ are projection layers mapping the input feature split into different subspaces, and $W_{i}^{P}$ is a linear layer that projects concatenated output features back to the dimension consistent with the input.

CGA computes the attention graph for each head in a cascade fashion by encouraging the Q, K, and V layers to learn projections on features with richer information, as shown in Fig. 5. It gradually refines the feature representation by adding the output of each header to the subsequent header: $X_{ij}{\prime} = X_{ij} + \tilde{X}_{{i\left( {j - 1} \right)}}$,1 < j ≤ h. Here, $X_{ij}{\prime}$ is obtained by adding the j-th input split $X_{ij}$ and the output $\tilde{X}_{{i\left( {j - 1} \right)}}$ of the (j− 1)-th head. $X_{ij}{\prime}$ replaces $X_{ij}$, as the new input feature for computing self-attention in the j-th head.

Fig. 5

Cascaded group attention network structure.

This cascade design has two main advantages. First, the diversity of the attention graph can be increased by providing different feature divisions for each attention head. Similar to other group convolution methods, CGA can reduce the number of input and output channels in the QKV layer without increasing the number of triggers and parameters. Second, by adding cascaded attention heads, the depth of the network can be increased to further enhance the capacity of the model without adding additional parameters. The computational cost incurred is also relatively low since the computations in each attention header use a smaller QK channel size. The Cascaded Group Attention mechanism (CGA) progressively optimizes the target location by cascading. Each attention head is computed based on the output and input features of the previous head, which gradually refines the feature representation and improves the accuracy of target localization. In addition, the IoU-aware query selection mechanism can further optimize the initialization of the target query, thus improving the accuracy of target localization.

Based on the above advantages, in this paper, the AIFI module is redesigned by replacing the traditional Multi-Head Self-Attention with Cascaded Group Attention. Compared with the previous MHSA, CGA provides different input segmentation for each attention head and cascades their output features together. This design approach not only reduces the computational redundancy in multi-head attention, but also enhances the capacity of the model by increasing the network depth. In addition, the efficiency of the model parameters is improved by expanding the channel widths of key network components to redistribute parameters and shrinking the components with lower hidden dimensions in the FFN.

Hierarchical scale-aware pyramid attention networks

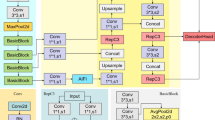
In PCB datasets, the task of defect recognition is challenged by the multi-scale problem due to the coexistence of multiple scales of defects on PCB boards of varying sizes, ranging from tiny scratches to larger breaks or shorts. To address this problem, this paper designs a Hierarchical Scale-aware Pyramidal Attention Network (HS-PAN) for multi-scale feature fusion, which allows the model to learn a more comprehensive array of PCB defect features.

The structure of HS-PAN is shown in Fig. 6. HS-PAN consists of three essential components: (1) Feature Selection Module; (2) Top-Down Feature Fusion Module; and (3) Integrated Feature Refinement Module. Firstly, the Feature Selection Module extracts the most discriminative and informative features by considering features at different scales and subjecting them to a selection process. Subsequently, guided by the Advanced Selective Feature Fusion (ASFF) mechanism, high-level and low-level information are fused together, aiming to synergistically integrate multi-level information, thereby generating richer semantic information for the model to accurately distinguish subtle defects. Finally, in the Integrated Feature Refinement Module, the fused features undergo further optimization and refinement to enhance the expression capability of local details, aiding in the accurate localization and identification of targets in complex scenes.

Fig. 6

HS-PAN network structure.

Feature Selection Module In this process, the CA module (Channelled Attention Module) and the DU module (Dimension Unification Module) play a key role. The CA module first inputs the feature map ${f}_{in}\in {R}^{C\times H\times W}$, where C, H, and W denote the number of channels, height and width of the feature map, respectively. Subsequently the feature mapping undergoes global average pooling and global maximum pooling and is combined to obtain a new feature, and finally the Sigmoid activation function is used to determine the weights for each channel, which ultimately yields the weight of each channel, i.e., ${f}_{CA}\in {R}^{C\times 1\times 1}$. The main objective of bi-level pooling is to downsize or compress the input data to reduce the number of computations and parameters and extract the most critical features from it to achieve invariance to translations, rotations and scales. As shown in Fig. 7, this process involves two steps, global average pooling and maximum pooling. Global average pooling is used to compute the average value for each channel, while maximum pooling is used to extract the most relevant data in each channel. With this dual pooling strategy, one can simultaneously retain the important information in each channel and minimize information loss. Maximum pooling focuses on the salient features within a channel, while average pooling obtains global features in a more balanced way to ensure the comprehensiveness and effectiveness of feature extraction. Subsequently, the weight information is multiplied by the corresponding scale of the feature maps to generate the filtered feature maps. Before feature fusion, it is crucial to ensure that these feature maps have matching dimensions due to the differences in the number of channels in the feature maps at different scales. For this reason, we design a Dimension Unification Module (DU) that uniformly reduces the number of channels of the feature maps at each scale to 256 by using a 1 × 1 convolution operation, thus ensuring that cross-scale feature maps can be fused effectively.

Fig. 7

CA module network diagram.

Top-down feature fusion module The multi-scale high-level features generated by the feature selection process contain rich semantic information but the localization of the target is relatively coarse; on the contrary, the low-level features present limited semantic information but accurate localization. Traditional methods usually directly sum the high- and low-level features pixel by pixel to enrich the semantic information of each layer. However, this simple approach lacks the process of feature selection. Therefore, in this paper, we design an SFF (Selective Feature Fusion) module that aims to take into account the importance of feature selection when synthesizing pixel values from multiple feature layers.

This module utilizes high-level features as weights to filter the basic semantic information in low-level features to strategically fuse features. As shown in Fig. 8 for the ASFF network structure, a high-level feature $f_{high} \in R^{C \times H \times W}$ and a low-level feature $f_{low} \in R^{{C \times H_{1} \times W_{1} }}$ are input respectively, low-level features go through an SE (Squeeze-and-Excitation) attention module to reduce attention to unimportant or redundant features and improve the model’s perceptual ability; and the high-level feature is expanded by transposed convolution (T-Conv) with step size 2 and convolution kernel 3 × 3, and subsequently obtains the feature size $f_{{\widehat{high}}} \in R^{C \times 2H \times 2W}$. Thereafter, in order to unify the dimensions of high-level and low-level features, this paper employs bilinear interpolation for downsampling the high-level feature, and finally obtains $f_{att} \in R^{{C \times H_{1} \times W_{1} }}$. Equations (5) and (6) represent the fusion process of feature selection:

$$\begin{array}{*{20}c} {f_{att} = BL\left( {T - Conv\left( {f_{high} } \right)} \right)} \\ \end{array}$$

(5)

$$\begin{array}{*{20}c} {f_{out} = f_{low} *CA\left( {f_{att} } \right) + f_{att} } \\ \end{array}$$

(6)

Fig. 8

ASFF module network structure diagram.

During the downsampling process, a combination of transposed convolution and bilinear interpolation is employed to restore the scale of high-level features. Bilinear interpolation is simple and effective, and can quickly compute the value of the target pixel, which accomplishes the scaling of the image. The advantages of transposed convolution include (1) strong learning ability, by learning the parameters of the trainable convolution kernel, so that the output not only enlarges the feature map, but also reconstructs the input in the form of convolution; (2) transposed convolution is also able to deal with the problem of non-uniform sampling, because it can sample different regions of the input image at different output positions.

Integrate feature refinement modules This module aims to combine different levels of feature information to fully utilize the target localization accuracy of low-level features and the rich semantic information of high-level features to further enhance the network model performance. Through feature selection and fusion operations, multi-level feature representations are integrated to enhance the performance of the target detection task. First, feature selection operations are performed on the output features from the previous stage to filter and enhance the features to be fused; then, starting from lower-level feature maps, features are gradually fused upwards, followed by strategic fusion of features by utilizing the ASFF module again, taking the high-level features as the weights, and filtering the basic semantic information in the low-level features in a targeted manner.

MPDIoU + NWD loss function

During the training process of RT-DETR, the use of the loss function to calculate the error between the predicted value and the true value in each iteration helps to optimize the performance of the model in the direction of convergence. RT-DETR uses GIoU as the regression loss function for the bounding box. The formula for GIoU loss can be expressed as follows:

$$\begin{array}{*{20}c} {IoU = \frac{{\left| {A \cap B} \right|}}{{\left| {A \cup B} \right|}}} \\ \end{array}$$

(7)

$$\begin{array}{*{20}c} {GIoU = IoU - \frac{{C - \left( {A \cup B} \right)}}{C}} \\ \end{array}$$

(8)

$$\begin{array}{*{20}c} {L_{GIoU} = 1 - GIoU} \\ \end{array}$$

(9)

Although the GIoU loss has been adopted by some advanced detectors (e.g., YOLOv3 and Faster R-CNN) and shows better performance compared to the MSE loss and the IoU loss, there is a problem of failure of the GIoU loss in the case where the prediction frames cover the real frames completely. To overcome this problem, MPDIoU Loss³⁰ is introduced in this paper to improve the original loss function. A comparison of MPDIoU and GIoU Loss is shown in Fig. 9. MPDIoU Loss is a bounding box similarity metric based on the minimum point distance, which integrates the intersection ratio of the predicted box and the real box, the distance between the centroids, as well as the width and height deviations. The design simplifies the calculation process to some extent, improves the convergence speed of the model, and the regression results are more accurate, as shown in Eqs. (10)–(13).

$$\begin{array}{*{20}c} {L_{{{\text{MPDIoU}}}} = 1 - {\text{MPDIoU}}} \\ \end{array}$$

(10)

$$\begin{array}{*{20}c} {{\text{MPDIoU}} = \frac{A \cap B}{{A \cup B}} - \frac{{d_{1}^{2} }}{{w^{2} + h^{2} }} - \frac{{d_{2}^{2} }}{{w^{2} + h^{2} }}} \\ \end{array}$$

(11)

$$\begin{array}{*{20}c} {d_{1}^{2} = \left( {x_{1}^{B} - x_{1}^{A} } \right)^{2} + \left( {y_{1}^{B} - y_{1}^{A} } \right)^{2} } \\ \end{array}$$

(12)

$$\begin{array}{*{20}c} {d_{2}^{2} = \left( {x_{2}^{B} - x_{2}^{A} } \right)^{2} + \left( {y_{2}^{B} - y_{2}^{A} } \right)^{2} } \\ \end{array}$$

(13)

where A and B denote the true and predicted frames, ($x_{1}^{A}$, $y_{1}^{A}$) and ($x_{2}^{A}$, $y_{2}^{A}$) denote the coordinates of the upper left and lower right corners of bounding box A, respectively. ($x_{1}^{B}$, $y_{1}^{B}$) and ($x_{2}^{B}$, $y_{2}^{B}$) denote the coordinates of the upper left and lower right corners of bounding box B, respectively.

Fig. 9

Comparison of GIoU Loss and MPDIoU Loss.

However, in our PCB dataset, small target defects account for a large proportion and the original model is prone to missing detection, which is closely related to the mechanism of IoU. As shown in Fig. 10, when a small target deviates from the real frame, its IoU drops rapidly. In contrast, the same deviation of a medium or large target defect does not cause a significant change in IoU. Therefore, the IoU-based loss function is very sensitive to the positional changes of small targets, which has a large impact on the detection accuracy. Although the MPDIoU used in this paper can alleviate this problem to some extent, it is still an IoU-based loss function. In order to better improve the detection performance of the model, on this basis, we introduce the loss function of Normalized Gaussian Wasserstein Distance (NWD Loss) NWD Loss firstly models the bounding box using a two-dimensional Gaussian distribution, and then calculates the similarity between the predicted box and the real box based on the corresponding Gaussian distribution. The formula of NWD Loss is as follows:

$$\begin{array}{*{20}c} {W_{2}^{2} \left( {N_{a} ,N_{b} } \right) = \left\| {\left( {\left[ {cx_{a} ,cy_{a} ,\frac{{w_{a} }}{2},\frac{{h_{a} }}{2}} \right]^{T} ,\left[ {cx_{b} ,cy_{b} ,\frac{{w_{b} }}{2},\frac{{h_{b} }}{2}} \right]^{T} } \right)} \right\|_{2}^{2} } \\ \end{array}$$

(14)

where $W_{2}^{2} \left( {N_{a} ,N_{b} } \right)$ is a distance measure that cannot be directly used as a similarity measure, Therefore, the normalized exponential form is used instead, as shown in the following equation:

$$\begin{array}{*{20}c} {NWD\left( {N_{a} ,N_{b} } \right) = \exp \left( { - \frac{{\sqrt {W_{2}^{2} \left( {N_{a} ,N_{b} } \right)} }}{C}} \right)} \\ \end{array}$$

(15)

Fig. 10

Analysis of IoU at different scales. Each small rectangular box in (a) represents 1 pixel; each small rectangular box in (b) represents 2 pixels. “A” is the true box; “B” and “C” represent the predicted box with a deviation of 1 pixel and 4 pixels, respectively.

Since there are not just only small target defects in dataset, we performed a probabilistic fusion of MPDIoU and NWD as the final loss function as shown in Eq. (16), where α takes the value of 0.5.

$$\begin{array}{*{20}c} {Loss = \alpha \times MPDIoU + \left( {1 - \alpha } \right) \times NWD} \\ \end{array}$$

(16)

Experiment

Dataset

This study adopted the PCB dataset provided by the Open Laboratory of Intelligent Robotics at Peking University (http://robotics.pkusz.edu.cn/resources/dataset/). This dataset is currently used by many scholars^14,15,31. The dataset encompasses six defect types: Short circuit, open circuit, mouse bite, spur, missing hole, and spurious copper, totaling 693 images, as shown in Fig. 11.

Fig. 11

Six types of defects in the PCB dataset, (a) Missing holes, (b) Mouse bites, (c) Open circuits, (d) Short circuits, (e) Spurs, (f) Spurious copper.

Due to the limited sample size, efforts were made to enhance model generalization and robustness. During the construction of the dataset, noise reduction and contrast adjustment were applied to improve image quality. The dataset was divided into training, testing and validation sets in an 8:1:1 ratio. The quantities of various types of defects in the dataset are shown in Table 2. The distribution of defect width and height in the dataset is shown in Fig. 12, indicating that PCB defects are primarily small targets, with a smaller portion being medium and large targets.

Table 2 Types and quantities of defects in the dataset.

Fig. 12

Distribution of defect width and height in the dataset.

In order to enhance the model generalization ability and robustness, this paper performs a series of data enhancement operations on the training data, including mix-up and mosaic. the mix-up operation mixes the feature maps and labels of two samples with a mixing ratio of 0.5. the mosaic operation splices the images of four samples to form a new image. In this paper, we use the open source library albumentations to implement the data enhancement operation. After data enhancement, the number of samples in the training dataset is increased by four times, the data distribution is more uniform, and the feature diversity is improved. Through comparison experiments, it is found that the mAP50 of the model is improved by 0.9% after using data enhancement, indicating that the data enhancement technique effectively improves the performance of the model.

Experimental environment

The experimental hardware environment is shown in Table 3. The operating system and software environment for the experiments are: Windows 10, Python 3.10, CUDA 11.8, PyTorch 2.0.1. In terms of programming implementation, this paper builds HSA-RTDETR model based on the PyTorch framework and uses the AdamW optimizer for model training. In addition this paper compares other model implementations that use different optimizers or learning rate scheduling methods on the same dataset, as well as tries other commonly used deep learning model structures such as YOLO or SSD. The code in this paper is written based on the API provided by PyTorch, and relevant code examples are available in the official RT-DETR open source deep learning library for reference.

Table 3 Experimental hardware environment.

For deep learning algorithms, the choice of hyperparameters has a significant impact on training time, storage costs, and the quality of the trained model. In this experiment, the AdamW optimizer is used, and the model is trained through backpropagation. In this experiment, the initial learning rate is set to 0.0001, and the learning rate is adjusted by cosine annealing to allow the model to quickly converge to a local optimum. The weight decay is set to 0.0001. The number of training epochs is set to 100, the batch size is 4, and the remaining parameters are kept at their default values.

Evaluation metrics

In order to objectively evaluate the performance of HSA-RTDETR model compared to the original RT-DETR model and other models under the same experimental conditions, the defect detection results are compared. Common evaluation metrics include precision (P), recall (R), average precision (AP), and mean Average Precision (mAP), the calculation formula is as follows:

$$\begin{array}{*{20}c} {Precision = \frac{TP}{{TP + FP}}} \\ \end{array}$$

(17)

$$\begin{array}{*{20}c} {Recall = \frac{TP}{{TP + FN}}} \\ \end{array}$$

(18)

$$\begin{array}{*{20}c} {AP = \mathop \smallint \limits_{0}^{1} P\left( R \right)dR} \\ \end{array}$$

(19)

$$\begin{array}{*{20}c} {mAP = \frac{{\mathop \sum \nolimits_{i = 1}^{N} AP_{i} }}{N}} \\ \end{array}$$

(20)

where TP represents the number of true positive samples, TN represents the number of true negative samples, FP represents the number of false positive samples, FN represents the number of false negative samples, and N represents the total number of classes. Additionally, there is FPS as an evaluation metric, where a higher FPS indicates a faster inference speed of the model and higher detection efficiency.

Results and discussion

Verification experiment of backbone improvement effectiveness

To validate the performance advantages of the proposed R18-Faster-EMA model, multiple backbone networks are trained on the PCB dataset in a single experimental environment, including: ResNet18/50/101, Fasternet³², Lsknet³³, EfficientViT³⁴, VanillaNet³⁵, Swim Transformer³⁶ and R18-Faster-EMA (The model proposed in this paper). As shown in Fig. 13, the comparison of different backbone networks indicates that R18-Faster-EMA exhibits significant improvements over the baseline R18 in terms of floating-point operations and mean Average Precision (mAP), outperforming all backbone networks except the ResNet series. Efficiency is crucial when deep learning networks perform recognition tasks. Although R18-Faster-EMA has a slightly lower mAP50 compared to R50 and R101 (by 0.8% and 1.2% respectively), its floating-point operations are much lower than R50 and R101. Lower floating-point operations imply higher inference speed and lower resource consumption, significantly reducing the computational cost of the model while maintaining relatively high performance. Therefore, the proposed R18-Faster-EMA, balancing performance and efficiency, maintains relatively high recognition accuracy while being more lightweight than the other 9 existing backbone networks.

Fig. 13

Comparison chart of different backbone networks.

Effectiveness experiment of cascaded group attention

To validate the effectiveness of the Cascaded Group Attention (CGA) module in this paper for small object detection, we conducted performance comparison experiments with the Multi-Head Self-Attention (MHSA) mechanism in the original RT-DETR. As shown in Table 4, the results demonstrate that Cascaded Group Attention outperforms MHSA in various metrics, with improvements of 2.9% in mAP50, 2.8% in precision (P), and 2.1% in recall (R). Additionally, the parameter count decreased by 0.4 m, while the frames per second (FPS) increased by 1.5.

Table 4 Performance comparison of different attention mechanisms.

To further validate the higher sensitivity of Cascaded Group Attention to small object defects, we compared the visualization effects of CGA and MHSA using Grad-CAM heatmaps. Grad-CAM heatmaps represent the importance of regions in the prediction output process by the brightness of certain areas in the class activation heatmap. The larger the area of bright color, the higher the attention paid to the prediction output. The heatmap results are shown in Fig. 14, with each group sequentially including the original image, the visualization effect of MHSA, and the visualization effect of CGA. Respectively, the red boxes on the original image represent the ground truth bounding boxes. Figure 14b shows the heatmap of the network output after using the MHSA module, it can be seen that the areas of focus in the network are relatively scattered, with the PCB defect areas having higher weights compared to their surrounding areas but not enough weight relative to the entire image. Figure 14c shows the heatmap of the network output after replacing MHSA with CGA, it can be observed that the CGA attention mechanism assigns higher weights to the prediction outputs of PCB defect features, even for less obvious defects, thus avoiding missed detections. Therefore, the method proposed in this paper has a significant effect.

Fig. 14

Visualization results of attention mechanism heatmaps.

Validation of the effectiveness of the MPDIoU + NWD loss function

To evaluate the effectiveness of the MPDIoU + NWD loss function incorporated into the RT-DETR model proposed in this paper, we established an experimental framework and tested seven different loss functions, including MPDIoU + NWD. The experimental results are shown in Table 5 and Fig. 15. After integrating the MPDIoU + NWD loss function into the model, a mAP50 of 93.1%, P of 91.6%, and R of 90.2% were achieved, which outperform the original model wisssth GIoU Loss. Compared to other loss functions, MPDIoU + NWD performs best across all metrics, demonstrating its higher mAP50 (93.1%) and improved bounding box regression loss compared to other loss functions, it is evident that the model using the MPDIoU + NWD loss function not only achieves the highest level of mean Average Precision but also performs optimally in bounding box regression loss. In contrast, the performance of SIoU and EIoU is not satisfactory. Further testing results validate the effectiveness of the proposed MPDIoU + NWD loss function in the model.

Table 5 Performance comparison of different loss functions.

Fig. 15

Performance comparison of loss functions.

Ablation experiment

To validate the effectiveness of the algorithmic improvement strategies proposed in this paper, ablation experiments were conducted using RT-DETR (ResNet 18) as the base model to compare the effects of different improvement strategies. The ablation experiment, by gradually removing or changing certain components in the network model and then evaluating the performance of the model under these changes, helps to verify the actual impact of various improvement strategies on the model performance and provides an objective evaluation basis for algorithm improvement. Specifically, the ablation experiment design is as follows: Using the original RT-DETR (ResNet18) algorithm without any improvements as the baseline, four individual modules were incrementally added: A. HS-PAN module, B. CGA attention mechanism, C. R18-Faster-EMA backbone network, and D. MPDIoU + NWD loss function. For each module, its impact on various data metrics of the RT-DETR model was evaluated separately. Finally, these four modules were simultaneously added to the RT-DETR model, and the data metrics were evaluated again.

The results in Table 6 indicate that the original RT-DETR achieves a precision of 91.3%, a recall of 86%, and mAP50 of 91.5%. Using this as a baseline, a series of improvements were made in this study, and the impact of each improvement on various metrics was observed. The results show that each improvement brought about a certain degree of performance enhancement. Ultimately, among all the improvement schemes, we achieved the optimal levels of precision at 97.1%, recall at 93.9%, and mAP50 at 96.9%. Compared to the baseline, precision increased by 5.8%, recall increased by 7.9%, mAP50 increased by 5.4%, and the Params count decreased by 2.5 m, making the overall model more lightweight. However, one limitation of this study is that, compared to the baseline model, the frames per second (FPS) of the improved algorithm is 66.2, a decrease of 17.8. Nonetheless, this still meets the frame rate requirements for online detection (> 25). Further validation of the improved algorithm’s feasibility was conducted through the aforementioned ablation experiments. As shown in Fig. 16, the comparison chart of the ablation experiments demonstrates that with the gradual introduction of each improvement module, performance steadily improves, validating the effectiveness of the improvement strategies. Figure 17 displays the extent of improvement for each individual aspect, showing that each improvement point contributes to a certain degree of enhancement.

Table 6 Ablation experiment metrics.

Fig. 16

Comparison chart of ablation experiments.

Fig. 17

Effectiveness chart of individual improvement points.

Analysis of other error components

To investigate the components of mAP, we categorized all false positives and false negatives in the model into six types, as shown in Fig. 18, they are Cls (classification error ratio), Loc (location error ratio), Cls + Loc (classification and localization error ratio), Duplicate (duplicate detection ratio), Bkgd (background false detection ratio), and Missed (missed detection ratio), respectively. Cls and Loc respectively measure the accuracy of the model in target classification and localization. Cls + Loc provides a comprehensive performance assessment. Duplicate and Bkgd reflect the model’s ability to handle duplicate detections and background. Missed indicates cases where targets are not detected. These metrics collectively aid in understanding the sources of model errors, guiding system optimization and improvement, and are crucial for evaluating the performance of object detection systems.

Fig. 18

Diagram of the six error types.

As shown in Table 7, in the unimproved scenario, Loc and Bkgd account for a significant proportion, respectively 1.83 and 1.86. The probability of misclassification and localization errors occurring simultaneously is 0. However, there are also issues with misclassification, duplicate detections, and missed detections, at 0.14, 0.53, and 0.34 respectively. After improvement, it can be observed that misclassification and missed detections are reduced from 0.14 to 0 and 0.34 to 0, respectively. However, localization errors still persist, albeit reduced to 0.6. Additionally, the problems of duplicate detections and background misjudgments have also been addressed, decreasing from 0.53 and 1.86 to 0.14 and 0.74 respectively. In summary, the algorithm proposed in this paper significantly improves the error associated with small target defects, but further optimization of localization errors is still needed to enhance the accuracy and stability of detection.

Table 7 Comparison of model errors before and after improvement.

Comparative experiment

The ablation experiments have confirmed the effectiveness of the HSA-RTDETR model proposed in this paper. To evaluate the performance of the proposed algorithm in PCB small target detection tasks, we conducted comparative experiments with 11 existing object detection models, including Faster-RCNN, CornerNet³⁷, YOLOv5, YOLOv7, YOLOv8n, DETR, Deformable DETR, Focus-DETR³⁸, RT-DETR. These experiments were conducted under the same training environment and using the same dataset, with each model being trained with recommended hyperparameters.

Table 8 presents the defect detection performance of different methods. It is evident that the proposed method achieves the best performance in terms of precision (P) and mean average precision at IoU 50% (mAP50), reaching 97.1% and 96.9% respectively. The recall rate (R) of 93.9% is second only to YOLOv7, but still superior to the other 10 models. The elevated precision (97.1%) and mAP50 (96.9%) scores demonstrate that the proposed HSA-RTDETR method consistently achieves high accuracy across diverse defect categories, including small and complex defects, as validated by experimental results on the PCB dataset.With a model parameter size of 17.6 m, the algorithm presented in this paper is relatively smaller compared to other algorithms, second only to YOLOv5s with 7.1 m parameters. This suggests that the proposed algorithm maintains high performance while having a more lightweight model structure, making it suitable for application in resource-constrained scenarios. In summary, the algorithm proposed in this paper demonstrates excellent performance in PCB small target detection tasks, with high precision, recall, and mAP50, and a smaller model size, making it suitable for rapid inference and deployment in practical application scenarios.

Table 8 Defect detection performance of different methods.

Actual scenario data testing

In order to evaluate the performance of the model in practical applications, the types of defects collected from actual scenes are difficult to cover the six defect types due to factors such as equipment limitations in the production environment. Therefore, in this paper, 180 images containing the three common defect types of OPEN, SHORT and SPUR are collected from the actual production and combined with another open source dataset PCB Defect (https://universe.roboflow.com/aakash-g0eoi/new_dataset-wdzks) A new validation set is constructed by combining it with the validation set in another open source dataset, PCB Defect (), resulting in 300 samples. This dataset provides richer defect types and scenarios for further validating the model’s performance in real-world applications.

Figure 19 shows the results of the visualization of the proposed method in this paper on real scene data, including bounding boxes and confidence scores. The model accurately detects and localizes each defect with high confidence. Table 9 lists the performance of the method proposed in this paper in real defect detection, including mAP50, mAP95, precision, and recall. The results indicate that the model achieves the highest performance in detecting missing hole defects, with a mAP50 of 99.5. In contrast, the model exhibits the lowest performance in detecting short defects, with a mAP50 of 92.9. The performance of spur defect detection is also less satisfactory, with a mAP50 of 94.3. The detection performance of the other three defect types (open circuit, mouse bite, spurious copper) is relatively similar, ranging from 96.9% to 98.7%.

Fig. 19

Actual scenario data test chart.

Table 9 The proposed method for PCB defect detection performance analysis.

Comparison of detection performance on PCB Dataset

The paper selects several models, including YOLOv5s, DETR, RT-DETR (R18), and HSA-RTDETR, for visual analysis of a PCB Dataset. Figure 20 shows the output results of the four models. It can be observed that the proposed model in this paper exhibits higher confidence and better detection performance.S

Fig. 20

Visualization results of four models.

Conclusions

This study aims to overcome the main limitations of the existing RT-DETR-based PCB defect detection models, especially the problems of complex background interference, large memory requirements and low detection accuracy. Therefore, this study proposes a new method for defect detection based on a hierarchical scale-aware attention mechanism, which improves the model in terms of feature extraction, transformer structure and loss function, achieving a 96.9% mAP50, the inference speed reaches 66.2 frames per second (FPS). Considering the computational complexity of the model, a new backbone network, R18-Faster-EMA, is designed in this paper to promote the combination of backbone network and attention mechanism, resulting is a simpler, more efficient and lightweight overall model with enhanced expressive capabilities. In order to improve the accuracy of detecting small target defects, this paper redesigns the AIFI module and adopts the cascade group attention to replace the original multi-head self-attention mechanism, to realize the selective feature attention and highlight the important features. Considering the PCB multi-scale and complex background interference, this paper designs a hierarchical scale-aware pyramid attention network (HS-PAN) to realize multi-scale feature fusion, allowing the model to learn a more comprehensive range of PCB defect features. Finally, this paper thoroughly investigates the shortcomings of the IoU mechanism, i.e., the large fluctuation of the defect location offset for small objects, which is prone to the phenomenon of missed detection, and designs a new MPDIoU + NWD loss function. which accelerates the model’s convergence speed of the model while paying more attention to the small object defects, and realizes more accurate regression results.

The experimental results show that the HSA-RTDETR proposed in this paper achieves an average precision of 96.9% in the PCB dataset, and improves the precision, recall, and mAP50 by 5.8%, 7.9%, and 5.4%, respectively, compared with the original RT-DETR algorithm in terms of precision and recall, and achieves an inference speed of 66.2 frames per second. The superiority and effectiveness of the method is demonstrated by comparing it with other methods using the same experimental setup and evaluation criteria, which shows that the algorithm in this paper not only detects small-target defects, but also effectively suppresses the complex background interference, and establishes a fast and accurate defect detection model, which is of great significance for PCB quality decision-making.