A chaotic arithmetic optimization algorithm with Cauchy perturbation and differential evolution for engineering design problems

Abstract

Although the arithmetic optimization algorithm (AOA) shows promising performance, it tends to suffer from premature convergence and poor scalability in high-dimensional problems. To address these challenges, we propose the Chaotic Differential Arithmetic Optimization Algorithm (CDAOA), which combines an improved Tent chaotic map for initializing a diverse population, Cauchy perturbation for enhanced exploration, and differential evolution with Lévy flight to strengthen exploitation. CDAOA is benchmarked on 16 classical functions, the CEC 2019 and 2021 test suites, and five real-world engineering problems. Results demonstrate that CDAOA achieves superior performance compared to AOA and several state-of-the-art algorithms in terms of convergence speed and solution quality.

Introduction

Optimization algorithms play a pivotal role in identifying global solutions for complex optimization problems involving one or multiple objectives. However, many real-world problems in scientific and engineering domains pose significant challenges due to their inherent complexity¹. These problems are often nonconvex and constrained by multiple linear or nonlinear equality and inequality conditions. Traditional optimization methods, such as gradient descent and Newton methods, demand strict assumptions like continuity and differentiability of the objective function, limiting their applicability. Furthermore, their reliance on initial values frequently leads to suboptimal solutions in cases where these values are poorly chosen. This has driven the search for more flexible and robust approaches to address such challenges.

Meta-heuristic optimization algorithms have emerged as a promising alternative to traditional methods, offering flexibility and the ability to handle complex, nonlinear problems without requiring strict assumptions. Therefore, there has been a proliferation of research on intelligent algorithms in recent years. They often draw inspiration from natural phenomena or human behaviors, making them both intuitive and effective. For example, GOOSE Algorithm (GOOSE)², Football Team Training Algorithm (FTTA)³, Spider Wasp Optimizer (SWO)⁴, Genetic Algorithm (GA)⁵, etc. The core concept of metaheuristic algorithms lies in their ability to explore and exploit the search space efficiently⁶. Exploration refers to the process of searching for new regions that may contain better solutions, while exploitation involves refining the current best solutions. Metaheuristics strike a balance between these two processes, ensuring that they do not get stuck in local minima and continue to search for globally optimal solutions.

Despite their widespread success, meta-heuristic algorithms encounter several challenges when applied to complex problems, particularly the risk of being trapped in local optima. This issue is exacerbated in high-dimensional spaces where intricate relationships exist among variables⁷. To overcome these limitations, researchers have proposed various improvement and hybridization strategies. For instance, Kong et al.⁸ proposed a novel artificial bee colony algorithm that combines cumulative binomial probability (CBABC) to balance exploration and exploitation. Farda et al.⁹ proposed a new adaptive differential evolution algorithm with multiple crossover strategy scheme (ADEMCS) to adapt to specific optimization problems. Widians et al.¹⁰ developed a hybrid ACO and GWO algorithm (ACO-GWO) to achieve an exploitation-exploration balance. Ahmed et al.¹¹ introduced the improved gray wolf optimizer (MELGWO), integrating memory mechanisms, evolutionary operators, and local search methods to boost performance. Pan et al.¹² created the dung beetle optimization algorithm guided by sine algorithm (MSADBO), merging sine algorithms with chaotic mapping and mutation operators for enhanced robustness. Su et al.¹³ proposed the hybrid hyper-heuristic whale optimization algorithm (HHWOA), combining adversarial learning and smoothing techniques to improve trajectory convergence, while Li et al.¹⁴ introduced the sand cat swarm optimization algorithm (CWXSCSO), utilizing elite dispersion and crossover strategies. Although these approaches have achieved significant results, the trade-offs in complexity and computational cost highlight the need for further research into more efficient and scalable solutions.

The Arithmetic Optimization Algorithm (AOA) is a relatively recent meta-heuristic algorithm inspired by the four basic arithmetic operations of addition, subtraction, multiplication, and division¹⁵. The AOA has gained attention due to its simplicity, minimal tuning parameters, and superior divergence rate, which enable efficient exploration of the search space and enhanced overall performance. As a result, AOA has outperformed numerous algorithms in the literature, such as PSO, GA, and DE, demonstrating its adaptability to diverse and complex optimization challenges. These strengths have led to its application in various domains, including engineering design problems¹⁶, image segmentation¹⁷, wireless sensor network deployment¹⁸, and hazard detection¹⁹. Nevertheless, the standard AOA suffers from notable weaknesses, including inadequate global exploration, poor population diversity, and susceptibility to local optima, especially in high-dimensional or multi-modal problems²⁰. Consequently, a variety of hybrid and improved variants have been proposed to enhance AOA’s search performance. For example, Kaveh et al.²¹ modified the original update structure to better balance exploration and exploitation, while Hu et al.²² incorporated neighborhood and point-set learning strategies to boost convergence speed and accuracy. Other approaches include integrating Nelder-Mead search into AOA (AOA-NM)²³, applying chaotic maps²⁴, or combining AOA with Aquila Optimizer (AO-AOA)²⁵. To provide a clearer understanding of the current state of research on AOAs, Table 1 summarizes the major strategies and applications of AOA improvements over the past two years. A comprehensive survey by Dhal et al.²⁶ offers further insights into AOA advancements.

Table 1 The research content of AOAs literature in the past two years.

According to Table 1, it is worth noting that although these hybridizations bring performance improvements, they often suffer from significant trade-offs, such as increased complexity, higher computation time, or limited effectiveness on large-scale or multi-objective problems. In light of these limitations, we propose a novel hybrid algorithm, named CDAOA, which differs from previous AOA variants in both design and purpose. Unlike other methods that apply isolated modifications or combine AOA with external metaheuristics, CDAOA employs a multi-level hybridization strategy wherein each component directly targets a specific deficiency in the original AOA. First, an improved chaotic mapping strategy is employed during initialization to enhance the population’s distribution diversity and promote better global exploration from the outset. This is distinct from general chaotic AOA variants in the literature, which often use standard maps without adaptive control or structural integration. Second, to overcome stagnation and improve escape from local optima, CDAOA introduces Cauchy perturbation to the best individual. This allows the algorithm to make occasional large jumps in the search space, enhancing its capacity to explore under-explored regions while retaining convergence focus. Lastly, the best-performing solution undergoes a tailored differential evolution process with Lévy flight mutation, which balances the depth of exploitation with controlled randomness, thereby refining solution quality without excessive parameter dependence or runtime overhead.

The contributions of this study can be outlined as follows:

• 1. An improved chaotic mapping strategy is designed to optimize the initial population. As a result, the AOA’s population diversity is enhanced and convergence rate become faster.

• 2. The Cauchy perturbation is added to adjust the position of the current solution, which enhances the global search ability and the diversity of search range.

• 3. The differential evolution operations with Lévy flight mutation factor is adopted to further enhance the quality of global best solution, which reduces the probability of AOA becoming trapped in local optima.

• 4. The performence of CDAOA outperforms its rival algorithms as well as other enhanced versions.

The subsequent sections of this paper are structured as follows. “Arithmetic optimization algorithm” presents an overview of the initial AOA. The proposed chaotic AOA with Cauchy perturbation and differential evolution algorithm is detailed in “The proposed CDAOA”. Comparative experimental outcomes are discussed in “Computational experiments”. In “Application to engineering design problems”, the practical effectiveness of CDAOA is demonstrated through its application to engineering design problems. Ultimately, “Conclusions” wraps up the paper.

Arithmetic optimization algorithm

The arithmetic optimization algorithm, proposed by Abualigah et al.¹⁵, is a newly developed intelligent optimization algorithm. The balance of this algorithm is achieved by emphasizing the precedence of mathematical operators, specifically division (D), multiplication (M), subtraction (S), and addition (A). By doing so, the algorithm efficiently seeks optimal solutions for a diverse range of optimization problems. The algorithm is primarily segmented into three components: the optimization strategy, determined by the mathematical optimizer acceleration (MOA) function section; the global search strategy, executed through multiplication and division operations; and the local search strategy, implemented via addition and subtraction operations.

The first step of the optimization process entails the creation of a random population of potential solutions, denoted as set (X). The population is generated randomly, and its mathematical representation is provided in Eq. (1).

$$\begin{aligned} X = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{x_{1,1}}}& {{x_{1,2}}}& \cdots & {{x_{1,n}}} \end{array}}\\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{x_{2,1}}}& {{x_{2,2}}}& \cdots & {{x_{2,n}}} \end{array}}\\ {\begin{array}{*{20}{c}} \vdots & {\mathrm{ } \vdots \mathrm{ }}& \vdots & {\mathrm{ } \vdots } \end{array}}\\ {\begin{array}{*{20}{c}} \vdots & {\mathrm{ } \vdots \mathrm{ }}& \vdots & {\mathrm{ } \vdots } \end{array}} \end{array}}\\ {\begin{array}{*{20}{c}} {{x_{m,1}}}& {{x_{m,2}}}& \cdots & {{x_{m,n}}} \end{array}} \end{array}} \right] \end{aligned}$$

(1)

where n is the quantity of variables to be optimized and m denotes the population size.

The elements ${x_{i,j}}\left( {i = 1 \ldots ,m;j = 1 \ldots ,n} \right)$ in the population X are generated using the Eq. (2).

$$\begin{aligned} {x_{i,j}} = L{B_j} + rand \times \left( {U{B_j} - L{B_j}} \right) \end{aligned}$$

(2)

where $L{B_j}$ and $U{B_j}$ represent the minimum bound and the maximum bound, respectively.

The solutions are confined within the limits of $L{B_j}$ and $U{B_j}$, thus confining the search process within these boundaries until the maximum iteration is reached.

MOA is a crucial function that serves as a determinant for the search method employed for population individuals. Its value is compared with a randomly generated number $r_1$, spans the range between 0 and 1. If $r_1<MOA$, the algorithm proceeds to the exploration phase, characterized as a global search. Otherwise, it transitions to the exploitation phase and carries out a local search. The mathematical model underlying MOA is detailed in Eq. (3).

$$\begin{aligned} MOA\left( {C\_Iter} \right) = MO{A_{\min }} + C\_Iter \times \left( {\frac{{MO{A_{\max }} - MO{A_{\min }}}}{{M\_Iter}}} \right) \end{aligned}$$

(3)

where $MO{A_{\min }}$ and $MO{A_{\max }}$ represent the constant values that define the initial and final values of the MOA function during each iteration. ${C\_Iter}$ stands for the current iteration count, while ${M\_Iter}$ represents the maximum iteration count.

The conceptual model of MOA based on four fundamental arithmetic operations is shown in Fig. 1. The execution of the potential solution is determined by the priority of mathematical operators. In AOA, the exploration stage involves division and multiplication expressions, while the exploitation stage follows subtraction and addition formulations. Therefore, AOA exhibits a divergent nature.

Fig. 1

The standard AOA.

During the exploration phase, individuals transition to a broader search, utilizing multiplication and division operators due to their precedence in solution selection. These operators finalize the search, updating the solution ${x_{i,j}}$ through a specified expression detailed in Eq. (4).

$$\begin{aligned} {x_{i,j}}\left( {C\_Iter + 1} \right) = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {best\left( {{x_j}} \right) \div \left( {MOP + \varepsilon } \right) \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu + L{B_j}} \right) ,}& {r_2 < 0.5} \end{array}}\\ {\begin{array}{*{20}{l}} {best\left( {{x_j}} \right) \times MOP \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu + L{B_j}} \right) ,}& {\text {otherwise}} \end{array}} \end{array}} \right. \end{aligned}$$

(4)

where $x_{i,j}$ represents the j-th position within the i-th solution, $\varepsilon$ is a fixed parameter to prevent zero, $\mu$ serves as a control parameter that governs the search processes, $r_2$ denotes a random value within the range from 0 to 1. Mop represents the math optimizer probability, with its mathematical model outlined in Eq. (5).

$$\begin{aligned} MOP\left( {C\_Iter} \right) = 1 - \frac{{{{\left( {C\_Iter} \right) }^{1/\alpha }}}}{{{{\left( {M\_Iter} \right) }^{1/\alpha }}}} \end{aligned}$$

(5)

where $\alpha$ serves as a constant parameter.

During the exploitation phase, population individuals utilize high-density addition and subtraction operators, leveraging their low precedence to effectively search for optimal values locally. Iteratively, these operators guide candidate solutions to optimal outcomes based on an update expression. Transitioning to the exploitation phase completes the search using a formula outlined in Eq. (6).

$$\begin{aligned} {x_{i,j}}\left( {C\_Iter + 1} \right) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {best\left( {{x_j}} \right) - MOP \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu + L{B_j}} \right) ,}& {{r_3} < 0.5} \end{array}}\\ {\begin{array}{*{20}{c}} {best\left( {{x_j}} \right) + MOP \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu + L{B_j}} \right) ,}& {\text {otherwise}} \end{array}} \end{array}} \right. \end{aligned}$$

(6)

where $r_3$ denotes a random value within the range from 0 to 1. For clarity, the pseudo-code of AOA is outlined in Algorithm 1.

Algorithm 1

Pseudo-code of the conventional AOA.

The proposed CDAOA

To further improve the local and global search ability of AOA with faster convergence speed, an improved AOA, called CDAOA, is proposed in this paper. First, an enhanced chaotic mapping strategy is employed to generate a high-quality initial population. Second, the position of the current solution is enhanced using random perturbations from a Cauchy distribution, leveraging its heavy-tail property to enlarge the search range and explore potential global optimal regions. Finally, within the previously identified search area, the Lévy differential evolution operator is applied to locally develop and fine-tune the current solution, balancing exploration and exploitation capabilities to further improve the quality of the solution. The subsequent subsections elaborate on the specifics of CDAOA.

An improved tent chaotic map optimization initial population

Chaotic mapping is a type of nonlinear mapping that generates random sequences. Its sensitivity to initial conditions ensures consistent production of uncorrelated encoding sequences. Among various chaotic mappings, the Tent chaotic mapping exhibits superior ergodic uniformity and a faster search speed⁵⁰, making it a highly effective tool for initializing the population due to its randomness and ergodicity. Hence, this paper introduces an improved Tent mapping for population initialization. By leveraging the randomness and regularity of Tent chaotic sequences, it enhances the diversity and uniform traversal of the population distribution. This approach effectively prevents the algorithm from falling into local optima, thus enhancing its global search capability. The mathematical representation of the Tent chaotic mapping is provided in Eq. (7).

$$\begin{aligned} {x_{i + 1}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{{{x_i}}}{\alpha }}& {0< {x_i} \le \alpha } \end{array}}\\ {\begin{array}{*{20}{c}} {\frac{{1 - {x_i}}}{{1 - \alpha }}}& {\alpha< {x_i} < 1} \end{array}} \end{array}} \right. \end{aligned}$$

(7)

where $\alpha \in \left( {0,1} \right)$ is the adjustment parameter, x denotes the initial value of the x(0). In this paper, $\alpha = 0.5$.

The Tent mapping function undergoes a Bernoulli shift transformation, which involves left-shifting the fractional part of the binary number in the interval (0, 1). This transformation facilitates efficient handling of large-scale data computations, enabling the Tent chaotic mapping function to iterate faster than the Logistic mapping function. The Bernoulli shift transformation is formally expressed in formula Eq. (8).

$$\begin{aligned} {x_{i + 1}} = \left( {2{x_i}} \right) \bmod 1 \end{aligned}$$

(8)

The Tent mapping in the interval (0, 1) generates a periodic chaotic sequence, but unstable periodic points also exist simultaneously. To avoid falling into small or unstable periodic points, an adaptive factor $rand(0,1) \times 1/N$ is introduced into the initial Tent chaotic mapping function. The optimized version is presented in Eq. (9).

$$\begin{aligned} {x_{i + 1}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{{{x_i}}}{\alpha } + rand(0,1) \times \frac{1}{N}}& {0< {x_i} \le \alpha } \end{array}}\\ {\begin{array}{*{20}{c}} {\frac{{1 - {x_i}}}{{1 - \alpha }} + rand(0,1) \times \frac{1}{N}}& {\alpha< {x_i} < 1} \end{array}} \end{array}} \right. \end{aligned}$$

(9)

where N is the number of particles within the Tent chaotic sequence. The expression after the Bernoulli shift transformation is shown in Eq. (10).

$$\begin{aligned} {x_{i + 1}} = \left( {2{x_i}} \right) \bmod 1 + rand(0,1) \times \frac{1}{N} \end{aligned}$$

(10)

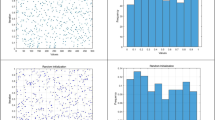
The scatter plots of the original and improved Tent mappings are shown in Fig. 2. In the Tent chaotic mapping experiment, the total number of particles is 5000. Analysis of the resulting data reveals that the original Tent mapping yields far fewer solution sets than the number of iterations, indicating a concentrated initial candidate set (Fig. 2a). Conversely, the improved Tent mapping exhibits superior iteration results, with a denser and more uniform distribution of points (Fig. 2b). This improvement is due to the adaptive factor, which avoids stationary and unstable periodic points, enhancing diversity while maintaining the chaotic mapping’s randomness, global traversal, and local regularity.

Fig. 2

Scatter plot comparison of tent chaotic mappings.

In AOA, random initialization of individuals leads to uneven population distribution, resulting in reduced accuracy and suboptimal solutions. To address this, the Tent mapping is used to improve the algorithm. The steps for initializing the population with the improved Tent chaotic mapping are as follows:

• Step 1: Randomly generate an initial value ${x_0} \in \left[ {0,1} \right]$.

• Step 2: Generate a chaotic sequence $\left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}$ of length n using Eq. (10).

• Step 3: Map the chaotic sequence to each dimension of the search space.

• Step 4: The mapped values are used as the initial candidate solutions, forming the initial population.

The model initialized by the Tent chaotic mapping is provided in Eq. (11).

$$\begin{aligned} x = {x_{\min }} + \delta \cdot \left( {{x_{\max }} - {x_{\min }}} \right) \end{aligned}$$

(11)

where $x_{\min }$ and $x_{\max }$ denote the minimum and maximum boundaries for the independent variables, respectively. $\delta$ represents a chaotic factor produced by the Tent map function.

Cauchy perturbation to enhance exploration

The Cauchy perturbation stems from the Cauchy distribution. The Cauchy distribution is a continuous probability distribution with a higher probability density at the origin. Its tails extend outward, generating random numbers that are further from the origin. This property allows it to perturb updates to the optimal solution, ensuring algorithmic diversity. In AOA, the update of each individual is influenced by the best individual from the previous iteration. Consequently, the algorithm often converges prematurely to local optima during the iterative process. Therefore, we address the above issue by combining Cauchy perturbation with AOA. The probability density function of the one-dimensional Cauchy distribution is presented in Eq. (12).

$$\begin{aligned} f\left( {x,\gamma ,\theta } \right) = \frac{1}{\pi }\left( {\frac{\gamma }{{{\gamma ^2} + {{\left( {x - \theta } \right) }^2}}}} \right) \end{aligned}$$

(12)

where $\theta$ represents the location parameter, and $\gamma$ denotes the scale parameter.

when $\gamma = 1,\theta = 0$, the specific formula for the probability density function is given in Eq. (13).

$$\begin{aligned} Cauchy(0,1) = \frac{1}{\pi }\left( {\frac{1}{{{x^2} + 1}}} \right) \end{aligned}$$

(13)

Subsequently, the Cauchy operator was used to perturb the current optimal individual, and the calculation formula was updated according to Eq. (14), enhancing AOA’s capability to escape from local optima.

$$\begin{aligned} x_{i,j}^{t + 1} = x_{best,j}^t + Cauchy(0,1) \oplus x_{best,j}^t \end{aligned}$$

(14)

After Cauchy perturbation, the fitness value of an individual is recalculated and compared with the current optimal. The individual with the best solution is chosen for the subsequent update.

Differential evolution with Lévy flight to strengthen exploitation

In AOA, DE can enlarge individual’s search range by means of cross-mutation selection so as to find the optimal solution better. Furthermore, the long jump property of Lévy flight accelerates the convergence rate, allowing the algorithm to approach the global optimal solution faster. The process is described as follows.

Differential evolution (DE), proposed by Storn et al.⁵¹, is a heuristic optimization algorithm with powerful global and local search ability. DE consists of three operators, i.e., mutation , crossover and selection. In this research, we utilized these three operators to improve the quality of the best solution of AOA. The detailed procedure is outlined as follows.

• Mutation

  The mutation operator of “DE/current-to-best/1” is adopted to make a mutation on the best solution at the current iteration to generate a experimental solution according to Eq.(15).

  $$\begin{aligned} V_{i,j}^t = X_{i,j}^t + F(X_{best,j}^t - X_{i,j}^t) + F\left( {X_{r1,j}^t - X_{r2,j}^t} \right) \end{aligned}$$

  (15)

  where $X_{best,j}^t$ denotes the optimal individual within the current generation t; ${r_1}$ and ${r_2}$ are two distinct integer number in [1, N]. F is the mutation factor controlling local search range. In previous studies, F is set to a fixed number or a random value between 0 and 1, which limits the search range of mutation operator. In this paper, the Lévy flight⁵² distribution is used to generate mutation factor to enlarge the search range. The Lévy flight distribution is shown in Eq. (16).

  $$\begin{aligned} Levy(s) \sim {\left| s \right| ^{ - 1 - \beta }},\quad 0 < \beta \le 2 \end{aligned}$$

  (16)

  where s denotes the flight step and $\beta$ is an exponent. s can be calculated using Eq. (17).

  $$\begin{aligned} s = \frac{\mu }{{{{\left| v \right| }^{\frac{1}{\beta }}}}},\quad \mu \sim N\left( {0,\sigma _\mu ^2} \right) ,v \sim N\left( {0,\sigma _v^2} \right) \end{aligned}$$

  (17)

  where $\beta$ is set to 1.5, and $\mu$ and v conform to the Gaussian distribution. $\sigma _\mu$ and $\sigma _v$ can be represented by Eq. (18).

  $$\begin{aligned} {\sigma _\mu } = {\left\{ {\frac{{\Gamma \left( {1 + \beta } \right) \cdot \sin \left( {\pi \beta /2} \right) }}{{\beta \cdot \Gamma \left[ {\left( {1 + \beta } \right) /2} \right] \cdot {2^{\frac{{\left( {\beta - 1} \right) }}{2}}}}}} \right\} ^{\frac{1}{\beta }}},{\sigma _v} = 1 \end{aligned}$$

  (18)

  where $\Gamma$ represents the standard Gamma function. The mutation operator with Lévy flight mutation factor can be expressed in Eq. (19).

  $$\begin{aligned} V_{i,j}^t = X_{i,j}^t + 0.5LR \cdot (X_{best,j}^t - X_{i,j}^t) + 0.5 LR \cdot ( {X_{r1,j}^t - X_{r2,j}^t}) \end{aligned}$$

  (19)

  where LR denotes a factor generated according to the Lévy distribution. Compared with the Gaussian distribution, the Lévy distribution has “heavy-tailed” pattern. The random number generated according to Lévy distribution exhibits long-distance jumping characteristic, which can help the algorithm escape from local optimum.

• Crossover

  To further enhance the quality of generated experimental solution, a crossover operation is followed, which is expressed as Eq.(20).

  $$\begin{aligned} U_{i,j}^t = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {V_{i,j}^t,}& {\mathrm{ }rand \le CR\,\mathrm{{ or }}\,j = {j_{rand}}} \end{array}}\\ {\begin{array}{*{20}{l}} {X_{i,j}^t\mathrm{{, }}}& {\mathrm{ }\text {otherwise}} \end{array}} \end{array}} \right. \end{aligned}$$

  (20)

  where $CR \in \left[ {0,1} \right]$ represents the crossover probability factor, ${j_{rand}} \in \left[ {1,2,...d} \right]$ denotes a random number.

• Selection

  Finally, we determine the final best solution using selection operator, which is expressed in Eq. (21).

  $$\begin{aligned} X_{best}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {X_{best}^t}& {f\left( {X_{best}^t} \right) \le f\left( {U_{i}^t} \right) } \end{array}}\\ {\begin{array}{*{20}{l}} {U_{i}^t}& \,\,{f\left( {X_{best}^t} \right) > f\left( {U_{i}^t} \right) } \end{array}} \end{array}} \right. \end{aligned}$$

  (21)

The structure of Lévy-DE operator based on “DE/current-to-best/1” is illustrated by the pseudo-code in Algorithm 2.

Algorithm 2

Pseudo-code of the Lévy-DE.

For clarity, the pseudo-code of the CDAOA is provided in Algorithm 3. The CDAOA flowchart is depicted in Fig. 3.

Algorithm 3

Pseudo-code of the CDAOA

Fig. 3

Flowchart of the CDAOA.

Computational complexity of CDAOA

The computational complexity of CDAOA depends on the population size N, the problem dimension D, and the number of iterations T. The initialization process based on chaotic mapping has a complexity of $O(N \times D)$, which is comparable to that of the original AOA in terms of asymptotic behavior. Although the exact complexity of fitness evaluation depends on the specific optimization problem, it is generally assumed to be proportional to D, and thus is included in the overall analysis. During each iteration, CDAOA performs operations such as Cauchy perturbation, Lévy-based differential evolution, and selection, all of which are applied to each individual across D dimensions. Therefore, the total time complexity of the proposed CDAOA algorithm can be expressed as $O(N \times D \times T)$. This complexity is comparable to that of other population-based metaheuristic algorithms.

Computational experiments

In this section, we comprehensively demonstrate the effectiveness of CDAOA from three aspects. First, the CDAOA is compared with AOA variants and other advanced meta-heuristic algorithms on 16 benchmark functions. Second, the superiority of CDAOA is verified through Wilcoxon signed rank sum test and Friedman mean rank test. Finally, the CEC 2019 and CEC 2021 test functions were employed to validate the performance of CDAOA in a highly complex environment. All the algorithms were programmed using MATLAB (R2020b) programming language and run on a computer equipped with a 11th Gen Intel(R) Core(TM) i7-1165G7 CPU and a 16G RAM, operating under Windows 10.

Improved strategy effectiveness test

CDAOA employs various tactics to enhance the efficiency of AOA. To evaluate the effectiveness of each improvement strategy, the AOA with improved chaotic mapping (ICAOA) and the NOA with Cauchy perturbation (CPAOA), and the NOA with DE operators with Lévy flight mutation factor (LDAOA) are also implemented for the purpose of comparison on the Goldstein-Price function. To ensure a fair comparison, the size of population is set to 30 and the maximum iteration count is set to 200. All the algorithms independently run 30 times.

$$\begin{aligned} \begin{array}{l} f\left( x \right) = \left[ {1 + {{\left( {{x_1} + {x_2} + 1} \right) }^2}\left( {19 - 14{x_1} + 3x_1^2 - 14{x_2} + 6{x_1}{x_2} + 3x_2^2} \right) } \right] \\ \times \left[ {30 + {{(2{x_1} - 3{x_2})}^2}\left( {18 - 32{x_1} + 12x_1^2 + 48{x_2} - 36{x_1}{x_2} + 27x_2^2} \right) } \right] \end{array} \end{aligned}$$

(22)

The Goldstein-Price function has multiple local minima and only one global minimum. Locating the global optimum of the Goldstein-Price function poses a challenge. Therefore, it is widely employed to assess the performance of optimization algorithms. Table 2 lists the optimization results of Goldstein-Price function found by AOA, LDAOA, ICAOA, CPAOA and CDAOA, in terms of best, mean and standard deviation (Std).

Table 2 The results of each improvement strategy impact.

According to Table 2, although ICAOA incorporates chaotic initialization, it performs poorly compared to the original AOA. It increases the best value by 168.99%, the mean value by 361.34%, and the standard deviation by 308.04%, indicating severe instability and degradation. This suggests that chaotic mapping alone is insufficient to improve AOA performance and may even introduce undesirable randomness. CPAOA, which includes only the Cauchy perturbation strategy, maintains the best value at 3.00 (an 90.00% improvement over AOA), but the mean and standard deviation are only reduced by 81.48% and 37.83%, respectively. LDAOA, enhanced with Lévy-based DE, also achieves a best value of 3.00, improves the mean by 81.90%, and reduces the standard deviation by 70.00% compared to AOA, reflecting stronger stability than CPAOA. Finally, the full version of the proposed CDAOA, which integrates all three strategies, yields the most remarkable performance improvements. Compared to the original AOA, CDAOA reduces the best value by 90.00%, the mean value by 91.20%, and the standard deviation by 99.80%. These results confirm that the hybrid integration of Tent chaotic mapping, Cauchy perturbation, and Lévy-based differential evolution delivers substantial gains in both optimization accuracy and robustness.

Description of benchmark functions

The adopted 16 test functions are described in Table 3. These functions are roughly categorized into unimodal and multimodal functions. Functions ${f_1} - {f_9}$ are unimodal functions, featuring a single global minimum with no local minima, which are usually utilized to assess the global search performance and convergence speed of algorithms. For these unimodal functions, ${f_1}$, ${f_3}$, ${f_4}$, ${f_5}$, and ${f_6}$ have larger search space, providing a good way to evaluate the convergence speed of algorithms. The gradient distribution of ${f_2}$, ${f_8}$ and ${f_9}$ exhibit a decreasing trend, which is beneficial to comprehensively assess the global search capability of algorithms. ${f_7}$ can more effectively test algorithm performance because it’s search space is smaller. ${f_{10}} - {f_{16}}$ are multimodal functions characterized by multiple local optima. They are widely adopted to evaluate both the convergence accuracy and the capability of algorithms to steer clear of local optima. It’s significant to point out that the Rosenbrock function (${f_{10}}$) poses a challenging optimization problem due to its special multimodal nature and the narrow valley that contains the global minimum, thereby rendering the task of locating the global minimum a formidable one.

Table 3 Benchmark functions.

Comparative algorithm and parameter settings

To better illustrate the superior performance of the proposed CDAOA, five advanced meta-heuristic algorithms and five AOA variants are selected as comparable algorithms. They are SWO⁴, EVO⁵³, KOA⁵⁴, GRO⁵⁵, GOOSE², as well as AOA and its variant LAOA⁴⁸, IAOA⁵⁶, COAOA⁴⁷, CAOA⁴¹. During the experiment, for all mentioned AOAs, the control parameters are set as $\alpha = 5$ and $\mu = 0.499$. The parameters $MO{A_{\max }}$ and $MO{A_{\min }}$ are 1 and 0.2, respectively. In the case of other comparison algorithms, their control parameter values were set to be the same as those in the referenced papers. To guarantee a equitable comparison, the population size and maximum iterations for all referenced algorithms were set to 30 and 1000, respectively. All the algorithms independently run 30 times.

Experimental results and discussion

The text outcomes of the 30-dimensional benchmark test functions among the 30 runs are statistically reported in Table 4, including the Best, Mean, and Std values. The Best indicates the minimum function value attained by each algorithm during 30 separate trials, which can assess algorithm’s convergence accuracy. The Mean represents the average function value attained by each algorithm during 30 separate trials, which can assess algorithm’s optimization capability. The Std shows the standard deviation attained by each algorithm during 30 separate trials, which can evaluate algorithm’s stability. In this paper, superior algorithm performance is indicated by smaller values of the Best, Mean, and Std. In Table 4, the optimal values of the Best, Mean and Std are emphasized in bold. According to Table 4, CDAOA excels over the other referenced algorithms on all 16 benchmark test functions.

Table 4 Comparative results of CDAOA with other algorithms on 16 benchmark functions.

For ${f_1}$, ${f_3}-{f_7}$, ${f_{10}}$, ${f_{15}}$ the Best, Mean and Std obtained by CDAOA are smaller than those by the other referenced algorithms. In the case of ${f_9}$, the STD obtained by the CDAOA was equal to that obtained by KOA. For ${f_2}$, ${f_8}$, ${f_{14}}$ and ${f_{16}}$, AOA and its variants can achieve better Mean than the other five algorithms. AOA, LAOA, CAOA, IAOA, COAOA, SWO, GRO and CDAOA approach the global minimum 0 on ${f_{11}}$. AOA, LAOA, CAOA, IAOA, COAOA, CDAOA and SWO can offer better Mean on ${f_{12}}$. SWO, GRO and CDAOA outperform the other eight algorithms on ${f_{13}}$ in terms of Mean and STD. In summary, AOA, LAOA, CAOA, IAOA and COAOA can get the optimal Mean on five (i.e. ${f_2}$, ${f_8}$, ${f_{11}}$, ${f_{12}}$, ${f_{14}}$ and ${f_{16}}$) functions, SWO can get the optimal Mean on ${f_{11}}$, ${f_{12}}$, and ${f_{13}}$ functions, and GRO can get the optimal Mean on ${f_{11}}$ and ${f_{13}}$ functions. It is surprised that CDAOA can get the optimal Mean on 16 functions. Notably, the best values of CDAOA is superior to all other algorithms. Moreover, CDAOA exhibits a more robust and stable comprehensive search capability compared to the other ten algorithms. It should be noted that GOOSE cannot compete with other ten algorithms on all functions. Evidently, CDAOA exhibits a superior global search capability compared to AOA, LAOA, CAOA, IAOA, COAOA, SWO, EVO, GRO, KOA and GOOSE.

Algorithm rank analysis

The Friedman mean rank test, a popular statistical tool in optimization, has been extensively utilized to evaluate the performance of various optimization algorithms. In this paper, the optimal solutions achieved by CDAOA and other competing algorithms across 30 independent runs were evaluated adopting the Friedman Mean Rank Test. Table 5 compares the ranking outcomes of CDAOA and other algorithms across 16 benchmark functions. Fig. 4 displays the Friedman mean ranks obtained by these algorithms across 16 benchmark functions. According to the Friedman Mean Rank Test findings presented in the Table 5 and Fig. 4, it is evident that the Friedman mean ranks of CDAOA are all smaller than other algorithms on all functions. This phenomenon illustrates the CDAOA comprehensively ranks first among all the algorithms.

Table 5 The Friedman mean rank test results for 16 benchmark functions.

Fig. 4

The Friedman mean ranks derived from the applied algorithms across 16 benchmark functions.

Statistical significance analysis

The Wilcoxon signed-rank test is widely employed for comparing the performance of various optimization algorithms. “R${^ + }$” signifies the positive rank sum, while“R${^ - }$” denotes the negative rank sum. “$+$” and“−” indicate superior and inferior performance compared to other algorithms, respectively. “$=$” denotes that the CDAOA algorithm shows no significant difference compared to other algorithms. Tables 6 and 7, as well as Fig. 5, present the experimental findings of CDAOA and other referenced algorithms from the conducted Wilcoxon signed-rank test under a significance level $\alpha = 0.05$. From Tables 6 and 7, we can see that the proposed CDAOA outperforms AOA, LAOA, CAOA, IAOA and COAOA on 10 functions, and show no difference on 6 functions. Notably, CDAOA outperforms GOOSE, EVO and KOA on all the 16 functions. In addition, CDAOA is superior to SWO on 13 functions, and to GRO on 14 functions, respectively.

Table 6 The Wilcoxon signed rank test results between CDAOA and other improved versions of AOA.

Table 7 The Wilcoxon signed rank test results between CDAOA and other intelligent algorithms.

Fig. 5

The Wilcoxon signed rank test results on 16 benchmark functions.

From the statistical viewpoint, although several algorithms achieve identical optimal values on certain functions, the proposed CDAOA demonstrates overall superior performance compared to other referenced algorithms, as evidenced by the consistent advantages shown in both the Wilcoxon signed-rank and Friedman mean rank tests.

Convergence performance analysis

For this section, we aim to analyze the convergence performance of CDAOA by comparing its convergence curves with those achieved by the AOA, LAOA, CAOA, IAOA and COAOA on the 16 benchmark functions, as illustrated in Figs. 6 and 7. The convergence curve clearly illustrates the convergence speed and accuracy of various algorithms in solving the benchmark functions. From Fig. 6, it can be seen that CDAOA achieves faster convergence compared to other algorithms on functions $f_3$, $f_5$ and $f_7$. For functions $f_1$, $f_4$ and $f_6$, the convergence speed of CDAOA is slower than other algorithms in the early phase, but faster than other algorithms in the later phase. For functions $f_2$ and $f_8$, the difference in convergence speed of CDAOA compared to other algorithms is relatively small. Nonetheless, it still outperforms the alternatives. From Fig. 7, it is evident that CDAOA shows a near-linear iteration curve in function $f_{16}$, while other algorithms are trapped in local optima. For functions $f_9$, $f_{13}$ and $f_{15}$, one can see that CDAOA converges faster than other AOA variants, and it converges to better solution. However, many other algorithms fall into local optimum and exhibit premature convergence. For function $f_{10}$, CDAOA demonstrates the fastest convergence speed among other AOA variants. AOA, LAOA, CAOA, IAOA and COAOA all become trapped in local optima. For the other functions, the convergence speed of CDAOA is not the fastest but is also not the slowest among the other AOA variants. In summary, for more complex optimization problems, CDAOA not only discovers more optimal solutions but also demonstrates excellent convergence characteristics. The reason is that other AOA variants tend to fall in local optima, leading to premature convergence and preventing further exploration of better solutions. In contrast, CDAOA employs a novel optimization strategy that enhances the search for more optimal solutions within the search space. This strategy also achieves a more effective balance between exploration and exploitation.

Fig. 6

Convergence curves of ${f_1}-{f_8}$.

Fig. 7

Convergence curves of ${f_9}-{f_{16}}$.

Runtime comparison

To verify the running speed of CDAOA, the average runtime of 30 independent runs of CDAOA was recorded and is shown in Table 8, with time units in seconds (s). From Table. 8, the ranking order of average runtime for 11 algorithms is GOOSE, COAOA, CAOA, AOA, LAOA, IAOA, SWO, KOA, GRO, CDAOA, and EVO, with GOOSE having the shortest average runtime. It can be observed that the proposed algorithm has a longer run time. This is due to the more complex computational process of CDAOA, which involves deeper searches or more refined optimization strategies. However, despite the longer run time, the algorithm achieves the best solution performance, indicating its superiority in finding optimal solutions. The longer run time may be attributed to more thoroughly exploring the solution space in high-dimensional or complex problems, resulting in significant improvements in accuracy or global optimality.

Table 8 Comparison of the average runtime of CDAOA with other algorithms on 16 benchmark functions.

Exploration and exploitation analysis

Effective exploration and exploitation are crucial components of any proposed algorithm. Fig. 8 illustrates the exploration and exploitation analysis of the referenced algorithms on the 8 representative benchmark functions, $f_1$, $f_5$, $f_6$ and $f_8$ are unimodal functions, $f_{11}$,$f_{12}$,$f_{14}$ and $f_{16}$ are multimodal functions. According to Fig. 8, it is evident that the exploration curve of CDAOA starts relatively high in the early stages and gradually decreases as iterations progress. Meanwhile, the exploitation curve of CDAOA begins relatively low and increases gradually, reaching higher levels as the algorithm approaches convergence. This demonstrates that compared to other competing algorithms, CDAOA achieves a good balance between global exploration and local exploitation, potentially leading to more effective discovery of global optimal solutions. In contrast, we observe that the exploration rate of SWO remains relatively high in the later stages, indicating that the algorithm may get stuck in local optima or fail to fully utilize its exploration capabilities.

Fig. 8

Exploration and exploitation plots of CDAOA against other algorithms.

Diversity analysis

To further verify the diversity of CDAOA, the diversity analysis is performed within this section. The diversity equation refers to Zhang et al.⁵⁷. The Branin function was selected to analyze the diversity of CDAOA and other improved versions. The Branin function has multiple local optima and one global optimum, which allows different optimization algorithms to demonstrate their capabilities in exploring both local and global solutions. Therefore, the function can better evaluate the algorithm’s performance. The mathematical model is depicted in Eq.(23). The diversity analysis of each algorithm are exhibited in Fig. 9.

$$\begin{aligned} \begin{array}{l} f\left( x \right) = {\left( {{x_2} - \frac{{5.1}}{{4{\pi ^2}}}x_1^2 + \frac{5}{\pi }{x_1} - 6} \right) ^2}+ 10\left( {1 - \frac{1}{{8\pi }}} \right) \cos {x_1} + 10 \end{array} \end{aligned}$$

(23)

where ${x_1} \in \left[ { - 5,10} \right]$ and ${x_2} \in \left[ { 0,15} \right]$ are variables.

Fig. 9

Diversity analysis curves of 5 algorithms on the Branin function.

From Fig. 9, CDAOA exhibits higher diversity in the early stages, which gradually decreases and begins to rise again after approximately 500 iterations, ultimately showing a sustained increase to a high diversity level. AOA experiences an initial decline in diversity, stabilizing at a lower level around 600 iterations, indicating convergence to a stable solution with slow recovery of diversity. CAOA initially shows significant fluctuations but later exhibits a trend similar to AOA, with some recovery in diversity towards moderate levels. IAOA demonstrates relatively stable diversity throughout, maintaining at a lower level without significant improvement in later stages, indicating lower diversity. LAOA initially decreases in diversity, then gradually recovers after 600 iterations and stabilizes, although the final diversity level remains relatively low despite some improvement. COAOA shows large fluctuations in diversity, similar to CDAOA in trend, with noticeable recovery in later stages, but its final diversity level is lower than that of CDAOA. Therefore, we conclude that CDAOA demonstrates superior diversity compared to other algorithms, mainly due to its enhanced population diversity through improved chaotic mapping.

Experimental comparisons on IEEE CEC 2019

The CEC 2019 test functions were chosen for additional testing to further evaluate the effectiveness and stability of the CDAOA. The mean value and Std are presented in Table 9. Table 9 further presents the statistical results of the Friedman ranking “Rank”. The optimal outcomes achieved by the eleven algorithms are highlighted in bold. Fig. 10 illustrates the behavior of some CEC 2019 functions and compares the convergence between CDAOA and other referenced algorithms. All the algorithms independently run 30 times.

Table 9 Comparative results of CDAOA with other compared algorithms on CEC 2019 test functions.

Fig. 10

Convergence curves of partial CEC 2019 functions.

According to the experimental outcomes outlined in Table 9, the proposed CDAOA approach stands out prominently due to its lowest average in 50% of functions (CEC01, CEC02, CEC03, CEC09 and CEC010), thus securing the top position. Following closely is the GRO (CEC04, CEC05 and CEC08), leading in 30% of functions. KOA and SWO have the lowest Mean in CEC06 and CEC07, respectively. Notably, the proposed CDAOA outperforms AOA and utilizes its advantages more effectively than other improved versions of AOA to broaden its search domain and reach optimal or near-optimal values. This highlights the ability of CDAOA to solve optimization problems effectively. In addition, in CEC04, CEC05, CEC06, CEC07 and CEC08, although CDAOA did not achieve the lowest average, its results surpass all improved versions of AOA. This performance demonstrates the effectiveness of enhanced algorithm strategies.

Furthermore, the Std test results in Table 9 encompassed a comprehensive assessment to gauge the stability and dispersion of data across the algorithms. Within this framework, the CDAOA consistently demonstrated strong performance across the majority of functions. Nevertheless, exceptions arose in instances such as CEC04 and CEC05, where stability exhibited a slight decrease.

From Fig. 10, it can be seen that the iteration curve of CDAOA is relatively smooth, indicating that it can converge stably to a solution during the optimization process without oscillating or exhibiting unstable behavior in the search space.

In conclusion, the tests conducted have provided comprehensive validation of the efficacy of the proposed CDAOA in this paper. While there may not be a stark variance in convergence accuracy across certain functions compared to other referenced algorithms, there has been a notable enhancement in algorithm performance when compared to AOA. Moreover, CDAOA exhibits a more robust and stable comprehensive search capability compared to the other ten algorithms.

Experimental comparisons on IEEE CEC 2021

The performance of CDAOA was further evaluated using the CEC 2021 test function, which include 10 benchmark functions: one unimodal, three basic, three hybrid, and three composite functions. The dimension of all test functions is 10, and the search space is [-100, 100]. CDAOA was compared with other state-of-the-art methods including SHADE (first ranked non-CMA-ES variant of IEEE CEC 2013)⁵⁸, L-SHADE (winner of CEC 2014 competition)⁵⁹, QMESSA, MELGWO, MSADBO and HHWOAA. The mean value and Std are presented in Table 10. The optimal outcomes achieved by the seven algorithms are highlighted in bold. Fig. 11 illustrates the behavior of four representative CEC 2021 functions and compares the convergence between CDAOA and other referenced algorithms. All the algorithms independently run 30 times.

Table 10 Comparative results of CDAOA with other compared algorithms on CEC 2021 test functions.

Fig. 11

Convergence curves of partial CEC 2021 functions.

From the analysis in Table 10, it is clear that CDAOA demonstrates superior performance compared to other algorithms, both in terms of the average and STD values across the ten functions. Although CDAOA produces the same value of 0 on function F8 as algorithms QMESSA, MELGWO, and MSADBO, it consistently outperforms other algorithms in other functions. This suggests that while its performance may be comparable to these algorithms in certain isolated cases, such as CEC08, CDAOA maintains an overall superior performance in terms of both average and standard deviation values for the majority of test functions. This highlights the algorithm’s robustness and reliability in achieving optimal results across diverse test cases.

As shown in Fig. 11a, CDAOA is relatively slow in the initial phase and faster in the final phase. However, CDAOA convergent to further more optimal solution and the other algorithms falls into local optimal solution. Based on Fig. 11c,d, it is evident that CDAOA not only converges more rapidly than other algorithms but also consistently reaches a superior solution. In contrast, several competing algorithms demonstrate premature convergence, becoming trapped in local optima, which hampers their ability to explore more optimal solutions. This underscores CDAOA’s advantage in balancing exploration and exploitation, thereby avoiding early stagnation during optimization. For Fig. 11b, while CDAOA does not exhibit the fastest convergence speed compared to GMESSA, it also does not rank among the slowest compared to other algorithms. Overall, CDAOA demonstrates excellent optimization capabilities, though at the expense of some convergence speed. This trade-off highlights the well-known “no free lunch” theorem in optimization, which suggests that no algorithm can excel in every aspect without some compromises. Thus, CDAOA strikes a balance between efficiency and solution quality, affirming its effectiveness in solving complex problems.

Application to engineering design problems

To further verify its feasibility, CDAOA is applied to solve five constrained engineering design problems and is contrasted with various optimization methods such as GSA⁶⁰, GWO⁶¹, WOA⁶², HHO⁶³, CSA⁶⁴, SO⁶⁵, DMO⁶⁶, TSA⁶⁷, GJO⁶⁸, AO⁶⁹, and CPSOGSA⁷⁰, which were commonly used as effective solutions for addressing various practical engineering design problems.

Case I: pressure vessel design

The construction of pressure vessels is an important issue in engineering design, as it involves creating structures capable of withstanding internal pressure. The objective of this problem is to achieve the minimization of overall costs, incorporating expenses for materials, fabrication and welding. The diagram illustrating the engineering design of the pressure vessel is presented in Fig. 12. The design parameters include the shell’s thickness $T_s (x_1)$, the dome’s thickness $T_h (x_2)$, the radial extent from the center to the interior boundary $R (x_3)$ and the axial extent of the cylindrical section $L (x_4)$. The mathematical representation is shown in Eq. (24).

$$\begin{aligned} \min f\left( x \right) = 0.6224{x_1}{x_3}{x_4} + 1.7781{x_2}x_3^2 + 3.1661x_1^2{x_4} + 19.84x_1^4{x_3} \end{aligned}$$

(24)

where the constraints g(x) are presented in Eq. (25).

$$\begin{aligned} \begin{array}{l} {g_1}\left( x \right) = - {x_1} + 0.0193{x_3} \le 0\\ {g_2}\left( x \right) = - {x_2} + 0.00954{x_3} \le 0\\ {g_3}\left( x \right) = - \pi x_3^2 - \frac{{4\pi x_3^3}}{3} + 1296000 \le 0\\ {g_4}\left( x \right) = {x_4} - 240 \le 0\\ 0 \le {x_1} \le 99,0 \le {x_2} \le 99,10 \le {x_3} \le 200,10 \le {x_4} \le 20 \end{array} \end{aligned}$$

(25)

Fig. 12

Pressure vessel design model.

Table 11 Optimal pressure vessel design results.

A comparison of the outcomes derived from the twelve algorithms is summarized in Table 11. According to the findings presented in Table 11, CDAOA yields the most cost-effective design scheme among the referenced algorithms. It proves that CDAOA exhibits superior performance in addressing pressure vessel design optimization issues.

Case II: tension/compression spring design

The tension/compression spring design refers to the process of designing springs to withstand tension or compression forces. The aim of this issue is to optimize the volumetric size of helical springs under constant tensile/compressive loads. The diagram illustrating the engineering design of the tension/compression spring is presented in Fig. 13. The design parameters include the spring wire diameter $W (x_1)$, spring outer diameter $O (x_2)$ and coil count of the spring. $C (x_3)$. The mathematical representation is presented in Eq. (26).

$$\begin{aligned} \min f\left( x \right) = \left( {{x_3} + 2} \right) {x_2}x_1^2 \end{aligned}$$

(26)

where the constraints g(x) are illustrated in Eq. (27).

$$\begin{aligned} \begin{array}{l} {g_1}\left( x \right) = 1 - \frac{{x_2^3{x_3}}}{{71785x_1^4}} \le 0\\ {g_2}\left( x \right) = \frac{{4x_2^2 - {x_1}{x_2}}}{{12566\left( {x_1^3{x_2} - x_1^4} \right) }} + \frac{1}{{5108x_1^2}} - 1 \le 0\\ {g_3}\left( x \right) = 1 - \frac{{140.45{x_1}}}{{x_2^2{x_3}}} \le 0\\ {g_4}\left( x \right) = \frac{{{x_1} + {x_2}}}{{1.5}} - 1 \le 0\\ 0.05 \le {x_1} \le 2,0.25 \le {x_2} \le 1.3,2 \le {x_3} \le 15 \end{array} \end{aligned}$$

(27)

Fig. 13

Tension/compression spring design model.

Table 12 Optimal tension/compression spring design results.

A comparative analysis of the outcomes derived from the twelve algorithms is presented in Table 12. According to the findings presented in Table 12, CDAOA proves to be notably more efficient than the other eleven algorithms when it comes to optimizing tension/compression spring design issues. The best solution of CDAOA is 0.012665. CDAOA aims to minimize the gravitational effects on this issue within specified constraints. The empirical findings additionally demonstrate that CDAOA excels beyond other methods regarding convergence accuracy and effectiveness for addressing tension/compression spring design problems.

Case III: welded beam design

Designing a welded beam involves creating a beam or structure for utilization in welded connections. The aim of this task is to reduce manufacturing costs to the minimum within specific constraints. The diagram depicting the engineering design of the welded beam is depicted in Fig. 14. The design parameters include the breadth $h (x_1)$, extent $l (x_2)$, profundity $d (x_3)$, and cross-sectional thickness $b (x_4)$. The constrains encompass normal stress $\tau$, critical load capacity of the bar $P_c$, displacement at the beam’s end $\delta$, and flexural stress within the beam $\sigma$. The mathematical representation is illustrated in Eq. (28).

$$\begin{aligned} \min f\left( x \right) = 1.10471x_1^2{x_2} + 0.04811{x_3}{x_4}({x_2} + 14) \end{aligned}$$

(28)

where the constraints g(x) are provided in Eq. (29).

$$\begin{aligned} \begin{array}{l} {g_1}\left( x \right) = \tau \left( x \right) - {\tau _{\max }} \le 0\\ {g_2}\left( x \right) = \sigma \left( x \right) - {\sigma _{\max }} \le 0\\ {g_3}\left( x \right) = \delta \left( x \right) - {\delta _{\max }} \le 0\\ {g_4}\left( x \right) = {x_1} - {x_4} \le 0\\ {g_5}\left( x \right) = P - {P_c}\left( x \right) \le 0\\ {g_6}\left( x \right) = 0.125 - {x_1} \le 0\\ {g_7}\left( x \right) = 1.10471x_1^2 + 0.04811{x_3}{x_4}\left( {14 + {x_2}} \right) - 5 \le 0\\ 0.1 \le {x_1} \le 2,0.1 \le {x_2} \le 10,0.1 \le {x_3} \le 10,0.1 \le {x_4} \le 2 \end{array} \end{aligned}$$

(29)

where

$\tau \left( x \right) = \sqrt{{{\left( {{\tau ^{'}}} \right) }^2} + 2{\tau ^{'}}{\tau ^{''}}\frac{{{x_2}}}{{2R}} + {{\left( {{\tau ^{''}}} \right) }^2}} ,\quad {\tau ^{'}} = \frac{P}{{\sqrt{2} {x_1}{x_2}}},\quad {\tau ^{''}} = \frac{{MR}}{J}$,

$M = P\left( {L + \frac{{{x_2}}}{2}} \right) ,\quad R = \sqrt{\frac{{x_2^2}}{4} + {{\left( {\frac{{{x_1} + {x_3}}}{2}} \right) }^2}},\quad J = 2\sqrt{2} {x_1}{x_2} {\frac{{x_2^2}}{4} + {{\left( {\frac{{{x_1} + {x_3}}}{2}} \right) }^2}}$,

$\sigma \left( x \right) = \frac{{6PL}}{{{x_4}x_3^2}},\delta \left( X \right) = \frac{{6P{L^3}}}{{Ex_3^2{x_4}}},\quad {P_c}\left( x \right) = \frac{{4.013E\sqrt{x_3^2x_4^6} }}{{{L^2}}}\left( {1 - \frac{{{x_3}}}{{2L}}\sqrt{\frac{E}{{4G}}} } \right) ,$

$P = 6000lb,L = 14ln,\,{\delta _{\max }} = 0.25ln,\,E = 30 \times {10^6}psi$,

$G = 12 \times {10^6}psi,\,{\tau _{\max }} = 13600psi,\,{\sigma _{\max }} = 30000psi$

Fig. 14

Welded beam design model.

Table 13 Optimal welded beam design results.

A comparative analysis of the outcomes derived from the twelve algorithms is presented in Table 13. According to the findings presented in Table 13, CDAOA achieves the best design scheme with the lowest cost among the referenced algorithms. It proves that CDAOA also exhibits superior performance in addressing welded beam design problems.

Case IV: hydro-static thrust bearing design problem

The design problem of hydrostatic thrust bearings involves designing and optimizing them to meet specific engineering requirements. These bearings are typically used to support rotating mechanical components such as turbines, centrifugal compressors, etc., to provide support and reduce friction. The diagram depicting the engineering design of the hydro-static thrust bearing is presented in Fig. 15. The design parameters include the bearing step radius $R(x_1)$, the recess radius $R_0(x_1)$, viscosity $\mu ({x_3})$, and flow rate $Q(x_4)$. The mathematical representation is provided in Eq. (30).

$$\begin{aligned} \min f\left( x \right) = \frac{{Q{P_0}}}{{0.7}} + {E_f} \end{aligned}$$

(30)

where the constraints g(x) are outlined in Eq. (31).

$$\begin{aligned} \begin{array}{l} {g_1}\left( x \right) = W - {W_s} \ge 0\\ {g_2}\left( x \right) = {P_{\max }} - {P_0} \ge 0\\ {g_3}\left( x \right) = \Delta {T_{\max }} - \Delta T \ge 0\\ {g_4}\left( x \right) = h - {h_{\min }} \ge 0\\ {g_5}\left( x \right) = R - {R_0} \ge 0\\ {g_6}\left( x \right) = 0.001 - \frac{\gamma }{{g{P_0}}}\left( {\frac{Q}{{2\pi Rh}}} \right) \ge 0\\ {g_7}\left( x \right) = 5000 - \frac{W}{{\pi \left( {{R^2} - R_0^2} \right) }} \ge 0 \end{array} \end{aligned}$$

(31)

where

$W = \frac{{\pi {p_0}}}{2}\frac{{{R^2} - R_0^2}}{{\ln \frac{R}{{{R_0}}}}},\quad {P_0} = \frac{{6\mu Q}}{{\pi {h^3}}}\ln \frac{R}{{{R_0}}},\quad p = \frac{{\log 10\log 10\left( {8.122e6\mu + 0.8} \right) - {C_1}}}{n},$

$h = {\left( {\frac{{2\pi N}}{{60}}} \right) ^2}\frac{{2\pi \mu }}{{{E_f}}}\left( {\frac{{{R^4}}}{4} - \frac{{R_0^4}}{4}} \right) ,\quad {E_f} = 9336Q\gamma C\Delta T,$

$\begin{array}{l} \Delta T = 2\left( {{{10}^p} - 560} \right) ,\gamma = 0.0307,C = 0.5,n = - 3.55,\\ {C_1} = 10.04,{W_s} = 101000,{P_{\max }} = 1000,{\Delta _{T\max }} = 50,\\ {h_{\min }} = 0.001,g = 386.4,N = 750.1 \le R,{R_0},Q \le 16,\\ 1e - 6 \le \mu \le 16e - 6. \end{array}$

Fig. 15

Hydrostatic thrust bearing model.

Table 14 Optimal hydro-static thrust bearing design results.

A comparative analysis of the outcomes derived from the twelve algorithms is presented in Table 14. According to the findings presented in Table 14, CDAOA proves to be notably more efficient than the other eleven algorithms when it comes to optimizing hydro-static thrust bearing design issues. The best solution of CDAOA is 1895.626. It is noteworthy that GSA, SO, AO, and CPSOGSA are not suitable for solving this engineering design problem.

Case V: weight minimization of a speed reducer

The weight minimization of a reducer refers to the process of reducing the weight of the gearbox or transmission system while maintaining or improving its functionality and performance. Reducing the weight of a reducer can lead to benefits such as improved fuel efficiency, increased payload capacity, and enhanced overall vehicle or machinery performance. The diagram depicting the engineering design of the speed reducer is presented in Fig. 16. The design parameters include the face width $(x_1)$, the module of teeth $(x_2)$, the quantity of teeth present on the pinion $(x_3)$, the dimension of the initial shaft spanned between bearings $(x_4)$, the dimension of the subsequent shaft spanned between bearings $(x_5)$, the diameter of the primary shaft $(x_6)$, and the diameter of the secondary shaft $(x_7)$. The mathematical representation is outlined in Eq. (32).

$$\begin{aligned} \begin{array}{l} \min f\left( x \right) = 0.7854{x_1}x_2^2\left( {3.3333x_3^2 + 14.9334{x_3} - 43.0934} \right) \\ - 1.508{x_1}\left( {x_6^2 + x_7^2} \right) + 7.4777\left( {x_6^3 + x_7^3} \right) + 0.7854\left( {{x_4}x_6^2 + {x_5}x_7^2} \right) \end{array} \end{aligned}$$

(32)

where the constraints g(x) are depicted in Eq. (33).

$$\begin{aligned} \begin{array}{l} {g_1}\left( x \right) = \frac{{27}}{{{x_1}x_2^2{x_3}}} - 1 \le 0\\ {g_2}\left( x \right) = \frac{{397.5}}{{{x_1}x_2^2{x_3}}} - 1 \le 0\\ {g_3}\left( x \right) = \frac{{1.93x_4^3}}{{{x_2}x_6^4{x_3}}} - 1 \le 0\\ {g_4}\left( x \right) = \frac{{1.93x_5^3}}{{{x_2}x_7^4{x_3}}} - 1 \le 0\\ {g_5}\left( x \right) = \frac{{{{\left( {{{\left( {\frac{{745{x_4}}}{{{x_2}{x_3}}}} \right) }^2} + 16.9 \times {{10}^6}} \right) }^{\frac{1}{2}}}}}{{110x_6^3}} - 1 \le 0\\ {g_6}\left( x \right) = \frac{{{{\left( {{{\left( {\frac{{745{x_5}}}{{{x_2}{x_3}}}} \right) }^2} + 157.5 \times {{10}^6}} \right) }^{\frac{1}{2}}}}}{{85x_7^3}} - 1 \le 0\\ {g_7}\left( x \right) = \frac{{{x_2}{x_3}}}{{40}} - 1 \le 0\\ {g_8}\left( x \right) = \frac{{5{x_2}}}{{{x_1}}} - 1 \le 0\\ {g_9}\left( x \right) = \frac{{x{EMPTY}_1}}{{12{x_2}}} - 1 \le 0\\ {g_{10}}\left( x \right) = \frac{{1.5{x_6} + 1.9}}{{{x_4}}} \le 0\\ {g_{11}}\left( x \right) = \frac{{1.1{x_7} + 1.9}}{{{x_5}}} \le 0 \end{array} \end{aligned}$$

(33)

where

$\begin{array}{l} 2.6 \le {x_1} \le 3.6,0.7 \le {x_2} \le 0.8,17 \le {x_3} \le 28,7.3 \le {x_4} \le 8.3\\ 7.3 \le {x_5} \le 8.3,2.9 \le {x_6} \le 3.9,5.0 \le {x_7} \le 5.5 \end{array}$

Fig. 16

Speed reducer design model.

Table 15 Optimal speed reducer design results.

A comparative analysis of the outcomes derived from the twelve algorithms is presented in Table 15. According to the findings presented in Table 15, CDAOA proves to be notably more efficient than the other eleven algorithms when it comes to optimizing speed reducer design issues. The best solution of CDAOA is 2994.4245. In terms of minimizing the speed reducer weight, CDAOA and DMO stand out as the most effective options. Notably, GSA is not suitable for solving this engineering design problem.

Conclusions

In this paper, a chaotic arithmetic optimization algorithm with Cauchy perturbation and differential evolution (CDAOA) is proposed. To overcome the inherent limitations of the original AOA, such as insufficient population diversity, weak global search capability, and slow convergence speed. By integrating multiple enhancement strategies, the proposed algorithm achieves a better balance between exploration and exploitation, leading to improved optimization performance.

Extensive numerical experiments validated the effectiveness of the proposed method. Compared to the original AOA, CDAOA achieved remarkable performance gains, reducing the mean optimization error by approximately 90% and significantly lowering the variance of solutions. Three groups of comparative tests are carried out on the classic test set, CEC 2019 and 2021 test functions, and the performances of the CDAOA are evaluated. Firstly, the influence of improvement strategies on AOA are studied by using 16 classical test problems. Meanwhile, the Wilcoxon rank-sum test, multiple-problem Wilcoxon’s test and Friedman test are used to evaluate the test results. It is concluded that the proposed CDAOA is the competitive improved AOA method. Secondly, to further evaluate the performance of CDAOA, based on the CEC 2019 and 2021 test suite, CDAOA is compared with the other 16 algorithms. The test results show that the performance of GRO is better than CDAOA in CEC2019-05. The performance of CDAOA is similar to QMESSA, MELGWO, MSADBO in CEC2021-08, and is better than the other algorithms. Therefore, the CDAOA has strong competitiveness in search performance. Finally, the CDAOA is compared with the other 11 algorithms on five practical engineering design problems, and the results show that the CDAOA can effectively solve real-world constrained optimization problems. Therefore, the proposed CDAOA algorithm in this paper can be used to solve complex numerical optimization problems and engineering optimization problems.

While CDAOA performs well in most scenarios, its efficiency may decrease when solving problems with dense local minima, and the runtime can be relatively long due to algorithmic complexity. Future work will focus on hybridization with efficient local search methods such as Nelder-Mead to further reduce runtime and extend the algorithm’s applicability to broader real-world optimization tasks.