Introduction

The COVID-19 pandemic highlighted the importance of early disease detection and isolation in order to prevent the spread of infection1,2,3. It is desirable, therefore, to have an effective system to continuously monitor an individual’s health state. Health monitoring systems consisting of wearable devices and artificial intelligence (AI) tools are portable, minimally invasive, and were shown to be able to detect COVID-19 infections4,5,6,7,8,9,10,11,12,13. For example, we developed a real-time infection prediction system using commercial-off-the-shelf (COTS) wearable devices and AI, which was capable of identifying COVID-19 infection on average 2.3 days before diagnostic testing with an Area Under the Receiver Operating Characteristic Curve (AUROC) of 0.82 6. Two other studies reported comparable performance from wearable physiological monitoring with AUROC = 0.804 and AUROC = 0.7714, respectively.

These health monitoring systems are typically powered by machine learning (ML) models4,5,6,7,14 or statistical methods10 that are sensitive to physiological changes caused by COVID-19 infection. The models gain intelligence through supervised learning on physiological data collected from the target populations of COVID-19 infection cases. However, training these models require data from a significant number of COVID-19 positive cases, which is challenging because infection data collection is time consuming and costly. Additional challenges of data collection include user compliance, physiologic context effects (such as traveling, intense exercises, etc.), and uncertainties in the timing of infection onset. These models cannot therefore be easily developed when they are most needed, such as at the beginning of novel infection outbreaks like the COVID-19 pandemic.

To this end, we propose that clinical decision support algorithms developed from data collected in hospitals can be utilized to significantly accelerate or provide a minimum viable starting point for wearable systems to monitor for infections in unconstrained, real-world environments. We previously developed a machine learning model that can identify hospital-acquired infection (HAI) patients up to 48 h before clinical suspicion of infection. The model used physiological measurements from hospital grade devices and demographic information collected in the hospital15. Here, we hypothesized that such infection prediction algorithms trained from hospital dataset (referred to in this article as the “hospital model”) can predict COVID-19 infection from the same set of physiological measurements collected through wearables outside of hospitals, provided that dataset shift16 – the changes in the joint distribution of the physiological features and the infectious disease labels between hospital and wearable datasets – are properly addressed. More specifically, if we define our physiological input features as X and our infectious disease labels as Y, we can typically have three types of dataset shifts:

  1. 1.

    Covariate shift: P(X) changes but P(Y|X) and P(Y) remain the same.

  2. 2.

    Label shift: P(Y) changes but P(Y|X) and P(X) remain the same.

  3. 3.

    Concept drift: P(Y|X) changes but P(X) and P(Y) remain the same.

where P(X), P(Y) and P(Y|X) are the probability distribution of X, probability distribution of Y, and the conditional probability distribution of Y given X, respectively.

In this study, we first performed retrospective analyses to identify sources of dataset shift between hospital dataset and wearable dataset, and then described two correction techniques – removing contextual confounders and applying a monotonic feature transformation – to reduce the differences in data distribution between the two datasets. We found that our infection prediction model trained from the hospital dataset performed best after applying both correction techniques, with an AUROC of 0.74, and detection of COVID-19 infection on average 2 days prior to diagnostic testing. Only a small sample of wearable data from healthy subjects (2 weeks of data from 25 healthy subjects) was required for the feature transformation. Our results suggest that a minimum viable wearable physiological monitoring system that detects early signs of COVID-19 infection can be developed and deployed without the need for data from COVID-19 cases.

Methods

Description of datasets

The two hospital datasets - MIMIC-III (Medical Information Mart for Intensive Care III)17 and Banner Health data - used to train the infection prediction model were described previously15. The two datasets were combined in this study to create a single hospital dataset to train the infection prediction model. Both MIMIC-III and Banner Health data comprise de-identified health-related data from patients during their hospital stay. The MIMIC-III data we used was from patients who stayed in critical care units of the Beth Israel Deaconess Medical Center (Boston, MA) between 2001 and 2012. Each patient encounter included in this study was from the MIMIC-III Waveform Database Matched Subset18. The Banner Health data was from patients who stayed in critical care units or low-acuity settings such as general wards in Banner Health hospitals (Phoenix, AZ). The patient cohort included in this study was collected between 2016 and 2017, where waveform records were available for a subset of the patient encounters.

The wearable dataset used to test hospital model’s ability to detect COVID-19 infection was collected in the framework of a study described previously6 and an extension of the study which focused on algorithm improvement and augmentation. This dataset comprises de-identified COTS wearable physiological and activity data from Garmin watch and Oura ring devices, collected from active military personnel recruited from multiple US Department of Defense (DoD) sites between June 2020 and May 2022. This dataset also included symptoms and diagnostic tests information from self-reported daily survey questionnaires.

Ethical approval

The MIMIC-III project was approved by the Institutional Review Boards of Beth Israel Deaconess Medical Center and the Massachusetts Institute of Technology (Cambridge, MA). The use of Banner Health data was a part of a retrospective deterioration detection study approved by the Institutional Review Board of Banner Health and by the Philips Internal Committee for Biomedical Experiments. For both hospital datasets, requirements for individual subject consent were waived because the project did not impact clinical care, was no greater than minimal risk, and all protected health information was removed from the limited dataset used in this study.

The collection and use of the wearable dataset was approved by the Institutional Review Boards of the US Department of Defense. Informed consent was obtained from all participants.

All methods were performed in accordance with the relevant IRB guidelines and regulations.

Cohort selection

Patient encounters used in this study to train the hospital-acquired infection prediction model were selected using the same methodology described previously15, namely a set of MIMIC-III and Banner Health patient encounters that had high-sampling frequency waveform recordings around the time of clinical suspicion of hospital-acquired infection. These data were acquired prior to the COVID-19 outbreak therefore included infection instances such as pneumonia, bloodstream infection, bone/joint/tissue/soft tissue infection, sepsis, urinary system infection and did not include instances of COVID-19 infections. We focused on patient encounters with waveform recordings, because we wanted to match the temporal resolution of the vital sign measurements from which the hospital model was trained, with the temporal resolution of the vital sign measurements in the wearable dataset to which the hospital model would be applied. The infection patients, as described previously, were those who had confirmed infection diagnoses and whose timing of clinical suspicion of infection could be localized by a microbiology culture test order. Note that we used as our reference the time when the microbiology culture test was ordered, not the time when the test result was returned. These infection patients were further screened into a hospital-acquired infection cohort if the earliest timing of the microbiology culture test order occurred at least 48 h after hospital admission.

Subjects used to validate the performance of the hospital model in predicting COVID-19 infection were extracted from the wearable dataset, as described previously6. Specifically, COVID-19 positive subjects were those who reported positive test results and symptoms, and COVID-19 negative subjects were those who reported at least 1 symptom-free negative test result, but no positive results. Condition for inclusion in both classes was the presence of data from a Garmin watch and an Oura ring simultaneously, and that at least 10 nights of physiologic data were collected during sleep within the 21-day period prior to their COVID-19 test (subjects were excluded post-hoc if they did not meet these criteria).

Feature extraction

The trained hospital model in this study used features derived from a subset of the demographics and vital sign measurements described previously15. We chose this subset because the same set of demographics and vital sign measurements were available and reliable in the wearable dataset. Specifically, the feature vector for training was composed of demographics (age, sex) and four statistic features - average, minimum, maximum and the standard deviation – of core body temperature, respiratory rate, heart rate, and RMSSD (Root Mean Square of Successive Differences between normal heartbeats – a standard measure of heart rate variability), collected in a 24-hour observation window prior to the observation time of 1-hour before clinical suspicion of infection. This resulted in a total set of 18 features in the feature vector. We required the feature vector to contain no missing values, and thus excluded patient encounters that had one or more types of vital sign measurements missing in the observation window. The majority of the vital sign measurements, except for temperature which was sporadically measured at the bedside, were derived from high temporal resolution waveforms and matched to the temporal resolution of the corresponding measurements provided by a Garmin watch and an Oura ring. In particular, heart rate and RMSSD were calculated after extracting inter-beat interval from photoplethysmography (PPG), and respiratory rate was derived from impedance-based measurements.

The same set of demographics and vital sign features were extracted from the wearable dataset. The Oura rings provided skin temperature and RMSSD measurements. Respiratory rate was measured from the Garmin watches. Concurrent heart rate measurements from the Garmin watch and Oura ring were combined before feature extraction. Plausibility filters were applied so that unrealistic values outside of a very broad physiological range were discarded6. For each subject, we extracted statistic features in 24-hour intervals within a 14-day window prior to their COVID-19 test (hence 14 observation times). Statistic features were derived from measurements collected in a 24-hour observation window prior to the observation time, similar to those used to train the hospital model. We extracted more than one day of features because we wanted to assess how early our model could detect COVID-19 infection prior to diagnostic testing. To examine the impact of daytime activity and other contextual factors on physiology, we extracted two sets of features: the first set used all vital sign measurements collected in the 24-hour observation window (“daily features”), and the second set used vital sign measurements collected during sleep in the 24-hour observation window (“sleep-only features”). Hypnogram information from the wearable devices were used to identify the sleep segments where the sleep-only features were extracted.

Hospital model training

The model for hospital-acquired infection prediction was trained using the same methodology described previously15. Specifically, we used the XGBoost algorithm19 to train and test the hospital model with stratified 5-fold cross-validation. Hyperparameters were optimized using grid search. No class-weighting was applied. Sampling was based on ambient data frequency. The set of hyperparameter that yielded the best model performance averaged from the 5 validation folds were used to train the final model for assessing its performance in the wearable dataset.

Testing the hospital model in the wearable dataset

To assess the performance of the hospital model in predicting COVID-19 infection, we defined a true positive as being a positive model prediction within the 14-day period prior to a positive COVID-19 test for the positive class, and a true negative as being a negative model prediction within the 14-day period prior to a negative COVID-19 test for the negative class. Because infection risk scores from the model were calculated in 24-hour intervals within a 14-day period, a positive model prediction was defined as one with at least one prediction within the 14-day period above the defined risk threshold, and a negative model prediction was defined as one with all predictions within the 14-day period below the defined risk threshold. In other words, we computed the hospital model outputs - which were probabilistic scores that estimated the likelihood of a given subject being infected – from the demographics and vital sign features for each day (or each sleep segment) and took the maximum score during the 14-day window for each subject. We then compared the maximum scores between COVID-19 positive and negative subjects and reported the model performance using the following metrics:

  • Area under the Receiver Operating Characteristic curve (AUROC),

  • Average Precision (AP),

  • True Negative Rate (Specificity),

  • True Positive Rate (Sensitivity, or Recall), including:

    • Sensitivity(Break-Even): Sensitivity at the break-even point, where Sensitivity and Precision are equal,

    • Sensitivity(80%): Sensitivity when Specificity = 0.8,

    • Sensitivity(90%): Sensitivity when Specificity = 0.9.

The confidence intervals for the performance metrics were estimated from bootstrap percentiles20,21. Specifically, given a total cohort of \(\:m\) COVID-19 positive subjects and \(\:n\) COVID-19 negative subjects, we performed random sampling with replacement 1000 times, each time drawing \(\:m\) random COVID-19 positive subjects and \(\:n\) random COVID-19 negative subjects. For each of the 1000 bootstrapping round, we calculated performance metrics such as AUROC and AP using the randomly drawn subjects and their maximum infection risk scores during the 14-day window. We then took the 2.5-th percentile and 97.5-th percentile of the 1000 bootstrap AUROCs as the 95% confidence interval for AUROC, and the 2.5-th percentile and 97.5-th percentile of the 1000 bootstrap APs as the 95% confidence interval for AP.

To compare model performance between different experiments, we used DeLong’s test22 to calculate p-values for whether one model has a significantly different AUROC than another model. To further correct for multiple comparisons, we reported adjusted p-values using Bonferroni correction23, where the adjusted p-value is the DeLong’s test p-value multiplied by the number of pairwise comparisons.

To estimate the overall lead time of positive classification, we identified the days (interpolated) in which the hospital model prediction exceeded a predefined threshold of sensitivity = 0.6 within the 14-day window prior to COVID-19 testing. The threshold was suggested by the study principal investigators in the US DoD sites. The lead time was then defined as the average across these positive days for each user and then aggregated across the cohort for the final mean estimate of the lead time for COVID-19 classification (False Negatives have lead time of 0 days). Similar as for AUROC and AP, we performed random sampling with replacement 1000 times to obtain confidence interval of the lead time. We also overlayed risk scores with time to have a visual representation of risk score elevation during the infection period.

To reduce the impact of dataset shift on model performance, we performed a monotonic feature transformation by first calculating percentile values of each feature in the hospital dataset and the wearable dataset respectively, and then replacing wearable feature values with the hospital feature values that shared the same percentile. The percentile values of a given feature were calculated in each dataset using all samples without distinguishing between positive and negative class labels. This way, we calibrated features from wearables to match the distribution in the hospital dataset without knowledge of the class labels. We then validated the performance of the hospital model on the calibrated wearable features and compared it with model performance on wearable features before feature transformation. Specifically, let’s denote the trained hospital model output for a given sample from the wearable dataset as \(\:H\left(\varvec{x}\right)\), where \(\:\varvec{x}=\left[{x}_{1}\:{x}_{2}\:\cdots\:\:{x}_{n}\right]\) is the feature vector of the given sample and \(\:{x}_{j}\) is the jth feature of \(\:\varvec{x}\) with a total of \(\:n\) features. The monotonic feature transformation is to find a feature vector \(\:\widehat{\varvec{x}}=\left[{\widehat{x}}_{1}\:{\widehat{x}}_{2}\:\cdots\:\:{\widehat{x}}_{n}\right]\) that satisfies \(\:\widehat{P}\left({\widehat{x}}_{j}\right)=P\left({x}_{j}\right)\) for all \(\:n\) features in the feature vector, where \(\:\widehat{P}\left({\widehat{x}}_{j}\right)\) is the percentile value of \(\:{\widehat{x}}_{j}\) in hospital dataset and \(\:P\left({x}_{j}\right)\) is the percentile value of \(\:{x}_{j}\) in wearable dataset. \(\:\widehat{\varvec{x}}\) is the calibrated feature vector of \(\:\varvec{x}\), and \(\:H\left(\widehat{\varvec{x}}\right)\) is the hospital model output for the sample after feature transformation. We describe the algorithm below to solve \(\:\widehat{P}\left({\widehat{x}}_{j}\right)=P\left({x}_{j}\right)\), where we denote the percentile values of each feature in the wearable dataset as matrix \(\:\varvec{v}=[{\varvec{v}}_{1}\:{\varvec{v}}_{2}\:\cdots\:\:{\varvec{v}}_{\varvec{n}}]\) and in the hospital dataset as matrix \(\:\widehat{\varvec{v}}=\left[{\widehat{\varvec{v}}}_{1}\:{\widehat{\varvec{v}}}_{2}\:\cdots\:\:{\widehat{\varvec{v}}}_{\varvec{n}}\right]\); \(\:{\varvec{v}}_{j}={\left[{v}_{j}^{1}\:{v}_{j}^{2}\:\cdots\:\:{v}_{j}^{100}\right]}^{T}\) and \(\:{\widehat{\varvec{v}}}_{j}={\left[{\widehat{v}}_{j}^{1}\:{\widehat{v}}_{j}^{2}\:\cdots\:\:{\widehat{v}}_{j}^{100}\right]}^{T}\) denote the column vector of 100 percentile values for the jth feature in the wearable dataset and hospital dataset respectively; \(\:{v}_{j}^{k}\) and \(\:{\widehat{v}}_{j}^{k}\) denote the kth percentile for the jth feature in the wearable dataset and hospital dataset respectively. We included the pseudocode and a diagram of monotonic feature transformation algorithm in Fig. 1.

Fig. 1
figure 1

Pseudocode and diagram of monotonic feature transformation algorithm. x-axis is the value of the jth feature, y-axis is the percentile values of the jth feature in a dataset. Blue and orange lines are the cumulative distribution of the jth feature in the wearable dataset and the hospital dataset respectively.

Full size image

To understand the data requirements for feature transformation, we performed additional benchmarking experiments with restrictions on the type and size of wearable data used for feature transformation, including: using wearable data acquired when the subjects were not under impact of COVID-19 infection; using wearable data from subjects that were not used to test the model performance; using the most recent days of wearable data prior to diagnostic testing; and using wearable data from randomly down-sampled cohorts or subject days (without replacement, 10 iterations).

Results

Cohorts and features for training and testing

The cohort selection criteria for training the hospital model resulted in a total dataset size of 9,517 patient encounters with waveform recordings around the time of clinical suspicion of hospital-acquired infections (not including COVID-19). Of these patient encounters, 3,951 (3,665 controls and 286 HAIs; 51% Banner Health and 49% MIMIC-III) had overlapping PPG waveforms and impedance-based measurements with good data quality, and therefore had the full set of 18 demographics and vital sign features (see METHODS) available at 1-hour before clinical suspicion of infection. These 3,951 patient encounters were used to train the hospital model of hospital-acquired infection prediction.

The cohort selection criteria for testing the trained hospital model resulted in 301 COVID-19 positive subjects and 2,111 COVID-19 negative subjects from the wearable dataset. Within the 14-day windows prior to COVID-19 tests from these subjects, a total of 33,164 subject days and 31,269 subject sleep segments had vital sign measurements that passed our plausibility filter. From these subject days, we extracted the feature vectors comprising the same set of 18 features that was used to train the hospital model, using either all available vital sign measurements or those measured during sleep (“daily features” and “sleep-only features”, see METHODS), to quantify the performance of the trained hospital model in predicting COVID-19 infections.

Differences between training and testing datasets

The joint distribution of inputs and outputs of the infection prediction model differed between the training scenario in the hospital dataset and the testing scenario in the wearable dataset – a problem known as “dataset shift”16. Here we describe five sources of dataset shift in our study.

First, the demographics of the training and testing cohorts were different. The patients from the hospital dataset were older than the subjects from the wearable dataset (Fig. 2A), and the wearable dataset had an imbalanced sex ratio than the hospital dataset (Figs. 2B, 20% female in the wearable dataset versus 47% female in the hospital dataset). Both age and sex may result in differences in physiology24,25,26,27,28,29,30,31,32,33,34.

Second, the health states of the training and testing cohorts were different. Patients in the hospital dataset are those who developed hospital-acquired infections during their stays in general wards or in some cases intensive care units, and are likely older adults with comorbidities and under medical treatments, therefore the physiological measurements in the hospital dataset were more likely to be abnormal and unstable compared to the physiological measurements in the wearable dataset where healthy young military personnel performing their daily duty were monitored. We found that patients in the hospital dataset had higher heart rate and higher respiratory rate than the subjects in the wearable dataset (see the Average and Maximum statistic feature in Supplementary Table 1), which were consistent with an overall declined health state34,35,36,37. The hospital patients also had larger variations in heart rate and respiratory rate than the subjects in the wearable dataset (see the Standard Deviation statistic feature in Supplementary Table 1).

Third, the data sources where the physiological features were extracted from were different between the hospital dataset and the wearable dataset. Temperature features were extracted from core body temperatures in the hospital dataset, whereas in the wearable dataset skin temperatures measured at the fingers were used. We found that skin temperature had lower values and larger variance compared with core body temperature (Fig. 2C, Supplementary Table 1), which was consistent with the literatures38,39,40,41.

Fourth, the processing methods to extract physiological signals were different between the two datasets. Heart rate variability measurement RMSSD were computed based on pulse estimates of heart beats. However, the signal processing algorithms that Oura ring used could be different from ours in detecting the fiducial points on the pulse waveforms, and in the validation of the resulted inter-beat intervals. We suspected that differences in the signal processing algorithms to obtain RMSSD also contributed to the distribution differences in the RMSSD features between the hospital dataset and the wearable dataset (Supplementary Table 1), in addition to the demographics and health state differences mentioned above.

Finally, wearable physiological data is acquired in an unconstrained, real-world environment, which is influenced by everyday activities and other contextual factors. In contrast, hospital physiological data is typically acquired when the patient is sedentary. Daytime activity such as physical exercise increases heart rate and respiratory rate34,35 which is a confounding factor to infection prediction because infections cause similar changes in vital signs36,42. Skin temperature also changes dynamically upon physical exercise, and the directionality of change depends on the intensity level of the exercise and whether the skin temperature is measured over active or non-active muscles43. When limiting feature extraction to wearable physiology data acquired during sleep, we found that sleep-only features have different data distributions compared to the daily features (Supplementary Table 1). For example, the data distribution of the mean temperature feature was shifted towards higher values when restricted to measurements during sleep (Fig. 2C).

We included a full comparison of feature values in Supplementary Table 1.

Fig. 2
figure 2

Comparison between hospital dataset and wearable dataset. (A) Age distribution of hospital dataset (white) and wearable dataset (black). (B) Sex distribution of hospital dataset (white) and wearable dataset (black). (C) Boxplot of mean temperature feature value from hospital dataset (left), wearable dataset (middle), and wearable dataset during sleep (right).

Full size image

Experiment design

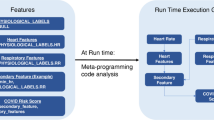
We explored two approaches to correct for differences in data distributions between hospital and wearable datasets. First, we limited feature extraction to wearable physiological data from wearable sensors acquired when the subject was sleeping. This approach directly mitigated dataset shift by removing contextual confounders of daytime activities. Second, we explored a monotonic feature transformation method to convert the data distribution of physiological features in the wearable dataset to match the data distribution in the hospital dataset. This approach addressed covariate shift – one of the three types of dataset shift (see INTRODUCTION) - due to differences in demographics and health state between hospitalized patients and subjects in the wearable dataset, as well as differences in physiological measurements between COTS wearables and hospital grade devices. We compared model performances with or without using such correction techniques (Experiments I, II, III, IV in Fig. 3), and in addition benchmarked data requirements (Experiments V, VI, VII):

  • Experiment I: a baseline comparison where the trained hospital model was directly applied to the daily features from the wearable dataset. Physiological measurements during both awake and sleep were used to extract the daily features.

  • Experiment II: the trained hospital model was tested on sleep-only features from the wearable dataset. Sleep-only features were extracted from the same window and time interval as the daily features but only using measurements during sleep segments.

  • Experiment III: the trained hospital model was tested on sleep-only features after the sleep-only features were transformed to match the distribution of the hospital dataset.

  • Experiment IV: the trained hospital model was tested on daily features after the daily features were transformed to match the distribution of the hospital dataset.

  • Experiments V, VI, VII: benchmarking the amount and type of wearable data needed for the monotonic feature transformation.

Fig. 3
figure 3

Schematic view of pipelines for training the hospital model (top box) and for testing the trained model in the wearable dataset (middle box). Similar steps of the two pipelines are aligned (bottom box). The trained hospital model was applied to the wearable dataset with or without the two dataset shift corrections (highlighted, middle box), which resulted in four experiments (Exp-I, II, III, IV in middle box) to compare model performance.

Full size image

Baseline comparison (Experiment I)

We directly applied the hospital model trained for hospital-acquired infection prediction to the wearable daily features and quantified its performance in predicting COVID-19 infections. We hypothesized that the hospital model would not generalize well in predicting COVID-19 infections, due to the differences between hospital and wearable physiological feature spaces. We found that the hospital model performed at Area under ROC Curve (AUROC) = 0.527, Average Precision (AP) = 0.132, Sensitivity = 0.163 and Specificity = 0.866 at break-even point, Sensitivity = 0.193 and 0.113 respectively when Specificity was at 0.8 and 0.9. This performance was at chance level (95% confidence interval: [0.498, 0.566] for AUROC, [0.122, 0.153] for AP), suggesting that the hospital model failed to generalize when directly applied to wearable dataset.

Removing contextual confounders (Experiment II)

When controlling for contextual factors like daytime activity, we found that the hospital model using the sleep-only features performed at AUROC = 0.644 (95% confidence interval: [0.632, 0.701]), AP = 0.260 (95% confidence interval: [0.258, 0.351]), Sensitivity = 0.279 and Specificity = 0.897 at break-even point, Sensitivity = 0.402 and 0.269 respectively when Specificity was at 0.8 and 0.9. Thus, using sleep-only features resulted a 22% boosting of performance in terms of AUROC, suggesting the importance of controlling for contextual confounders when extracting the likelihood of infection from wearables physiological data.

Applying feature transformation after removing contextual confounders (Experiment III)

We hypothesized that a monotonic feature transformation procedure which transforms the wearable feature values to match the distribution in hospital dataset (see METHODS) could improve performance of the hospital model. Using mean temperature feature as an example (Fig. 4), the feature transformation procedure based on matching feature values that share the same 0-100 percentile value in their corresponding datasets resulted in an almost identical data distribution of the mean temperature feature between the two datasets, despite large discrepancies in the data distributions before transformation. Hence, we performed the same feature transformation procedure independently on each feature, and evaluated the performance of hospital model on the wearable dataset after all the features were transformed. We found that the hospital model performed at AUROC = 0.740 (95% confidence interval: [0.740, 0.808]; Fig. 5A, red solid line), AP = 0.330 (95% confidence interval: [0.330, 0.442]; Fig. 5B, red solid line), Sensitivity = 0.379 and Specificity = 0.910 at break-even point, Sensitivity = 0.588 and 0.409 respectively when Specificity was at 0.8 and 0.9, using transformed wearable sleep-only features. Applying feature transformation on the sleep-only features resulted an additional 15% boosting of performance in terms of AUROC (0.740 versus 0.643, red solid line versus green dashed line in Fig. 5A).

Fig. 4
figure 4

Monotonic feature transformation of mean temperature feature. Red, hospital dataset; green, wearable dataset (sleep-only features); blue, transformed wearable dataset (sleep-only features). (A) Data distribution of mean temperature feature: red and green shaded areas describe data distribution from hospital and wearable sleep data respectively. Vertical lines mark the 0-100 percentile values in 5% intervals on the x-axis corresponding to each dataset. (B) Monotonic feature transformation curve (black) where feature values with the same percentile value are mapped between two datasets. Dashed lines mark the 0-100 percentile values in 5% intervals on the x-axis for wearable sleep data (green) and on the y-axis for hospital data (red). (C) Data distribution of mean temperature feature: red, green and blue shaded areas describe data distribution from hospital dataset, wearable sleep dataset and transformed wearable sleep dataset respectively. Vertical lines mark the 0-100 percentile values in 5% intervals on the x-axis corresponding to each dataset; blue vertical lines are overlapped with red vertical lines.

Full size image

Applying feature transformation without removing contextual confounders (Experiment IV)

We further investigated whether the same feature transformation procedure could improve the performance of the hospital model on wearable features without removing the contextual confounder of awake versus sleep. Similarly, we calculated percentile values of daily wearable features derived from awake and sleep data combined, replaced the feature value with the corresponding value from the hospital dataset, and evaluated the performance of the hospital model on the transformed features. The model had an AUROC = 0.566 (95% confidence interval: [0.554, 0.622]; Fig. 5A, orange dotted line), AP = 0.158 (95% confidence interval: [0.153, 0.205]; Fig. 5B, orange dotted line), Sensitivity = 0.256 and Specificity = 0.844 at break-even point, Sensitivity = 0.296 and 0.146 respectively when Specificity was at 0.8 and 0.9, when applied to the transformed wearable features without using sleep data exclusively. The model performance was slightly better than before feature transformation (AUROC: 0.565 versus 0.526, orange dotted line versus blue dash-dot line in Fig. 5A), but the improvement was not as substantial as when applying feature transformation to the sleep-only features (AUROC: 0.740 versus 0.643, red solid line versus green dashed line in Fig. 5A). These results suggested that both controlling for contextual cofounders and applying feature transformation to address dataset shift were important to enable good model performance.

Statistical analysis and comparison with previous work

We performed DeLong’s test22 to compare model performance between each pair of the four experiments and use Bonferroni method to correct for multiple comparisons23. We included the z-score, the p-value and the adjusted p-value in Supplementary Table 2. We found significant differences (p-value < 0.01; adjusted p-value < 0.05) in AUROC from all pairs of comparisons.

We have shown that the hospital model trained for hospital-acquired infection prediction performed the best in detecting early signs of COVID-19 infection on wearable dataset when feature transformations were performed and when only sleep data were considered (AUROC = 0.740, Experiment III). Although this performance is viable for a system, it was lower than our previously reported solution using a model trained directly on wearable dataset with COVID-19 labels (AUROC = 0.82)6. This was expected because the hospital model was designed to be an economical minimal viable solution that uses no COVID-19 labels for training, and thus not capable of controlling for concept drifts and/or label shifts.

When overlaying risk scores with time from the Experiment III hospital model, on average subjects with positive COVID-19 test results showed risk score elevations around COVID-19 test time (Fig. 5C, black), whereas subjects with negative COVID-19 test maintained their baseline risk scores (Fig. 5C, blue). Based on a cut-off risk threshold of 15 (yielding 60% Sensitivity and 78% Specificity), we identified the days in which the model output exceeded the defined threshold within the 14-day window prior to COVID-19 testing to estimate the lead time of positive classification (see METHODS). We found that the Experiment III hospital model successfully predicted COVID-19 infection, on average, 2.2 days prior to testing (95% confidence interval: [1.95, 2.61] days). This lead time was slightly lower but comparable to our previously reported wearable solution of 2.3 days prior to testing6.

Fig. 5
figure 5

Hospital model performance and risk scores in detecting COVID-19 infection from wearable dataset. (A) Receiver Operating Characteristic (ROC) curves. Experiment I (blue dash-dot line): hospital model directly applied to wearable daily features. Experiment II (green dashed line): hospital model applied to wearable sleep-only features. Experiment III (red solid line): hospital model applied to wearable sleep-only features after feature transformation. Experiment IV (orange dotted line): hospital model applied to wearable daily features after feature transformation, without using sleep data exclusively. Area under the ROC curve (AUROC) for each experiment is included in the figure legend. (B) Precision-recall curve. Colors are the same as described in subplot A. Average Precision (AP) score for each experiment is included in the figure legend. (C) Mean infection risk score based on the output of the best generalized hospital model (Experiment III: sleep-only features + feature transformation) in 301 COVID-19 positive subjects (black) and 2,111 COVID-19 negative subjects (blue) as a function of number of days relative to the COVID-19 test time (red). Grey and light-blue shaded area depicts 95% confidence interval calculated from the standard error.

Full size image

Data requirements for feature transformation (Experiments V, VI, VII)

Given that our best generalized hospital model (Experiment III) performed reasonable but inferior to our previous wearable model6, it is most sensible to use a hospital model for predicting COVID-19 in the absence of the wearable model, e.g. at the onset and during the early stage of the outbreak when data from COVID-19 positive cases were limited or unavailable to train a wearable model. Therefore, we investigated the data requirements of the generalized hospital model in Experiment III, in particular, the type and amount of wearable sleep data needed for the feature transformation. A favorable solution should require minimal COVID-19 positive instances. We performed three sets of additional experiments.

First, we asked whether illness data of COVID-19 were required for feature transformation (Experiment V). Interestingly, we found that baseline healthy data was sufficient because (1) using wearable sleep data from subjects that only reported negative test results for the feature transformation resulted in similar AUROC of 0.741 (Experient V-a, Supplementary Table 3), and (2) using wearable sleep data 4 weeks to 2 weeks before COVID-19 test – a time range when subjects were not infected - achieved similar results (AUROC = 0.741; Experient V-b, Supplementary Table 3).

Second, we asked whether wearable sleep data for feature transformation needed to be from the same subjects (Experiment VI, Supplementary Table 3). We randomly split the subjects in the wearable dataset into 5 folds, and for each subject we used subjects from the other four folds to transform the features of the given subject. The model performed with an AUROC of 0.741, suggesting that the wearable data used for feature transformation do not need to come from the same subjects used to test the model.

Third, we examined the minimum sleep data needed for feature transformation by benchmarking model performance against using sleep data from reduced number of days or from reduced number of subjects (Experiment VII). We gradually decreased the number of days from the 14 days prior to COVID-19 test where the wearable data were used for feature transformation (Experiment VII-a, Supplementary Table 3). We found that the model performed at AUROC of 0.74 when more than 2 days immediately preceding the COVID-19 test were used for feature transformation, and the model performed at AUROC = 0.73 when using data from the day before or two days before COVID-19 test for feature transformation. We also benchmarked against data from randomly selected days within the 14-day window prior to the COVID-19 test for feature transformation and found that the model performed at AUROC of 0.74 for all experiments - randomly selecting number of N days where N ranges from 1 to 13 days (Experiment VII-b, Supplementary Table 3). Further, we pooled all subject days and used random down-samples for feature transformation (Experiment VII-c, Supplementary Table 3). We found that the model performed at AUROC of 0.74 for all experiments of reduced subject days (number of reduced subject days: 25,000, or 20,000, or 15,000, or 10,000, or 7,500, or 5,000, or 3,000, or 1,000, or 500, or 300), even when only 300 subject days were used. Regarding the number of subjects needed, we used data from randomly down-sampled subjects for feature transformation and found that the model performed at AUROC of 0.74 for all experiments of reduced number of subjects (number of reduced subjects: 2,000, or 1,500, or 1,000, or 500, or 250, or 100, or 50, or 25), even when the number of subjects was reduced to 25 (Experiment VII-d, Supplementary Table 3).

Summarizing all the experiments (Supplementary Table 3), we concluded that healthy wearable data from 25 subjects collected in a period of 14 days for feature transformation would be sufficient to ensure the same model performance of AUROC = 0.74.

Discussions

This study demonstrated the feasibility of applying a machine learning model trained on hospital data to detect early signs of COVID-19 infection in physiological data from COTS wearables outside of hospitals. Our hospital model was trained from hospitalized patients and vital signs collected from hospital grade devices to test against a set of common hospital-acquired infections (prior to the COVID-19 outbreak), therefore had no prior knowledge of COVID-19 infections and no exposure to physiological data collected through COTS wearables. Nevertheless, after controlling for dataset shift, the hospital model performed at AUROC = 0.74 in alerting COVID-19 infection before diagnostic testing from wearable physiology monitoring in military personnel under unrestrained use. This performance was lower than our previously reported solution using a model trained directly on wearable dataset with COVID-19 labels6 but is nevertheless viable for a system, and can detect COVID-19 infection 2 days before diagnostic testing, with no need of model retraining. Importantly, our approaches in addressing dataset shift did not require any labeled data of COVID-19 cases; rather, a small dataset from healthy subjects – e.g. 2 weeks of wearable data from 25 subjects – was sufficient to generalize the hospital model to predict COVID-19 infection from wearable data with an AUROC of 0.74. Therefore, our efficient solution of generalizing the hospital model of infection prediction to wearable physiological monitoring would be most economical and useful at early onset of outbreaks of novel infections when data from positive cases are limited or unavailable to train an pathogen-specific model – such as our previously reported COVID-19 wearable model6. Because a small amount of healthy baseline data is feasible to collect prior to any infection outbreak, the transformation function to calibrate the feature values can be derived to enable rapid deployment of a pre-trained model. We anticipate such a solution could create a big impact in infectious disease control, as transmission prevention at the onset and during the early outbreak of an infectious disease is critical.

The two enablers of our solution of generalized hospital model were (1) the isolation of contextual confounders, focusing on sleep-only wearable data, and (2) feature transformations that calibrated the wearable feature values to match the distribution of the hospital model training data and that do not rely on positive labels. Both reduced the differences in the joint distribution of the physiological features X and the infectious disease labels Y between the hospital dataset and the wearable dataset, therefore mitigating dataset shift. The model performed at chance level without these two corrections and performed at AUROC of 0.74 when and only when both corrections were used. This is likely because the two methods controlled for different aspects of dataset shift. Feature transformation is a correction technique for covariate shift (see INTRODUCTION) because it modifies the probability distribution of the physiological features P(X). Removing contextual confounder of daytime activities, on the other hand, controls for both covariate shift P(X) and to some extent concept drift P(Y|X). For example, increases in heart rate in hospitalized patients are associated with increased risk of infection42; in contrast, increases of heart rate in the subjects from the wearable monitored cohort could be normal physiology change, e.g. if the subjects are exercising34. Therefore, daytime activities such as physical exercises affect the wearable physiology data in such a way that increases the likelihood that they will be misclassified by the hospital model as infection cases. Hence it is beneficial to use sleep-only features in our study, and that it is not sufficient to perform feature transformations on the daily features without isolating sleep periods.

In our study we used hypnogram information from wearables to identify measurements during sleep to compute sleep-only features so that both P(X) and P(Y|X) were more similar to the hospital dataset, where the physiological measurements were acquired when patients were sedentary. We could also apply the hospital model to the wearable dataset in other similar scenarios such as during wakefulness, but limited to resting/sedentary states. It is possible that there are other contextual confounders that we could identify and isolate from the wearable dataset to further improve the model performance of the generalized hospital model. Identifying contextual factors does not require any explicit knowledge of data distributions of the training nor testing datasets but replies on domain knowledge of the model training and application scenarios. Removing contextual factors, however, relies on the availability of data elements that can be used to isolate the contextual factors.

It is challenging to address all aspects of dataset shift. Transfer learning techniques aim to improve the performance of a machine learning model at the presence of dataset shift, however, the effectiveness of these techniques has a large variation, and is depended on the extent of the dataset shift (e.g. how different is the test scenario from the training scenario) as well as whether labeled data is present44. In particular, label shift and concept drift would likely require labels from both the training and testing scenario to be properly addressed. Previous work that corrected dataset shift using unlabeled data typically addressed covariate shift, and involved re-training using resampling weights that were either estimated from the biasing densities45,46,47 or inferred by comparing nonparametric distributions between training and testing samples48. Recent work49,50,51,52,53 in the deep regime may tackle all three types of dataset shift, but methods based on neural network are difficult to interpret, computationally expensive, mostly need labels, and often require fine-tuning of a large set of trainable parameters. In contrast, the monotonic feature transformation technique described in our study requires no labels, no re-training, is a straightforward mathematical operation operating on linear time complexity, and that preserves the rank order of data but modifies the shape of the distribution. By doing so, we are minimizing the dataset differences in physiological signals caused by the differences in individual and group baselines, and by the differences in measurement devices, yet preserving the relative rank of infection risk among individuals. Our hospital model was based on ensembles of decision tree which makes aggregated decisions from individual features on each tree split. This makes it possible for us to manipulate the distribution of each feature independently without altering the overall decision from the tree ensembles based on the feature ranks (e.g. P(Y|X) is unchanged for monotonic transformations of X, where X is the physiological features and Y is the infection labels). Algorithms based on decision trees are particularly suitable for disease modeling, as typically lower and/or higher clinical measurements are associated with declined health. In other words, infection risk as a function of clinical measurements resembles a U-shape curve or a monotonic function. This is the reason why preserving the rank of feature values worked in our solution as it preserved the rank of infection risk, e.g. both a high rank of skin temperature and a high rank of core temperature are associated with high infection risk, therefore the conditional probability of COVID-19 infection risk given skin temperature P(Y_covid|X_skin) can be monotonically mapped to the conditional probability of infection risk given core temperature P(Y_infection|X_core). It is important to note that we need a feature transformation method that both matches the data distribution and preserves the data rank. For example, algorithms in optimal transport problem54 match the data distribution but do not preserve the data rank, linear transformation algorithms such as PCA55 keeps the data rank but only matches data distribution up to 2nd order statistics and does not capture the more complex nonlinear relationship in the data.

In summary, our feature transformation technique requires no labels (therefore is “unsupervised”), no re-training, and is computationally inexpensive and interpretable, compared with previous work that corrected dataset shift45,46,47,48,49,50,51,52,53. It is device-agnostic by nature, and we demonstrated its effectiveness in addressing the dataset shift due to differences in measurement devices, e.g. the skin temperature feature from Oura ring was transformed to have almost identical distribution as the core temperature feature from hospital grade device (Fig. 4). Removing contextual confounders have its challenges in first identifying the relevant context and then finding data elements that can be used to isolate the context, but theoretically has the potential to make our solution context-agnostic. Our generalized hospital model of infection prediction performed well in detecting COVID-19, despite pathogen differences in COVID-19 infection and the set of hospital-acquired infections used to train the hospital model. This is likely because the hospital model was trained from data that included a large range of different infection types, therefore had learned the change of physiological signatures caused by many different types of pathogens including those that are similar as COVID-19. In other words, even though label shift and concept drift were present, P(Y|X) and P(Y) were more similar between the hospital dataset and the wearable dataset than that they were different. Therefore, we believe the generalized hospital model can be easily adapted to deploy in other scenarios of infection prediction, and it is not restricted to a specific set of wearable devices, a specific population, or a specific context. For example, the hospital model of infection prediction may be used to track the health state of healthcare professionals during flu season with a different set of wearables, given that similar types of vital sign signals are collected, and appropriate dataset shift transformations are applied. We acknowledge that in the case where a new pathogen alters the physiological signatures in a way that is significantly different than the set of infection types that we used to train the model, then just correcting for the covariant shift would not be sufficient. Some amount of labeled data from the new pathogen would be needed to properly address label shift and concept drift.

Conclusions

We found that an infection prediction model developed for hospitalized patients can detect early signs of COVID-19 infection from wearable physiological monitoring (AUROC = 0.74), on average 2 days earlier than diagnostic testing, provided that a small sample (e.g. 25 subjects in a period of 14 days) of wearable data from healthy subjects is available to address the dataset shift between hospital dataset and wearable dataset, and that sleep markers can be extracted to control for contextual effects in wearable dataset. Our approaches to transform features between datasets and isolate contextual confounders can enable rapid deployment of a pre-trained infection prediction model at the onset of novel infection outbreaks.