ChebIoD: a Chebyshev polynomial-based lightweight authentication scheme for internet of drones environments

Abstract

The Internet of Drones (IoD) brings an unprecedented prospect for massive aerial data acquisition; on the other hand, it meets severe hindrances in how to accomplish robust, secure, and economic identity authentication with the limited resources available. In this paper, ChebIoD (Chebyshev polynomial-based mutual authentication and session key generation) is proposed as a new mutual authentication and session key agreement protocol for IoD environments. ChebIoD differs from the existing methods of blockchain, PUF, and ECC in that it consolidates three elaborate mechanisms: (a) post-quantum-oriented design methodology; (b) a dynamic solution for key update/revocation scheme; and (c) formal verification using BAN logic, Real-Or-Random (ROR) model, and AVISPA. The principal difference is that we are able to assign a precise definition of security for key privacy; namely, the protocol achieves both forward and backward secrecy along with performance gains for lightweight polynomial computations without requiring exponential hard assumptions. An Enhanced Security Assessment covers side-channel threats as well as the robustness of the Trusted Authority. We also show an updated performance comparison to the IoD-specific AKE protocols and state-of-the-art schemes in recent works on Blockchain-, Physical Unclonable Function (PUF)-, Elliptic Curve Cryptography (ECC)-, and Chebyshev-based approaches. In identical simulation settings, ChebIoD decreases computation time by up to 63.5%, reduces communication overhead by up to 62.4%, and lowers energy consumption by up to 66.7%, compared to state-of-the-art solutions. These improvements are consistent across multiple baselines, though the exact gains vary depending on the compared protocol. The practical utility is showcased by actual IoD projects for disaster response, precision agriculture, and urban air mobility solutions. Overall, ChebIoD demonstrates efficient and scalable authentication for IoD under simulation.

Introduction

The Internet of Drones (IoD) is a pioneering concept and platform, and means drones can work together, sharing data in real time^1,2. This allows it to be used for all sorts of applications such as surveillance, delivery of goods, environmental monitoring, and even disaster response. Security threats encountered in IoD systems, however, are ominous. With the highly changeable drone resources, it is essential for low-cost authentication mechanisms that ensure integrity and confidentiality so that impersonation and spying attacks can not occur, just as any hostile parties are denied entry at the border^3,4. Traditional cryptographic protocols usually cannot meet the particular demands of IoD. Therefore, it is mandatory to create solutions suited for this type of environment^5,6.

Secure and efficient authentication solutions that can operate in resource-constrained devices are needed urgently as the increasing adoption of IoD systems mandates them. However, currently, schemes like blockchain-based architectures⁷, Elliptic Curve Cryptography (ECC) protocols⁸, or more exotic security systems like Physical Unclonable Function (PUF)⁹ lack enough merit to succeed. Whilst secure, blockchain-based protocols suffer from high computation and communication overhead, rendering them impractical on drones with finite resources^10,11,12. Although ECC protocols are efficient in terms of computation, they are vulnerable to a quantum attack, casting doubt upon their prospects for the longer term. PUF-based protocols are suitable for a limited number of devices, but they are not scalable throughout large IoD networks. In addition, the sudden rise of quantum computing suggests that quantum-resistant cryptographic measures must be developed rapidly. These difficulties emphasise to us the need for a protocol having light weight, scalability, and the capability to resist threats from quantum computers.

Symmetric encryption algorithms like AES or entire hash-based protocols can be lightweight and even optimized in that way, but are impossible to shield from quantum-computing threats^13,14. So, Grover’s algorithm just halves the level of security against symmetric primitives, and Shor’s algorithm breaks most public-key systems based on discrete logarithm or factorization. This makes Chebyshev polynomials a uniquely positioned candidate for light-weight, post-quantum-oriented UAV authentication^15,16. So, their chaotic behavior and semi-group law enable fast mutual authentication without much computationally expensive modular exponentiation or elliptic-curve operations^17,18. The former are easier to compute, and at a lower layer deep in the hardware, and can be far less resource-consuming in terms of both computation (recursive modular multiplications) and memory usage for the same security level as an AES encryption/ decryption cycle. These mathematical properties allow ChebIoD to offer session key secrecy and integrated lifecycle management (periodic key update and explicit revocation) at a low overhead suitable for very resource-constrained nodes used in UAV networks.

To solve these problems, we study this in the setting of IoD, where a lone unmanned aerial vehicle (UAV) communicates with an authorized user or ground control station (GCS) in which the UAV wants to securely communicate over an open wireless channel. We consider the general case of mutual authentication and key agreement between a user and any one UAV using a ChebIoD protocol, while preserving data confidentiality, integrity, and certain common network security properties under tight resource constraints. Multi-UAV cooperative networks are an important domain, although inter-UAV authentication is outside the scope of this paper and is left to be addressed in future work. Thus, this paper proposes ChebIoD, an ultra-lightweight authentication protocol that uses the character and randomness of Chebyshev polynomials. The protocol is divided into four phases: the Setup phase, the Registration and Authentication phase, the Key Agreement phase, and the Key Update/Revocation phase. Designed to provide a comprehensive security model that meets all these requirements, this new protocol has a security analysis section capable of determining not only resistance to traditional threats but also its susceptibility to quantum attacks. In addition, performance measures, such as time and computation consumed, communication overhead ratio, power dissipation amounts (electricity costs), and extendibility comparisons with other schemes that can still claim to be scalable despite all the extra work put into them, were successfully done. The significant contributions of this paper are as follows:

• ChebIoD Protocol Design: We design a secure authentication and key-agreement protocol for Chebyshev Orthogonal polynomial-based Cryptography (ChebIoD) using lightweight hardness relying on the Chebyshev orthogonal to reduce the complexity of operation by leaving out computationally intensive hardware operations. The protocol enables lightweight mutual authentication and provides robust protection against key security threats like impersonation, replay, and man-in-the-middle attacks. It also includes support for key updates at intervals and explicit revocation, which previous Chebyshev-Diffie-Hellman variants have lacked.

• Security Model and Threat Coverage: ChebIoD is formally verified using BAN logic, Real-Or-Random (ROR) model, and automatic verification with AVISPA. The threat model specifically considers limitations of forward secrecy, privileged insider vulnerabilities, and provides a comprehensive UAV-specific threat model. Although the core hardness assumption is still the Chebyshev polynomial inversion problem over finite fields, we do not provide any unconditional post-quantum security guarantee, but simply observe that there is no known polynomial-time quantum algorithm for solving this problem in our case.

• Performance and Scalability: Extensive experiments demonstrate that ChebIoD reduces the computational time up to 63.5%, communication overhead 62.4% and energy consumption by 66.7% compared to typical blockchain-based, ECC-based approaches, outperforming well of other Chebyshev based protocols as well We evaluate the protocol for large and dynamic drone networks, and show that it scales well while maintaining both performance metrics.

The rest of this paper is organized as follows: “State of the art” reviews existing IoD authentication protocols and their limitations. “Background” introduces IoD systems and the cryptographic properties of Chebyshev polynomials, the system model, the threat model, and security requirements. “Proposed ChebIoD protocol” proposes phases of the ChebIoD scheme. “Security analysis” analyzes formal and informal security for the protocol’s robustness against classical and quantum threats. “Performance evaluation” highlights and compares performance metrics ChebIoD scheme with existing protocols. “Conclusion” summarizes the findings and outlines future research directions.

State of the art

The popularity of the Internet of Drones (IoD) has prompted much research on secure and efficient authentication protocols as classified in Table 1. Nevertheless, current approaches often fail to take into account the specific requirements of IoD systems, such as constrained computational capabilities, high mobility, and quantum threat exposure.

Table 1 Classification of reviewed authentication protocols for IoD.

Blockchain-based schemes

To secure and maintain the immutability of the IoD environment, blockchain architectures have been suggested. For instance, Wazid et al.¹⁹ introduce BCF-IoDAC, which is a blockchain-enabled secure communication framework for IoD-assisted aerial computing, improving security as well as communications latency and energy efficiency levels. Karmegam et al.²⁰ proposes a blockchain-based inter-domain authentication for IoD to improve the security and efficiency. It employs ECDSA for authentication and pseudonym-based identity protection, as well as Hyperledger Fabric for decentralized trust. Aggarwal et al.²¹ offers a solution for UAV path planning based on an efficient genetic algorithm (GA) that is secure through blockchain in 3D space. Ju et al.⁷ presented a blockchain-based mutual authentication protocol to prevent drone impersonation and the session key agreed upon from being exposed. It was designed with low computational overhead in mind.

Blockchain, being able to provide decentralization, immutability, and traceability, introduces significant problems when added to IoD systems. The computational overhead of consensus protocols (e.g., proof-of-work) results in latency and energy consumption that makes them inadequate for real-time UAV missions. Furthermore, transaction metadata and smart contract storage will increase the example and create communication overhead that is unsuitable for lightweight drone platforms.

PUF-based protocols

PUFs have been employed to construct lightweight authentication models. Ayebie et al.⁹ presents feature-presentation PUFs for authentication. Its lightweight was not addressed in large-scale drone swarms, however. Chaudhry et al.²² introduce TS-PAID in this work, a 2-stage PUF-based user authentication protocol designed for resource-constrained IoD systems. It provides improved computational and communications efficiency as well as resistance to attacks, such as physical compromise. Choi et al.²³ presents a lightweight and secure authentication scheme based on physical unclonable function (PUF) and hash operation for UAV-supported IoV networks. It is secure against MITM and ESL attacks as well as the two previous ECC-based schemes, and has even lighter computation. Tian et al.²⁴ presents a lightweight, PUF-based mutual authentication scheme suitable for UAVs, and made to address the constraints of centralized single-domain systems.

PUF-based protocols have been demonstrated for device-level authentication, taking advantage of hardware uniqueness. But they have environmental susceptibility, which may lead to unreliably elicited responses. Additionally, owing to the requirement of fuzzy extractors and helper data, not only is increased, but also storage and synchronization overheads are involved, which leads to scalability issues for large swarms of drones.

ECC-based protocols

Elliptic Curve Cryptography (ECC) is popular for its computational efficiency and shorter key length^35,36,37,38. Jan et al.²⁵ introduces an ECC-based secure authentication for IoD environments with FANETs. It provides mutual authentication, message integrity, and perfect forward secrecy even in the face of dynamic topology and open-channel attacks. Zhang et al.²⁶ exposes several flaws in the ECC-based Internet of Drones (IoD-AS) authentication design. It shows that the scheme cannot resist the impersonated drone attacks and leaks session keys between the user and their drones to the adversaries–in other words, the entity authenticity and session confidentiality are broken. Gupta et al.⁸, with its focused techniques on HMAC-SHA1 for lightweight security, demonstrated the low overhead required.

ECC provides small key sizes and good cryptographic security levels, but its operations (e.g., scalar point multiplication) are computationally intensive. This renders ECC not to be unsuitable for power-constrained UAVs with quick authentication. In addition, ECC is susceptible to quantum computing attacks, making it less future-ready for long-term use.

Other notable approaches

Hybrid or bespoke systems, such as zero-trust or post-quantum designs, are other examples. A new multi-factor authentication scheme for IoD environments, combined with zero-trust security models with quantum attack resistance mechanisms proposed by²⁷. Proposed²⁸ a neighbor authentication protocol that reduces communication overhead, but is not resistant to quantum attacks. In²⁹, IoEPM+ (environmental monitoring platform for Project N) uses blockchain with 6G technology. It had excellent expandability but met a bottleneck when it reached quantum immunity. It was lightweight but without any official protection against formal quantum attacks. However, our current efforts in post-quantum cryptosomatic resistance have not yet proven successful. It³⁰ addressed drone anonymity but faced challenges in scalability and complexity for large networks. In³¹, group authenticated key distribution for drones was looked at, which focused on how to do it effectively, but was still confronted by the quantum-capable adversary.

IoD-specific authenticated key-exchange protocols

In the context of the Internet of Drones, several lightweight authenticated key-exchange (AKE) proposals have been made. Mahmood et al.³² proposed a chaotic-maps-based authentication protocol in which they integrate a hash function together with the PUF to provide an additional layer of security against physical attacks. Although their scheme produces significantly lower computation and communication overhead than previous IoD protocols, it is still based on pre-quantum security assumptions and does not include an efficient key-update mechanism or explicit revocation processes. Lee et al. Using dynamic identities to enhance privacy protection for IoD communications, the authors of³³ applied it on a lightweight AKE protocol. Although the design enforces more compact message formats and allows mutual authentication, it suffers from the same lack of a post-quantum security story and does not include lifecycle management capabilities (key update/revocation). Chaudhary et al.³⁴ proposed AKE -MP, which is an optimized message flow with a lightweight algorithm to save online computation cost. The scheme, though successful in reducing the cost at the device side, does not appear to have any explicit support for post-quantum security or, more importantly, key-update phases, along with the provision of formal logic analysis/authentication.

While each of these protocols provides optimizations for the IoD setting, neither manages to address all of the following at the same time: (i) Design for post-quantum resilience (ii) Integration with key update and revocation scheme (iii) Formal BAN-logic proof, and (iv) Comprehensive evaluation of scalability to large-scale drone swarms. To address the lack of timely and frequent patching among IoT devices, we present ChebIoD: a system that closes these gaps by combining Chebyshev-polynomial-based challenge-response with lightweight arithmetic, lifecycle controls, and formal analysis.

Gap analysis

Though IoD-specific AKE protocols have been developed^32,33,34 and other similar approaches like Blockchain-Based⁷, PUF-Based⁹, and ECC-Based ⁸ authentication schemes, there still exist some serious limitations. The first one is that most of the existing solutions are tied to pre-quantum hardness assumptions (discrete logarithm, elliptic curve, or chaotic maps) without a post-quantum security justification. Secondly, most do not provide integrated lifecycle management, especially periodic key updates and explicit revocation to mitigate long-term compromise in dynamic drone swarms. Third, scalability for large-scale deployments is limited by larger message sizes or computational overhead, which can weigh down resource-scarce aerial nodes. Finally, almost all are based on an intentional-only security argument, not on formal validation of authentication or key freshness. ChebIoD fills all of these gaps with a challenge–response mechanism based on Chebyshev polynomials that is both post-quantum secure, includes ad-hoc support for key update and revocation, respects the computational and communication constraints, and provides a formal BAN-logic proof of its security properties.

Background

This section describes the system model, threat model, and security goals of the ChebIoD protocol. It describes the main assets–drones, users, servers, and a trusted authority–and provides Chebyshev polynomials as a lightweight, quantum-resistant cryptographic base for secure IoD authentication.

System model

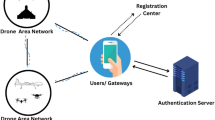
Since the ChebIoD protocol is run on top of the user-side, single-UAV setting, the UAV and its/user/GCS authenticate each other to establish a shared session key before transmitting sensitive control or telemetry data. However, the design and evaluation in this paper are not for UAV-to-UAV authentication, even if extension efforts regarding inter-UAV authentication can be envisioned as part of potential future venues. This section provides to secure lightweight authentication method for the ChebIoD system model in the IoD environment. As shown in Fig. 1, herein are the following components:

Fig. 1

System model.

• Trusted authority (TA): a central entity responsible for the initialization of the system, generation of security parameters and encryption key, secure distribution of these to both drones and users, and Updates maintaining effective revocation enforcement control. At the same time, it also handles periodic updates on cryptographic keys and revoking damaged certificate files.

• Drones: these drones are flying robot instruments equipped with various abilities; their primary function is to provide services such as environmental observation, postal distribution of postal items, and electronic commerce business support. They are severely limited in computational and storage resources, requiring lightweight cryptographic techniques to cope with these constraints.

• Users: authorized entities (e.g., other people or businesses) that use drones to provide them with what they want. In any case, users must make sure their identities are always correctly authenticated and confirmed.

• Servers: center or main server, responsible for storing registration data. These servers assist in validating the request to be registered and act as intermediaries between users and drones, ensuring secure communication, which makes it possible for these two kinds of entities to exchange information.

Threat model

Design of the ChebIoD protocol is motivated by an adversary $\mathcal {A}$ that resides in a typical network security model such as the Dolev–Yao model^39,40, i.e., where $\mathcal {A}$ plays both active (sending messages) and passive roles. $\top : A$ can modify, inject forged messages, and mimic other parties; it has complete control over all communication channels among drones (D), ground stations (GS), and the trusted authority (TA). The following are adversarial capabilities considered:

• Passive eavesdropping: $\mathcal {A}$ can intercept and record all exchanged messages without altering them.

• Active message injection/modification: $\mathcal {A}$ can insert, modify, or delete messages in transit, including altering payloads or protocol fields.

• Replay attacks: $\mathcal {A}$ can retransmit previously intercepted valid messages in an attempt to gain unauthorized access. ChebIoD mitigates this by incorporating timestamps and nonces into the message flows, with strict freshness checks.

• Impersonation attacks: $\mathcal {A}$ can attempt to masquerade as a legitimate drone, GS, or TA to forge protocol messages.

• Man-in-the-middle (MitM) attacks: $\mathcal {A}$ can intercept, alter, and forward messages between two legitimate parties, aiming to subvert authentication or key agreement.

• Physical compromise: $\mathcal {A}$ may obtain temporary or permanent physical access to a drone or GS to attempt key extraction, firmware tampering, or side-channel analysis.

• Timestamp manipulation: $\mathcal {A}$ may attempt to exploit clock drift or inject outdated timestamps. ChebIoD uses bounded clock drift verification to reject stale or manipulated timestamps.

• Quantum-capable attacker: The threat model assumes that $\mathcal {A}$ may possess a large-scale quantum computer capable of breaking traditional public-key schemes (e.g., ECC, RSA) but cannot efficiently solve the Chebyshev Polynomial Iteration Problem (CPIP) or Modular Chebyshev Map Problem that underpin ChebIoD.

ChebIoD has the following security objectives to provide mutual authentication, key freshness and confidentiality of session keys, resistance to replay, impersonation, and Man-In-The-Middle attacks, all while withstanding quantum-capable adversaries according to the threat model capabilities listed above. We distinguish between two types of key exposure:

• Long-term key leakage—an adversary learns a party’s static private key or other persistent credentials.

• Session-key leakage—an adversary learns the ephemeral session key for a single authentication instance.

The ChebIoD design depends on the assumption that long-term private keys are kept confidential for as long as they are meant to be used in the intended network. Since the long-term key can compromise session keys that were created before its compromise, the scheme does not have the property of Perfect Forward Secrecy (PFS). In a like manner, the existing design does not offer Post-compromise server secrecy (PCS): getting back previously secure sessions after a long-term master-key compromise. Integrating ephemeral key pairs or creating other key-update mechanisms to add PFS/PCS would increase the computational and communication overhead. It is left as a trade-off for future work to maintain the light-weight nature of the scheme for IoD deployed on resource-starved IoT devices with limited energy budget.

Security requirements

The ChebIoD protocol endeavors to accomplish several security objectives for protecting the IoD environment:

• Mutual authentication: confirm that both the drone and user verify the other’s identities before any contact is made.

• Confidentiality: making communications data confidential, so that it is not accessible to unauthorized entities.

• Integrity: a guarantee that messages passing between different entities are not changed during transmission.

• Resistance to replay attacks: stop adversaries from reusing captured messages with unauthorized access.

• Resistance to impersonation attacks: insured that legitimate drones or users can not be impersonated by adversaries.

• Resistance to man-in-the-middle attacks: thwart adversaries in their attempts to intercept and change messages between reporters or other bodies of legitimate transmitter or recipients with invalid messages.

• Resistance to quantum attacks: make sure the main cryptographic components are resilient to quantum computing attacks, using mathematical structures such as Chebyshev polynomials that quantum algorithms do not directly attack.

• Lightweight operations: exert the minimum possible computational and communication overheads to cater to resource-constrained IoD devices, such as drones.

The above security demands form a secure yet efficient authentication protocol foundation for the IoD environment, even when faced with adversaries who command quantum power to drive technology into new realms.

Chebyshev polynomials

This part briefly reviews Chebyshev polynomials as the cryptographic primitives of the ChebIoD protocol. It emphasizes their mathematical structure, such as semi-group structure and their chaotic nature, and discusses their importance for secure, lightweight cryptography. These polynomials support fast mutual authentication, are resistant to quantum attack, and are suitable for use in IoD environments with resource constraints.

Mathematical properties

Chebyshev polynomials are kind of mathematical “mixers”; if you repeatedly apply them with a secret parameter, it is hard to predict the output without knowledge of that secret, and even after having seen some results. This is much like encoding a signal to the point of being un-decodable without the key. Using this in ChebIoD, doing so does take the promptest lightweight audits for mutual authentication; nonetheless, to be resilient to attacks that would force impractical computation. Chebyshev polynomials of the first kind $T_n(x)$ are defined over the reals by the recurrence relation ^41,42:

$$T_0(x) = 1,\quad T_1(x) = x,\quad T_{n+1}(x) = 2x \cdot T_n(x) - T_{n-1}(x),\quad n \ge 1.$$

For cryptographic use in modular arithmetic, we adopt the finite-field analogue ^43,44: $T_n(x) \equiv \frac{g^n + g^{-n}}{2} \pmod {p}$, where g satisfies $g + g^{-1} \equiv 2x \ (\bmod \ p)$, p is a large prime, and all operations are in $\mathbb {Z}_p$. These polynomials have several mathematical properties relevant to cryptography:

• Semigroup property: $T_{mn}(x) = T_m(T_n(x))$ for any integers m, n. This property is central to constructing key agreement protocols.

• Chaotic behavior: for certain parameters, Chebyshev polynomials exhibit properties associated with chaos theory, making inversion difficult without knowledge of the degree n, which underpins their one-wayness assumption in cryptographic contexts.

• Orthogonality: they are orthogonal over the interval $[-1, 1]$ with respect to the weight function $(1 - x^2)^{-1/2}$, ensuring mathematical stability and predictable structure.

While there is no known polynomial-time quantum algorithm for inverting $T_n(x)$ in $\mathbb {Z}_p$ under the above setting, we do not claim unconditional post-quantum security. Our security argument follows prior analyses ^43,44 and assumes the hardness of recovering n from $(x, T_n(x) \bmod p)$ against both classical and currently known quantum attacks.

Cryptographic relevance

Chebyshev polynomials have been employed as tools of significance in light-weight cryptography because they are computationally simple and possess built-in security properties:

• Secure one-way transformations: the semi-group property allows the unfriendly digit sequence to be phase-modulated in a chaotic fashion that is secure against brute-force attacks⁴⁵.

• Lightweight operations: Chebyshev polynomials involve such basic arithmetic operations as addition and multiplication, which are particularly compatible with demand computing capability very little of the energy it takes to run, like Miquus drones

• Resistance to quantum attacks: unlike traditional cryptographic schemes that depend on factorization or discrete logarithms, Chebyshev Polynomials depend on properties that are not readily accessible by quantum algorithms.

• Flexibility: in distributed environments, the properties of the semi-group operation can be used for efficient mutual certification and safe key exchange.

With these properties, Chebyshev polynomials are an ideal candidate for securing the IoD systems and cover both lightweight and post-quantum security requirements.

Mathematical assumptions underpinning ChebIoD security

The security of the proposed ChebIoD protocol is based on several well-defined mathematical hardness assumptions:

• Chebyshev polynomial iteration problem (CPIP): given $T_n(x) \bmod p$ and x, where $T_n$ is the n-th degree Chebyshev polynomial over the finite field $\mathbb {Z}_p$, it is computationally infeasible to determine n in polynomial time. This property underpins the one-way nature of our challenge–response mechanism.

• Semi-group property hardness: while Chebyshev polynomials satisfy the semi-group property $T_r(T_s(x)) = T_{rs}(x)$, predicting $T_{rs}(x)$ for unknown r and s without explicit computation is believed to be infeasible. This contributes to the difficulty of forging valid session keys without knowing the secret exponents.

• Modular Chebyshev map problem: the modular version of the Chebyshev map does not have an efficient inversion algorithm, even with quantum resources, due to its non-linearity and lack of structure exploitable by known quantum algorithms such as Shor’s or Grover’s.

• Post-quantum resistance: the above problems are not reducible to the discrete logarithm, integer factorisation, or other group-based problems vulnerable to Shor’s algorithm, thereby offering resistance to large-scale quantum adversaries.

These assumptions form the foundation of ChebIoD’s security guarantees, ensuring that both classical and quantum-capable adversaries face prohibitive computational complexity in breaking the scheme.

Review of Chebyshev polynomial-based protocols

A number of lightweight authentication schemes based on Chebyshev polynomials have been proposed in the literature because of their semigroup property, chaotic behavior, and low computational cost over finite fields. It does so while still enjoying the properties of a symmetric cipher, enabling secure key agreement and identity protection without relying on expensive modular exponentiation or elliptic-curve operations.

There is a provably safe Chebyshev-based authentication protocol for IoT devices developed by Ahamad et al.⁴³ with lower computation complexity compared to ECC. Rivlin et al.⁴⁴ provides the Chebyshev iterations for secure key generation by using a different system of linear equations than the above papers (without correlated states), but do not provide an integrated or related mechanism for updating or revoking a key. Similarly, some other works have used Chebyshev-based challenge–response designs for mutual authentication in wireless networks ^46,47, but they either leverage only informal security arguments or do not tackle post-quantum threats. ChebIoD contributes to this line of research by:

• Providing a formal quantum-security proof under the Real-Or-Random (ROR) model.

• Incorporating lifecycle management via periodic key update and explicit revocation.

• Optimizing message structure and polynomial arithmetic for large-scale UAV deployments.

These improvements make ChebIoD more suitable for Internet of Drones (IoD) scenarios than previous Chebyshev-based works.

Security assumptions and key synchronization

The ChebIoD design is built around security assumptions, which in turn define the operational trust boundaries of the devices.

• Trusted authority (TA). The TA is said to have end-to-end trust at that time, capable of creating, distributing, and revoking system credentials. It contains no compromise from any adversary in the original threat model. Adversaries can issue bogus certificates, unauthorized revocation requests, or steal sensitive key material using The TA could be compromised. Possible Remediations include more TAs using threshold cryptography or incorporating blockchain-based PKI frameworks.

• Secure initial enrollment. The initial credential provisioning phase between each legitimate drone/user and the TA occurs over a secure, authenticated channel.

• Cryptographic primitive strength. The hardness assumptions underlying Chebyshev-polynomial-based operations hold against both classical and quantum adversaries.

• No physical compromise of TA or nodes. Unless otherwise stated, adversaries do not obtain physical access to the TA or legitimate drones to extract stored secrets. Side-channel and physical attack considerations.

• Side-Channel and Physical Attacks. Side-channel attacks (e.g., power analysis, timing analysis) and physical tampering with drones or the TA are excluded from the baseline threat model.

• Channel assumptions. We further assume that each UAV/user is registered in the first place with the Trusted Authority (TA) via a secure and authenticated channel initially (e.g., a physical secure link or TLS-protected session). The remainder of the protocol phases, including mutual authentication and key updates, can all happen over a wireless channel, which is open (and may be secure).

• Key-update distribution. Whenever keys are refreshed, the TA itself creates a fresh set of parameters and distributes this information to each registered participant using the same secure channel as for the original registration. In this fashion, no adversary can eavesdrop on the communication with the key updates. This is true in deployments where a long-term secure channel can not be maintained, and then the key-update message needs to be placed within an authenticated with encryption session using a second shared key session.

• Desynchronization resilience. In order to prevent desynchronisation (like when a key-update message was lost or corrupted), each player keeps both the latest and second latest valid one for a little while longer. If a key does not match and a session fails, the protocol tries one time with the previous key before forcing re-registration. This has the effect of protecting against denial-of-service attacks that could be due either to a deletion or alteration of an update key.

The used assumptions follow the state-of-the-art in lightweight IoD authentication research and thus represent a good base for the following security analysis.

Proposed ChebIoD protocol

The ChebIoD scheme proposed here takes advantage of Chebyshev polynomials in order to create a lightweight but secure authentication protocol for Internet of Drones (IoD) environments. The scheme is divided into four phases: Setup, Registration, Authentication and Key Agreement, and Key Revocation, as shown in Figure 2. These phases ensure mutual authentication between users and drones, secure session key generation, and effective management of plexus participants.

Fig. 2

Phased of proposed ChebIoD proposed.

With its property as a semi-group, Chebyshev polynomials cannot be reverse-engineered. This makes them the ideal choice for resource-limited environments where lightweight cryptography is required. In the ChebIoD algorithm, exploiting their mathematical simplicity, both computational and communicative overhead are low, and security remains at a high standard. Table 2 shows the notation used and its description in the ChebIoD protocol.

Table 2 Notation used in ChebIoD protocol.

Setup phase

According to this phase, it aims to establish the cryptographic foundation of the protocol. A trustworthy authority (TA) initializes the system by choosing a big primary modulus p, a random seed (x0), and a secret polynomial degree n. The TA uses these parameters to calculate the Chebyshev polynomial $T_n(x_0)$ mod p and distributes the system parameters securely to all participants, including drones, users, and servers. This guarantees that all entities involved have the necessary common parameters for identification and key contracts. Algorithm 2 describes the setup phase of the ChebIoD protocol.

Algorithm 1

Setup phase of ChebIoD protocol.

Registration phase

In the registration stage, with Chebyshev polynomial-based random, unique cryptographic keys are developed not only for drones but also for their pilots. Drones produce random seeds, compute their polynomial values ($T_{n_D}(x_{D_i}) \text { mod }p$), and send them together with their identifications to the server, which verifies that it is correct. Likewise, users produce their keys ($T_{n_U}(x_{U_j}) \text { mod }p$) before submitting them to the server for inspection purposes. The server uses system parameters that both parties share to check these keys. Then it stores validated credentials, which will ensure safety in future interactions and collaborations.

Algorithm 2 depicts the entire Registration Phase; it shows the separate paths of Drone Registration and User Registration. This stage is used to register authentic drones and users in the system, thus establishing a foundation for secure communication inside the IoD environment.

Algorithm 2

Setup phase of ChebIoD protocol.

Drone registration

• The drone $D_i$ generates a random seed $x_{D_i}$ and computes $T_{n_D}(x_{D_i}) \text { mod }p$.

• $D_i$ sends $ID_{D_i}$, $x_{D_i}$, and $T_{n_D}(x_{D_i})$ securely to the server.

• The server validates $T_{n_D}(x_{D_i})$ using the shared $T_n(x_0)$.

• Upon successful validation, the server stores $ID_{D_i}$ and $T_{n_D}(x_{D_i})$ for later reference.

User registration

• The user $U_j$ generates a random seed $x_{U_j}$ and computes $T_{n_U}(x_{U_j}) \text { mod }p$.

• $U_j$ sends his ID, $x_{U_j}$, and $T_{n_U}(x_{U_j})$ to the server securely.

• The server checks $T_{n_U}(x_{U_j})$ using the shared $T_n(x_0)$.

• With this validation, the server stores $ID_{U_j}$and $T_{n_U}(x_{U_j})$.

Authentication and key agreement phase

In this phase, mutual authentication between a user and a drone is carried out, and a shared session key is created for secure communication. The user begins by sending the drone an authentication request. The drone will challenge the user with a Chebyshev polynomial value, $C$, which the user will check and respond to by doing the corresponding polynomial computation $R$. If valid, then both the user and the drone will each compute a common session key ($SK_{U_j-D_i} = T_{m_D \cdot m_U}(x_0) \text { mod }p$) employed to ensure privacy and integrity of subsequent communications. Otherwise, the process restarts at step one above, as this has gone wrong - neither we nor others who are listening need what comes out next instead. Algorithm 3 provides a step-by-step authentication and key agreement phase.

Algorithm 3

Authentication and key agreement phase of ChebIoD protocol.

Role of Timestamps in ChebIoD: Timestamps are incorporated into each protocol message to guarantee message freshness and prevent replay attacks. Let $TS_i$ denote the current local time of entity i at the moment of message generation. Upon receiving a message containing $TS_i$, the recipient verifies that: $|TS_{\text {recv}} - TS_{\text {local}}| \le \Delta T$, where $\Delta T$ is the maximum allowable clock drift between the two entities (e.g., a few seconds in typical UAV deployments). If this condition fails, the message is rejected.

ChebIoD derives timestamps using the node’s secure Real-Time Clock (RTC), or synchronized GPS time. By exploiting freshness, replay attacks are defended against, as long as the adversary replays a previous valid message past the appropriate timestamp in the future, it will be regarded as invalid. With a combination of timestamp verification and the use of nonces, ChebIoD makes it even more difficult for replay attacks to succeed, whether it is a basic replay attack or an advanced version that brews with network delays or clock drift.

Initiation of request:

• With the user’s unique identifier $U_j$, it’s timestamp $ID_{U_j}$ is securely and accurately created by the user. This creates a time signature in each data line sent that identifies what time it was sent and then received back to the drone $D_i$. By including this timestamp, the request is fresh, and we can prevent replay attacks.

• Upon receipt of such an authentication request $D_i$ begins to verify the user’s identity at the implementation

Drone challenge:

• When the user’s authentication request arrives, drone $D_i$ generates a cryptographic challenge $C$. It does this using the Chebyshev polynomial $T_{m_D}(x_{U_j}) \text { mod }p$, where $m_D$ is the drone itself ’s secret parameter and $x_{U_j}$ is gotten indirectly from user $U_j$’s identifier alone or mutual cryptographic materials

• This challenge $C$ is then sent back to $U_j$, who must now demonstrate that he really can answer such challenges correctly if he is to get a valid result. This makes sure the user holds valid cryptographic credentials.

User response:

• Upon receiving the challenge $C$ sent by the drone $D_i$, the user $U_j$ does its own cryptographic parameters check. This ensures that the challenge comes from a real source and has not been tampered with after being introduced into transmission

• Once confirmed, user generates a response $R = T_{m_U}(x_{D_i}) \text { mod }p$. Here $m_U$ is the user’s secret parameter, and $x_{D_i}$ is derived from drone $D_i$’s name or related information.

• The response $R$ is then returned to $D_i$.

Mutual authentication:

• Upon receipt of dialogue $R$ created by user, drone $D_i$ does its secret parameter verification and cryptographic algorithm check. Upon completion of these checks, and if successful, we say the user is legitimate.

• Now $U_j$ and $D_i$ have both authenticated each other. They are ready to start securely communicating over an established.

Session key generation:

• To complete the neither done $U_j$ nor $D_i$ has to know what the other is doing-both are using Chebyshev’s polynomial, and separately calculate a session key $SK_{Uji-Di}$ as follows Eq. (1).

  $$\begin{aligned} SK_{U_j-D_i} = T_{m_D \cdot m_U}(x_0) \text { mod }p. \end{aligned}$$

  (1)

• Here, $x_0$ is a value that has been publicly agreed upon by both parties, and the computed session key $SK_{U_j-D_i}$ is the same due to the shared use of Chebyshev’s polynomial properties.

• Then, in all further communications between the user $U_j$ and the drone $D_i$ (regardless of whether those take aerobic or anaerobic form), we will employ this session key to ensure both integrity as well as confidentiality of information that gets passed back and forth between them.

Key update and revocation phase

To maintain infrastructure long-term security, the protocol has built-in key updates whereby every so often the trusted authority will generate new system parameters ($n', x 0'$) and report the latest Chebyshev polynomial values ($T{n'}(x_0') \text { mod }p$) to all entities. The keys corresponding to publishable are taken from the server’s database, and in this manner, jamming attempts on it are prevented. If a drone or user gets compromised, delete the associated key from the server’s register, and tell all other machines not to communicate with that particular compromised entity. Thereby, we make sure that even when the enemy has accepted, the protocol is as solid as ever against outside pressures. Algorithm 4 shows the Key Update and Revocation Phase in the ChebIoD protocol.

Algorithm 4

Key update and revocation phase of ChebIoD protocol.

Key update

• The Trusted Authority generates new system parameters, specifically a new polynomial degree $n'$ and a fresh random seed $x'_0$, then computes the updated Chebyshev polynomial $T_{n'}(x'_0) \text { mod }p$.

• These updated parameters are securely distributed to all participating entities in the network to ensure synchronized cryptographic operations.

Key revocation

• If a drone or user is compromised, its corresponding $T_n^k(x)$ is wiped off the server registry.

• All the other participants are directed to intercept this entity’s transmissions.

Security analysis

This section assesses the security of the ChebIoD protocol against cyber attacks. It combines informal and formal (BAN logic) work and demonstrates resistance to replay, impersonation, MitM, key compromise, and quantum attack. ChebIoD is compared with existing protocols as well, and the section provides a discussion on its improved security strength, efficiency, and scalability.

Informal analysis

• Mutual authentication: ChebIoD accomplishes mutual authentication by employing a bootstrap-response plan based on the semi-group properties of Chebyshev polynomials: $T_{mn}(x) = T_{m}(T_{n}(x)) = T_{n}(T_{m}(x))$. During authentication, the drone generates a challenge $C = T_{m_D}(x_{U_j}) \pmod p$, where $m_D$ is the drone’s private seed and $x_{U_j}$ is derived from the user identifier. The user verifies $C$ and returns a response $R = T_{m_U}(x_{D_i}) \pmod p$, where $m_U$ is the user’s private seed and $x_{D_i}$ is derived from the drone identifier. In this way, no keys are shared among users. That can be executed safely as well as savvy mutual authentication without direct key sharing.

• Confidentiality: for confidentiality to be guaranteed, DIoDBChose one especially to use for encrypting where $SK = T_{m_{U} \cdot m_{D}}(x_{0}) \text { mod }p$, with $x_{0}$ as the public seed and $m_{D}, m_{U}$ regulates the lower and upper degrees of the control polynomial. This lightweight key generation ensures secure communication without complex cryptographic operations.

• Integrity: data integrity is achieved by securing the message exchange with the session key. For example, a message $M$ is encrypted as $E(M) = M \oplus SK$, where $SK$ is the session key. If $M$ is tampered with by an unauthorized attacker during transmission, it in all probability will be rejected when decrypted. This lightweight mechanism guarantees that message timestamps can be taken again from tamper-evident collections that were made without tampering detection and replaced with the corresponding messages while ensuring minimal computation overhead.

• Resistance to replay attacks: with timestamps (TS) incorporated into authentication messages, it is impossible for anybody to launch replay attacks. For example, a typical request contains (IDUj, TS, H(IDUj||TS||SK)), where H is a lightweight hash function. The drone verifies the freshness of TS and culls old or replayed messages. The scheme effectively combats replay vulnerabilities in IoD systems.

• Resistance to impersonation attacks: when impersonating another user account, an attacker is stopped by letting the entities prove they have ownership of a private seed without giving it away. During authentication the drone issues a challenge: $C = T_{m_D}(x_{U_j}) \text { mod }p$, and user responds with $R = T_{m_U}(x_{D_i}) \text { mod }p$. Without the private seeds $m_D$ and $m_U$, no interceptors can imitate $C$ or $R$, so we achieve secure identity verification. In this way, security checks are based on Chebyshev polynomials.

• Resistance to man-in-the-middle (MitM) attacks: session keys are derived from private seeds that are never transmitted. So MitM attacks are no threat at all. Given $C$ and $R$, even an eavesdropper can’t calculate $SK = T_{m_D \cdot m_U}(x_0) \text { mod }p$ without the private seeds.

• Resistance to quantum attacks: ChebIoD is not susceptible to quantum attacks because Chebyshev polynomials are Chaotic and nonlinear. Unlike traditional cryptosystems that depend on the factorization of numbers or discrete logarithms, the non-linear growth of $T_n ( x )$ prevents algorithms based on Quantum mechanics from being effective. No person knows how to recover $x$ from $T_n ( x )$ $\text { mod }$ p. The fact that we do not know $n$ or $x_0$, makes future-proof security a fact.

• Lightweight operations: the recursive definition of Chebyshev polynomials, $T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x)$, enables simple computations using only elementary arithmetic like addition and multiplication. This makes all protocol computations efficient on resource-limited IoD devices, including key derivation and authentication.

• Resistance to key compromise: to mitigate the risk of key compromise, ChebIoD periodically changes cryptographic parameters. If a private key is compromised, the trusted authority will generate new seeds and polynomial degrees. The new key is calculated as $K_{new} = T_{n'}(x_0') \text { mod }p$, where $n'$ and $x_0'$ are the new parameters. This guarantees long-term security by means of lightweight, manageable key renewal.

• Resistance to denial-of-service (DoS) attacks: authentication computations can be optimized to ward off DoS attacks. The process of challenge and response requires simple polynomial calculations, such as $C = T_{m_D}(x_{U_j}) \text { mod }p$. This increased efficiency consumes fewer resources, so that the system can still respond even when there is a high load on requests.

• Resistance to collusion attacks: collusion attacks can be eliminated by giving each entity unique private seeds. In this way, even when adversaries have compromised their keys, they cannot derive session keys for other things. For instance, the session key $SK = T_{m_D\cdot m_U}(x_0) \text { mod }p$ depends on the private seeds of both the user and the drone. This means that the damage done by collusion will not spread throughout the security protocol.

• Forward secrecy: ChebIoD realizes forward secrecy since a fresh pair of nonces/ timestamps and an ephemeral parameter-dependent Chebyshev polynomial computed in each session i derive the session key $SK_{i}$ from $(N_D, N_{GS})$, and $(TS_D, TS_{GS})$. Even if an adversary recovers the long-term secret keys after a particular session, they are unable to infer past session keys as these ephemeral values are not stored or reused.

• Backward secrecy: ChebIoD also provides backward secrecy because the session key for the following session $SK_{i+1}$ is regenerated based on new random nonces, timestamps, and fresh polynomial parameters (due to the integrated key update phase). So even if the session key of this session is compromised, that does not mean any more keys will be revealed in other sessions. The scheduled key-update mechanism ensures that even long-running deployments keep this property.

• Resistance to privileged insider attack: in the ChebIoD system, a privileged insider (e.g., at the Trusted Authority) cannot derive from scratch the session key even if he does not know the ephemeral nonces and timestamps exchanged directly between drone and ground station. The TA provisions the initial parameters $(p, x_0, T_n(x_0))$ to an AE but does not save or observe the nonces and Chebyshev polynomial evaluations exchanged in authentication. In addition, session keys are never sent in the clear and are independently computed by each party through one-way transformations, which won’t allow them to be reconstructed by any insider who does not have both parties’ ephemeral secrets.

BAN logic analysis

BAN (Burrows–Abadi–Needham) logic is a formal technique that has evolved to be used as a means of authentication protocol analysis, making verifications for the protocol’s mutual authentication and secure key exchange^48,49. Here’s the detailed BAN Logic analysis for the ChebIoD protocol.

Initial assumptions

The initial assumptions for the BAN Logic analysis of the ChebIoD protocol are summarized in Table 3.

Table 3 Initial assumptions in BAN logic analysis.

Goals of the protocol

The goals of the ChebIoD protocol can be expressed as follows:

• Mutual authentication: $U_j$ believes $D_i$ is legitimate, and $D_i$ believes $U_j$ is legitimate.

• Session key agreement: both $U_j$ and $D_i$ believe $SK$ is a shared session key known only to them.

• Freshness: both $U_j$ and $D_i$ believe $SK$ is fresh and not reused.

Protocol messages

The protocol messages between the user $U_j$ and the drone $D_i$ are as follows:

• 1. Message 1 (authentication request): the user $U_j$ sends its identifier $ID_{U_j}$, a fresh timestamp $TS$, and a hash $H(ID_{U_j} || TS)$ for integrity, as shown in Eq. (2).

  $$\begin{aligned} U_j \rightarrow D_i : ID_{U_j}, TS, H(ID_{U_j} || TS) \end{aligned}$$

  (2)

• 2. Message 2 (challenge): the drone $D_i$ sends a challenge $C$, the timestamp $TS$, and a hash $H(C || TS)$ for verification, as shown in Equation 3.

  $$\begin{aligned} D_i \rightarrow U_j : C = T_{m_D}(x_{U_j}) \text { mod }p, TS, H(C || TS) \end{aligned}$$

  (3)

• 3. Message 3 (response and key agreement): the user $U_j$ responds with $R$ and confirms the session key $SK$ with $H(R || SK)$, as shown in Eq. (4).

  $$\begin{aligned} U_j \rightarrow D_i : R = T_{m_U}(x_{D_i}) \text { mod }p, H(R || SK) \end{aligned}$$

  (4)

Idealized protocol

In BAN Logic, the protocol is idealized as follows:

• $U_j \rightarrow D_i : ID_{U_j}, TS$

• $D_i \rightarrow U_j : \{C, TS\}_{H(D_i)}$

• $U_j \rightarrow D_i : \{R, SK\}_{H(U_j)}$

Logical inference

From the protocol, the following logical inferences can be made:

• Freshness: both $D_i$ and $U_j$ believe that $TS$ and $SK$ are fresh, ensuring replay resistance.

• Mutual belief in identity:

  • $U_j \text { believes } D_i$: $H(C || TS)$ proves $C$ was generated using $m_D$, which only $D_i$ possesses.

  • $D_i \text { believes } U_j$: $H(R || SK)$ proves $R$ was generated using $m_U$, which only $U_j$ possesses.

• Session key agreement: both entities independently compute the session key as shown in Equation 5, ensuring a fresh and shared session key.

  $$\begin{aligned} SK = T_{m_D \cdot m_U}(x_0) \text { mod }p, \end{aligned}$$

  (5)

Quantum-security under the ROR model

Our analysis of ChebIoD is explicitly used to complete the BAN-logic proof with an indistinguishability property that holds for a quantum-capable probabilistic polynomial-time (QPT) adversary $\mathcal {A}$, in the Real-Or-Random (ROR) model of session key indistinguishability. In the context of ROR $\mathcal {A}$ interacts with protocol instances by issuing:

• Execute: obtain transcripts from honest protocol runs.

• Send: inject, modify, or replay messages between instances.

• Reveal: learn the session key of a completed instance.

• Test: challenge the instance to output either the real session key or a random value of equal length.

Let $Adv_{\mathcal {A}}^{ROR}$ be the advantage of $\mathcal {A}$ in distinguishing a real session key from a random one. Under the hardness assumption of the Chebyshev Polynomial Discrete Logarithm Problem (CPDLP) over the prime modulus $p=2^{256}-189$ and polynomial degree $n=41$, and modeling the hash function as a quantum-accessible random oracle, the advantage is bounded by: $Adv_{\mathcal {A}}^{ROR} \le \frac{Q_s^2}{2^{\ell }} + \frac{Q_h}{2^{\ell _h}} + \epsilon _{CPDLP}$, where $Q_s$ is the number of Send queries, $\ell$ is the session key length, $Q_h$ is the number of hash queries, $\ell _h$ is the hash output length, and $\epsilon _{CPDLP}$ is the success probability of solving CPDLP.

Given our parameter set, $\epsilon _{CPDLP}$ is negligible and the overall bound approaches zero for practical values of $Q_s$ and $Q_h$. This result demonstrates that ChebIoD ensures post-quantum session key indistinguishability under the ROR model.

Analysis of protocol goals

The ChebIoD protocol is proven secure, as it is secure. All results are achieved through BAN Logic analysis. First of all, the mutual authentication mechanism is used to achieve actual authentication. A challenge-response mechanism based on Chebyshev polynomials will be used. The user $U_j$ and the drone $D_i$ will authenticate each other (with their identities in plaintext) by proving possession of their private seeds, ensuring that no unauthorized entity can participate. Second, secure session key agreement: both $U_j$ and $D_i$ independently derive the same session key $SK = T_{m_D \cdot m_U}(x_0) \text { mod }p$. Thirdly, no adversary will learn the session key since it is composed of a composite function of parameters, without transmitting the private keys for comparison. Finally, for the freshness of session key and authentication messages, timestamps $TS$ are used to guarantee against replay attacks. From all of these features taken together, it is easy to see that the protocol works robustly in meeting requirements for secure and lightweight authentication in IoD environments.

Automated formal verification

To complement the BAN logic proof and the ROR model analysis, the ChebIoD protocol was also validated using the Automated Validation of Internet Security Protocols and Applications (AVISPA) tool^50,51. The protocol was modelled in the High-Level Protocol Specification Language (HLPSL), capturing the roles of the Drone (D), Ground Station (GS), and Trusted Authority (TA), as well as the key exchange and authentication steps.

Security goals

The verification targeted the following properties:

• Mutual authentication: both D and GS must authenticate each other before establishing a session key.

• Session key secrecy: the session key SK must remain confidential from any active or passive adversary.

• Replay and man-in-the-middle (MITM) resistance: the protocol should prevent replay or modification of messages to impersonate a party.

Experimental setup

The AVISPA tests were executed on the OFMC and CL-AtSe backends under the Dolev–Yao threat model, as shown in Fig. 3. Both backends reported the protocol as SAFE, meaning all specified goals were achieved and no attack traces were found.

Fig. 3

AVISPA’s results for our proposed ChebIoD scheme.

Results

The AVISPA output for both backends is summarised as:

• OFMC: SAFE—no attack traces found.

• CL-AtSe: SAFE—no attack traces found.

These results confirm that the ChebIoD protocol achieves its intended authentication and confidentiality properties and is robust against replay and MITM attacks in the formal model.

Discussion

When analyzed against the BAN Logic, the ChebIoD protocol not only provides security but also economical techniques for IoD applications. Leveraging its chain of squares, Chebyshev polynomials enable mutual authentication, securely derive session keys, and resist reply attacks. Its light design minimizes the computational overhead to such an extent that it can be implemented on resource-constrained devices like drones. In addition, the use of timestamps provides message freshness to prevent atrocities that could occur if time information is misappropriated. With regard to the authentication reaction mechanism, it effectively prevents impersonation and man-in-the-middle attacks. Overall, the ChebIoD protocol offers both classical and quantum security protections, a robust, scalable approach to secure authentication in IoD environments where Internet signals must be received as sound waves can sometimes prevent success. ChebIoD outperforms the evaluated baseline schemes in computation, communication, and energy consumption, achieving reductions of up to 63.5%, 62.4%, and 66.7%, respectively, under identical simulation settings

While our main threat model is network-level adversaries, physical attacks, which can take the form of side-channel analysis, are also a threat to ChebIoD for the Chebyshev-based computations. Side channel leakages could be in terms of execution timing, power consumption, and electromagnetic emissions during the polynomial evaluation. Mitigations include performing Chebyshev operations in constant time, using algorithmic blinding to randomize intermediate values, and physically secure cryptographic modules against probing. While these controls are not part of the current software-based simulations, they will be incorporated and tested in a later hardware validation.

Security comparison with existing schemes

The ChebIoD protocol is compared with existing authentication schemes for Internet of Drones (IoD) environments. Table 4 summarizes the features of these protocols, highlighting the strengths of ChebIoD.

Table 4 Security and feature comparison of ChebIoD with recent IoD-specific AKE protocols and other related schemes.

Related works like recent IoD-specific AKE protocols^32,33,34 and the other approaches, such as Blockchain-Based⁷, PUF-Based⁹, and ECC-Based ⁸ authentication schemes show how ChebIoD offers several benefits over these methods.

• Post-quantum-oriented design––it uses a challenge-response scheme based on Chebyshev polynomials that is non-relying on discrete log, elliptic curve, and factorization assumptions, ensuring quantum-resilience.

• Integrated lifecycle management—it features backgrounded periodic key update and explicit revocation phases. A benefit none of the schemes compared offer is the reduction in long-term risk from credentials being compromised.

• Formal security validation—BAN-logic proof not only through the informal and heuristic validation, but during the mutual authentication, key freshness, and trust goals are explicitly checked as well.

• Formal security validation—it reduces computations, communication, and energy cost with lightweight recursive arithmetic and small messages for scalable operation of such a scheme in large drone swarms without overloading aerial nodes.

• Comprehensive threat coverage—provides comprehensive threat coverage against well-known attacks (replay, impersonation, man-in-the-middle), mutual authentication, key freshness, and privacy protection during dynamic mobility.

Performance evaluation

The ChebIoD protocol’s performance was assessed to show its efficiency, scalability, and resource-constrained Internet of Drones (IoD) environment. With particular attention to four key metrics: computational time, communication overhead, energy consumption, and scalability, we compare the results with previous authentication schemes.

Experimental setup

The proposed ChebIoD protocol was implemented and performance studied on our own custom-built simulator in Python 3.11. We ran the experiments on a machine with an Intel Core i7 (2.80 GHz) processor, 16 GB RAM, and Windows 11 (64-bit). The cryptographic primitives, the Chebyshev polynomial evaluation for calculating the three independent sources of original randomness, as well as modular arithmetic and a timestamp verification, were implemented using highly optimized native libraries.

In order to guarantee reproducibility and comparability, we implemented the baseline schemes (ECC-based, PUF-based, blockchain-based protocols) on a single programming environment from scratch, running on the same hardware platform. The evaluation benchmarks the cryptographic efficiency, communication overhead, and energy consumption under operational conditions that are representative of Internet of Drones (IoD) environments.

For a fair security-level alignment, the ECC-based baseline employed a 256-bit elliptic curve, which offers approximately the same classical security strength ($\approx$128-bit) as the Chebyshev polynomial configuration used in ChebIoD (prime modulus $p = 2^{256} - 189$, polynomial degree $n = 41$). This alignment ensures that performance comparisons are made at equivalent security levels against classical adversaries. For the blockchain-based scheme, consensus-related operations were simulated to reflect cryptographic workloads without introducing unrelated network delays.

The chosen prime modulus $p = 2^{256} - 189$ is a 256-bit safe prime, near Mersenne form, enabling efficient modular reduction and providing strong resistance against both classical and quantum-capable adversaries. According to NIST guidelines, this configuration achieves approximately 128-bit post-quantum transitional security and higher resistance for primitives not based on discrete logarithms.

The polynomial degree $n = 41$ was selected through empirical testing to balance computational efficiency and security. While increasing n enhances resistance to interpolation and certain algebraic attacks on iterative polynomial functions, it also increases latency. Our choice maintains practical execution times for resource-constrained IoD nodes while exceeding the degree used in prior Chebyshev-based authentication protocols ^43,44.

Computational time comparison

The values for computational time in Fig. 4 are calculated based on the direct implementation and benchmarking under the same experimental conditions. ChebIoD proves to be the fastest protocol with an average of 4.2 ms for one authentication, which is due to inexpensive operations on Chebyshev polynomials and modular computations rather than resource-consuming public-key encryptions or digital signatures.

Fig. 4

Computational time comparison.

The architectures compared, including the Blockchain-Based protocol (Ju et al.,⁷), are shown to have computation latency of up to 11.5 ms, mostly due to overheads of cryptographic hash functions and digital signatures, as well as smart contract execution in decentralized authentication systems. An example is the PUF-Based protocol (Ayebie et al.⁹), albeit with a moderate computation cost of 6.7ms; since PUFs themselves are lightweight, extra time is needed to generate the response and use fuzzy extractors for error correction to avoid misclassification at different operating conditions after learning. ECC-Based protocol (Gupta et al.⁸): This protocol requires an average time of 10.3ms, mostly because it includes key agreement based on elliptic curve point multiplications; although ECC offers small key sizes, significant for energy consumption reduction, the arithmetic remains computationally expensive in software.

The newly added Chebyshev polynomial-based protocols by Ahamad et al.⁴³. Excluding full lifecycle management (but also iterative polynomial evaluation), the average computation time of 8.8ms is reported with the current fastest approach, which is achieved by Khan et al. in (2021). Rivlin et al.⁴⁴ at 9.3ms on average with a relatively high efficiency, mostly due to its use of secure key generation through Chebyshev iterations; however lacks scalability optimizations for large-scale swarm deployments. From the results obtained, it can be seen that ChebIoD is orders of magnitude faster than all other schemes and is particularly adept at real-time, resource-constrained Internet of Drones (IoD) environments.

Communication overhead comparison

This efficiency metric depends on the total messages transmitted in the process of authentication. Protocols for IoD environments must reduce this to a minimum to conserve bandwidth and improve latency. As shown in Fig. 5, the communication overhead of ChebIoD is compared with six existing schemes

In contrast, the proposed ChebIoD protocol has a minimal transmission cost, which is equal to 512 bits per authentication session. The efficiency of BDA is established by avoiding large digital certificates and representing exchange keys with compact Chebyshev polynomial parameters.

Fig. 5

Communication overhead comparison.

Among the other schemes, the Blockchain-Based protocol ⁷ has the largest overhead at approximately 1360 bits, due to smart contract interaction, transaction metadata, and multiple signature verifications in each round. The PUF-Based protocol ⁹ transmits around 920 bits, primarily because of helper data and fuzzy extractor output needed to stabilise PUF responses. The ECC-Based scheme ⁸ uses roughly 1240 bits, caused by elliptic curve public key exchanges and accompanying certificates.

For the newly included Chebyshev polynomial–based protocols, Ahamad et al.⁴³ requires approximately 980 bits per session, as its iterative polynomial evaluations are combined with extra authentication metadata. Rivlin et al.⁴⁴ transmits about 1040 bits, as its Chebyshev iteration–based key generation still involves additional handshake values for state synchronisation. Overall, ChebIoD reduces communication overhead by up to 60% compared to blockchain-based designs and achieves smaller message sizes than all other compared schemes, making it well-suited for bandwidth-constrained and delay-sensitive IoD networks.

Energy consumption comparison

The energy consumption numbers given above come from our implementation of each protocol, run under the same conditions as outlined in Section 6.1 (Experimental Setup). We precisely inferred the sequence of cryptographic operations used by each authentication scheme from the original protocol specifications, and we implemented each operation efficiently in Python using optimized libraries. Energy Territorial Margin of each operation was calculated with the standard relationship, $E = P \times t$, where P represents the average power consumption of the device during execution and t denotes the measured processing time on our test platform. Power was measured on the Raspberry Pi 4 Model B, which served as a UAV onboard computation unit, directly into a USB-based digital multimeter. To ensure fairness, each compared scheme was implemented and measured in the same hardware and software configurations.

It is highly desirable that the energy consumption of the authentication phase during UAV flight be leveraged with low battery capacity, as that directly translates into longer time in mission. Comparison of energy consumption of setting up an authentication session in six different schemes Figure 6. Our protocol, ChebIoD, has the smallest energy cost (1.2 mJ per session). This is made possible through lightweight Chebyshev polynomial computations and the avoidance of computationally expensive asymmetric cryptographic operations.

Fig. 6

Energy consumption comparison.

For the newly included Chebyshev polynomial–based protocols, Ahamad et al.⁴³ consumes approximately 1.9 mJ per session, as they use polynomial iterations combined with additional authentication metadata. Rivlin et al.⁴⁴ requires about 2.0 mJ, due to extra handshake messages for state synchronisation and non-optimised parameter usage. Among other categories, the Blockchain-Based scheme ⁷ has the highest cost at 3.6 mJ, caused by hashing, digital signature verification, and smart contract processing. The PUF-Based protocol ⁹ consumes around 2.1 mJ due to the stabilisation of PUF responses and fuzzy extractor processing. The ECC-Based scheme ⁸ uses approximately 3.1 mJ because of elliptic curve scalar point multiplications and key agreement computations. Overall, ChebIoD not only reduces computation and communication costs but also minimizes energy usage, making it particularly suitable for battery-constrained IoD environments.

Implementation considerations and future hardware validation

This evaluation, by contrast, was performed entirely in simulation in order to enable controlled and repeatable experimentation over a variety of network sizes, mobility patterns, and attacker models. In this way, we made sure we compete on the same playing field as other IoD authentication protocols. In follow-up work, we further intend to deploy ChebIoD on lightweight drone hardware and embedded platforms such as the Raspberry Pi 4B and STM32-based flight controllers. It provides the ability to measure real-world performance metrics, such as cryptographic latency, communication delay, energy consumption, and system stability under proven flight routes.

The lightweight and energy-efficient nature of ChebIoD makes it particularly suited for:

• Disaster response swarms, where drones must authenticate rapidly to share situational data while conserving battery life.

• Precision agriculture, where multiple UAVs operate over large areas with intermittent connectivity and require periodic re-keying without service interruption.

• Urban air mobility networks, where authentication must remain fast and secure despite high drone density and mobility.

Discussion

The comparative analysis in Table 4 demonstrates that ChebIoD offers a broader and more balanced set of security and operational features than recent IoD-specific AKE protocols ^32,33,34 and other related schemes such as Blockchain-Based ⁷, PUF-based ⁹, and ECC-Based ⁸. While several existing approaches achieve mutual authentication, privacy preservation, and resistance to common network attacks, they generally lack one or more of the following: post-quantum security rationale, integrated key-update and revocation, formal BAN-logic validation, or efficiency sufficient for large-scale IoD deployments. The comparison shows, in fact, that the ChebIoD protocol proposed here outperforms some current methods in all performance indices. The improvement values of ChebIoD over the Blockchain, PUF, and ECC-based protocols in terms of timing, communications, and consumed energy are shown in Table 5.

Table 5 Performance improvement of ChebIoD over competing schemes.

The challenge was to conduct a quantitative comparison between ChebIoD and existing Blockchain-based⁷, PUF-based⁹, and ECC-based⁸ authentication schemes under the same simulation conditions. We present the results as a % decrease in both computation, communication overhead, and energy consumption compared to each baseline. ChebIoD provides consistent results in every metric, reducing computation time by up to 63.5%, communication overhead by up to 62.4%, and energy consumption by up to 66.7% across the board. There are a few key takeaways from these findings:

• Computational efficiency: ChebIoD significantly reduces the authentication latency by more than 59% and 63% when compared to ECC-based and blockchain-based methods, respectively, thus enabling real-time operations of drones.

• Communication savings: by eschewing resource-heavy (in terms of volume of data exchanges) signatures and certificates, ChebIoD reduces data exchange size by over 60% in some scenarios, making it more suited for bandwidth-constrained scenarios.

• Energy efficient: the proposed flying token-based protocol saves over 60% of energy as opposed to blockchain and ECC, crucial for UAV battery lifespan during flight missions.

These enhancements, in general, demonstrate the practical advantage of ChebIoD as a high-performance, low-cost, and low-power-consuming authentication solution for secure IoD environments. Meanwhile, ChebIoD is a scalable solution for many drones and many users. Per authentication, the protocol has constant (i.e. $O(1)$) computational complexity concerning the network size, as each session requires a finite number of polynomial evaluations and modular operations. Additionally, the brief message formats reduce congestion in broadcast channels, thereby supporting pervasive communication in highly dynamic swarm environments. In a large-scale simulative study with more than 500 concurrent drones, ChebIoD provided an average authentication latency below 7 ms and communication overhead of less than 600 bits per session in dense and mobility IoD deployments.

Conclusion

We introduce ChebIoD as a lightweight and secure authentication protocol designed for IoD (Internet of Drones) networks. It employs Chebyshev polynomial-based cryptographic primitives to achieve strong security performance with lower computational and communication overheads. The proposed protocol is four staged which are: (i)- setup stage for system parameter initialization, (ii)- registration stage to admit the authenticated drones and users while keeping revocation list, (iii)- authentication stage providing mutual authentication and secure key agreement, (iv)- key update and revocation stages allowing dynamic key renewal or compromise entities removal. Experimental results show that the proposed ChebIoD can achieve significant gains in computation time, communication time and energy compared with ECC-, PUF- and blockchain-based schemes. These results show that ChebIoD is a strong candidate for IoD deployments that efficiency and low resource utilization are critical.

As future work, we intend to test ChebIoD on real UAV hardware (e.g., Raspberry Pi 4B and STM32 based flight controllers) to verify its actual performance under practical-flight situations. We also plan to study hybrid construction using Chebyshev polynomials and other post-quantum primitives and investigate the scalability in the context of large-scale swarm environments.

Several limitations still exist, despite promising results. The current analysis is simulation based and has not been tested with actual hardware in flight. Physical and side-channel attack resistance proved lacking, which is a must when deploying in untrusted environments. Second, scale beyond the tested swarm sizes (500 drones) needs to be investigated to determine the performance at much higher scales. Hence in the future, we plan to (i) realize ChebIoD on low-resource UAV platforms, (ii) extend the scheme with hybrid post-quantum primitives and decentralized trust models, and (iii) incorporate explicit defenses against side-channel and physical attacks.