Evaluating generative AI tools for visual communication design using the CoCoSo method under interval valued spherical fuzzy environment

Abstract

At the age of intelligent design, generative AI tools are leading to a revolution in visual communication as the creative process is shifting to being fully automated, ideation is augmented, and production pipelines are fast-tracked. This paper will present a robust multi-criteria decision-making (MCDM) approach to analyze the comparative efficiency of prevalent tools of generative AI based on the combined compromise solution (CoCoSo) approach in an interval-valued (IVSF) spherical fuzzy framework. The IVSF framework is used to faithfully reflect the differences in how much or how little an expert would like to assign a particular degree of membership, non-membership, or abstinence, for the interval-valued membership, non-membership, and abstinence of degrees. These IVSF values are summed up, defuzzified, and then combined in the CoCoSo algorithm to provide an overall rating of the alternatives. One of the key features of this writing is the creation of a practical case study based on seven assessment criteria, including creativity, cost, customization, integration capability, and others, as well as ten generative AI platforms. DeepArt is presented as the most relevant tool by the proposed IVSF-CoCoSo approach, as it achieves a higher rate of creativity improvement, yields the best results in terms of output quality, and offers customization. Through comparison with other MCDM approaches, as well as sensitivity analysis, the proposed model proves to be highly reliable and flexible. The proposed study will provide practical knowledge to designers, researchers, and other industry stakeholders who aim to implement generative AI in visual communication processes successfully.

Introduction

Generative AI has culminated in recent years to revolutionize the discipline of visual communication design, as machines can now autonomously generate creative outputs in the form of graphics, layouts, illustrations, and interactive media¹. Generative adversarial networks and diffusion-based models are generations of AI trained on vast volumes of data to generate novel visual media that closely mimic the work of human creativity. The transformation aids designers in ideation, prototyping, and personalization, and saves them significantly on the time and effort required to develop stimulating visuals. Consequently, generative AI has become a crucial tool for enhancing user engagement rates, branding efficiency, and the overall aesthetic quality of both digital and print communication.

Generative AI is enhancing the efficiency of design in visual communication and offering new perspectives on collaboration between people and AI. Still, however, there are different approaches to using generative AI tools, practices, and design requirements, which is why decision-makers can hardly know which solution would best fit their aesthetic and functional requirements. This complexity necessitates an orderly system of assessment that approaches several standards, such as originality, adaptability, coherence, usability, and the capacity to be automated. Additionally, these standards are often subjective and interrelated, and the judgment of experts can vary in uncertain conditions. Hence, in this complex environment of decision-making, multi-criteria decision-making (MCDM) methods are necessary to manage the environment effectively.

The critical nature of evaluating generative AI tools lies in their high dimensionality and imprecision, due to linguistic preferences, fuzzy thinking, and differences of opinion among various stakeholders. Conventional decision-making tools are not suitable for dealing with unquantifiable and ambiguous expert inputs. In contrast to them, fuzzy MCDM techniques (or, more specifically, techniques based on interval-valued spherical fuzzy sets (IVSFS) enable a more detailed description of uncertainty, indecisiveness, and diversity of opinion. By using such approaches, it is possible to make the comparison of AI design options appear more realistic, as well as to increase their stability in the face of the dynamics of aggregate support and evaluation. As such, there is an apparent need to integrate IVSFS into the CoCoSo method due to its ability to reflect the complexity of selecting elements for multimodal visual design.

MCDM methods provide a systematic approach to evaluating multiple competing criteria in a structured manner. MCDM in a generative AI-based visual communication context can enable stakeholders to assess and rank the AI solutions based on the opinions of various experts. Nevertheless, human decisions are unpredictable and often inaccurate, particularly in cases involving subjective design criteria. In this regard, fuzzy set theory has been extensively incorporated in MCDM. Classical fuzzy sets (FS), as initially proposed by Zadeh², model uncertainty through a membership degree (MD) taking its values in $\:\left[\text{0,1}\right]$. However, FS does not indicate the possibility of hesitation or non-membership. As an extension of this, Atanassov³ introduced intuitionistic fuzzy sets (IFS) with non-membership (NMD), and circular IFS (CIFS)⁴. Yager⁵ introduced Pythagorean fuzzy sets (PyFS) and q-rung orthopair fuzzy sets (q-ROFS)⁶, which are more flexible. Later on, picture fuzzy sets (PFS) by Cuong⁷ were introduced with an abstinence degree (AD). Spherical fuzzy sets (SFS)⁸ went one step ahead by ensuring that the sum of MD, AD, and NMD squares adds up to at most one. Comprehensive comparative analyses in recent works such as^9,10 highlight the increasing importance of sophisticated fuzzy extensions in uncertain environments. To further approximate interval-based uncertainty, IVSFS¹¹ were proposed, where MD, AD, and NMD can take interval values, introducing a more detailed and subtle representation of expert opinion. In comparison to other older fuzzy models like IFS, PFS, Fermatean fuzzy sets (FFS)¹² or interval-valued PFS (IVPFS)¹², IVSFS has greater expressiveness as it combines the spherical constraint and the interval uncertainty, thus enabling a more fine-grained and trustworthy representation of complex design-related uncertainty. This is particularly beneficial in situations in which expert opinions can be uncertain or even conflicting, in which case, extraordinarily precise values may fall short.

Since the study requires a superior decision-making support mechanism in the presence of such uncertainty, the study considers the CoCoSo method, one of the most recent and effective MCDM techniques proposed by Yazdani et al.¹³. The CoCoSo method combines simple additive weighting (SAW), weighted aggregated sum product assessment (WASPAS), and exponential ways of ranking alternatives more efficiently. Its flexibility to different aggregation schemes and scoring functions renders it suitable for evaluating complex systems such as generative AI-based design tools. Nevertheless, crisp or single-valued fuzzy models, which are typically used in this manner, might lack the properties of complex expert opinions that are received in such creative and ambiguous circumstances. To address this, the study employs IVSFS, which offers a robust mathematical framework for handling the degree of membership, non-membership, and hesitancy that have interval ranges. Combined with IVSFS, CoCoSo becomes a powerful decision model capable of managing the ambiguity and variability of human judgments in creative tasks. This hybridization makes the model highly effective, as it not only considers more than just two dimensions when evaluating the criteria, but also incorporates the desired uncertainty in the expert’s opinion.

The paper also demonstrates a comparative analysis with the available MCDM techniques, including TOPSIS¹⁴, VIKOR¹⁵, EDAS¹⁶, DEMATEL¹⁷, and MARCOS¹⁸, to prove this methodology’s strengths and validity. The IVSF-CoCoSo method proposed here does not have the limitations of traditional fuzzy MCDM models and, unlike them, creates additional benefits based on the improved expressiveness of IVSFS and more accurate representation of uncertainty. It allows the inclusion of expert uncertainty, vague, and contradictory views in decision data in a more granular form. Further, a sensitivity analysis is performed by perturbing the compromise coefficient ($\:\lambda\:$) to see the stability of the rankings. These analyses demonstrate the efficiency of the IVSF-CoCoSo approach in providing consistent and reliable results, particularly in subjective and complex design environments.

Thus, the paper suggests a new IVSF-CoCoSo-based decision model that can assess the value and effectiveness of generative AI to support visual communication design improvement. In the proposed approach, the uncertainties in the expert scores are modelled through IVSF data, and the final ranks of AI-based design solutions are calculated via the CoCoSo method. Such a methodology helps to fill the gap between the theoretical models of fuzzy logic and its applications to the creative industries.

Objectives and contributions of the study

The research aims to investigate and assess how generative AI can be used to improve the visual communication design using a solid and adaptable decision-making framework. In particular, the research will attempt to:

• i. Determine key criteria that affect the introduction of generative AI in visual design practices.

• ii. Manage uncertainty and imprecision in the expert judgments with IVSFS.

• iii. Rank the possible alternatives using the CoCoSo MCDM technique.

The proposed study contributes to the decision-making and visual communication design in several important ways. Firstly, it presents a new decision-making model, combining the IVSFS with the CoCoSo MCDM method, which can better reflect experts’ uncertainty and great hesitation in complex assessment scenarios. Second, it deals with the increasing significance of generative AI in visual design by simulating a realistically positioned decision problem incorporating seven extensive evaluation aspects and ten realistic alternatives valued by three expert decision-makers. Third, the given approach is verified with the help of the sensitivity analysis and the comparative assessment against the well-known MCDM methods, including TOPSIS, VIKOR, EDAS, MARCOS, and DEMATEL, showing superiority in terms of flexibility, exactness, and the soundness of decisions. In addition, the study provides theoretical developments through benchmarking the performance of IVSFS with the traditional fuzzy models, such as FS, IFS, PFS, PyFS, q-ROFS, PFS, and SFS, in terms of better capability of dealing with interval uncertainty and consistency in complex environments. Finally, the research offers practical and managerial implications to stakeholders interested in adopting generative AI in visual communication, filling the gap between theoretical modelling and practice.

Research gap and motivations

Although the application of generative AI is rapidly growing in visual communication design, the existing body of research focuses mainly on the creative output or the development of the algorithms, without a formal model of decision-making in uncertainty. Conventional MCDM procedures may be unable to deal with imprecise, hesitant, and interval-valued assessments typical of expert opinions. The IVSFS offers a more realistic and flexible modelling environment as it encapsulates the MD, AD, and NMD within bounds of intervals. Although recent literature has used IVSFS to study different fields, none of the available literature has examined the possibility of integrating the IVSF-CoCoSo approach to assess the role of generative AI in visual communication design. The presence of such a significant gap justifies the relevance of a robust and uncertainty-aware framework capable of supporting decision-makers in prioritizing and evaluating generative AI contributions based on several criteria related to design.

Driven by this gap, this paper suggests a new IVSF-CoCoSo MCDM model that examines and evaluates alternatives entirely using experts’ opinions. Such a strategy will increase the accuracy of decisions and open the path to informed implementation of generative AI in the creative and design sectors.

MCDM in generative AI for enhancing visual communication design

The recent development of generative AI in such areas as visual communication has raised the urgent necessity of effective decision-making models adaptable to various and frequently competing assessment standards. As generative AI tools become more utilized to automate and improve visual storytelling, branding, and interactive design, stakeholders will need to evaluate such tools beyond a measure of creativity, to include adaptability, computing efficiency, and user experience. When faced with such intricate situations, MCDM techniques offer an effective analytical model that can be used to assess and rank the alternatives concurrently. For example, Seiti et al.¹⁹ showed the usefulness of a causal MCDM methodology in human-related generative AI uses in supply chain risk management applications, where structured, criterion-based analysis is essential in an AI-assisted world. Within the framework of visual communication design, generative AI has already demonstrated significant potential in changing picture creation, graphical arrangements, and visual narratives²⁰²¹;. Such innovations require decision models capable of addressing the design selection’s subjective and multi-dimensional nature. As an illustration, Zhao²² examined intelligent poster creation with the help of such generative AI models as GANs and VAEs, and it seems essential to generate a balance between technical correctness and aesthetic quality. Likewise, the significance of MCDM in measuring the creative potential in sustainable product design was highlighted by Kaljun and Kaljun²³, who discussed how generative AI tools improve creativity.

Besides, within the scope of business visualization, Mazumder²⁴ used generative AI to facilitate the interpretation of big data, demonstrating how MCDM techniques assist in ensuring that the AI result is strategically decision-aligned. This synergy is also applicable to the educational sector; Bukar et al.²⁵ suggested using MCDM to create a decision framework that can be used to assess generative AI models such as ChatGPT in the classroom. The tendency towards recognizing MCDM as an instrument necessary to optimize GAI tools and reduce the gap between AI capability and domain-specific expectations becomes evident with these studies. Overall, MCDM is an essential facilitator in the assessment of generative AI in visual communication design, helping to make informed decisions by considering qualitative and quantitative factors through a combination. The proposed study is part of these efforts as it uses an innovative IVSF-CoCoSo methodology to manage the ambiguity and complexity of human judgments in creative decision-making situations.

CoCoSo MCDM method

One of the most recent approaches to the MCDM problem is the CoCoSo method suggested by Yazdani et al.¹³, which attempts to incorporate the strengths of compromise and aggregation approaches to achieve higher accuracy in the created decision. The CoCoSo method has demonstrated considerable applicability over time in various fields. As an illustration, Popović²⁶ successfully applied it to personnel selection issues, showing its advantage in ranking human-centered alternatives. Likewise, Peng et al.²⁷ combined CoCoSo with CRITIC and PyFS to assess firms within the 5G sector, demonstrating its adaptability to complex environments and sophisticated data structures. Cui and Liu²⁸ applied an interval neutrosophic number-based CoCoSo methodology with superhypersoft logic in evaluating rural competitiveness in tourism development. They demonstrated the effectiveness of this methodology in a complex MAGDM situation. The model’s effectiveness is based on the hybrid approach (PyF-AHP and CoCoSo) aimed at evaluating the adoption of AI technology, which was also developed by Nguyen et al.²⁹.

In addition, Kamber³⁰ employed the fuzzy CoCoSo method to evaluate AI-based accessibility tools in higher education among students with disabilities, thereby overcoming the drawbacks of traditional MCDM methods in handling imprecise or verbal information. Karami et al.³¹ also extended the technique by using SWARA to weight the criteria and IVF-CoCoSo to rank the final decisions in cases where a more solid solution is required in interval-valued fuzzy cases. Further developments like IF-CoCoSo³², PyF-CoCoSo³³, and PF-CoCoSo³⁴ have also been presented to reflect more on the tendency of hesitancy, uncertainty, and imprecision of experts in various applications. These frameworks demonstrate the growing belief that more expressive fuzzy settings are necessary in the complex determination of such issues. These studies confirm CoCoSo as a versatile and robust MCDM method that can handle complex, uncertain, and multidimensional decision problems. In this case, the study employs the IVSF-CoCoSo approach to address the uncertainty and ambiguity in evaluating the role of generative AI in enhancing visual communication design, where prevailing subjective judgments and unclear criteria are evident. The incorporation of IVSFS into CoCoSo further strengthens the possibilities of decision modeling by adopting interval-valued degrees of membership, abstention, and non-membership, providing a finer scale and more agreeable valuation in imaginative and uncertain settings.

Studies applied the Interval-Valued spherical fuzzy sets

The IVSFS is a further development of the theory of fuzzy sets, which is a more liberal theory to manage and model uncertainty. This powerful representation has drawn much attention in many decision-making and system analysis areas. For example, Aydoğdu and Gul³⁵ introduced new entropy measures designed explicitly for IVSFS. They extended the additive ratio assessment (ARAS) approach into the ARAS-IVSFS, thereby expanding the methodological range in MCDM. In the same light, Yu et al.³⁶ integrated the IVSFS-based CODAS method into a safety assessment scheme of the LNG tank system, suggesting a new scoring function and weight summation plan, which properly handled the obscurity in the professional appraisals. Within the safety and sociotechnical systems domain, Zarei et al.³⁷ used IVSFS to improve a systemic safety model with an extensive taxonomy of performance shaping factors, demonstrating the framework’s flexibility to complex, interdependent system performance. Okine et al.³⁸ presented the IVSFS-FRAM (functional resonance analysis method) to assess aviation wake turbulence operations. The fuzzy environment offered a subtle reading of uncertain causalities in the dynamic flight conditions. In addition, Almulhim³⁹ extended the IVSFS to the well-known DEMATEL methodology to account for the early-stage investment decisions and incorporated the expert weightings to capture the different levels of expertise and enhanced the methodological rigor of the fuzzy structural modelling.

The above studies establish that IVSFS models are helpful and can embrace uncertainty, vagueness, and expert hesitancy in different decision-making environments. The increased use of IVSFS in safety analysis, investment planning, functional causation modelling, and risk evaluation apps highlights that IVSFS is recognized as a powerful and multifunctional intelligent decision support system tool. The proposed study uses the IVSFS framework to make the evaluations of interest in generative AI in visual communication design more precise and expressive when human perception, aesthetics, and subjective judgments must be used under uncertain circumstances.

Structure of the study

The structure of this study is organized into several sections to systematically address the application of the IVSF-CoCoSo method for evaluating the role of generative AI in enhancing visual communication design. Section “Preliminaries” outlines the basic concept related to IVSFS. Section "Interval-valued spherical fuzzy CoCoSo MCDM method" proposed the IVSF-CoCoSo methodology with a detailed algorithm for exploring the role of generative AI in visual communication design. Section "Exploring the role of generative AI in enhancing visual communication design" examines the role of generative AI in visual communication design by employing the proposed methodology and discusses its results. Section “Comparison analysis” performs a comparison analysis with existing MCDM methods and a sensitivity analysis by changing a parameter value to check the stability of the ranking. Also, the study’s practical and managerial implications, advantages, and limitations will be discussed. Finally, Sect. “Conclusion” concludes with key findings and future research directions.

Preliminaries

This section outlines the context and mathematical expressions needed to understand the proposed framework. It integrates IVSFS into the CoCoSo method, exploring generative AI’s role in visual communication design.

Definition 1

⁸ Let$\:\:U$ is the discourse universe that includes MD $\:\left(\mathfrak{m}\right)$, AD $\:\left(\mathcal{a}\right)$, and NMD $\:\left(\mathfrak{n}\right)$. The SFS $\:\mathcal{H}$ is defined as:

$$\:\mathcal{H}=\left\{\left({\mathfrak{m}}_{\mathcal{H}}\left(u\right),{\mathcal{a}}_{\mathcal{H}}\left(u\right),{\mathfrak{n}}_{\mathcal{H}}\left(u\right)\right):u\in\:U\right\}$$

Where

$$\:{\mathfrak{m}}_{\mathcal{H}}\left(u\right),{\mathcal{a}}_{\mathcal{H}}\left(u\right),{\mathfrak{n}}_{\mathcal{H}}\left(u\right)\in\:\left[\text{0,1}\right]$$

Under these conditions:

$$\:0\le\:{\left({\mathfrak{m}}_{\mathcal{H}}\left(u\right)\right)}^{2}+{\left({\mathcal{a}}_{\mathcal{H}}\left(u\right)\right)}^{2}+{\left({\mathfrak{n}}_{\mathcal{H}}\left(u\right)\right)}^{2}\le\:1$$

Furthermore, the refusal degree (RD) is well-known by:

$$\:{\pi\:}_{\mathcal{H}}\left(u\right)={\left(1-\left({\left({\mathfrak{m}}_{\mathcal{H}}\left(u\right)\right)}^{2}+{\left({\mathcal{a}}_{\mathcal{H}}\left(u\right)\right)}^{2}+{\left({\mathfrak{n}}_{\mathcal{H}}\left(u\right)\right)}^{2}\right)\right)}^{\frac{1}{2}}$$

Definition 2

¹¹ Let $\:U$ is the discourse universe that includes MD$\:\mathfrak{\:}\left(\mathfrak{m}\right)$, AD$\:\mathcal{\:}\left(\mathcal{a}\right)$, and NMD$\:\mathfrak{\:}\left(\mathfrak{n}\right)$. The IVSFS $\:\mathcal{H}$ is defined as:

$$\:\mathcal{H}=\left\{\left([{\mathfrak{m}}_{\mathcal{H}}{\left(u\right)}^{l},{\mathfrak{m}}_{\mathcal{H}}{\left(u\right)}^{u}],[{\mathcal{a}}_{\mathcal{H}}{\left(u\right)}^{l},{\mathcal{a}}_{\mathcal{H}}{\left(u\right)}^{u}],[{\mathfrak{n}}_{\mathcal{H}}{\left(u\right)}^{l},{\mathfrak{n}}_{\mathcal{H}}{\left(u\right)}^{u}]\right):u\in\:U\right\}$$

Where:

$$\:[{\mathfrak{m}}_{\mathcal{H}}{\left(u\right)}^{l},{\mathfrak{m}}_{\mathcal{H}}{\left(u\right)}^{u}],[{\mathcal{a}}_{\mathcal{H}}{\left(u\right)}^{l},{\mathcal{a}}_{\mathcal{H}}{\left(u\right)}^{u}],[{\mathfrak{n}}_{\mathcal{H}}{\left(u\right)}^{l},{\mathfrak{n}}_{\mathcal{H}}{\left(u\right)}^{u}]\in\:\left[\text{0,1}\right]$$

Under these conditions:

$$\:0\le\:{\left({\mathfrak{m}}_{\mathcal{H}}{\left(u\right)}^{u}\right)}^{2}+{\left({\mathcal{a}}_{\mathcal{H}}{\left(u\right)}^{u}\right)}^{2}+{\left({\mathfrak{n}}_{\mathcal{H}}{\left(u\right)}^{u}\right)}^{2}\le\:1\:\:$$

Furthermore, the RD is well-known by:

$$\:{\pi\:}_{\mathcal{H}}\left(u\right)={\left(1-\left({\left({\mathfrak{m}}_{\mathcal{H}}{\left(u\right)}^{u}\right)}^{2}+{\left({\mathcal{a}}_{\mathcal{H}}{\left(u\right)}^{u}\right)}^{2}+{\left({\mathfrak{n}}_{\mathcal{H}}{\left(u\right)}^{u}\right)}^{2}\right)\right)}^{\frac{1}{2}}$$

Definition 3

¹¹Let $\:\:{\mathcal{H}}_{1}=([{\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l},{\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}],$$[{\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l},{\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}],[{\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l},$${\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}])$, $\:\:{\mathcal{H}}_{2}=([{\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l},{\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}],$$[{\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l},{\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}],[{\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l},{\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}]t)$ be two interval-valued spherical fuzzy values (IVSFVs) and$\:\:\rho\:>0$,$\:\:\rho\:$ be any scalar number, then it satisfies the following operations:

$$\:{\mathcal{H}}_{1}\oplus\:{\mathcal{H}}_{2}=\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}+{\left({\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l}\right)}^{2}-{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}.{\left({\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l}\right)}^{2}},\\\:\sqrt{{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}+{\left({\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right)}^{2}-{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}.{\left({\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right)}^{2}}\end{array}\right]\:,\\\:\left[{\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}{\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l},\:{\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}{\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right],\\\:\left[{\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}{\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l},\:{\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}{\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right]\end{array}\right)$$

$$\:{\mathcal{H}}_{1}\otimes\:{\mathcal{H}}_{2}=\left(\begin{array}{c}\left[{\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}{\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l},\:{\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}{\mathfrak{m}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right],\\\:\left[\begin{array}{c}\sqrt{{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}+{\left({\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l}\right)}^{2}-{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}.{\left({\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l}\right)}^{2}},\\\:\sqrt{{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}+{\left({\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right)}^{2}-{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}.{\left({\mathcal{a}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right)}^{2}}\end{array}\right]\:,\\\:\left[\begin{array}{c}\sqrt{{\left({\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}+{\left({\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l}\right)}^{2}-{\left({\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}.{\left({\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{l}\right)}^{2}},\\\:\sqrt{{\left({\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}+{\left({\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right)}^{2}-{\left({\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}.{\left({\mathfrak{n}}_{{\mathcal{H}}_{2}}{\left(u\right)}^{u}\right)}^{2}}\end{array}\right]\:\end{array}\right)$$

$$\:{\uprho\:}.{\mathcal{H}}_{1}=\left(\begin{array}{c}\left[\sqrt{1-{\left(1-{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}\right)}^{\rho\:}},\sqrt{1-{\left(1-{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}\right)}^{\rho\:}}\right],\\\:\left[{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{{\uprho\:}},{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{{\uprho\:}}\right],\left[{\left({\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{{\uprho\:}},{\left({\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{{\uprho\:}}\right]\end{array}\right)$$

$$\:\:{\mathcal{H}}_{1}^{\rho\:}=\left(\begin{array}{c}\left[{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{{\uprho\:}},{\left({\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{{\uprho\:}}\right],\\\:\left[\sqrt{1-{\left(1-{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}\right)}^{{\uprho\:}}},\sqrt{1-{\left(1-{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}\right)}^{{\uprho\:}}}\right],\\\:\left[\sqrt{1-{\left(1-{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l}\right)}^{2}\right)}^{{\uprho\:}}},\sqrt{1-{\left(1-{\left({\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}\right)}^{2}\right)}^{{\uprho\:}}}\right]\end{array}\right)$$

$$\:{\mathcal{H}}_{1}^{c}=\left([{\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l},{\mathfrak{n}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}],\:[{\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l},{\mathcal{a}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}],[{\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{l},{\mathfrak{m}}_{{\mathcal{H}}_{1}}{\left(u\right)}^{u}]\right)$$

Additionally, the following steps can be used to add and multiply IVSFSs.

$$\:{\mathcal{H}}_{1}\oplus\:{\mathcal{H}}_{2}={\mathcal{H}}_{2}\oplus\:{\mathcal{H}}_{1}$$

$$\:{\mathcal{H}}_{1}\otimes\:{\mathcal{H}}_{2}={\mathcal{H}}_{2}\otimes\:{\mathcal{H}}_{1}$$

Definition 4

The score and accuracy functions have been created to evaluate and compare IVSFS. Equations (1) and (2) provide the accuracy and score functions for each IVSFS.

$$Score function:\:{Sc}_{\mathcal{H}}=\frac{{\left(\left[{\mathfrak{m}}_{\mathcal{H}}^{l}+{\mathfrak{m}}_{\mathcal{H}}^{u}\right]-\left[{\mathfrak{n}}_{\mathcal{H}}^{l}+{\mathfrak{n}}_{\mathcal{H}}^{u}\right]\:\right)}^{2}-{\left(\left[{\mathcal{a}}_{\mathcal{H}}^{l}+{\mathcal{a}}_{\mathcal{H}}^{u}\right]-\left[\left({\mathfrak{n}}_{\mathcal{H}}^{l}+{\mathfrak{n}}_{\mathcal{H}}^{u}\right)\:\right]\right)}^{2}\:\:\:}{2}$$

(1)

 

$$Accuracy function:\:{Ac}_{\mathcal{H}}=\frac{\left[{{\mathfrak{m}}^{l}}_{\mathcal{H}}^{2}+{{\mathfrak{m}}^{u}}_{\mathcal{H}}^{2}\right]+\left[{{\mathcal{a}}^{l}}_{\mathcal{H}}^{2}+{{\mathcal{a}}^{u}}_{\mathcal{H}}^{2}\right]+\left[{{\mathfrak{n}}^{l}}_{\mathcal{H}}^{2}+{{\mathfrak{n}}^{u}}_{\mathcal{H}}^{2}\right]}{2}$$

(2)

In this study, these functions are offered, as far as the authors consider them to be the first attempt to assess and compare IVSFSs. It has a score function as given in Eq. At that, (1) is created to highlight the total positivity of an IVSFS by focusing on the contrast between the cumulative MD, AD, and NMD. The squared terms contribute to intensifying greater differences between alternatives and also make the ranking exercise more sensitive to changes in uncertainty. There is a monotonicity of the function regarding the increase of MD and the decrease of NMD, as well as its consistency and boundedness. This makes it more intuitive compared to the values in IVSF and thus provides a solid mathematical foundation in the pursuit of decision processes.

Interval-valued spherical fuzzy CoCoSo MCDM method

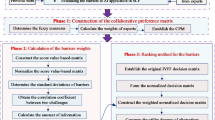
The IVSF-CoCoSo approach combines IVSFS and CoCoSo, offering the incorporation of uncertain and subjective environmental information to enhance decision-making. With this integration, modeling can become more flexible, realistic, and accurate, which is necessary for complex decisions, such as the adoption of generative AI in visual communication design. Thanks to IVSFS, hesitancy, imprecision, and expert preferences that varied on different criteria are captured well to produce accurate alternative ordering. Figure 1 illustrates the detailed steps of the IVSF-CoCoSo MCDM algorithm.

Fig. 1

Flowchart of the methodology.

Step 1

Development of the initial decision matrix.

The initial stage in MCDM approaches is to create a decision matrix, as shown below. Consider $\:R=\left\{{R}_{1},{R}_{2},\cdots\:,{R}_{m}\right\}$ as the collection of alternatives, $\:C=\left\{{C}_{1},{C}_{2},\cdots\:,{C}_{j},\cdots\:,{C}_{n}\right\}$ representing the specified criteria, and $\:W=\left\{{w}_{1},{w}_{2},\cdots\:,{w}_{n}\right\}$ as the array of weights with $\:{w}_{j}\in\:\left[\text{0,1}\right]$. The matrix $\:\mathcal{H}={\left({\mathcal{H}}_{ij}\right)}_{m\times\:n}$ represents the evaluation of choice A by the decision-maker number $\:D$ using criterion $\:n$. The matrix is generated using linguistic concepts.

$$\:\mathcal{H}={\left({C}_{j}\left({d}_{i}\right)\right)}_{m\times\:n}=\left[\begin{array}{ccc}{\mathcal{H}}_{11}&\:\cdots\:&\:{\mathcal{H}}_{1n}\\\:\vdots&\:\ddots\:&\:\vdots\\\:{\mathcal{H}}_{m1}&\:\cdots\:&\:{\mathcal{H}}_{mn}\end{array}\right]$$

(3)

Step 2

Transforming linguistic variables into IVSFVs.

In the second stage, the identified linguistic variables from step 1 are transformed to IVSFVs using Table 1, and the decision matrix is generated using Eq. 4.

$$\:\mathcal{H}={\left({C}_{j}\left({d}_{i}\right)\right)}_{m\times\:n}=\left[\begin{array}{ccc}{f}_{11}&\:\cdots\:&\:{f}_{1n}\\\:\vdots&\:\ddots\:&\:\vdots\\\:{f}_{m1}&\:\cdots\:&\:{f}_{mn}\end{array}\right]$$

(4)

Step 3

The creation of an Aggregated Decision Matrix.

This stage involves combining experts’ opinions while considering the specified weight for each opinion. The aggregated decision matrix was created using the IVSFWA operators, as shown in Eq. 5. This is done to make sure that each of the fuzzy evaluations made by individuals is aggregated into a judgment that is collectively made via weighted ways of aggregation dependent upon the importance specific to the expert. The aggregation preserves the interval-based nature of the information to maintain uncertainty.

$$\:IVSFWA=\left\{\begin{array}{c}\left[{\left(1-{\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{\left(1-{{\mathfrak{m}}^{l}}^{2}\right)}^{{w}_{\mathfrak{i}}}\right)}^{\raisebox{1ex}{$1$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.},{\left(1-{\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{\left(1-{{\mathfrak{m}}^{u}}^{2}\right)}^{{w}_{\mathfrak{i}}}\right)}^{\raisebox{1ex}{$1$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.}\right],\\\:\left[{\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{{\mathfrak{n}}^{l}}^{{w}_{\mathfrak{i}}},{\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{{\mathfrak{n}}^{u}}^{{w}_{\mathfrak{i}}}\right],\\\:\left[\begin{array}{c}{\left({\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{\left(1-{{\mathfrak{m}}^{l}}^{2}\right)}^{{w}_{\mathfrak{i}}}-{\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{\left(1-{{\mathfrak{m}}^{l}}^{2}-{{{a}}^{l}}^{2}\right)}^{{w}_{\mathfrak{i}}}\right)}^{\raisebox{1ex}{$1$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.},\\\:{\left({\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{\left(1-{{\mathfrak{m}}^{u}}^{2}\right)}^{{w}_{\mathfrak{i}}}-{\prod\:}_{\mathfrak{i}=1}^{\mathfrak{n}}{\left(1-{{\mathfrak{m}}^{u}}^{2}-{{{a}}^{u}}^{2}\right)}^{{w}_{\mathfrak{i}}}\right)}^{\raisebox{1ex}{$1$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right\}$$

(5)

Step 4

Computation of the Score function.

Using Eq. 1, the score value for each IVSFV is calculated, resulting in the matrix $\:{\mathcal{H}}^{\text{*}}={\left({f}_{ij}^{\text{*}}\right)}_{m\times\:n}$. The score function does so by converting the IVSFVs into crisp score values by representing the overall effect of MD, AD, and NMD. Such a transformation makes them compatible with the classical operations of CoCoSo.

Step 5

The decision matrix’s normalization.

Normalization is generally used across all MCDM approaches. In this stage, Eq. 6 is used to modify the decision matrix for positive and negative variables based on the relationships illustrated below. $\:{f}_{j+}^{\text{*}}$ and $\:{f}_{j-}^{\text{*}}$ are the maximum and minimum values for each variable column, respectively.

$$\:\frac{\mathcal{H}}{{\mathcal{H}}_{ij}}=\left\{\begin{array}{ll}\frac{{f}_{ij}^{\text{*}}-{f}_{{j}^{-}}^{\text{*}}}{{f}_{{j}^{+}}^{\text{*}}-{f}_{{j}^{-}}^{\text{*}}}&\:\text{if}\;j\in\:B\\\:\frac{{f}_{{j}^{+}}^{\text{*}}-{f}_{ij}^{\text{*}}}{{f}_{{j}^{+}}^{\text{*}}-{f}_{{j}^{-}}^{\text{*}}}&\:\text{if}\;j\in\:C\end{array}\right.$$

(6)

Where,

$$\:{f}_{{j}^{-}}^{\text{*}}=\underset{i}{\text{m}\text{i}\text{n}}\:{f}_{ij}^{\text{*}}\;\text{and}\;{f}_{{j}^{+}}^{\text{*}}=\underset{i}{\text{m}\text{a}\text{x}}\:{f}_{ij}^{\text{*}}$$

(7)

Step 6

Calculate the power weight of comparability and the sum of weighted comparability sequences.

At this point, the power weight of comparability (Ƥ_i) and cumulative weighted comparability (Ṧ) sequences for each alternative are computed. The CoCoSo technique uses the weight of variables, represented by $\:W$, as input. The values of Ṧ and Ƥ_i were obtained using the SAW and WASPAS techniques, respectively.

(8)

(9)

Step 7

Evaluation scores are assessed using three unique procedures.

This section provides the scores of the alternatives determined from three different evaluation procedures, using Formulas 10–12. Equation 10 expresses the arithmetic mean of the scores for WSM and WPM, while Eq. 11 expresses the relative scores of WSM and WPM to optimal performance. Equation 12 represents an exact equilibrium of WSM and WPM. In Eq. 12, an expert assigns $\:\lambda\:$, however, a value of $\:\lambda\:=0.5$ provides greater flexibility.

(10)

(11)

(12)

Step 8

Evaluation of the appraisal score and ranking of the alternatives.

This section defines the process of calculating the final score using Eq. 13, which illustrates the combination of the arithmetic mean and geometric mean derived from the preceding three strategies. Consequently, the alternatives with the highest $\:\:{\mathbbm{k}}_{i}$ score are the most optimal.

$$\:{\mathbbm{k}}_{i}={\left({\mathbbm{k}}_{i{a}}*{\mathbbm{k}}_{ib}{\mathbb{*}\mathbbm{k}}_{ic}\right)}^{\frac{1}{3}}+\frac{1}{3}\left({\mathbbm{k}}_{i{a}}+{\mathbbm{k}}_{i\text{b}}+{\mathbbm{k}}_{ic}\right)$$

(13)

It should be remembered that the values $\:{\mathbbm{k}}_{i\mathcal{a}},\:{\mathbbm{k}}_{ib},{\mathbbm{k}}_{ic}$ are calculated with the help of the scalar scores that are based on the IVSF assessments. These scalar scores are then obtained through the score function defined in Definition 4 (Eq. 1), calculating the ratings of all alternatives in each of the criteria. This transformation allows one to aggregate IVSF data along with others in the aggregation process of CoCoSo. Thus, Eq. Those scalar scores are combined to generate $\:{\mathbbm{k}}_{i}$, an overall appraisal index based upon the three methods of aggregation, and on that basis, ranking on the final basis is done.

Exploring the role of generative AI in enhancing visual communication design

Generative AI has become more relevant in improving visual communication design in recent years. Generative AI describes cutting-edge machine learning models that can generate original content, such as graphics, illustrations, typography, layout, and even motion design. Such AI tools are transforming visual communication in terms of how designers think and create visual artefacts, through automation, customization and ideation on a scale never before seen. Not only are these tools diminishing the time and effort involved in production, but they are also broadening the creative potential of designers. Due to this, the conceptualization and appraisal of the role played by generative AI in visual communication design has risen to become an essential issue to both academia and industry.

Generative AI does more than automate tasks; it transforms the conceptual basis of visual communication design. With the help of cutting-edge algorithms, including diffusion models and generative adversarial networks (GANs), these systems may understand ambiguous textual instructions and turn them into elaborate and visually striking results. This feature allows designers to leave the old trial-and-error designing behind and pursue as many design directions in real-time as they wish. Moreover, generative AI promotes inclusivity and democratization in designing, which allows people with less technical expertise to create high-quality images, thus opening up access to creativity. It serves as a co-creative collaborator in pedagogical and professional settings, assisting users to distill their vision, explore aesthetic propositions, and swiftly iterate. With visual narratives taking center stage in branding, marketing, and social communication, the strategic use of generative AI in design processes can help organizations ensure visual consistency, quick prototype campaigns, and be dynamic in response to ever-changing cultural trends. The paradigm shift highlights the importance of guided assessment frameworks, such as the one presented in the current paper, to comprehend and maximize the use of generative AI in visual communication.

MCDM offers a useful structure for systematically evaluating this role. Considering the underlying uncertainties and subjective judgments, which are part of the process of assessing creative tools and processes, the study uses the IVSF-CoCoSo MCDM approach. The method admits the consideration of unclear or inexact expert views by using them in the in IVSF setting, which renders it a good fit whenever assessing qualitative and uncertain criteria. A decision-making situation is created wherein three decision-makers are involved: a graphic designer, a creative director, and a branding consultant, who all provide expertise on the situation regarding their varying professional backgrounds.

The analysis is performed against seven dimensions selected to thoroughly cover the major determinants of the usefulness of generative AI tools in visual design. Such criteria are:

• Creativity Enhancement ($\:{C}_{1}$): This criterion evaluates the AI tool in terms of generating new innovative ideas. It is essential because visual communication is all about creativity and any tool ought to add value to the ideation process.

• User-Friendliness ($\:{C}_{2}$): This gauges the interface simple and learnability. Designers have to meet strict deadlines regularly so the tools should be readily available with little learning curves to be useful.

• Cost-Effectiveness ($\:{C}_{3}$): This analyses the cost and license type of the AI tools. Cost is therefore a crucial factor in long term adoption and scale as many generative AI platforms are run on subscription models or per output cost.

• Customization Capability ($\:{C}_{4}$): Support of contextually relevant designs must be provided by the possibility to customize outputs according to the user input or brand necessities. Inflexible tools are not so helpful in practical branding situations.

• Output Quality ($\:{C}_{5}$): This criterion measures the resolution, aesthetics quality and the professional finishing of the generated designs, which directly influences the usability in the commercial projects.

• Integration with Design Pipelines ($\:{C}_{6}$): This considers the smoothness of the AI tool to be used with regard to the existing design programs like Adobe Creative Suite or Figma, which is essential to the continuation of the workflow.

• Time Efficiency ($\:{C}_{7}$): One of the most important aspects of the tool performance, both to agencies and to freelancers, is time saved in the design process.

The seven evaluation criteria were determined based on the expertise consultation and backed by appropriate literature in the generative AI and visual design⁴⁰. To measure these criteria, ten alternatives are chosen, comprising prominent generative AI tools and platforms applicable in the visual design. These alternatives include:

• $\:{A}_{1}$ (Midjourney): Created by an independent research organization, the AI tool shares the same principles of focusing on aesthetic appeal as is popular with artists and designers, primarily to create stylized imagery.

• $\:{A}_{2}$ (DALL·E 3): is the follow-up to DALL·E 2 with an advanced understanding of prompts, image fidelity, and direct integration with ChatGPT, which has made it more precise and accessible to design.

• $\:{A}_{3}$ (Adobe Firefly): This is a tool that comes with the Adobe Creative Cloud suite and focuses on being simple to use and the end product being commercially licensed.

• $\:{A}_{4}$ (Canva AI): This tool is baked into Canva and delivers AI-driven design assistants, image creation, and layout to make user-friendly visual content creation.

• $\:{A}_{5}$ (RunwayML): provides real-time of image and video creation supported by the AI model, which can find practical application among creative people in multimedia creation.

• $\:{A}_{6}$ (NightCafe): A versatile service that allows using different types of AI models to make prompts to create images is easy to get acquainted with, and accompanied by a community.

• $\:{A}_{7}$ (DeepArt): Applies to the user images using deep neural networks to transform them into art in the style of renowned artists, making it ideal to reinterpret artistically.

• $\:{A}_{8}$ (Artbreeder): Allows collaborative mixing and morphing of images with the aid of generative models, which are often applied with character and concept design.

• $\:{A}_{9}$ (Dream by Wombo): Get a mobile application that creates stylish images based on a prompt and provides easy and fast creativity.

• $\:{A}_{10}$ (Designify): A piece of AI software that augments and improvises product photo editing, background removal, and visual optimization in different marketing and design undertakings.

These tools are selected based on the criteria of popularity, availability, and certain features related to designing. All the alternatives offer distinct combinations of sources of strength, such as the generation of fine art or professional graphic design support, which makes them appropriate to compare.

IVSF-CoCoSo methodology has been adopted and implemented on the aggregated decision matrix extracted from the panel of experts, where the linguistic terms are used to represent any uncertain or approximate assessment. Table 1 displays the linguistic review of IVSFS.

Table 1 Linguistic evaluation of interval-valued spherical fuzzy sets.

Table 2 shows the IVSF decision matrix based on decision-makers’ preferences, as shown in Table 1.

Table 2 Interval-valued spherical fuzzy decision matrix.

Using Eq. (5), aggregate the IVSFVs as shown in Table 3. The weights of the criteria are $\:{\left(\text{0.11,0.08,0.05,0.21,0.30,0.07,0.18}\right)}^{T}$ and these weights are hypothetically taken. The above weights are chosen in order to indicate a reasonable hierarchy of design factors in relation to application in generative AI evaluation. The goal is to show how the proposed IVSF-CoCoSo approach can and will be used, and how its functionality can prove to be robust.

Table 3 Interval-valued spherical fuzzy aggregated decision matrix.

We get Table 5 by normalizing the score values using Eqs. (6)- (7), here$\:\:{C}_{3}$ is the cost criterion. We apply Eqs. (8)-(13) to find the ranking of alternatives shown in Table 6.

Table 5 Normalized decision matrix.

Table 6 Ranking of alternatives.

Figure 2 shows the graphical representation of the ranking of alternatives.

Fig. 2

Ranking of alternatives.

Result discussion

The IVSF-CoCoSo framework suggested was used to test the efficacy of ten popular generative AI tools ($\:A_1$–$\:A_{10}$) to stimulate the improvement of visual communication design. The resulting total scores obtained through the CoCoSo methodology provided a decisive ranking of the alternatives based on the performance of each tool in the seven criteria defined in the study. According to the results, $\:{A}_{7}$ (DeepArt) is ranked first and, on the whole, is the most suitable generative AI tool that can be applied to visual communication design as it has performed very well in creativity enhancement, the quality of the output, and the customization capability. Also among the factors that made it rise to the top was its ability to transform images passed to it faithfully into works of art with high aesthetic.

It is in line with the current trends in the industry that DeepART is most useful and well-suited in artistic transformation and style transfer, particularly in areas where artistic fidelity and uniqueness are essential. In the second place was $\:{A}_{8}$ (Artbreeder), which is known to have strong customization capabilities and a collaborative image-editing workspace with the support of iterative refinement of visual output. $\:{A}_{6}$ (NightCafe) was ranked third, with a convenient interface and a diverse stylistic spectrum, making it a convenient tool for both inexperienced and professional designers. Conversely, $\:{A}_{4}$ (Canva AI) and $\:{A}_{2}$ (DALL-E 3) ranked last. Although both have powerful generative features, their performance weakness was dictated by the restrictions of more advanced customization and connection to professional design pipelines, which can be important in high-end visual communication pipelines.

However, the one that got the fifth place unexpectedly was $\:{A}_{3}$ (Adobe Firefly) with its great brand recognition and output quality. Still, the key factor influencing the decision-makers was its cost and, arguably, quite sharp learning curve. $\:{A}_{1}$ (Midjourney) and $\:{A}_{5}$ (RunwayML) reached mid-ranking, which means that their performance is average but not outstanding on all metrics. $\:{A}_{9}$ (Dream by Wombo) and $\:{A}_{10}$ (Designify) were in the lower middle category, ranking eighth and fourth, respectively, with particular strong points, e.g., time efficiency, but were not versatile overall. These findings indicate the subtle trade-offs between generative AI tools, as judged overall in an uncertain situation. The IVSF-CoCoSo approach helped handle subjective evaluation and could perform a multi-facet assessment. Results of the ranking reflect actual use and the generally accepted expertise in creative industries and support the validity of the framework in practice. The conclusions of the ranking provide practical knowledge to designers, educators, and creative directors in choosing the most suitable generative AI tools depending on concrete visual communication tasks.

Theoretical implications

The present study makes significant theoretical contributions to the interconnection of generative AI, visual communication design, and fuzzy MCDM techniques. It provides a structured and quantitative framework to assess generative AI tools in the field, where the subjective judgment has been dominant by combining the IVSF environment with the CoCoSo technique. The given approach resolves the creative choice’s ambiguity and unpredictability, diversifying the theoretical sphere of AI-assisted design criticism. Besides, the offered model adds a multi-criteria outlook on visual communication as a field that has been insufficiently investigated in available literature. It reaffirms the relevance of diverse, expert-based decision-making in assessing design tools, as suggested theoretically, and that heterogeneous inputs can enhance the accuracy of the decisions made. Finally, the research extends to the theory of fuzzy sets, which demonstrates the flexibility of IVSFVs in the creative field. It paves the additional theoretical inquiry into the co-creativity with the AI and human-AI interaction in design activities.

Comparison analysis

The comparison analysis of Table 7 reveals the benefits of the stated method, namely the IVSF-CoCoSo, when compared to several of the most used MCDM techniques, i.e., TOPSIS¹⁴, VIKOR¹⁵, EDAS¹⁶, DEMATEL¹⁷, MARCOS¹⁸, MABAC⁴¹, and ELECTRE⁴². According to the table, the traditional approaches tend to work effectively in situations with structured decisions but have weaknesses regarding uncertainty, imprecise information, and creative, subjective situations like visual communication design. Conversely, the IVSF-CoCoSo approach suggested in this paper shows better capabilities for managing uncertainty by combining IVSF information, efficiently dealing with different decision-makers, and using opinion-based evaluation measures. It is also more stable and accurate in ranking, and it is flexible and can be applied to design-oriented real-world applications. The analyses of the criteria weighting are done using the DEMATEL method and are thus represented in this comparison according to their methodological characteristics and the nature of their use in most cases during the determination of criteria weights, rather than as a ranking tool to come up with answers concerning alternatives. Therefore, it can be considered that the IVSF-CoCoSo method is more holistic and solid, and perfectly adapted to complex, fuzzy, and creative decision-making situations.

Table 7 Comparison analysis with existing MCDM methods.

Table 8 compares the IVSFS with the conventional fuzzy models, such as FS, IFS, PyFS, q-ROFS, PFS, and SFS. Although the previous models provide partial or limited representation of the uncertainty and complexity of decision, IVSFS can be distinguished because it considers the combination of interval-valued MD, AD, and NMD with a strict spherical constraint. It allows a more flexible and expressive way of modelling vague, imprecise, and contradicting expert opinions. It is highly optimized to work in complicated decision-making contexts such as visual communication design augmented with generative AI. It is noteworthy that the comparison is made on the grounds of fuzzy set characteristics of definition and properties, whereas numerical comparisons under varying fuzzy settings in terms of performance are left to further inquiries.

Table 8 Comparison analysis of IVSFS with existing fuzzy models.

Sensitivity analysis

Sensitivity analysis has been carried out by changing the parameter$\:\:\lambda\:$ from $\:0.1$ to $\:0.9\:$to check the robustness and consistency of the generated IVSF-CoCoSo approach in considering the most suitable alternative to improve the visual communication design using generative AI. Figure 3 helped to realize that $\:{A}_{7}$ had the highest performance scores for all values of $\:\lambda\:$, proving this alternative’s stability and superiority. Other high-scoring variants like $\:{A}_{6},\:{A}_{8}$ and $\:{A}_{10}$ also performed consistently with slight variations as $\:\lambda\:$ varied. Instead, alternatives like $\:{A}_{4}$ and $\:{A}_{2}$ stayed at the bottom, which might imply their comparatively low suitability irrespective of weight modification. Overall, this discussion supports the conclusion that the suggested approach gives consistent and robust decision-making results, and the change of the balancing parameter$\:\:\lambda\:$ does not essentially influence the preference of alternatives. This study also attests to the stability of the model when the weighting focus is varied, which makes it very feasible in the actual practice of decision-making, where uncertainty regarding preferences is a common factor. All the above stability across the range of options at a given value of $\:\lambda\:$ and across the range of $\:\lambda\:$ values, which reflects the sound stability of the IVSF-CoCoSo technique.

Fig. 3

Sensitivity analysis by changing parameter values.

Practical and managerial implications

The research has both practical and management implications for the stakeholders of visual communication design and AI. In practice, the IVSF-CoCoSo framework suggested is a flexible and structured method that comprises evaluating and ranking generative AI methods applied to visual communication. This model can be used by designers, developers, and other technology practitioners to determine the best AI-powered tools and approaches depending on various real-life factors, including creativity, cost, flexibility, performance, and human-computer interaction. This speaks in favor of implementing AI solutions that are selected based on particular design requests and project objectives. There might, however, be practical obstacles to their use in the real world. There could be some practical difficulties in real life, which include the complexity of IVSFS, expert assessment is subjective, and more computatio.nal demands in the form of large-scale problems. They can be eradicated using decision-support software, expert training, and an incremental implementation of the model to current work processes, which may be required to achieve both validation and the ability to use.

The study offers, on a managerial level, a decision support tool that can help managers and strategic planners make transparent and informed decisions when modifying the design processes with the aid of AI. The uncertainty and the divergent expert opinion are imbued into the model with the help of IVSF information that helps organizations to reduce decision risks, substantiate the investment in the novel AI technology, and prevent contradictions between the AI adoption and the objectives of the business operation. This congruence eventually strengthens innovation, competitiveness, and long-term strategic orientation in the creative and digital industry. In order to make the paper more accessible to practitioners who may not be conversant with fuzzy logic, the paper will provide a number of mitigation measures. They involve: support of software, levels of training by experts, and facilitation of phased implementation. The purpose of such proactive measures is to facilitate the learning curve and to stimulate confidence in the procedure, and also to encourage the mainstreaming of the IVSF-CoCoSo by industries.

Advantages of the study

The suggested research has several significant strengths. First, it incorporates the IVSFS usage, which is more flexible and precise in representing the uncertainty and hesitation in the expert assessment than the conventional fuzzy models. Second, the combination of IVSFS with the CoCoSo approach makes the study balanced and thorough in guaranteeing that compromise, aggregation, and weighting strategies are simultaneously considered during the decision-making process. Third, the approach accommodates qualitative or quantitative standards, which means it can address real-world, complicated issues such as assessing the role of generative AI in visual communication design. The model is also scalable, domain-adapted, and can deal with interval-based data, thereby increasing its real-life usefulness. Lastly, it enhances openness and uniformity in decision-making, thus being beneficial to all researchers, practitioners, and managers.

Limitations, operational considerations, and ethical constraints

Even though the present study is quite broad in its applicability, several limitations outline its scope and guide further research. The fact that there are a limited number of decision-makers (three), criteria (seven), and alternatives (ten) is one of the limitations that might not reflect all the viewpoints in the large-scale implementations. This was, however, deliberately made to keep things simple and easy to manage and to keep sight of making valuable insights. In the same way, using IVSFS necessitates a complicated calculation and knowledge of fuzzy logic as a basis, which is a limitation that some practitioners might face. Still, it is more accurate in modelling uncertainty.

Operationally, application of the IVSF-CoCoSo methodology requires integrated contributions of expertise, IVSF data and access to computational capabilities. The assumptions and fuzzy parameters incorporated in the model must be properly understood. In a real environment, the use of the method may need technical training on the part of the decision-makers. Ethical limitations are also essential, particularly when generative AI participates in creative work. Issues like the protection of intellectual property, prevention of biased work, transparency in content creation, and preservation of people’s trust will have to be hurdled. The paper demonstrates the significance of ethical considerations regarding AI-powered visual communication solutions in order to assume a responsible and inclusive design.

Conclusion

This paper presented an entire decision-making model, the IVSF-CoCoSo approach, to formally analyze the place of generative AI in improving the visual communication design. Conventional decision-making in this area is usually based on subjective expert opinions, which can be biased, inconsistent or unable to deal with uncertainty formally. The limitations are overcome by using the interval-valued spherical fuzzy environment proposed by us, which is more flexible in modelling uncertainty because it considers the membership, abstention, and non-membership degrees simultaneously in interval form, which is reasonable in dealing with imprecise and contradictory human inputs in creative evaluations. The procedure was carried out in a systematic scenario with three domain experts, seven criteria based on technical and creative dimensions, and ten realistic alternatives based on various uses of generative AI. It is important to note that $\:{A}_{7}$ appeared to be the most productive alternative, meaning that some generative design solutions are much more productive than others in terms of adaptability, creativity support, and user interaction. The comparative analysis demonstrated that, in contrast to the traditional MCDM methods, the IVSF-CoCoSo method is more suited to model human cognitive uncertainty and provided more solid results in terms of ranking. The stability of the technique in varying parameter settings was further confirmed by sensitivity analysis.

Through the combination of a compromise-based MCDM structure and the ability of fuzzy reasoning to consider nuances of reasoning, the study offers a replicable example that design professionals, managers, and researchers can follow to examine AI-driven innovations with higher accuracy and less bias. The results indicate that generative AI can be evaluated systematically regarding its input in visual communication, helping to introduce it in an informed manner and using it ethically. The approach enables a well-rounded decision-making process, which considers subjective knowledge and measurable standards currently under-represented in design decisions. Finally, the study contributes to the theory and practice, filling in the gap between smart algorithmic assessment and human-oriented creative decision making, presenting an effective strategic implementation of generative AI into current design practice.

The IVSF-CoCoSo framework can be extended to structured decision-making with AHP and interval-valued PFS⁴³, and educational assessments with complex PFS⁴⁴. The decision accuracy can be further enriched by prioritizing the neutrosophic operators⁴⁵, the PyFS-based rough set theory⁴⁶, p,q-Quasirung orthopair fuzzy⁴⁷ and the IF rough aggregations⁴⁸ additions to the model. Also, it can be integrated with interval-valued t-spherical fuzzy sets⁴⁹ and domain-specific models such as circular intuitionistic fuzzy EDAS in automotive decisions⁵⁰ to increase the model to the real world and make it more adaptive. We shall also numerically confirm the robustness of the model proposed in the future work using rank correlation methods like the Spearman rho, and the Kendall tau⁵¹.