Introduction

The South China Sea (SCS) is a vital marine region globally, renowned for its rich natural resources, unique ecosystems, and strategic importance as a major international shipping route1,2,3,4. Accurate trajectory prediction enhances the efficiency of search and rescue operations, optimizes the monitoring and mitigation of marine pollutants, including oil spills and plastic debris, and provides critical support for decision-making in fisheries management, marine resource development, and navigation safety5,6,7,8. However, the region’s complex ocean current systems, strong internal waves and tides, frequent typhoons, extreme weather conditions, intricate terrain, and steep temperature and salinity gradients, present significant barriers for precise drifter trajectory prediction9,10.

Traditional methods for predicting drifter trajectories are typically divides into two main categories: numerical model-based methods and statistical approaches. Numerical models simulate ocean dynamics by iteratively calculating an object’s drift using approximate solutions to the partial differential equations that govern ocean state variables11 Van Sebille et al.12 combined historical drifter position data with numerical models to analyze the formation and evolution of oceanic garbage patches, effectively demonstrating the utility of numerical models in trajectory prediction. Liu and Weisberg13 introduced a new skill score based on normalized cumulative Lagrangian separation distances, effectively evaluating numerical trajectory models in regions with varying current strengths. However, despite their widespread use, traditional numerical simulation methods have limitations in providing long-term, continuous spatial and temporal forecasts14. However, due to the limitation of traditional numerical methods, recent studies have explored the application of deep learning techniques to enhance the accuracy of drifter trajectory predictions. For example, Shen et al.15 successfully integrated deep learning to improve the precision of numerical models.

Statistical methods for drifter trajectory prediction typically rely on analyzing and modeling historical data. By examining past drifter trajectory observations, methods such as regression analysis, time series analysis, and probabilistic models are commonly employed to predict future drifter trajectories. For instance, regression models have been applied to forecast drifter speeds and trajectories under various environmental conditions, constructing models tailored to both normal and extreme scenarios16,17. Qiao et al.18 utilized probabilistic density models, such as Hidden Markov Models, to predict drifter positions or regions by extracting time series features and analyzing the probability distribution of drifter movement. Although these models effectively identify patterns in drifter behavior, challenges persist in their application to complex ocean dynamics and nonlinear datasets. This challenge arises primarily because statistical models generally rely on a predefined structure with parameters estimated from observational data. While traditional methods provide some capability for trajectory prediction, they are hindered by high computational demands, limited accuracy in complex marine environment, and a dependency on high-quality input data. These limitations have prompted the exploration of alternative approaches, such as deep learning methods, which demonstrate superior adaptability and higher predictive accuracy in complex conditions.

Predicting drift trajectories of objects is essentially a time series forecasting task. Deep learning, as an advanced approach in high-performance computing, offers innovate solutions in this domain. Common deep learning models for time series forecasting include Recurrent Neural Networks (RNN), Long Short-Term Memory (LSTM), Gated Recurrent Unit (GRU), Convolutional Neural Networks (CNN), as well as Transformer and Informer models19,20,21,22,23,24,25. RNN and its variants, LSTM and GRU, are effective in capturing short-term dependencies in sequence but face limitations with long-term dependencies. These include issues like vanishing or exploding gradients and excessive reliance on previous time steps, which restricts parallel computation. Despite its advance, the Transformer model mitigates these challenges by incorporating an attention mechanism that effectively avoids long-term dependencies, improving both performance and computational efficiency. However, the Transformer requires substantial memory when handling long sequences. The Informer model addresses a sparse attention mechanism that reduces computational complexity to linear time and incorporates self-attention distillation to enhance efficiency further. Compared to the Transformer, the Informer retains its advantages while being more suitable for long sequence time series forecasting. Consequently, this study adopts the Informer as the predictive model.

In the context of the swift progression of machine learning and deep learning, an escalating number of researchers have been applying methodologies such as Random Forest, LSTM, and Transformer to the prediction of drift trajectories. Song et al. put forward a hybrid model which integrates a CNN, a Bidirectional Gated Recurrent Unit (BiGRU), and Attention mechanism, aiming to precisely forecast the zonal and meridional velocities of drifters and subsequently calculate their drifter trajectories22,26. Similarly, Zhang et al. developed the DBASformer model, based on Transformer architecture, which improves drifter trajectory prediction accuracy by incorporating adaptive span attention and double-branch attention to capture cross-time and cross-dimension dependencies in multivariate sequences27,28. Furthermore, Ning et al.29 proposed the TSFFAM model, which amalgamates temporal and spatial characteristics. By leveraging historical Argo drifter trajectory data and satellite observations, it achieves more precise trajectory predictions. Zeng et al.30 exploited the Relational Graph Attention (RGA) model, which fuses ResNet, GRU, and Attention, to consummately forecast the trajectories of drifters in inland rivers. Although these methods leverage the individual strengths of LSTM, GRU, and Transformer architectures, they fail to fully integrate the comprehensive advantages each model offers. Therefore, this study proposes a novel approach based on the Informer and CNN models, aiming to address the temporal limitations of Transformer and LSTM while incorporating spatial data, thereby better tackling the challenges of drift trajectory prediction in complex oceanic environments.

This study proposes a deep learning approach for predicting drifter trajectories, integrating CNN and Informer architectures in an innovative manner. The proposed method comprehensively considers drifter trajectory data along with oceanic environmental variables, including zonal velocity (U), meridional velocity (V), sea surface temperature (SST), and sea surface salinity (SSS) during the training process. The structure of this paper is organized as follows: Section Data and data preprocessing details the data used and the preprocessing steps. Section Experiment outlines the experimental design and the framework of the proposed fusion model (Informer-CNN). Section Result presents the experimental results and comparative analysis. Finally, Section Conclusion concludes with a summary of the key findings.

Data and data preprocessing

Data

Drifter trajectory data

The drifter trajectory data used in this study was obtained from the Global Drifter Program (GDP)31. The GDP provides comprehensive data on various oceanographic parameters, including SSTt (in this context, SSTt refers to the SST measured by drifters), as well as current speed and direction. For this study, we extracted data specific to the SCS region, defined by the coordinates 10°-25°N and 105°-125°E, from the global dataset, spanning the period from 2010 to 2023.

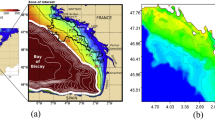
Figure 1(a) depicts the trajectories of all drifters in this region over the study period, and Fig. 1(b) presents the spatial distribution of the amount of drifter observation data density, aggregated into spatial bins with a resolution of 0.33°×0.25°. It is evident from the figures that there are significant spatial variations in data density across different regions.

Fig. 1
figure 1

(a) All the 578 drifter trajectories in the SCS from 2010 to 2023 in the study region (10–25°N, 105–125°E). (b) Drifter observations counts aggregated into spatial bins with a resolution of 0.33°×0.25°.Created by Python(version 3.9.19, https://www.python.org/downloads/release/python-3919/), Cartopy(version 0.22.0, https://scitools.org.uk/cartopy/docs/latest/), Matplotlib(version 3.8.3, https://matplotlib.org).

Full size image

Each drifter trajectory records 9 types of data every 6 h (at 00:00, 06:00, 12:00, and 18:00 UTC), including latitude (LAT), longitude (LON), SSTt, eastward velocity (VE), northward velocity (VN), speed magnitude (SPD), latitude variance (VAR_LAT), longitude variance (VAR_LON) and SSTt variance (VAR_SSTt).

To more effectively extract latent information, this study derives a total of 17 motion features. In addition to the previously mentioned 9 features, it also includes differences between previous time steps and the current time step, encompassing attributes such as bearing (BRNG), distance (DISTANCE), change in latitude (DIF_LAT), change in longitude (DIF_LON), eastward and northward velocity components (DIF_VE and DIF_VN), change in SSTt (DIF_SSTt) and change in speed (DIF_SPD). Comprehensive details for each feature are provided in Table 1.

Oceanic environmental data

Observational and theoretical research has demonstrated that oceanic environmental impacts the movement of free-floating drifters directly or indirectly through a variety of physical processes. Ocean currents and wind are the primary drivers of drifter displacement, whereas variables such as temperature and salinity influence drifter trajectories indirectly by altering the seawater density and hydrodynamic properties32. Considering these environmental variables comprehensively is crucial for establishing accurate prediction models for free-floating drifters. Therefore, this study selects U, V, SSTe (in this context, SSTe refers to the SST derived from HYCOM reanalysis data), and SSSe (in this context, SSSe refers to the SSS derived from HYCOM reanalysis data) as key input parameters for the deep learning model.

HYCOM reanalysis data provide high-resolution global ocean data, with a temporal resolution of up to 3 h (at 00:00, 03:00, 06:00, 09:00, 12:00, 15:00, 18:00 and 21:00 UTC) and a spatial resolution typically at 0.08° (approximately 9 km). These reanalysis data offer detailed, time-varying oceanic conditions, which are critical for precise modeling and analysis of ocean dynamics. In this study, we select HYCOM reanalysis data with a temporal resolution of 3 h, spanning from 2010 to 2023, are selected for the SCS region (10°-25°N, 105°-125°E) to provide accurate oceanic environmental variables for model training.

To ensure feature independence, drifter-measured sea surface temperature (SSTt) and reanalysis-derived SST and sea surface salinity (SSTe, SSS) are explicitly treated as distinct data sources. The HYCOM product used here is a gridded, global reanalysis field that does not directly assimilate individual GDP drifter observations at this scale, thereby minimizing the risk of data leakage between observation-based and reanalysis-based features. SSTt captures localized in situ conditions, while SSTe and SSS represent the regional background environment, enabling the predictive model to integrate both fine-scale variability and large-scale context.

Feature importance evaluation (random forest)

Given the substantial number of features (17) involved in the time series prediction of drifter trajectories, this section outlines the methodology for conducting feature importance analysis on drifter trajectory dataset using a Random Forest algorithm prior to constructing the deep learning-based time series prediction model. The importance of oceanic environmental variable features (SSTe, SSSe, U, and V data within a 1°×1° area centered on the drifter location) will be highlighted through comparative analysis of the prediction results in Section Prediction based on drifter trajectory and ocean environmental data.

Feature importance analysis helps identify the key features that significantly contribute to model performance. Random forest can determine the relative importance of different features in prediction by assessing each feature’s contribution to information gain during decision tree splits33,34. This analysis not only aids in reducing unimportant or redundant features, thereby lowering model complexity, but also enhances training efficiency and improves the overall predictive performance.

During the training of each tree, only part of the dataset is used through random sampling, and the remaining unused data is referred to as out-of-bag (OOB) samples. These OOB samples act as an internal test set, providing an independent validation of each tree’s prediction results, thus offering an unbiased performance assessment for the entire model. This method enables evaluation of the model’s generalization ability without requiring an additional validation set, and through feature importance analysis, identifies the features most influential for the model’s predictions, thereby enhancing model interpretability and predictive performance.

The results of evaluating the impact of the 17 trajectory features Table 1 are shown in Fig. 2. Shown in Fig. 2(a), highlight the relative importance of each feature. The most significant features for predicting the drifter’s longitude and latitude of the drifter over the next 72 h include DIF_LAT, BRNG, DIF_VE, and DIF_VN. These features significantly improve prediction accuracy, while features such as SSTt and VAR_LAT are of lower importance. The OOB score, obtained by sequentially adding features based on their importance, reaches its maximum when the current 14 features are included (Fig. 2(b)). This result indicates that DIF_LAT, BRNG, DIF_VN, DIF_VE, and the remaining features constitute the optimal feature set for the time series prediction model.

Fig. 2
figure 2

(a) Importance of each feature based on the Random Forest method. (b) The OOB scores corresponding to different feature combinations (red dots indicate the maximum value).

Full size image
Table 1 The short and full name of features.
Full size table

Experiment

Experiment design

The purpose of this study is to predict the drifter movements over the next 6 to 24 h by utilizing drifter trajectory data and surrounding oceanic environmental data form the preceding 72 h. Given that the maximum forecast horizon is 24 h (4 trajectory points) and the input sequence length is 72 h (12 trajectory points), drifters with a lifespan shorter than 96 h were excluded from the analysis. The input-prediction sequence samples obtained through a sliding window approach were chronologically divided into three groups: training set, validation set, and test set. A total of 98,303 samples were collected, with 90% used for training and the remaining 10% for validation. The test set consists of 1,967 samples.

To accurately match the oceanic environmental variable data with the drifter trajectory data, this study extracts relevant oceanic environmental data for each point in the trajectory. These data are centered on each trajectory point and extend outward to cover a surrounding area that includes SSTe, SSSe, U, and V data within the drifter’s environmental field, forming a regional dataset. Given that the HYCOM reanalysis data have a resolution of 0.08°×0.04°, the extracted grid size is 13 × 25, which corresponds to a 1°×1° area containing 325 data points, with each data point representing an accurate oceanic environmental value.

Informer-CNN

This research introduces a hybrid model named Informer-CNN, constructed within the PyTorch deep learning framework, designed to integrate heterogeneous data sources and improve the precision of spatiotemporal sequence forecasting. The model combines the strengths of CNN and the Informer encoder-decoder architecture. The input data comprises oceanic features, including U, V, SSTe, and SSSe, along with drifter trajectory data represented as Track. Ocean data features are first extracted using CNN, generating feature maps that are processed through convolution operations and subsequently stacked into a feature matrix for further analysis. For drifter trajectory data, location encoding and time encoding are integrated into the input and subsequently passed into the Informer encoder. This part is highlighted in a red box in Fig. 3, with the specific structure illustrated in Fig. 4. The encoder progressively extracts critical spatiotemporal dependencies from the input data, and the decoder utilizes Masked Multi-head ProbSparse Attention to ensure that only past data is leveraged during prediction, thereby maintaining temporal causality. Finally, a fully connected layer integrates the extracted ocean and trajectory features, mapping the high-dimensional data into the output space and thus completing the model’s prediction process. Figure 3 illustrates the specific model structure, and Table 2 provides detailed structural information regarding the CNN component of the model.

Fig. 3
figure 3

The model framework and network of Informer-CNN. Red boxes indicate location encoding and time encoding are incorporated into the input.

Full size image
Fig. 4
figure 4

The structure of the Embedding layer.

Full size image
Table 2 The architecture of each layer in the CNN component of the Informer-CNN model.
Full size table

Unlike RNN, which process input sequentially across time steps, the Informer model processes input sequences in parallel. To enable the model to distinguish between data at different time points and effectively capture long-term dependencies and trends in time series data, Positional Encoding is introduced. As drifters move across the sea surface, both temporal and spatial dimensions change. Since drifters move across the sea surface with variations in both time and space, Positional Encoding in this study incorporates both time (Global Time Stamp) and location information (Location Position). As illustrated in Fig. 4, the embedding is partitioned into four parts: Scalar, Local Time Stamp, Global Time Stamp, and Location Position. These components convert temporal, spatial, and drifter trajectory data into vectors, facilitating efficient processing by the model. The Scalar component projects drifter trajectory data into vector form. The Local Time Stamp encodes specific time information for each drifter (e.g., TE0, TE1, …, TE8), thereby improving the model’s temporal sensitivity. The Global Time Stamp captures broader periodic patterns, such as daily, weekly, monthly, and annual cycles, while Location Position encodes spatial information to enhance the model’s spatial awareness.

Results

Prediction based on drifter trajectory data

In addition to the Informer model, this study also constructed four other models—RNN, LSTM, GRU, and Transformer—utilizing the same training data for comparative analysis. Each of these models possesses distinct characteristics: RNN excel at capturing short-term dependencies but hindered by the vanishing gradient problem; LSTM and GRU improve the ability to capture long-term dependencies through gating mechanisms; the Transformer utilizes global self-attention to capture long-term dependencies, although it incurs relatively high computational complexity. Through comparative experiments involving the Informer model, this study aim to comprehensively understand the performance of different models in long-time series forecasting tasks and verify Informer’s advantages in computational efficiency and prediction accuracy.

During the training process, we adopted a batch size of 256, 100 epochs, and 256 neurons in the hidden layers to ensure the model has sufficient learning capacity. Additionally, to mitigate the risk of overfitting, an Early Stopping technique was implemented to monitor the loss function on the validation set. The training process was automatically terminated when no further improvement in performance was observed on the validation set, thereby preventing overfitting to the training data and improving the model’s generalization on unseen data.

In Table 3, the mean absolute distance errors (in kilometers) predicted by five deep learning models (RNN, LSTM, GRU, Transformer, and Informer) are presented across forecast intervals of 6, 12, 18, and 24 h. The Informer model consistently demonstrates superior performance across all forecast intervals, as evidenced by the bolded values. Specifically, the Informer achieves the lowest prediction errors, with mean absolute distance errors of 8.6226 km, 8.4038 km, 11.7772 km, and 15.5273 km for 6, 12, 18, and 24 h forecasts intervals, respectively. These results highlight the Informer model’s enhanced accuracy in long-term trajectory forecasting, markedly surpassing the performance of other models such as RNN and GRU, which exhibit higher error rates, particularly within the 12 h to 24 h range.

Table 3 Comparison of the mean absolute distance errors (km) predicted by multiple deep-learning models. Bold values highlight the best performance.
Full size table

As shown in Fig. 5, the distribution of absolute mean distance errors for five neural network models (RNN, LSTM, GRU, Transformer, and Informer) at forecast intervals of 6, 12, 18, and 24 h is presented using a boxplot. The blue dots represent the mean error values for each model. It is evident that the Informer model consistently demonstrates lower median errors and reduced error variance compared to the other models, particularly for longer forecast intervals. The boxplots further indicate that Informer not only achieves the lowest average error but also exhibits the most stable performance across different prediction intervals, characterized by a narrower spread of errors. In contrast, the Transformer and GRU models show greater variability and higher mean errors, especially at the 18 h and 24 h intervals, suggesting a decline in performance for longer-term predictions. Although the Transformer performs well for shorter intervals, its increased error variability at longer intervals suggests that its attention mechanism, while effective, may be less robust for the specific environmental and drifter trajectory data applied in this study.

Fig. 5
figure 5

The absolute-average-distance boxplot for five types of neural networks (RNN, LSTM, GRU, Transformer, and Informer) generating forecasts for 6–24 h at 6 h intervals.

Full size image

Prediction based on drifter trajectory and oceanic environmental data

The results of Prediction based on drifter trajectory data have demonstrated the advantages of the Informer in time series prediction of drifter trajectories. To further enhance the model’s prediction performance, this study thoroughly considers the influence of oceanic environmental factors, specifically SSTe, SSSe, U, and V. A CNN is used to extract the spatial features from the oceanic environmental data, thereby obtaining local spatial structure information of the environmental factors through convolution operations. The features derived from these spatial structures are then integrated with temporal features to construct the Informer-CNN model.

To systematically evaluate the enhancement effects of ocean environmental field data on different model architectures, this study adopts a unified multimodal fusion framework. Within this consistent feature fusion paradigm, we construct corresponding multimodal prediction models (RNN_Sea, LSTM_Sea, GRU_Sea, and Transformer_Sea) based on RNN, LSTM, GRU, and Transformer architectures, respectively. To more accurately evaluate model performance, our study introduces two traditional numerical validation approaches. The first method (denoted as hycom) calculates the drifter’s position after 6 h based on HYCOM-provided ocean current data at its current location and time. The second approach (denoted as hycom_mean) generates a local 1°×1° current field by expanding 0.5° outward from the drifter’s current position and time, then computes the mean current using HYCOM velocity data within this region to determine the 6-hour trajectory. As shown in Table 4, we compare the performance of these seven models across four prediction horizons (6-hour, 12-hour, 18-hour, and 24-hour). The bolded RMSE (°) and MAE (km) values indicate the optimal prediction results at each temporal scale.

The results in Table 4 demonstrate that the Informer-CNN model achieves the best performance across all forecast intervals. Specifically, for the critical 24-hour prediction task, the Informer-CNN yields a MAE of 12.9916 km, which is 1.0006 km lower than the second-best model, LSTM_Sea, and 8.2753 km lower than the worst-performing model, GRU_Sea. In short-term forecasting, the Informer-CNN also exhibits low prediction error, with a 6-hour MAE of only 4.0633 km. In contrast, traditional models show clear limitations: RNN_Sea suffers from memory decay inherent to recurrent neural networks, leading to a sharp increase in error for long-term predictions (with a 24-hour MAE of 17.5756 km); while Transformer_Sea performs better than RNN-based models, its 24-hour error reaches 17.8375 km due to computational redundancy, still higher than that of Informer-CNN. Moreover, Informer-CNN consistently outperforms the traditional numerical validation approaches. These results confirm the effectiveness of Informer-CNN in accurately predicting drifter trajectories under complex oceanic conditions.

To complement these results, Fig. 6 provides a detailed visualization of absolute distance errors for trajectories predicted before and after model optimization. Each row corresponds to a forecast lead time (6 h, 12 h, 18 h, and 24 h), with the left column (“before”) representing errors before optimization and the right column (“last”) showing errors after optimization. The color scale indicates error magnitude in kilometers. From this figure, it is evident that model optimization significantly reduces prediction errors, cutting them by more than half in most scenarios. Errors increase with forecast horizon, reaching their highest levels at 24 h. Before optimization, Informer-CNN predictions were often less accurate than HYCOM-driven results, but after optimization, the deep learning model consistently outperforms physics-based forecasts, demonstrating superior short-term (6–18 h) accuracy and improved long-term robustness. This performance gain results from the model learning task-specific features from the training dataset during optimization, improving alignment with observational data and enhancing its ability to represent drifter movement dynamics. This analysis highlights that the optimized Informer-CNN model not only surpasses physics-based trajectory prediction methods but also demonstrates strong adaptability and precision, particularly in short-term forecasts.

Table 4 Comparative analysis of multimodal trajectory prediction models.
Full size table
Fig. 6
figure 6

Mean absolute distance errors of HYCOM-driven baseline trajectories across forecast horizons.

Full size image

To investigate the impact of the four oceanic environmental field variables on the multimodal drifter trajectory prediction model and observe the contribution of different feature combinations to the model’s predictive performance, this study conducted an ablation experiment.

Table 5 presents a comparison of the root mean square errors (RMSE) and mean absolute distance error for four groups of Informer-CNN models, each integrating different environmental features (SSTe, SSSe, “SSTe and SSSe”, “U and V”). The evaluation is conducted at forecast intervals of 6, 12, 18, and 24 h. The RMSE values reflect the model’s accuracy in predicting latitude and longitude, while the distance values represent the absolute error in kilometers for the trajectory prediction. The model that integrates the U and V (ocean current velocity) data consistently shows the lowest RMSE and distance errors, especially at shorter forecast intervals. For instance, at 6 h, the RMSE of the Informer-CNN model using the variables U and V (in the following text, use “Informer-CNN: U + V” as a substitute) in the oceanic environmental data is 0.0494, and an mean absolute distance error of 4.3279 km, which is significantly lower than those of the other models. This trend continues across all forecast intervals, with “U and V” integration resulting in more accurate predictions compared to models that rely solely on SSTe, SSSe, or their combination.

The box plot illustrating the mean absolute distance error provides a more intuitive comparison of the performance across different models (Fig. 7). It shows the error distances (in kilometers) for four distinct configurations of the Informer-CNN models at forecast intervals of 6, 12, 18, and 24 h. The four models include: the model that uses the SSTe variable in the oceanic environmental data (referred to as Informer-CNN: SSTe hereafter), the model that uses the SSSe variable in the oceanic environmental data (referred to as Informer-CNN: SSSe hereafter), the model that uses both SSTe and SSSe variables in the oceanic environmental data (referred to as Informer-CNN: SSTe+SSSe hereafter), and Informer-CNN: U + V. The box plot illustrates the distribution of errors, with the red line representing the median, the blue dot indicating the mean, the box showing the interquartile range (spanning from the 25th to the 75th percentile), and the whiskers marking the maximum and minimum error values.

As the forecast duration extends, the distribution of error distances shows a clear increase. For the 6 h forecast, the errors are relatively minor, with most values falling within a 10 km range. In contrast, for the 24 h forecast, the error increases significantly, with the maximum value approaching 30 to 40 km. The error distributions of the models in the short-term forecasts (6 and 12 h) are quite similar, with the Informer-CNN: U + V model having relatively lower median and mean errors, indicating better performance. In the long-term forecasts (18 and 24 h), the error distributions of the models converge, displaying similar median errors, which suggests comparable performance across models for extended time predictions.

Table 5 Comparison of drifter trajectory data combining different environmental features. RMSE is the root mean square error of latitude and longitude(°), and the distance is the mean absolute distance error (km).
Full size table
Fig. 7
figure 7

The absolute-average-distance boxplot for four groups of Informer-CNN models, each integrating SSTe, SSSe, and “U and V” oceanic environmental data, generating forecasts for 6–24 h at 6 h intervals.

Full size image

From the perspective of feature influence, the models incorporating SSTe and SSSe show similar performance in the short-term forecasts (6 and 12 h), although they perform slightly worse than the model incorporating U and V components. This indicates that U and V play a greater role in improving short-term predictions. The model that integrates both SSTe and SSSe shows no significant differences in error across the forecast intervals, especially after 12 h, where its performance aligns with the other models, suggesting limited impact of the SSTe and SSSe combination on long-term forecasts. Overall, the Informer-CNN: U + V model performs the best in short-term forecasts among the four ablation models, while in long-term forecasts, the errors increase significantly for all models, and the combination of multiple features does not lead to substantial improvements, with the error primarily influenced by the forecast duration.

The scatter density plot in Fig. 8 shows the comparison between the predicted and actual drifter trajectories in terms of latitude and longitude at different prediction times intervals (6, 12, 18, and 24 h). The left plot represents latitude prediction, while the right plot represents longitude prediction, with the color bar indicating the drifter’s speed (in meters per second). For the 6 h prediction, the Spearman correlation coefficient (SCC) of the model is 1.000, and the standard deviation error (SDE) and RMSE are 0.041 and 0.057, indicating a close alignment between the model’s predictions and the actual values. The data points are densely distributed and close to the scatter plot of actual values and fitted line of predicted values, reflecting the model’s high prediction accuracy. For the 12 h prediction, the SCC remains above 0.999, and although the SDE and RMSE increase slightly, the errors are still minimal, and the model performs well. As the prediction time extends to 18 and 24 h, the SCC decreases to 0.999 and 0.998, respectively, with notable increases in both SDE and RMSE, indicating a decline in accuracy over longer forecast intervals. The prediction error becomes more pronounced, particularly for slower-moving drifters, and the data points gradually deviate from the scatter plot of actual values and fitted line of predicted values. In the 18-hour and 24-hour predictions, a larger number of values deviate from the actual values and fitted line, particularly within the 20°–23°N latitude range. This deviation may be associated with more complex drifting dynamics or environmental factors specific to this region.

Fig. 8
figure 8

Scatter plot distributions of latitude and longitude predictions. The color bar represents the maximum current speed, including the latitude and longitude forecasts at 6, 12, 18, 24 h.

Full size image

Figure 9(a) and Fig. 9(b) display comparative heatmaps of predicted versus observed values at a 1°×1° resolution throughout the entire forecasting period. The strong consistency in color distribution between both figures indicates close agreement between predicted and actual values across these regions. The proximity between predicted and observed values further demonstrates the model’s accuracy in hotspot prediction. In the highlighted regions (18°N, 119°E) and (21°N, 118°E), the predicted values of 544 and 492 show minimal discrepancies of 2.9% and 1.2% relative to the observed values (560 and 498, respectively), indicating high prediction precision in these areas of concentrated drifter activity. However, greater variance is observed at (18°N, 107°E), where the predicted value of 36 differs from the observed value of 16 by 125.0%. Overall, the model achieves a prediction accuracy of 96.3%, demonstrating robust forecasting performance.

Fig. 9
figure 9

Drifter Trajectory Density Heatmaps: (a) Predicted Values (b) Observed Values.

Full size image

Figure 10 illustrates the predicted trajectories of free-floating drifters across four distinct regions of the SCS. This visualization enables a regional comparison of trajectory predictions, highlighting spatial variations and model performance across different areas. The background color represents SSTe, the arrows indicate the direction and strength of ocean currents, and the RMSE and Distance (km) in the upper left corner represent the errors between the predicted trajectories and the true trajectories. Overall, ocean currents and temperature data significantly influence the model’s trajectory predictions. In areas characterized by stronger and more consistent currents (e.g., the upper left and upper right panels), the predicted trajectories closely match the observed ones, especially for the model incorporating ocean current components U and V, highlighting the critical role of current information in drifter trajectory prediction. Conversely, in regions with weaker or more complex currents (e.g., the lower left and lower right panels), the prediction errors of all models increase significantly. Models relying solely on SSTe or SSSe show particularly large errors, indicating that these features have limited predictive power in complex marine environments. The distribution of the temperature data also influences the model’s performance: in regions with larger temperature gradients, stronger currents help improve prediction accuracy, while in areas with more uniform temperature data, prediction becomes more challenging. In summary, the ocean current components U and V play a decisive role in improving prediction accuracy, while models that only use SSTe and SSSe features perform less effectively in complex marine environments compared to those that integrate current information.

Fig. 10
figure 10

Comparison of observed trajectory and predicted future trajectory using Informer-CNN in four different regions under oceanic environmental data conditions. The shading indicates the distribution of SSTe in the area.

Full size image

Discussion

The experimental results presented in this study demonstrate that the proposed Informer-CNN model significantly enhances the accuracy of drift trajectory predictions in the SCS. The main innovations of this study include:

(1) Integration of “U and V” data—among the various oceanic environmental data evaluated (SSTe, SSSe, “SSTe and SSSe”, “U and V”), the integration of “U and V” data (zonal velocity and meridional velocity) has proven to be the most effective method for reducing prediction errors. This superior performance is attributed to the model’s ability to accurately capture the influence of ocean currents on drifter movement.

(2) Multi-head ProbSparse Attention and Location Position—by utilizing the Multi-head ProbSparse Attention mechanism and incorporating Location Position, the Informer model can effectively handle long-term dependencies between temporal and spatial data in drifter trajectory datasets. This ensures that the model can accurately capture the movement trends and variation patterns of drifting objects during trajectory prediction.

(3) Integration of CNN and Informer—the Informer model can learn the temporal and spatial patterns of drifter movement from drifter trajectory data, while CNN extracts key spatial features from oceanic environmental data through its convolutional layers. By combining the drifter trajectory data extracted by the Informer model with the essential spatial features derived from oceanic environmental data by CNN, these components effectively complement each other, achieving an efficient integration of spatiotemporal information.

(4) High prediction accuracy—the SCC value is close to 1, indicating a strong correlation between the observed and predicted values. The distance error for 6–12 h forecasts is within 5 km, and for 24 h forecasts, the error is within 15 km. Compared to models like RNN, LSTM, GRU, and Transformer, the prediction errors are significantly reduced.The accurate long-term predictions provided by the Informer-CNN model are crucial for applications such as search and rescue operations, oil spill tracking, and marine ecosystem management.

Building on the current study, which primarily focuses on the use of SSTe, SSSe, U, and V variables in the SCS, future work could explore the incorporation of additional environmental variables and extend the model’s application to other ocean regions.

In constructing the trajectory prediction model, this study simplified computational complexity by not fully considering the effects of tidal forces, near-inertial circular motions induced by surface inertial currents, and wind fields on the model. Future research could incorporate high-resolution tidal and inertial current data to analyze the impact of these ocean dynamic factors on prediction errors in different marine regions, and develop error compensation mechanisms to further improve the model’s prediction accuracy.

For practical applications, the application of the Informer-CNN model in real-time forecasting systems could provide significant benefits for operational oceanography, improving decision-making in real-time search and rescue missions, navigation, and disaster response efforts. For example, we will mount several Popup Data Communication Beacons (PDCB) on the main body of the underwater mooring. When the PDCB is released and rises to the sea surface, it enters a drifting state mode. Utilizing the Informer-CNN model to accurately predict the future drift trajectory of the PDCB can significantly enhance its operational efficiency.

In conclusion, the Informer-CNN model represents a significant step forward in the accurate and efficient prediction of drifter trajectories in dynamic ocean environments. The integration of critical oceanic environmental data such as sea surface currents and the model’s ability to handle long-term dependencies in time-series data mark a notable advancement in the data of oceanographic forecasting.