A generalized framework for the collinear restricted four-body problem with a central dominant mass

Abstract

This study extends the classical circular restricted three-body problem (CR3BP) by introducing a dominant central primary, forming a collinear restricted four-body problem (CR4BP) that better reflects the dynamics of real planetary systems. The model remains dynamically consistent and non-degenerate when the central mass parameter μ₀ lies in (½, 1) and the peripheral mass μ satisfies 0 < μ < ½ (1 – μ₀). It generalizes to the CR3BP by setting μ₀ = 0, recovering classical results. The system exhibits six libration points: four collinear and two symmetric non-collinear points forming an isosceles triangle with the peripheral primaries. Non-collinear points emerge via a saddle-node bifurcation at a critical μ = μ_c and as μ increases further within the range μ_c < μ < ½ (1 – μ₀), these points move away from the x-axis and gradually align closer to the y-axis, while remaining symmetric with respect to the x-axis. The stability analysis reveals that collinear libration points L₁, L₃ and L₄ are linearly unstable under all conditions while L₂ is stable in the interval 0 < μ < μ^* where μ^* is a critical threshold for L₂. The non-collinear points are linearly stable within a defined interval μ_c < μ < μ_c1. Finally, these results are applied to the Saturn–Janus–Epimetheus system to illustrate the model’s practical relevance.

Introduction

The restricted three-body problem (R3BP) is a foundational model in celestial mechanics, widely used to study the motion of an infinitesimal mass under the gravitational influence of two dominant bodies, typically referred to as the primaries. Its mathematical simplicity and physical relevance make it an ideal framework for analyzing satellite trajectories, planetary motion, and stability regions in space dynamics. Over time, researchers have extended the classical R3BP to more complex configurations, including the restricted four-body, five-body, six-body, and even up to n-body problems. These extensions allow for the inclusion of additional gravitational influences, leading to more realistic and nuanced models that better represent the dynamical behavior observed in natural and artificial celestial systems. Such generalizations have significantly enriched the theoretical landscape and have practical applications in mission planning and understanding multi-body interactions in astrophysical contexts.

The foundational analytical work on the circular restricted four-body problem (CR4BP) was introduced by Michalodimitrakis¹, marking the beginning of extensive research in this area. Roy and Steves² expanded the study by examining special configurations in both symmetric and asymmetric four-body systems. Leandro³ focused on central configurations in the planar CR4BP, while Papadakis⁴ provided asymptotic solutions for the same. Furthering the dynamical understanding, Burgos-Garcia and Delgado⁵ investigated symmetric periodic orbits. The role of oblateness on stability regions was explored by Kumari and Kushvah⁶, and Alvarez-Ramirez et al.⁷ conducted a nonlinear stability analysis in the equilateral configuration. Singh and Vincent⁸ incorporated radiation pressure effects into the analysis of equilibrium points, whereas Barrabés et al.⁹ studied spatial collinear configurations under a repulsive Manev potential. Zotos¹⁰ examined equilibrium points and basins of convergence in a linear CR4BP framework with angular velocity. Chakraborty and Narayan¹¹ extended the problem to its elliptic case. The influence of triaxiality on equilibrium dynamics was demonstrated by Muhammad et al.¹². More recently, Suraj et al.¹³ and Alrebdi et al.¹⁴ analyzed the equilibrium dynamics in the collinear CR4BP involving non-spherical primaries. Meena and Kishor¹⁵ investigated periodic motion in the photo-gravitational planar elliptic variant, while Ma and Gao¹⁶ explored the dynamics of variable mass in a CR4BP framework considering radiating and oblate primaries.

The restricted five-body problem (R5BP) has attracted increasing attention due to its ability to model more complex gravitational systems. Ollongren¹⁷ performed an early analytical study using computer algebra techniques to analyze a specific configuration of the R5BP. Moeckel¹⁸ introduced a family of transition tori within the planar case, highlighting intricate dynamical structures. Papadakis and Kanavos¹⁹ investigated the photogravitational R5BP through numerical methods, while Zotos and Papadakis²⁰ contributed by classifying orbits and constructing networks of periodic solutions in the planar circular configuration. Gao and Wang²¹ conducted a numerical study of zero velocity surfaces and transfer trajectories in the circular R5BP. The impact of variable mass on system dynamics was analyzed by Suraj et al.²², providing new insights into evolving mass conditions. Kashif and Shoaib²³ examined a concave kite configuration, adding to the diversity of geometric setups. Ullah and Idrisi²⁴ explored a particular variant known as the concentric Sitnikov problem, and subsequent work by Idrisi et al.²⁵ delved into the motion of an infinitesimal mass in this framework. Most recently, Kumar and Awasthi²⁶ studied the influence of perturbing forces on motion states within the R5BP, further enriching the understanding of multi-body gravitational systems.

Idrisi and Ullah²⁷ proposed a mathematical model for the restricted six-body problem (R6BP), introducing a configuration with a dominant central primary located at the system’s center of mass. Building upon this, Idrisi et al.²⁸ investigated the effects of perturbations due to centrifugal and Coriolis forces, revealing their influence on the system’s equilibrium structure. Kumar et al.²⁹ further contributed by examining the basins of attraction, shedding light on the system’s stability landscape. In an extension to three-dimensional analysis, Idrisi and Ullah³⁰ explored out-of-plane equilibrium points, enriching the spatial understanding of the R6BP. A rhomboidal configuration of the R6BP was analyzed by Siddique and Kashif³¹, while Suraj et al.³² discussed the associated basins of convergence, offering insight into the convergence behavior of equilibrium solutions. Additionally, Llibre and Mello³³ extended the scope of multi-body configurations by studying families of planar central configurations in the more complex seven-body problem, broadening the theoretical foundation for multi-body celestial mechanics.

Idrisi et al.³⁴ introduced a mathematical model for the circular restricted eight-body problem (R8BP), focusing on the identification and linear stability analysis of equilibrium points. Building on this framework, Saravanamoorthi et al.³⁵ examined how radiation from a central primary affects the in-plane equilibrium points in a photo-gravitational version of the R8BP. Further advancing the model, Idrisi et al.³⁶ extended the analysis to out-of-plane equilibrium points, providing a more comprehensive understanding of the spatial dynamics. Earlier foundational work on multi-body configurations includes Pacella’s³⁷ application of equivariant Morse theory to the study of central configurations in the n-body problem, and Llibre’s³⁸ identification of various central configurations. A significant contribution to the global theory was made by Qiu-Dong³⁹, who offered a solution to the restricted n-body problem. Kalvouridis⁴⁰ proposed the “ring problem”, a planar variant of the n + 1 body problem, emphasizing symmetric mass distributions. Golov and Petrusevich⁴¹ conducted a comprehensive analysis of the Sloan Digital Sky Survey (SDSS) Data Release 14 (DR14) dataset, which compiles extensive statistical information on a wide array of astronomical objects, including stars, galaxies, and quasars. Gilliam and Bettinger⁴² formulated a version of the circular restricted n-body problem tailored to the Jovian system, highlighting its practical relevance in planetary dynamics.

Recent research has explored the dynamics and trajectory design in realistic multi-body environments. For instance, Zhang et al.⁴³ investigated the transfers from lunar distant retrograde orbits (DROs) to Earth orbits via optimization in the four-body problem, demonstrating the practical application of multi-body dynamics to mission planning in the Earth–Moon–Sun system. Similarly, Zhang et al.⁴⁴ analyzed libration points and periodic orbit families near a binary asteroid system with different shapes of the secondary, highlighting how variations in body shape affect equilibrium point locations and orbital stability. In another related study, Shi et al.⁴⁵ examined equilibrium points and associated periodic orbits in the gravity of binary asteroid systems, using (66,391) 1999 KW4 as an example, providing valuable insight into the stability and orbital structure of small-body systems. These works collectively emphasize that extending restricted multi-body models to realistic mass distributions and geometries can yield significant advancements in both theoretical understanding and space mission design, a direction closely aligned with the present study’s adoption of the Saturn–Janus–Epimetheus system as a physically consistent example of the collinear restricted four-body problem.

The restricted four-body problem (R4BP) has been widely used to model the motion of a negligible-mass particle under the gravitational influence of three primaries. However, most studies assume equal or nearly equal masses for the primaries, which limits the applicability of the classical formulation to real planetary systems. In many natural configurations, one central primary is overwhelmingly massive, and the two remaining primaries are much smaller but may share nearly identical orbital periods as in certain co-orbital moon systems or binary–satellite configurations. The present work focuses on such a collinear restricted four-body problem with a dominant central mass, which can accurately describe hierarchical gravitational systems satisfying the constant angular velocity condition. A prime example is the Saturn–Janus–Epimetheus system, where Janus and Epimetheus are co-orbital moons with nearly identical semi-major axes and mean motions. This choice not only ensures the model’s physical realism but also offers insights into stability properties relevant to mission planning, station-keeping strategies, and the general dynamics of co-orbital celestial bodies. By extending the CR4BP framework to include a dominant central primary and realistic mass distributions, this study bridges the gap between theoretical models and observationally consistent planetary–satellite systems.

The structure of the paper is laid out systematically: Section "Introduction" introduces notable research contributions pertinent to the study’s theme. Section "Model description and equations of motion" lays down the system’s mathematical model, detailing the equations of motion for the infinitesimal mass. Section "Existence and stability of LPs: A qualitative approach" presents both graphical and numerical solutions pertaining to the libration points. The stability of these libration points is meticulously addressed in Sect. "Existence and stability of LPs". A real application to the proposed dynamical system is shown in section "An application to the Saturn-Janus-Epimetheus system". Finally, the paper concludes with a succinct discussion and conclusion in the closing section.

Model description and equations of motion

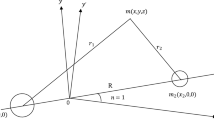
The system consists of three primary bodies P_i with masses m_i (where i = 0, 1, 2). Among them, m₀ is the most massive, while m₁ and m₂ are less massive, with m₁ > m₂ and (m₁ + m₂) < m₀. The less massive bodies are positioned along a straight line and move in concentric circular orbits with radii a and b (where a < b) around most massive primary, m₀, remains libration at the origin, as depicted in Fig. 1. Let r_i represent the distances of the infinitesimal mass m from the primary bodies P_i. We consider a synodic coordinate system Oxyz, which initially coincides with the inertial system OXYZ and rotates with angular velocity ω = nk about the Z-axis (with the z-axis aligned with the Z-axis). By choosing the time unit such that G = 1, Σm_i = 1 and a + b = 1, the two-dimensional equations of motion for the infinitesimal mass m in the synodic reference frame and dimensionless system are given by:

$$\left. \begin{gathered} \ddot{x} - 2n\dot{y} = \Theta_{x} \,\,\, \hfill \\ \ddot{y} + 2n\dot{x} = \Theta_{y} \hfill \\ \end{gathered} \right\}$$

(1)

Fig. 1

The collinear concentric restricted four-body problem (CR4BP) configuration with a dominant central primary m₀ and two smaller peripheral primaries m₁ and m₂. The rotating coordinate system (x, y) is centered at m₀, with the x-axis along the line of primaries.

The potential function Θ(x, y) can be expressed as:

$$\Theta (x,y) = \frac{{n^{2} }}{2}(x^{2} + y^{2} ) + \frac{{\mu_{0} }}{{r_{0} }} + \frac{{1 - \mu - \mu_{0} }}{{r_{1} }} + \frac{\mu }{{r_{2} }}.$$

(2)

Here n is the mean-motion of the primaries, and.

$\mu_{0} = \frac{{m_{0} }}{M},\,\mu = \frac{{m_{2} }}{M},\,M = \sum\limits_{i = 0}^{2} {m_{i} } = 1$,

$$r_{0}^{2} = x^{2} + y^{2} ,\,\,\,r_{1}^{2} = \left( {x - a} \right)^{2} + y^{2} ,\,\,\,r_{2}^{2} = \left( {x + b} \right)^{2} + y^{2} ,$$

$$a = \frac{\mu }{{1 - \mu_{0} }},\,b = \frac{{1 - \mu - \mu_{0} }}{{1 - \mu_{0} }};0 < \mu < \,\frac{{1 - \mu_{0} }}{2}\,\,{\text{and}}\,\,\frac{1}{2} < \mu_{0} < 1.$$

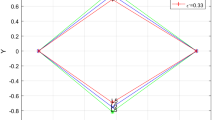
The permissible range for the mass parameters (μ₀, μ) is displayed in Fig. 2. There is a triangular-shaped area (highlighted in grey color) representing the acceptable combination of these mass parameters, within which the numerical study can be conducted.

Fig. 2

Permissible range of the mass parameters (μ₀, μ) in the CR4BP. The triangular grey-shaded region represents the acceptable combinations of μ₀ and μ for which the numerical study is carried out.

Mean-motion of the primaries

In order to maintain the configuration of the primaries in a rotating reference frame, the sum of the gravitational forces exerted by P₀ and P₂ on P₁ must balance the centrifugal force acting on P₁. This condition ensures that P₁ remains in a stable orbit and does not deviate from its position relative to the other bodies. The gravitational attractions from the two primary bodies, P₀ and P₂, pull P₁ towards them, while the centrifugal force, caused by the rotation of the system, pushes it outward. The equilibrium between these forces ensures that the system’s configuration is maintained, i.e.,

$$m_{1} an^{2} = \frac{{Gm_{1} m_{0} }}{{a^{2} }} + \frac{{Gm_{1} m_{2} }}{{(a + b)^{2} }}.$$

(3)

Similarly,

$$m_{2} bn^{2} = \frac{{Gm_{2} m_{0} }}{{b^{2} }} + \frac{{Gm_{2} m_{1} }}{{(b + a)^{2} }}.$$

(4)

Simplifying and then adding Eqs. (3) and (4) under the assumptions G = 1 and a + b = 1, we get

$$n^{{2}} = { 1 }{-}\kappa \mu_{0}$$

(5)

where $\kappa = \left( {1 - \frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right) < 1$ for all μ and μ₀. It is worth noting that when μ₀ = 0, the problem reduces to the classical circular restricted three-body problem (CRTBP), which has been extensively studied, including the work of Szebehely⁴⁶.

Existence and stability of LPs: a qualitative approach

In celestial mechanics, libration points (LPs), also known as equilibrium points or Lagrange points, refer to locations in space where an infinitesimal mass, influenced by the gravitational forces of the primaries, experiences no net force. At these points, the gravitational pull of the primaries balances with the centrifugal force due to the orbital motion of infinitesimal mass, allowing it to remain in a fixed position relative to the larger bodies.

The libration points are determined by solving the equations Θ_x = Θ_y = 0, i.e.,

$$\,\left. \begin{gathered} n^{2} x - \frac{{\mu_{0} }}{{r_{0}^{3} }}x - \frac{{(1 - \mu - \mu_{0} )}}{{r_{1}^{3} }}(x - a) - \frac{\mu }{{r_{2}^{3} }}(x + b) = 0,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y\left( {n^{2} - \frac{{\mu_{0} }}{{r_{0}^{3} }} - \frac{{(1 - \mu - \mu_{0} )}}{{r_{1}^{3} }} - \frac{\mu }{{r_{2}^{3} }}} \right) = 0. \hfill \\ \end{gathered} \right\}$$

(6)

The solution of Eq. (6) gives the locations of libration points in dimensionless system.

In the orbital plane of the primaries, libration points are represented graphically by the intersections of the iso-contours curves Θ_x(x, y) and Θ_y(x, y), as shown in Fig. 3, which identifies six such points, denoted as L_j (j = 1, 2, …, 6). The libration points L_1,2,3,4 lie along the x-axis, while L_5,6 are situated in the xy-plane, forming a symmetric triangular configuration relative to the primaries. Specifically, L₁ and L₄ are positioned to the left and right of P₂ and P₁, respectively, L₂ lies between the primaries P₀ and P₂, and L₃ is located between P₀ and P₁. This arrangement highlights the dynamic gravitational balance in the system.

Fig. 3

Representation of Libration points locations (rubin red dots) derived from intersections of iso-contours curves Θ_x(x, y) = 0 (in green) and Θ_y(x, y) = 0 (in grey) in the concentric restricted four body problem where μ₀ = 0.75 and μ = 0.1

Figure 4 illustrates the dynamics and stability characteristics of the collinear libration points for μ₀ = 0.75, while μ varies within the interval (0, 0.125). As μ increases, the libration point L₁ shifts progressively closer to the secondary mass m₂. Meanwhile, L₂ initially moves toward m₂ but then slightly reverses course, edging back toward the central mass m₀. The third collinear point, L₃, steadily migrates toward the primary mass m₁, and L₄ consistently moves away from m₁. In terms of stability, among the collinear libration points, only L₂ exhibits stability for μ values below a critical threshold μ^* = 0.0448. Beyond this value, and for the other collinear points regardless of μ, instability prevails. It is important to note that this stability threshold is specific to the case of μ₀ = 0.75, and variations in μ₀ may yield different critical values of μ^*.

Fig. 4

Variation in position and linear stability of the collinear libration points for μ₀ = 0.75 as μ varies in the interval (0, 0.125). L₁ shifts toward m₂, L₂ moves toward m₂ and then slightly back toward m₀, L₃ approaches m₁, and L₄ recedes from m₁. Stability analysis shows that only L₂ remains stable for μ < μ^∗  = 0.0448; all other collinear points are unstable for the full range of μ.

Figure 5 illustrates the behavior and stability of the non-collinear libration points L_5,6 for μ₀ = 0.75 and μ ∈ (0, 0.125). Graphical results reveal that at μ = 0.046, a bifurcation occurs, giving rise to two additional non-collinear points, L₅ and L₆, which emerge near the collinear point L₂. As μ continues to increase, these points drift away from the x-axis and gradually align closer to the y-axis, maintaining symmetry with respect to the x-axis. Regarding their stability, L_5,6 are found to be stable within a critical interval I_c = (0.046, 0.062); outside this range, i.e., for μ ≤ 0.046 and μ ≥ 0.062, they become unstable. This analysis is specific to μ₀ = 0.75, and the critical interval I_c may shift for different values of μ₀.

Fig. 5

Examining the parametric evolution of the positions of the LPs, L_j, j = 1, 2, …, 6 in the concentric circular restricted four body problem, when μ₀ = 0.75 and 0 < μ < 0.125. The arrows indicate the movement direction of the LPs as μ increases. The olive green dots shows the value of μ just greater than zero whereas for black dots, μ = 0.125; red dots, μ = 0.04480061; grey dots, μ = 0.046; and pink dots, μ = 0.062.

Existence and stability of LPs

In this section, we perform a numerical analysis to investigate the existence and stability of all libration points, including both collinear and non-collinear configurations. By solving the system of Eq. (6), we locate the equilibrium points and assess their stability through linearization techniques and eigenvalue analysis. This approach allows for a comprehensive understanding of the dynamic behavior near each libration point, providing insights into the nature of small perturbations and their impact on orbital stability.

Libration points

In this section, we focus on the numerical locations of collinear and non-collinear LPs for different values of μ₀ and μ.

Collinear LPs

The libration points on the x-axis can be obtained by setting y = 0 in Eq. (6, we have

$$f(x) = n^{2} x - \mu_{0} \frac{x}{{|x|^{3} }} - (1 - \mu - \mu_{0} )\frac{(x - a)}{{|x - a|^{3} }} - \mu \frac{(x + b)}{{|x + b|^{3} }} = 0.$$

(7)

The Eq. (7) has three singularities at x = –b, 0 and a, and thus we have the following observations:

$$\left. \begin{gathered} \mathop {\lim }\limits_{x \to \, - \infty } f(x) = - \infty ,\,\mathop {\lim }\limits_{{x \to \, - b^{ - } }} f(x) = + \infty , \hfill \\ \mathop {\lim }\limits_{{x \to \, - b^{ + } }} f(x) = - \infty ,\,\mathop {\lim }\limits_{{x \to 0^{ - } }} f(x) = + \infty , \hfill \\ \mathop {\lim }\limits_{{x \to 0^{ + } }} f(x) = - \infty ,\,\mathop {\lim }\limits_{{x \to a^{ - } }} f(x) = + \infty , \hfill \\ \mathop {\lim }\limits_{{x \to a^{ - } }} f(x) = - \infty ,\mathop {\lim }\limits_{x \to \infty } f(x) = + \infty \,.\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} \right\}$$

(8)

In the view of Eq. (6), it is evident that Eq. (7) possesses exactly one real root within each of the intervals (–∞, –b), (–b, 0), (0, a) and (a, ∞). Thus, the solution of Eq. (7) yields four real roots, denoted as x_j (j = 1, 2, 3, 4), which correspond to the positions of the collinear libration points L_j(x_j, 0) located within the aforementioned intervals, respectively. Due to the complexity of Eq. (7), a general analytical solution is not feasible; thus, specific solutions are computed for selected values of the parameter μ₀, namely μ₀ = 0, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90 and 0.95. The mass parameter μ, constrained within the interval (0, (1 – μ₀)/2) where ½ < μ₀ < 1, experiences a narrowing range as μ₀. It is important to highlight that the collinear libration point L₁ does not exist for sufficiently small values of μ. Observationally, with increasing μ in the given range, the libration point L₁ shifts closer to m₂, L₂ initially approaches m₂ and then slightly shifts toward the central mass m₀, L₃ moves toward m₁, and L₄ progressively recedes from m₁. A graphical representation of the dynamics of these libration points is presented in Fig. 4 and summarized numerically in Table 1.

Table 1 Numerical positions of collinear LPs.

Non-collinear LPs

The non-collinear libration points are determined by solving the equations Θ_x = Θ_y = 0, y ≠ 0, i.e.,

$$n^{2} x - \frac{{\mu_{0} }}{{r_{0}^{3} }}x - \frac{{(1 - \mu - \mu_{0} )}}{{r_{1}^{3} }}(x - a) - \frac{\mu }{{r_{2}^{3} }}(x + b) = 0,$$

(8)

$$\,n^{2} - \frac{{\mu_{0} }}{{r_{0}^{3} }} - \frac{{(1 - \mu - \mu_{0} )}}{{r_{1}^{3} }} - \frac{\mu }{{r_{2}^{3} }} = 0.$$

(9)

On plugging Eq. (9) into Eq. (8), we get r₁ = r₂ which gives x = a – ½. Now, substitute this value of x in the Eq. (9), we have

$$\,n^{2} - \frac{{\mu_{0} }}{{\left[ {(a - 1/2)^{2} + y^{2} } \right]^{3/2} }} - \frac{{(1 - \mu_{0} )}}{{\left( {1/4 + y^{2} } \right)^{3/2} }} = 0.$$

(10)

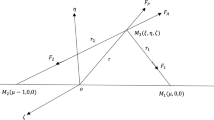
The coordinates of the non-collinear libration points are therefore given by

$$L_{5,6} \left( {a - \frac{1}{2},\,y^{*} } \right);\,a = \frac{\mu }{{1 - \mu_{0} }}.$$

(11)

where y^* represents the symmetric real roots of Eq. (10).

It should be noted that for μ₀ = 0, the conditions r₁ = r₂ = 1 satisfy Eqn. (8) and (9), thereby verifying the classical case. However, for μ₀ ≠ 0, the libration points L_5,6(a – ½, ± y^*) form an isosceles triangle with the m₁ and m₂. Since a general analytical solution to Eq. (10) is not feasible, we solve it numerically for various values of μ₀ and μ. All corresponding results are compiled and presented in Table 2.

Table 2 Numerical positions of L_5,6 for μ₀ = 0.55.

For μ₀ = 0.55, 0 < μ < 0.225, it is observed that the Eq. (110 has no real roots in the interval 0 < μ ≤ 0.078233 while in the interval 0.078233 < μ < 0.225 it has two symmetric real roots as mentioned in the Table 2. Hence at the critical value μ_c ≈ 0.078233 the two non-collinear equilibria L_5,6 born in a classic saddle-node bifurcation. For μ < μ_c there are no off-axis solutions (y = 0 is the only root), but exactly at μ_c, the double root at y = 0 splits into two symmetric branches: one with y > 0 (the upper triangular point L₅) and with y < 0 (the lower point L₆). As μ increases beyond μ_c, these branches rapidly separate, with | y | growing. The accompanying bifurcation diagram (Fig. 6) clearly shows that the emergence of the two off-axis solutions from a single degenerate root at μ_c, making the onset of the triangular configuration.

Fig. 6

Bifurcation diagram for μ₀ = 0.55 showing the emergence of non-collinear libration points L₅ and L₆ as μ increases. No off-axis solutions exist for 0 < μ ≤ μ_c ≈ 0.0782330. At μ = μ_c, a saddle-node bifurcation occurs, where the double root at y = 0 splits into two symmetric branches corresponding to L₅ (y > 0) and L₆ (y < 0). For μ > μ_c, these points separate with ∣y∣ increasing as μ grows.

Similarly, for a specific μ₀ there exist a critical interval 0 < μ < μ_c in which non-collinear libration points do not exist. At μ = μ_c, a saddle-node bifurcation occurs, and giving rise to two symmetric non-collinear libration points. As μ increases further within the range μ_c < μ < (1 – μ₀)/2, these points move away from the x-axis and gradually align closer to the y-axis, while remaining symmetric with respect to the x-axis. This critical value μ_c for different μ₀ is given in Table 3. The plot of μ_c versus μ₀ reveals a steadily decreasing trend, indicating an inverse or exponential decay-like relationship between the two variables, Fig. 7. As μ₀ increases from 0.55 to 0.98, the corresponding values of μ_c drop sharply from approximately 0.078 to 0.0037. This suggests that small increases in μ₀ initially cause significant reductions in μ_c, while further increases have diminishing effects.

Table 3 μ_c for different μ₀.

Fig. 7

Variation of the critical mass parameter μ_c with μ₀. The curve shows a decreasing trend resembling an inverse relationship: as μ₀ increases from 0.55 to 0.98, μ_c drops from about 0.078 to 0.0037, with the rate of decrease diminishing at higher μ₀ values.

Stability of LPs

To discuss the linear stability of libration points L_i, (i = 1, 2, …, 6), we perturb the libration point L(x₀, y₀) to L^*(x₀ + ξ, y₀ + η), where ξ, η <  < 1. Now, linearizing the system (1), we get the variational equations of motion as:

$$\left. \begin{gathered} \ddot{\xi } - 2\,n\dot{\eta } = \xi \mathop \Theta \limits^{o}_{xx} \, + \,\eta \,\mathop \Theta \limits^{o}_{xy} \hfill \\ \ddot{\eta } + 2n\dot{\xi } = \xi \mathop \Theta \limits^{o}_{yx} \, + \,\eta \,\mathop \Theta \limits^{o}_{yy} \,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} \right\}$$

(12)

where ‘o’ indicates that the partial derivatives are to be calculated at the libration points under consideration.

The partial derivatives in system of Eq. (11) are defined as follows:

$$\begin{gathered} \mathop \Theta \limits^{o}_{xx} \, = n^{2} - \frac{{\mu_{0} }}{{r_{00}^{3} }} - \frac{{1 - \mu - \mu_{0} }}{{r_{10}^{3} }} - \frac{\mu }{{r_{20}^{3} }} + \frac{{3\mu_{0} x_{0}^{2} }}{{r_{00}^{5} }} + \frac{{3(1 - \mu - \mu_{0} )(x_{0} - a)^{2} }}{{r_{10}^{5} }} + \frac{{3\mu (x_{0} + b)^{2} }}{{r_{20}^{5} }}, \hfill \\ \mathop \Theta \limits^{o}_{xy} \, = \frac{{3\mu_{0} x_{0} y_{0} }}{{r_{00}^{5} }} + \frac{{3(1 - \mu - \mu_{0} )(x_{0} - a)y_{0} }}{{r_{10}^{5} }} + \frac{{3\mu (x_{0} + b)y_{0} }}{{r_{20}^{5} }}, \hfill \\ \mathop \Theta \limits^{o}_{yy} \, = n^{2} - \frac{{\mu_{0} }}{{r_{00}^{3} }} - \frac{{1 - \mu - \mu_{0} }}{{r_{10}^{3} }} - \frac{\mu }{{r_{20}^{3} }} + \frac{{3\mu_{0} y_{0}^{2} }}{{r_{00}^{5} }} + \frac{{3(1 - \mu - \mu_{0} )y_{0}^{2} }}{{r_{10}^{5} }} + \frac{{3\mu y_{0}^{2} }}{{r_{20}^{5} }}. \hfill \\ \end{gathered}$$

$$r_{00} = \sqrt {x_{0}^{2} + y_{0}^{2} } ,\,\,r_{10} = \sqrt {(x_{0} - a)^{2} + y_{0}^{2} } ,\,\,\,r_{20} = \sqrt {(x_{0} + b)^{2} + y_{0}^{2} } .$$

The characteristic equation that corresponds to the system of Eq. (12) is given by

$$\lambda^{4} + \left( {4n^{2} - \mathop \Theta \limits^{0}_{xx} (x_{0} ,y_{0} ) - \mathop \Theta \limits^{0}_{yy} (x_{0} ,y_{0} )} \right)\,\lambda^{2} + \,\mathop \Theta \limits^{0}_{xx} (x_{0} ,y_{0} )\mathop \Theta \limits^{0}_{yy} (x_{0} ,y_{0} ) - \left( {\mathop \Theta \limits^{0}_{xy} (x_{0} ,y_{0} )} \right)^{2} \, = 0.$$

(13)

A libration point L(x₀, y₀) is considered stable if all characteristic roots of Eq. (13) have either a strictly negative real value, if they are real, or negative real part, if they are complex. This ensures that small perturbations about the libration point will decay with time and all trajectories in the system’s phase space will converge to the libration point L(x₀, y₀) or at least orbit close to it. In simpler terms, there is no tendency towards uncontrolled growth or oscillations that move away from equilibrium. As such, the sign of the real part of the characteristic roots determines most of the local stability behavior close to the libration point.

Stability of collinear LPs

For the collinear libration points, L_1,2,3,4(x_1,2,3,4, 0) the characteristic Eq. (13) reduces to

$$\Lambda^{2} + \Xi (x_{i} )\,\Lambda + \Gamma (x_{i} )\, = 0$$

(14)

where $\Lambda = \lambda^{2} ,\,\,\Xi (x_{i} ) = 4n^{2} - \mathop \Theta \limits^{0}_{xx} \left( {x_{i} ,0} \right) - \mathop \Theta \limits^{0}_{yy} \left( {x_{i} ,0} \right);\,\,\Gamma (x_{i} ) = \mathop \Theta \limits^{0}_{xx} \left( {x_{i} ,0} \right)\mathop \Theta \limits^{0}_{yy} \left( {x_{i} ,0} \right),\,\,i = 1,2,3,4$

The roots of the characteristic Eq. (14) for collinear libration points L_1,2,3,4(x_1,2,3,4, 0) are given by

$$\Lambda_{1,2} = \frac{1}{2}\left( { - \Xi (x_{i} ) \pm \sqrt {\Xi (x_{i} )^{2} - 4\Gamma (x_{i} )} } \right).$$

Consequently, the eigenvalues of characteristic Eq. (12) can be expressed as:

$$\lambda_{1,2} = \pm \sqrt {\Lambda_{1} } \,{\text{and}}\,\lambda_{3,4} = \pm \sqrt {\Lambda_{2} } .$$

When plotting the values of Λ_1,2 for μ₀ = 0.75 within the range 0 < μ < 0.125 for the libration point L₁, it is observed that Λ₁ > 0 while Λ₂ < 0, as shown in Fig. 8. This indicates that the libration point L₁ is a saddle-center point and hence linearly unstable. This behavior is not limited to this specific case but holds true for other values of μ₀ as well, across the collinear libration points L_1,3,4(x_1,3,4, 0), confirming their inherent linear instability.

Fig. 8

Variation of the characteristic roots Λ_1,2 for the libration point L₁ with μ₀ = 0.75 and 0 < μ < 0.125. The condition Λ₁ > 0 and Λ₂ < 0 indicates a saddle–center configuration, confirming the linear instability of L₁.

In contrast, for libration point L₂, Λ_1,2 < 0 in the interval 0 < μ < μ^* where μ^* = 0.0448 as illustrated in Fig. 9. As a result, the eigenvalues of the characteristic Eq. (14) are purely imaginary within this range, indicating that L₂ behaves as a center and is thus linearly stable. This result holds for other values of μ₀ as well, although the corresponding value μ^* of will vary accordingly.

Fig. 9

Variation of the characteristic roots Λ_1,2 for the libration point L₂ with μ₀ = 0.75. For 0 < μ < μ^∗  = 0.04480, both Λ₁ and Λ₂ are negative, yielding purely imaginary eigenvalues of the characteristic Eq. (14) and indicating that L₂ behaves as a center and is linearly stable.

Stability of non-collinear LPs

The characteristic Eq. (12) for non-collinear libration points L_5,6 reduces to

$$\Pi^{2} + \varphi \left( {a - \frac{1}{2},y^{*} } \right)\,\Pi + \Psi \left( {a - \frac{1}{2},y^{*} } \right)\, = 0$$

(15)

where

$$\begin{gathered} \Pi = \lambda^{2} ,\,\,\varphi \left( {a - \frac{1}{2},y^{*} } \right) = 4n^{2} - \mathop \Theta \limits^{0}_{xx} \left( {a - \frac{1}{2},y^{*} } \right) - \mathop \Theta \limits^{0}_{yy} \left( {a - \frac{1}{2},y^{*} } \right),\,\, \hfill \\ \Psi \left( {a - \frac{1}{2},y^{*} } \right) = \mathop \Theta \limits^{0}_{xx} \left( {a - \frac{1}{2},y^{*} } \right)\mathop \Theta \limits^{0}_{yy} \left( {a - \frac{1}{2},y^{*} } \right) - \left[ {\mathop \Theta \limits^{0}_{xy} \left( {a - \frac{1}{2},y^{*} } \right)} \right]^{2} . \hfill \\ \end{gathered}$$

The roots of the characteristic Eq. (14) are therefore given by

$$\Pi_{1,2} = \frac{ - \varphi \pm \sqrt \Delta }{2}$$

(16)

where Δ = φ² – 4Ψ.

As previously discussed, for a fixed value of μ₀ there exist an open interval μ_c < μ < (1 – μ₀)/2 within which non-collinear LPs exist. In order to analyze the characteristic roots of the Eq. (15), we consider μ₀ = 0.55, leading to the interval 0.078233 < μ < 0.225. Within this range, it is observed that both φ > 0 and Ψ > 0, indicating certain stability conditions. However, the discriminant Δ > 0 only within the narrower interval 0.078233 < μ < 0.0897961, as depicted in Fig. 10. Consequently, Π_1,2 < 0 within this same subinterval as depicted in Fig. 11, implying that the characteristic roots of Eq. (13) are purely imaginary. This confirms that the non-collinear libration points are linearly stable within this narrower subinterval.

Fig. 10

Variation of the stability parameters φ, Ψ, and discriminant Δ for the non-collinear libration points with μ₀ = 0.55. While φ > 0 and Ψ > 0 for the full range 0.078233 < μ < 0.225, the discriminant satisfies Δ > 0 only in the narrower interval 0.078233 < μ < 0.0897961, indicating potential stability in this subinterval.

Fig. 11

Variation of Π_1,2 for the non-collinear libration points with μ₀ = 0.55. Both Π_1,2 < 0 only within the interval 0.078233 < μ < 0.0897961, implying that the characteristic roots of Eq. (13) are purely imaginary and confirming the linear stability of the non-collinear points in this range.

For other values of μ₀, there always exists an interval μ_c < μ < μ_c1 within which the non-collinear libration points exhibit linear stability. In this context, μ_c and μ_c1 represent the critical lower and upper bounds, respectively, of the interval where the conditions φ > 0, Ψ > 0 and Δ > 0 are simultaneously satisfied. These conditions are both necessary and sufficient to ensure the linear stability of the libration points. The existence of such an interval for varying μ₀ highlights the sensitivity of the stability behavior to changes in system parameters, and it emphasizes the importance of precisely identifying the ranges of μ for which the stability criteria are met.

An application to the Saturn-Janus-Epimetheus system

To illustrate the applicability of the proposed collinear restricted four-body problem (CR4BP) with a central dominant mass, we consider a dynamical configuration involving Saturn and two of its co-orbital moons: Janus and Epimetheus orbit with nearly the same angular velocity in an inertial frame. This configuration satisfies the assumptions of our model namely, a dominant central mass with two peripheral primaries in concentric and nearly circular orbits. It provides a realistic example of a gravitational system where libration points and their stability can be meaningfully studied.

From the astrophysical data, Lang ⁴⁷, we have:

Mass of Saturn (m₀): 5.683 × 10²⁶ kg.

Mass of Janus (m₁): 1.98 × 10¹⁸ kg.

Mass of Epimetheus (m₂): 5.6 × 10¹⁷ kg.

Mean orbital radius of Janus (a): 151,472 km.

Mean orbital radius of Epimetheus (b): 151,422 km.

In dimensionless system, we have

$$\mu_{0} = \, 0.{999999996},\mu = { 9}.{85395 } \times {1}0^{{{-}{1}0}} ,a = \, 0.{5}000{\text{83 and}}b = \, 0.{499917}$$

Therefore, on solving Eq. (6), the libration points in the Saturn-Janus-Epimetheus system are determined, as presented in Table 4. The analysis reveals the existence of four collinear libration points (L₁, L₂, L₃ and L₄) and two symmetric non-collinear points (L_5,6). The first two points lie on the Saturn–Epimetheus side, one between Saturn and Epimetheus and the other outside Epimetheus, while the remaining two points are situated analogously on the Saturn–Janus side. The positions of the collinear points reflect the near-symmetry of the system, with only minute asymmetries due to the small difference in orbital distances of Janus and Epimetheus from Saturn. Meanwhile, the non-collinear libration points L_5,6 exhibit a symmetric layout, forming an isosceles triangle with Janus and Epimetheus. This geometric arrangement emphasizes the balanced gravitational dynamics and highlights the structural symmetry inherent in the system.

Table 4 Libration points in Saturn–Janus–Epimetheus system.

Furthermore, we have examined the linear stability of the libration points by evaluating the characteristic Eq. (13) at each equilibrium configuration. The computed eigenvalues indicate that all collinear libration points possess one real pair and one purely imaginary pair of roots, corresponding to a saddle–center structure in the phase space. This confirms their linear instability, as perturbations along the unstable manifold grow exponentially. In contrast, the non-collinear libration points exhibit purely imaginary eigenvalues forming two center modes, which implies linear stability in the sense of Lyapunov. The numerical values of the characteristic roots for each point, which substantiate these conclusions, are listed in Table 4.

Discussion

This study presents a generalized framework of the circular restricted four-body problem (CR4BP) by introducing a centrally dominant primary mass positioned at the system’s center of mass. This extension not only encapsulates more realistic gravitational dynamics seen in planetary systems such as the Sun–Jupiter–Saturn configuration but also preserves theoretical continuity with the classical circular restricted three-body problem (CR3BP), which is recovered as a limiting case when the central mass parameter μ₀ approaches zero.

Through analytical derivation and numerical validation, we identified the conditions under which the system admits equilibrium points and remains dynamically viable. Specifically, it was shown that equilibrium configurations exist for 0.5 < μ₀ < 1 and 0 < μ < (1 – μ₀)/2, ensuring the non-degeneracy of primary placements. The system exhibits six libration points: four collinear and two symmetric non-collinear points. A critical bifurcation value μ_c was established, beyond which the non-collinear libration points emerge and gradually transition toward the y-axis while maintaining symmetry.

Stability analysis revealed that collinear points L₁, L₃, and L₄ are linearly unstable, while L₂ maintains stability for μ < μ^*. Moreover, the non-collinear libration points exhibit linear stability within a well-defined mass range μ_c < μ < μ_c1, varying with the central mass μ₀. These findings contribute significantly to our understanding of equilibrium structures and their stability in multi-body gravitational systems.

Finally, by applying the model to the Saturn-Janus-Epimetheus system, we demonstrated its practical relevance in astrophysical contexts. The model offers valuable insights for future studies in celestial mechanics, mission trajectory design, and the long-term dynamical evolution of multi-planet systems. Future work may extend this model to include additional forces such as radiation pressure, relativistic corrections, or non-circular primary orbits for broader applicability.

Conclusion

We have presented a comprehensive analysis of the collinear restricted four-body problem with a dominant central mass, supported by both analytical derivations and numerical computations. By adopting the Saturn–Janus–Epimetheus system as a physically consistent real-world application, we ensured that the constant angular velocity assumption of the CR4BP is closely satisfied. The computed mean motion, equilibrium positions, and corresponding stability properties reveal that all collinear libration points in this configuration are linearly unstable, while non-collinear libration points are found linearly stable.

This study underscores the importance of selecting dynamically consistent planetary systems when applying the CR4BP to real-world scenarios. The results may serve as a reference for future work exploring similar co-orbital satellite systems or artificial multi-body configurations. Potential extensions of this work include incorporating small perturbations such as solar radiation pressure, oblateness, and orbital eccentricity to examine how these effects might alter the existence and stability of equilibrium points in both natural and engineered space environments.