Using ensemble learning for classifying artistic styles in traditional Chinese woodcuts

Abstract

As one of the oldest art fields, Chinese woodcut represent the rich history and culture of China, and have so far seen various artistic styles and diverse techniques. However, an automated method for identifying and classifying the artistic styles of these works has not yet been proposed. In this work, we propose a new method that consists of three main steps: The first step involves the compilation and preprocessing of the images of the woodblocks and their conversion into colored form to extract important features. The second step will use an ensemble model based on Convolutional Neural Network (CNN), which allows for the prediction of the time period and artistic style of the works. In the third step, the predicted results from the basic models are combined with a regression tree-based meta-model Classification and Regression Tree (CART) to improve the prediction accuracy. This hybrid and multi-stage approach seeks to provide an efficient solution for the automatic identification and classification of Chinese woodcut and can contribute to scientific and applied advances in the field of Chinese art. The results of experiments conducted on our proposed method show remarkable success in achieving high levels of accuracy and precision in the identification and classification of Chinese woodcut. Specifically, this method has been able to achieve an accuracy increase of 4.7% and a precision increase level of 4%, which represent significant improvements compared to the compared methods. These results demonstrate the model’s ability to more accurately and efficiently identify different artistic styles and time periods in woodcut.

Introduction

The use of woodcut in Asia emerged as a significant role in the dissemination of culture. Using woodcut to create amulets was a popular folk tradition during the Eastern Jin Dynasty. With the rise of Buddhism in China, a lot of Buddhist sutras had been translated and circulated in woodcut form. In ancient Chinese societies, woodcut was normally used to produce calendars, New Year paintings, and texts on agricultural knowledge and techniques. Popular in northern Vietnam, Đông Hồ paintings depicted the folk and traditional religions and livings. Ukiyo-e (literally pictures of the floating world) that thrived in the seventeenth century during the Edo Era vividly depicted the daily life, landscapes, and cultures with rich colors in Japan¹.

At the onset of the twentieth century, influenced by Western culture, woodcut in Asia experienced creative forms and groundbreaking ideas. In the 1920 s, following his exposure to German and Russian social realist woodcuts, Lu Xun posited that, unlike traditional Chinese ink paintings and Western art, woodcuts functioned as a potent medium for reflecting social phenomena due to their straightforward creation process and striking stylistic boldness; their proliferation could invigorate national consciousness and the proletarian revolutionary endeavor. Subsequently, led by Lu Xun and other avant-garde painters, the modern woodcut movement thrived during the Sino-Japanese War and the ensuing revolution, extending its impact to popular movements in Japan, Vietnam, Korea, and beyond. By addressing social issues and marginalized individuals, woodcut printing evolved into a form of “popular art” where the populace emerged as the political subject. Consequently, the individualism and materialism inherent in Western Modernism have been eclipsed by a “anti-modern modern avant-garde cultural movement,” a phrase introduced by the historian Tang^1,2.

Woodcut is one of the most ancient and fundamental kinds of printmaking, including the cutting of reverse images onto a wooden block and subsequently printing them onto paper for aesthetic assessment³. Traditional woodcut prints are primarily monochromatic, utilizing black and white, which facilitates repeatability and promotion. They have significant mastery over light and shadow⁴. The pronounced color contrasts and the texture of woodcut marks produce a striking visual impact, rendering it an appealing design style that is likely to captivate the viewer’s attention. Several constraints have contributed to the downfall of woodcut printing. The woodcut block printing technique necessitates that designers compose in mirror image, showcasing light fluctuation through alterations in line density rather than grayscale, presenting a formidable design challenge⁵. Once the knife penetrates, a line cannot be obliterated. Typically, a single individual oversees the entire process, from the initial draft to engraving and printing, resulting in a production that is both time-consuming and labor-intensive. The outcome of each printed copy is comparatively inconsistent, and the influence of paper cannot be immediately reflected during the engraving process in woodcut prints, necessitating numerous revisions and adjustments⁶.

Despite their high efficiency, image processing and automatic classification techniques have not yet been widely used in the field of classification or identification of artistic styles related to this category of works. In this research, an attempt is made to improve this research gap by presenting a new model, which includes the assembly of a dedicated dataset of Chinese woodcuts. Our goal is to use new technologies and advanced models to apply image processing and classification capabilities in a way that improves the process of identifying and classifying artistic styles and thus achieve a better understanding of the artistic and stylistic characteristics of these works. This action will not only contribute to scientific progress in this field, but also provide new tools for artists, researchers, and art enthusiasts.

The present study is accompanied by two main innovations. The first innovation is dedicated to the discussion of the topic; in a way that this topic has not been comprehensively investigated in previous research so far. The second innovation is related to the model structure that our proposed method presents as an ensemble system. This ensemble model is designed as a stack and is a combination of deep learning and decision tree-based learning techniques. In this structure, we have used CNN to create models or stack learning components and we have used the decision tree structure to form a meta-model. The goal of this approach is to improve the performance of the ensemble system compared to conventional ensemble structures, and we expect that with this innovation, the accuracy and efficiency of art identification and classification will increase significantly. This paper provides the following contributions:

• Investigating a new topic in the field of art style identification and classification.

• Presenting a decision tree and deep learning-based ensemble model for art style identification and classification, whose performance is enhanced compared to conventional methods.

• Collecting a dataset including different styles of Chinese woodcut.

The remainder of the paper is organized as follows: Sect. 2 examines the related research; Sect. 3 delineates the proposed method in depth, whilst Sect. 4 analyzes the implementation results. Section 5 delineates the conclusions regarding the outcomes of the proposed approach.

Related work

This section reviews the work done in the field of art in recent years. The related works in the field of analyzing artistic styles using machine learning can be grouped into several main categories. In the continuation of the section, we review some of the previous works in each category and highlight the gaps which this research attempts to fill.

Deep learning for artistic style classification

CNNs and similar deep learning models are widely used now in the automatic classification of artistic styles and related features because they can easily learn the hierarchical features found in images.

Yang and Min⁷ adopted the deep CNN architecture to classify media such as oil paint, pastel, pencil, and watercolor into art works; for this, the DenseNet performed very close to trained human performance. It also utilized synthesized oil paint images for fourteen key works of literature. Lin et al.⁸ investigated the relationship between deep learning-based visual recognition systems and fine arts, demonstrating that these systems can proficiently analyze paintings through interactive segmentation tools, thus enhancing feature quality and evaluating domain adaption strategies.

Yi⁹ presented an art education image classification method via an enhanced deep learning model, attaining an accuracy of 86.49%, which surpassed conventional models by 26.29%, while effectively extracting both comprehensive and specific information. Castellano et al.¹⁰ proposed a framework for visual link retrieval and knowledge discovery in digital painting datasets, employing a deep CNN, an unsupervised closest neighbor approach, and graph analysis.

Jalandoni et al.¹¹ introduced a machine learning technique employing deep learning to detect painted rock art pictures, evidencing its effectiveness with Australian data and showing its applicability in other geographical contexts within rock art research. Mohammadi and Rustaee¹² proposed a hierarchical classification approach for the automated fine-art painting style classification. The styles were divided into super-styles, called parents, where one parent classifier and several child classifiers were employed. This approach resulted in a remarkable enhancement of the average F1 score of the DenseNet121 network.

Yang et al.¹³ proposed a technique for categorizing painting art forms through the use of CNN. They employed the VGG-19 mixed transfer learning model to identify various painting styles. The algorithm identified three categories of painting techniques, and when juxtaposed with human observation, it proved to be more effective for classification. Zhao et al.¹⁴ evaluated seven transfer learning models for the classification of artworks by genres, styles, and artists, demonstrating that enhancing the model architecture augmented performance. Moreover, displaying style and genre classification facilitated comprehension of the challenges encountered by the computer.

Imran et al.¹⁵ aimed to create a software application for the analysis and categorization of fine art photographs utilizing Deep CNNs (DCNNs) and shallow neural networks, showcasing enhanced accuracy and precision. Yu and Shi¹⁶ introduced a new approach in the classification of digital paintings according to the attribution of the artist by a multi-scale pyramid representation, CNN algorithm, and Markov Random Fields. Agha et al.¹⁷ investigated the use of a DCNN in recognizing contemporary conceptual art from galleries based on two working hypotheses: that the DCNN relies on exhibitable properties including shape and color while ignoring the non-exhibited properties.

Advanced deep learning and ensemble techniques for art analysis

Apart from basic CNN applications, researchers have also looked into more advanced deep learning techniques, such as using several models together for better accuracy and providing explanations for model decisions.

Menis-Mastromichalakis et al.¹⁸ investigated the application of deep networks to the recognition of art style in the digitization of artworks, comparing eight architectures on two datasets and attaining state-of-the-art accuracy by using a stacking ensemble method. Conde and Turgutlu¹⁹ utilized Contrastive Language-Image Pre-Training (CLIP) to train a neural network on pairings of art images and text, with the objective of tackling attribute identification and instance retrieval difficulties by anticipating the most pertinent natural language description for each image.

Castellano and Vessio²⁰ proposed DELIUS, a DEep learning approach to cLustering vIsUal artS, which employed a pre-trained convolutional network combined with a deep embedded clustering model to optimize the mapping of data and centroids of clusters.

Fumanal-Idocin et al.²¹ have proposed an explainable artificial intelligence method that contributes to improving the generalization and performance of the artistic classification system by using deep learning features along with fuzzy rules, and they achieve up to 19% more accurate results.

Knowledge-driven and feature-based approaches in art analysis

Apart from deep learning, some other approaches have been applied to art analysis and interpretation, including those based on natural language processing, hand-crafted features, and knowledge graphs to highlight different parts of artworks.

Zhao et al.²² presented a new Natural Language Processing (NLP)-based approach to the automatic analysis of paintings in large amounts, with a graph convolutional network and artistic comments used for type, school, timeframe, and author classification.

Liu et al.²³ proposed a new feature-based model for the recognition of artistic movements in portrait paintings by utilizing features such as modified color distance, color ratio feature, and weber’s law-based texture feature. This model was superior to other methods and showed high accuracy.

Raleiras et al.²⁴ investigated the development of automatic learning style predictions for learning systems, which could be divided into literature-based and data-driven approaches. The advantages, disadvantages, and challenges of each are also discussed to improve the quality of research.

Castellano et al.²⁵ proposed a novel fine art classification method using a Knowledge Graph (KG)-enabled approach for attribute prediction based on WikiArt and DBpedia. This work tries to bridge the gap between the Humanities and Computer Science communities in order to increase understanding and promote cultural spread.

Zhang et al.²⁶ presented the Deep Learning Algorithm for modern art education, taking into consideration the problem faced by an art teacher in explaining the meaning of art. The proposed DLA could perform feature engineering autonomously, supported comprehensive teaching, outlined standards, and evaluated student outcomes.

Research gap and contribution

Although a lot has been achieved in using computers to analyze art, there is still a particular gap in identifying and sorting the styles of traditional Chinese woodcuts. Most of the existing approaches center on Western art, typical painting types, or use extra information from outside sources. Also, a detailed approach that combines several visual aspects and time-related information for this cultural heritage has not been fully explored yet. The study aims to solve this problem by suggesting a new ensemble learning approach for accurately classifying traditional Chinese woodcut styles.

Research method

Traditional Chinese woodcut is a very interesting and diversified art, representative of abundant visual information with which the analysis may form certain indications of historical trends, cultural characteristics, and trends in artistic development. Still, classification and analysis require large amounts of human labor and are greatly subjective and easily mistaken. To handle the challenge, this section shows a completely automated approach with the use of machine learning techniques to classify Chinese woodcuts with high accuracy according to their artistic styles. First, this section describes how the dataset was collected, how contextual categorization is determined, and then presents the proposed strategy details for automating this process.

Data

This research utilizes a dataset including 900 high-quality photographs of traditional Chinese woodcuts, categorized into nine distinct artistic styles. Each style is regarded as a distinct category, encompassing 100 photographs that offer a thorough visual representation of this abundant artistic legacy. Equal number of instances for each category results in a balanced dataset. This dataset has been assembled from multiple web sources to guarantee extensive diversity and representation of diverse artistic genres. All images in the collection utilize the RGB color scheme, each exemplifying a distinct style of traditional Chinese woodcuts. The image dimensions in the dataset are inconsistent, requiring preprocessing to provide uniformity and compliance with machine learning models. All pictures have been downsized to a uniform dimension of 200 × 200 pixels to accomplish this objective. Furthermore, owing to the restricted sample size within each category, data augmentation methods such as random cropping, rotation, and flipping have been utilized to enhance data diversity and bolster the model’s generalization capacity. The identification of the artistic style for each sample has been conducted in conjunction with three art specialists. In this classification, each sample is initially segmented into three primary categories according to its origination time: (1) Early period (Tang to Ming dynasty), (2) Secondary period (Late Ming to Qing dynasty), and (3) Modern period (20th century and beyond). Each principal category is thereafter broken into three more specialized subcategories according to creative style. Each expert designates the target category for a sample, and the ultimate target category for each sample is established through majority voting. The agreement rate of 88.44% (perfect concordance on 796 out of 900 samples in the total dataset) signifies acceptable validity and precision of the categorization established by the experts. Figure 1 illustrates multiple instances of the photos contained inside this collection.

The samples in the dataset have been categorized based on the experts’ opinions into the following groups:

Early Period (Tang to Ming Dynasty):

• 1. Religious: Most of them were Buddhist themes, featuring intricate patterns, bright colors, and often depicting deities and other mythical creatures.

• 2. Literary: Images related to classic Chinese literature, such as novels and poetry, typically illustrating landscapes, historical figures, and allegorical scenes.

• 3. Decorative: Decorative prints for home décor, including auspicious symbols, floral patterns, and geometric designs.

Secondary Period (Late Ming to Qing Dynasty):

• 4. Nianhua (New Year Pictures): Colorful prints associated with Chinese New Year celebrations, often depicting gods of wealth, historical figures, and mythical creatures.

• 5. Suzhou Prints: Delicate prints produced in the Suzhou region, known for their fine lines, soft colors, and intricate depictions of landscapes and figures.

• 6. Yangliuqing Prints: Bright prints from the Yangliuqing region, in bold colors with dynamic composition, often presenting historical and mythological scenes.

Modern Period (20th Century and Beyond):

• 7. Modern Woodcut Movement: Influenced by Western art and social realism, these woodcuts often convey social and political messages through imagery and intense symbolism.

• 8. Revolutionary Woodcuts: Produced during the Chinese Revolution and the Cultural Revolution, these woodcuts frequently depict heroic figures, revolutionary scenes, and propaganda themes.

• 9. Contemporary Woodcuts: A diverse range of styles that incorporate both traditional and modern elements, exploring a wide array of themes and techniques.

Fig. 1

Some examples of images in the dataset.

The next section is dedicated to detailing the proposed model for the automatic classification of database samples based on the above categorization.

Proposed method

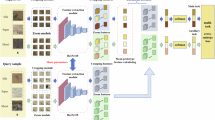
This section presents a cumulative learning-based strategy for the automatic classification of Chinese woodcuts based on their artistic styles. The proposed method aims to achieve a more accurate prediction system by combining the knowledge acquired from various deep learning models. Since the temporal information of the woodcut can be effective in narrowing down the categorization of its artistic styles, a CNN is employed to estimate the time period. Additionally, two separate CNN models analyze the image information to predict the artwork’s artistic style based on existing patterns. This combined model utilizes a meta-model based on decision trees and regression to ensemble the results from the three aforementioned models. The detection process in the proposed strategy can be summarized as follows (Fig. 2):

• 1. Preprocessing of samples.

• 2. Image analysis by CNN s to predict time period and artistic style.

• 3. Ensemble of results using a meta-model based on decision trees and regression.

Fig. 2

Diagram of the Proposed Approach for Artistic Style Classification.

The proposed method involves several steps, starting with the preprocessing of input images. According to Fig. 2, the preprocessing procedure consists of normalizing the dimension of the images and converting the color system of each sample into the RGB color model. This step is necessary in adapting the samples to image-processing models and eliminating redundant information. These preprocessed images are utilized simultaneously by three CNN models. First $\:CN{N}_{1}$ in Fig. 2 is to predict the time period in which the artwork was created; each preprocessed sample would be classified into one of three categories: early period, secondary period, or modern period. Since the detailed categorization of artistic styles is based on temporal information, this data can play a significant role in achieving a more accurate detection model. Alongside this CNN model, two other CNN process the input sample (denoted as $\:CN{N}_{2}\:$and $\:CN{N}_{3}\:$in Fig. 2). $\:CN{N}_{2}$, similar to $\:CN{N}_{1}$, is a two-dimensional CNN that is fed by the preprocessed images, aiming to extract patterns related to the artistic style of each artwork based on the visual features present in the image. In contrast, $\:CN{N}_{3}\:$obtains its required input from a feature descriptor component. This one-dimensional CNN processes a set of statistical features and the Gray Level Co-occurrence Matrix (GLCM) of the image, rather than directly processing the images, and attempts to identify the artistic style of the artworks through a shorter set of image descriptor features. Each of the $\:CN{N}_{2}$and $\:CN{N}_{3}\:$models generates a predicted label for the artistic style variable. The predicted labels, along with the time period predicted by $\:CN{N}_{1}$, are used as inputs for a decision tree and regression model CART. This CART model is trained based on the relationships between the predicted labels from the learning models and the target variable, allowing for a more efficient final output compared to conventional ensemble techniques.

Preprocessing

The database of images has varying dimensions, which makes it challenging to use them as inputs for machine learning models. Therefore, in the first step of the proposed method, the dimensions of all samples have been changed to 200 × 200 pixels to achieve a unified structure for introducing these samples to the machine learning models. All images were resized using bicubic interpolation. This method was chosen to maintain image quality during resizing without cropping, ensuring that the entire content of the woodcut is preserved. After resizing the samples, the preprocessing process targets the description of images in the color system. The initial images are described in RGB format, where the pixels of each sample are represented by intensity values for each of the three color layers in the range of [0, + 255]. Color features are significant in identifying the artistic style of the artworks; however, the intensity feature, which is visually represented as brightness, can be disregarded. To eliminate features related to intensity, the color system of each image is first converted from RGB to HSI. This action isolates the intensity feature in a separate layer from the image. Next, the I layer in the converted image is removed so that each image is described using the two layers H and S. Doing this results in each image being represented in a matrix format of 2 × 200 × 200. The resulting set forms the input for the learning models in the second phase of the proposed method.

Image analysis by CNNs for predicting the time period and artistic style of the artwork

In the process of identifying the artistic style of Chinese woodcuts, the stacked ensemble will use three CNN models to analyze the pre-processed images. The first CNN model will predict the time period, and the other two will attempt to identify the related artistic style category of the Chinese woodcut by processing the hidden patterns in the image. These three models have a similar architecture in layers, but the details of hyperparameter configuration are different among them. Figure 3 shows the structure of layer arrangement in these three CNN models.

Fig. 3

Layer Arrangement Structure in the CNN Models of the Proposed Stacked Ensemble.

The two CNN models, CNN₁ and CNN₂, are fed with preprocessed images; thus, their layer architectures are two-dimensional. On the other hand, CNN₃ differs in input from the other two models. This CNN obtains its input data through statistical features and GLCM extracted from the initial image; consequently, its overall architecture is one-dimensional.

According to Fig. 3, all three CNN models used in the proposed stacked ensemble consist of 5 convolutional blocks. The first CNN model (for predicting the time period of the artwork) and the second CNN model (for predicting the artistic style of the artwork) accept HS layers with dimensions of 200 × 200 as input. The activation layers of these two models include a combination of LeakyReLU and ReLU functions in various blocks. Additionally, the pooling layers of these two networks use max and average functions. Considering the nature of the output of each model, the first CNN includes 3 neurons in its output layer (corresponding to the time periods), while the second CNN includes 9 neurons in this layer (corresponding to the artistic styles). In contrast, the third CNN feeds on 265 features described by the statistical properties and GLCM of the image, using a combination of sigmoid and ReLU functions in its activation layers. All pooling layers in this model are of the max type, and the final layer includes 9 neurons for determining the artistic style of the artwork. The configuration of each model has been conducted independently using a grid search strategy. In this process, various values for hyperparameters, including dimensions and the number of filters in the convolutional layers, the type of activation function, the type of pooling layer, and the size of the fully connected layer (FC1), have been examined. The search range for the filter dimensions of the convolutions has been established as a set, while the search range for the number of filters in each layer has been defined accordingly. Possible options for the activation function parameters in the activation layers have been considered as $\:\left\{ReLU,LeakyReLU,Sigmoid\right\}$. Additionally, during the grid search process, different scenarios for using $\:\left\{max,average,global\right\}$ functions in the pooling layers of the CNN models have been examined. The most suitable configurations obtained for each CNN model in the proposed stacked ensemble are presented in Table 1.

Table 1 Layer configuration details in the CNN models of the proposed stacked ensemble.

It is worth mentioning that during the grid search process, the training parameters for each model, including the $\:\left\{SGDM,\:Adam\right\}$optimization algorithm and minimum batch sizes of $\:\left\{\text{16,32,64,128}\right\}$ were also examined. Based on the search results, the use of the Adam optimizer for CNN models 2 and 3 and SGDM for CNN₁ yielded the best training performance. Additionally, the minimum batch size for all three CNN models was set to 32.

Cross-Entropy Loss was used for training all three CNN models (CNN₁, CNN₂, and CNN₃), since it is designed for multi-class classification. Early stopping was used to avoid overfitting and make sure the training process did not run too long. If the validation loss remained the same for 10 consecutive epochs, training stopped. Training for 100 epochs gave the early stopping criterion the chance to decide when to end the training. For CNN₂ and CNN₃, which applied the Adam optimizer, the initial learning rate was 0.001, but for CNN₁, which used SGDM, the learning rate was set to 0.01. The model used a step decay scheduler for learning rate, which cut the learning rate by 0.1 every 30 epochs. In addition, all CNNs had L2 weight decay with a factor of $\:{10}^{-4}$ on their convolutional layers to help prevent overfitting. After the FC1 layers in every CNN, dropout layers with a rate of 0.3 were added. We chose a batch size of 32 because our experiments showed it gave the best balance between stable training, efficient use of resources, and the model’s performance, considering the type of data and model we were using.

As mentioned, the necessary input for model CNN₃ is obtained through a feature descriptor component that extracts statistical properties and GLCM from the initial RGB image. It is important to note that this component extracts the mentioned features from the original RGB image. The continuation of this section is dedicated to explaining the process of preparing the necessary input data for model CNN₃.

The first strategy employed for feature extraction from the initial images is the color correlation of pixels. To do this, the input image X in the RGB color system is mapped to 64 colors in the RGB space with dimensions of 4 × 4 × 4. This process is repeated using quantization for each pixel²⁷.

$$\:{q}_{i,j}=\: \lceil N\times\:\frac{{p}_{i,j\:}}{{\text{m}\text{a}\text{x}}_{\text{p}}} \rceil$$

(1)

In the above equation, N represents the number of levels associated with the current layer, $\:{p}_{i,j\:}$denotes the pixel value at row i and column j in the current layer, and $\:{\text{m}\text{a}\text{x}}_{\text{p}}\:$refers to the maximum value corresponding to this layer. The quantized matrix is considered as the image X’ with a limited color space.

In the image X’, each color layer has four levels, allowing each pixel to adopt one of the 64 colors available in the mapped space. A radius is considered for the neighborhood of the image pixels. For each pixel in the image, a list of neighboring pixels within the radius of the current pixel is obtained, and then the current pixel is compared with its neighbors. If the value of the current pixel is the same as that of its neighbor, the count for that pixel’s color is increased by one. By doing this, a 64-element vector of pixel color correlation based on the neighborhood radius is derived. The values of this vector are then mapped to the range of [0, + 1] through normalization. In the proposed method, this process is conducted for four different neighborhood radii, and the resultant output is stored as a feature vector that indicates the pixel-based color correlation. The pixel color correlation features perform the image description at the pixel level. The proposed method also utilizes layer-level features to describe the database images. This set of features is referred to as the layer color properties. To extract this category of features, the input color image is decomposed into its constituent layers. For each layer, the mean and standard deviation of the brightness of the pixels in that layer are then calculated. By doing so, for each layer, we describe the feature vector indicating the color properties of the image as $\:<{M}_{R},{S}_{R},\:{M}_{G},\:{S}_{G},{M}_{B},{S}_{B}>$, where $\:{M}_{R}$ represents the mean brightness of the red layer and $\:{S}_{R}$ indicates the standard deviation associated with the red layer. Additionally, the indices B and G correspond to the properties of the blue and green layers, respectively.

The second type of image descriptor characteristics is the GLCM²⁸. The GLCM is a probabilistic model utilized to characterize the distribution of pixel intensity values among neighboring pixels in a picture. GLCM is a bidimensional probability function that evaluates the intensity of pixel i at one position in conjunction with the intensity of pixel j at a different location. GLCM features are statistical metrics derived from the GLCM that characterize image properties. These attributes can be employed to discern and characterize diverse patterns in photographs. GLCM characteristics applicable for picture characterization comprise:

• Correlation: This feature calculates the degree of correlation between the intensity values of neighboring pixels. A high value of correlation would mean that the neighboring pixels are highly related in intensity. It finds application in identifying areas that show regular patterns.

• Variance: This feature is a measure of the dispersion of data. It returns a high value when data is spread out. With the help of this feature, one can identify which area has a high degree of diversity.

• Flatness: This feature calculates the uniformity in the distribution of intensity values. A high value for flatness will indicate that the distribution of intensity values is uniform. This feature can then be used to identify regions that exhibit a uniform intensity distribution.

Thus, the above feature set is organized in vector format to produce the necessary input for model CNN₃.

Ensemble of results using a meta-model based on decision trees and regression

The third phase of the proposed method involves predicting the artistic style of the artwork by ensemble the results provided by the CNN models in the previous step. To this end, a stacked ensemble learning strategy is employed. Ensemble learning is a technique for combining multiple models to improve predictive performance, which has seen significant use in recent years. Among various ensemble methods, stacking has emerged as a powerful approach to combining the strengths of diverse base models. In the proposed method of this paper, a stacked ensemble model is suggested to address the multi-class classification problem, where the three CNN models described in the previous section serve as base models, and a CART acts as the meta-model.

In the three base CNN models used in the proposed ensemble system, $\:CN{N}_{1}$is used to predict the time period of the artwork, while the other two models, $\:CN{N}_{2}$ and $\:CN{N}_{3}$, are used to predict the artistic style of the artwork. Each of the base models is trained on training samples from the dataset. Once the output of each model is determined, a CART-based meta-model is employed to ensemble the outputs of the three base models. In other words, in the proposed stacked ensemble system, the step of merging the outputs of the base models is replaced with a learning model. It proposes the integration of temporal information regarding the artwork in the style prediction results given by other models for more accurate prediction. The CART model was then trained based on the relationships among the predicted labels of the learning models and the target variable, which allows the final output to be obtained with higher efficiency than conventional techniques of ensemble.

Tree-based algorithms are one of the popular families of non-parametric and supervised methods related to classification and regression. A decision tree is an upside-down tree with a decision rule at the root, where decision rules are expanded in the lower sections of the tree. Every tree has a root node through which inputs pass. This root node splits into a set of decision nodes where results and observations are processed based on a set of conditions. The process of splitting a node into multiple nodes is called branching. If a node is not split into any further nodes, it is called a leaf node or terminal node. Each sub-section of the decision tree is referred to as a branch or subtree. However, the CART model can also be applied for classification or regression purposes. In the present research, it acts like a classification model.

We chose CART as the meta-model because it offers several important benefits for this particular application. First, it is important that CART can find non-linear relationships between the CNN’s outputs and the true style labels. Although single CNNs are good at extracting features, their combined results may show interactions that a single linear prediction cannot see. In addition, CART models are naturally easy to understand. Since the model is built like a tree, it is easy to see how predictions from CNNs and the estimated time period combine to give the final classification, which is useful in art classification. Also, considering that the meta-model is given a small number of predicted labels (time period from CNN₁, in addition to style from CNN₂, and CNN₃), CART is faster and less likely to overfit than more advanced meta-learners. CART is also strong against outliers in the predictions, so it can be helpful in an ensemble where some base models may sometimes give unreliable results.

The applied CART model in the suggested ensemble system uses the Gini index as the impurity criterion²⁹:

$$\:Gini\left(t\right)=1-\sum\:_{j=1}^{J}{p}^{2}\left(j|t\right)$$

(2)

In the above equation, $\:p\left(j|t\right)\:$is the estimated probability that data t belongs to class j, and j indicates the number of classes. The Gini impurity is used to measure the probability that a randomly selected sample would be incorrectly classified by a specific node. This criterion is known as the “impurity” measure because it shows how much the model differs from a pure split. The degree of Gini impurity always ranges from 0 to 1, where 0 indicates that all elements belong to a specific class (or it is a pure split), and 1 indicates that elements are randomly distributed across different classes. A Gini impurity of 0.5 indicates that elements are evenly distributed among some classes.

In the training process of the CART meta-model in the proposed stacked ensemble system, the outputs of the base models are defined as input variables, and the target variable is defined as the output. In other words, the CART meta-model attempts to model the relationship between the labeling pattern of the samples by the base models and the target variable.

Research finding

We evaluated the proposed method employing MATLAB 2020a, using a 10-fold cross-validation for evaluation. For every fold, 810 samples (90%) were used for training and validation, with 80% of them used for training and 10% for validation, and the remaining 90 samples (10%) were set aside for testing. The average is taken from the results of the 10 folds.

Our proposed method is investigated in three different modes. The first mode, introduced as Proposed, is presented in Sect. 3. The second mode, CNN₁ + CNN₂, refers to the situation in which the first model is used for age estimation and the CNN₂ model is used for registration assessment or prediction. Also, in this case, the CART model is used to ensemble the results. The third mode, CNN₂ + CNN₃, refers to the situation in which age estimation of the work is not performed and only artistic registration prediction is performed using the CNN₂ and CNN₃ models. In this case, results of these two models are combined together and the CART model is used to predict the target (artistic style) in the ensemble model. Furthermore, a comparison of the proposed method was conducted using the publications of Mohammadi et al.¹², Yang¹³, and Zhao et al.¹⁴. These compared methods were re-implemented using the architectures based on original specifications and trained on our dataset.

Accuracy, Precision, Recall and F-Measure, criteria have been employed as evaluation metrics in this section. The following cases can occur for a single test instance by comparing the system-generated predicted label with the actual label:

• True Positive (TP): The number of actual positive instances correctly predicted as positive.

• True Negative (TN): The number of actual negative instances correctly predicted as negative.

• False Negative (FN): The number of actual positive instances incorrectly predicted as negative.

• False Positive (FP): The number of actual negative instances incorrectly predicted as positive.

Accuracy is the major metric used for performance evaluation. It can be explained as the percent of properly predicted samples out of the total number of predictions. This may be calculated by using Eq. (3). Precision tells about the exactness of the projected observations that come out to be positive. The precision comes by dividing the number of correctly predicted positive cases by the total number of positive predictions, as shown in Eq. (4). Recall is the metric for quantifying the ratio of correctly anticipated positive observations. According to Eq. (5), it is calculated as the ratio of correctly predicted positive cases to the total number of positive observations. F-measure is the harmonic average of the precision and recall values for each classifier. The F-measure is determined by using Eq. (6).

$$\:Accuracy=\:\frac{TP+TN}{TP+FP+TN+FN}$$

(3)

$$\:Precision=\frac{TP}{TP+FP}$$

(4)

$$\:Recall=\frac{TP}{FN+TP}$$

(5)

$$\:F-Measure=\frac{2\times\:Precision\times\:Recall}{Precision+Recall}$$

(6)

Results

Figure 4 shows the accuracy metric. In Fig. 4a, the accuracy of different models across different folds is depicted. The proposed method in this graph shows the highest accuracy compared to other models. By examining the methods, it is clear that the accuracy of the proposed model remains consistently above 90% and in some folds even reaches close to 100%. In contrast, other hybrid methods such as CNN₁ + CNN₂ and CNN₂ + CNN₃, as well as models proposed by other researchers (Mohammadi et al. and Yang and Zhao) show fluctuations in their accuracy values, none of which reach the stability and accuracy of the proposed model. Figure 4b shows the box of the average accuracy of the proposed method and the comparative methods. The proposed method, with the highest in accuracy of 93.67%, is at the center of the plot, meaning that it always has high consistency in performing its accuracy. The median line (mean) inside the box shows the highest for the proposed method, emphasizing the reliability and efficiency of this method in classifying Chinese woodcuts. The methods for CNN₁ + CNN₂ and CNN₂ + CNN₃ have a greater fluctuation in their values of accuracy, which is 85.44% and 83.78%, respectively. Also, the comparative methods of Mohammadi et al.¹², Yang¹³, and Zhao¹⁴ provide accuracies ranging from 82.11% to 88.89%, which is accompanied by greater fluctuations and dispersion in the data. This box plot clearly demonstrates the importance and efficiency of using deep learning combinations in the automatic classification of Chinese woodcuts and emphasizes the superiority of the proposed method in this field.

Fig. 4

Evaluation of (a) accuracy during CV folds and (b) average accuracy in classification of artistic styles.

Figure 5 clearly presents how our proposed stacked ensemble method performs compared to several simple and previous methods^12,13,14. The Precision, Recall, and F-Measure for each model are clearly shown in subfigures (a), (b), and (c) for all 10 cross-validation folds. The stability and strength of a model can be judged by these plots; a similar performance in every fold suggests that the model is not affected much by different data partitions. It is clear from the results of the subplots that our proposed method performs best in all 10 folds for Precision, Recall, and F-Measure, indicating its strong stability and ability to generalize. Overall, subfigure (d) shows the average performance of each model across all the folds. The bar chart makes it clear that the ‘Proposed’ stacked ensemble method achieves the highest average Precision, Recall, and F-Measure when compared to other tested methods, including CNN combinations (for example CNN₁ + CNN₂ and CNN₂ + CNN₃) and those found in the literature. The fact that our approach performs better than others in all aspects proves that it is effective in classifying traditional Chinese woodcuts.

Fig. 5

Performance Comparison of Proposed Ensemble Method against Baseline Models. Subplots (a), (b), and (c) illustrate the stability and consistency of Precision, Recall, and F-Measure, respectively, for each model across 10 cross-validation folds. Subplot (d) presents the overall average performance metrics (Precision, Recall, and F-Measure) for all compared models, providing a consolidated view of their classification quality.

Figure 6 shows the obtained Precision, Recall, and F-Measure metrics for different categories. As can be seen, the proposed method performs very well in the Precision criterion in all categories except the revolutionary category. This indicates the model’s ability to correctly identify positive samples and reduce false positive errors, and shows that the model has well identified the specific features of each category. In the Recall criterion, the proposed method has also shown good performance in most of the 9 categories, which indicates the model’s ability to identify all true positives and increase its reliability in identifying positive woodcuts. In addition, in the F-Measure criterion, the Replication Guide has shown good results in all categories compared to the comparative methods. This clearly indicates a proper balance between Precision and Recall, which leads to increased accuracy and efficiency of the model in identifying and classifying Chinese woodcuts. We can conclude that our results indicate that the proposed method has been able to well meet the needs related to identifying and classifying Chinese woodcuts.

Fig. 6

The classification rates obtained for each category: (a) Precision, (b) Recall, and (c) F-Measure metrics.

Figure 7 shows the confusion matrix. The confusion matrix is an essential resource for evaluating classification model performance. The approach we propose has an accuracy of 93.67%, helping us to analyze its effectiveness in detecting Chinese woodcuts. This high accuracy indicates the high ability of the model in identifying different woodcuts and well reflects the ability of this method to extract unique features of woodcuts and successfully identify them. In addition, this method has also achieved a 4.7% advantage over comparative approaches, including Zhao et al.¹⁴.

Fig. 7

Evaluation of the confusion matrices obtained through classification of artistic styles.

Figure 8 introduces the ROC (Receiver Operating Characteristic) curve as an effective tool for evaluating the performance of classification models, particularly in identifying Chinese woodcuts. This curve displays the relationship between the True Positive Rate (TPR) and the False Positive Rate (FPR) at various thresholds, allowing us to carefully assess the overall performance of the proposed method. To calculate TPR and FPR in a multi-class problem with C classes, each class is considered positive while the rest are considered negative. For every class k, the TPR, which is also called Recall or Sensitivity, is given by Eq. (7):

$$\:TP{R}_{k}=\frac{T{P}_{k}}{T{P}_{k}+F{N}_{k}}$$

(7)

$\:T{P}_{k}$ is the number of class k samples that are correctly classified as class k; and $\:F{N}_{k}$ is the number of class k samples that are incorrectly classified as a different class. This number shows how many positive instances of class k were identified correctly. The FPR for a class k is computed by using Eq. (8):

$$\:FP{R}_{k}=\frac{F{P}_{k}}{F{P}_{k}+T{N}_{k}\:}$$

(8)

$\:F{P}_{k}$ represents the number of samples that are not part of class k and are still predicted as class k. $\:T{N}_{k}$ means the number of samples from a different class that are correctly identified as not belonging to class k. This value shows how many negative instances were wrongly labeled as class k. In Fig. 8, each curve represents the micro-average performance of the model for every class.

The main objective of this method is to maximize TPR while minimizing FPR. Identifying woodcuts, as one of the traditional forms of Chinese art, requires a high degree of accuracy because it involves intricate details and unique characteristics that the proposed model must be able to extract and analyze.

Fig. 8

Evaluation of ROC curves of various methods in classification of artistic styles.

Table 2 comprehensively presents the comparative performance of different models in identifying Chinese woodcuts and clearly shows the results of our proposed method. This method has the highest accuracy with Precision equal to 0.9372, which indicates its ability to reduce false positive errors and correctly identify samples. Also, the Recall with 0.9367 of this criterion indicates its good capability in identifying true positive samples. The F-measure with a value of 0.9367 gives this model a good balance between Precision and Recall, while the Accuracy of this model is 93.67%, indicating that the model is highly accurate in the identification of woodcuts. Overall, these results reflect the great superiority of the proposed method in identifying Chinese woodcuts and its capacity to extract the complex features of these traditional artworks.

Table 2 Results obtained from the proposed method and comparative methods.

The proposed stacked ensemble method has also been compared to the pre-trained fine-tuned ResNet-50 and ViT-B/16³⁰ models in Table 2. These two models are pre-trained on ImageNet-21k. In the experiments, the two models were fine-tuned on the Chinese woodcuts dataset with the same training, validation, and testing splits to make a fair and direct comparison with our proposed ensemble approach.

The accuracy of the suggested approach (93.67%) is much higher than that of the fine-tuned ResNet-50 (90.22%). Such a difference of 3.45% points could be explained by the hybrid nature of our model. Unlike a typical CNN which only operates on raw pixels, we are fusing three streams of information i.e., temporal context, visual patterns and statistical textures which are intelligently fused by a CART meta-learner. This multifaceted method gives a more detailed insight into the work of art, which results in better classification.

Further, we compared our model with the ViT-B/16 that showed a very high accuracy of 91.89 and confirms the power of new transformer architectures. Nevertheless, there is also a clear advantage of our model, and it is that it performs better than the ViT by 1.78% points. In our opinion, this has been achievable due to the hierarchical nature of our model which is domain-informed. This is a major background that our model takes into account first by forecasting the time frame and then using it to categorize the final artistic style. An architecture such as ViT that is general-purpose will have to implicitly learn this two-level relationship. This observation leads to the fact that the domain-specific architecture constructed based on domain knowledge can achieve better results on subtle tasks, even compared to the powerful and state-of-the-art models.

Ablation study for meta-classifier

A study was done to prove that using a classification and regression tree as the meta-model is beneficial in our stacked ensemble. This study analyzes how well our proposed ensemble (CART) works compared to other methods of combining the predictions from the base CNN models. The simpler or more common strategies used in the alternatives let us measure the extra benefit of using CART. Several meta-classifier configurations were tested in the experiment:

• Proposed (CART Meta-model): This case refers to the full proposed model, in which a CART is trained based on the outputs of $\:{\text{C}\text{N}\text{N}}_{1}$, $\:{\text{C}\text{N}\text{N}}_{2}$, and $\:{\text{C}\text{N}\text{N}}_{3}$ to predict the target variable.

• Simple Averaging: The predicted artistic style is determined by averaging the probabilities given by $\:{\text{C}\text{N}\text{N}}_{2}$ and $\:{\text{C}\text{N}\text{N}}_{3}$. In this case, the prediction from $\:{\text{C}\text{N}\text{N}}_{1}$ is not included in the averaging process.

• Logistic Regression Classifier: The meta-model is a linear Logistic Regression, and it uses the outputs of $\:CN{N}_{1}$, $\:CN{N}_{2}$, and $\:CN{N}_{3}$ as input. It checks whether a basic combination of the base model’s predictions is adequate.

• Single Dense Neural Layer: A single dense neural layer with SoftMax activation is the meta-model, and it is fed with the outputs of all three CNN base models combined. This is how a basic neural network approach can be compared.

Table 3 shows the results of the ablation study.

Table 3 Performance comparison of different Meta-Classifier Strategies.

As can be seen in Table 3, the stacked ensemble with CART as the meta-model is always better than the other meta-classifier strategies in all evaluated metrics. The Simple Averaging method, not using a meta-learner, achieved the lowest results, meaning that just mixing base models without considering their connections is not the best approach. Applying “Logistic Regression” as a meta-model made the predictions better than just averaging the base models, proving that a simple linear model can still make use of base predictions. The “Single Dense Neural Layer” showed that a simple non-linear combination of neurons can lead to better performance.

Our CART model recorded the highest scores, reaching an accuracy of 93.67%, precision of 0.9372, recall of 0.9367, and F1-measure of 0.9367. CART increased the accuracy by 2.89% over the single dense neural layer, which means it can better model the links between CNN predictions, resulting in more accurate final classifications. The results we obtained from the experiments prove that CART is a suitable choice as a meta-model, as it makes use of the strengths of the individual base learners to improve the classification of artistic styles.

Ablation study on individual components

To check the effectiveness of our proposed stacked ensemble architecture, we ran an ablation study to see the impact of its main parts. The purpose of this study is to show that using an ensemble of models is better than using single models or simple combinations. To evaluate the configurations, Accuracy, Precision, Recall, and F1-measure were used. The following arrangements were tested for the purpose of classifying artistic styles:

• $\:CN{N}_{2}$ (Standalone Style Predictor): This setup depends on $\:CN{N}_{2}$, which works on the preprocessed HS images to predict the style of the painting. This forms the basis for an image-based deep learning model.

• $\:CN{N}_{3}$ (Standalone Style Predictor): only uses $\:CN{N}_{3}$ to process the statistical and GLCM features and predict the style of the image. This forms the basis for a deep learning model that uses features.

• Ensemble ($\:CN{N}_{2}+\:CN{N}_{3}$ - Averaged Probabilities): In this case, the final style prediction is determined by averaging the SoftMax probabilities from $\:CN{N}_{2}$ and $\:CN{N}_{3}$. It shows that using two different style-prediction paths together works well, without the need for temporal information or a more advanced meta-learner.

• Ensemble ($\:CN{N}_{1}+\:CN{N}_{2}+\:CN{N}_{3}$ with Logistic Regression Meta-model): In this configuration, the outputs of all three CNNs ($\:CN{N}_{1}$ for period and $\:CN{N}_{2}$ and $\:CN{N}_{3}$ for style) are combined by a simple linear Logistic Regression classifier. It demonstrates that using all base learners can be more useful than the particular benefits of the CART meta-model.

• Proposed Stacked Ensemble (CART): This case refers to the approach suggested in this research for classification of artistic styles.

Table 4 shows the results for each of the configurations tested.

Table 4 Performance comparison of individual components and ensemble Configurations.

Table 4 makes it clear that our approach of stacking ensembles leads to improved performance. $\:CN{N}_{2}$ and $\:CN{N}_{3}$ are used as basic baselines to show what each model can do in classifying artistic styles. The $\:CN{N}_{2}$ model, trained on processed images, was slightly better than $\:CN{N}_{3}$, which uses only statistical and GLCM features, but both performed well on their own for such a tough task.

When the predictions from $\:CN{N}_{2}$ and $\:CN{N}_{3}$ were averaged, the model reached an accuracy of 88%. It proves that using various feature representations and models, even with a basic fusion, is beneficial. When $\:CN{N}_{1}$’s period prediction and a linear meta-model (Logistic Regression) were used in the ensemble, the accuracy increased to 89.56%, proving that considering the time period is important for improving the classification of art styles.

Our Proposed Stacked Ensemble with the CART meta-model achieved the greatest performance in all the metrics, with an accuracy of 93.67%, precision of 0.937, recall of 0.937, and an F1-measure of 0.937. The fact that CART performed better than Logistic Regression (by 4.11%) demonstrates how well it can handle complex and time-related connections between the base model outputs for the final classification. As a result, this study proves that every component, including different CNN base learners and the CART meta-model, plays an important role in achieving the high accuracy and stability of our suggested approach.

Conclusion

In this research, a novel method was developed to address the general problem of identifying and categorizing Chinese woodcut prints, a unique form of art that was uniquely representative of the traditional Chinese culture. In our proposed work, which was divided into three main steps, that involved image preprocessing, the use of an ensemble model of CNN, CART meta-model, we recorded an impressive improvement which amounted to 4.7% in terms of accuracy and a precision improvement of 4%. These results not only demonstrated how our framework outperformed the available methods but also displayed how the current sophisticated deep learning methodologies can contribute to future art historical research. With the ability to classify different artistic styles and their respective epochs, our model helped fill the gap of understanding between Chinese woodcut and modern technology. In general, this research provided the foundation for future advancements and development of interdisciplinary projects in the Chinese art studies strengthening both theoretical knowledge and its application in other fields. The following are the limitations and future work listed:

• One of the limitations of this research is related to the data. This research has tried to collect a dataset to solve the problem, but due to the limitations of resources and collection methods, this dataset cannot cover a wide range of samples. Therefore, we could not ensure the generalizability of the model to classify unobserved samples. We hope that in our future research, this limitation may be overcome by increasing the number of samples and including different types of works in the given field.

• The second limitation is related to the computational complexity of the model. Based on the experiments, the use of an ensemble combination of deep learning systems has been effective in increasing the accuracy. The results have shown that each of the components used in the ensemble system has a suitable effect on increasing the accuracy of the system. However, each of these components imposes an additional burden on the system, which can limit the generalizability of using different models. In future research, we will try to reduce this limitation by improving the computational model and utilizing computational load reduction techniques such as quantization.

• Even though XAI is very helpful for understanding why models make certain decisions, especially in cultural heritage applications, the focus of this study was on developing a strong classification framework. We plan to use Grad-CAM and LIME in future studies to improve how understandable our models are and learn more about the visual aspects that affect our classifications.