Introduction

With the increasing integration of distributed energy resources–mainly wind, solar, and electric vehicle charging stations–modern power systems are experiencing increasingly complex power quality disturbances (PQDs). This shift is reshaping grid dynamics and posing challenges to reliable monitoring. As integration of power electronics systems grows1,2, two key features emerge: (1) proliferation of large-scale disturbance sources and (2) coupling and superposition of PQDs3. These disturbances are often non-stationary and resulted in degraded power quality, equipment damage, data loss, increased energy consumption, and in severe cases, large-scale outages4. consequently, accurate and efficient PQD detection, localization and classification are vital for grid stability and safe energy use.

Traditionally, PQD recognition relied on manual feature extraction using signal processing techniques like Fourier Transform5, S-Transform combines with LightGBM6, and S-Transform followed by kernel SVM7, Wavelet Transform8, Decision Trees9, and Deep Belief Networks10, as well as wavelet-based feature selection with probabilistic neural networks11 and RBF neural networks with growing/pruning mechanisms12. While effective for simple disturbances, these methods have proven effective, but often require domain expertise and lack adaptability. As PQDs grow more complex with renewable integration, traditional techniques struggle to accommodate their diversity and temporal variability.

Deep learning has revolutionized PQD recognition by enabling autonomous feature extraction and enhanced generalization. CNNs and RNNs have been used for classification, with CNNs extracting spatial features and RNNs capturing temporal patterns13,14,15. However, 1D CNNs often fail to fully capture temporal dynamics and face gradient issues, which limit their effectiveness on complex PQDs. To overcome this, researchers have adopted signal visualization techniques to convert 1D signals into 2D representations like Gramian Angular Field (GAF) images, enabling the use of ResNet and CNNs. Studies16,17 show GAF improves accuracy but is computationally heavy, prone to noise, and unsuitable for real-time use in large systems. Efficient signal-to-image conversion methods that preserve key features are still needed. While attention-based CNNs enhance accuracy, DenseNet models augmented with static modules like Convolutional Block Attention Module (CBAM)18,19,20 are resource-intensive and less adaptable to diverse PQDs, limiting real-time applicability. Other deep architectures, including sequence-to-sequence Bi-GRU models21, CNNs with GAF encoding22, and improved fully convolutional networks (FCN)23, have further advanced PQD recognition but still lack validation under real-time constraints. Addressing these challenges is critical for the advancement of practical PQD recognition systems..

Solar power, a sustainable and cost-declining energy source, benefits from ongoing innovations and economies of scale24. As a DG technology, it supports varied uses and boosts grid resilience during outages25. Solar PV integration improves voltage support and reliability but causes PQ issues like voltage/frequency instability, harmonics, reverse power flow, and flicker26,27. These effects vary with PV size, grid connection, load ratio, and voltage control28,29,30,31. A Zagreb study showed high current harmonics (3rd, 5th, 7th, 9th) during shading and increased voltage harmonics at high PV penetration32. In Puducherry, PV caused the most PQ degradation, including voltage fluctuations, harmonics, flicker, and lower power factor33. Grid-connected PV systems cause varied PQ issues based on size and grid conditions. A 3.45 kW system in Portugal showed voltage fluctuations, dips, swells, and harmonics affected by grid strength and load34. A 12-kW system in Brazil improved voltage and lowered THDU but risked overvoltage at high PV levels; harmonics were mainly load-related35. Larger systems reported over/undervoltage, power fluctuations, frequency spikes, low power factor, inrush currents, and rising harmonics at low power and due to grid voltage distortion36. In Maribor, Slovenia, PV systems caused voltage issues and high harmonic currents under low short-circuit impedance, especially with multiple inverters on one bus37. Studies show PV size alone doesn’t dictate harmonics; module connections, irradiance, and PV location impact THDU and voltage support38. In Thailand and single-phase systems, voltage sags, flickers, transient and subharmonic currents were linked to grid faults, shading, and MPPT design, highlighting the inverter’s key role in PQ39.

To address the above mentioned challenges, this paper presents a low-latency, recurrence-plot-based framework for real-time detection, zonal localization, and classification of power quality disturbances (PQDs) in a solar-penetrated IEEE 13-bus distribution system. The proposed pipeline uses recurrence plots (RPs) to preserve non-linear and temporal structure of three-phase voltage waveforms and a Cosine Similarity Index (CSI) computed against a healthy reference RP for fast anomaly triggering. For classification we employ an EfficientNet-B0 backbone augmented with adaptive Squeeze-and-Excitation (SE) blocks (EfficientNet-SE) tailored to RP texture learning. A zone-wise localization rule, based on CSI comparisons from three strategically placed measurement nodes, enables real-time identification of affected regions. The entire detection \(\rightarrow\) localization \(\rightarrow\) classification chain is validated end-to-end using Real-Time Digital Simulator (RTDS) experiments and Hardware-in-the-Loop (HIL) testing. Results demonstrate high detection and classification performance under varying SNRs and solar operating conditions, while meeting stringent timing requiOscillatory Transientsrements for near-real-time operation.

Main contributions of the proposed work

  • A practical, low-latency RP\(\rightarrow\)CSI detector that triggers PQD processing on a 10-cycle moving buffer updated at sub-millisecond rates, enabling rapid anomaly detection with a simple, interpretable thresholding mechanism.

  • A compact RP\(\rightarrow\)EfficientNet-B0 classifier enhanced with adaptive SE modules (EfficientNet-SE) that improves discrimination of 39 single/multi-event PQD classes while increasing noise robustness.

  • A zone-based localization approach using three measurement nodes selected for voltage observability; the method is validated in RTDS+HIL and achieves detection accuracy of 95.5% and zonal localization accuracy of 89.44% on the test cases considered.

  • A sensitivity analysis across SNR levels, representative solar operating scenarios, and grid strength (SCR) variations that quantifies performance degradation and provides recommended CSI threshold adaptations for weak grids.

Addressing limitations in the prior literature

Several limitations remain in the PQD literature (see Table 6). Below we explicitly map representative prior shortcomings to how this work addresses them and where supporting evidence appears in the manuscript.

Objectives

The specific objectives of this work are to:

  1. 1.

    Develop and validate a low-latency recurrence-plot + CSI anomaly detector that operates on a 10-cycle moving window updated at 250 \(\mu\)s increments.

  2. 2.

    Design, train, and evaluate an EfficientNet-SE classifier for RP images to reliably recognize 39 PQD classes with strong noise resilience and modest inference cost.

  3. 3.

    Implement an end-to-end detection \(\rightarrow\) localization \(\rightarrow\) classification pipeline and validate it using RTDS and HIL on a solar-integrated IEEE 13-bus testbed, reporting accuracy, confusion characteristics, and timing metrics.

  4. 4.

    Quantify sensitivity to grid strength (SCR), solar operating conditions, and additive noise; compare the proposed approach with representative state-of-the-art baselines and report tradeoffs in accuracy, latency, and complexity.

The remainder of this paper is structured as follows: Section “ Procedure for the data visualization of PQD’s using recurrence plots” explains the process of visualizing PQDs using recurrence plots, section “PQD classification based on Efficient-Net with adaptive SE blocks” introduces the PQD classification technique based on EfficientNet with adaptive Squeeze-and-Excitation (SE) blocks, section “Proposed power quality detection, classification, and localization framework” presents the proposed methodology along with the zone-based detection strategy and classification of power quality events, section “Real time validation using RTDS” outlines the experimental setup, including the RTDS and HIL environments. Section “Validation of PQD algorithm in real time for power quality detection and zone identification” presents the validation of the PQD detection and localization algorithm in real time, and section “Conclusion” concludes with key findings.

Procedure for the data visualization Of PQD’s using recurrence plots

Acquiring complex PQD data from real-world systems is challenging; thus, this paper uses mathematical modeling based on IEEE Std 201919. Nine basic disturbances that includes sag, swell, interruption, harmonic, oscillatory transient, pulse, flicker, gap, and spike are modeled, as shown in Table 1. Complex PQDs arise from superimposing multiple disturbances of different types and timings, producing irregular waveforms that complicate accurate classification.

Table 1 PQDs description and their mathematical models.
Full size table

Recurrence plot

Recurrence plots (RPs) have been shown to outperform Gramian Angular Fields (GAF) and Markov Transition Fields (MTF)20 in Power Quality Disturbance (PQD) analysis by effectively capturing the non-linear, non-stationary characteristics of signals. Unlike GAF and MTF, which encode angular relationships or state transitions, RPs visualize the recurrence of states in phase space, revealing dynamics like periodicity, chaos, and abrupt transitions. This capability makes RPs perticularly well suited for identifying complex PQD patterns. RPs also preserve temporal structures more effectively and exhibit greater robustness to noise, while GAF and MTF plots tend to be sensitive to parameter selection and are computationally demanding. The distinct visual patterns produced by RPs enhance image-based classification approaches, leading to improved accuracy in real-world PQD recognition tasks.

To generate a Recurrence Plot (RP) from a univariate time series \(X = \{x_i\}_{i=1}^N\), where \(x_i\) denotes the data value at time \(t_i\) and N is the total number of time points, the process begins with phase space reconstruction. In this step, state vectors \(\mathbf{y}_i\) are constructed using an embedding dimension m and a time delay \(\tau\), as expressed in Equation (1):

$$\begin{aligned} \begin{aligned} \mathbf{y}_i = \big [ x_i,\, x_{i+\tau },\, x_{i+2\tau },\, \dots ,\, x_{i+(m-1)\tau } \big ], \\ \quad i = 1, 2, \dots , N - (m - 1)\tau \end{aligned} \end{aligned}$$
(1)

Next, the distance matrix \(\mathbf{D}\) is computed using the Euclidean norm to quantify the differences between state vectors. This is expressed in Equation (2):

$$\begin{aligned} D_{i,j} = \sqrt{ \sum _{k=0}^{m-1} \left( x_{i + k\tau } - x_{j + k\tau } \right) ^2 } \end{aligned}$$
(2)

Based on a predefined threshold \(\varepsilon\), the recurrence matrix \(\mathbf{R}\) is constructed using the Heaviside step function \(\Theta (\cdot )\), which determines whether two state vectors are recurrent or not. This is formally defined in Equation (3):

$$\begin{aligned} R_{i,j} = \Theta (\varepsilon - D_{i,j}), \quad \Theta (x) = {\left\{ \begin{array}{ll} 1, & \text {if } x \ge 0 \\ 0, & \text {if } x < 0 \end{array}\right. } \end{aligned}$$
(3)

Finally, the binary matrix \(\mathbf{R}\) is visualized as an image, as shown in Fig. 1 effectively capturing the key temporal patterns present in non-linear, non-stationary signals such as power quality disturbances.

Fig. 1
figure 1

Visualization of recurrence plot generation process.

Full size image

Parameter selection and robustness: The choice of embedding parameters \((m, \tau )\) and the recurrence threshold \(\varepsilon\) is critical for stable RP generation. In this work, m and \(\tau\) were selected via the False Nearest Neighbours (FNN) and Average Mutual Information (AMI) methods16,17,18,19,20, respectively, using representative healthy and disturbed signals. The threshold \(\varepsilon\) was set to the 5th percentile of the pairwise distance distribution computed over a 10-cycle healthy operation buffer. Sensitivity analysis showed that the RP texture statistics and the subsequent classification accuracy remain stable for \(\pm 20\%\) variations in \(\varepsilon\), confirming robustness of the chosen values.

PQD signal visualization

To visualize PQD data while preserving temporal and detailed signal features, this study employs Recurrence Plots (RPs) to convert one-dimensional signals into two-dimensional images. Based on the PQD models in Table 1 and the method described in section “Recurrence plot”, signals are sampled at 1920 Hz over 10 cycles (60 Hz base), generating RP-based images for nine PQD types (Fig. 2). These images exhibit distinct textural patterns that spatially differentiate PQDs. The clarity of these features, even under superimposed conditions, enables effective feature extraction and supports accurate classification by deep learning models.

Fig. 2
figure 2

Recurrence Plots (a) Normal Operation (b) Voltage Sag (c) Voltage Swell (d) Harmonics (e) Oscillatory Transients (f) Spike (g) Notching (h) Flicker (i) Gap (j) Interruption.

Full size image

PQD classification based on efficient-net with adaptive SE blocks

Traditional CNNs often suffer from overfitting due to their large number of parameters and limited training data, while shallow architectures struggle to extract complex features. Although deeper networks mitigate this issue, they are prone to vanishing or exploding gradients, which can slow down or destabilize the training process24. To overcome these challenges, advanced models such as DenseNet, EfficientNet, and MobileNetV3 have been developed. DenseNet improves gradient flow and promotes feature reuse through dense connections, thereby reducing redundant learning and lowering the number of parameters19. EfficientNet applies compound scaling to simultaneously optimize network depth, width, and resolution, achieving higher accuracy with fewer computational resources. The integration of Squeeze-and-Excitation (SE) blocks enables adaptive channel-wise attention, enhancing relevant features and improving model robustness. Figure 3 illustrates the structure of EfficientNet.

Efficient-Net model

EfficientNet, designed via Neural Architecture Search (NAS), balances depth, width, and resolution for high accuracy and low computational cost. EfficientNet-B0, the baseline variant, is employed in this study for feature extraction and PQD classification. Its core component, the MBConv block, as shown in Fig. 3, includes an expansion phase with convolution, Batch Normalization (BN), and Swish activation, followed by a depthwise convolution. The integrated Squeeze-and-Excitation (SE) block adaptively recalibrates channel-wise features. A final convolution layer restores dimensions, with Dropout enhancing generalization.

Fig. 3
figure 3

Structure of MBConv.

Full size image

Batch Normalization (BN) stabilizes training by normalizing layer inputs using mini-batch statistics, which helps to mitigate the internal covariate shift and accelerates convergence. The Swish activation function, defined in Equation (4), combines smoothness with non-linearity and is given by:

$$\begin{aligned} f(x) = x \cdot \sigma (\alpha x), \quad \text {where } \alpha = 1 \text { by default} \end{aligned}$$
(4)

where \(\sigma (\cdot )\) denotes the sigmoid function.

To convert the final layer activations into class probabilities, the Softmax function is used as shown in Equation (5):

$$\begin{aligned} j_i = \frac{e^{a_i}}{\sum _{k=1}^{R} e^{a_k}} \end{aligned}$$
(5)

where \(j_i\) is the predicted probability for class i, \(a_i\) is the activation corresponding to class i, and R is the total number of classes.

The model is optimized using the cross-entropy loss function, which measures the discrepancy between the predicted probabilities and the true labels. It is defined in Equation (6):

$$\begin{aligned} \text {Loss} = -\sum _{i=1}^{C} \hat{j}_i \log (j_i) \end{aligned}$$
(6)

where \(\hat{j}_i\) is the ground truth label (1 for the correct class and 0 otherwise), and \(j_i\) is the predicted probability for class i. This architecture supports accurate and efficient PQD classification

Fig. 4
figure 4

Sequence Diagram of EfficientNet Implementation.

Full size image

Convolutional block attension module (CBAM)

CBAM20 enhances convolutional neural networks by applying attention in both channel and spatial dimensions through two sequential modules: the Channel Attention Module (CAM) and the Spatial Attention Module (SAM).

Channel attention module (CAM)

Given an input feature map \(F \in \mathbb {R}^{C \times H \times W}\), CAM first applies global average pooling (GAP) and global max pooling (GMP) across the spatial dimensions to obtain channel descriptors.

$$\begin{aligned} F_{\text {avg},c} = \text {GAP}(F), \quad F_{\text {max},c} = \text {GMP}(F) \end{aligned}$$
(7)

These are passed through a shared multilayer perceptron (MLP) consisting of two fully connected layers with ReLU and sigmoid activations:

$$\begin{aligned} M_{\text {avg},c} = \sigma (W_1 \delta (W_0 F_{\text {avg},c})), \quad M_{\text {max},c} = \sigma (W_1 \delta (W_0 F_{\text {max},c})) \end{aligned}$$
(8)

The final channel attention map is computed as:

$$\begin{aligned} M_c = \sigma (M_{\text {avg},c} + M_{\text {max},c}), \quad M_c \in \mathbb {R}^{C \times 1 \times 1} \end{aligned}$$
(9)

The refined feature map \(F'\) is obtained via element-wise multiplication:

$$\begin{aligned} F' = M_c \odot F \end{aligned}$$
(10)

Spatial attention module (SAM)

To capture spatial attention, SAM first applies average and max pooling across the channel axis of \(F'\) to produce two spatial feature maps. These are concatenated and passed through a convolution layer followed by a sigmoid activation:

$$\begin{aligned} M_s = \sigma (\text {Conv2D}([F_{\text {avg},s}; F_{\text {max},s}])) \end{aligned}$$
(11)

The final output of CBAM is obtained as:

$$\begin{aligned} F'' = M_s \odot F' \end{aligned}$$
(12)

Squeeze-and-excitation (SE) block

The SE block improves representational power by modeling channel-wise interdependencies.

Squeeze

Global context is captured by applying GAP across spatial dimensions:

$$\begin{aligned} Z_c = \frac{1}{H \times W} \sum _{i=1}^{H} \sum _{j=1}^{W} X_{i,j,c} \end{aligned}$$
(13)

Excitation

The squeezed vector is passed through a two-layer fully connected (FC) network with a bottleneck structure and sigmoid activation:

$$\begin{aligned} S = \sigma (W_2 \cdot \text {ReLU}(W_1 Z)) \end{aligned}$$
(14)

Recalibration

The original feature map is scaled channel-wise using the excitation weights:

$$\begin{aligned} \hat{X}_{i,j,c} = S_c \cdot X_{i,j,c} \end{aligned}$$
(15)

EfficientNet with CBAM integration

EfficientNet scales depth, width, and resolution of the network using a compound scaling coefficient \(\phi\), under the constraint:

$$\begin{aligned} d = \alpha ^\phi , \quad \omega = \beta ^\phi , \quad r = \gamma ^\phi \quad \text {subject to } \alpha \cdot \beta ^2 \cdot \gamma ^2 \approx 2 \end{aligned}$$
(16)

EfficientNet employs Mobile Inverted Bottleneck Convolution (MBConv) blocks, which consist of:

  • 1\(\times\)1 pointwise expansion,

  • 3\(\times\)3 depthwise convolution,

  • SE block for channel recalibration,

  • 1\(\times\)1 projection.

CBAM modules are inserted at selected layers to enhance feature refinement. Downsampling is performed via stride-2 depthwise convolutions. The network concludes with a global average pooling layer and a fully connected layer of 1280 dimensions. Figure 4 illustrates the complete architecture of EfficientNet integrated with CBAM and the recurrence plot-based preprocessing for PQD (Power Quality Disturbance) classification.

Cosine similarity

Cosine similarity measures the cosine of the angle \(\theta\) between two non-zero vectors in a high-dimensional space, as given by equation (17). Cosine similarity suits Recurrence Plots as both use angular patterns, emphasizing directional and shape similarity over magnitude. It is also scale-invariant and handles high-dimensional data efficiently40. The range of cosine similarity is from − 1 to + 140 however to avoid negative values, the range has been scaled from 0 to 2 by adding + 1 for the computed Cosine Similarity Index (CSI) values.

$$\begin{aligned} \text {Cosine Similarity} = \frac{\mathbf{A} \cdot \mathbf{B}}{\Vert \mathbf{A}\Vert \, \Vert \mathbf{B}\Vert } \end{aligned}$$
(17)

Where:

  • \(\mathbf{A} \cdot \mathbf{B} = \sum _{i=1}^{n} A_i B_i\)    (dot product),

  • \(\Vert \mathbf{A}\Vert = \sqrt{\sum _{i=1}^{n} A_i^2}\)    (magnitude of vector A),

  • \(\Vert \mathbf{B}\Vert = \sqrt{\sum _{i=1}^{n} B_i^2}\)    (magnitude of vector B).

Normalization and thresholding: To ensure interpretability, the raw cosine similarity (range \([-1,1]\)) was shifted to [0, 2] by adding \(+1\), yielding the Cosine Similarity Index (CSI). Under healthy operation, CSI values remain close to 2. A global threshold of 1.55 was obtained by Receiver Operating Characteristic (ROC) curve analysis on validation data16,17 to maximize detection sensitivity while limiting false alarms. For improved localization, zone-specific thresholds were derived: \(Z1=1.25\), \(Z2=1.31\), \(Z3=1.32\). This threshold design balances fast detection with robustness to noise, as further validated in section “Validation of PQD algorithm in real time for power quality detection and zone identification”.

Proposed power quality detection, classification, and localization framework

The raw PQD signal x(t) generated using the mathematical models (Table 1) are sampled at fs=1920 Hz over 10 cycles at the base frequency f0=60 Hz, yielding 640 samples per signal. These 1D time-domain signals are transformed into 2D images via Recurrence Plots (RPs) (Fig. 2) to retain temporal structures and enable spatial feature learning. The recurrence plot is compared with a healthy reference pattern using cosine similarity index to detect the power quality event when the similarity index is above the reference value. Leveraging the imaging strengths of recurrence plots alongside the deep feature extraction and efficiency of EfficientNet enhanced with Adaptive SE Blocks, this paper introduces a novel method for PQDs classification. As illustrated in Fig. 4, the proposed framework consists of three key modules: a signal visualization module, a dense feature learning module, with attention enhancement module, and a final classification module. IEEE 13 bus test system will be modelled and simulated by considering various power quality events as per Table 1 to validate the above method in real time for detection, classification and localization of power quality events using real time digital simulator and a real time power quality detection hardware implemented on a high speed x86 based hardware. In the coming sections, initially the performance of the proposed algorithm is validated for classification of power quality events by simulating the power quality events as per the mathematical equations mentioned in Table 1. Subsequently validated in real time on IEEE 13 bus system modelled in RTDS for detection, classification and localization of power quality events.

Validation using simulated data

This work develops a PQD classification model using the TensorFlow framework in Python 3.9. In accordance with IEEE Std 1159–2019, a total of 30 composite disturbances are synthesized from nine basic disturbance types, comprising 15 double, 10 triple, and 5 quadruple disturbance combinations based on Table 1. Each type consists of 800 samples generated with uniformly distributed amplitude and phase, under SNR levels of 0, 20, 30, and 40 dB. The PQD signals are transformed into 2D representations using recurrence plots, resulting in a 39-class image dataset as explained in section “PQD signal visualization” and Fig. 1. Experiments are carried out on a system equipped with an Intel Core i9-13900K CPU, 64 GB RAM, and an NVIDIA RTX 3090 GPU. A 5-fold cross-validation scheme is used to divide the dataset into training, validation, and testing subsets in a 6:2:2 ratio, with model selection based on the highest validation accuracy. The dataset used for PQD classification consists of 39 distinct classes as shown in Table 2. The EfficientNet-SE model is trained over 50 epochs with a batch size of 64 using Stochastic Gradient Descent (SGD), a momentum of 0.9, and a weight decay of \(1 \times 10^{-4}\) for regularization. The initial learning rate is set to 0.001 and decayed by a factor of 10 halfway through training. Categorical cross-entropy is used as the loss function for multi-class classification.

Model training and complexity

The EfficientNet-B0 backbone with SE blocks was trained on recurrence plot images resized to \(224 \times 224\). Training was implemented in TensorFlow 2.x using Stochastic Gradient Descent (SGD) with momentum of 0.9, an initial learning rate of \(10^{-3}\) (decayed by a factor of 0.1 at epoch 25), and weight decay of \(1 \times 10^{-4}\) for regularization. A batch size of 64 and a maximum of 50 epochs were used, with categorical cross-entropy as the loss function. In addition, early stopping (patience = 8) was applied based on validation loss to prevent overfitting. To enhance robustness, data augmentation included small rotations (\(\pm 5^\circ\)), horizontal/vertical shifts (\(\pm 5\%\)), and intensity jitter, which improved generalization under noisy conditions. Model complexity was quantified in terms of trainable parameters and floating-point operations (FLOPs) as shown in Table  3 , confirming suitability for near-real-time operation. Latency measurements were conducted separately for detection (on the Intel Atom module) and classification (on the workstation GPU), with results presented in section “Validation of PQD algorithm in real time for power quality detection and zone identification”.

Model performance is assessed using Accuracy Averaged across all classes as given in the equation below:

$$\begin{aligned} \text {Accuracy} = \left( \frac{1}{N} \sum _{j=1}^{N} \frac{\text {TP}_j}{T_j} \right) \times 100\% \end{aligned}$$

where N is the number of classes, \(\text {TP}_j\) the correct predictions, and \(T_j\) the total samples in class j.

Model complexity is evaluated based on trainable parameters and FLOPs to ensure suitability for edge deployment. Noise robustness is tested by adding Gaussian noise at SNR levels ranging from 20 dB to 60 dB. Latency is analyzed by measuring detection, data transfer, and classification times, confirming the system’s capability for real-time operation. This configuration delivers high classification accuracy with low computational overhead and strong resilience to noise, making it well-suited for real-time power quality monitoring applications.

The EfficientNet-SE model is assessed against a baseline EfficientNet without the SE attention module under identical training settings. After 50 epochs, validation trends show that EfficientNet-SE converges faster, stabilizing at \(\sim\)98.5% accuracy and \(\sim\)0.06 loss, while the baseline fluctuates near 95% accuracy and 0.15 loss.

Table 2 Class description of power quality events.
Full size table
Table 3 Model complexity and latency comparison.
Full size table

Under SNR levels of no noise, 50 dB, 30 dB, and 20 dB, the baseline achieves 96.12%, 94.78%, 92.41%, and 91.65% accuracy, respectively, while EfficientNet-SE reaches 98.45%, 97.33%, 95.76%, and 92.18%. These results highlight the SE module’s role in enhancing noise robustness and feature discrimination. Grad-CAM41 visualizations confirm improved focus and spatial consistency with SE, capturing key texture areas in RP images more precisely, especially under multi-disturbance scenarios as shown in Fig. 5. The SE module enables better global feature learning by adaptively reweighting channels, making the model more effective for real-time PQD classification.

Fig. 5
figure 5

Heat Map of EfficientNet-SE and EfficientNet-Without SE for a PQD Event (a) Voltage Sag, and (b) Voltage Sag + Harmonics.

Full size image

To evaluate the noise resilience of the proposed EfficientNet-SE model under challenging conditions, its performance was tested on 39 types of PQD signals at a 20 dB SNR level. These disturbance patterns, including single, double, triple, and quadruple combinations, were converted to recurrence plot images and classified using the EfficientNet-SE architecture. Despite the noise, the EfficientNet-SE model achieved a recognition accuracy of 95.76%, notably surpassing the previously reported EfficientNet-without SE model accuracy of 91.65% under the same conditions. This improvement of 4.11 percentage points highlights the effectiveness of recurrence-based texture mapping combined with SE attention mechanisms.

Key observations:

  • Single disturbances such as Sag, Swell, Interruption, and Harmonics are classified with near-perfect accuracy, showing enhanced feature sensitivity in the EfficientNet-SE backbone.

  • Double disturbances involving harmonics and flicker (e.g., C12, C18, C25) showed minimal confusion due to the model’s superior ability to focus on texture localization via squeeze-and-excitation modules.

  • In contrast to EfficientNet-without SE, triple and quadruple disturbances involving oscillatory transient and notch (e.g., C29 \(\rightarrow\) C30, C36 \(\rightarrow\) C37) exhibit fewer misclassifications, confirming better generalization to complex scenarios.

  • Overall, misclassifications are sparse and concentrated around classes with high spectral overlap, yet less frequent than in EfficientNet-SE.

Real time validation using RTDS

The proposed algorithm is tested on modified IEEE 13-node distribution systems modelled and simulated in Real Time Digital Simulator (RTDS), with network data sourced from42. The 13-node system operates at 5 MVA, 60 Hz, with voltage levels of 0.48 kV and 4.16 kV. It connects to the utility via station transformer, which has a neutral-to-ground impedance of (0.5 + j0.005) \(\Omega\), as shown in Fig. 6. Distributed generation is incorporated in IEEE 13 bus system as follows—a 400-kW solar unit at node 680 via a suitable interconnection transformers as shown in Fig. 6. Parameters for solar power generation are adopted from43.

Fig. 6
figure 6

Modified IEEE 13 bus distribution system.

Full size image

RTDS simulation set-up

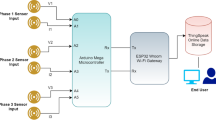
Fig. 7 shows the hardware setup for the implementation and testing of Power quality detection (PQD), localization and classification algorithm. It consists of RTDS workstation which is connected to RTDS hardware capable of interfacing digital and analog Input and output modules with target hardware to be tested, and also used to design the test system (IEEE 13 bus system). The target hardware architecture is shown in Fig. 8. it consists of Intel Atom D525 Dual Core 1.8 GHz Processor module operated on QNX based Real Time Operating System (RTOS), one high speed Analog/Digital Input / Output (I/O) card capable of acquiring data at the rate of 1 micro second, and 3 normal I/O cards that can capture the data at 50 micro second. All the cords communicate and exchange data through PCI-e based hardware back plane. The data transfer between processor and work station is TCI/Ip based ethernet communication.

Zone selection and observability

In the IEEE 13-bus system, as shown in Fig. 6, three zones were identified to enable disturbance localization with minimal measurement overhead: Z1 (632, 633, 634, 645, 646), Z2 (611, 652, 684), and Z3 (671, 675, 692, 680). Voltage measurements were taken at node 650 in Zone 1, at node 684 in Zone 2, and at node 692 in Zone 3. These nodes were selected after analyzing system observability using the Jacobian-based voltage sensitivity matrix42, ensuring that each measurement point provides maximum coverage of its respective zone and that disturbances anywhere within a zone manifest as measurable deviations at the selected bus. The analog signals from these buses were interfaced to a high-speed data acquisition card through the GTAO (analog output) card of RTDS. The processor module received the analog samples at 250 \(\upmu\)s intervals and processed them in real time for recurrence plot generation using a 10-cycle moving window buffer, which was updated at every 250 \(\upmu\)s step. An observability summary for the selected zones is provided in Appendix A.

Fig. 7
figure 7

hardware setup for the implementation and testing of PQD detection, localization and classification algorithm.

Full size image
Fig. 8
figure 8

Power Quality Detection hardware architecture.

Full size image

Classification of power quality events using efficient-net model with SE technique

Solar PV operational parameters impacting power quality include system size, grid strength, load ratio, and module connection mode. Factors such as shading and irradiance variations can introduce flicker, transients, and sub-harmonics, while voltage levels and harmonic distortions are influenced by PV location, ambient temperature, and simultaneous inverter operation. High-order harmonics tend to increase during low output power conditions. To evaluate the impact of changing solar PV operating conditions on power quality in the 13-bus system, simulations were conducted at each bus by varying key solar generation parameters. Example test cases included scenarios such as partial shading under moderate irradiance, high ambient temperature with low load ratio, weak grid conditions with simultaneous inverter operation, and rapid irradiance fluctuations due to cloud movement. A total of 15 such distinct operating scenarios were simulated per bus, resulting in 180 test cases across the system.

Fig. 9
figure 9

Cosine similarity heatmap at measurement nodes for each fault bus.

Full size image
Fig. 10
figure 10

Zone-wise confusion matrix (with Misclassifications).

Full size image

Validation Of PQD algorithm in real time for power quality detection and zone identification

The generated recurrence plot in each zone at each bus using the moving window data of 3 phase voltages updated at every 1 millisecond is compared with the normal operation recurrence plot generated and stored in the historian using cosine similarity index as explained in section  “Cosine similarity”. Cosine similarity index of 2 signifies the status of normal operation and no power quality event at that instant. The deviation from the value of 2 signifies the system operation away from normal operation. Global cosine similarity index (CSI) threshold below which the power quality event being detected is 1.55 for avoiding spurious power quality detection. Zone wise thresholds for the 3 zones being considered are Z1-1.25, Z2-1.31, Z3: 1.32. When the event triggers 2 zones simultaneously, for the event in one Zone, then the algorithm considers the zone with lowest CSI as the affected zone. With these thresholds, the accuracy achieved in power quality event detection is 95.5% (172 out of 180 events were correctly detected). Fig. 9 describes the heat map of the cosine similarity at measurement nodes for each bus for the case studies described in section “Classification of power quality events using Efficient-Net model with SE technique”. Fig. 10 shows the zone wise confusion matrix including the zone wise misclassifications. The accuracy achieved for zonal wise detection is 89.44%. The zone-wise performance shows that Z1 achieved a precision of 0.86, recall of 0.76, and F1-score of 0.81, Z2 had a precision of 0.75, recall of 0.80, and F1-score of 0.77, while Z3 recorded a precision of 0.75, recall of 0.83, and F1-score of 0.79.

Table 4 Classification of power quality events using real time events.
Full size table

PQD detection using single point voltage measurements at substation bus

The case studies considered in the previous section are repeated by considering the 3-phase voltage measurements only at the sub-station bus. The corresponding Cosine Similarity Index (CSI) values obtained using recurrence plots generated with the help of substation voltage bus measurements shows that these measurements are able to detect the power quality events at nearer buses such as 632, 633, 645, 671, 684, 692 with an accuracy of 95.5%. For the far away buses such as 646, 634, this technique has achieved an accuracy of 80%, and the remaining buses resulted in a poor accuracy of less than 50%. With the selection zones as described in Section V (A) the accuracy has been greatly improved to 95.5% for power quality event detection and zonal location finding.

Classification of power quality event using efficient-net with SE model in real time

Following the detection of power quality event, the detection signal will be sent to the high-speed work station through TCP/IP to consider the 10-cycle buffered voltage samples just before the power quality detection signal received, for the generation of recurrence plot using 3-phase voltage samples. The generated image will be given as input to the application that is using the trained EfficientNet model with SE technique as described in section “PQD classification based on Efficient-Net with adaptive SE blocks” to classify the power quality event from the 39 different combinations of power quality events being considered. Table  4 shows the detected PQD classes for the total 180 cases considered.

Timing analysis

In the Power quality detection hardware considered for this work, the timing analysis has been done in real time to find the time to detect the power quality event and the corresponding Zone location finding. the maximum value of time to detect the power quality event and zonal location finding is 18.95 milli seconds, and the maximum value of power quality event classification using real time data after power quality event detection signal is 38.5 milli seconds.

SCR sensitivity for PQD detection

Grid strength was varied by changing the Thevenin equivalent impedance at the point of common coupling/ Substation Bus in IEEE 13 Bus system. For a target SCR we set \(S_{SC}=\text {SCR}\times P_{rated}\) and computed \(Z_{th}=V_{LL}^2/S_{SC}\), where \(V_{LL}\) is the PCC line-to-line RMS voltage and \(P_{rated}\) the installed PV rating. The resulting \(Z_{th}\) was split into series R and X using an X/R ratio of 5, and implemented as a series R–L branch feeding the IEEE 13-bus network. We tested three SCR conditions representative of strong, moderate and weak grids (SCR = 10, 7, 3). For each SCR we performed the identical set of PQD events and recorded recurrence plots, CSI traces, detection/localization decisions and classification outputs as shown in Table  5

Table 5 Impact of grid strength (SCR) on PQD detection and classification performance.
Full size table
Table 6 Comparative analysis of PQD classification methods from literature and the proposed approach.
Full size table

Comparative analysis with state-of-the-art methods

To contextualize the effectiveness of the proposed RP + EfficientNet-SE framework, we benchmarked it against representative state-of-the-art methods reported in the literature. The selected baselines include traditional feature-based classifiers, image-based CNNs, and recent deep learning architectures that have been widely applied to PQD recognition tasks. Table 6 summarizes the key characteristics and performance of these methods in terms of data representation, number of disturbance classes considered, classification accuracy, noise robustness, and validation environment.

As shown in Table 6, traditional feature-based methods such as DWT + PNN11 and RBF-NN12 achieve accuracies around 94–95% but are limited in scalability and robustness under noise. S-Transform-based classifiers6,7 slightly improve performance but remain constrained by handcrafted features and lack real-time validation. Image-based approaches such as GAF + CNN22 and CBAM-DenseNet18 achieve higher accuracy (96–97%) but incur higher computational cost and do not provide latency analysis. Recent sequence models like Bi-GRU21 and fully convolutional networks23 show promise, yet are tested on fewer classes and remain simulation-only. By contrast, the proposed RP+EfficientNet-SE framework demonstrates superior classification accuracy (98.5%), robustness under noisy conditions (92.2% at 20 dB), and uniquely provides full real-time validation on an RTDS + HIL testbed for PQD’s detection, classification and localization together using a real time hardware platform in a renewable energy integrated IEEE 13 bus system. This combination of accuracy, scalability to 39 disturbance classes, and end-to-end real-time feasibility highlights the novelty and practical significance of the proposed method.

Discussion of overall results of the proposed work

The proposed RP + EfficientNet-SE based framework was evaluated extensively under RTDS and HIL environments. Key findings are summarized below:

  • High accuracy across tasks: The framework achieved a detection accuracy of 95.5%, zonal localization accuracy of 89.44%, and classification accuracy of 98.5% across 39 single and composite PQD classes.

  • Noise robustness: Performance remained stable under adverse measurement conditions, maintaining 92.2% classification accuracy at 20 dB SNR, demonstrating resilience to noise.

  • Real-time feasibility: End-to-end real-time validation showed a detection latency of less than 18.95 ms and classification latency of less than 38.5 ms, satisfying practical requirements for near real-time power quality monitoring.

  • Advantages of zonal monitoring: By adopting a zone-based observability strategy, the number of measurement points was reduced without sacrificing detection accuracy. This minimizes hardware overhead while maintaining comprehensive grid coverage.

Overall, these results highlight the practicality of the proposed system for deployment in modern distribution networks with high renewable penetration, where low latency, scalability, and robustness are essential.

Limitations and future work

While the proposed RP + EfficientNet-SE framework shows strong detection, localization, and classification performance in the IEEE 13-bus test system, several limitations remain:

  • The study is validated on a single benchmark feeder; generalization to larger and unbalanced distribution systems needs further exploration.

  • The analysis considers limited PV penetration levels; scenarios with very high inverter-based generation ( greater than 80%) require investigation.

  • Although RTDS and HIL validation confirm real-time feasibility, deployment on embedded hardware platforms with restricted resources remains future work.

  • While robustness under varying SNR and SCR levels was quantified, cyber-physical aspects such as communication delays or data loss were not modeled.

  • The proposed CSI thresholding adapts to weak grids, but dynamic, self-learning threshold selection remains an open research direction.

Conclusion

The propose work presented a framework for real-time detection, localization, and classification of power quality disturbances (PQDs) in a solar-integrated IEEE 13-bus distribution system. Using recurrence plots and a cosine similarity index (CSI)-based anomaly detector, the zonal monitoring approach achieved a PQD detection accuracy of 95.5% and a localization accuracy of 89.44%. The CSI thresholds were calibrated both globally and zone-wise, balancing sensitivity and specificity and thereby reducing false positives.

Classification was performed using an EfficientNet-B0 model with Squeeze-and-Excitation (SE) blocks, which achieved an overall accuracy of 98.5% under nominal operating conditions and maintained 92.2% accuracy at 20 dB SNR across 39 single and composite PQD classes. Frequent PQD types, such as Voltage Harmonic + Flicker (65/180), Voltage Harmonic + Sag (53/180), and Voltage Harmonics alone (49/180), were reliably identified. Validation in both RTDS and Hardware-in-the-Loop (HIL) environments confirmed the method’s feasibility for real-time operation with detection latency below 18.95 ms and classification latency below 38.50 ms.