Circular hole pose estimation of porous workpiece based on binocular vision system

Abstract

The workpiece with multi-hole is common in the field of machine production and manufacturing. Robot-oriented automated docking is an important means to improve product assembly efficiency. How to accurately estimate the position and the circular hole pose of porous workpiece is drawing more and more attention. In this paper, we propose a new binocular vision method for circular hole pose estimation. First, an ellipse detection method is used to extract the hole feature. It uses three geometry constraints to ensure the accuracy of the ellipse detection. Second, the vanishing point and vanishing line of the workpiece plane are calculated using the ellipse information. Then the real projection point of the circle center can be accurately obtained through the vanishing line. The position of the circle center is reconstructed by the triangulation technology in our method. Last, the structural characteristics of the multi-hole workpiece are fully employed in the step of pose estimation. The posture is calculated by fitting the plane of those 3D points of circle center in order to reduce the error. Experiments are performed. The precision error of position estimation could be within 0.15mm and the precision error of pose estimation could be within 0.5$\phantom{0}^\circ$, meeting the operation requirements of machine production and manufacturing. These results verified the high accuracy and strong robustness of our proposed method.

Introduction

Circular holes are one of the common geometric features on industrial parts. Measuring the pose of circular hole is an important content in the production and manufacturing process. For example, by the pose measurement of circular hole, the pose of the part can be estimated for robot grasping, and hole docking is implemented more easily for assembly. Therefore, accurate measurement of circular hole pose is of great significance for industrial applications.

Binocular vision is a commonly used method for measuring the pose of circular hole features. Compared with monocular vision, binocular vision not only reduces detection errors caused by noise and distortion in a single view, but also enables accurate plane fitting by reconstructing multiple hole centers, thereby improving the stability and accuracy of pose estimation. Generally, the pose measurement of a circular hole using binocular vision first detects the circular hole in the image, i.e. ellipse detection, and then estimate the pose by feature matching and 3D reconstruction. However, due to image distortion and noise, it is still a challenge to precisely estimate the pose of circular hole.

In recent years, there has been a lot of work on binocular visual measurement of circular hole pose. Many researchers focused on the accuaracy of ellipse detection which is the projection of the round hole on the workpiece, i.e., carrying out a voting procedure in a parameter space^1,2,3,4, detecting short line segments in the edge diagram or arc-support line and then combining them^5,6,7, And then the pose measurement step which is based on monocular vision or binocular vision is estimated by using the algebraic method, elliptic information or using the geometric method^{8,9,10,11,12,13,14,15,16,17,18}. However, all popular pose calculation of porous workpiece only involves one of the ellipses and it doesn’t make full use of the characteristics of the features of multi-hole workpiece. In order to improve accuracy, the proposed method use all of the ellipses geometry information to estimate the vanishing points, and the vanishing line. In the method, we also make full use of the structural characteristic of the multi-hole workpiece and make full use of the information of each ellipse which contributes to the final pose estimation result.

Based on the above discussions, we proposed a pose estimation process. Firstly, we detect the ellipse feature on the image by the edge detection method which detects the arcs that belong to the same ellipse based on the set constraint, relative point position constraint and geometry constraint. The direct least square is fitting to estimate the parameters of the ellipses, we can get the basic features accurately. Secondly, we estimate the position and pose by the point features. We extract the accurate projected point of circle and reconstruct the position of it based on binocular vision system. Then the high precise pose of the supported plane of the circular holes can be obtained by fitting the plane of these center points.

Related work

In most existing vision-based pose measurement methods, feature extracting and pose measurement are two basic steps.The round hole on the surface of the mechanical workpiece becomes an ellipse on the image after projection transformation. And the ellipse, as a geometric figure with important properties, is often extracted as the most important feature. Hough transform (HT)¹ is one of the popular algorithms. However, this method is to perform brute force search in the parameter space, which takes an extremely long time. Many researches are working to reduce the calculation time of traditional HT^2,3,4. On the other hand, the type of arc linking based method has a good detection rate. Kim⁵ first detect short line segments in the edge diagram, and then combine them into arc segments based on the line segments, and finally determine the geometric parameters of detecting ellipses with the geometric constraint. Fornaciari⁶ directly connect the edge points into arc segments and divide them into four areas, use the relationship between the centerline of a set of chords of the ellipse and the center of the ellipse to judge whether the three arcs can be combined together, and use the voting-based parameter space decomposition method to estimate the geometric parameters of the ellipse. Qi⁷ followed the basic idea of Fornaciari’s method, while introducing the concept of the number of features of lines and arcs. Based on the feature number of lines, the Qi method can eliminate a large number of invalid line segments. Lu¹⁹ proposed an industry-oriented ellipse detector by arc-support line segments, which follows a four-stage ellipse detection framework: arc-support groups forming, initialellipse set generation, clustering, and candidate verification. Moreover, CNN-based ellipse detectors such as ElDet²⁰ have achieved strong performance in generic vision tasks. Nevertheless, these learning-based methods often require large annotated datasets and suffer from lower computational efficiency, which limits their applicability in real-time industrial scenarios. Geometry-based approaches are therefore more suitable for our task. However, within this category, most existing methods rely on only one or two geometric constraints, aiming to balance accuracy and generality in complicated environments. In our case, the simplicity of the target environment makes it possible to exploit more geometric constraints and achieve more accurate ellipse detection.

In circular target pose estimation, a lot of research have been done. There are two main categories in this field, one is implemented in monocular vision. Shiu and Ahmad⁸ proposed a closed-formed solution for the 3D position and orientation of a circular feature. Safaee⁹ proposed an analytical method based on two parts, first estimate and then calculate. Chen¹⁰ proposed a geometric pose determination method which is directly based on two particular chords of the circular object. It derived the closed-form solution to the circle pose problem based on the geometric properties of the 2D and 3D feature points of the circular object. Wu¹¹ simplified the circular object pose measurement with determining a suitable intersection between an elliptic cone surface and a sphere. Fu¹² presented a new method for measurement pose of the coplanar circle .The linear constraint is added on the known radius of the target firstly, and then the mathematical model is established based on the relation- ship between the features and their projections. On the other hand, as the orientation duality¹³ is also a long-term studied problem. Researchers proposed some solutions by adding a camera in order to obtain more constraints. Circular feature pose esti- mation based on binocular vision is this type of method. Ma¹⁴ gave the analytical solution of the space circle pose in their research, and combined the left and right camera rotation and translation relations of binocular vision. Xu¹⁵ proposed a solution using simple mathematics. It calculated the pose of target in left camera coordinate and right coordinate respectively. It determines the unique solution by combining the two sets of solutions into the reference coordinate. Moreover, it calculated the radius of target. Peng¹⁶ proposed a method in which the algebraic method is used. On the basis of Ahmad’s work, the two solutions in the left and right camera coordinate systems are also solved separately, and then the solutions in the two camera coordinate systems are unified under the same coordinate system. Liu¹⁷ also used binocular vision measurement when solving the problem of non-cooperative target space docking. Different from Xu’s geometric observation model solution, Liu used the camera imaging model and space coordinate transformation to obtain the analytical solution of the reconstruction pose based on ellipse parameters and calibration parameters. Liu¹⁸ used the special vectors that are irrelevant to the unknown radius to calculate the normal vector of the circular plane, and then obtained the position of center by triangulation technology of binocular vision and the radius. The method estimates the pose of one hole to represent the real pose of its supported plane. However, there are two main issues with existing methods. Most methods use the two endpoints on the diameter to calculate the center position, which is easily affected by ellipse fitting errors, resulting in large error of center position estimation. In addition, the results are given in the form of analytical solutions, and the geometric parameters of the detected ellipse are used as inputs to the analytical solution, thus, the ellipse fitting error can greatly affect the pose estimation results. Different from the existing methods, this paper employs the coefficients of the vanishing line and the principle of projective geometry transformation to estimate the center of the ellipse imaging. The optimal triangulation technology in binocular vision is introduced to calculate the new matching points that comply with epipolar geometric constraint, which makes the position calculation of the center projection more accurate. Thus, the pose measuring error is effectively reduced.

Ellipse detection and feature extraction

The first step of visual measurement is to process the image and extract the significant features. In our measurement scenario, our detected object is a workpiece with multi-hole. The circles on the surface could be viewed as the geometry feature to extract and these circles could be mapped into ellipses in images. There are many ellipses in the image, so we can detect these ellipses firstly. To ensure the accuracy of the following measurement procedure, we should detect the ellipses as accuracy as possible.The flow chart of the ellipse detection is as Fig. 1 shows :

Fig. 1

The flowchart of ellipse detection.

Arc extraction

In this phase, we extract the arcs of the ellipse firstly and classify them into four categories according to the property of the concavity and convexity.

Edge detection

Before the edge detection, image pre-processing techniques like Gaussian filtering (kernel size = $5\times 5$ with a standard deviation $\sigma$ = 1.0) was used to improve the effect of edge extraction. We use the Canny detector to localize the edge point and after the processing every edge point $e_{i}$ has position coordinate ($x_{i}$,$y_{i}$) and Sobel derivates in X and Y direction ($dx_{i}$,$dy_{i}$)(which is already calculated in Canny algorithm). We use to denote the gradient angle.

$$\begin{aligned} \varphi _{i}=arctan(dy_{i}/dx_{i}) \end{aligned}$$

(1)

Because of the image digitalization and noise, the accurate value of gradient is hard to estimate. To prevent its influence, we just use the main direction of the gradient angle.

Arc detection

The edge point whose $dx_{i}=0$ or $dy_{i}=0$ is the sudden change of main gradient direction. An arc is formed by linking the connected edge points in its eight neighborhoods whose gradient directions are the same. The number pixel points of an arc $\tau ^k$ is denoted as $N^k$, we also denote $L^k$ as the leftmost pixel point of the arc,$R^k$ as the rightmost pixel point of the arc and $M^k$ is the middle point which lies in the $\big \lceil N^k/2 \big \rceil$ position of the arc.

Arc elimination

After edge detection, a large number of arc candidates are obtained, among which some are nearly straight segments or very short arcs caused by noise. We here filter out these degenerate cases by applying the threshold $Th_{len}$ and $Th_{OBB}$. We denote $OBB_{k}$ as the minimum oriented bounding box which encloses all edge points of an arc $\tau ^k$. When $\tau ^k$ satisfies one of the following conditions, it proves that this arc is likely not to be a part of an ellipse and it should be discarded.

• (1) The size of $N^k$ is less than the threshold $Th_{len}$ (16 is our default setting). These arcs occur mainly due to noise as the arc is short.

• (2) The length of the short side of $OBB_k$ is less than the threshold $Th_{OBB}$ (3 is our default setting). When the short side is not large enough, the arc $\tau ^k$ is likely to contain the collinear points which has little contribution to compose an arc of ellipse.

Arc classification

Based on the main direction of the gradient angle, we have two big categories—$Dir(\tau ^k)>0$ or $Dir(\tau ^k)<0$. Each direction group is divided into two sets according to the concavity and convexity. Connect the $L^k$ and $R^k$ pixel points and calculate the equation of this line based on the pixel coordinate, as is shown in Fig. 2. We split each group into two subgroups by determining whether the position of $M^k$ is above the line $\overline{L^kR^k}$ or not. Finally, we divide the total arc segments into four independent sets based on the direction of arc and the concavity and convexity of the arc:

$$\begin{aligned} \tau = {\left\{ \begin{array}{ll} \tau _{I},Dir(\tau ^k)>0\hspace{5.0pt}and\hspace{5.0pt}M^k\hspace{5.0pt}is\hspace{5.0pt}above\hspace{5.0pt}the\hspace{5.0pt}line\hspace{5.0pt}\overline{L^kR^k} \\ \tau _{II},Dir(\tau ^k)<0\hspace{5.0pt}and\hspace{5.0pt}M^k\hspace{5.0pt}is\hspace{5.0pt}above\hspace{5.0pt}the\hspace{5.0pt}line\hspace{5.0pt}\overline{L^kR^k} \\ \tau _{III},Dir(\tau ^k)>0\hspace{5.0pt}and\hspace{5.0pt}M^k\hspace{5.0pt}is\hspace{5.0pt}behind\hspace{5.0pt}the\hspace{5.0pt}line\hspace{5.0pt}\overline{L^kR^k} \\ \tau _{IV},Dir(\tau ^k)<0\hspace{5.0pt}and\hspace{5.0pt}M^k\hspace{5.0pt}is\hspace{5.0pt}behind\hspace{5.0pt}the\hspace{5.0pt}line\hspace{5.0pt}\overline{L^kR^k} \end{array}\right. } \end{aligned}$$

(2)

Fig. 2

Convexity classification.

Ellipse detection

In the previous section, we have extracted arcs which are likely to compose an ellipse and grouped them into four sets. To form an ellipse, three arc selection strategies should be conducted to group arcs which belong to an ellipse:(a) Set constraint (b) Relative point constraint (c) Geometry constraint based on Pascal Hexagon Theorem. Then, direct least square fitting is used to estimate the ellipse parameters for the first time.

Set constraint

In ideal circumstances, four complete arcs which are not affected by noise or occlusion from four different sets can form an integrated ellipse. However, arcs could be broken into two segments or brought the absence from arcs sets by reason of noise. So we pick out three arcs from three different arc sets, and there are four choices in total:($\tau _{I},\tau _{II},\tau _{III}$),($\tau _{I},\tau _{II},\tau _{IV}$),($\tau _{I},\tau _{III},\tau _{IV}$), ($\tau _{II},\tau _{III},\tau _{IV}$). If we choose two different arcs from the same arc set, it is impossible to form an ellipse.

Relative point constraint

After selecting three different arcs, the position of end point should satisfy the fundamental relative relation. Taking the sets ($\tau _{I},\tau _{II}$) for example, if the rightmost extrema of the $\tau _{II}$ is on the right side of the leftmost extrema of the $\tau _{I}$, the two arcs could never form an ellipse.

We denote $L_{I}^k.x$ as the x coordinate of the leftmost extrema of arc $\tau _{I}^k,L_{I}^k.y$ as the y coordinate of the leftmost extrema of arc $\tau _{I}^k$,and $R_{I}^k.x$ as the x coordinate of the rightmost extrema of arc $\tau _{I}^k$, $R_{I}^k.y$ as the y coordinate of the rightmost extrema of arc $\tau _{I}^k$. The remaining arcs are labeled in the same way and we can obtain the following end points constraints in Table 1:

Table 1 The valid arc combinations.

Geometry constraint based on Pascal hexagon theorem

Any ellipse can be transformed into a circle by affine transformation and affine transformation has a series of geometry invariants, such as parallelism. Therefore, some geometry properties about circle are likely to be extended to ellipses. Among the geometry properties, Pascal Theorem is an important and succinct property. It proves that if a hexagon is enclosed in a circle, its three opposite sides intersect on the same line. As is shown in Fig. 3a, we pick six different points from the ellipse:$A_{1},A_{2},A_{3}$ and $B_{1},B_{2},B_{3}. \overline{A_{1}B_{2}}$ and $\overline{A_{2}B_{1}}$ intersect at point P, $\overline{A_{2}B_{3}} and \overline{A_{3}B_{2}}$ at point Q, $\overline{A_{3}B_{1}}$ and $\overline{A_{1}B_{3}}$ intersect at point M and the three points P,Q,M lie in the same line. According to the invariant property under affine transformation, it is also applicable to ellipse, which is shown in Fig. 3b. The three selected arcs are considered valid if they satisfy the set constraints and relative point constraints, then we verify whether the arcs satisfy the geometry constraint or not.

Fig. 3

(a) The graphic explanation of Pascal’s hexagon theorem on circle (b) The graphic explanation of Pascal’s hexagon theorem on ellipse.

Taking ($\tau _{I},\tau _{II},\tau _{III}$) for example, the three arcs have six end points in total and we label these points with $A_{1},A_{2},A_{3},B_{1},B_{2},B_{3}$ in counterclockwise order. As is shown in Fig. 4.

Fig. 4

The six key points of the three arcs.

Then we connect $(A_{1},B_{1}),(A_{1},B_{2}),(A_{2},B_{1}),(A_{2},B_{3}),(A_{3},B_{2}),(A_{3},B_{3})$ and calculate the equations of the six lines in pixel coordinate respectively. Subsequently, the point P which is the intersection of $\overline{A_{2}B_{1}}$ and $\overline{A_{3}B_{2}}$ ,the point Q which is the intersection of $\overline{A_{1}B_{2}}$ and $\overline{A_{2}B_{3}}$, the point M which is the intersection of $\overline{A_{1}B_{1}}$ and $\overline{A_{3}B_{3}}$ are calculated by these equations. In the real image, P, Q and M are hardly collinear. In order to estimate the degree of the collinearity, we calculate the angle between $\overrightarrow{MP}$ and $\overrightarrow{MQ}$ The range of angle is (0,180]$\phantom{0}^\circ$, the larger the angle is, the more collinear the three points are. We define

$$\begin{aligned} Angle(PQM)=arccos(\overrightarrow{MP},\overrightarrow{MQ}) \end{aligned}$$

(3)

If $(180-Angle(PQM))$ of an arc combination is less than $Th_{angle}$. It proves that the arcs selection is valid for the following ellipse fitting since it meets the constraint of geometry based on Pascal Hexagon Theorem. The flowchart of the geometry constraint is detailed in Algorithm 1.

Algorithm 1

Geometry constraint based on Pascal theorem

With the three constraints, Algorithm 2 shows the picking process for the set combination, and the remaining three arcs grouping are labeled and calculated in the same way. Finally, we have obtained all the valid arcs combinations which are ready to fit the ellipse for the first time in the next section.

Algorithm 2

Picking strategy from arc combinations

Ellipse fitting

In the previous section, we obtain all the effective three arcs groups after arcs elimination operations, such as set constraint, relative point constraint and geometry constraint. Most invalid arcs or arc combinations which have no contribution to ellipse fitting are discarded. There are five parameters to determine an ellipse: the position of center (x and y), the major axis, the minor axis and the orientation angle. In this paper, we use the direct least square fitting algorithm which is proposed by Fitzgibbon²¹ to estimate the parameters. In direct least square fitting, the goal is to minimize the sum of the square of the distances between data points and the fitting ellipse which is described in the form of quadratic curve

$$\begin{aligned} F(x,y)=Ax^2+Bxy+Cy^2+Dx+Ey+F \end{aligned}$$

(4)

It uses a non-iterative method to get the optimal parameters. Since the algorithm is for the ellipse, it produces the solution which takes all the data points into consideration no matter whether they are correct or not. However, the pixel points in the three arcs which meet the previous constraints are more likely to lie in the same ellipse, it can attenuate the effect of the outer points. The transformation between coefficient (A, B, C, D, E, F) and the five geometry parameters is as follows: The center position

$$\begin{aligned} c_{x}=\frac{BE-2CD}{4AC-B^2} \end{aligned}$$

(5)

$$\begin{aligned} c_{y}=\frac{BD-2AE}{4AC-B^2} \end{aligned}$$

(6)

The major semi-axis and the minor semi-axis

$$\begin{aligned} a^2=\frac{2(Ac_{x}^2+Cc_{y}^2)+Bc_{x}c_{y}-1}{A+C-\sqrt{(A-C)^2+B^2}} \end{aligned}$$

(7)

$$\begin{aligned} b^2=\frac{2(Ac_{x}^2+Cc_{y}^2)+Bc_{x}c_{y}-1}{A+C+\sqrt{(A-C)^2+B^2}} \end{aligned}$$

(8)

The orientation angle

$$\begin{aligned} \theta =\frac{1}{2} arctan(\frac{B}{A-C}) \end{aligned}$$

(9)

Post processing

Although we have obtained the initial ellipse set by using the ellipse parameter fitting, the false detections may still be included. A validation step is necessary in the initial ellipse set. Moreover, multiple three arcs groups may be found on the boundary of the same ellipse, generating multiple detections of the same ellipses. We should label these arcs whose fitting ellipses are the same and merge these arcs to get a better ellipse result.

Validation

We use two steps to validate whether an ellipse is a true positive or not⁶. The first step measures how many pixel points fitting the corresponding ellipse. There exists error between the fitting ellipse and the pixel points which belong to the three arcs combinations. We substitute every point data to the ellipse equation and estimate how well it fits the equation. We count the number of points that are close to the boundary constraint which we set, and calculate the ratio to the total points of three arcs. If the value is less than $Th_{score}$, it is likely not to be a real detected ellipse. If it meets the requirement of the first step, we continue the second step.

Even it satisfies the first requirement, it is possible to fit the ellipse by chance. We will compute the total projection length of the three arcs combination to the major axis and minor axis direction, and calculate the ratio to the four times the sum of major semi-axis a and minor semi-axis b. If the value is less than $Th_{rel}$,it is likely to be discarded.

Clustering and second fitting

In practical, an arc could be divided into small arcs due to noise. Also, the same object may be detected in a few of times because every three arcs of an ellipse could be merged into a detected ellipse. By the method of Prasad²², it assesses the similarity of two ellipses.

$\varepsilon _{i}=(C_{i}.x,C_{i}.y,a_{i},b_{i},\theta _{i})$ and $\varepsilon _{j}=(C_{j}.x,C_{j}.y,a_{j},b_{j},\theta _{j})$ comparing the distances between center, axis and orientation:

$Cond1:\sqrt{(C_{i}.x-C_{j}.x)^2+(C_{i}.y-C_{j}.y)^2}<min(b_{i},b_{j})\times 0.1$

$Cond2:\vert a_{i}-a_{j}\vert < max(a_{i},a_{j})\times 0.1$

$Cond3:\vert b_{i}-b_{j}\vert < min(b_{i},b_{j})\times 0.1$

$Cond4:\vert \theta _{i}-\theta _{j}\vert < \pi \times 0.1$

If the four conditions are all satisfied, it means that there exist the ellipses which belong to the same object. The arcs of detected ellipses which belong to the same object can be marked. Finally, we can get all of validation arcs of the same object, they provide more sufficient pixels than previous. We can fit the ellipse again by these pixels in order to improve the accuracy. Figure 5 shows the merge procedure. Figure 5a shows a detected ellipse which is composed with arc I, arc II, arc IV(1), Fig. 5b shows a detected ellipse which is composed with arc I, arc II, arc IV(2), Fig. 5c shows a detected ellipse which is composed with arc I, arc II, arc III, these detected ellipses are similar and the composed arcs can be labeled as belonging to the same ellipse. We fit the five arcs again to get a more accurate ellipse.

Fig. 5

Merge all of arcs belonging to the same ellipse.

Pose estimation

Preliminaries

Fig. 6

The model of binocular vision and the space coordinate systems.

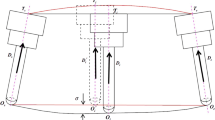
The formation of image is modeled as the “pinhole camera model”, which is commonly used in studies²³. We use the model of binocular vision, as Fig. 6 shows. Taking the left camera as an example, a space coordinate system is established–the world coordinate $O_{w} - X_{w}Y_{w}Z_{w}$ , the camera coordinate $O_{cl} - X_{cl}Y_{cl}Z_{cl}$,the image coordinate $O_{il} - X_{il}Y_{il}$ and the pixel coordinate $O_{pl} - X_{pl}Y_{pl}$ For a specific space point X,we can locate the point in two different Euclidean coordinate systems–world coordinate system and camera coordinate system. The two coordinate systems are related via rotation and translation.

Vanishing line and projected center

In the previous section, we established a model of image formation of the camera, which is a perspective projection transformation. Perspective projection is not a shape preserving transformation. The objects in 3D dimension are usually distorted if they are not parallel with image plane. Specifically, a circle in space is projected into an ellipse if the supported plane of the circle is not parallel with image plane. Only when the surface is parallel with image plane, projections remain circular. It is important to note that the ellipse center is not coincidence with the actual projected center of the circle. The geometry distance between them is larger when the size of the circle and the angle between the circular plane and image plane are bigger. In projective geometry, the transformation of a point mapped into the image plane is expressed as follows

$$\begin{aligned} O' = HO \end{aligned}$$

(10)

where H is the projective transformation matrix, O is an arbitrary space point. Under a point transformation, a conic can be transformed to

$$\begin{aligned} E = H^{-T}CH^{-1} \end{aligned}$$

(11)

where C is a conic coefficient matrix, as previously mentioned, a circle in space is distorted into an ellipse in projective transformation. In this case, C represents the form of the circle and E represents the corresponding ellipse coefficient matrix.Moreover, line in space is expressed as follows in similar form with the point transformation

$$\begin{aligned} l'=H^{-T}l \end{aligned}$$

(12)

l denotes a line in space. Among the countless space lines in space, there is a special line called the line at infinity, denoted by the vector $l_{\infty }=(0,1,1)^T$ .According to Eq. (10) and (11),the product of ellipse coefficient matrix and the projected center can be expressed as follows

$$\begin{aligned} EO=H^{-T}CH^{-1}HO=H^{-T}CO \end{aligned}$$

(13)

A 3D circle centered at $(X_{0},Y_{0})$ with the radius r can be represented as

$$\begin{aligned} X_{w}CX_{w}^T=0 \end{aligned}$$

(14)

Where C is

$$\begin{aligned} C = \begin{bmatrix} 1 & 0 & -X_{0} \\ 0 & 1 & -Y_{0} \\ -X_{0} & -Y_{0} & X_{0}^2+Y_{0}^2-r^2 \end{bmatrix} \end{aligned}$$

(15)

Finally, we can obtain

$$\begin{aligned} EO=H^{-T}\begin{bmatrix} 0\\ 0\\ -r^2 \end{bmatrix} \end{aligned}$$

(16)

By comparison, the equations of $l_{\infty }$ and EO are the same up to a non-zero scale factor. Namely,

$$\begin{aligned} EO\propto l_{\infty }' \end{aligned}$$

(17)

According to this equivalence relation, the accurate projected center of a 3D circle can be obtained from the vanishing line of the supported plane and the ellipse matrix produced by the ellipse detection.

$$\begin{aligned} O'=E^{-1}l_{\infty }' \end{aligned}$$

(18)

In ellipse detection procedure, we finally get the geometric description parameters of every ellipse in image. There are five parameters to determine an ellipse uniquely-the major semi-axis a, the minor semi-axis b, the center point coordinate $(c_{x},c_{y})^T$ and the rotation angle. As transformation matrxi H is unkown here, how to get the vanishing line of the surface plane from the image information is the key point. The vanishing point and line are two significant concepts in projective transformation since it can show the point of infinity or the line of infinity in an image and we can use the invariant geometry properties.

Fig. 7

Vanishing line formation (a) The two sets parallel lines on the chessboard converge to the vanishing points v1 and v2. (b) The two sets parallel lines on three coplanar circles.

As Fig. 7 shows, the two sets of parallel lines on the same scene plane converge to the vanishing points v1 and v2 in the image, the line l through v1 and v2 is the vanishing line of the plane. The tangent lines of two circles of the same size are parallel in 3D space. The intersection point of the two parallel lines are infinity but it can be mapped into an image point under projective transformation. There are N round holes of the same size on the surface of a multi-hole feature workpiece. $C_{N}^2$ pairs of tangent lines can be calculated and the corresponding vanishing points can also be obtained from these parallel lines. Because the vanishing points of lines parallel to the same plane lie on the vanishing line of the plane, we can obtain the vanishing line equation of the workpiece surface plane from these vanishing points. Picking any two detected ellipses on the picture and the ellipse expressions are as follows, respectively

$$\begin{aligned} A_{1}x^2+B_{1}xy+C_{1}y^2+D_{1}x+E_{1}y+F_{1}=0 \end{aligned}$$

(19)

$$\begin{aligned} A_{2}x^2+B_{2}xy+C_{2}y^2+D_{2}x+E_{2}y+F_{2}=0 \end{aligned}$$

(20)

The common tangent line of the two ellipses is set as

$$\begin{aligned} y=kx+b \end{aligned}$$

(21)

where k denotes slope and b denotes intercept in image pixel coordinate. Substituting Eq. (21) into Eqs. (19) and (20), they can be transformed into as follows

$$\begin{aligned} (A_{1}+B_{1}+C_{1}k^2)X^2+(B_{1}b+2C_{1}kb+D_{1}+E_{1}k)X+(C_{1}b^2+E_{1}b+F_{1})=0 \end{aligned}$$

(22)

$$\begin{aligned} (A_{2}+B_{2}+C_{2}k^2)X^2+(B_{2}b+2C_{2}kb+D_{2}+E_{2}k)X+(C_{2}b^2+E_{2}b+F_{2})=0 \end{aligned}$$

(23)

Based on the observation, they are quadratic equations. The line is tangent with two ellipses at the same time when Eqs. (22) and (23) have multiple roots. According to discriminant equation $\bigtriangleup =b^2-4ac=0$, the following two formulas can be calculated

$$\begin{aligned} (B_{1}b+2C_{1}kb+D_{1}+E_{1}k)^2-4(A_{1}+B_{1}k+C_{1}k^2)(C_{1}b^2+E_{1}b+F_{1})=0 \end{aligned}$$

(24)

$$\begin{aligned} (B_{2}b+2C_{2}kb+D_{2}+E_{2}k)^2-4(A_{2}+B_{2}k+C_{2}k^2)(C_{2}b^2+E_{2}b+F_{2})=0 \end{aligned}$$

(25)

k and b can be solved by the two equations, both of them have two solutions. At the end four common tangent line equations are obtained by combining different k and b. Of these four equations, two of them are internal common tangent line equations and the other two are external common tangent line equations. The correct choice of k and b can be judged by the relative position relationship between the centers of the ellipses and the common tangent line. If the centers of the two ellipses are on the opposite sides of the common tangent line, then this common tangent line is the inner common tangent line. As line $\textcircled {3}$ and line $\textcircled {4}$ show in Fig. 8.

If the centers of the two ellipses are on the same sides of the common tangent line, then this common tangent line is the external common tangent line. As line $\textcircled {1}$ and line $\textcircled {2}$ show in Fig. 8.

Fig. 8

The model of binocular vision and the space coordinate systems.

The intersection coordinates of the two external common tangent lines are solved by the linear equations. The intersection coordinate must exist when the camera imaging plane is not completely parallel to the workpiece surface plane. If these two common tangent lines are completely parallel, it means that the circular hole on the workpiece surface plane is projected into a circle, and the projected center point is the detected ellipse center. But this scenario is rare in practical application environments.

If the two common tangent lines are not parallel, the intersection coordinate is a vanishing point. Owing to the random combinations of detected ellipses, a lot of vanishing points can be obtained. In order to obtain a more accurate vanishing line, it can be calculated by the least square fitting method to these vanishing points on the image. Then, the accurate projected center points can be obtained with ellipse parameters and vanishing line equation according to Eq. (18).

Center position estimation

In binocular vision, image matching is the pre-stage of reconstructing the three-dimensional coordinates of points for depth estimation. However, there are no dominant feature points in a circle. The only special point is the center of circle. Since the method by projective geometry gives the accurate projection points of the center of the circle in left and right image. The location of the center of the circle can be calculated using triangulation.

As shown in Fig. 6, epipolar geometry is used as a geometry model to express the relation of the left image and right image. Specifically, given a pair of correspondence points $x_{l}$ and $x_{r}$ in two different perspective images, $x_{r}$ must lie in the epipolar line of $x_{l}$ in right image, namely $l_{r}$. Similarly, $x_{l}$ must lie in the epipolar line of $x_{r}$ in left image, namely $l_{l}$.

Considering $O_{l}$ and $O_{r}$ as the projection points of the center of the circle in left and right image respectively. Their homogeneous coordinates are expressed as $\tilde{O_{l}}$ and $\tilde{O_{r}}$ respectively. According to the epipolar geometry, the two matching points should meet the following equation

$$\begin{aligned} \widetilde{O_{r}^T}F\widetilde{O_{l}}=0 \end{aligned}$$

(26)

F denotes the fundamental matrix in epipolar geometry which relates the two cameras in pixel coordinate and it can be estimated in camera calibration procedure. But in practical environments, because of the presence of noise and calibration error, the two correspondence points can’t satisfy the epipolar geometry model accurately. The real correspondence image points should lie in around the measurement points and they are subject to the Eq. (26) precisely. For locating the two new matching points $\widehat{O_{l}}\leftrightarrow \widehat{O_{r}}$,we could define a cost function

$$\begin{aligned} Cost(O_{l},O_{r})=d(O_{l},\widehat{O_{l}})+d(O_{r},\widehat{O_{r}}) \end{aligned}$$

(27)

Where $d(*,*)$ is the geometric distance between two points. To solve the global minima of the cost function, we use the optimal triangulation method proposed by Hartley²⁴. It uses a non-iterative algorithm and it is proved to be optimal. Finally, the accurate position of center of the circle is calculated, then they can be used to obtain the pose of the workpiece surface plane in camera coordinate.

Pose estimation

Since the specific workpiece has some holes on its surface, and the accurate position of the circle center has been calculated. All of them can be used to estimate the real pose of the surface in MLE to reduce the error compared with the traditional pose estimation algorithm for single circular target object. The detailed computation procedures are as follows: Suppose there are M space points, whose coordinates are $(x_{i},y_{i},z_{i}),i=1\sim M$. The fitting plane equation is

$$\begin{aligned} ax+by+cz-d=0 \end{aligned}$$

(28)

a, b and c are the unit normal vector and d is the distance from the origin of the space coordinate to the fitted plane. The restriction on a,b,c is $a^2+b^2+c^2=1$ and the optimization goal is to make the total distances between the point $(x_{i},y_{i},z_{i})$ and the fitted plane the smallest. The prior knowledge about the plane fitting is that the average value of the total points must lie in the fitted plane.

$$\begin{aligned} a\overline{x}+b\overline{y}+c\overline{z}-d=0 \end{aligned}$$

(29)

Where $\bar{x}$, $\bar{y}$ and $\bar{z}$ are the average value. So the core part is to estimate the normal vector of the fitted plane. Eqs. (28) and (29):

$$\begin{aligned} a(x_{i}-\overline{x})+b(y_{i}-\overline{y})+c(z_{i}-\overline{z})=0 \end{aligned}$$

(30)

Because three point can specify a unique plane, so M should be larger than 3 at least. The M equations can compose a matrix equation,

$$\begin{aligned} \begin{bmatrix} x_{1}-\overline{x} & y_{1}-\overline{y} & z_{1}-\overline{z} \\ x_{2}-\overline{x} & y_{2}-\overline{y} & z_{2}-\overline{z} \\ x_{3}-\overline{x} & y_{3}-\overline{y} & z_{3}-\overline{z} \\ \ldots & \ldots & \ldots \\ x_{M}-\overline{x} & y_{M}-\overline{y} & z_{M}-\overline{z} \\ \end{bmatrix}\begin{bmatrix} a\\ b\\ c \end{bmatrix}=0 \end{aligned}$$

(31)

The left matrix is A, and the right matrix is X. The objective function is

$$\begin{aligned} cost=min \Vert AX\Vert \end{aligned}$$

(32)

Where $\Vert X\Vert =1$. In general, such a set of equations will not have an exact solution because some of the points set are not exactly lie in the plane. In the absence of an exact solution for the equation, we will normally seek a least-squares solutions. Firstly, the matrix A is decomposed in SVD method:

$$\begin{aligned} A=UDV^T \end{aligned}$$

(33)

Where U and V are unitary matrixes, and D is diagonal matrix. Then the objective function can be transformed

$$\begin{aligned} cost=min\Vert UDV^TX\Vert =min\Vert DV^TX\Vert where \Vert V^TX\Vert =1 \end{aligned}$$

To simplify the notation, we denote $Y=\Vert V^TX\Vert$ and the problem is: minimize $\Vert DY\Vert$ which is subject to $\Vert Y\Vert =1$. Because D is a diagonal matrix with its diagonal elements in descending order. When $Y=[0\hspace{5.0pt}0\hspace{5.0pt}0\hspace{5.0pt}\ldots \hspace{5.0pt}1]^T$ , the objective function $\Vert DY\Vert$ can get the minimum value. The original solution X is simply the last column of V. Finally, the normal coefficients of the plane are calculated by the method of SVD to fit a plane. Namely, the coefficient vector(a, b, c), which corresponds to the last column of V , is the plane normal vector obtained from the singular value decomposition of matrix A.

Experimental results and discussion

We conduct a series of experiments on the accuracy of the proposed method with different relative angles. Since the feature extraction of the corner point and 3D reconstruction of the space point is more convincing, we can use a calibration board and calculate its pose as the compared group. We calculate the absolute value between our measurement method and the compared chess board as the precision error.

Experiment setup

As shown in Fig. 9, the camera sensors which are used in experiments are two CMOS industrial cameras with 24482048 pixels. They are mounted on the mental platform. The calibration chessboard contains 11 corner points evenly distributed, and the distance of the adjacent points is 25 mm in horizontal and vertical directions.

Fig. 9

The experimental platform.

The intrinsic parameters of the cameras, as well as the distortion parameters, can be calibrated using OpenCV or the MATLAB toolbox²⁵. As shown in Table 2, the 3$\times$3 matrices represent the intrinsic parameters of the two cameras, while the vectors (DL, DR) correspond to their respective radial parameters. Since the tangential distortion is negligible–due to the high manufacturing precision of the lenses and the nearly parallel alignment of the optical axis with the imaging plane–it is optimized to zero in the MATLAB toolbox and thus omitted.

Table 2 The calibration parameters.

The quality of camera calibration is evaluated by the reprojection error. We collected 14 sets of calibration images at different distances and angles, and obtained a mean reprojection error of 0.13 pixel, with most errors within ±0.3 pixels, demonstrating satisfactory calibration accuracy.

Ellipse detection experiment

The first step of the pose estimation is to extract the ellipses on the image. As for the dataset, we use CMOS industrial camera and mobile phone camera to shoot standard circular objects in life scenes, so that their projections on the images have strictly elliptical shapes. The CMOS data set taken by CMOS camera has 105 pictures, and the Phone data set has 231 pictures.

We conduct experimental verification of the proposed ellipse detection method by performing detection on the two data sets described above, comparing with the current popular ellipse detection algorithms, such as Fornaciari⁶,Qi⁷ and Lu¹⁹. We use precision, recall, and F-measure values with an IoU threshold of 0.8 to measure the results, defined as follows:

$$\begin{aligned} Precision = \frac{number \hspace{5.0pt}of \hspace{5.0pt}ecllipses \hspace{5.0pt}detected \hspace{5.0pt}correctly}{number \hspace{5.0pt}of \hspace{5.0pt}ecllipses \hspace{5.0pt}detected \hspace{5.0pt}in \hspace{5.0pt}all} \end{aligned}$$

(34)

$$\begin{aligned} Recall = \frac{number \hspace{5.0pt}of \hspace{5.0pt}ecllipses \hspace{5.0pt}detected \hspace{5.0pt}correctly}{number \hspace{5.0pt}of \hspace{5.0pt}real \hspace{5.0pt}ecllipses \hspace{5.0pt}in \hspace{5.0pt}all} \end{aligned}$$

(35)

$$\begin{aligned} F{\text {-}}measure = \frac{2\times Precision \times Recall}{Precision + Recall} \end{aligned}$$

(36)

The results, including the highest precision, recall, and F-measure scores emphasized in boldface, are shown in Table 3.

Table 3 Comparison of ellipse detection results.

Our method outperforms Fornaciari method, Qi method and Lu method in precision value by 8.23%, 11.3% and 10.4% respectively in CMOS dataset, and by 18.5%, 21.3% and 11.11% respectively in Phone dataset. The Lu method groups together arc support segments with similar geometric features, clusters the initial ellipses, and finally verifies the clustered ellipses to ensure high geometric features and good fitting effect. As a result, it makes a good recall rate in CMOS data set, which improve the overall detection effect. The Qi method is developed on the basis of Fornaciari method, and both preform well on recall in Phone data set. Thus, in terms of recall, our method performs slightly lower than Lu on the CMOS dataset and lower than Qi and Fornaciari on the Phone dataset. This is mainly because our approach imposes stricter geometric constraints in the arc aggregation process, which ensures high reliability of detected ellipses but may reject some true ellipses with blurred or incomplete boundaries. Overall, our method still achieves competitive F-measure scores, ranking second on the CMOS dataset (0.7790) and the highest on the Phone dataset (0.8103), demonstrating a strong balance between precision and recall. These results confirm that our method provides more accurate and robust ellipse detection, especially in scenarios where high precision is crucial (as shown in Fig. 10).

Fig. 10

The 1st column is the result of the Fornaciari method; the 2nd column is the result of the Qi method;the 3rd column is the method of Lu method;the 4th column is the result of our method.

In addition, we will process some typical porous workpiece pictures to verify the actual fitting effect of the ellipse detection algorithm. As shown in Fig. 11, it is the ellipse detection results of our method based on accurate aggregation of arc segments, which provides a basic guarantee for the subsequent pose measurement of porous workpieces based on ellipse features. It should be noted that this method can fit a complete ellipse from three arc segments, so this method has a certain degree of fault tolerance.

Fig. 11

Ellipse detection results of real porous workpieces.

Center position estimation experiment

In order to unify the coordinate system and verify the accuracy of our method, we can use a chessboard as a reference. The corners on the black and white chessboard can be extracted easily and the 3D reconstruction point of the corner can be estimated precisely using Optimal Triangulation.

We draw a chessboard with four equal sized circles on it, which is shown in Fig. 12. It is easily to count distance between the center of the circle and the four corner. We use a 0.02 mm precision Vernier scale to measure the true distance (21.80 mm), and evaluate the size of the position error by comparing the difference between the two.

Fig. 12

The chessboard for comparison.

The inner corners of the chessboard can be accurately extracted in opencv algorithm, and the reconstructed space point can also be calculated with a high accuracy. The average spatial position of the four corners around the circle can be used as a reference position of the center. We take photos from different angle and different distance which is shown in Fig. 13. Table 4 presents the measurement errors of the distance to the four corners (d1–d4) based on 12 tests. The errors were minimal, with mean ± standard deviation values of d1 = − 0.0306 ± 0.0609 mm, d2 = − 0.0603 ± 0.0454 mm, d3 = − 0.0102 ± 0.0502 mm, and d4 = − 0.0268 ± 0.0780 mm. A t-test further revealed statistically negative biases for d1, d2, and d4 (p < 0.05), indicating systematic underestimation, whereas d3 showed no significant bias (p = 0.1663), suggesting its error likely due to random variation.

Fig. 13

The partial tested images of center position. The first row is the left images and the second row is the corresponding right image.

Table 4 Position measurement error data.

To verify the effectiveness of our proposed method, we compared our results with the traditional Xu’s method¹⁵, as Fig. 14 shows. It is obvious that our proposed method can achieve a higher accuracy (the absolute mean error of our method is 0.060 mm, standard variance is 0.022). It greatly reduces the deviation of circular hole center caused by asymmetric projection.

Fig. 14

The center position estimation experiment result.

Moreover, to investigate the validity of our proposed method, we can calculate the center distance of each circle and the other circles respectively and compare them with the real physical distance measured by vernier caliper. The measured distance between the centers of two adjacent circles on the screen is 61.80 mm, exactly twice the distance between squares. Compared with real physical distance, the maximum error using our measurement method could be controlled in 0.15 mm.

Normal vector estimation experiment

In order to estimate the error between the accurate result and our proposed method, we put the flange plate and the chessboard on the same plane. As described in the previous section, we can extract the corners accurately and reconstruct its space position. Three points determine a unique plane and we pick out three corners p1, p2 and p3 on the boundary, as is shown in Fig. 15.

Fig. 15

The three corners on the boundary.

the corresponding position is calculated as P1, P2and P3, then the accurate normal vector can be obtained as follows:

$$\begin{aligned} \vec {n}=\frac{\overline{P1P2}\times \overline{P1P3}}{\vert \overline{P1P2}\times \overline{P1P3}\vert } \end{aligned}$$

The result of $\vec {n}$ can be viewed as a reference. Because the detected object and the chessboard are on the same plane, so their normal vector of supported plane are same in the reference of camera coordinate. We could use the angle between two vectors as the error between them.

In Fig. 16, we compare the absolute error of them. The absolute error is greatly reduced by using our method than that by Xu’s method. The maximum error of ours doesn’t exceed 0.5$\phantom{0}^\circ$ and the average orientation error is 0.269$\phantom{0}^\circ$.

Fig. 16

The orientation of norm vector estimation experiment result.

Parameters selection

Our proposed method of ellipse detection is used to extract the hole feature. We have three parameters to adjust. The first is $Th_{angle}$ which is the geometric constraint threshold. The smaller this value is, the stronger constraints exist. For example, if it equals to 1, this fact means only few arcs could pass the geometric constraints and enter the next fitting procedure. At the same time, the total running time is relatively short. The second is $Th_{score}$ that estimate how well the point data fits the ellipse equation. The larger value it is, the better fit it does. The third is $Th_{rel}$ whose value determines the reliability of whether the three arcs are in the same ellipse after they satisfy the $Th_{score}$.

Fig. 17

Performance impact curve of (a) $Th_{angle}$, (b) $Th_{score}$, (c) $Th_{rel}$.

To find the suitable values for these three parameters, we first determine a (relatively small) initial changing region for each parameter, i.e., $Th_{angle}$ varies from 1 to 25 with interval 1, $Th_{score}$ varies from 0.3 to 1 with interval 0.1, and $Th_{rel}$ varies from 0.3 to 1 with interval 0.1. In Fig. 17a, We then observe the performance results and find out that, when the geometric constraint is 10, there are more feasible combinations of arc segments that pass the geometric constraints, and the final F-measure value tends to be stable. We also find out when $Th_{score}$ is 0.7 and $Th_{rel}$ is 0.7, we can get the maximal F-measure in two datasets, as shown in Fig. 17b, c. This is because when the threshold is set larger, the true detection samples will be falsely filtered out, and when the threshold is set lower, the false detection samples will pass the index test, which will lead to a decrease in the overall F-measure value.

Conclusion

In this paper, we propose an effective method to measure the 3D position and pose of the specific workpiece which has multi-hole on its surface. Firstly, in the process of the graphic feature extraction, we choose to detect the ellipse in the image by the edge following method which detects the arcs that belong to the same ellipse based on the set constraint, relative point position constraint and geometry constraint. Then by using the direct least square fitting method, we get the basic feature information of the ellipses. Secondly, we estimate the position and pose by the point feature. We extract each accurate projected point of the circle centers using the property of vanishing line and reconstruct the positions of them based on the triangulation technology. Then the high precision pose of the supported plane of these circular holes can be obtained by fitting the plane of these center points. Experiments are conducted. The experimental results prove that our method can achieve a high accuracy and robustness.

There are still some limitations of the method in this paper. Firstly, for the pose measurement of the workpiece, this paper mainly focuses on the extraction and processing of ellipse features. The algorithm processing of image feature extraction now will consume a certain amount of time while using the pictures of megapixels or even tens of millions of pixels. Actually, in industrial scenes, the detected objects on the captured pictures often only occupy a small area. Therefore, introducing deep learning technology to locate the ROI region of the specific workpiece fast and accurately would be considered in the future. Secondly, for porous workpieces, the current pose measurement algorithm requires at least three circular holes to be detected. In the future, we would explore how to reconstruct the pose of the spatial circular hole under the premise that only two detection ellipses exist.