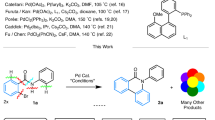
Abstract
The statistical design of experiment (sDoE) enables efficient exploration of complex chemical space by screening multiple factors simultaneously, overcoming the limitations of the one-factor-at-a-time (OFAT) approaches. In this study, Plackett–Burman design (PBD) was applied to screen five factors: electronic effect and Tolman’s cone angle of phosphine ligands (4), catalyst loading (2), bases (2), and solvent polarity (2) across twelve (12) C–C cross-coupling reactions for the Mizoroki–Heck, Suzuki–Miyaura, and Sonogashira–Hagihara reactions. While the importance of these factors is well established in cross-coupling chemistry, this study aimed to demonstrate how statistical PBD can compare and rank factors’ effect via high-throughput screening (HTS) context. The outcome identified influential factors for each reaction, indicating the efficiency of integrating HTS and sDoE. This proof-of-concept study demonstrates an initial screening approach for future optimisation using advanced designs such as response surface methodologies (RSM), providing a deeper understanding of complex chemical spaces by investigating factor interactions, catalyst design, and process development.
Similar content being viewed by others
Introduction
Catalytic systems often involve multiple factors that interact synergistically or antagonistically. Therefore, screening and optimising factors are essential to achieve an optimal system. However, chemists often rely on the one-factor-at-a-time (OFAT) approach for screening catalytic reactions. The OFAT approach ignores interactions between factors by varying one factor while keeping all other factors constant. Given the complexity of catalytic systems, neglecting such interactions can result in the development of suboptimal systems1,2.
The statistical design of experiment (sDoE) addresses limitations of the OFAT approach and is more reliable in scientific research. The sDoE allows for simultaneous screening of multiple factors to determine both their individual and interaction effects on a reaction system3. The increasing use of sDoE in scientific research is driven by the inefficiency of OFAT, which requires a large number of experiments and consumes time, resources, and money. The sDoE, however, has more merits than the OFAT experimentation. In contrast, sDoE minimises the number of experiments while maximising the information obtained, thus conserving resources and time4,5.
The core principle of sDoE involves identifying important factors and selecting at least two reasonable levels for each factor. Factor levels are defined, and experiments are performed based on the experimental design. The significance of each factor is then assessed using statistical analysis of experimental data, leading to objective and data-driven conclusions6,7. In recent years, sDoE has contributed to improving product quality and reliability. It has been widely applied in decision-making processes related to manufacturing, product development, and process optimisation across various industries, including petrochemical and chemical6, chromatography7, hospitals8, food9, energy10, pharmaceutical11, and architecture12.
Various sDoE designs can be used in screening and optimising different systems, including central composite design (CCD)13, mixture design (MD)14, full factorial designs (FFD)15, Box-Behnken design (BBD)16, definitive screening design (DSD)17, space-filling design (SFD)18, Taguchi design (TD)19, response surface methodology (RSM)20, and Plackett–Burman design (PBD)21.
Among these, PBD is widely used for initial screening to identify significant factors in reaction systems22. It is also known as a saturated design because effects are estimated using all degrees of freedom. The PBD is suitable for screening because it identifies the main effects of factors23.
Additionally, PBD is based on performing n experiments to screen up to n−1 factors (parameters), where n is a multiple of four (4). For example, a twelve-run (12) run design can screen up to eleven (11) factors. In each run, factors are set at two levels: low (–1) and high (+ 1). If the factors screened are fewer than n−1, then the remaining factors in the design are used as dummy factors. The dummy factors are used to estimate experimental standard errors and identify statistically significant factors in a reaction system24,25,26.
In this study, a 12-factor PBD is implemented to simultaneously screen key factors in the Mizoroki–Heck, Suzuki–Miyaura, and Sonogashira–Hagihara carbon-carbon (C–C) cross-coupling reactions. These coupling reactions were chosen because they are among academia and industry’s most widely applied palladium-catalysed reactions. For instance, the Mizoroki–Heck reaction can be used to synthesise functionalised alkenes, which are key intermediates in agrochemicals, pharmaceuticals, and advanced materials27. The Suzuki–Miyaura reaction is a versatile transformation that provides scalable access to different functional groups with broad applications in large-scale synthesis and medicinal chemistry28. The Sonogashira–Hagihara reaction provides an efficient path to synthesising aryl-alkyne groups, which are used to synthesise organic electronic materials, natural products, and bioactive molecules. These benchmark reactions are ideal for demonstrating the impact of HTS and sDoE on catalyst and conditions screening because they provide diverse transformation and synthetic applications29.
The PBD was selected because it systematically evaluates numerous factors at defined levels and provides insights into their individual and interaction effects. Key factors investigated include the electronic effect of phosphine ligands and Tolman’s cone angle (steric bulkiness) of phosphine ligands, catalyst loading, base strength, and solvent polarity. This sDoE offers a robust approach for identifying, screening, and optimising parameters in cross-coupling reactions and can be extended to explore interactions in other catalysed reactions.
Materials and methods
Materials
All reagents were purchased from Sigma-Aldrich (Johannesburg, South Africa) and used without further purification. The reagents included bromobenzene (PhBr, 99%), iodobenzene (PhI, 98%), butylacrylate (99%), 4-fluorophenylboronic acid (95%), and phenylacetylene (98%). The catalysts include potassium tetrachloropalladate (II) (K2PdCl4, 98%) and palladium acetate [Pd(OAc)₂, 99%]. Bases included sodium hydroxide (NaOH, 99.08%) and triethylamine (Et3N, ≥ 99%). Solvents included dimethylsulfoxide (DMSO, ≥ 99.9%), acetonitrile (MeCN, ≥ 99.8%), and dichloromethane (DCM). Dodecane (≥ 99.9%) was used as an internal standard. A list of phosphine ligands screened is provided in Table 1.
Methodology
In the screening of the C–C cross-coupling reaction, a two-level, 12-run Plackett–Burman design (PBD) was used to evaluate the significance of key factors by minimising the number of required experiments. Experimental runs were randomised to reduce the influence of uncontrolled factors that can affect the reliability and accuracy of results. Four phosphine ligands of different electronic effect, Tolman’s cone angle, a weak and a strong base, two solvents of different polarity, and catalyst loadings were assigned to factor columns A to E in the PBD table. The remaining six columns were assigned to dummy factors F-G. All eleven factors were defined as high levels (+ 1) and low levels (–1). Refer to Table 2 below, a summary of Table SI 2 in the supplementary information (SI).
Phosphine ligands
The electronic effect [vCO (cm–1)] and Tolman’s cone angles (θ) factors of phosphine ligands were investigated to determine how they affect the C–C coupling reactions. Stretching frequency (vco) is used to determine the electronic effect of ligands as a factor, and Tolman’s cone angle (θ) is another factor investigated (see Table 3). Figure 1 shows a graph comparing the electronic effect and Tolman’s cone angle of phosphine ligands.
An amount of 0.1- and 0.2-mmol of phosphine ligands were used in the Sonogashira–Hagihara reaction, and Mizoroki–Heck and Suzuki–Miyaura reactions, respectively. Table 4 demonstrates how the ligands were assigned to the PBD table columns for screening purposes.
Catalyst
Two metal precursors were used as catalysts in the reactions. Potassium tetrachloropalladate (II) (K2PdCl4) was used to catalyse the Mizoroki–Heck and Suzuki–Miyaura reactions, while palladium acetate [Pd(OAc)₂] was used as a catalyst for the Sonogashira–Hagihara reactions. A loading of 1- and 5-mol% were chosen; 5 mol% was chosen as a high level (+ 1) and 1 mol% as a low level (–1) [see Tables 6 and 7].
Base
Sodium hydroxide (NaOH), a high level (+ 1), and triethylamine (Et3N), as a low level (–1), were chosen based on their basic strength. Amounts of 2- and 4-mmol of these bases were used in the Sonogashira–Hagihara reaction, and Mizoroki–Heck and Suzuki–Miyaura reactions, respectively. See Tables 6 and 7.
Reaction solvent
The polarity of dipolar aprotic solvents, dimethylsulfoxide (DMSO) and acetonitrile (MeCN), was evaluated in this study, with DMSO as the low level (–1) and MeCN as the high level (+1). Solvent selection was based on the principal component analysis (PCA) solvent space framework developed by Murray et al.3, which classifies solvents based on their diverse physicochemical properties: polarity, dipolarity, hydrogen bonding, van der Waals interactions, and donor/acceptor characteristics. Table 5 represents physicochemical properties of DMSO and MeCN, including dielectric constant, Hansen Solubility Parameters (HSP), and Kamlet − Taft parameters (KTP).
An equal volume of 5 mL of DMSO (–1) and MeCN (+ 1) was used in all reactions. See Tables 6 and 7.
General description of the C–C cross-coupling reactions
Mizoroki–Heck reactions were performed using iodobenzene (PhI, 2 mmol) with butylacrylate (nucleophile, 2.4 mmol), Suzuki–Miyaura reactions using bromobenzene (PhBr, 2 mmol) with 4-fluorophenylboronic acid (nucleophile, 2.4 mmol), and Sonogashira–Hagihara reactions using iodobenzene (PhI, 1 mmol) with phenylacetylene (nucleophile, 1.2 mmol). All reactions were performed at 60 ℃ for 24 h in carousel tubes (Figure SI 1, SI). The reaction temperature was chosen to accommodate the large temperature difference in boiling points between DMSO (189 ℃) and MeCN (82 ℃), to ensure effective use of both solvents under the same thermal conditions with minimum evaporation or decomposition. The duration of the reaction was selected to ensure sufficient screening time. The progress of the reactions was monitored using gas chromatography flame ionisation detection (GC-FID), and gas chromatography mass spectrometry (GC-MS) was used to identify products.
Mizoroki–Heck reactions
In a typical reaction, using the 12-run PBD (see Table 2), a mixture of 345.50 µL of butylacrylate and 223.82 µL of iodobenzene was dispensed to 12 carousel tubes. Followed by the addition of ligands: 0.0105 g of ligand T1 was dispensed in reaction tubes for runs 1, 4, and 5, and 5.2 µL of T2 in runs 2, 6, and 10 tubes. On the other hand, 0.0056 g of T3 was dispensed in runs 3, 9, and 11 tubes, and 2.85 µL of T4 in runs 7, 8, and 12 reaction tubes. For bases: 0.1599 g of NaOH was dispensed in runs 1 to 3, 7, and 9 to 10 tubes, and 557.52 µL of Et3N in runs 4 to 6, 8, and 11 to 12 tubes. As an internal standard, 454.54 µL of dodecane was dispensed in all 12 runs. Lastly, A 0.0065 g (1 mol%) of metal precursor, K2PdCl4, was dispensed in runs 1, 5 to 7, 9, and 12, and 0.0326 g (5 mol%) of K2PdCl4 in runs 2 to 4, 8, and 10 to 11 tubes. Reaction runs 1 to 2, 6, 8 to 9, and 11 were performed in DMSO (5 mL), and reaction runs 3 to 5, 7, 10, and 12 were performed in MeCN (5 mL).
Suzuki–Miyaura reactions
The same procedure, reagents (excluding substrates), and order of dispensing reagents were used for the Suzuki–Miyaura reactions (see the Mizoroki–Heck reaction procedure). However, a mixture of 0.3358 g of 4-fluorophenylboronic acid and 210.61 µL of bromobenzene was used to perform these reactions.
Sonogashira–Hagihara reactions
Similarly, the same procedure, reagents (excluding substrates and metal precursor), and order of dispensing reagents used for the Mizoroki–Heck reactions were used for this part, except that a mixture of 131.78 µL of phenylacetylene and 112 µL of iodobenzene was used to perform these reactions. For this part, 10 mol% of the same ligands were used: 0.0523 g of ligand T1 was dispensed in reaction tubes for runs 1, 4, and 5, and 26.21 µL of T2 in runs 2, 6, and 10 tubes. Moreover, 0.0280 g of T3 was dispensed in runs 3, 9, and 11 tubes, and 14.22 µL of T4 in runs 7, 8, and 12 reaction tubes.
For bases, 0.0799 g of NaOH was dispensed in runs 1 to 3, 7, and 9 to 10 tubes, and 278.76 µL of Et3N in runs 4 to 6, 8, and 11 to 12 tubes. About 227.27 µL of dodecane was dispensed in all 12 runs as an internal standard. Lastly, 0.0022 g (1 mol%) of metal precursor, Pd(OAc)₂, was dispensed in runs 1, 5 to 7, 9, and 12, and 0.0112 g (5 mol%) of Pd(OAc)₂ in runs 2 to 4, 8, and 10 to 11 tubes. Reactions were performed under the same conditions as described above.
GC-FID and GC-MS analysis
A volume of 100 µL was taken from each reaction before the start (0 h) and at the end (24 h) to determine the reactions’ conversions and identify products formed. However, after reactions, reaction mixtures were subjected to a small silica column to remove inorganic species, and a syringe was used to remove any solid particles before 24-hour samples were prepared. Samples were then diluted (1:10) with dichloromethane (DCM) for analysis.
Substrate conversions (Eq. 1) were calculated using 0-hour and 24-hour sample GC-FID results. In each sample, peak intensity/area was used for the calculations, together with the peak intensity/area of the internal standard (dodecane). The equation is defined as:
Where C is the conversion rate of the substrate, Isubstrate is the intensity of substrate (at 24 and 0 h), and Idodecane is the intensity of decane (at 24 and 0 h). Products were confirmed using GC-MS.
Results and discussion
The application of Plackett–Burman design (PBD) in key cross-coupling reactions, Mizoroki–Heck, Suzuki–Miyaura, and Sonogashira–Hagihara, enabled rapid and statistically efficient screening of multiple reagent factors in a large experimental space. This approach reduces the number of required experiments while identifying the most significant factors on substrate reactions, than the traditional one-factor-at-a-time (OFAT) approach, which is time- and resource-intensive. However, PBD is inherently limited to evaluating factors at two levels (–1 and + 1), limiting its ability resolving nonlinear effects or interactions. As such, this study focused on efficiently identifying the most significant factors, rather than fully exploring the effects of individual reagent properties in detail.
Five key reagent factors were selected: (1) electronic effects of ligands and Tolman angle (steric bulkiness) of ligands, (3) catalyst loading, (4) base strength, and (5) solvent polarity. These were chosen based on their critical roles in influencing the catalytic activities, reaction kinetics, and product yield in cross-coupling reactions. Among these, ligand properties modulate the electron density at the metal (Pd) center, influencing catalytic steps such as oxidative addition, transmetalation, and reductive elimination rates33,34. Thus, they stabilise PdNPs formed in the reactions and are responsible for catalytic activity35.
The synergistic effects of electronic and steric properties of biaryl- and triaryl-phosphine ligands facilitate the rate of oxidative addition, transmetalation, and reductive elimination steps in the catalytic cycle of the coupling reactions. These occur as follows: these ligands’ electronic effect and bulkiness play a role in stabilising the monoligated L1Pd intermediate, a key species in the catalytic cycle. In the presence of these ligands, oxidative addition of aryl halide takes place faster with the L1Pd(0) complex, which is smaller in size than the L2Pd(0) complex. As a result, they accelerate the overall reaction rate36. Systematic variation of electronic and steric properties allows for valuable insight into the synergistic interaction between ligand and metal and catalyst design37,38,39.
Base strength has a mechanistic significance in transition metal-catalysed cross-coupling reactions, such as facilitating oxidative addition, transmetalation, and reductive elimination by stabilising intermediates and maintaining the catalytic cycle. Literature consistently reports that bases play numerous roles in these reactions and that no general rule is used to select a base due to base structure, strength, and solubility. In Mizoroki–Heck and Suzuki–Miyaura reactions, a base transforms the L2Pd(H)X to L2Pd(0) complex to complete the catalytic cycle. A base causes the equilibrium to shift to the Pd(0) complex by quenching the HX species. In the Suzuki–Miyaura reactions, a base facilitates transmetalation by replacing a halide in the palladium complex36,40.
The nature of the base, organic or inorganic, affects the reaction efficiency and outcome. Weaker or sterically hindered organic bases, such as Et3N, can be less efficient in reactions due to reduced basicity, leading to possible catalyst deactivation or incomplete deprotonation. In contrast, strong inorganic bases such as NaOH under the same catalytic conditions are generally more effective, leading to higher reaction rates and better conversions by effectively deprotonating intermediates. In addition, other equally important properties include the solubility of base in a reaction solvent and the ability to avoid side reactions. Therefore, screening base strength can provide a deeper understanding of its impact on catalytic performance: rate, yield, and selectivity41,42,43.
Solvent choice plays an important role in palladium-catalysed cross-coupling reactions by influencing catalyst activity, stability, and selectivity. Key physicochemical properties, such as polarity, polarisability, hydrogen bonding characteristics, and boiling point, can influence reagent solubility, polar intermediate stability, and overall catalytic efficiency44,45. Solvents can act as hydrogen bond donors or acceptors that can compete with ligands for metal bonding sites, which can affect catalyst activity and deactivation pathways. In some instances, solvents can enhance the activity of acids or bases in reactions and help control the separation of by-products from products through precipitation or partitioning of products46.
In this study, solvent choice was guided by the principal component analysis (PCA) solvent framework developed by Murray et al.3 which mapped solvents based on key physicochemical descriptors. Using the PCA mapping, two polar aprotic solvents, DMSO and MeCN, were chosen not only based on their widespread use in cross-coupling reactions, but also due to their different polarities, van der Waals forces, polarisability/dipolarity, hydrogen bonding capacities, and boiling point. These solvents occupy distinct positions in the PCA solvent map, showing differences in physicochemical properties3,47. Solvent screening provides insight into understanding the influence of solvents on catalyst activity, reaction selectivity, yield, and optimising factors using a statistical experimental design48.
Statistics design of experiment (sDoE) calculations
After running 3 sets of 12 experimental runs for five (5) factors at only two levels: low level (–1) and high level (+ 1), the significance of factors on reactions was determined using substrate conversions to products. Factors include electronic effects and Tolman’s cone angle of phosphine ligands, catalyst loading, base strength, and solvent polarity. The experimental data obtained were fitted into the first-order (linear) polynomial model given by the following equation for regression analysis49:
Where Y is the predicted conversion in this study, \(\:{\beta\:}_{0}\) is the average conversion, \(\:{\beta\:}_{i}\) is the observed effect of factors, Xi is the level of factors (–1 or + 1), and k is the number of factors.
Main effect plot of factors
Conversion of low- and high-level factors were used to calculate average substrate conversions of factors using Eq. 3, contrast (Δ). The main effect plot of each factor was plotted using factor levels (–1, + 1) on the x-axis against average conversions on the y-axis50:
Where \(\:\sum\:\left(y-1\right)\) is the sum of the conversions at a low level and \(\:\sum\:\left(y+1\right)\) is the sum of conversions at a high level of factors. The slope of the line in the main effect plots indicates the significance of each factor on conversions: significant factors have a steep slope, and insignificant factors have a flat slope. If a factor line increases from a low level to a high level, that factor positively affects reactions; a factor with a line decreasing from a low level to a high level has a negative effect on reactions. Slopes of factors were compared to identify the most influential factors. Therefore, the main effect chart indicates the impact of increasing and decreasing factors on reaction performance. The plots are given in Figs. 3a and 5a, and 7a, respectively.
Estimated and disentangled effect of factors
The estimated effects allow determination of both the magnitude and direction (positive or negative) of each factor’s influence and help identify which factors have statistically significant impacts on reaction conversion. Estimated effects of each variable were calculated using the following Eq. 451:
Where Eeff is the factor effect, \(\:\sum\:\left(y-1\right)\) and \(\:\sum\:\left(y+1\right)\) are the sum of the conversions at low and high levels, respectively, and N is the total number of experimental runs. Using minimal runs to determine the effects of PBD can cause an increase in confounding between factors. When factors are confounded, the estimated effects can be distorted by hidden interrelationships, hindering the accurate identification of significant factors. Therefore, factors are systematically disentangled to avoid confounding and to assess their significance in reactions. Disentangled effects are given by Eq. 4: a negative value of the disentangled effect indicates increased conversion at the factor’s low level (–1), and a positive value indicates increased conversion at the factor’s high level (+ 1). Results for the Mizoroki–Heck, Suzuki–Miyaura, and Sonogashira–Hagihara reactions are given in Tables 8, 9, and 10, respectively.
Standardised Pareto chart
Effects of dummy factors were used to calculate experimental error (ER) which is given by Eq. 5:
Where Ed is the effect of dummy factors at high and low levels, and n is the total number of dummy factors. Standard error (SE) is the square root of experimental error. The standardised effect (t-test) of factors were calculated using Eq. 652:
A minimum significant effect (MSE) value was calculated using the t-critical value (t-value) and standard error (SE), using Eq. 7:
The t-value of 3.707 was calculated using a statistical significance level of 1% (\(\:\alpha\:=0.01\)) and a degree of freedom, n = 6, which is the number of dummy factors. A standardised Pareto chart was plotted using the absolute standardised effects of factors. The bar length of the factors indicates the significance of the factors. The bars are in order of significant factor at the top of the chart and the least/significant factor at the bottom. Factors whose standardised effects exceed the MSE threshold are statistically significant at \(\:\alpha\:=0.01\). See plots in Figs. 4b, 7b, and 10b.
Normal probability plot
Firstly, normal quantiles (pi) of each factor were calculated using Eq. 853:
Where pi is the normal quantile (cumulative probability), i is the data rank from most negative to most positive (ascending order), and n is the total number of data points. Standard normal quantiles were calculated as the inverse of normal quantiles [\(\:{\varPhi\:}^{-1}\) (pi)], see Eq. 954:
Normal probability plots were determined by comparing the absolute standardised effects against standard normal quantiles (zi). If factor points are closer to the straight line, they are insignificant; if points deviate from the linearity, they are significant. Therefore, this visual approach supports the Pareto chart by confirming factor significance. Figures 4c and 7c, and 10c represent normal probability plots. The effects of each factor are discussed below.
Mizoroki–Heck coupling reactions
The coupling of butylacrylate with iodobenzene to form butyl-3-phenylpropionate was investigated (see Fig. 2). Sample data from GC-FID were used to calculate conversions of iodobenzene substrate to butyl-3-phenylpropionate product; see Table 8. A reaction with the highest conversion was identified to have optimal reaction conditions. The product structure was confirmed with GC-MS analysis; refer to Figure SI 2 to Figure SI 4, which shows the chromatogram and spectrum of the product in the SI appendices. The effects of ligand, base, solvent, and catalyst were systematically evaluated using the PB design.
The Mizoroki–Heck reaction proceeds through a Pd(0)/Pd(II) catalytic cycle: oxidative addition, migratory insertion, and beta (β)-hydride elimination, as shown in Fig. 3. In this study, K2PdCI4 was used as a palladium (Pd) source, where it undergoes in situ ligand- and base-assisted reduction reaction to form the active Pd(0) species that catalyse reactions. Phosphine ligands facilitate this process by undergoing oxidation to phosphine oxides while reducing Pd(II) to Pd(0), thereby stabilising the formed Pd(0) species and preventing aggregation to a less catalytically active Pd black. Concurrently, base facilitates halide removal, enhancing the reduction process and solubility of reactive intermediates55,56. The generated active Pd(0) species generated in situ undergoes oxidative addition with iodobenzene to form I–Pd(II)-phenyl complex, followed by butylacrylate coordination and migratory insertion to the Pd centre, β-hydride elimination to release the butyl-3-phenylpropionate and base-mediated regeneration (reductive elimination) of Pd(0)57.
Experimental runs show that ligand properties significantly influence the oxidative addition step. A positive observed or estimated effect (+ 0.020) for electronic effects consistently shows that electron-withdrawing ligands, such as tris(pentaflurophenyl)phosphine (T1), stabilise the Pd(0) centre and accelerate oxidative addition, producing the highest conversion of (87.68%, run 1). Electron-deficient ligands make Pd(0) more electrophilic, lowering barriers for the insertion of iodobenzene. This outcome is consistent with Amatore et al.‘s study, which demonstrates the impact of electron-withdrawing ligands on oxidative addition in the Mizoroki–Heck reactions58,59.
In contrast, the negative effect (–0.015) of Tolman’s cone angle reflects the negative influence of the ligand’s steric hindrance (factor B). Sterically bulkier ligands hinder butylacrylate coordination to the Pd(0), reducing efficiency. For instance, replacing T1 (run 1) with a bulkier ligand T3 (run 9), caused a decrease in conversion from 87.68% to 15.73% under the same reaction conditions. Literature similarly highlights that bulkier ligands can block alkene coordination and insertion to the Pd in Heck reactions33,57.
A negative observed effect (–0.008) of catalyst loading (factor C) shows that an increase in catalyst loading from 1 mol% to 5 mol% does not significantly improve conversion. This trend is supported by a decrease in conversion from 87.68% (run 1) to 71.89% (run 2) when catalyst loading was increased in the same conditions, potentially leading to catalyst deactivation at higher loading. Similarly, this has been reported in the literature60.
Base strength (D) was the most crucial factor influencing reaction conversions. A strongly positive effect (+ 0.031) for NaOH, a strong inorganic base, produced the highest conversion of 87.68% in run 1, whereas Et3N, a weaker organic base, produced only a conversion of 20.93% in run 6. This shows that a strong inorganic base, such as NaOH, has mechanistic properties to promote deprotonation of Pd–H species to regenerate Pd(0), ensuring high conversion. In contrast, a weak organic base such as Et3N can bind to the Pd centre, inhibiting catalysis61. This is consistent with the literature, which shows that inorganic bases such as NaOH often lead to high turnover in polar, anhydrous conditions57. Although only NaOH and Et3N were tested based on the nature of the PBD used in this study, literature shows that intermediate bases such as potassium carbonate (K2CO3), cesium carbonate (Cs2CO3) and sodium carbonate (Na2CO3), can provide moderate basicity and solubility which promote efficient catalysis62,63.
A negative effect (–0.005) of solvent polarity (factor E) shows that solvent choice has minimal impact but still influences conversion. A polar aprotic solvent, DMSO (71.89%, run 2), outperformed MeCN (48.07%, run 10), due to its high dielectric constant, excellent base solubilisation ability, and superior hydrogen-bond acceptor strength, which can stabilise Pd species during oxidative addition. Literature shows that polar aprotic solvents such as dimethylformamide (DMF) and N-methyl-2-pyrolidone (NMP) have a similar influence of facilitating oxidative addition and β-hydride elimination64. In contrast, non-polar solvents such as toluene, cyclopentyl methyl ether (CPME), and chloroform are less effective due to the limited solubility and stability of a base; however, they are used in industries for selective purposes57. All these observations highlight how physicochemical properties govern reaction outcome, which guide HTS and DoE-based optimisation65.
Analysis of DoE data, show that base strength (D) has the highest effect on reaction conversion (NaOH is more favourable than Et3N), electronic effect (A) and Tolman angle/steric effect (B) have significant influence on conversions, improved reaction conversion does not necessarily depends on higher catalyst loading (C), and solvent polarity (E) has minor influence on the reaction but DMSO is slight favoured. The main effect plot (Fig. 4a) shows that factor D has a steeper slope than the other factors, followed by factors A and B, respectively. The insignificance of factors C and E is shown by their smaller slope.
The Pareto chart (Fig. 4b) shows that all factors are significant because their standardised effects exceed the minimum significant effect (MSE) value. However, the bar length shows that factors D, A, and B are the most significant, respectively. In the normal probability plot (Fig. 4c), factors D, A, and B are the most significant because they are far from the straight line, whereas factors C and E are closer to the straight line.
Suzuki–Miyaura coupling reactions
Based on the same approach, the coupling of 4-fluorophenylboronic acid with bromobenzene to form 4-fluoro-1,1’-biphenyl was investigated, as shown in Fig. 5. The 4-fluoro-1,1’-biphenyl product was confirmed by GC-MS analysis, and conversions were evaluated using GC-FID based on sDoE. Refer to Figure SI 5 to Figure SI 7 in the SI to confirm the product’s structure and Table 9 for results.
A plausible mechanism for the Suzuki–Miyaura reaction involves three key steps within the Pd(0)/Pd(II) cycle, as shown in Fig. 6: oxidative addition, transmetalation, and reductive elimination. In these reactions, active Pd(0) species are produced in situ from the reduction reaction of Pd (II) precursor (K2PdCl4). Electron-rich phosphine ligand facilitates the reduction reaction while undergoing oxidation reaction to phosphine oxide, and base assists the removal of halide, accelerating the reduction reaction and preventing the aggregation of Pd black. The active Pd(0) undergoes oxidative addition with bromobenzene to form a Br–Pd(II)–phenyl complex. Afterwards, 4-fluorophenylboronic acid is activated by a base to form 4-fluorophenyl boronate anion (intermediate), either via direct protonation in the presence of NaOH or via indirect protonation in the presence of Et3N. Polar solvents such as DMSO have hydrogen bond accepting properties that promote the formation of hydrogen species in situ and stabilise boronate intermediates. The boronate intermediate undergoes transmetalation with the Pd(II)–aryl complex to produce a bis-aryl Pd(II) intermediate, followed by reductive elimination to produce the 4-fluoro-1,1’-biphenyl product and regeneration of Pd(0)66,67.
Influence of the electronic effect of ligands (factor A) on oxidative addition is highlighted in run 9, where tricyclohexylphosphine (T3, electronic-rich ligand) resulted in the highest conversion of 95.15% (1 mol% K2PdCl4, NaOH, and DMSO). In contrast, tris(pentaflurophenyl)phosphine (T1, electron-withdrawing) ligand produced slightly lower conversion (86.71%, run 1) under the same conditions. This outcome indicates that the electron-donating ligands efficiently stabilise Pd(0) and accelerate oxidative addition of bromobenzene. The positive (0.025) estimated effect of electronic properties (A) shows that reaction performance can be improved with ligands of a certain electronic property. Miyaura and Suzuki’s41 study supports the report that stronger donor ligands can promote faster oxidative addition and better catalytic efficiency.
The steric influence of ligands (factor B) has minimal influence in these reactions. For instance, conversions are moderately decreased from 38.95% (run 5, T1) to 28.46% (run 12, T4-bulkier ligand) under comparable conditions. The small estimated effect (–0.001) supports that the steric effect has a secondary impact compared to the electronic effect, aligning with literature reports59.
Catalyst loading (factor C) has a negative estimated effect (–0.015), indicating that increasing Pd loading from 1- to 5-mol% does not improve reaction performance. This is supported by a decrease in conversions from 38.95% (1 mol%, run 5) to 35.88% (5 mol%, run 4), under the same conditions. The decrease is attributed to Pd aggregation of Pd species or catalyst deactivation at higher loading, which is supported by literature68.
The strongly positive observed effect (0.025) of base strength (factor D) indicates that stronger bases improve reaction performance. Run 9 produced a conversion of 95.19% (NaOH), whereas run 6 produced 89.60% (Et3N), under the same conditions: DMSO and 1 mol% Pd loading. The difference in conversion is attributed to the ability of NaOH to protonate 4-fluorophenylboronic acid to ensure efficient transmetalation, while Et3N depends on solvents to activate the boronate. Notably, the high efficiency of Et3N in DMSO, as shown by the conversion 89.60% (run 6), shows how solvent properties (hydrogen bond acceptor and high polarity) can compensate for weaker bases by stabilising boronate species and Pd intermediate. Therefore, Et3N can stabilise the palladium intermediate and facilitate transmetalation, especially in polar solvents. A study by Allan Watson and co-workers demonstrates the viability of Et3N in highly polar solvents in Suzuki–Miyaura reactions. The base trend is supported by Watson et al.‘s work, demonstrating the key role of hydroxide in transmetalation.
The highest positive estimated effects (0.056) of solvent polarity (factor E) show that conversions can be strongly enhanced by a highly apolar solvent (DMSO). Polar aprotic DMSO consistently outperformed MeCN; this is observed by a decrease in conversion from 67.71% (DMSO, run 2) to 38.12% (Et3N, run 3) under similar conditions. The physicochemical properties of DMSO: a high dielectric constant, the ability to dissolve bases and intermediates, a strong hydrogen bond accepting ability, and the ability to stabilise Pd species and intermediates, are key in facilitating oxidation addition and transmetalation. Lennox et al.‘s study supports that reaction rate and intermediate stability can be influenced by solvent choice69. Comparable solvents such as DMF and NMP can enhance catalytic efficiency, whereas non-polar solvents such as toluene or CPME have poor base and intermediate solubility, limiting conversions57.
The DoE data analysis diagrams in Fig. 7 show the following observations: solvent polarity (E) strongly improves reactions, base strength (D) and electronic effect (A) are crucial and significant in improving conversions, low catalyst loading (C) increases reaction performance, and Tolman angle/steric hindrance (B) does not play a significant role in this reactions. The significance of factor E is shown by its steeper slope in the main effect plot (Fig. 7a). Factors D and A have the same slope, indicating their equal significance.
The bar length of factors in the Pareto chart (Fig. 7b) shows that factors E, D, A, and C are respectively significant in this reaction because their standardised effects are above the MSE value compared to factor B, which is insignificant. The normal probability plot (Fig. 7c) shows the same observations: factor B is closer to the straight line (insignificant), and factors E, D, A, and C, respectively, are far away from the straight line.
Sonogashira–Hagihara coupling reactions
The same ligands, catalyst loading, base, and solvent polarity were further evaluated using the Sonogashira–Hagihara coupling of phenylacetylene with iodobenzene to form diphenylacetylene, as shown in Fig. 8, using PBD. Refer to Figure SI 8 to Figure SI 10 to confirm the product’s structure. The reaction conversions of substrates to the diphenylacetylene product are listed in Table 10.
A mechanism for the Sonogashira–Hagihara reaction involves three key steps in the Pd(0)/Pd(II) cycle (Fig. 9). The active Pd(0) species are generated from Pd(II) precursor, Pd(OAc)₂, in situ through the reduction reaction facilitated by electron-rich phosphine ligands and base-assisted removal of halide70. This process ensures the availability of active Pd(0) species by preventing the aggregation of Pd. Under copper-free conditions, iodobenzene undergoes oxidative addition with active Pd(0) species to form an I–Pd(II)–phenyl complex. The terminal alkyne (phenylacetylene) is then deprotonated by the base (NaOH or Et3N) to form an alkynyl species, which subsequently transfers to the Pd(II)–aryl complex to form a Pd(II)-aryl-alkynyl intermediate71.
In the absence of copper [Cu(I)], the transfer of the alkynyl fragment to the Pd(II) complex may not take place through the classical transmetalation pathway. Instead, alternative mechanistic pathways have been proposed, including: (i) direct base-assisted coordination and deprotonation of the alkyne to the Pd(II) centre72,73, (ii) a direct nucleophilic substitution of the halide by a solvated alkynyl anion74, and (iii) a Pd-Pd transmetalation step where a Pd species first form a Pd-alkynyl intermediate that transfers the alkynyl group to the oxidative addition Pd centre75,76. All these alternative pathways achieve the net transfer of the alkynyl fragment depending on the ligand, base, and solvent used. Subsequent reductive elimination produces the diphenylacetylene product, regenerating the Pd(0) species and completing the catalytic cycle77.
The electronic effect (factor A) of ligands on conversions was minor but notable, as highlighted by a minimal adverse effect (–0.005). An electron-rich ligand such as triphenylphosphite (T2) stabilises Pd(0) and promotes oxidative addition, producing the highest conversion of 97.55% in run 2 (5 mol%). Therefore, using a slightly electron-rich ligand T2 produced a lower conversion of 47.16% in run 1 (1 mol%) under similar conditions, indicating that although the electron-donating properties of ligands enhance stability and activity of Pd(0), it is less significant than the solvent effect and base strength. This is supported by literature highlighting that electron-rich ligands have a secondary effect in oxidative addition of the Sonogashira–Hagihara reaction compared to base strength and solvent roles.
The minimal observed effect of (+ 0.002) indicates that the steric effect/bulkiness of ligands (B) has a minimal effect on reaction performance. The significant drop in conversions from 97.55% (T2, run 2) to 69.86% (T3, run 9) is attributed to the bulkiness or steric hindrance limiting substrate access to the Pd centre. Using a bulkier ligand in run 9, under similar conditions, is the reason for the conversion drop. While a bulky ligand can improve the activity of Pd species, it has a slightly negative impact on overall reaction performance59.
The positive estimated effect (+ 0.021) shows increased catalyst loading (C) can slightly increase conversion. Increasing catalyst loading from 1 mol% (run 1) to 5 mol% (run 2) significantly increased conversion from 47.16% to 97.55%. This shows that higher Pd loading promotes the availability of Pd(0) species for oxidative addition step with minimal or catalyst deactivation. Literature reports that low catalyst loading likely deactivates the catalyst71.
Base strength (factor D) emerges as the most critical factor with the largest positive effect (+ 0.036). Strong bases such as NaOH successfully deprotonate phenylacetylene and reduce Pd(II) to Pd(0), producing the highest conversion (97.55%, run 2) compared to a weaker base such as Et3N, which produces a lower conversion (57.65%, run 8) due to a slower formation of acetylide and reduced transmetalation efficiency43.
A moderate positive estimated effect (+ 0.024) of solvent polarity (E) indicates the importance of solvent polarity in the Sonogashira–Hagihara reaction. The role of solvent polarity is shown by improved conversion from 57.01% (MeCN, run 2) to 97.55% (DMSO, run 3) under comparable conditions. Although both solvents are polar, MeCN has limited solubility of substrates and bases, and its coordinating ability allows for competition with substrates for the Pd binding sites, thereby slowing down catalytic turnover. In contrast, DMSO provides a favourable environment for substrates and base solubility, strong hydrogen bond accepting ability, stabilising charged intermediates, and Pd species. These properties collectively promoted oxidative addition, acetylide transmetalation, and overall catalytic efficiency. Similar solvent effects have been reported in the literature71.
The following trends in Fig. 10 were observed for the overall Sonogashira–Hagihara reaction reactions: Base strength (D) has the most influential factor on the reactions, solvent polarity (E) and catalyst loading (C) have positive effect on conversions, electronic effect (A) has negligible effect on reaction and steric effect/Tolman angle (B) has no significant influence on this reaction.
The main effect plot (Fig. 10a) shows that factor D has the steepest slope, followed by factors E and C, respectively. Factor A has a slight slope, and factor B has the smallest slope, indicating that it is the least significant. Factors D, E, and C have long bar lengths in the Pareto chart (Fig. 10b), indicating their respective significance on the reactions. Comparably, factors A and B have short bar lengths. In the normal probability plot (Fig. 10c), factors A and B are closer to the straight line as they are the least significant. However, factors D, E, and C are far away from the straight line because of their significant effects on these reactions.
It is important to note that the application of PBD to these cross-coupling reactions provides two main insights. First, while the influence of ligands, base, solvent, and catalyst loading in catalytic systems is well established, PBD allows a statistical comparison of these factors. As a result, this provides a workflow to systematically compare and rank factors’ effects across different reactions in the HTS context. Secondly, the PBD workflow shows efficiency by identifying significant factor effects from a minimal number of experimental runs. In contrast, traditional OFAT would require more experimental runs and fails to account for possible interactions and potential confounding effects between factors. Thus, our results highlight that even preliminary screening designs such as PBD can capture trends and guide subsequent screening designs.
The integration of HTS and sDoE in this study provided a synergistic advantage: rapid screening of multiple conditions accelerated data collection, while sDoE provides a statistical framework for analysis of collected data. Together, these approaches enabled rapid screening and the identification of significant or influential factors on reaction outcome. Although this initial PBD analysis does not intend to provide a fully optimised catalytic system, it demonstrates how outcomes from an initial screening can guide future detailed experimental designs, such as response surface methodologies (RSM) that can be used for an in-depth further exploration of factor interactions to provide potential synergistic effects and identification of true optimal systems. This proof-of-concept work demonstrates how PBD can be used as an initial or early workflow where HTS and sDoE can accelerate the discovery and development of catalytic systems.
Combining sDoE, specifically PBD, and HTS provides novel qualitative insights beyond conventional methods. Unlike traditional OFAT approaches, sDoE allows for identifying and ranking the most influential parameters on reactions using minimal experimental runs by enabling simultaneous statistical evaluation of multiple factors. While the influence of ligands, base, solvents, and catalyst loading is well established in literature, applying PBD in this study allowed for quantitative assessment that reveal how these factors act synergistically, compensatively, and antagonistically across benchmark cross-coupling reactions. For instance, in the Suzuki–Miyaura reaction, the statistical approach showed that a weaker organic base like Et3N could still improve reaction conversion in the presence of a highly polar solvent like DMSO, highlighting how polarity can compensate for a weak base. Similarly, it was revealed that electron-rich ligands positively impact oxidative addition efficiency, which is contrary to high steric hindrance, an insight not readily accessible from conventional studies. These results provide chemical significance by showing how multiple factors collectively shape catalytic performance. The novelty of integrating sDoE with HTS thus lies in its ability to accelerate the discovery of optimal reaction conditions and advance mechanistic understanding of factors in organometallic catalysis. It provides a statistical framework to guide further optimisation and rational selection of reagents.
Conclusion
In this study, a high-throughput screening (HTS) approach was combined with statistical design of experiments (sDoE), specifically Plackett–Burman design (PBD), to systematically investigate the influence of electronics and steric (Tolman cone angle) effects of ligands, catalyst loading, base strength, and solvent polarity on palladium-catalysed cross-coupling reactions. Given that the importance of these factors is well established in cross-coupling chemistry, the applications of statistical PBD were compared and ranked the effects across three benchmark coupling reactions. This enabled the identification of the most influential factors using minimal experimental runs, highlighting the practicality and efficiency of this approach compared to traditional OFAT approaches. Overall, this work demonstrates the synergistic power of combining HTS with sDoE as an efficient initial screening for the reaction development workflow. The insights gained provide a basis for future optimisation studies investigating factor interactions, catalyst design, and process development.
Data availability
Data is provided within the manuscript or supplementary information files.
Abbreviations
- sDoE:
-
Statistical Design of Experiment
- PBD:
-
Plackett–Burman design
- CCD:
-
Central composite design
- MD:
-
Mixture design
- FFD:
-
Full factorial designs
- BBD:
-
Box-Behnken design
- DSD:
-
Definitive screening design
- SFD:
-
Space-filling design
- TD:
-
Taguchi design
- OFAT:
-
One-factor-at-a-time
- HTS:
-
High-throughput screening
- C–C:
-
Carbon–Carbon coupling
- HSP:
-
Hansen Solubility
- KTP:
-
Kamlet–Taft parameters
- NP:
-
Nanoparticles
- PdNP:
-
Palladium nanoparticles
- K2PdCl4 :
-
Potassium tetrachloropalladate
- Pd(OAc)₂:
-
Palladium acetate
- PhBr:
-
Bromobenzene
- PhI:
-
Iodobenzene
- Et3N:
-
Triethylamine
- DMSO:
-
Dimethylsulfoxide
- DCM:
-
Dichloromethane
- DMF:
-
Dimethylformamide
- NaOH:
-
Sodium hydroxide
- MeCN:
-
Acetonitrile
- mmol:
-
Millimole
- µL:
-
Microlitre
- GC-FID:
-
Gas chromatography flame ionisation detection
- GC-MS:
-
Gas chromatography mass spectrometry
References
Gilman, J., Walls, L., Bandiera, L. & Menolascina, F. Statistical design of experiments for synthetic biology. ACS Synth. Biol. 10, 1–18. https://doi.org/10.1021/acssynbio.0c00385 (2021).
Beg, S., Swain, S., Rahman, M., Hasnain, M. S. & Imam, S. S. Application of Design of Experiments (DoE) in Pharmaceutical Product and Process Optimization (Elsevier Inc., 2019). https://doi.org/10.1016/B978-0-12-815799-2.00003-4.
Murray, P. M. et al. The application of design of experiments (DoE) reaction optimisation and solvent selection in the development of new synthetic chemistry. Org. Biomol. Chem. 14, 2373–2384. https://doi.org/10.1039/c5ob01892g (2016).
Taylor, C. J. et al. A brief introduction to chemical reaction optimization. Chem. Rev. 123, 3089–3126. https://doi.org/10.1021/acs.chemrev.2c00798 (2023).
Taylor, C. J. et al. Flow chemistry for process optimisation using design of experiments. J. Flow. Chem. 11, 75–86. https://doi.org/10.1007/s41981-020-00135-0 (2021).
Tsay, C., Pattison, R. C., Piana, M. R. & Baldea, M. A survey of optimal process design capabilities and practices in the chemical and petrochemical industries. Comput. Chem. Eng. 112, 180–189 (2018).
Peng, L. et al. Design of experiment techniques for the optimization of chromatographic analysis conditions: A review. Electrophoresis 43, 1882–1898. https://doi.org/10.1002/elps.202200072 (2022).
Durakovic, B. Design of experiments Application, Concepts, examples: state of the Art. Periodicals Eng. Nat. Sci. 5, 421–439. https://doi.org/10.21533/pen.v5i3.145 (2017).
Verdooren, L. R. History of the statistical design of agricultural experiments. J. Agric. Biol. Environ. Stat. 25, 457–486 (2020).
Ginocchi, M., Penthong, T., Ponci, F. & Monti, A. Statistical design of experiments for power system protection testing: A case study for distance relay performance testing. IEEE Access. 12, 27052–27072. https://doi.org/10.1109/ACCESS.2024.3367591 (2024).
Dhoot, A. S., Fernandes, G. J., Naha, A., Rathnanand, M. & Kumar, L. Design of experiments in pharmaceutical development. Pharm. Chem. J. 53, 730–735. https://doi.org/10.1007/s11094-019-02070-4 (2019).
Schlueter, A., Geyer, P. & Linking, B. I. M. Design of experiments to balance architectural and technical design factors for energy performance. Autom. Constr. 86, 33–43. https://doi.org/10.1016/j.autcon.2017.10.021 (2018).
Hossain, M. S., Rahim, N. A., Aman, M. M. & Selvaraj, J. Application of ANOVA method to study solar energy for hydrogen production. Int. J. Hydrogen Energy. 44, 14571–14579. https://doi.org/10.1016/j.ijhydene.2019.04.028 (2019).
Li, N., Shi, C., Zhang, Z., Wang, H. & Liu, Y. A review on mixture design methods for geopolymer concrete. Compos. B Eng. 178, 107490. https://doi.org/10.1016/j.compositesb.2019.107490 (2019).
Yolmeh, M. & Jafari, S. M. Applications of response surface methodology in the food industry processes. Food Bioproc Tech. 10, 413–433. https://doi.org/10.1007/s11947-016-1855-2 (2017).
Emeji, I. C. & Patel, B. Box-Behnken assisted RSM and ANN modelling for biodiesel production over titanium supported Zinc-Oxide catalyst. Energy 308, 132765. https://doi.org/10.1016/j.energy.2024.132765 (2024).
Errore, A., Jones, B., Li, W. & Nachtsheim, C. J. Using definitive screening designs to identify active first-and second-order factor effects. J. Qual. Technol. 49, 244–264. https://doi.org/10.1080/00224065.2017.11917993 (2017).
Joseph, V. R., Gu, L., Ba, S. & Myers, W. R. Space-Filling designs for robustness experiments. Technometrics 61, 24–37. https://doi.org/10.1080/00401706.2018.1451390 (2019).
Asghar, A., Raman, A. A. A. & Daud, W. M. A. W. A comparison of central composite design and Taguchi method for optimizing Fenton process. Sci. World J. 2014, 869120. https://doi.org/10.1155/2014/869120 (2014).
Aouici, H., Bouchelaghem, H., Yallese, M. A., Elbah, M. & Fnides, B. Machinability Lnvestigation in hard turning of AISI D3 cold work steel with ceramic tool using response surface methodology. Int. J. Adv. Manuf. Technol. 73, 1775–1788. https://doi.org/10.1007/s00170-014-5950-0 (2014).
Spadi, A. et al. Using a Plackett–Burman design to maximise yield of Rosemary essential oil by distillation. Ind. Crops Prod. 166, 113488. https://doi.org/10.1016/j.indcrop.2021.113488 (2021).
Eng, C., Darani, K., Abolhasan, S. & Ali, S. S. Application of Plackett Burman design for citric acid production from pretreated and untreated wheat straw. Iran. J. Chem. Eng. 27, 91–104 (2008).
Gregor, M., Grznar, P., Mozol, S. & Mozolova, L. Plackett–Burman design. Acta Simulatio. 10, 5–9 (2024).
Smith, Z. D. et al. Sandoval, Plackett–Burman experimental design to facilitate syntactic foam development. J. Appl. Polym. Sci. 133, 1–37. https://doi.org/10.1002/app.42892 (2016).
Bouziane, L., Bendebane, F., Ismail, F. & Delimi, R. Removal of zinc and cadmium from an aqueous solution using sawdust as a Low-Cost adsorbent: application of Plackett–Burman design. Desalin. Water Treat. 49, 189–199. https://doi.org/10.1080/19443994.2012.719318 (2012).
Ekpenyong, M. G., Antai, S. P., Asitok, A. D. & Ekpo, B. O. Design and response surface optimization of medium trace nutrients for glycolipopeptide biosurfactant production. Iran. Biomed. J. 21, 249–260. https://doi.org/10.18869/acadpub.ibj.21.4.249 (2017).
Koranne, A. et al. The Mizoroki–Heck reaction between in situ generated alkenes and Aryl halides: Cross-Coupling route to substituted olefins. RSC Adv. 13, 22512–22528. https://doi.org/10.1039/d3ra03533f (2023).
Takale, B. S., Kong, F. Y. & Thakore, R. R. Recent applications of Pd-Catalyzed Suzuki–Miyaura and Buchwald–Hartwig couplings in pharmaceutical process chemistry. Organics 3, 1–21. https://doi.org/10.3390/org3010001 (2022).
Yan, F., Zhang, X., Li, D., Zhu, N. & Bao, H. Recent applications of the Sonogashira reaction in the synthesis of drugs and their derivatives: A review. Appl. Organomet. Chem. 39, 1–27. https://doi.org/10.1002/aoc.7932 (2025).
Bell, N. L., Kupper, M. & Cronin, L. Design of experiments for optimization of polyoxometalate syntheses. Chem. Mater. 33, 7263–7271. https://doi.org/10.1021/acs.chemmater.1c01401 (2021).
Fernandez, A. L., Reyes, C., Prock, A. & Giering, W. P. The stereoelectronic parameters of Phosphites. The quantitative analysis of ligand effects (QALE). J. Chem. Soc. Perkin Trans. 2, 1033–1041. https://doi.org/10.1039/a909250a (2000).
Jordan, A., Hall, C. G. J., Thorp, L. R. & Sneddon, H. F. Replacement of Less-Preferred dipolar Aprotic and ethereal solvents in synthetic organic chemistry with more sustainable alternatives. Chem. Rev. 122, 6749–6794. https://doi.org/10.1021/acs.chemrev.1c00672 (2022).
Tolman, C. A. Steric effects of phosphorus ligands in organometallic chemistry and homogeneous catalysis. Chem. Rev. 77, 313–348. https://doi.org/10.1021/cr60307a002 (1977).
Johansson Seechurn, C. C. C., Kitching, M. O., Colacot, T. J. & Snieckus, V. Palladium-Catalyzed Cross-Coupling: A historical contextual perspective to the 2010 nobel prize. Angewandte Chemie - Int. Ed. 51, 5062–5085. https://doi.org/10.1002/anie.201107017 (2012).
Trzeciak, A. M. & Augustyniak, A. W. The role of palladium nanoparticles in catalytic C–C Cross-Coupling reactions. Coord. Chem. Rev. 384, 1–20. https://doi.org/10.1016/j.ccr.2019.01.008 (2019).
Martin, R. & Buchwald, S. L. Palladium-Catalyzed Suzuki – Miyaura Cross-Coupling reactions employing dialkylbiaryl phosphine ligands. Acc. Chem. Res. 41, 1461–1473. https://doi.org/10.1021/ar800036s.Palladium-Catalyzed (2008).
Barder, T. E., Walker, S. D., Martinelli, J. R. & Buchwald, S. L. Catalysts for Suzuki–Miyaura coupling processes: scope and studies of the effect of ligand structure. J. Am. Chem. Soc. 127, 4685–4696. https://doi.org/10.1021/ja042491j (2005).
Sperger, T., Sanhueza, I. A., Kalvet, I. & Schoenebeck, F. Computational studies of synthetically relevant homogeneous organometallic catalysis involving Ni, Pd, Ir, and rh: an overview of commonly employed DFT methods and mechanistic insights. Chem. Rev. 115, 9532–9586. https://doi.org/10.1021/acs.chemrev.5b00163 (2015).
Schoenebeck, F. & Houk, K. N. Ligand-Controlled regioselectivity in Palladium-Catalyzed cross coupling reactions. J. Am. Chem. Soc. 132, 2496–2497. https://doi.org/10.1021/ja9077528 (2010).
Jagtap, S. Heck Reaction—State of the Art. Catalysts 7, 267. https://doi.org/10.3390/catal7090267 (2017).
Suzuki, A. & Miyaura, N. Palladium-Catalyzed Cross-Coupling reactions of organoboron compounds. Chem. Rev. 95, 2457–2483 (1995).
Phan, N. T. S., Van Der Sluys, M. & Jones, C. W. On the nature of the active species in palladium catalyzed Mizoroki–Heck and Suzuki–Miyaura Couplings - Homogeneous or heterogeneous Catalysis, A critical review. Adv. Synth. Catal. 348, 609–679. https://doi.org/10.1002/adsc.200505473 (2006).
Ruiz-Castillo, P. & Buchwald, S. L. Applications of Palladium-Catalyzed C-N Cross-Coupling reactions. Chem. Rev. 116, 12564–12649. https://doi.org/10.1021/acs.chemrev.6b00512 (2016).
Akkoç, S. Importance of some factors on the Suzuki–Miyaura Cross-Coupling reaction. J. Chin. Chem. Soc. 68, 942–951. https://doi.org/10.1002/jccs.202000351 (2021).
Williams, D. B. G. & Lawton, M. Drying of organic solvents: quantitative evaluation of the efficiency of several desiccants. J. Org. Chem. 75, 8351–8354. https://doi.org/10.1021/jo101589h (2010).
Sherwood, J., Clark, J. H., Fairlamb, I. J. S. & Slattery, J. M. Solvent effects in palladium catalysed Cross-Coupling reactions. Green Chem. 21, 2164–2213. https://doi.org/10.1039/c9gc00617f (2019).
Shaughnessy, K. H. Hydrophilic ligands and their application in Aqueous-Phase Metal-Catalyzed reactions. Chem. Rev. 109, 643–710. https://doi.org/10.1021/cr800403r (2009).
Collins, K. D. & Glorius, F. A robustness screen for the rapid assessment of chemical reactions. Nat. Chem. 5, 597–601. https://doi.org/10.1038/nchem.1669 (2013).
Dayana Priyadharshini, S. & Bakthavatsalam, A. K. Optimization of phenol degradation by the microalga chlorella pyrenoidosa using Plackett–Burman design and response surface methodology. Bioresour Technol. 207, 150–156. https://doi.org/10.1016/j.biortech.2016.01.138 (2016).
Djenouhat, M., Bendebane, F., Bahloul, L., Samar, M. E. H. & Ismail, F. Optimization of methylene blue removal by stable emulsified liquid membrane using Plackett–Burman and Box–Behnken designs of experiments. R Soc. Open. Sci. 5, 171220. https://doi.org/10.1098/rsos.171220 (2018).
Bouasla, C. Optimization of electrochemical oxidation for the degradation of acid yellow 99 via sulfate and hydroxyl radicals activation: A study using Plackett–Burman and Box–Behnken designs. J. Water Process. Eng. 68, 106362. https://doi.org/10.1016/j.jwpe.2024.106362 (2024).
Habache, N., Bechiri, O., Djaghout, I., Djenouhet, M., Optimizing Orange, G. & Modelling and Removal by Heat-Activated persulfate using Two-Step statistical strategies: Plackett–Burman and Box–Behnken designs. Desalin. Water Treat. 244, 291–301. https://doi.org/10.5004/dwt.2021.27904 (2021).
Boylan, G. L. & Cho, B. R. The normal probability plot as a tool for Understanding data: A shape analysis from the perspective of Skewness, Kurtosis, and variability. Qual. Reliab. Eng. Int. 28, 249–264. https://doi.org/10.1002/qre.1241 (2012).
Chung, J. H. & Bin Lim, Y. A modified LGB method for detecting significant effects based on a Half-Normal probability plot. J. Korean Stat. Soc. 48, 568–577. https://doi.org/10.1016/j.jkss.2019.01.002 (2019).
Amatore, C. & Jutand, A. Anionic Pd(0) and Pd(II) intermediates in Palladium-Catalyzed heck and Cross-Coupling reactions. Acc. Chem. Res. 33, 314–321. https://doi.org/10.1021/ar980063a (2000).
Biffis, A., Centomo, P., Del Zotto, A. & Zecca, M. Pd metal catalysts for Cross-Couplings and related reactions in the 21st century. Crit. Rev. Chem. Rev. 118, 2249–2295. https://doi.org/10.1021/acs.chemrev.7b00443 (2018).
Beletskaya, I. P. & Cheprakov, A. V. Heck reaction as a sharpening stone of palladium catalysis. Chem. Rev. 100, 3009–3066. https://doi.org/10.1021/cr9903048 (2000).
Trzeciak, A. M. & Ziółkowski, J. J. Structural and mechanistic studies of Pd-Catalyzed C-C bond formation: the case of carbonylation and heck reaction. Coord. Chem. Rev. 249, 2308–2322. https://doi.org/10.1016/j.ccr.2005.02.001 (2005).
Littke, A. F. & Fu, G. C. Palladium-Catalyzed coupling reactions of Aryl chlorides. Angewandte Chemie - Int. Ed. 41, 4176–4211. https://doi.org/10.1002/1521-3773(20021115)41:22%3C4176::AID-ANIE4176%3E3.0.CO;2-U (2002).
Yin, L. & Liebscher, J. Carbon-Carbon coupling reactions catalyzed by heterogeneous palladium catalysts. Chem. Rev. 107, 133–173. https://doi.org/10.1021/cr0505674 (2007).
Amatore, C. & Jutand, A. Mechanistic and kinetic studies of palladium catalytic systems. J. Organomet. Chem. 576, 254–278. https://doi.org/10.1016/S0022-328X(98)01063-8 (1999).
Hajipour, A. R., Sadeghi, A. R. & Khorsandi, Z. Pd nanoparticles immobilized on magnetic Chitosan as a novel reusable catalyst for green heck and Suzuki Cross-Coupling reaction: in water at room temperature. Appl. Organomet. Chem. 32, 1–11. https://doi.org/10.1002/aoc.4112 (2018).
Cacchi, S. & Fabrizi, G. Synthesis and functionalization of Indoles through Palladium-Catalyzed reactions. Chem. Rev. 105, 2873–2920. https://doi.org/10.1021/cr040639b (2005).
Dounay, A. B. & Overman, L. E. The asymmetric intramolecular heck reaction in natural product total synthesis. Chem. Rev. 103, 2945–2964. https://doi.org/10.1002/9780470716076.ch16 (2003).
Farina, V. High-Turnover palladium catalysts in Cross-Coupling and heck chemistry: A critical overview. Adv. Synth. Catal. 346, 1553–1582. https://doi.org/10.1002/adsc.200404178 (2004).
D’Alterio, M. C. et al. Mechanistic aspects of the Palladium-Catalyzed Suzuki–Miyaura Cross-Coupling reaction. Chem.---Eur. J. 27, 13481–13493. https://doi.org/10.1002/chem.202101880 (2021).
Lennox, A. J. J. & Lloyd-Jones, G. C. Selection of Boron reagents for Suzuki–Miyaura coupling. Chem. Soc. Rev. 43, 412–443. https://doi.org/10.1039/c3cs60197h (2014).
Bedford, R. B., Cazin, C. S. J. & Holder, D. The development of palladium catalysts for C-C and cheteroatom bond forming reactions of Aryl chloride substrates. Coord. Chem. Rev. 248, 2283–2321. https://doi.org/10.1016/j.ccr.2004.06.012 (2004).
Lennox, A. J. J. & Lloyd-Jones, G. C. Transmetalation in the Suzuki–Miyaura coupling: the fork in the trail. Angewandte Chemie - Int. Ed. 52, 7362–7370. https://doi.org/10.1002/anie.201301737 (2013).
Fantoni, T. et al. Mastering Palladium-Catalyzed Cross-Coupling reactions: the critical role of in situ Pre-Catalyst reduction design. Org. Chem. Front. 12, 1982–1991. https://doi.org/10.1039/d4qo02335h (2025).
Chinchilla, R. & Nájera, C. The Sonogashira reaction: A booming methodology in synthetic organic chemistry. Chem. Rev. 107, 874–922. https://doi.org/10.1021/cr050992x (2007).
García-Melchor, M., Pacheco, M. C., Nájera, C., Lledós, A. & Ujaque, G. Mechanistic exploration of the Pd-Catalyzed Copper-Free Sonogashira reaction. ACS Catal. 2, 135–144. https://doi.org/10.1021/cs200526x (2012).
Gazvoda, M., Virant, M., Pinter, B. & Košmrlj, J. Mechanism of Copper-Free Sonogashira reaction operates through Palladium-Palladium transmetallation. Nat. Commun. 9, 1–9. https://doi.org/10.1038/s41467-018-07081-5 (2018).
Mohajer, F., Heravi, M. M., Zadsirjan, V. & Poormohammad, N. Copper-Free Sonogashira Cross-Coupling reactions: an overview. RSC Adv. 11, 6885–6925. https://doi.org/10.1039/d0ra10575a (2021).
Martek, B. A., Gazvoda, M., Urankar, D. & Košmrlj, J. Designing homogeneous Copper-Free Sonogashira reaction through a Prism of Pd-Pd transmetalation. Org. Lett. 22, 4938–4943. https://doi.org/10.1021/acs.orglett.0c01227 (2020).
Ivančič, A., Košmrlj, J. & Gazvoda, M. Elucidating the reaction mechanism of a Palladium-Palladium dual catalytic process through kinetic studies of proposed elementary steps. Commun. Chem. 6, 1–14. https://doi.org/10.1038/s42004-023-00849-x (2023).
Palladino, C. et al. New mechanistic insights into the Copper-Free Heck-Cassar-Sonogashira Cross-Coupling reaction. ACS Catal. 13, 12048–12061. https://doi.org/10.1021/acscatal.3c02787 (2023).
Acknowledgements
We thank Shimadzu South Africa (Pty) for their analytical instruments. This work was supported by the National Research Foundation (NRF) of South Africa and the University of Johannesburg. We acknowledge Dr Kariska Potgieter for mentorship.
Funding
This research was supported by the National Research Foundation (NRF) of South Africa (Grant number BCSA210302588432) and the University of Johannesburg.
Author information
Authors and Affiliations
Contributions
Professor Reinout Meijboom conceived the project and designed the experiments. Fulufhelo Radzilani performed experiments and analysed the data. Dr Orpah Zinyemba contributed to the manuscript preparation. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Radzilani, F., Zinyemba, O. & Meijboom, R. Application of statistical design of experiment to identify key factors in cross coupling reactions. Sci Rep 15, 42800 (2025). https://doi.org/10.1038/s41598-025-27005-w
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-27005-w