Introduction

Strength training plays a critical role in various sports; however, the biomechanical mechanisms underlying upper-limb strength training remain insufficiently quantified, often leading to a lack of individualized load prescription. This is particularly evident in lower-limb-dominant sports, where upper-body strength development is frequently overlooked, ultimately impairing overall athletic performance and muscular balance1. The push-up, a widely adopted upper-body exercise valued for its practicality and minimal equipment requirements2,3,4, is effective not only for improving upper-limb strength5 and local muscular endurance6 but also commonly incorporated into physical fitness assessments7. By modifying hand and foot positions to perform different push-up variations, this exercise can enhance upper-body muscle activation while reducing joint stress, making it a efficient option for home-based training8,9,10. Nevertheless, predictive models for estimating ground reaction forces under different inclination angles and movement tempos are still underdeveloped, limiting the precision of intensity modulation in practice. This study aims to develop a biomechanics-based predictive model to address this gap and provide a theoretical foundation for individualized load quantification in push-up training.

Velocity-Based Training (VBT) is grounded in the well-established physiological principle that movement velocity is closely related to the percentage of one’s one-repetition maximum (%1RM), providing an objective basis for regulating training intensity in real time11,12. This approach allows coaches and athletes to monitor neuromuscular performance and adjust loads dynamically based on daily readiness13,14,15. The present study is conceptually situated within the VBT framework, with the aim of extending its application to inclined push-up exercises—a common yet understudied closed-chain upper-body movement. While prior research has examined the effects of movement speed on push-up performance16,17, the load-velocity profile and force characteristics of push-ups performed under different inclination angles and tempos remain poorly quantified. This gap is particularly relevant given the growing use of push-ups in both athletic and recreational training settings. By investigating the relationship between kinematic variables (inclination and tempo) and kinetic outputs (vertical ground reaction forces), this study seeks to establish a predictive model that can support evidence-based application of VBT principles in upper-limb training. The findings are expected to contribute to more individualized and precise programming of push-up exercises, thereby enhancing both performance outcomes and training safety.

The simplicity of the push-up technique makes it suitable for both beginners and experienced trainers. It is frequently incorporated into dynamic warm-ups and bodyweight training routines, and is widely used in upper limb rehabilitation, especially for patients with shoulder injuries17. Additionally, push-ups are an effective method for assessing upper limb muscle strength and endurance18. The primary resistance in standard push-ups comes from the individual’s body mass19,20,21, making them a valuable strength-building exercise that can easily fit into daily workout routines17,18.

For home-based training, adjusting push-up positions to modify force output offers a practical and feasible approach. In the early stages of training, frequent 1RM upper limb strength tests can induce physical and mental fatigue. To address this, our study introduces a predictive model for estimating force during elevated push-ups, which broadens the application of upper limb strength assessments. Incorporating this digital testing method into training not only alleviates the psychological fatigue associated with repeated testing but also provides a clearer understanding of performance levels. This model has significant practical value for both beginners and experienced trainers in designing and executing personalized training programs.

This study applies the load-velocity relationship—a foundational concept in strength training—to push-up exercises under various inclines and tempos. While well-established for free-weight exercises, this relationship remains under-explored in closed-chain movements like push-ups. We use movement velocity to predict external load (measured as vertical ground reaction force), extending velocity-based training principles to bodyweight exercise. The goal is to develop a quantitative framework for prescribing and monitoring push-up intensity based on individual biomechanics.

Methods

Participants

Sample size was determined a priori using G’Power 3.1. A repeated-measures ANOVA (within factors) with an assumed medium effect size (f = 0.25), α = 0.05, and power = 0.95 indicated a required sample of 22 participants. Accounting for 20% potential attrition, 27 male undergraduates from Beijing Sport University were recruited. Inclusion criteria included: (1) ≥ 1 year of sports training; (2) no recent injuries; (3) proficiency in push-ups per Bushman22. Exclusion criteria were: (1) inadequate sports experience; (2) recent injuries; (3) inability to perform proper push-ups. All 27 participants completed the study (Table 1).

Table 1 Participant demographics.
Full size table

Human ethics and consent to participate declarations

This study adhered to the Declaration of Helsinki and was approved by the Institutional Review Board of the Beijing Sport University Ethics Committee (approval number: 2022002H). The research design met ethical standards, and participants were fully informed about the study’s purpose, benefits, risks, and their rights before providing written consent. They were also informed of their right to withdraw from the study at any time without affecting their future services, and any data from withdrawn participants would be excluded from the analysis.

Experimental design

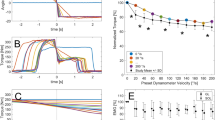
After familiarization with the experimental protocol, all 27 participants completed push-up trials under three elevation conditions in randomized order: (1) 10° incline (Fig. 1A), (2) 20° incline (Fig. 1B), and (3) 30° incline (Fig. 1C). The inclination angles were precisely set and verified using a digital inclinometer prior to each testing session. The platform height was individually adjusted according to each participant’s lower limb length to ensure biomechanical consistency and angle accuracy across participants.

Fig. 1
figure 1

Different inclination angle push-up exercises. (A) 10°angle, (B) 20°angle, (C) 30°angle.

Full size image

These angles were selected to systematically examine the effect of progressively increasing intensity on muscle activation and performance. The 10° condition served as a mild elevation commonly used in rehabilitative and introductory strength training, while the 20° and 30° inclines introduced graduated challenges to the upper body musculature. All participants wore standardized compression clothing to minimize clothing-related measurement variance and facilitate consistent motion capture.

Each condition was performed in a separate session with a 48-h interval between tests to minimize fatigue. Within each session, participants performed push-ups at three different tempos (7 push-ups/10 s, 5/10 s, and 4/10 s), guided by a metronome16,23,24,25. Vertical ground reaction forces were recorded using a Kistler force platform (Model 9281EA, Winterthur, Switzerland), and movement velocity was recorded with a GymAware linear position transducer (PowerTool, Kinetic Performance Technology, Australia). A 15-min rest period was enforced between sets. Prior to testing, anthropometric data including height and weight were measured. Warm-up consisted of joint mobilization, dynamic stretching, activation exercises, and light jogging, followed by 5 min of rest.

Intervention

Feet-elevation height calculation and angle verification

With the participant standing in anatomical position, we measured: c = torso length (acromion to greater trochanter, cm), a = arm length (acromion to wrist center with the elbow fully extended, cm), and d = force-platform height (floor to top plate, cm). For a target incline angle θ (relative to the horizontal, defined by the line from the acromion to the greater trochanter when the body is held rigid in a plank), the required feet-elevation height e was computed as:

$$e=(c\times sin\theta )+a+d$$

We verified θ before each trial using a digital angle finder (DL7306, Deli, Ningbo, China; accuracy ± 0.05°) placed along the acromion–greater-trochanter line while the participant held the start position. Figure 2 shows the geometry and includes only the variables a, c, d, e, θ.

Fig. 2
figure 2

Diagram of feet-elevation height. a, arm length (acromion to wrist center with the elbow extended); c, torso length (acromion to greater trochanter) in standing; d, force-platform height; e, required feet-elevation height; θ, target incline angle.

Full size image

Definition of average concentric velocity (X₂) and tempo enforcement

A metronome enforced three tempos: 7 reps/10 s (1.43 s/rep), 5/10 s (2.00 s/rep), and 4/10 s (2.50 s/rep). Participants performed symmetrical repetitions (eccentric and concentric each occupying half of the rep duration) without intentional pauses. The linear position transducer provided rep-level velocity. For each repetition, concentric velocity was computed over the positive-displacement phase (from the sign change of velocity to zero velocity at the top). X₂ was defined as the mean concentric velocity across valid repetitions within each angle-by-tempo condition. Force- and velocity–time series were time-synchronized.

Push-up force value testing

Participants started in a standard push-up position, lifting their bodies in a straight line and bending their arms until their foreheads touched a yoga block. Before testing, the appropriate angle for each participant was calibrated based on group-specific requirements. Attempts where the body was not straight or the forehead did not touch the yoga block were invalid. Force values at different incline angles were recorded using a Kistler force platform (Model 9281EA) at 1000 Hz, low-pass filtered at 10 Hz, with peak-picking for maximum and minimum vertical forces.

Data analysis

Data were analyzed using SPSS (Version 26.0, IBM Corp., USA) and are presented as mean ± standard deviation (M ± SD). For within-subject factors angle (10°, 20°, 30°) and rhythm (fast, medium, slow), we used a two-way repeated-measures ANOVA (α = 0.05); Shapiro–Wilk tested residual normality and Mauchly’s test assessed sphericity, with Greenhouse–Geisser corrections as needed and Bonferroni post hoc tests. Effect sizes are partial η2.

Associations were examined with Pearson correlations. Multiple linear regression predicted vertical ground reaction force from body mass, angle, and average concentric velocity (X₂); standard assumptions were checked (linearity, independence, homoscedasticity, multicollinearity, influence). Agreement between measured and predicted forces was summarized using Bland–Altman mean bias and 95% limits of agreement; paired t-tests were not used for validation.

Results

Variation characteristics among angle, rhythm, body mass, and force values

A multivariate linear regression analysis was conducted to evaluate the influence of body mass, incline angle, and execution rhythm on vertical ground reaction force values. Prior to modeling, key regression assumptions were thoroughly examined. The linearity between each independent variable and the outcome was assessed using partial regression plots, while the independence of residuals was verified with the Durbin-Watson test (d ≈ 2.0). Homoscedasticity was confirmed by visual inspection of standardized residual versus predicted value plots.

Multicollinearity was evaluated using variance inflation factors (VIFs), with all predictors yielding VIF values below 5, indicating absence of multicollinearity. Outliers and influential cases were examined through studentized residuals (all < 3), leverage values (all < 0.2), and Cook’s distance (all < 1). Normality of the residuals was confirmed visually via a normal P-P plot and formally with the Shapiro–Wilk test (p > 0.05).

All three predictors significantly contributed to the model (p < 0.05). Detailed regression equations and coefficients are reported in Table 2. Agreement between measured and predicted forces is summarized in Table 3. Mean biases were small across conditions (− 0.02 to 16.66 N), with 95% limits of agreement ranging approximately from ± 104 to ± 206 N depending on condition. To avoid back-substitution bias, we did not use paired t-tests for validation.

Table 2 Relationships between various factors and force values.
Full size table
Table 3 Agreement between measured and predicted forces across conditions(mean bias and 95% limits of agreement).
Full size table

Significant correlations between movement rhythm and force values were observed across all incline angles, with the strength and direction of correlations structured as follows:

10° Incline: Fast rhythm showed a moderate correlation with maximum force values (r = 0.58, p = 0.005), while medium rhythm exhibited a strong correlation (r = 0.69, p < 0.001).

20° Incline: All rhythms significantly influenced maximum force values (p < 0.05). Fast rhythm demonstrated a moderate correlation (r = 0.36, p = 0.006), while both medium (r = 0.58, p = 0.007) and slow rhythms (r = 0.74, p < 0.001) showed strong correlations. Minimum force values were also strongly correlated with medium (r = 0.61, p < 0.001) and slow rhythms (r = 0.75, p < 0.001).

30° Incline: Both fast (r = 0.55, p = 0.009) and slow rhythms (r = 0.54, p = 0.010) significantly predicted maximum force values with moderate to strong correlations.

Variations between angle and force values

A two-way repeated-measures ANOVA (angle × rhythm), with Greenhouse–Geisser corrections where necessary, showed a significant main effect of angle on maximum force (F = 5.943, p = 0.003). When collapsing across angles, the main effect of rhythm on maximum force was not significant (p > 0.05), and the angle × rhythm interaction was not significant. Overall, maximum force decreased as the incline angle increased, indicating an inverse angle–force relationship. Bonferroni-adjusted pairwise comparisons for the angle main effect (ignoring rhythm) yielded non-weighted marginal means of 666.72 N at 10°, 663.10 N at 20°, and 595.61 N at 30° (Table 5). Accordingly, the maximum force at 10° exceeded 30° by 71.12 N (95% CI: 25.28–116.96, p = 0.03), and 20° exceeded 30° by 67.50 N (95% CI: 21.66–113.34, p = 0.04), whereas 10° vs 20° was not significant (Table 4).

Table 4 Bonferroni-adjusted pairwise comparisons for the main effect of angle on maximum force.
Full size table

Pairwise comparison analysis of main effects of incline angles—conducted to evaluate the independent impact of inclination on force output—revealed non-weighted marginal means of 666.72 at 10°, 663.10 at 20°, and 595.61 at 30°. These results clarify the fundamental force-angle relationship without the influence of rhythm. Ignoring rhythm, maximum force value at 10° was significantly higher than at 30° by 71.12 (95% CI 25.28–116.96, p = 0.03), and at 20° was higher than at 30° by 67.50 (95% CI 21.66–113.34, p = 0.04) (Table 5). These findings highlight a consistent decline in force production with increasing inclination, supporting the presence of a significant inverse force-angle relationship.

Table 5 Estimates of maximum force values at different tilt angles.
Full size table

Variation characteristics between rhythm and force values

The study found no significant main effects of rhythm on either minimum or maximum force values (F = 0.813, p = 0.445; F = 0.253, p = 0.777), indicating that, overall, rhythm variations did not exert a systematic influence on force outputs. However, post hoc correlation analyses revealed more nuanced, angle-specific relationships. Pearson correlation analysis showed no general significant correlations across all conditions, but several rhythm- and angle-dependent associations were identified. These included a moderate positive correlation between fast rhythm and maximum force specifically at 20° (r = 0.50, p < 0.05), and strong positive correlations for medium-tempo rhythm with maximum force at 10°, 20°, and 30° (r = 0.63, 0.60, 0.80 respectively; p < 0.01). Slow rhythm demonstrated a moderate positive correlation at 10° (r = 0.49, p < 0.05) and very strong correlations at 20° and 30° (r = 0.63, p < 0.01), alongside a moderate negative correlation with minimum force at 20° (r = − 0.50, p < 0.05) (Table 6). When collapsing across angles, the main effect of tempo on maximum or minimum force was not significant; however, angle-specific associations emerged in correlation analyses. This pattern indicates that the influence of tempo is angle-dependent rather than a uniform main effect across all angles.

Table 6 Relationships between rhythms and force values.
Full size table

Discussion

Biomechanical Impact of Incline Angles on Push-Up Force Output

Adjustments in hand or leg positions can lead to various biomechanical changes, affecting muscle recruitment, activation, and joint forces26,27,28. Our study also found that maximum force values decrease with increasing angles for different rhythms, showing an inverse relationship. Notably, for push-ups at a 20° incline angle, force values significantly decrease across all three rhythms. At a 10° incline, force values for fast push-ups show a clear upward trend. However, when performing 20° incline push-ups at a moderate rhythm, force values rise and exceed those of fast rhythms. After accounting for rhythm (i.e., marginal means), maximum force at 10° exceeded 30° by 71.12 N (95% CI 25.28–116.96, p = 0.03) and 20° exceeded 30° by 67.50 N (95% CI 21.66–113.34, p = 0.04) (Tables 4–5). Previous studies have shown that force values in conventional push-ups28 and knee-flexion push-ups29 differ slightly from earlier results, ranging from about 64% to 66% and 49% to 53% of body mass, respectively. Changes in hand positions result in force values ranging from 52.9% to 72.9% of body mass. Further exploration revealed that push-ups with hands elevated to 60.96 cm produce vertical forces as low as 41% of body mass, whereas elevating the feet to the same height can increase vertical forces up to 74% of body mass30.

Our findings can be explained through biomechanical principles. At 10° or 20° inclines, the center of mass shifts horizontally relative to the support surface (hands), directly affecting the moment arm lengths at the shoulder and elbow joints31. The moment arm is a key factor in torque production; a longer moment arm can generate greater torque with the same muscle force output, thereby enhancing the force exerted by the muscles around the joints32,33,34. At a 20° incline, the moment arm lengths at the shoulder and elbow reach a balance, allowing the upper limb muscles (such as the pectoralis major, anterior deltoid, and triceps brachii) to work at an optimal mechanical advantage35. This optimal positioning not only maximizes force output but also reduces joint shear forces, thereby lowering the risk of injury36. Furthermore, the core muscles are more effectively engaged to stabilize the body at this angle, resulting in more direct and efficient force transmission37,38.

When the incline angle increases to 30° or higher, although the center of mass continues to move forward and the moment arm length increases, the shear forces at the shoulder joint significantly increase24. This additional stress requires the shoulder muscles to contribute more to joint stabilization, reducing the overall efficiency of force output39. Therefore, a 20° incline provides an ideal balance, maximizing force output while maintaining joint stability and safety35,36,40.

In our study, participants maintained a standardized hand position with shoulder-width spacing and kept the body in a straight line from head to toe throughout the movement. Hand position was individually adjusted to ensure consistency, as it plays a role as critical as inclination angle in determining exercise intensity and biomechanical output30. These observations align with the predictive model proposed in our study, which integrates body posture, joint kinematics, and timing parameters to estimate force output under various configurations.

Prior work has reported that modifying limb positioning can increase push-up loading by approximately 33%37. Our findings are directionally consistent with this evidence, although quantifying percentage increases was not the aim of the present study. Moore et al. reported that integrating standard postures, knee-flexed push-ups, and elevated-hand or elevated-foot variations into training regimens significantly enhances ground reaction forces—particularly in feet-elevated push-ups compared to other modalities38. This reinforces the importance of posture and limb placement, factors that our model systematically incorporates to improve prediction accuracy concerning force output and joint loading.

Thus, while hand and foot adjustments are often overlooked in conventional practice, their biomechanical effects are captured and quantifiable through our model, enhancing its applicability and explanatory power.

Influence of push-up rhythm on force generation

The choice of rhythm in push-up execution significantly influences performance, as excessively fast or slow rhythms may compromise technique or induce premature fatigue, thereby reducing the number of repetitions performed24,39,40. Numerous training protocols—with or without prescribed rhythm and time constraints—have been employed in push-up assessments41,42,43,44,45. This study identified a moderate to strong positive correlation between medium-to-fast rhythms and maximum force across various angles, underscoring that movement rhythm substantially affects ground reaction force. Efficient shifting between eccentric and concentric muscle contractions optimizes the stretch–shortening cycle (SSC), which facilitates elastic energy storage and release, thereby augmenting force production41. Conversely, overly rapid rhythms may curtail the efficacy of the SSC due to inadequate time for energy storage, while very slow rhythms can diminish force output as a result of reduced dynamic muscle activation.

The interplay between inclination angle, rhythm, and force further complicates this relationship. At a 10° incline, faster rhythms appear to enhance force output, likely owing to the elasticity and brief tension periods inherent in dynamic contractions. At 20°, a moderate rhythm proves most beneficial, balancing favorable joint moments with sufficient SSC utilization. At steeper inclines (e.g., 30°), both fast and slow rhythms correlate with decreased force, likely due to increased shoulder shear forces and compromised mechanical advantage.

These findings directly inform practical training applications. For instance, incorporating feet-elevated push-ups—which elicit higher ground reaction forces—into structured programs may maximize strength development44,45,46,47,48. As push-up variations continue to proliferate in fitness contexts49,50, it becomes possible to modulate external loading according to individual athlete mass and skill level51,52,53. Lighter individuals may use additional load to achieve comparable intensity to heavier athletes, who may instead use technique modifications to reduce load.

Notably, the predictive model introduced in this study offers a practical tool for estimating force output under various conditions, which can help customize push-up intensity for home-based or team training. However, the model has limitations: it does not fully account for inter-individual variability in biomechanics, muscle composition, or neuromuscular efficiency. Moreover, its accuracy may diminish under extreme angles or highly irregular rhythms. Future iterations could benefit from incorporating real-time biomechanical feedback or personal performance data.

Ultimately, this research provides a foundational model for force estimation in standard and modified push-ups, facilitating the design of individualized training programs and supporting load selection in group settings to improve athletic performance.

Conclusion

Across 10°, 20°, and 30° inclines and three tempos, the regression model integrating body mass, angle, and average concentric velocity provided moderate predictive performance with acceptable agreement between predicted and measured vertical ground reaction forces (Bland–Altman mean bias − 0.02 to 16.66 N; 95% limits of agreement ≈ ± 104–206 N). For minimum force, models at 20° performed most reliably under medium and slow tempos. Because body mass was a positive predictor across angles, it should be incorporated when prescribing push-up intensity.

These findings support condition-specific use of the model to program and monitor body-weight push-ups within the tested ranges of angles and tempos. In practice, coaches may adjust angle and tempo alongside body mass to achieve targeted force demands.

Limitations and future directions

This study was conducted with a homogeneous sample of male students from a sports university under controlled laboratory conditions with predefined tempos, and it did not explicitly model individual biomechanical differences such as limb segment lengths, muscle insertion geometry, or neuromuscular efficiency. These features limit external validity and may influence prediction accuracy when the model is applied beyond the tested context.

Future research should prioritize external validation and, where necessary, recalibration in women, competitive athletes, and tactical populations, as well as in field settings that introduce greater ecological variability. Incorporating anthropometric and biomechanical covariates would enable more personalized predictions and would allow assessment of model transportability across different body mass strata. It is also important to extend analyses to additional push-up variants, including decline push-ups, weighted push-ups, and unilateral push-ups, and to broader tempo schemes, and to report fold level performance metrics when k fold cross validation is used to document generalization.

Finally, translation into practice will benefit from the development and evaluation of sensor based real time prescription workflows that suggest angle and tempo to achieve a target force. These workflows should be tested in supervised, remote, and home environments and benchmarked against standard programming. These steps would help advance the framework into a more generalizable, individualized, and deployment ready tool for upper limb strength prescription using body mass exercise.