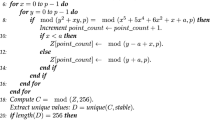An optimized substitution box generator based on cubic pell curves and its application in image encryption

Abstract

In today’s digital landscape, safeguarding confidential data from cyber threats and unauthorized breaches is more crucial than ever. A key component in modern cryptographic systems is the substitution box (S-box), which ensures data security through complex transformations. Designing S-boxes with high nonlinearity and computation efficiency is still challenging. In this paper, we propose a novel S-box generator based on cubic Pell curves. The key idea of our generator is to utilize the randomness of the points over the cubic Pell curves by using their binary strings. The optimized S-boxes are obtained by performing swapping operations on initial S-boxes that ensure high nonlinearity. Cryptographic evaluations including nonlinearity (NL), strict avalanche criterion (SAC), bit independence criterion (BIC), differential approximation probability (DAP), linear approximation probability (LAP) and algebraic complexity (AC) demonstrate the strength of our method. The proposed S-boxes achieve optimal nonlinearity (108), outperform existing schemes in speed and security, and pass NIST randomness tests. Image encryption results demonstrate the robustness of the generated S-boxes against statistical attacks, further validating their cryptographic strength.

Introduction

Researchers have explored multiple strategies to develop highly secure S-boxes for cryptographic applications. As a fundamental element in block cipher encryption and decryption, the substitution box (S-box) plays a vital role in establishing confusion between the secret key and ciphertext. S-boxes generally fall into two categories: static and dynamic. While static S-boxes maintain a fixed structure, dynamic S-boxes can adapt in size, offering greater resistance against subkey extraction and data analysis attacks. Due to this flexibility, dynamic S-boxes are often considered more effective in strengthening cryptographic security¹. Several studies have introduced S-box constructions based on elliptic curve cryptography (ECC), highlighting their potential in modern encryption systems. Both dynamic and optimized S-box generation techniques play a crucial role in enhancing the security and efficiency of cryptographic protocols.

Elliptic Curve Cryptography (ECC) is currently the most widely used public key cryptographic system. However, the cubic Pell curve (CPC) cryptosystem provides a more efficient alternative with higher performance. The cubic Pell curves offer several unique advantages over Elliptic curves in the construction of substitution boxes (S-boxes) for cryptographic applications. These advantages stem from their distinct algebraic properties, computational efficiency, and strong security features. The cubic Pell curves are defined by the formula $\mathscr {x}^3 + \alpha \mathscr {y}^3 + \alpha ^2\mathscr {z}^3 - 3\alpha \mathscr {x}\mathscr {y}\mathscr {z} \equiv 1 \pmod {p}$, which results in a larger group order compared to elliptic curves for the same prime field. This property enables cubic Pell curves to generate more set of points, thereby offering greater randomness and variation for the construction of the S-boxes. Despite their larger group order, arithmetic operations on cubic Pell curves such as point addition law are computationally comparable to those on elliptic curves. This ensures efficient S-box generation without compromising performance. The deterministic nature of point generation on cubic Pell curves reduces computational overhead compared to the probabilistic methods often used in some elliptic curve based S-box constructions. The points on cubic Pell curves exhibit strong pseudorandom behavior due to the curve nonlinear structure. The complexity of solving the Discrete Logarithm Problem in CPC is at least as challenging as in ECC, assuming the group orders of PEC and ECC are comparable. Unlike ECC, which is based on the algebraic properties of elliptic curve point groups, CPC cryptography operates on a different class of curves derived from the solutions of a cubic Pell equation². The cubic Pell curves offer flexibility in parameter selection, such as the non-cubic residue $\alpha$ and prime p enabling dynamic S-box generation designed to meet specific security requirements. The cubic Pell curve cryptosystem is proposed to work on a higher order but with comparable computational complexity compared to well known elliptic curve cryptosystems. Recently³, presented a new public key cryptosystem founded on the arithmetic of the cubic Pell curve $\mathcal{P}\mathcal{C}_\alpha (N): x^3 + \alpha y^3 + \alpha ^2z^3 - 3\alpha xyz = 1$ over $\mathbb {Z}/ N \mathbb {Z}$, with $N=p^rq^s$as a multi prime power integer. The security of this system is based on the difficulty of factoring composite integers and the one way trapdoor function introduced by Rabin. In this unique method, arithmetic operations are carried out on a cubic Pell curve, which is exclusively known to the sender and receiver of the message. The arithmetic operations on cubic Pell curves known as the generalized Brahmagupta product can be implemented efficiently in both hardware and software, making cubic Pell curves based S-boxes practical for real world applications. Efficiency in large scale S-box generation has also been a key research focus.

In this manuscript, we used a particular cubic Pell curve over large primes to design an S-box of good cryptographic strength with respect to elliptic curve-based S-boxes. So far, there is no S-box on the cubic Pell curve in the literature. We generate the points using arithmetic of the cubic Pell curve to construct a dynamic S-box. Both hardware and software can implement cubic Pell curve operations efficiently.

Related work

Dynamic S-box generators are developed to create S-boxes with high variability while maintaining minimal computational complexity. These generators enhance encryption performance by improving efficiency and reducing the processing overhead of encryption algorithms. Various techniques have been explored for S-box construction. Reference⁴ introduced an S-box design approach that integrates two methods. Initially, they created an S-box based on a non-permutation power function, followed by a heuristic algorithm that ensures the final S-box is bijective, mapping 8-bit inputs to 8-bit outputs. While⁵ introduced an efficient algorithm for generating random bijective S-boxes by combining chaotic maps with a composition method. This approach constructs new S-boxes through compositions of a fixed initial set, where the sequence of S-box selection is determined by chaotic sequences. Performance tests demonstrate that the resulting S-boxes exhibit strong cryptographic properties. The key advantages of this method include low computational complexity and the ability to achieve a large key space. Reference⁶ proposed an algorithm to construct an $8\times 8$ S-box by applying a fractional linear transformation over the Galois field $GF(2^8)$, designed to achieve strong cryptographic properties. Additionally⁷, proposed an algorithm that leverages a novel chaotic system for S-box generation. Other approaches incorporate mathematical structures and optimization methods. Reference⁸ introduced coset graphs and symmetric groups as foundational elements for constructing robust S-boxes. Reference⁹ presented a chaos-based S-box technique for secure image encryption. Their improved coupling quadratic map efficiently eliminates fixed and reverse fixed points, thereby strengthening resistance to cryptographic attacks. Elliptic curves have also been widely adopted in S-box construction. Reference¹⁰ formulated an approach utilizing ordered elliptic curves over a prime field, achieving a time complexity of $\mathcal {O}(p^2)$ and a space complexity of $\mathcal {O}(p)$, where p represents the prime number associated with the elliptic curve. They later proposed an S-box generation method based on Mordell elliptic curves. Reference¹¹ explored ordered isomorphic elliptic curves to develop secure S-boxes, requiring $\mathcal {O} (2^m)$ space and $\mathcal {O} (2^{m}p)$ time. Further refinement was provided by¹², who leveraged elliptic curve properties such as ordering and isomorphism to enhance cryptographic strength. Reference¹³ applied Mordell elliptic curves in their S-box design methodology. Efficiency in large-scale S-box generation has also been a key research focus. Reference¹⁴ Ibrahim and Abbas (2021) introduced the fastest technique for producing an $m \times m$ S-box using large elliptic curves (ECs). Using given EC parameters and an integer N, the approach generates 3N points on the curve through two steps: first, a nondeterministic algorithm identifies N valid points on the curve; second, 2N more points are computed via the group law operation. These points are then utilized to perform swapping on an initial S-box, resulting in the final S-box. Experimental findings demonstrate that this method can quickly generate 8$\times$8 S-boxes across prime fields of varying bit sizes, with processing times reducing as bit length grows. However, the total computation time is largely influenced by the nondeterministic first step, which increases exponentially with N. A novel S-box generator is proposed by¹⁵, based on a deterministic algorithm over elliptic curves, to generate highly dynamic and secure S-boxes with low computational cost. Experimental results demonstrate that the generator is i times faster than the fastest available S-box generator¹⁴, where $i \in [6.720, 1.3 \times 10^5]$, for generating S-boxes of an input size $2^m, m = 4, 6, 8, 10, 12, 14, 16$ over large elliptic curves. This significant improvement enables significantly higher encryption throughput compared to the state-of-the-art schemes. Reference¹⁶ proposed a new pseudo random encryption key and constructed a novel S-boxes from the hyperchaotic 4D Chen system and the Mersenne Twister. An efficient and secure color image encryption scheme by¹⁷ based on a novel chaotic structure and dynamical strong S-box are built by full chaotic maps. Reference¹⁸ proposed a $16 \times 16$ S-box based on the hyperchaotic system with high nonlinearity and high cryptographic strength. A method proposed by¹⁹ generated an $8 \times 8$ S-box based on LA ring of order 1024 that is viewed as a large class of non associative rings. The use of a non associative LA ring enhances the robustness of the S-box. Reference²⁰ proposes a new construction of substitution boxes $n \times n$ (S-boxes) using integer quaternion in order to enhance cryptographic strength. Reference²¹ designed a novel substitution box construction method using a chaotic fractional order nonlinear coupled map lattice system combined with an elementary cellular automaton. Reference²² introduced a method for designing dynamic S-boxes using an extended Two Dimensional Hyperchaotic Effect Coupled Map Lattice (2DHECML) system. The system is also used to enhance its chaotic behavior and cryptographic properties. Reference²³ proposed two S-box methods based on the continuous time Lu Chen chaotic system for image encryption, which encompass row and column rotation and zigzag transformations.

Optimization techniques have played a crucial role in improving S-box cryptographic properties, particularly in maximizing nonlinearity. Several recent studies have focused on such methods to improve their resistance and overall performance. An efficient color image encryption algorithm was proposed by²⁴ based on a two dimensional Sine Logistic Gaussian (2D-SLG) chaotic system and a multi-objective optimized S-box. The 2D-SLG system combines chaotic complexity with computational efficiency, while particle swarm optimization enhances the substitution performance with a nonlinearity of 106. This combination strengthens security without compromising encryption speed. Reference²⁵ proposed a discrete chaotic map integrated with an improved Grey Wolf Optimizer (GWO), enhanced by a novel crossover operator to improve the optimization process. Their method produced high performance S boxes with a nonlinearity value of 106, highlighting the potential of combining chaotic systems with metaheuristic optimization for cryptographic purposes. An improved cryptographic system was developed by²⁶ first employing ergodic chaotic maps to enhance the Particle Swarm Optimization (PSO) algorithm. The optimized PSO was then used to generate highly effective chaotic S-boxes, achieving an excellent nonlinearity value of 104. This approach demonstrates how chaotic systems can significantly boost the performance of both optimization algorithms and cryptographic components. Reference²⁷ presented a new hybrid chaotic function created by connecting various one dimensional maps. The map’s performance was confirmed through Lyapunov exponent and entropy analysis. Additionally, the chaotic Jaya optimization algorithm was employed to create an optimized substitution box with a nonlinearity of 104. A new method combining a discrete chaotic map (DCM) with the firefly optimization algorithm (FOA) was introduced by²⁸ to create cryptographically strong S-boxes. An initial S-box was generated using the DCM and then enhanced its nonlinearity through FOA. Their S-box achieved a nonlinearity value of 106, outperforming many other optimization based generators, though it remains below the optimal level. A method for designing robust S-boxes was introduced by²⁹ in which chaos theory was combined with the teaching learning based optimization algorithm. They claimed that their resultant S-boxes have superior cryptographic properties than known techniques. However, the most significant drawback of this technique is that the cryptographic properties of their resultant S-box was achieved the nonlinearity value of 104 which are not near to ideal values. Reference³⁰ proposed a metaheuristic approach that combines Ant Colony Optimization (ACO) with chaotic maps to construct a robust $8 \times 8$ substitution box (S-box). In this method, the initial S-box is transformed into a Traveling Salesman Problem (TSP) using an edge matrix. An optimal path, identified through ACO, directs the rotation of the intermediate S-box, resulting in a high-performance design with a nonlinearity value of 106. Reference³¹ introduced a 1D discrete chaotic map that leverages sensitivity to initial conditions and randomness in generated sequences to construct a strong S-box with a nonlinearity of 106. First, the chaotic map is iterated to generate initial S-box candidates, which then seed the population of a Cuckoo Search (CS) algorithm to further optimize cryptographic strength. Reference³² proposed a novel hybrid method using the Harris Hawks optimization algorithm (HHO) and the Booster algorithm for generating highly nonlinear S-boxes with low computational time. The (HHO) algorithm is employed in order to search in the large permutation search space to find an S-box of suitable cryptographic properties. Reference³³ presented a robust S-box design through the use of the intrinsic physical randomness of phase noise and the SHA-256 hash function. The design method significantly improves security for the S-boxes along with improved performance in nonlinearity, SAC, and BIC tests. Reference³⁴ designed a new technique for the construction of $8 \times 8$ S boxes that have selected cryptographic properties according to the ABO (African Buffalo Optimization) algorithm and a random function. Hybrid Adaptive Genetic Algorithm (HAGA)³⁵, integrates genetic algorithms with local search to construct nonlinear S-boxes possessing strong cryptographic properties. The Chaotic Opposition based Learning Initialized Hybrid Algebraic-Heuristic (COBLAH) algorithm³⁶, construct S-boxes by unifying algebraic methods with heuristic techniques using Galois field inversion, affine mapping, and genetic algorithms.

Contributions

This paper aims to present a dynamic methodology for constructing S-boxes with superior cryptographic strength. The key contributions of this work are outlined as follows:

• A novel S-box generation technique is introduced, capable of rapidly producing highly dynamic and secure S-boxes. By leveraging binary sequences obtained from points on cubic Pell curves, this approach ensures efficient encryption with minimal computational overhead.

• A comprehensive security evaluation and comparative analysis confirm the superiority of the proposed S-box generator over existing techniques^{10,11,14,15,37,38,39,40,41,42,43,44,45,46,47,48,49}.

• The proposed generator produces optimized S-boxes with higher nonlinearity than those generated by previous optimization methods^{24,25,26,27,28,29,30,31}.

• With an optimal nonlinearity score of 108, the generated S-boxes provide both high-speed encryption and strong resistance against cryptographic attacks.

• The use of these optimized S-boxes significantly strengthens the security of image encryption, enhancing protection against statistical and differential attacks.

The paper is structured as follows: Section 2 covers fundamental concepts related to cubic Pell curves. Section 3 details the design and construction of the proposed S-box generators. Section 4 presents an in-depth security analysis and comparison with conventional S-box generators. Section 5 explores the practical implementation of the proposed generator in image encryption. Finally, Section 6 concludes the study with key findings and future research directions.

Preliminaries

Definition 1

Reference³: An integer $\alpha$ is considered a cubic residue modulo p, if there exists at least one solution to the congruence equation:

$$\begin{aligned} \mathscr {x}^3 \equiv \alpha \pmod {p} \end{aligned}$$

where a prime number p . If no such solution exists, $\alpha$ is a cubic non-residue modulo p.

Definition 2

Reference³: An integer $\alpha$ is defined as a quadratic residue modulo $p^r$, if there exists at least one solution to the equation

$$\begin{aligned} \mathscr {x}^2 \equiv \alpha \pmod {p^r} \end{aligned}$$

where a prime number p and a non-negative integer r. If no such solution exists, $\alpha$ is a quadratic non-residue modulo $p^r$.

Definition 3

Reference³: Cubic Pell Discrete Logarithm Problem (CPDLP):

Given a prime number p, a non-cubic integer $\alpha$ modulo p, a point $P_1(\mathscr {x}_1, \mathscr {y}_1, \mathscr {z}_1)$, and a point $P_{\lambda }(\mathscr {x}_{\lambda }, \mathscr {y}_{\lambda }, \mathscr {z}_{\lambda })$ on the curve with the cubic pell equation $\mathscr {x}^3 + \alpha \mathscr {y}^3 + \alpha ^2\mathscr {z}^3 - 3\alpha \mathscr {x}\mathscr {y}\mathscr {z} \equiv 1 \pmod {p}$, find $\lambda$, if any, such that $P_{\lambda }=\lambda P_1$.

The Cubic Pell Discrete Logarithm Problem (CPDLP) is as challenging as the Elliptic Curve Discrete Logarithm Problem (ECDLP).

The theory of cubic Pell curves over fields

Let $\mathcal {K}$ be a field and $\alpha \in \mathcal {K}$. Consider the quotient ring $\mathcal {R}_{\alpha }= \frac{\mathcal {K}[t]}{(t^3 - \alpha )}$. It is known that $\mathcal {R}_{\alpha }$ forms a field if $\alpha$ is a cubic non-residue in $\mathcal {K}$.The expression for any element $\omega \in \mathcal {R}_{\alpha }$ can be written as $\omega = \mathscr {x} + \mathscr {y}\mathscr {t} + \mathscr {z}\mathscr {t}^2$, where $(\mathscr {x},\mathscr {y},\mathscr {z}) \in \mathcal {K}^3$. For two elements $\omega _1 = \mathscr {x}_1 + \mathscr {y}_1 \mathscr {t} + \mathscr {z}_1 \mathscr {t}^2$ and $\omega _{1} = \mathscr {x}_2 + \mathscr {y}_2 \mathscr {t} + \mathscr {z}_2 \mathscr {t}^2$ in $\mathcal {R}_{\alpha }$, their product is given by:

$$\omega _{1} \cdot \omega _{2} = \left[ \mathscr {x}_1 \mathscr {x}_2 + \alpha (\mathscr {y}_2 \mathscr {z}_1 + \mathscr {y}_1 \mathscr {z}_2)\right] + \left[ \mathscr {x}_2 \mathscr {y}_1 + \mathscr {x}_1 \mathscr {y}_2 + \alpha \mathscr {z}_1 \mathscr {z}_2\right] t + \left[ \mathscr {y}_1 \mathscr {y}_2 + \mathscr {x}_2 \mathscr {z}_1 + \mathscr {x}_1 \mathscr {z}_2\right] t^2 .$$

The norm of an element $\omega = \mathscr {x} + \mathscr {y}\mathscr {t} + \mathscr {z}\mathscr {t}^2$ is defined as²:

$$\begin{aligned} \mathcal {N}_\alpha (\omega ) = \mathscr {x}^3 + \alpha \mathscr {y}^3 + \alpha ^2 \mathscr {z}^3 - 3 \alpha \mathscr {x} \mathscr {y} \mathscr {z}. \end{aligned}$$

Now, define the set of unitary elements in $\mathcal {R}_{\alpha }$ as:

$$\mathfrak {U}_\alpha = \{\mathscr {x} + \mathscr {y}t + \mathscr {z}t^2 \in \mathcal {R}_{\alpha } \mid \mathscr {x}^3 + \alpha \mathscr {y}^3 + \alpha ^2 \mathscr {z}^3 - 3 \mathscr {x}\mathscr {y}\mathscr {z} = 1 \}.$$

This corresponds to the cubic Pell curve over $\mathcal {K}$, given by:

$$\begin{aligned} \mathcal{C}\mathcal{P}^3_\alpha (p): = \{ (\mathscr {x},\mathscr {y},\mathscr {z}) \in \mathcal {K}^3 \mid \mathscr {x}^3 + \alpha \mathscr {y}^3 + \alpha ^2 \mathscr {z}^3 - 3 \mathscr {x}\mathscr {y}\mathscr {z} = 1 \}. \end{aligned}$$

The natural product on $\mathfrak {U}_\alpha$ induces a generalized Brahmagupta product, which is defined for two points $\omega _1 = (\mathscr {x}_1, \mathscr {y}_1, \mathscr {z}_1)$ and $\omega _2 = (\mathscr {x}_2,\mathscr {y}_2, \mathscr {z}_2)$ in $\mathcal{C}\mathcal{P}^3_\alpha (p)$ as:

$$\omega _1 \oplus \omega _2 = \mathscr {x}_1 \mathscr {x}_2 + \alpha (\mathscr {y}_2 \mathscr {z}_1 + \mathscr {y}_1 \mathscr {z}_2) ,\mathscr {x}_2 \mathscr {y}_1 + \mathscr {x}_2 \mathscr {y}_1 + \alpha \mathscr {z}_1 \mathscr {z}_2 , \mathscr {y}_1 \mathscr {y}_2 + \mathscr {x}_2 \mathscr {z}_1 + \mathscr {x}_1 \mathscr {z}_2.$$

The set $(\mathcal{C}\mathcal{P}^3_\alpha (p), \oplus )$ forms a group with the identity element (1, 0, 0) . The inverse of any element $\omega = (\mathscr {x}, \mathscr {y}, \mathscr {z})$ in this group is given by:

$$\omega ^{-1} = (\mathscr {x}^2 - \alpha \mathscr {y}\mathscr {z}, \alpha \mathscr {z}^2 - \mathscr {x}\mathscr {y},\mathscr {y}^2 - \mathscr {x}\mathscr {z}).$$

Proposition 1

Reference³: Let $p^r$ represent a prime power and $\alpha \in \mathbb {Z}/ p^r \mathbb {Z}$. The set of solutions to the cubic Pell equation

$$\begin{aligned} \mathscr {x}^3 + \alpha \mathscr {y}^3 + \alpha ^2 \mathscr {z}^3 - 3 \alpha \mathscr {x} \mathscr {y} \mathscr {z} \equiv 1 \pmod {p^r}. \end{aligned}$$

is denoted by $\mathcal{C}\mathcal{P}_\alpha (p^r)$.

Lemma 1

Reference³: Let $p^r$ represent a prime power such that $p \equiv 1 \pmod 3$, with $r\ge 1$. Consider $\alpha \in \mathbb {Z}/ p^r \mathbb {Z}$ where gcd$(\alpha , p)=1$. The size of the set $\mathcal{C}\mathcal{P}_\alpha (p^r)$ is given by:

$$\left| \mathcal{C}\mathcal{P}_\alpha (p^r) \right| = {\left\{ \begin{array}{ll} (p-1)^2 p^{2(r-1)} & \\ \text {if } \alpha \text { is a cubic residue modulo} ~p,\\ (p^2+p+1) p^{2(r-1)} & \\ \text {if } \alpha~ \text {is a cube non-residue modulo}~p. \end{array}\right. }$$

The proposed S-box generator based on cubic Pell curve

This section provides a detailed description of the dynamic S-box generator we have developed, highlighting the optimization techniques used to improve its performance. Our approach employs points derived from a cubic Pell curve to determine the locations for swapping operations within the initial S-box. By utilizing a deterministic method to generate these points, we effectively reduce the computational burden, improving efficiency compared to the approach proposed by¹⁵. This offers an alternative to the optimized S-box generators outlined in Table 10. The method presented here focuses on generating S-boxes with superior nonlinearity.

To explain the process, let $\mathcal{C}\mathcal{P}_\alpha (p^r)$ denote the set of solutions to the cubic Pell curve equation:

$$\begin{aligned} \mathscr {x}^3 + \alpha \mathscr {y}^3 + \alpha ^2 \mathscr {z}^3 - 3 \alpha \mathscr {x} \mathscr {y} \mathscr {z} \equiv 1 \pmod {p^r} \end{aligned}$$

where p is a prime number, $\alpha \in \mathbb {Z}/ p^r \mathbb {Z} \backslash \{0\}$ is a non-cubic integer, and r is a positive integer. Our generator starts with the non-identity point $G_i = (\mathscr {x}_i, \mathscr {y}_i, \mathscr {z}_i)$ $\in \mathcal{C}\mathcal{P}_\alpha (p^r)$ where i is the $i^{th}$ generated point. We generate n points $2G,3G,\ldots , nG$ over $\mathcal{C}\mathcal{P}_\alpha (p^r)$ by using the addition law³. For the two points $(\mathscr {x}_1, \mathscr {y}_1,\mathscr {z}_1)$ and $(\mathscr {x}_2, \mathscr {y}_2, \mathscr {z}_2) \in \mathcal{C}\mathcal{P}_\alpha (p^r)$. The addition law in $\mathcal{C}\mathcal{P}_\alpha (p^r)$ is defined as

$$\begin{aligned} (\mathscr {x}_3,\mathscr {y}_3, \mathscr {z}_3):= (\mathscr {x}_1,\mathscr {y}_1, \mathscr {z}_1) \oplus (\mathscr {x}_2,\mathscr {y}_2, \mathscr {z}_2) \end{aligned}$$

(1)

where

$$\begin{aligned} {\mathscr {x}_3} \equiv \alpha \mathscr {y}_1 \mathscr {z}_2 +\mathscr {x}_1 \mathscr {x}_2 + \alpha \mathscr {y}_2\mathscr {z}_1 \pmod {p^r}, \end{aligned}$$

$$\begin{aligned} {\mathscr {y}_3} \equiv \mathscr {x}_1 \mathscr {y}_2 + \alpha \mathscr {z}_1 \mathscr {z}_2 + \mathscr {x}_2 \mathscr {y}_1 \pmod {p^r}, \end{aligned}$$

$$\begin{aligned} {\mathscr {z}_3} \equiv \mathscr {x}_2 \mathscr {z}_1 + \mathscr {y}_1 \mathscr {y}_2 + \mathscr {x}_1 \mathscr {z}_2 \pmod {p^r}. \end{aligned}$$

For the generated n points $2G,3G,\ldots , nG$ on the cubic Pell curve, then calculate a new point $G'_i = (\mathscr {x}'_i, \mathscr {y}'_i, \mathscr {z}'_i)$ on each coordinate point of $G_i = (\mathscr {x}_i, \mathscr {y}_i, \mathscr {z}_i)$ as:

$$\begin{aligned} {\mathscr {x}'}:= \mathscr {y}_i \oplus \mathscr {z}_i , \end{aligned}$$

$$\begin{aligned} {\mathscr {y}'}:= \mathscr {x}_i \oplus \mathscr {z}_i , \end{aligned}$$

$$\begin{aligned} {\mathscr {z}'}:= \mathscr {x}_i \oplus \mathscr {y}_i . \end{aligned}$$

where $\oplus$ denote the XoR operation, and $\mathscr {x}_i, \mathscr {y}_i$ and $\mathscr {z}_i$ are the $i^{th}$ generated points using the addition law in the $\mathcal{C}\mathcal{P}_\alpha (p^r)$ Algorithm 1. Next, compute the binary representations $\textrm{bin}(\mathscr {x}'_{iG'}) = \mathscr {x}'_{i1}, \mathscr {x}'_{i2}, \dots , \mathscr {x}'_{it}$, $\textrm{bin}(\mathscr {y}'_{iG'}) = \mathscr {y}'_{i1}, \mathscr {y}'_{i2}, \dots ,\mathscr {y}'_{it'}$ and $\textrm{bin}(\mathscr {z}'_{iG'}) = \mathscr {z}'_{i1}, \mathscr {z}'_{i2}, \dots , \mathscr {z}'_{it''}$ of the ${\mathscr {x}'}, {\mathscr {y}'}$ and ${\mathscr {z}'}$ coordinates of the points $iG' = (\mathscr {x}'_{iG'}, \mathscr {y}'_{iG'},$ $\mathscr {z}'_{iG'})$, $i = 1, 2, \ldots , n$. Let $\textrm{bin}(iG') = \mathscr {x}'_{i1}, \mathscr {y}'_{i1}, \mathscr {z}'_{i1}, \dots , \mathscr {x}'_{ik},$ $\mathscr {y}'_{ik},\mathscr {z}'_{ik}$ denote the complete binary sequence $\mathcal {M}_i$ obtained by merging $\textrm{bin}(\mathscr {x}'_{iG'}), \textrm{bin}(\mathscr {y}'_{iG'})$, and $\textrm{bin}(\mathscr {z}'_{iG'})$, where $k = \min \{t, t', t''\}$. For the generated n points the resulting binary sequence $\mathcal {M}_i$ has a length of at least $m 2^m$, and divide this binary sequence $\mathcal {M}_i$ into $2^m$ subblocks, each of size m then onvert each m-bit subblock of $\mathcal {M}_i$ into its integer value, producing an integer sequence $\mathcal {I}_i$. Denote the current S-box S using the decimal values of the integer sequence $\mathcal {I}_i$. If this S-box S has repeated integer values, then S is not a bijective S-box. Our goal is to place all integer values in all positions of length $2^m$ without repetitions, ensuring we get a bijective S-box. Find the repeated integer values in the current S-box S. Set a sequence $S'$ and assign $-1$ to the repeated integer values of S. Generate a new sequence $T_s$ by assigning the number 1 to the corresponding position of $T_s$ if it appears in the index value of $S'$; otherwise, assign 0 to that position i.e $T_s[i]=1$ if $S'[i]=-1$, else $T_s[i]=0$. Generate a sequence K by assigning the missing index values of $T_s$. Set the final required S-box $S_b$ as initial S-box $S'$, where $\beta$ is the length of the sequence $S'$ and $\omega$ is the length of the sequence K. If the $S'[i]=-1$, then use the equation $\delta = 1+\mod ((\omega -j), S_{b}[i-1])$ to get the values. The dynamic S-box generated by our generator is represented by S, and its generation method is detailed in Algorithm 2.

The optimised S-box generator is designed by eliminating swap operations that minimize nonlinearity. The optimized S-box $S_{opt}$ is obtained by performing swapping operations that ensure high nonlinearity, as given in Algorithm 3.

Algorithm 1

Addition in $\mathcal{C}\mathcal{P}_\alpha (p^r)$.

Algorithm 2

Dynamic S-Box Generation.

Algorithm 3

Optimised S-Box Generation.

Security analysis and comparison

A comprehensive evaluation of our method was carried out, focusing on computational efficiency, dynamic behavior, and cryptographic strength. We compared the execution time of our S-box generation approach with the fastest known methods, specifically the one introduced by¹⁵. The cryptographic and dynamic characteristics of the S-boxes generated by our method were thoroughly examined and compared to those produced by other established techniques. In addition, we assessed the nonlinearity of the S-boxes and evaluated their security performance in relation to existing generators.

Experimental setup: The dynamic and optimized generated S-boxes used the recommended elliptic curve domain parameters from⁵⁰, using primes of sizes 128, 224, 256, and 521 bits, generated with MATHEMATICA 14.0 on a machine with 16GB of RAM and an AMD Ryzen 7 5700U @ 1.80 GHz. We employed primes of different sizes with the parameters p, c, and G The parameters p, c, and G are detailed in the supplementary material.

Experimental results and comparative analysis

Analysis of number of points

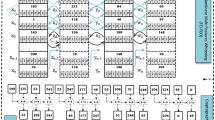
Our experimental analysis focused on the number of points required to generate S-boxes of sizes $(8 \times 8)$, $(9 \times 9)$ and $(10 \times 10)$ using prime numbers with bit sizes of 16, 32, 64, 128, 256, 521, and 1024. The results indicate that our method generates [2, 26], [3, 55], and [4, 118] points for constructing $(8 \times 8)$, $(9 \times 9)$ and $(10 \times 10)$ S-boxes, respectively. In contrast, the method proposed by¹⁵ requires [2, 77], [3, 190], and [6, 381] points to generate the same S-box sizes. A comparison of the points generated by both methods is shown in Fig. 1, illustrating that our generator requires significantly fewer points than the method by¹⁵.

Fig. 1

The number of points generated by the proposed S-box generator for $(8 \times 8)$, $(9 \times 9)$, and $(10 \times 10)$ S-boxes is compared with the generator by¹⁵.

Computational time analysis

We measured the time taken to generate $(8 \times 8)$-S-boxes and $(10 \times 10)$-S-boxes using prime numbers with bit sizes of 128, 224, 256, and 521. The generation process was repeated five times, and the results showed that our generator produces an $(8 \times 8)$-S-box in the range of [0.0059, 0.0085] seconds and a $(10 \times 10)$-S-box in [0.0199, 0.0356] seconds. In comparison, the method by¹⁵ takes [0.00689, 0.00922] seconds and [0.0377, 0.06441] seconds, respectively. These results confirm that our proposed generator is significantly faster and more efficient than the current fastest method available.

The time complexity of the proposed dynamic S-box generator can be determined by evaluating each step separately of Algorithm 2. Line 1: Taking a non-identity point $G:= (\mathscr {x}_0, \mathscr {y}_0, \mathscr {z}_0)$ on the cubic Pell curve the time is $\mathcal {O}(1)$. Line 2: The generation of n points on the cubic Pell curve using the addition law with Algorithm 1 repeatedly, has a time complexity of $\mathcal {O}(n \cdot \log p)$, as each addition requires a fixed number of modular arithmetic operations. Line 3: Compute the modified coordinates $(\mathscr {x}'_i, \mathscr {y}'_i, \mathscr {z}'_i)$ using XOR operations has a time complexity of $\mathcal {O}(n)$. Line 4: Conversion of $(\mathscr {x}'_i, \mathscr {y}'_i, \mathscr {z}'_i)$ into binary sequences, which takes $\mathcal {O}(n \cdot \log p )$ time as each coordinate is expressed with $\log p$ bits. Lines 5 to 8: The process of merging and partitioning the binary sequences into $2^m$ sub-blocks, along with converting them into decimal values to form the initial S-box requires $\mathcal {O}(2^m)$ time. Lines 9 to 20: Detecting and replacing duplicate entries to ensure bijectivity requires a linear traversal of $2^m$ entries, adding an additional $\mathcal {O}(2^m)$ time. Since $2^m$ is a small fixed constant (256 for an $8 \times 8$ S-box) and $n \ll p$ (i.e that the number of points n generated on the cubic Pell curve is significantly smaller than the underlying prime p). Therefore, the overall time complexity of the proposed dynamic S-box generator is

$\mathcal {O}(n \cdot \log p+2^m) \approx \mathcal {O}(\log p)$,

for fixed $m=8$ and the number of points n is also small in the range [2, 26].

Dyanmic S-box performance analysis

We generated 10,000 dynamic S-boxes using the approach outlined in Section 3 and conducted an extensive security evaluation to assess their cryptographic strength. This evaluation included a variety of important properties, such as nonlinearity (NL), differential approximation probability (DAP), strict avalanche criterion (SAC), linear approximation probability (LAP), bit independence criterion (BIC), and algebraic complexity (AC).

Nonlinearity (NL)

NL of an S-box is a crucial factor in enhancing the confusion between the ciphertext and plaintext, improving its cryptographic security. One of the primary measures of the effectiveness of an S-box is its nonlinearity, as defined by⁵¹. NL is quantified as the minimum Hamming distance between the S-box function $\sigma :Z_2{^m} \rightarrow Z_2{^m}$ and the set of all affine functions. This property plays a pivotal role in the security of the encryption system, as it helps prevent attackers from exploiting linear relationships between inputs and outputs. Mathematically, the nonlinearity of an S-box is given by:

$$\begin{aligned} NL(S) \triangleq \min _{(\omega , \alpha , \beta )} \{ {x} \in Z_2^{m} \vert \omega .S(x) \ne (\beta \oplus \alpha .x)\}, \end{aligned}$$

(2)

where $\omega \in Z_2^{m},\alpha \in Z_2^{m}$ and $\beta \in Z_2$. The NL(S) is required to be as close as possible to its maximum value, given by $(2^{m-1}-2^{\frac{m}{2}-1})$ for perfectly non-linear functions⁵¹.

The nonlinearity of an S-box can be determined by computing its Walsh spectrum. The Walsh spectrum is defined as:

$$\begin{aligned} \mathcal{W}\mathcal{S}(\omega ) \triangleq \sum _{\alpha \in Z_2^{m}} (-1)^{S(x) \oplus \alpha .\omega }, \end{aligned}$$

(3)

where $\omega \in Z_2^{m}$, and $\alpha .\omega$ denotes the dot product, calculated as $\alpha .\omega = \alpha _1\oplus \omega _1,........ \alpha _n\oplus \omega _n$. Based on this, the nonlinearity NL(S) of the S-box is given by:

$$\begin{aligned} NL(S) \triangleq 2^{m-1} (1-2^{-m} \max _{\alpha \in Z_2^{m}}\vert \mathcal{W}\mathcal{S}(\omega ) \vert ) \end{aligned}$$

(4)

The nonlinearity values with respect to eight boolean functions of the 10,000 S-boxes generated by our method are shown in Fig. 2. As reflected in Table 1, 93% of the generated S-boxes exhibited a nonlinearity at least 96. This demonstrates that our proposed generator is highly efficient in producing S-boxes that offer strong resistance to linear cryptanalysis, reinforcing their cryptographic security. We compared the nonlinearity due to eight boolean functions of 10,000 S-boxes produced by our method with those produced by several existing generators, including those from^{5,10,14,15,42,44,52} as shown in Table 2. The results revealed that our generator consistently outperformed the others in terms of minimum nonlinearity across all generated S-boxes. Moreover, the maximum nonlinearity achieved by our method was also higher than that of other approaches, including those by^5,10,42,44, further demonstrating its superior capacity for generating cryptographically secure S-boxes.

The S-boxes ($\mathcal {S}_{\mathcal {P}})$, listed in Table 3, reached the optimal nonlinearity due to eight boolean functions of 106 with the input parameters $(m, p, \alpha ,r,G_i)$, where,

$m=8, \alpha =9, r=2$,

$p= 11579208923731619542357098500868790785326998466564056403945758400 7908834671663$,

$x_{G_1} = {78678897980110680189937615394517648981960744210695720077288090136718124162276}$,

$y_{G_1} = {105316748987465574731669528188867710098205080952350007334827872052771392502134},$

$z_{G_1} = {15955009163358243145477188650123601990859004833262966782397166421349909202929}$.

Additionally, we compared the nonlinearity due to eight boolean functions and 256 boolean functions of our dynamic S-box $(\mathcal {S}_{\mathcal {P}})$ to that of other methods listed in Table 4. This solidifies the proposed generator’s effectiveness in cryptographic applications, outperforming methods presented by^{16,17,18,20,21,22,37,39,44,47,48,49}.

Fig. 2

Results of nonlinearity with eight boolean functions for 10,000 randomly generated S-boxes.

Table 1 The percentage of nonlinearity with eight boolean functions achieved by the proposed generator for 10,000 S-boxes.

Table 2 Comparison of the nonlinearity over eight boolean functions results of 10,000 randomly generated S-boxes.

Table 3 The dynamic S-box $(\mathcal {S}_{\mathcal {P}})$ by proposed method.

Table 4 Comparison between the proposed dynamic S-box ($\mathcal {S}_{\mathcal {P}})$ and other existing S-box generators.

Linear approximation probability (LAP)

LAP was first introduced by⁵⁴, quantifies the probability that a specific input bit correlates with a corresponding output bit in a cryptographic function. This metric helps assess the strength of a cipher by evaluating the potential for linear relationships between inputs and outputs, which could lead to vulnerabilities if the probability is too high. To calculate the LAP of the S-box, we can apply the following formula:

$$\begin{aligned} LAP(S)\triangleq \frac{1}{2^{n}}\{\max _{\alpha ,\beta \ne 0} \left| N(\alpha ,\beta ) \right| \}, \end{aligned}$$

(5)

where $N(\alpha ,\beta ) \triangleq {\#\{ {x} \in Z_2^{n} \vert x \cdot \alpha =S(x) \cdot \beta \}}-2^{n-1}, \alpha \in Z_2^{n}$ and $\beta \in Z_2^{n}$. Smaller LAP(S) values provide higher resistance to linear cryptanalysis.

LAP values for the 10,000 S-boxes produced by our approach are presented in Fig. 3, with a range from [-0.0156, 0.1406] and an average of 0.0466. These results suggest that our S-boxes exhibit a strong resistance to linear cryptanalysis. In comparison with other S-box generators, as shown in Table 4, the LAP values of our S-boxes are significantly lower. This indicates that our approach yields more secure S-boxes, with reduced susceptibility to linear attacks, compared to the methods in^{10,11,16,17,18,20,21,22,37,38,39,40,41,42,43,44,46,47,48,49,52,53}.

Fig. 3

The LAP results of 10,000 randomly generated S-boxes.

Differential approximation probability (DAP)

DAP measure, introduced by⁵⁵, evaluates the susceptibility of an S-box to differential cryptanalysis. An S-box with high differential uniformity is considered more secure against such attacks. A lower DAP value implies that the S-box has a greater ability to resist differential cryptanalysis, making it more robust in cryptographic applications. The DAP is calculated as follows:

$$\begin{aligned} DAP(S) \triangleq \max _{\delta {x} \ne 0,\delta {y}\in Z_2^{n} } \left( \frac{ D (\delta {x},\delta {y})}{2^{n}} \right) \end{aligned}$$

(6)

where $D(\delta {x},\delta {y})\triangleq \#\{ {x} \in Z_2^{n} \vert S(x)\oplus S(x\oplus \delta {x}) =\delta {y}\}, \delta {x} \in Z_2^{n}$ and $\delta {y} \in Z_2^{n}$.

DAP values for the 10,000 S-boxes produced by our proposed generator are shown in Fig. 4. The DAP values for all the S-boxes lie within the ideal range of [0.039, 0.063], indicating strong resistance to differential cryptanalysis. The DAP of the proposed S-box ($\mathcal {S}_{\mathcal {P}}$) is 0.047. The DAP results for the proposed S-box are presented in Table 4, indicating that its performance is comparable to that of the existing S-box generators^{10,11,16,17,18,20,21,22,37,38,39,40,41,42,43,44,46,47,48,49,52,53}.

Fig. 4

The DAP value results of 10,000 randomly generated S-boxes.

Strict avalanche criterion (SAC)

SAC, introduced by⁵⁶, is a method for testing S-boxes that combines the concepts of avalanche behavior and completeness. It measures the ability of the S-box to induce confusion in the cipher. An S-box satisfies the SAC if a small variation in the input bits leads to a change in the output bits with a probability of 0.5, ensuring that the cipher is highly sensitive to input alterations.

$$\begin{aligned} \mathcal {S}(i,j)\triangleq \frac{1}{2^{n}}\left[ \ (S_i(\nu )\oplus \omega (S_i(\nu \oplus \delta _j)))\right] , \end{aligned}$$

(7)

where $\omega (\delta _j)=1$ is the number of non-zero bits in $\delta _j$, $1\le i,j \le 8$ and $\delta _j \in Z_2^{n}$.

We conducted an extensive SAC analysis on 10,000 S-boxes generated by our proposed method. The results, shown in Figs. 5 and  6, highlight the average, minimum, and maximum SAC values. The SAC values for the generated S-boxes were found to fall within the ranges of [0.2969, 0.4531] for the minimum, [0.5469, 0.7188] for the maximum, and [0.3982, 0.6049] on average. These values are in close proximity to the ideal value of 0.5, confirming that the generated S-boxes comply with SAC requirements. This ensures that the S-boxes offer significant resistance to attacks exploiting Boolean functions. Furthermore, a comparison of the SAC values for our S-boxes with other generators is provided in Table 4, showing that our method performs favorably compared to existing methods^{10,11,16,17,18,20,21,22,37,38,39,40,41,42,43,44,46,47,48,49,52,53}.

Fig. 5

The maximum and minimum SAC values of 10,000 randomly generated S-boxes.

Fig. 6

Average SAC results of 10,000 randomly generated S-boxes.

Algebraic complexity (AC)

The concept of AC was introduced by⁵⁷ as a key measure for evaluating the resistance of an S-box to algebraic attacks. The AC of an S-box refers to the number of non-zero terms in its corresponding polynomial representation. The higher the AC, the more difficult it is for an attacker to perform algebraic attacks successfully. S-boxes with higher AC values provide a stronger cryptographic defense, with a maximum AC value of 255 indicating significant protection against such attacks. Thus, a higher AC value is crucial for enhancing the cryptographic security of S-boxes. The AC values of the 10,000 S-boxes, ranging from 249 to 255, are depicted in Fig. 7. From Table 5, it is clear that over 99% of our generated S-boxes have an AC value $\ge 251$, which is higher than⁵⁸. Additionally, Table 4 compares the AC results of the S-box ($\mathcal {S}_{\mathcal {P}}$) with the other S-box generators^{10,11,16,17,18,20,21,22,37,38,39,40,41,42,43,44,46,47,48,49,52,53}.

Fig. 7

AC results of 10,000 randomly generated S-boxes.

Table 5 The AC results of 10,000 S-boxes generated by the proposed generator are compared with the method presented in⁵⁸.

Bit independence criterion (BIC)

BIC, introduced by⁵⁶, is a method for evaluating how the output bits of an S-box change when a single input bit is modified. This criterion, similar to the strict avalanche criterion, is used to assess the resilience of an S-box against potential Boolean function-based attacks.

To analyze the BIC, we computed the values for 10,000 S-boxes generated by our proposed method. The results, including the minimum, maximum, and average BIC values, are illustrated in Figs. 8, 9. The computed ranges for the BIC values are: average [0.4708, 0.5332], minimum [0.4316, 0.4941], and maximum [0.5098, 0.5723]. Additionally, we compared the BIC values of the S-box generated by our method ($\mathcal {S}_{\mathcal {P}})$ with those of other S-box generators^{10,11,16,17,18,20,21,22,37,38,39,40,41,42,43,44,46,47,48,49,52,53}, as listed in Table 4. The comparison indicates that our proposed generator excels at producing dynamic S-boxes with strong BIC values, reinforcing their effectiveness in cryptographic applications.

Fig. 8

The maximum and minimum BIC values of 10,000 randomly generated S-boxes.

Fig. 9

Average BIC results of 10,000 randomly generated S-boxes.

Absolute indicator (AI)

An absolute indicator of a boolean function f is defined as the largest absolute value of auto correlation is given by⁵⁹

$$\begin{aligned} \mathcal {A}_\mathscr {f} \triangleq \max _{\gamma \ne 0,\gamma \in Z_2^{m} }\left| \Lambda _f(\gamma ) \right| , \end{aligned}$$

(8)

where $\Lambda _f(\gamma )$ is the autocorrealtion of the function f over $Z_2^{m}$ is calculated as

$$\begin{aligned} \Lambda _f(\gamma ) \triangleq \sum _{\mathscr {x} \in Z_2^{m}} (-1)^{f(x) \oplus f(x+\gamma )}. \end{aligned}$$

The comparison of the AI values for our proposed dynamic S-box $(\mathcal {S}_{\mathcal {P}})$ with other generators is provided in Table 4, showing that our method performs favorably compared to existing methods^44,46.

Boomerang uniformity (BU)

The concept of boomerang uniformity was introduced by⁶⁰, is defined as the maximum value in the boomerang connectivity table, excluding the row and column corresponding to index 0.

$$\begin{aligned} \mathcal {B_U} \triangleq \max _{\alpha , \beta \ne 0,\alpha , \beta \in Z_2^{m} }\left| \mathcal {B_S}(\alpha , \beta ) \right| , \end{aligned}$$

(9)

where $\mathcal {B}_\mathscr {c}(\alpha , \beta )$ is the boomerang connectivity table of $\mathcal {S}$ is given by

$$\begin{aligned} \mathcal {B}_\mathscr {c}(\alpha , \beta ) \triangleq \#\{ {x} \in Z_2^{m} \vert S^{-1}(S(x)\oplus \beta ) \oplus S^{-1}(S(x \oplus \alpha )\oplus \beta )=\alpha \}, \alpha , \beta \in Z_2^{m}. \end{aligned}$$

The comparison of the BU values for our proposed dynamic S-box $(\mathcal {S}_{\mathcal {P}})$ with other generators is provided in Table 4, showing that our method performs favorably compared to existing methods^{11,18,20,37,44,48,49,52}.

Optimized S-box performance analysis

In order to generate optimized S-boxes of size $(8 \times 8)$, we leveraged elliptic curve domain parameters as suggested by⁵⁰, utilizing prime sizes of 128, 224, 256, and 521 bits. The optimized S-boxes were constructed by applying the swapping procedure outlined in Algorithm 3, resulting in a nonlinearity value of 108. The generated optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$ are presented in Tables 6, 7, 8 and 9.

• 1. A comparison of the NL due to eight boolean functions and 256 boolean functions of our optimized S-boxes with those of existing optimized S-box generators^{24,25,26,27,28,29,30,31,33,34} is provided in Table 10. Our optimized S-boxes $\mathcal {S}_{128}$, $\mathcal {S}_{224}$, $\mathcal {S}_{256}$, and $\mathcal {S}_{521}$, with a nonlinearity due to eight boolean functions of 108, show superior performance in comparison with other generators^{24,25,26,27,28,29,30,31,33,34}, confirming the high nonlinearity achieved by our method.

• 2. LAP values of the optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}$, $\mathcal {S}_{256},$ and $\mathcal {S}_{521}$ are evaluated and listed in Table 10. These values are notably higher than those of existing S-box generators^{24,25,26,27,28,29,30,31,33,34}, indicating that the optimized S-boxes produced by our method exhibit stronger resistance to linear cryptanalysis.

• 3. DAP values for the optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$ are presented in Table 10. The DAP values for the optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$ are 0.047, 0.039, 0.047, and 0.039. The DAP results for the proposed S-box are presented in Table 10, indicating that its performance is comparable to that of the existing S-box schemes^{24,25,26,27,28,29,30,31,33,34}, making them more resilient against differential cryptanalysis attacks.

• 4. AC values of our optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$, shown in Table 10, outperform those from other generators^{24,25,26,27,28,29,30,31,33,34}. Higher AC indicates that the proposed S-boxes are more secure against algebraic attacks, providing enhanced cryptographic strength.

• 5. BU and AI values of our optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$, shown in Table 10, perform favorably compared to existing methods^{24,25,26,27,28,29,30,31,33,34}.

• 6. SAC values of our optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$ are close to the ideal value of 0.5, demonstrating strong confusion properties. As indicated in Table 10, these S-boxes have better SAC results than compared to other S-box generation schemes^{24,25,26,27,28,29,30,31,33,34}. Therefore, the S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$ demonstrate resistance to cryptanalysis by the Boolean function.

• 7. Finally, BIC values of the optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}$, $\mathcal {S}_{256},$ and $\mathcal {S}_{521}$, as presented in Table 10, are found to be comparable to those from other state-of-the-art S-box generation schemes^{24,25,26,27,28,29,30,31,33,34}. This confirms that our method produces optimized S-boxes with excellent BIC performance, ensuring robust cryptographic security.

Table 6 The generated S-box, $\mathcal {S}_{128}$.

Table 7 The generated S-box, $\mathcal {S}_{224}$.

Table 8 The generated S-box, $\mathcal {S}_{256}$.

Table 9 The generated S-box, $\mathcal {S}_{521}$.

Table 10 Comparison of the proposed optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}$, $\mathcal {S}_{256},$ and $\mathcal {S}_{521}$ with existing generators.

NIST statistical randomness test

The statistical test results for randomness carried out using the tool provided by NIST 800-22⁶¹ on the roposed S-boxes $\mathcal {S}_{p}$, $\mathcal {S}_{128}$, $\mathcal {S}_{224}$, $\mathcal {S}_{256}$ and $\mathcal {S}_{521}$. These tests are designed to find any non-randomness in the range [0,255] of the output sequence. Each S-box contains 256 values ranging from 0 to 255 were transformed into binary sequences to form the input for the NIST tests. Every byte of the S-box was encoded as an 8-bit binary string, all of which were concatenated to create a long string of binary digits. The NIST Statistical Test Suite (NIST) was used to test the randomness of the binary sequences that were generated. The tests verify various statistical characteristics such as frequency distribution, runs and linear complexity to identify deviations from randomness. The NIST suite calculates the probability of $p_\text {value}$ for each sequence, and if $p_\text {value}$ $\ge \lambda$ (or $p_\text {value}$ < $\lambda$ ), the sequence is considered random (or non-random), where $\lambda$ is a predefined threshold known as the significance level. For cryptographic purposes, $\lambda$ is usually set between 0.001 and 0.01⁶¹. The results for 14 tests including (random occurrence, random occurrence variant, etc.), which are some of the most significant for cryptographic use. These have been selected because they examine properties directly related to S-box security, such as uniformity, independence, and unpredictability. The results of the statistical randomness test of the proposed S boxes through the tool provided by NIST 800-22⁶¹ are listed in Table 11. The Universal Statistical Test was excluded, as it is intended for longer input sequences.

Table 11 The NIST results of the proposed S-boxes $\mathcal {S}_{p}$, $\mathcal {S}_{128}$, $\mathcal {S}_{224}$, $\mathcal {S}_{256}$ and $\mathcal {S}_{521}$.

Application of optimized S-boxes in image encryption

S-boxes used in image encryption applications are further employed to assess their strength. The process takes a plain image as input and produces an encrypted cipher image as output. The image coefficients are substituted using the proposed optimized S-boxes: $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$. An encrypted image is generated by mapping these optimized S-boxes, each of size $16 \times 16$, onto plain text images sized $256 \times 256$.

The Majority Logic Criterion (MLC) can be utilized to evaluate the encryption capabilities of the S-boxes⁶². To evaluate the randomness of the encrypted image, MLC employs several analyses, including entropy, energy, homogeneity, contrast, correlation, and the mean of absolute deviation (MAD). Additionally, differential statistical analysis is performed to assess the Number of Pixel Change Rate (NPCR) and the Unified Average Changing Intensity (UACI). Cryptographic images can be identified by examining homogeneity and energy. A correlation test compares the plaintext and encrypted images to assess their similarity, with encryption reducing the correlation value, indicating greater distortion. Contrast is used to estimate the loss of brightness in the original image, with higher contrast scores indicating more effective encryption. MAD analysis helps quantify the quality difference between the encrypted and original images. The quality of the S-box is determined by the statistical features that emerge from the distortions introduced during the encryption process.

For the image encryption application, we used $256 \times 256$ images of a clock, a cameraman, and a baboon, applying our generated optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$. The encrypted images were obtained after a single round of applying the optimized S-box to evaluate the randomness of the S-box. Figures 10,  11,  12 and  13 show the results of image encryption using these optimized S boxes after applying a single round, where (a) Display the plain images; (b) provide the histograms of the plain images; (c) display the encrypted images using $\mathcal {S}_{128}$, $\mathcal {S}_{224}$, $\mathcal {S}_{256}$ and $\mathcal {S}_{521}$; and (d) present their histograms. To prevent information leakage, multiple rounds were carried out to obtain the encrypted images as shown in Fig. 14 and their corresponding histograms are shown in Fig. 15. As evident from the Figs. 14 and  15, the results are robust and effectively prevent information leakage. We analyze the encrypted images using MLC tests, comparing the results with the encryption performance of the AES S-box and the APA S-box. The results of the MLC test are shown in Table 12, while additional results for the number of pixel changes (NPCR) and the unified average change intensity (UACI) are presented in Table 13. These results demonstrate that the image encryption performance of the generated optimized S-boxes is satisfactory and consistent.

Fig. 10

“Plain image, encrypted image and their histograms using the optimized S-box $\mathcal {S}_{128}$.

Fig. 11

Plain image, encrypted image and their histograms using the optimized S-box $\mathcal {S}_{224}$.

Fig. 12

Plain image, encrypted image and their histograms using the optimized S-box $\mathcal {S}_{256}.$.

Fig. 13

Plain image, encrypted image and their histograms using the optimized S-box $\mathcal {S}_{521}$.

Fig. 14

Images (a–d) show the encrypted results of the plain images generated using optimized S-boxes over multiple rounds.

Fig. 15

Images (a–d) show the histograms of encrypted images from Fig. 14.

Table 12 The MLC results for image encryption using the S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}.$.

Table 13 NPCR and UACI results for image encryption using optimized S-boxes.

Conclusion

The task of generating S-boxes with high nonlinearity while maintaining low computational time is a significant challenge. In this work, we present a novel substitution S-box generator based on cubic Pell curves. The main idea behind this approach is to leverage the randomness inherent in the points on cubic Pell curves, using their binary representations. Our S-box generation method produces dynamic and optimized S-boxes that exhibit high nonlinearity and strong cryptographic properties. Through comprehensive cryptographic analysis, we have compared our dynamic S-box generation method with various existing methods^{10,11,14,16,17,18,20,21,22,37,38,39,40,41,42,43,44,45,46,47,48,49,52,53,58}, including the fastest dynamic S-box generation technique¹⁵. Our security analysis shows that the S-boxes generated by our method demonstrate superior cryptographic strength in comparison to others. We evaluated the nonlinearity due to eight boolean functions of 10,000 S-boxes generated by our approach and found that these S-boxes possess highly nonlinear characteristics, outperforming those generated by other methods^{5,10,14,15,42,44,52}. The NL due to eight boolean functions of our optimized S-boxes $\mathcal {S}_{128}$, $\mathcal {S}_{224}$, $\mathcal {S}_{256}$, and $\mathcal {S}_{521}$ is 108, which is notably higher than the NL values of other existing optimized generators^{24,25,26,27,28,29,30,31,33,34}. This indicates that our optimized S-box method is capable of generating highly secure S-boxes with exceptional cryptographic properties, including nonlinearity (NL), strict avalanche criterion (SAC), linear approximation probability (LAP), bit independence criterion (BIC), differential approximation probability (DAP), and algebraic complexity (AC). The proposed S-boxes also satisfies the randomness properties when evaluated using the tests provided by NIST test suite. In addition, we tested the effectiveness of the optimized S-boxes $\mathcal {S}_{128}, \mathcal {S}_{224}, \mathcal {S}_{256},$ and $\mathcal {S}_{521}$ in the context of image encryption. The results demonstrated that the generated S-boxes contribute significantly to enhancing the security of image encryption applications. Overall, our proposed S-box generation method shows great potential for use in cryptographic systems requiring high security and robustness against various types of attacks.

Future work could focus on applying the S-box generator to real-world encryption tasks, such as securing multimedia data (images, videos) and sensitive communications. Research could also explore more efficient algorithms and mathematical approaches to improve performance without compromising security.