Introduction

Overview of research problem

Unmanned Aerial Vehicles (UAVs) have become integral to modern applications such as surveillance, defence, environmental monitoring, and autonomous logistics due to their adaptability and ability to perform in hazardous or inaccessible environments1,2. Quadrotors, in particular, are favoured because of their hovering capability, vertical take-off and landing (VTOL), and agility in constrained spaces3,4. Despite these advantages, quadrotors are nonlinear, underactuated, and strongly coupled systems, making stable control and precise trajectory tracking challenging under disturbances and uncertainties.

Traditional controllers such as Proportional–Integral–Derivative (PID) are widely used due to simplicity, but they exhibit limited performance in nonlinear and uncertain operating conditions5. Linear Quadratic Regulator (LQR) control offers an optimal trade-off between performance and control effort6, but its effectiveness depends heavily on the proper selection of weighting matrices Q and R. Conventionally, these are chosen by heuristic or trial-and-error approaches, which often result in suboptimal outcomes. This motivates the development of systematic optimization methods for gain tuning.

Literature review

Several advanced control strategies have been explored to overcome the nonlinearities of quadrotors. Sliding Mode Control (SMC) provides robustness against uncertainties and external disturbances7, while Back stepping Control ensures global asymptotic stability through recursive design8. However, both approaches have drawbacks, such as chattering (SMC) and computational complexity (Backstepping).

Among optimal control strategies, LQR has been widely studied for quadrotor stabilization and trajectory tracking9,10. Early works designed LQR controllers using full six-degree-of-freedom models10, while later research proposed Integral Effect LQR to reduce steady-state errors11,12. Nevertheless, the tuning of Q and R matrices remains a key limitation. To address this, metaheuristic algorithms have been applied, including Particle Swarm Optimization (PSO), Whale Optimization Algorithm (WOA), and Grey Wolf Optimizer (GWO)13. While these methods improve performance compared to manual tuning, standalone approaches are often prone to premature convergence or limited exploitation of the search space14,15. This motivates the exploration of hybrid optimization frameworks. Advances in hybrid metaheuristics have greatly improved the performance of UAV control systems through their efficient solving of intricate optimization issues like trajectory tracking, path planning, and obstacle evasion. Paper16 conducted an extensive systematic review of metaheuristic strategies in autonomous UAVs, pointing out the increasing use of hybrid algorithms to increase robustness and adaptability in dynamic environments. Their research highlighted the importance of integrating complementary optimization methods to mitigate the limitations of each method and enable more effective and trustworthy UAV navigation.

Research in17 developed a new hybrid Hunger Games Search optimization with neural networks for UAV trajectory tracking, namely, controlling cable suspended loads. This method proved to have better control performance by taking advantage of the exploration power of metaheuristics and the learning capacity of neural networks, leading to better accuracy and stability.

Further advancing the field, paper18 proposed a hybrid HAOAROA metaheuristic with a fractional order PID controller for obstacle avoidance and path planning in UAVs. Their hybrid approach enhanced path optimization with uncertain and dynamic scenarios beyond that of classical control strategies. The integration of metaheuristic optimization with fractional control showed a potential avenue for future UAV control architectures.

Novelty and contributions

This work proposes a hybrid optimization-based LQR framework that integrates the Grey Wolf Optimizer (GWO) with Cuckoo Search (CS) to improve quadrotor control performance. The novelty lies in exploiting the global search ability of GWO while enhancing local refinement through CS, ensuring both convergence speed and solution quality. The LQR–GWO–CS controller is designed to minimize a performance index based on the Integral of Absolute Error (IAE), leading to improved transient response and robustness. A simplified schematic of the methodology is presented to illustrate the framework.

The novelty and contributions of this work are:

  • Development of a comprehensive nonlinear quadrotor model using Newton–Euler formalism.

  • Implementation of an LQR controller for altitude and position control with a novel integration of GWO and CS for systematic tuning of LQR weighting matrices.

  • Comparative evaluation with conventional LQR, LQR–GWO, and LQR–WOA methods, highlighting quantitative improvements in settling time, overshoot, and IAE.

  • Validation of the proposed controller through Hardware-in-the-Loop testing on OPAL-RT.

The rest of this article is structured as follows. The section “System details” presents the nonlinear modeling of the quadrotor system. The section “Control methodology” describes the control methodology and the proposed LQR–GWO–CS framework. The section “Results and discussion” discusses simulation setup, performance evaluation, and robustness analysis. The section “Validation of results through OPAL-RT” presents Hardware-in-the-Loop validation using OPAL-RT. Section “Conclusions” concludes the work and outlines future research directions.

System details

Assumptions and coordinate frames

The quadrotor is modelled as a rigid-body, symmetric aerial vehicle with six degrees of freedom (DOF) and four independent inputs (rotor thrusts). Two coordinate frames are used: the earth-fixed inertial frame I and the body-fixed frame B. The rotor model is explained in Fig. 1 and the following assumptions are considered:

Fig. 1
figure 1

Comprehensive schematic of quadcopter showing body-fixed and inertial frames, thrust and torque vectors, rotor motions.

Full size image

Assumptions are as follows:

  1. 1.

    The quadrotor body is rigid and symmetric.

  2. 2.

    The inertia matrix is diagonal, I = diag(Jx, Jy, Jz).

  3. 3.

    Aerodynamic drag is negligible near hover and treated as a disturbance.

  4. 4.

    Rotor dynamics are faster than body dynamics; thrust is assumed proportional to rotor speed squared.

Nonlinear dynamics

Using the Newton–Euler formalism, the translational and rotational dynamics are written in Eqs. (1) and (2), respectively.

$$\:m*{d}^{2}p/d{t}^{2}=-m*g*{e}^{3}+R\left(\phi\:,\theta\:,\psi\:\right)*\left[\text{0,0},T\right]^{T}+{f}_{d}$$
(1)
$$\:I*d\omega\:/dt+\omega\:\times\:\left(I*\omega\:\right)=\tau\:+{\tau\:}_{d}$$
(2)

Here, p= [x y z]T is the position vector, ω= [p q r]T is the angular velocity vector, T is the total thrust, and τ is the torque vector.

Rotor-to-force/torque mapping

The control inputs are generated from the four rotor thrusts F1, F2, F3, and F4. The relation is given in Eq. (3).

$$\:\left[\:T\:\:\:\:\:\:\:\:\right]\:\:\:\left[\:1\:\:\:1\:\:\:1\:\:\:1\:\right]\:[F_{1}]$$
$$\:[\:\tau\:\_\phi\:\:\:\:\:\:\:]\:=\:[\:0\:\:-\mathcal{l}\mathcal{\:}\mathcal{\:}\mathcal{\:}0\:\:\:\mathcal{l}\mathcal{\:}]\mathcal{\:}[F_{2}]$$
$$\:[\:\tau\:\_\theta\:\mathcal{\:}\mathcal{\:}\mathcal{\:}\mathcal{\:}\mathcal{\:}\mathcal{\:}]\mathcal{\:}\mathcal{\:}\mathcal{\:}[-\mathcal{l}\mathcal{\:}\mathcal{\:}\mathcal{\:}0\:\:\:\mathcal{l}\mathcal{\:}\mathcal{\:}\mathcal{\:}0\:]\:[F_{3}]$$
$$\:[\:\tau\:\_\psi\:\:\:\:\:\:\:]\:\:\:[\:b\:\:-b\:\:\:b\:\:-b\:]\:[F_{4}]$$
(3)

State-space modelling

$$A=\:\left[\begin{array}{cc}\begin{array}{c}\begin{array}{cc}\begin{array}{ccc}0&\:1&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:1&\:0&\:0\end{array}\end{array}\\\:\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:1\\\:0&\:0&\:0\end{array}\end{array}\end{array}&\:\begin{array}{c}\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\end{array}\\\:\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\end{array}\end{array}\\\:\begin{array}{c}\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\end{array}\\\:\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\end{array}\end{array}&\:\begin{array}{c}\begin{array}{cc}\begin{array}{ccc}0&\:1&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:1&\:0&\:0\end{array}\end{array}\\\:\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:1\\\:0&\:0&\:0\end{array}\end{array}\end{array}\end{array}\right]$$
$$B=\:\left[\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:g&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\\\:\begin{array}{ccc}0&\:-g&\:0\\\:0&\:0&\:0\\\:0&\:0&\:1/m\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\\\:\begin{array}{c}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\\\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\end{array}&\:\begin{array}{c}\begin{array}{ccc}0&\:0&\:0\\\:1/{j}_{x}&\:0&\:0\\\:0&\:0&\:0\end{array}\\\:\begin{array}{ccc}0&\:1/{j}_{y}&\:0\\\:0&\:0&\:0\\\:0&\:0&\:1/{j}_{z}\end{array}\end{array}\end{array}\right]$$
$$\:C=\:\left[\begin{array}{ccc}\begin{array}{ccc}1&\:0&\:0\\\:0&\:0&\:1\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:1&\:0\end{array}&\:\begin{array}{cc}\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\end{array}\\\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}&\:\begin{array}{cc}\begin{array}{ccc}1&\:0&\:0\\\:0&\:0&\:1\\\:0&\:0&\:0\end{array}&\:\begin{array}{ccc}0&\:0&\:0\\\:0&\:0&\:0\\\:0&\:1&\:0\end{array}\end{array}\end{array}\right]$$
$$\:D\: = \:0_{{12 \times 4}}$$
(4)

In the mathematical modelling of a quadrotor, the state-space representation plays a critical role in formulating the control strategy. The final state space matrix is given in Eq. (4). The state matrix A encapsulates the intrinsic system dynamics by defining how each state variable-such as position, velocity, and angular rates-evolves over time as a function of the current system state. The input matrix B characterizes the influence of control actions, such as thrust and torques from the rotors, on the system dynamics, effectively mapping how each input contributes to changes in the state variables. The output matrix C serves to map the internal system states to the measurable output variables, which are crucial for feedback control and system monitoring. Together, these matrices form the foundation of the state-space model used in the LQR framework. Accurate modelling of A, B, and C ensures precise simulation of quadrotor behaviour and forms the basis for designing the optimal control law. In this work, these matrices are used to construct the LQR formulation, whose weighting matrices Q and R are optimally tuned using a hybrid Grey Wolf Optimization-Cuckoo Search (GWO-CS) algorithm to enhance quadrotor stability and trajectory tracking performance.

Fig. 2
figure 2

Workflow of proposed control methodology.

Full size image

Control methodology

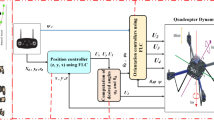
The proposed control methodology shown in Fig. 2 combines the strengths of optimal control and metaheuristic optimization to enhance quadrotor position regulation. A Linear Quadratic Regulator (LQR) is selected for its ability to generate optimal feedback control by minimizing a quadratic performance index involving the state and control weighting matrices, Q and R. These matrices critically shape the controller’s trade-off between state deviation and control effort. Rather than selecting Q and R through trial-and-error, a fitness function based on the Integral of Absolute Error (IAE) is used to quantify system performance, enabling a more systematic and performance-driven tuning process. To optimize the LQR parameters, a hybrid Grey Wolf Optimizer–Cuckoo Search (GWO-CS) algorithm is employed. The GWO component facilitates robust global exploration by mimicking the social hierarchy and cooperative hunting strategies of grey wolves, while the CS component refines local search using Lévy flight-based behavior to escape local optima. This hybrid approach ensures both broad search space coverage and fine-tuned exploitation, leading to faster convergence and improved controller performance. The resulting GWO-CS–tuned LQR controller offers enhanced trajectory tracking and stability in the presence of system nonlinearities and external disturbances, making it highly suitable for real-world quadrotor applications.

Linear quadratic regulator (LQR)

The Linear Quadratic Regulator (LQR) serves as a powerful and widely accepted method for designing optimal state feedback controllers, particularly in systems that can be modeled linearly or linearized around an operating point. It formulates a control law by minimizing a quadratic cost function that balances state deviations and control efforts, governed by the weighting matrices Q and R. Conceptually, this trade-off can be likened to selecting the most efficient mode of transport, such as train, bus, taxi, or aircraft, for a journey based on time, cost, or a combination of both. Similarly, in control system design, the goal is to drive the system’s state from an initial condition to the desired state efficiently, considering performance and energy constraints. LQR provides a systematic approach to achieve this balance by computing the optimal gain matrix that ensures stability, responsiveness, and energy-efficient operation. Its mathematical elegance and computational simplicity make it a preferred technique in modern control design, particularly when enhanced through optimization techniques for fine-tuning Q and R to suit nonlinear or complex systems. The basic block diagram of the LQR approach is provided in Fig. 3.

Fig. 3
figure 3

LQR Block diagram.

Full size image

In LQR, the implementation of state feedback resembles pole placement in structure but differs in formulation and purpose. While pole placement designs the feedback gain to assign desired closed-loop poles, LQR determines the gain by minimizing a cost function that balances state deviations and control effort. This optimal gain is obtained by solving the Discrete Matrix Riccati Equation (DMRE), which emerges from the Lagrangian formulation of a constrained optimization problem, where the plant dynamics serve as constraints. By leveraging this approach, LQR provides a systematic and optimal way to design controllers that guide the system from its initial state to a desired target while optimizing performance and respecting input constraints.

Here, it is assumed that all the states are measurable, and the linear system description is given as,

$$\:\stackrel{\bullet\:}{x}\left(t\right)=A\left(t\right)x\left(t\right)+B\left(t\right)u\left(t\right)$$
(5)

Now, let us define a general performance index that takes into account the state vector and input vector,

$$\:J=\frac{1}{2}{x}^{t}\left({t}_{f}\right)G\left({t}_{f}\right)x\left({t}_{f}\right)+{\int\:}_{{t}_{0}}^{{t}_{f}}\left[{x}^{t}\left(t\right)Q\left(t\right)x\left(t\right)+{u}^{t}\left(t\right)R\left(t\right)u\left(t\right)\right]dt$$
(6)

This PI is quadratic in nature as it gives unique minima, and also prevents the solution of the problem from converging at infinity.

Here, Q is the weight attached to the state, and R is attached to the input vector. Usually, for design purposes, these matrices are chosen according to the trial-and-error approach. But technically, these weights represent the degree of freedom attached to the particular state or input. Assume that if the weight attached to a particular input is high, it means the designer wants to minimize the cost function (or stabilize the system) with less of that particular input. Alternatively, if the weight is low, it means the designer can use that input freely13.

Also, \(\:G\left({t}_{f}\right)\) and \(\:Q\left(t\right)\) are the positive semi-definite matrices. And \(\:R\left(t\right)\) is the positive definite matrix. The states can be self-regulating, but all the inputs must have some reflection on the output. Minimizing Eq. (6) gives the following solution, given in Eq. (7)

$$\:\stackrel{\bullet\:}{M}\left(t\right)=-Q\left(t\right)-M\left(t\right)A\left(t\right)-{A}^{T}\left(t\right)M\left(t\right)+M\left(t\right)B\left(t\right){R}^{-1}\left(t\right){B}^{T}\left(t\right)M\left(t\right)$$
(7)

This equation is known as the differential matrix Riccati equation (DMRE).

GWO-CS optimizer

To enhance the performance of the LQR controller for quadrotor regulation, this study employs a hybrid Grey Wolf Optimizer–Cuckoo Search (GWO-CS) algorithm for optimal tuning of the LQR weighting matrices Q and R. The hybridization leverages the complementary strengths of both optimization techniques: Grey Wolf Optimizer (GWO) offers superior global exploration capabilities inspired by the leadership hierarchy and social hunting behavior of grey wolves, whereas Cuckoo Search (CS) provides strong local exploitation via Lévy flight-based solution generation. Together, they form a synergistic framework that improves convergence speed, solution diversity, and robustness against local minima.

In the proposed framework, the objective is to minimize a performance index defined by the Integral of Absolute Error (IAE), which captures deviations in trajectory tracking. The GWO-CS algorithm begins by initializing a population of candidate solutions representing different combinations of QQQ and RRR matrices. During each iteration, the top three solutions in GWO are treated as alpha, beta, and delta wolves, guiding the search process of the remaining candidates. Concurrently, the CS mechanism introduces randomization through Lévy flights to escape local traps and refine the search near promising regions of the solution space. The hybridization is implemented by interleaving GWO updates with CS-inspired solution perturbations. The balance between exploration and exploitation is dynamically managed, resulting in rapid convergence to a globally optimal solution with reduced computational overhead. As shown in the MPPT optimization context by14, the GWO-CS technique significantly outperformed standalone GWO, PSO, CS, and MVO algorithms in terms of convergence rate and tracking accuracy. The same strategic advantage is expected in this study, where GWO-CS is applied to optimize LQR gains for improved quadrotor stability and responsiveness. Hybrid Grey Wolf Optimizer–Cuckoo Search (HCSGWO) Mathematical Modeling is provided in the given equations.

  • Grey Wolf Optimizer (GWO) modelling.

The hunting strategy of grey wolves is mathematically modelled as follows:

  1. i.

    Encircling the prey.

$$\:{X}^{t+1}={X}_{p}^{t}-A\cdot\:\left|C\cdot\:{X}_{p}^{t}-{X}^{t}\right|$$
(8)

Here, \(\:{X}^{t}\) is the position vector of a wolf at iteration t, \(\:{X}_{p}^{t}\)​ is the prey position, and A, C are coefficient vectors controlling the exploration and exploitation.

  1. ii.

    Coefficient vectors.

$$\:A=2a{r}_{1}-a,\hspace{1em}C=2{r}_{2}$$
(9)

where r1, r2 ∈ [0, 1] are random numbers, and a decreases linearly with iterations to balance exploration and exploitation.

  1. iii.

    Convergence factor.

$$\:a\left(t\right)=2-\frac{2t}{{t}_{max}}$$
(10)

where t is the current iteration and \(\:{t}_{max}\:\) the maximum number of iterations.

  1. iv.

    Position updates based on top three wolves (α, β, δ).

$$\:{X}_{1}^{t}={X}_{{\upalpha\:}}-{A}_{1}\cdot\:\left|{C}_{1}{X}_{{\upalpha\:}}-X\right|$$
(11)
$$\:{X}_{2}^{t}={X}_{{\upbeta\:}}-{A}_{2}\cdot\:\left|{C}_{2}{X}_{{\upbeta\:}}-X\right|$$
(12)
$$\:{X}_{3}^{t}={X}_{{\upgamma\:}}-{A}_{3}\cdot\:\left|{C}_{3}{X}_{{\upgamma\:}}-X\right|$$
(13)

where \(\:{X}_{\alpha\:}\), \(\:{X}_{\beta\:}\), and \(\:{X}_{\gamma\:}\) denote the three best wolves guiding the search.

  1. xxii.

    Final wolf position update.

$$\:{X}^{t+1}=\frac{{X}_{1}^{t}+{X}_{2}^{t}+{X}_{3}^{t}}{3}$$
(14)

This equation averages the influence of the three best wolves to update the position of each wolf.

  • Cuckoo Search (CS) modeling

The cuckoo search employs Levy flights to generate new solutions.

  1. i.

    Levy flight-based position update.

$$\:{x}_{i}^{t+1}={x}_{i}^{t}+{\upalpha\:}\oplus\:\text{Levy}\left({\uplambda\:}\right)$$
(15)

where α is the step size scaling factor, and ⊕ indicates element-wise multiplication.

  1. ii.

    Levy distribution.

$$\:\text{Levy}\left({\uplambda\:}\right)\sim\:{t}^{-{\uplambda\:}},\hspace{1em}0<{\uplambda\:}\le\:3$$
(16)

which allows both local and global search through random walks.

  • Hybrid GWO–CS (HCSGWO) integration

The hybridization aims to overcome the static control problem in GWO by dynamically selecting parameters using CS.

  1. i.

    Dynamic nest updating (via CS).

$$\:{x}_{\text{new}}=\frac{{x}_{\text{best}}+{x}_{\text{rand}}}{2}+{\upalpha\:}\oplus\:\text{Levy}\left({\uplambda\:}\right)$$
(17)

where \(\:{x}_{\text{best}}\)​ is the best solution found so far, and \(\:{x}_{\text{rand}}\)​ is a randomly chosen solution.

  1. ii.

    Refinement using GWO equations.

After CS-based parameter tuning, wolf positions are updated using the GWO update rules (Eqs. 11–14). This ensures better exploration (via CS) and faster convergence (via GWO).

This hybrid algorithm thus enables intelligent parameter tuning that is otherwise difficult to achieve using conventional trial-and-error or gradient-based methods. By optimizing the feedback gain indirectly through Q and R, the LQR controller achieves faster settling time, lower overshoot, and improved tracking accuracy under dynamic and nonlinear conditions typical of quadrotor flight.

Results and discussion

To evaluate the effectiveness of the proposed LQR–GWO–CS controller, three different tests were carried out in simulation and real-time environments. These tests were designed to validate nominal performance, robustness against external disturbances, and practical feasibility through hardware-in-the-loop experiments. The test scenarios and their objectives are summarized in Table 1.

Table 1 Test cases and their objectives.
Full size table

Based on these tests, the proposed controller is benchmarked against conventional LQR, LQR–GWO, and LQR–WOA methods using standard performance metrics, as discussed in the following subsections.

Basic transient analysis (T1)

In this work, the authors have developed a detailed quadrotor simulation model in MATLAB/Simulink, utilizing the system parameters listed in Table 2. A Linear Quadratic Regulator (LQR) controller was subsequently designed and integrated with the quadrotor model to enhance trajectory tracking and dynamic stability. The transient response of the system with the conventional LQR controller was evaluated using standard time-domain performance metrics, including settling time (ST) and maximum overshoot (MO). To improve the tuning precision of the LQR controller, a hybrid Grey Wolf Optimizer–Cuckoo Search (GWO-CS) algorithm was employed to optimize the cost function weighting matrices Q and R. This hybrid optimization approach enables a more effective balance between state regulation and control effort, thereby enhancing the overall control performance under nonlinear and coupled dynamic conditions. The optimized LQR weighting matrices obtained through the GWO-CS algorithm are presented in Table 3.

Table 2 Parameter values for quadrotor model.
Full size table
Table 3 LQR weight parameters tuned using GWO-CS.
Full size table

Herein, the results obtained from the proposed LQR-WOA method have been evaluated and compared with the LQR-only approach and are appended in Table 4. The parameters in Table 3 were optimized using the Whale Optimization Algorithm (WOA), which minimizes a fitness function constructed using the integral absolute error (IAE) of positional deviations in the X, Y, and Z axes. WOA iteratively explores the search space by simulating whale behavior, such as encircling prey or bubble-net feeding, to adjust the LQR weight parameters. This process ensures an optimal trade-off between control effort and error minimization, leading to the final set of weight values in Table 3 after the algorithm converges to the best solution.

Table 4 Comparison of results using LQR and WOA-tuned LQR.
Full size table
Fig. 4
figure 4

Transient characteristics curves for the quadrotor for: (a) X-dimension, (b) Y-dimension, (c) Z-dimension.

Full size image

The optimization of LQR weight parameters using the whale optimization algorithm involves the minimization of the fitness function. Herein, the fitness function is constructed by taking the integral absolute error values for the positional error values for X, Y & Z. The IAE values for X, Y & Z are provided in Table 4.

The proposed LQR–GWO–CS method was compared against conventional LQR, LQR–GWO, and LQR–WOA controllers. These methods were selected because: (a) LQR is a widely used baseline for quadrotor control9,10,11,12, (b) LQR–GWO represents a common single-algorithm metaheuristic approach13, and (c) LQR–WOA is another recent state-of-the-art optimizer that has been applied to quadrotor control. This set of comparisons ensures both fairness (classical vs. optimized) and relevance to existing metaheuristic-based tuning approaches.

The comparative performance of the proposed LQR–GWO-CS controller with conventional LQR, LQR–WOA, and LQR–GWO controllers is evaluated across all three translational axes (X, Y, and Z) using key time-domain metrics: settling time, overshoot, and Integral of Absolute Error (IAE). The results, summarized in Table 4, clearly demonstrate the effectiveness of the hybrid GWO-CS-based optimization in enhancing quadrotor regulation. For the X-axis as shown in Fig. 4(a), the LQR–GWO-CS controller achieves a settling time of 1.70 s, significantly faster than the conventional LQR (4.077 s), LQR–GWO (7.36 s), and LQR–WOA (2.89 s). Notably, it also maintains zero overshoot, unlike LQR–WOA, which exhibits a 4.1% overshoot. Although WOA shows a slightly lower IAE (0.6884 vs. 0.7081), the faster response and zero overshoot of GWO-CS make it more suitable for applications demanding fast and smooth control. In the Y-axis, as shown in Fig. 4(b), the LQR–GWO-CS once again outperforms all counterparts by achieving the lowest IAE (0.6978) with a fast-settling time of 1.64 s and zero overshoot. While LQR–WOA offers a marginally faster settling time (1.539 s), it introduces a 4.2% overshoot, compromising stability. LQR and LQR–GWO lag in both response time and tracking accuracy. As shown in Fig. 4(c), the Z-axis, where altitude control is often the most sensitive, the proposed controller shows the best balance. It achieves a settling time of 1.96 s with only 2% overshoot and a lower IAE (0.9023) compared to LQR (1.2629) and WOA (0.9858). Although LQR–GWO yields a slightly lower IAE (0.8914), it suffers from the highest overshoot (4.4%), indicating poorer transient behavior.

Overall, the LQR–GWO-CS controller consistently delivers faster convergence with either zero or minimal overshoot while maintaining low tracking errors. The combination of GWO’s global search capability with CS’s efficient local exploitation allows the controller to fine-tune the LQR weighting matrices for optimal performance. These results highlight the robustness and adaptability of the proposed control strategy, making it a strong candidate for real-time UAV deployment in dynamic and uncertain environments.

Validation of results through OPAL-RT (T2)

To validate the proposed LQR-GWO-CS controller in real-time, a Hardware-in-the-Loop (HIL) simulation was conducted using the OPAL-RT OP4520 real-time simulator. The optimized controller, along with the nonlinear quadrotor model, was deployed in the real-time environment to assess the fidelity and robustness of the proposed algorithm under hardware constraints. Figure 5 displays the time-domain responses of the quadrotor system on all three axes (X, Y, and Z), as captured from the oscilloscope during the OPAL-RT test. These outputs represent the tracking performance of the quadrotor’s position control with respect to a unit step reference input.

Figure 5(a) shows the real-time response of the X-axis, highlighting a rapid rise time and negligible overshoot. The waveform exhibits high repeatability, validating the controller’s stability under real-time constraints. Figure 5b) (Green Trace) represents the Y-axis trajectory, again showing a smooth transition with minimal deviation from the desired value. Figure 5(c) (Pink Trace) illustrates the Z-axis response. While a minor overshoot is observed initially, the system stabilizes quickly and maintains the desired set point. The traces demonstrate tightly coupled settling behavior with negligible oscillations, confirming the effectiveness of the GWO-CS optimized LQR in real-time implementation.

Fig. 5
figure 5

Validation of quadrotor transient response for: (a) X-dimension, (b) Y-dimension, (c) Z-dimension.

Full size image

The results affirm that the proposed LQR-GWO-CS controller performs reliably not only in simulation but also in real-time conditions. The accurate trajectory tracking and reduced settling time observed across all axes validate the practicality of this approach for UAV applications requiring precision and robustness, such as surveillance, payload transport, and autonomous navigation.

Robustness analysis (T3)

To evaluate the robustness and disturbance rejection capability of the proposed LQR-GWO-CS controller, an external disturbance of 0.05 magnitude was applied to the output response between 2 and 7 s. This scenario mimics real-world conditions such as wind gusts or load variations commonly encountered during UAV missions. The position responses along the X, Y, and Z axes under the disturbance are illustrated in Fig. 6. It is observed that the controller manages to limit the deviation and swiftly restores the trajectory to the desired reference once the disturbance ceases, without introducing instability or oscillations.

Fig. 6
figure 6

Transient response characteristics under the disturbance case.

Full size image

In addition to disturbance rejection, the robustness of the proposed controller was also validated under varying initial conditions and parameter mismatches. The controller-maintained stability and acceptable performance even when slight variations in mass and inertia were introduced in the simulation model. The system consistently showed a bounded response and returned to equilibrium after disturbances, verifying its resilience against modeling uncertainties. These results confirm that the LQR-GWO-CS controller provides a robust and reliable control framework suitable for practical UAV applications operating in uncertain and dynamic environments.

Conclusions

In this study, an advanced control strategy was proposed by integrating the Linear Quadratic Regulator (LQR) with a hybrid Grey Wolf Optimizer–Cuckoo Search (GWO-CS) algorithm for optimal regulation of a quadrotor UAV. A comprehensive mathematical model of the quadrotor was developed using the Newton–Euler formalism, capturing both translational and rotational dynamics. The LQR controller was employed as the core regulator due to its optimal state-feedback capability. To overcome the limitations of manual tuning, the GWO-CS algorithm was utilized to optimally adjust the cost function weighting parameters (Q and R matrices), thereby enhancing controller performance.

Extensive simulation results demonstrated that the proposed LQR-GWO-CS framework significantly outperforms the conventional LQR, LQR-GWO, and LQR-WOA approaches in terms of key time-domain metrics such as settling time, overshoot, and Integral of Absolute Error (IAE). The results validated that the proposed method ensures faster response, better accuracy, and robust behavior under disturbances and parameter uncertainties. For instance, in the X-axis response, the proposed controller achieves a reduced settling time of 1.70 s and zero overshoot, compared to 4.077 s with the standard LQR. Furthermore, OPAL-RT-based real-time simulations confirmed the controller’s reliability in practical implementation. These outcomes establish the LQR-GWO-CS approach as a highly effective and robust solution for UAV control tasks, suitable for applications in defense, surveillance, and autonomous delivery. Future work will focus on hardware experimentation and extending this optimization framework to more complex multi-agent UAV systems and adaptive mission scenarios.