Double event-triggered fault tolerant consensus of nonlinear heterogeneous multiagent systems under inconsistent Markov

Abstract

This paper addresses the fault-tolerant control of nonlinear heterogeneous multi-agent systems with actuators and sensors affected by faults under inconsistent Markov switching topology. A double event-triggered strategy is introduced to reduce the communication burden in the network and to improve the effectiveness. Moreover, to avoid Zero behavior, the considered event-triggered conditions are dependent on sampled-data. Based on this, the state observers and fault estimators are designed to estimate the system states and faults, and the estimation results are utilized to design the fault-tolerant controllers. The stability criterion of the estimated error system can be obtained based on Lyapunov theory and some inequality techniques. Finally, the effectiveness of the proposed method is verified by a numerical simulation.

Introduction

With the rapid development of computer and communication technologies, multi-agent systems (MASs) have received extensive interest. The characteristics of high efficiency and flexibility have facilitated wide applications of MASs in many fields, such as unmanned aerial vehicles (UAVs)^1,2, wireless sensor networks³, smart grids⁴ and so on. However, in real systems, the system parameters or structures are usually different, such as UAVs may face different nonlinearities in a UAV show due to their different ages or location, or a system consisting of UAVs and unmanned ground vehicles (UGVs)^5,6. Therefore, in recent years, heterogeneous MASs (HMASs) with different characteristics have gradually received wide attention^7,8,9. Considering the increasing complexity of the tasks in practice, the dynamic characteristics of the agents in the system tend to be different. Therefore, it seems more relevant that the HMASs considered in this paper are composed of first order (FO) and second order (SO) agents.

In current industrial sectors, with the increasing scale and complexity, MASs are also exposed to numerous unexpected failures, especially HMASs with more sensors and actuators. Therefore, it is significant theoretical significance and engineering application value to study the fault-tolerant control of HMASs to ensure the system is sufficiently safe and reliable. In recent years, numerous works have been carried out by scholars on HMASs with faults, for example, the system faults is considered in^10,11, the actuator faults is considered in the system^12,13, the sensor faults is considered in^14,15. In these studies, only single faults were considered, while concurrent faults involving actuators and sensors (composite faults) are relatively common in actual HMAS. For example, damage to a drone motor (actuator fault) may occur simultaneously with the loss of GPS signals (sensor fault). Some research results have also been obtained on related fault-tolerant control issues in homogeneous MASs^16,17,18. Nevertheless, for HMASs with different dynamic characteristics, these methods may not be fully applicable due to their more complex system structure, and there are still few studies addressing the related problems in the existing research results, which motivates this paper.

In the above literature and even in most of the literature on the consensus problem, the communication topology between agents is assumed to be fixed. However, the operating environment of HMASs is often subject to internal or external uncertainties that lead to topology changes in HMASs. Markov has been introduced to characterize this phenomenon. In recent years, the consensus problem of HMASs under Markov switching topologies has also been gradually attracted more attention and many important results have been obtained^19,20. However, assuming that state transition probabilities are homogeneous is often unrealistic in many cases. For example, the evolution between operating modes of DC motor equipment is determined by state transition probabilities that vary over time. Furthermore, delays or packet losses in network control systems vary over time, leading to time-varying transition probabilities. For such cases, inconsistent Markov processes are more suitable for describing these real-world systems. Currently, inconsistent Markov processes have been considered in some systems, such as neural networks^21,22 and Markov jump systems^23,24. In HMASs, agents may be affected by different environments or communication delays. For example, the low mobility of FO agents results in slow topological changes, while the high mobility and complex aerodynamic characteristics of SO agents lead to frequent/discontinuous link changes, which also causes inconsistent communication topology switching between agents. Therefore, this paper introduces inconsistent Markov processes into HMASs.

In addition, since communication resources in a system are usually limited, it is important to improve network resource utilization while ensuring system security. Event-triggered strategy (ETS) is one of the common methods to improve communication efficiency and save computational resources, and have been applied in several works^25,26,27. In traditional control systems, most of them only need to design event triggers from sensors to observers/controllers and from controllers to actuators to reduce redundant data transmission in the network channel. In contrast, it is necessary to consider information from both the agent itself and from its neighbors in HMASs, which makes the complexity of the network structure and the communication burden greatly increased. On the other hand, unnecessary data transmission can also be reduced by designing appropriate ETS, which have also been used in some literatures for fault-tolerant control of HMASs to reduce the transmission of fault messages. Inspired by^28,29, a double ETS is introduced to HMASs in this paper, which means that ETS are designed on both sensor-to-observer and observer-to-controller channels. Furthermore, to avoid Zeno behavior, the double ETS rely on sampled-data, which means that the events occur only at the instant of the sampling time.

Inspired by previous discussions, the primary target is to design event-triggered controllers that rely on sampled-data to address the consensus of nonlinear HMASs with actuator and sensor failures subject to inconsistent Markov processes. The main contributions are listed as:

(i) Unlike the results in^30,31, where all agents are considered to follow the identical Markov chain. In practice, due to the different dynamic characteristics of agents in HMASs, making their topological switching more likely to follow inconsistent Markov jumping rules. Therefore, the inconsistent Markov is introduced in HMASs in this paper, namely, the FO agent and the SO agent systems follow different Markov chains.

(ii) In contrast to the existing results in^32,33, which only considered single faults in the system. However, when both actuators and sensors in the system are affected by faults, composite faults simultaneously disturb control inputs and state measurements, these methods are inadequate for handling composite faults. Therefore, a fault-tolerant control method is designed for HMASs with actuator and sensor failures to ensure that the system maintains consensus.

(iii) Since HMASs consisting of agents with different dynamic characteristics have more sensors and actuators, to minimize the transmission of information, combining the advantages of sampled-data and ETS as well as inspired by^28,29, double ETS is introduced into HMASs, where the ETS is designed between the sensor to the observer and the observer to the controller.

Moreover, to more clearly illustrate the contributions of this paper, Table 1 is provided to summarize and compare the relevant literature mentioned, focusing on System model type, whether communication topologies involve Markov switching, the types of faults present in the systems, and the types of ETS. In Table 1, ’NO’ indicates they are not involved.

Table 1 Summarization and comparison of the mentioned articles.

Preliminaries

Notations: ${\mathscr {I}}_m$ is a identity matrix of dimension m. $\mathscr {P} > (\ge )$ 0 denotes that $\mathscr {P}$ is a positive definite (positive semi-definite) matrix. ${\mathscr {Q}}^{-1}$ and ${\mathscr {Q}}^\textrm{T}$ mean the inverse and transpose matrix of matrix ${\mathscr {B}}$, respectively. $\otimes$ represents the Kronecker product. $*$ indicates the terms derived from the omission of symmetry. For simplicity, the time parameter t is omitted in this paper, such as $x_i = x_i (t)$. Besides, the abbreviations are defined: $\hbar _\eta \buildrel \Delta \over = \hbar \left( {t - \eta } \right)$, where $\hbar = x, v, {\delta _{xi}}, {\delta _{vi}}, \delta , \Delta , e$, which will be detailed later.

Assume that ${ {\mathscr {G}}^{{\sigma _1} \left( t \right) }} = \left( { {\mathscr {N}}, { {\mathscr {E}}^{{\sigma _1} \left( t \right) }}, {A^{{\sigma _1} \left( t \right) }}} \right)$ is a weighted directed graph, with ${\mathscr {N}} = \left\{ {1, 2,..., n} \right\}$ is the set of n nodes, and ${{\mathscr {E}}^{{\sigma _1}\left( t \right) } \subseteq \mathscr {N} \times \mathscr {N}}$ represents the edge set. An edge is characterized by $e_{ij}^{\sigma _1 \left( t \right) } = \left( {j, i} \right)$. ${\mathscr {N}}_j = \{i | (i, j) \in {\mathscr {E}} \}$ is the neighbors set of agent j. ${A^{{\sigma _1} \left( t \right) }} = \left[ {a_{ij}^{{\sigma _1}\left( t \right) }} \right] \in { {\mathscr {R}}^{n \times n}}$ denotes the adjacent matrix, and ${a_{ij}} > 0$ if $\left( {{v_j}, {v_i}} \right) \in {\mathscr {E}}^{{\sigma _1}\left( t \right) }$. The degree matrix ${\mathscr {D}} = \textrm{diag}\{d_1, d_2,..., d_n \}$ with $d_i = \sum \limits _{j \in {\mathscr {N}}_i} {a_{ij}^{{\sigma _1}\left( t \right) }}$. The Laplacian matrix $L = \left( {l_{ij}^{{\sigma _1}\left( t \right) }} \right) \in {{\mathscr {R}}^{n \times n}}$ is defined as $L = {\mathscr {D}} - A$ can be characterized as:

$$\begin{aligned} l_{ij}^{{\sigma _1}\left( t \right) } = \left\{ \begin{array}{l} - a_{ij}^{{\sigma _1}\left( t \right) }, {\hspace{18.0pt}} j \ne i,\\ \sum \limits _{j = 1, j \ne i}^n {a_{ij}^{{\sigma _1}\left( t \right) }} , j = i. \end{array} \right. \end{aligned}$$

${\sigma _1} \left( t \right)$ denotes a continuous-time Markov process, the definition of which will be given later.

Problem formulation

Assume that the considered nonlinear HMASs are described as:

$$\begin{aligned} \left\{ \begin{array}{l} \left\{ \begin{array}{l} {{\dot{x}}_i} = u_i^f + f\left( x_i \right) + {w_i},\\ {y_i} = x_i^f, \end{array} \right. {\hspace{12.0pt}} i \in {N_1},\\ \left\{ \begin{array}{l} {{\dot{x}}_i} = {v_i}, \\ {{\dot{v}}_i} = u_i^f + f\left( {{x_i},{v_i}} \right) + {w_i}, \\ {y_i} = \left[ \begin{array}{l} x_i^f\\ v_i^f \end{array} \right] , \end{array} \right. i \in {N_2}, \end{array} \right. \end{aligned}$$

(1)

where ${N_1}\mathrm{{ = }} \left\{ {1, 2,..., m} \right\}$ and ${N_2}\mathrm{{ = }} \left\{ {m+1, m+2,..., n} \right\}$, which implies that HMASs (1) involves m FO and $n-m$ SO agents. ${x_i}$ and ${v_i}$ represent the state and velocity of ith agent, respectively. $y_i$ is the measurement output. $x_i^f$, $v_i^f$, $u_i^f$ represents the positions, velocities, and inputs involving fault information. $f (\cdot )$ is a nonlinear function that satisfies the Lipschitz condition. ${w_i}$ denotes external disturbance. Furthermore, the adjacency matrix ${A^{\sigma \left( t \right) }}$ for HMASs (1) is given as:

$$\begin{aligned} {A^{\sigma \left( t \right) }} = \left[ {\begin{array}{*{20}{c}} {A_{ss}^{{\sigma _1}\left( t \right) }}& {A_{sf}^{{\sigma _2}\left( t \right) }}\\ {A_{fs}^{{\sigma _1}\left( t \right) }}& {A_{ff}^{{\sigma _2}\left( t \right) }} \end{array}} \right] . \end{aligned}$$

(2)

According to the matrix (2), the matrix $A^{(\sigma (t))}$ can be considered as including four blocks. $A_{ss}^{{\sigma _1}\left( t \right) } \in {R^{n \times n}}$ denotes the adjacent matrices of SO agents, $A_{ff}^{{\sigma _2}\left( t \right) } \in {R^{m \times m}}$ is the adjacent matrices of FO agents. $A_{sf}^{{\sigma _2}\left( t \right) }$ and $A_{fs}^{{\sigma _1}\left( t \right) }$ are the adjacent matrices from SO agents to FO agents and from FO agents to SO agents, respectively. Based on this, the Laplacian matrix $L^{\sigma (t)}$ of the HMASs (1) can be divided as follows:

$$\begin{aligned} {L^{\sigma (t)}} = \left[ {\begin{array}{*{20}{c}} {L_{ss}^{{\sigma _1}\left( t \right) } + D_{sf}^{{\sigma _1}\left( t \right) }}& { - A_{sf}^{{\sigma _1}\left( t \right) }}\\ { - A_{fs}^{{\sigma _2}\left( t \right) }}& {L_{ff}^{{\sigma _2}\left( t \right) } + D_{sf}^{{\sigma _2}\left( t \right) }} \end{array}} \right] . \end{aligned}$$

where $L_{ss}^{{\sigma _1}\left( t \right) } = \left[ {l_{sij}^{{\sigma _1}\left( t \right) }} \right] \in {R^{n \times n}}$ is the laplace matrix of SO agents. $L_{ff}^{{\sigma _2}\left( t \right) } = \left[ {l_{fij}^{{\sigma _2}\left( t \right) }} \right] \in {R^{m \times m}}$ indicates the laplace matrix of FO agents. $D_{sf}^{{\sigma _1}\left( t \right) } = diag\left\{ {\sum \limits _{j \in {N_{i,f}}} {a_{ij}^{{\sigma _1}\left( t \right) }}, i \in {N_1}} \right\}$ and $D_{fs}^{{\sigma _2}\left( t \right) } = diag\left\{ {\sum \limits _{j \in {N_{i,s}}} {a_{ij}^{{\sigma _2}\left( t \right) }}, i \in {N_2}} \right\}$ denote the in-degree matrices of different order agents.

Furthemore, ${\sigma _1}\left( t \right) (t > 0)$ represents a continuous-time Markov process with right continuous trajectories and taking values in a finite set ${S_1} = \left\{ {1, 2,..., {s_1}} \right\}$ with transition probability matrix $\Pi = {\left( {{\pi _{ij}}} \right) _{s_1 \times s_1}}$ given by

$$\begin{aligned} {P_r} \left\{ {{\sigma _1}\left( {t + \Delta t} \right) = j|{\sigma _1}\left( t \right) = i} \right\} = \left\{ \begin{array}{l} {\pi _{ij}}\Delta t + o\left( {\Delta t} \right) {\hspace{15.0pt}} , i \ne j,\\ 1 + {\pi _{ii}}\Delta t + o\left( {\Delta t} \right) , i = j, \end{array} \right. \end{aligned}$$

where $\Delta t > 0$, ${\lim _{\Delta t \rightarrow 0}}\left( {o\left( {\Delta t} \right) /\Delta t} \right) = 0$ and ${\pi _{ij}} \ge 0$ $\left( \textrm{for} {\hspace{3.0pt}} i \ne j \right)$ is the transition rate from mode i at time t to mode j at time $t + \Delta t$ and ${\pi _{ii}} = - \sum \limits _{j = 1,j \ne i}^s {{\pi _{ij}}}$. ${\sigma _2}\left( t \right) (t > 0)$ stands for another Markov process that taking values in the set ${S_2} = \left\{ {1,2,...,{s_2}} \right\}$ and is related to ${\sigma _1}\left( t \right)$ as follows:

$$\begin{aligned} {P_r} \left\{ {{\sigma _2}\left( t \right) = h | {\sigma _1}\left( t \right) = l} \right\} = {p_{lh}}.\end{aligned}$$

Review the system (1), in which both sensors and actuators are subject to partial loss of effectiveness (PLOE). Specifically, the position and velocity outputs are affected by sensor failures, which are described as:

$$\begin{aligned} x_i^f = \left\{ \begin{array}{l} {x_i}, {\hspace{21.0pt}} t< {t_{fxi}},\\ {x_i} + {f_{xi}}, t \ge {t_{fxi}}, \end{array} \right. v_i^f = \left\{ \begin{array}{l} {v_i}, {\hspace{21.0pt}} t < {t_{fvi}},\\ {v_i} + {f_{vi}}, t \ge {t_{fvi}}, \end{array} \right. \end{aligned}$$

(3)

where ${f_{xi}}$ and ${f_{vi}}$ are sensor efficiency faults, namely, ${f_{xi}} = p_{xi} x_i$, ${f_{vi}} = p_{vi} v_i$, $-1< p_{xi}, p_{vi} <0$. $t_{fxi}$ and $t_{fvi}$ indicate the time of sensor failure.

Similarly, the actuator fault is depicted as:

$$\begin{aligned} u_i^f = \left\{ \begin{array}{l} {u_i}, {\hspace{21.0pt}} t < {t_{fui}},\\ {u_i} + {f_{ui}}, t \ge {t_{fui}}, \end{array} \right. \end{aligned}$$

(4)

where $u_i$ is control input, $t_{fui}$ indicates the time of actuator failure.

Assumption 1

¹⁶ The noise disturbance is limited to a known and positive upper limit, it satisfies: $\left\| {{w_i}} \right\| \le {w_{i1}}$, and $\left\| {{{\dot{w}}_i}} \right\| \le {w_{i2}}$.

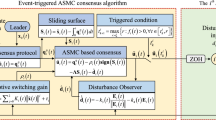
Due to multiple actuator/sensor failures in the system, the coupling effect of sensor and actuator failures further increases the complexity of system dynamics. Furthermore, inconsistent Markov also complicates changes in system topology. This coupling of inconsistent Markov and dual failures makes traditional fault-tolerant control methods difficult to apply directly, requiring the design of new observers and event-triggered strategies. To alleviate the communication burden, two event triggers are employed for sensor-to-observer and observer-to-controller. The schematic diagram of the overall design scheme is depicted in Fig. 1.

Fig. 1

Schematic diagram of the overall design scheme.

First, the following errors and fault estimation errors are defined: ${e_{xi}} = x_i^f - {\hat{x}_i} - {\hat{f}_{xi}}$, ${e_{vi}} = v_i^f - {\hat{v}_i} - {\hat{f}_{vi}}$, ${e_{fxi}} = {f_{xi}} - {\hat{f}_{xi}}$, ${e_{fvi}} = {f_{vi}} - {\hat{f}_{vi}}$. Then, based on the scheme in Fig. 1, the state observer is designed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \left\{ \begin{array}{l} {{\dot{\hat{x}}_i}} = {u_i} + f \left( {{{\hat{x}}_i}} \right) + (H_1 + F_1) {e_{xi}} ( t^i_{k} ), \\ {\hat{y}_i} = {\hat{x}_i}, \end{array} \right. {\hspace{58.0pt}} i \in {N_1}, \\ \left\{ \begin{array}{l} {{\dot{\hat{x}}_i}} = {{\hat{v}}_i}, \\ {{\dot{\hat{v}}_i}} = {u_i} + f \left( {{{\hat{x}}_i}, {{\hat{v}}_i}} \right) + {H_2} {e_{xi}} ( t^i_{k} ) + (H_3 + F_3) {e_{vi}} ( t^i_{k} ), \\ {\hat{y}_i} = \left[ \begin{array}{l} {\hat{x}_i}\\ {\hat{v}_i} \end{array} \right] , \end{array} \right. i \in {N_2}, \end{array} \right. \end{aligned}$$

(5)

and the sensor fault estimators are devised:

$$\begin{aligned} \begin{array}{l} {\dot{\hat{f}}_{xi}} = \left\{ \begin{array}{l} - {{\hat{f}}_{xi}} - F_1 {e_{xi}} ( t^i_{k}), i \in {N_1}, \\ - {{\hat{f}}_{xi}} - F_2 {e_{xi}} ( t^i_{k} ), i \in {N_2}, \end{array} \right. \\ {\dot{\hat{f}}_{vi}} = - {\hat{f}_{vi}} - F_3 {e_{vi}} ( t^i_{k} ), i \in {N_2}, \end{array} \end{aligned}$$

(6)

where ${\hat{x}}_i$, ${\hat{v}}_i$, ${\hat{f}}_i$ and $\hat{y}_i$ denote the estimate of state, velocity, fault and measurement output, respectively. Parameters $H_1$, $H_2$, $H_3$, $F_1$, $F_2$ and $F_3$ need to be devised. $e_{xi} ( t^i_{k}) = x_i^f ( t^i_{k1})- {\hat{x}_i} ( t^i_{k2}) - {\hat{f}_{xi}} ( t^i_{k2})$ and $e_{vi} ( t^i_{k}) = v_i^f ( t^i_{k1})- {\hat{v}_i} ( t^i_{k2}) - {\hat{f}_{vi}} ( t^i_{k2})$, $t^i_{k1}$ and $t^i_{k2}$ represent the last triggering moments of ETS-a and ETS-b, respectively, suppose $t_0^i = 0$.

In this paper, the considered ETS-a and ETS-b rely on sampled-data to avoid the Zeno behavior. Let $t_s$ be the sampling instants with $0 = t_0< t_1<...< t_s <...$. Based on this, when $t = t_s$, the event-triggered condition of ETS-a for the ith agent in HMASs (1) is expressed as:

$$\begin{aligned} \begin{array}{l} \delta _{xi}^T \left( {t_s} \right) {\Omega _{1}} {\delta _{xi}} \left( {t_s} \right) \le {\sigma _{1}} e_{xi}^T \left( {t_s} \right) {\Omega _{1}} {e_{xi}} \left( {t_s} \right) , i \in {N_1}, \\ \delta _{xi}^T \left( {t_s} \right) {\Omega _{2}} {\delta _{xi}} \left( {t_s} \right) \le {\sigma _{2}} e_{xi}^T \left( {t_s} \right) {\Omega _{2}} {e_{xi}} \left( {t_s} \right) , i \in {N_2}, \\ \delta _{vi}^T \left( {t_s} \right) {\Omega _{3}} {\delta _{vi}} \left( {t_s} \right) \le {\sigma _{3}} e_{vi}^T \left( {t_s} \right) {\Omega _{3}} {e_{vi}} \left( {t_s} \right) , i \in {N_2}, \end{array} \end{aligned}$$

(7)

where the error ${\delta _{xi}} \left( {t_s} \right) = {x_i^f} \left( {t_s} \right) - {x_i^f} \left( {t_{k1}^i} \right)$ and ${\delta _{vi}} \left( {t_s} \right) = {v_i^f} \left( {t_s} \right) - {v_i^f} \left( {t_{k1}^i} \right)$ represent the difference between the position and velocity at the current sampled moment and the last event-triggered instant, respectively. ${\sigma _{1}} > 0$, ${\sigma _{2}} > 0$ and ${\sigma _{3}} > 0$ denote the threshold parameter. $\Omega _1$, $\Omega _2$ and $\Omega _3$ are adjustment parameter matrix to be designed.

Similarly, the event-triggered conditions of ETS-b represented as:

$$\begin{aligned} \begin{array}{l} \theta _{xi}^T \left( {t_s} \right) {\Omega _{4}} {\theta _{xi}} \left( {t_s} \right) \le {\sigma _{4}} \varphi _{xi}^T \left( {t_s} \right) {\Omega _{4}} {\varphi _{xi}} \left( {t_s} \right) , i \in {N_1}, \\ \theta _{xi}^T \left( {t_s} \right) {\Omega _{5}} {\theta _{xi}} \left( {t_s} \right) \le {\sigma _{5}} \varphi _{xi}^T \left( {t_s} \right) {\Omega _{5}} {\varphi _{xi}} \left( {t_s} \right) , i \in {N_2}, \\ \theta _{vi}^T \left( {t_s} \right) {\Omega _{6}} {\theta _{vi}} \left( {t_s} \right) \le {\sigma _{6}} \varphi _{vi}^T \left( {t_s} \right) {\Omega _{6}} {\varphi _{vi}} \left( {t_s} \right) , i \in {N_2}, \end{array} \end{aligned}$$

(8)

where ${\theta _{{\hat{x}}_i}} \left( {t_s} \right) = \sum \limits _{j \in {{\mathscr {N}}_i}} {{a_{ij}} \left( {e_{{\hat{x}}_i} \left( {t_s} \right) - {e_{{{\hat{x}}_j}}} \left( {t_s} \right) } \right) }$, ${e_{{\hat{x}}_i}} \left( {t_s} \right) = {\hat{x}_i} \left( {{t_s}} \right) - {\hat{x}_i} \left( {t_{{k_2}}^i} \right)$, $\varphi _{{\hat{x}_{i} }} \left( {t_{s} } \right)\; = \;$$\sum\limits_{{j \in {\mathcal{N}}_{i} }} {a_{{ij}} }$$\left( {\hat{x}_{i} \left( {t_{s} } \right) - \hat{x}_{j} \left( {t_{s} } \right)} \right)$; ${\theta _{{\hat{v}}_i}} \left( {t_s} \right) = \sum \limits _{j \in {{\mathscr {N}}_i}} {{a_{ij}} \left( {e_{{\hat{v}}_i} \left( {t_s} \right) - {e_{{{\hat{v}}_j}}} \left( {t_s} \right) } \right) }$, ${e_{{\hat{v}}_i}} \left( {t_s} \right) = {\hat{v}_i} \left( {{t_s}} \right) - {\hat{v}_i} \left( {t_{{k_2}}^i} \right)$, ${\varphi _{{\hat{v}}_i}} \left( {t_s} \right) =\;$$\sum \limits _{j \in {{\mathscr {N}}_i}} {{a_{ij}} \left( {{\hat{v}}_i \left( {t_s} \right) - {{\hat{v}}_j} \left( {t_s} \right) } \right) }$. ${\sigma _{4}} > 0$, ${\sigma _{5}} > 0$ and ${\sigma _{6}} > 0$ denote the threshold parameter. $\Omega _4$, $\Omega _5$ and $\Omega _6$ are adjustment parameter matrix to be designed.

Remark 1

The double ETS (ETS-a and ETS-b) proposed in this paper rely on sampled data, which means event-triggered occurs only at discrete sampling instants, thereby fundamentally avoiding Zeno behavior. Compared with general ETS in^25,26,27 or double ETS in^28,29, the double ETS are applied to HMASs with inconsistent Markov and compound failures, significantly reducing communication overhead while ensuring system consistency.

Defining $0 \le \eta = t - {\tau _s}h \le {\eta _k} = {t_{k + 1}} - {\tau _s}h \le {\eta _M}$ with $\dot{\eta }\left( t \right) = 1$, from ${\delta _{xi}} \left( {t_s} \right) = {x_i^f} \left( {t_s} \right) - {x_i^f} \left( {t_{k1}^i} \right)$, it has $x_i^f \left( {t_{k1}^i} \right) = x_{i\eta }^f - \delta _{x_ {i\eta }}$. Likewise, $v_i^f \left( {t_{k1}^i} \right) = v_{i\eta }^f - \delta _{v_ {i\eta }}$. Similar to the transformation, define a transition variable ${\delta _{fi}}\left( {{\tau _s}h} \right) = {\hat{f}_{xi}}\left( {{\tau _s}h} \right) - {\hat{f}_{xi}}\left( {t_{{k_2}}^i} \right)$.

Let $\tilde{e}_i = \mathrm{{col}}$$\{ e_1, e_2, e_3 \}$, $e_1 = \mathrm{{col}}$$\{ e_{x_1}, e_{x_2}, \;$$\ldots , e_{x_m} \}$, $e_2 = \mathrm{{col}}$$\{ e_{x_{m+1}}, e_{x_{m+2}},$$\;\ldots , e_{x_n} \}$, $e_{3} \; = \; {\text{col}}$$\{ e_{{v_{{m + 1}} }} ,e_{{v_{{m + 2}} }} ,\;$$\ldots ,e_{{v_{n} }} \}$, $\tilde{e}_{f_i} = \mathrm{{col}}$$\{ e_{f_1}, e_{f_2}, e_{f_3} \}$, $e_{f_1} = \mathrm{{col}}$$\{ e_{f_{x_1}}, e_{f_{x_2}},$$\;\ldots , e_{f_{x_m}} \}$, $e_{{f_{2} }} = {\text{col}}$$\{ e_{{f_{{x_{{m + 1}} }} }} ,e_{{f_{{x_{{m + 2}} }} }} ,$$\;\ldots ,e_{{f_{{x_{n} }} }} \}$, $e_{f_3} = \mathrm{{col}}$$\{ e_{f_{v_{m+1}}}, e_{f_{v_{m+2}}},$$\;\ldots , e_{f_{v_n}} \}$, $\tilde{\delta }_i = \mathrm{{col}}$$\{ \delta _1, \delta _2, \delta _3 \}$, $\delta _1 = \mathrm{{col}}$$\{ \delta _{e_{x_1}}, \delta _{e_{x_2}},$$\;\ldots , \delta _{e_{x_m}} \}$, $\delta _2 = \mathrm{{col}}$$\{ \delta _{e_{x_{m+1}}}, \delta _{e_{x_{m+2}}},$$\;\ldots , \delta _{e_{x_{n}}} \}$, $\delta _3 = \mathrm{{col}}$$\{ \delta _{e_{v_{m+1}}}, \delta _{e_{v_{m+2}}},$$\;\ldots , \delta _{e_{v_{n}}} \}$, ${\tilde{f}}_i = \mathrm{{col}}$$\left\{ {f(x_{i} )} \right.$$- f(\hat{x}_{i} ),$$f(x_{i} ,v_{i} )\; - \;$$f\left( {\hat{x}_{i} ,\hat{v}_{i} } \right)v_{i} \; - \;$$\left. {f\left( {\hat{x}_{i} ,\hat{v}_{i} } \right)} \right\}$, $\varpi = \mathrm{{col}}$$\{ \omega ,f_{{xi}} ,f_{{xj}} ,f_{{vj}} ,$$f_{{ui}} ,\dot{f}_{{xi}} ,\dot{f}_{{xj}} ,\dot{f}_{{vj}} \}$, $i \in N_1$, $j \in N_2$. From the definition of error and the fault estimation error, one obtains:

$$\begin{aligned} {\dot{\tilde{e}}}_i= & B \tilde{e}_i - B {{\tilde{e}}_f} - {H} \tilde{e}_{i\eta } + {H} \tilde{\delta }_{i\eta } + C \tilde{f} + {E_1} \tilde{\varpi }_i, \end{aligned}$$

(9)

$$\begin{aligned} {\dot{\tilde{e}}_{fi}}= & - {\tilde{e}}_{fi} -F \tilde{e}_{i\eta } + F \tilde{\delta }_ {i \eta } + {E_2} \tilde{\varpi }_i, \end{aligned}$$

(10)

where

$$\begin{aligned} B = \left[ {\begin{array}{*{20}{c}} 0 & 0 & 0 \\ 0 & 0 & I_2 \\ 0 & 0 & 0 \end{array}} \right] , C = \left[ {\begin{array}{*{20}{c}} I_1 & 0 \\ 0 & 0 \\ 0 & I_2 \end{array}} \right] , {E_1} = \left[ {\begin{array}{*{20}{c}} I_3 & I_1 & 0 & 0 & I_1 & I_1 & 0 & 0 \\ 0 & 0 & I_2 & 0 & 0 & 0 & I_2 & 0 \\ I_4 & 0 & 0 & I_2 & I_2 & 0 & 0 & I_2 \end{array}} \right] , \\ H = \left[ {\begin{array}{*{20}{c}} H_1 & 0 & 0 \\ 0 & - F_2 & 0 \\ 0 & H_2 & H_3 \end{array}} \right] , F = \left[ {\begin{array}{*{20}{c}} F_1 & 0 & 0 \\ 0 & F_2 & 0 \\ 0 & 0 & F_3 \end{array}} \right] , {E_2} = \left[ {\begin{array}{*{20}{c}} 0 & I_1 & 0 & 0 & 0 & I_1 & 0 & 0 \\ 0 & 0 & I_2 & 0 & 0 & 0 & I_2 & 0 \\ 0 & 0 & 0 & I_2 & 0 & 0 & 0 & I_2 \end{array}} \right] . \end{aligned}$$

with $I_1= {\mathscr {I}}_m$, $I_2={\mathscr {I}}_{n-m}$, $I_3 = \textrm{diag} \{{\mathscr {I}}_m, 0_{n-m}\}$, $I_4 = \textrm{diag} \{0_m, {\mathscr {I}}_{n-m}\}$.

Let ${\tilde{\varepsilon }}_i = \mathrm{{col}} \{ {\tilde{e}}_i, {\tilde{e}}_{fi} \}$, based on (9) and (10), the following augmented system can be derived:

$$\begin{aligned} \begin{array}{l} {\dot{\tilde{\varepsilon }}_i} = \tilde{B} \tilde{\varepsilon }_i - \tilde{H} \tilde{I} \tilde{\varepsilon }_{i \eta } + \tilde{H} \tilde{\delta }_{i \eta } + \tilde{C} {{\tilde{f}}_i} + {\tilde{E}} \tilde{\varpi }_i, \end{array} \end{aligned}$$

(11)

where

$$\begin{aligned} \tilde{B} = \left[ {\begin{array}{*{20}{c}} B& { - B}\\ 0& -{I_5} \end{array}} \right] , \tilde{H} = \left[ \begin{array}{l} {H} \\ {F} \end{array} \right] , \tilde{I} = \left[ {\begin{array}{*{20}{c}} {I_5}&0 \end{array}} \right] , \tilde{C} = \left[ \begin{array}{l} C\\ 0 \end{array} \right] , \tilde{E} = \left[ \begin{array}{l} {E_1}\\ {E_2} \end{array} \right] , \\ I_5 = {\mathscr {I}}_{2n+m} = \mathrm{{diag}} \{{\mathscr {I}}_m, {\mathscr {I}}_{n-m}, {\mathscr {I}}_{n-m}\}. \end{aligned}$$

In this step, the objective is to address the fault-tolerant estimation for HMASs with inconsistent Markov topology by designing the observer (5), adaptive fault tolerant laws (6) and ETS-a (7), so that the augmented system (11) can be stable and satisfy:

(1) for $\varpi _i = 0$, the system (11) is stable;

(2) under the zero-initial condition, for all non-zero $\varpi _i = 0$, the system (11) satisfies the ${H_\infty }$ performance index requirement ${\left\| {\tilde{\varepsilon }_i} \right\| _2} \le \beta {\left\| {\varpi _i} \right\| _2}$.

Based on the above analysis, the fault tolerant controller will next be designed by using the estimation information as compensation to enable the heterogeneous multi-agent system can achieve consensus.

Let ${X_1} = \mathrm{{col}} \{ \hat{x}_1, \hat{x}_2, \ldots , \hat{x}_m \}$, ${X_2} = \mathrm{{col}} \{ \hat{x}_{m + 1}, \hat{x}_{m + 2}, \ldots , \hat{x}_n \}$, ${X_3}= \mathrm{{col}} \{ \hat{v}_{m + 1}, \hat{v}_{m + 2}, \ldots , \hat{v}_n \}$. Define the consensus error as: ${e_{\hat{x}_i}} = {\hat{x}_1} - {\hat{x}_i}$, $i \in N_1$, ${e_{\hat{x}_j}} = {\hat{x}_{m + 1}} - {\hat{x}_j}$, $i \in N_2$, ${e_{\hat{v}j}} = {\hat{v}_{m + 1}} - {\hat{v}_j}$, $j \in N_2$. Then, for $i \in N_1$, one has ${e_{\hat{x}i}} = \left( {{C_1} \otimes {I_p}} \right) {X_1}$, ${X_1}\left( t \right) = \left( {{D_1} \otimes {I_p}} \right) {e_{\hat{x}i}}\left( t \right) + \left( {{\mathbf{{1}}_{m - 1}} \otimes {I_p}} \right) {\hat{x}_1}\left( t \right)$, with ${C_1} = \left[ {1, - {I_{m - 1}}} \right]$, ${D_1} = \left[ {0, - {I_{m - 1}}} \right] ^T$. For $i \in N_2$, there’s a similar transformation. Based on this, the consensus error system can be described:

$$\begin{aligned} \dot{\bar{e}}_i = B \bar{e}_i - \left( {\bar{L} \otimes K} \right) \bar{e}_{i \eta } + \left( {\bar{L} \otimes K} \right) \bar{\Delta }_{i \eta } + C \bar{f} + D \bar{\varpi }_i, \end{aligned}$$

(12)

where ${\bar{e}_i} = \mathrm{{col}} \{ e_{\hat{x}_i}, e_{\hat{x}_j}, e_{\hat{v}_j} \}$, $\bar{\Delta }_i = \left( {C_1} \otimes {I_p} \right) {\bar{\delta }_i}$, $\bar{\delta }_i = \mathrm{{col}} \{ \bar{\delta }_1, \bar{\delta }_2, \bar{\delta }_3 \}$, $\bar{\delta }_1 = \mathrm{{col}}$$\{ \delta _{e_{\hat{x}_1}}, \delta _{e_{\hat{x}_2}},$$\;\ldots , \delta _{e_{\hat{x}_m}} \}$, $\bar{\delta }_2 = \mathrm{{col}}$$\{ \delta _{e_{\hat{x}_{m+1}}}, \delta _{e_{\hat{x}_{m+2}}},$$\;\ldots , \delta _{e_{\hat{x}_{n}}} \}$, $\bar{\delta }_3 = \mathrm{{col}}$$\{ \delta _{e_{\hat{v}_{m+1}}}, \delta _{e_{\hat{v}_{m+2}}},$$\;\ldots , \delta _{e_{\hat{v}_{n}}} \}$. $\bar{\varpi }_i =$$\;\{ {\mathscr {E}}_{i \eta }, \Delta _{e_{i \eta }} \}$, ${\mathscr {E}}_{i \eta } =$$\;{C_1} \otimes {I_p} \tilde{e}_i$, $\Delta _{e_{i \eta }} =\;$${C_1} \otimes {I_p} \tilde{\delta }_i$, $D = \left[ { - \bar{L} \otimes H, \bar{L} \otimes H} \right]$.

The main target is to deal with the consensus problem for HMASs, the controller and event-triggered scheme (8) are proposed so that the consensus error system is stable and meet condition: ${\left\| {\bar{e}} \right\| _2} \le {\beta _2} {\left\| {\varpi _2} \right\| _2}$.

Assumption 2

³⁴ For the nonlinear function $f \left( \cdot \right)$, there exists constants ${\eta _1}$, ${\eta _2} > 0$ for any x, v, $x'$, $v'$, such that

$$\begin{aligned} \left\| {f\left( {x, v} \right) - f\left( {x', v'} \right) } \right\| \le {\eta _1}\left\| {x - x'} \right\| + {\eta _2}\left\| {v - v'} \right\| .\end{aligned}$$

Main results

In this part, sufficient conditions for addressing the fault estimation and consensus control problems of HMASs (1) will be obtained. For convenience, the symbols present in the paper are summarized in Table 2.

Table 2 Symbol and its physical meaning.

Theorem 1

Assuming the graph ${\mathscr {G}}$ exists directed spanning tree. For given scalars $\eta _1$, $\eta _2$, $\eta _3$, $\beta$, $\vartheta _1$, $\eta _M$, the augmented system (11) is stable, if there exist real matrices $\tilde{P}$, $\tilde{Q}_1$, $\tilde{Q}_2$ > 0 and appropriate dimensions matrix $\tilde{W}_1$, $\tilde{W}_2$, $\tilde{\Omega }$ such that:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\Sigma _{1}}} & {{\Sigma _{2}}}\\ {*} & {{\Sigma _{3}}} \end{array}} \right] < 0, \end{aligned}$$

(13)

where

$$\begin{aligned} \begin{array}{l} \Sigma _1 = \left[ {\begin{array}{*{20}{c}} {\Sigma _{11}} & {{\tilde{\Upsilon }}_{12}} & {{\tilde{\Upsilon }}_{13}} & {{\tilde{\Upsilon }}_{14}} & {{\tilde{\Upsilon }}_{15}} & {{\tilde{\Upsilon }}_{16}} & {{\tilde{\Upsilon }}_{17}} \\ {*} & {{\tilde{\Upsilon }}_{22}} & {{\tilde{\Upsilon }}_{23}} & 0 & 0 & 0 & {{\tilde{\Upsilon }}_{27}} \\ {*} & * & {{\tilde{\Upsilon }}_{33}} & 0 & 0 & 0 & 0 \\ {*} & * & * & {{\tilde{\Upsilon }}_{44}} & 0 & 0 & {{\tilde{\Upsilon }}_{47}} \\ {*} & * & * & * & {{\tilde{\Upsilon }}_{55}} & 0 & {{\tilde{\Upsilon }}_{57}} \\ {*} & * & * & * & * & {{\tilde{\Upsilon }}_{66}} & {{\tilde{\Upsilon }}_{67}} \\ {*} & * & * & * & * & * & {\Sigma _{77}} \end{array}} \right] , \\ {\Sigma _{2}} = {\mathrm{{diag}} \left\{ {{\eta _1} {I_1}, \sqrt{2} {\eta _2} {I_2}, \sqrt{2} {\eta _3} {I_2}} \right\} \tilde{P}}, {\Sigma _{3}} = - I_5, \end{array} \end{aligned}$$

(14)

with

$$\begin{aligned} \begin{array}{l} {{\tilde{\Upsilon }}_{11}} = \sum \limits _{n = 1} ^\lambda {{\pi _{lq}} I_5 \otimes \tilde{P}} + 2 \tilde{B} \otimes \tilde{P} + I_5 \otimes {{\tilde{Q}}_1} - I_5 \otimes {{\tilde{W}}_1}, {{\tilde{\Upsilon }}_{12}} = L \otimes Y_1 + I_5 \otimes {{\tilde{W}}_1} - I_5 \otimes {{\tilde{W}}_2}, \\ {{\tilde{\Upsilon }}_{13}} = I_5 \otimes {{\tilde{W}}_2}, {{\tilde{\Upsilon }}_{14}} = - L \otimes Y_1, {{\tilde{\Upsilon }}_{15}} = \tilde{C}, {{\tilde{\Upsilon }}_{16}} = \tilde{E}, {{\tilde{\Upsilon }}_{22}} = I_5 \otimes ({- 2{\tilde{W}}_1} + {{\tilde{W}}_2} + \tilde{W}_2^\mathrm{{T}} + \Phi ),\\ \Phi = \left[ { \sigma \tilde{\Omega },0} \right] , {{\tilde{\Upsilon }}_{23}} = I_5 \otimes ({{\tilde{W}}_1} - {{\tilde{W}}_2}), {{\tilde{\Upsilon }}_{33}} = - I_5 \otimes ( {{\tilde{Q}}_1} - {{\tilde{W}}_1}), {{\tilde{\Upsilon }}_{44}} = - I_5 \otimes \tilde{\Omega }, \\ {{\tilde{\Upsilon }}_{55}} = - {I_{n + m}}, {{\tilde{\Upsilon }}_{66}} = - {\beta ^2} I_5, {{\tilde{\Upsilon }}_{17}} = {\left( {\tilde{B} \otimes \tilde{P}} \right) ^\mathrm{{T}}}, {{\tilde{\Upsilon }}_{27}} = {\left( {L \otimes Y_1} \right) ^\mathrm{{T}}}, {{\tilde{\Upsilon }}_{47}} = - {\left( {L \otimes Y_1} \right) ^\mathrm{{T}}},\\ {{\tilde{\Upsilon }}_{57}} = {\left( {\tilde{C} \otimes \tilde{P}} \right) ^\mathrm{{T}}}, {{\tilde{\Upsilon }}_{67}} = {\left( {\tilde{E} \otimes \tilde{P}} \right) ^\mathrm{{T}}}, {{\Sigma }_{77}} = I_5 \otimes ( {\vartheta ^2} \eta _M^{ - 2} {{\tilde{Q}}_2} - 2 \vartheta \tilde{P}), \end{array} \end{aligned}$$

and satisfies the ${H_\infty }$ performance. Moreover, the observer parameters can be obtained: $\tilde{H} = Y_1 \tilde{P}^{-1}$.

Proof

Choose the following Lyapunov function:

$$\begin{aligned} {V_1} \left( {t, \sigma \left( t \right) } \right) = {{\tilde{\varepsilon }}^T} {P_{\sigma \left( t \right) }} \tilde{\varepsilon }+ \int _{t - {\eta _M}}^t {{{\tilde{\varepsilon }}^T} \left( s \right) {Q_1} \tilde{\varepsilon }\left( s \right) ds} + {\eta _M} \int _{ - {\eta _M}}^0 {\int _{t + \theta }^t {{\dot{\tilde{\varepsilon }}^T} \left( s \right) {Q_2} \dot{\tilde{\varepsilon }} \left( s \right) ds d\theta } }. \end{aligned}$$

(15)

When $\sigma \left( t \right) = l$, by the weak infinitesimal operator $\mathscr {L}$ in , one yields

$$\begin{aligned} \begin{array}{l} L{V_1}\left( {t,\sigma } \right) = \textrm{E} \left\{ {2{{\tilde{\varepsilon }}^T} {P_l} \left( \tilde{B} \tilde{\varepsilon }_i - \tilde{H} \tilde{I} \tilde{\varepsilon }_i + \tilde{H} \tilde{\delta }_i + \tilde{C} {{\tilde{f}}_i} + {\tilde{E}} \tilde{\varpi }_i \right) + {{\tilde{\varepsilon }}^T} \sum \limits _{n = 1}^\lambda {{\pi _{lq}}{P_l}} \tilde{\varepsilon }} \right. \\ {\hspace{58.0pt}} \left. { + {\tilde{\varepsilon }^\textrm{T}} {Q_1}\tilde{\varepsilon }- {\tilde{\varepsilon }^T}\left( {t - {\eta _M}} \right) {Q_1} \tilde{\varepsilon }\left( {t - {\eta _M}} \right) } + \eta _M^2 {\dot{\tilde{\varepsilon }}^T} {Q_2} \dot{\tilde{\varepsilon }} \right. \\ {\hspace{58.0pt}} \left. { - {\eta _M} \int _{t - {\eta _M}}^t {{\dot{\tilde{\varepsilon }}^T} \left( s \right) {Q_2} \dot{\tilde{\varepsilon }} \left( s \right) ds} } \right\} . \end{array} \end{aligned}$$

(16)

From Assumption 1, one obtains

$$\begin{aligned} & f^\mathrm{{T}} \left( {{x_i}} \right) f \left( x_i \right) \le {\eta _1} e_{xi}^T {e_{xi}}, \end{aligned}$$

(17)

$$\begin{aligned} & f^\mathrm{{T}} \left( {{x_i}, {v_i}} \right) f \left( {{x_i}, {v_i}} \right) \le 2 \eta _2^2 e_{xi}^T {e_{xi}} + 2 \eta _3^2 e_{vi}^T {e_{vi}}. \end{aligned}$$

(18)

Furthermore, according to Jensen’s inequality³⁵ and Lemma 3 in³⁶, it follows that

$$\begin{aligned} {\hspace{7.0pt}} - {\eta _M}\int _{t - {\eta _M}}^t {\dot{\tilde{\varepsilon }}^T \left( s \right) {Q_2} \tilde{\varepsilon }\left( s \right) ds} \le \varsigma ^T_0 \Upsilon _0 \varsigma _0, \end{aligned}$$

(19)

where

$$\begin{aligned} \begin{array}{l} \varsigma _0 = \mathrm{{col}} \left[ {\tilde{\varepsilon }, \tilde{\varepsilon }_\eta , \tilde{\varepsilon }( {t - {\eta _M}} )} \right] , \\ \Upsilon _0 = \left[ {\begin{array}{*{20}{c}} - W_1 & W_1 - W_2 & W_2 \\ {*} & -2 W_1 + W_2 + W^T_2 & W_1 - W_2 \\ {*} & * & - W_1 \end{array}} \right] . \end{array} \end{aligned}$$

(20)

Combining the above formula, ETS-a and Kronecker product, one has

$$\begin{aligned} \begin{array}{l} \mathrm{{E}} \left\{ {{\mathscr {L}} V \left( {t,\sigma \left( t \right) } \right) } \right\} \le \varsigma _1^\mathrm{{T}} {\Upsilon _1} {\varsigma _1} + \eta _M^2 {\dot{\tilde{\varepsilon }}^T} {Q_2} \dot{\tilde{\varepsilon }} - {{\tilde{\varepsilon }}^\mathrm{{T}}} \tilde{\varepsilon }+ {\beta ^2} {\varpi ^\mathrm{{T}}} \varpi \\ {\hspace{62.0pt}} \le \varsigma _1^\mathrm{{T}} \left( {{\Upsilon _1} + \Upsilon _2^\mathrm{{T}} \left( {\eta _M^2{Q_2}} \right) {\Upsilon _2}} \right) {\varsigma _1} - {{\tilde{\varepsilon }}^\mathrm{{T}}} \tilde{\varepsilon }+ {\beta ^2} {\varpi ^\mathrm{{T}}} \varpi , \end{array} \end{aligned}$$

(21)

where $\varsigma _1 = \mathrm{{col}} \left[ {\tilde{\varepsilon }, \tilde{\varepsilon }_\eta , \tilde{\varepsilon }( {t - {\eta _M}} ), \tilde{\delta }_\eta , F, \varpi } \right]$, by using Schur complement³⁷, $\Upsilon$ can be obtained as following:

$$\begin{aligned} \Upsilon = \left[ {\begin{array}{*{20}{c}} {\Upsilon _1}& {\Upsilon _2^\mathrm{{T}}}\\ {*} & {\Upsilon _3} \end{array}} \right] , \end{aligned}$$

(22)

where

$$\begin{aligned} {\Upsilon _1} = \left[ {\begin{array}{*{20}{c}} {\Upsilon _{111}} & {\Upsilon _{112}} & {\Upsilon _{113}} & {\Upsilon _{114}} & {\Upsilon _{115}} & {\Upsilon _{116}} \\ {*} & {\Upsilon _{122}} & {\Upsilon _{123}} & 0 & 0 & 0 \\ {*} & * & {\Upsilon _{133}} & 0 & 0 & 0 \\ {*} & * & * & {\Upsilon _{144}} & 0 & 0 \\ {*} & * & * & * & {\Upsilon _{155}} & 0 \\ {*} & * & * & * & *& {\Upsilon _{166}} \end{array}} \right] , \\ {\Upsilon _2} = \left[ {\begin{array}{*{20}{c}} {\tilde{B}}&{ - L \otimes \tilde{K}}&0&{L \otimes \tilde{K}}&{\tilde{C}}&{\tilde{E}} \end{array}} \right] , {\Upsilon _3} = - {\left( {\eta _M^2{Q_2}} \right) ^{ - 1}}, \end{aligned}$$

with

$$\begin{aligned} \begin{array}{l} {\Upsilon _{111}} = \sum \limits _{n = 1}^\lambda {{\pi _{lq}} I_5 \otimes {P_l}} + 2{P_l} \otimes \tilde{B} + I_5 \otimes {Q_1} - I_5 \otimes {W_1} + {\Upsilon _{1111}}, \\ {\Upsilon _{1111}} = \mathrm{{diag}} \left\{ {\eta _1^2 {I_1}, 2 \eta _2^2 {I_2}, 2 \eta _3^2 {I_2}, 0, 0, 0} \right\} , {\Upsilon _{112}} = - {P_l} \left( {L \otimes \tilde{K}} \right) + I_5 \otimes {W_1} - I_5 \otimes {W_2},\\ {\Upsilon _{113}} = I_5 \otimes {W_2}, {\Upsilon _{114}} = {P_l} \left( {L \otimes \tilde{K}} \right) , {\Upsilon _{115}} = {P_l} \otimes \tilde{C}, {\Upsilon _{116}} = {P_l} \otimes \tilde{E},\\ {\Upsilon _{122}} = I_5 \otimes (- 2{W_1} + {W_2} + W_2^\mathrm{{T}} + \tilde{\Omega }), \tilde{\Omega }= \left[ { \sigma \Omega ,0} \right] , {\Upsilon _{123}} =I_5 \otimes ({W_1} - {W_2}),\\ {\Upsilon _{133}} = - I_5 \otimes ({Q_1} + {W_1}), {\Upsilon _{144}} = - I_5 \otimes \Omega , {\Upsilon _{155}} = - {I_{n + m}}, {\Upsilon _{166}} = - {\beta ^2_1}I_5. \end{array} \end{aligned}$$

Defining $\tilde{P} = P_l^{ - 1}$, ${\tilde{Q}_1} = \tilde{P}{Q_1}\tilde{P}$. Then, pre- and post-multiplying both sides of (15) by $\mathrm{{diag}}\left\{ {\tilde{P},\tilde{P},\tilde{P},\tilde{P},I,I,I} \right\}$ and its transpose, one has

$$\begin{aligned} \tilde{\Upsilon }= \left[ {\begin{array}{*{20}{c}} {{\tilde{\Upsilon }}_{11}} & {{\tilde{\Upsilon }}_{12}} & {{\tilde{\Upsilon }}_{13}} & {{\tilde{\Upsilon }}_{14}} & {{\tilde{\Upsilon }}_{15}} & {{\tilde{\Upsilon }}_{16}} & {{\tilde{\Upsilon }}_{17}} \\ {*} & {{\tilde{\Upsilon }}_{22}} & {{\tilde{\Upsilon }}_{23}} & 0 & 0 & 0 & {{\tilde{\Upsilon }}_{27}} \\ {*} & * & {{\tilde{\Upsilon }}_{33}} & 0 & 0 & 0 & 0 \\ {*} & * & * & {{\tilde{\Upsilon }}_{44}} & 0 & 0 & {{\tilde{\Upsilon }}_{47}} \\ {*} & * & * & * & {{\tilde{\Upsilon }}_{55}} & 0 & {{\tilde{\Upsilon }}_{57}} \\ {*} & * & * & * & * & {{\tilde{\Upsilon }}_{66}} & {{\tilde{\Upsilon }}_{67}} \\ {*} & * & * & * & * & * & {{\tilde{\Upsilon }}_{77}} \end{array}} \right] , \end{aligned}$$

(23)

with

$$\begin{aligned} \begin{array}{l} {{\tilde{\Upsilon }}_{11}} = \sum \limits _{n = 1} ^\lambda {{\pi _{lq}} I_5 \otimes \tilde{P}} + 2 \tilde{B} \otimes \tilde{P} + I_5 \otimes {{\tilde{Q}}_1} - I_5 \otimes {{\tilde{W}}_1} + {{\tilde{\Upsilon }}_{111}},\\ {{\tilde{\Upsilon }}_{111}} = \mathrm{{diag}}\{ {\eta _1^2 {I_1}}, {2 \eta _2^2 {I_2}}, {2\eta _3^2 {I_2}}, 0, 0, 0 \} {{\tilde{P}}^2}, {\tilde{\Upsilon }_{77}} = - I_5 \otimes {\left( {\eta _M^2 {Q_2}} \right) ^{ - 1}}. \end{array} \end{aligned}$$

Moreover, from Lemma3 in³⁸, one has the following:

$$\begin{aligned} \begin{array}{l} {\tilde{\Upsilon }_{77}} = - I_5 \otimes {\left( {\eta _M^2{Q_2}} \right) ^{ - 1}} = - I_5 \otimes \tilde{P} \left( {\eta _M^2 {\tilde{Q}}_2} \right) ^{-1} \tilde{P} \\ {\hspace{16.0pt}}\le I_5 \otimes ({\vartheta ^2_1} \eta _M^2 {{\tilde{Q}}_2} - 2 \vartheta _1 \tilde{P}) = {{\Sigma }_{77}}. \end{array} \end{aligned}$$

(24)

Further, apply Schur complement to $\tilde{\Upsilon }$, $\Sigma$ is obtained as shown in Theorem 1.

If $\Sigma < 0$ hold, then one yields

$$\begin{aligned} \mathrm{{E}}\left\{ {V\left( {e\left( { + \infty } \right) } \right) } \right\} - \mathrm{{E}}\left\{ {V\left( {e\left( 0 \right) } \right) } \right\} \le \mathrm{{E}} \left\{ {\int _0^{ + \infty } {\left( { - {{\tilde{e}}^\mathrm{{T}}} \tilde{e} + {\beta ^2}{\varpi ^\mathrm{{T}}} \varpi } \right) dt} } \right\} . \end{aligned}$$

(25)

Under zero initial condition $V\left( {e\left( 0 \right) } \right) = 0$, it is easy to show that $\mathrm{{E}}\left\{ {V\left( {e\left( { + \infty } \right) } \right) } \right\} = \mathrm{{E}}\left\{ {\int _0^{ + \infty } {LV\left( {t,\sigma \left( t \right) } \right) dt} } \right\} \ge 0$. Furthermore, one can get $\mathrm{{E}}\left\{ {\int _0^{ + \infty } {{{\tilde{e}}^\mathrm{{T}}}\tilde{e}dt} } \right\} \le {\gamma ^2}\mathrm{{E}}\left\{ {\int _0^{ + \infty } {{\varpi ^\mathrm{{T}}} \varpi dt} } \right\}$. It completes the proof. $\square$

Theorem 2

Assuming the graph ${\mathscr {G}}$ exists directed spanning tree. For given scalars $\eta _4$, $\eta _5$, $\eta _6$, $\beta _2$, $\vartheta _2$, $\eta _M$, the estimation error system 12 is stable, if there exist real matrices $\bar{R}$, $\bar{Q}_3$, $\bar{Q}_4$ and appropriate dimensions matrix $\bar{W}_3$, $\bar{W}_4$, $\bar{\Omega }$ such that:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} \Xi _{1} & \Xi _{2} \\ {*} & \Xi _{3} \end{array}} \right] < 0, \end{aligned}$$

(26)

where

$$\begin{aligned} \begin{array}{l} \Xi _1 = \left[ {\begin{array}{*{20}{c}} \Xi _{11} & \Xi _{12} & \Xi _{13} & \Xi _{14} & \Xi _{15} & \Xi _{16} & \Xi _{17} \\ {*} & \Xi _{22} & \Xi _{23} & \Xi _{24} & 0 & 0 & \Xi _{27} \\ {*} & * & \Xi _{33} & 0 & 0 & 0 & 0 \\ {*} & * & * & \Xi _{44} & 0 & 0 & \Xi _{47} \\ {*} & * & * & * & \Xi _{55} & 0 & \Xi _{57} \\ {*} & * & * & * & * & \Xi _{66} & \Xi _{67} \\ {*} & * & * & * & * & * & \Xi _{77} \end{array}} \right] , \\ {\Xi _{2}} = \mathrm{{diag}} \left\{ {{\eta _1} {I_n}, \sqrt{2} {\eta _2} {I_m}, \sqrt{2} {\eta _3} {I_m}} \right\} \bar{R}, {\Xi _{3}} = - I_6, \end{array} \end{aligned}$$

with

$$\begin{aligned} \begin{array}{l} I_6 = {\mathscr {I}}_{2n-m-3} = \mathrm{{diag}} \{{\mathscr {I}}_{m-1}, {\mathscr {I}}_{n-m-1}, {\mathscr {I}}_{n-m-1}\}, {{\Xi }_{11}} = I_6 \otimes (\sum \limits _{n = 1}^\lambda {{\pi _{lq}} \bar{R}} + {{\bar{Q}}_3} - {{\bar{W}}_3})+ 2B \otimes \bar{R},\\ {{\tilde{\Upsilon }}_{12}} = - L \otimes {Y_2} + I_6 \otimes ({{\bar{W}}_3} - {{\bar{W}}_4}), {{\Xi }_{13}} = I_6 \otimes {{\bar{W}}_4}, {{\Xi }_{14}} = L \otimes {Y_2}, {{\Xi }_{15}} = C, {{\Xi }_{16}} = D,\\ {{\Xi }_{17}} = {\left( {B \otimes \bar{R}} \right) ^\mathrm{{T}}}, {{\Xi }_{22}} = I_6 \otimes (- 2{{\bar{W}}_3} + {{\bar{W}}_4} + \bar{W}_4^\mathrm{{T}}) + \alpha {{\bar{D}}^T} {L^T} \Lambda L \bar{D} \otimes \bar{\Omega }, \\ {{\Xi }_{23}} = I_6 \otimes ({{\bar{W}}_3} - {{\bar{W}}_4}), {{\Xi }_{24}} = \alpha {{\bar{D}}^T} {L^T} \Lambda Z L\bar{D} \otimes \bar{\Omega }, {{\Xi }_{27}} = - {\left( {L \otimes {Y_2}} \right) ^\mathrm{{T}}},\\ {{\Xi }_{33}} = - I_6 \otimes ({{\bar{Q}}_3} + {{\bar{W}}_3}), {{\Xi }_{44}} = - I_6 \otimes \bar{\Omega }+ \alpha {{\bar{D}}^T} {L^T} \Lambda L \bar{D} \otimes \bar{\Omega }, {{\Xi }_{47}} = {\left( {L \otimes {Y_2}} \right) ^\mathrm{{T}}},\\ {{\Xi }_{55}} = - {I_{n + m}}, {{\Xi }_{57}} = {\left( {C \otimes \bar{R}} \right) ^\mathrm{{T}}}, {{\Xi }_{66}} = - {\beta ^2}I_6, {{\Xi }_{67}} = {\left( {D \otimes \bar{R}} \right) ^\mathrm{{T}}}, \\ {{\Xi }_{77}} = - I_6 \otimes ({\vartheta ^2_2} \eta _M^{ - 2} {{\tilde{Q}}_2} + 2 \vartheta \tilde{P}), \end{array} \end{aligned}$$

and satisfies the prespecified constraints. In addition, the controller parameters can be obtained: $K = Y_2 \tilde{R}^{-1}$.

Proof

Choose the following Lyapunov function:

$$\begin{aligned} {V_2} \left( {t, \sigma \left( t \right) } \right) = {{{\bar{e}}}^T} {P_{\sigma \left( t \right) }} {\bar{e}} + \int _{t - {\eta _M}}^t {{{{\bar{e}}}^T} \left( s \right) {Q_3} {\bar{e}} \left( s \right) ds} + {\eta _M} \int _{ - {\eta _M}}^0 {\int _{t + \theta }^t {{\dot{{\bar{e}}}^T} \left( s \right) {Q_4} \dot{{\bar{e}}} \left( s \right) ds d\theta } }. \end{aligned}$$

(27)

The following proof steps is similar to Theorem 1. These details are omitted for brevity. $\square$

Simulation study

The validity of the previous results will be illustrated in this section by an numerical example presented below.

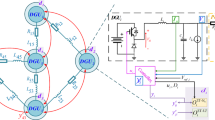
Assume that the considered HMASs (1) consist of four agents, labeled 1, 2, 3, and 4, where agents 1 and 2 are FO agents and agents 3 and 4 are SO agents. As shown in Fig. 2, the communication topology of the agents switches between the two topologies, which follows an inconsistent Markov process. It is assumed that all weights of topology 1 are all 1 and the weights of topology 2 are represented in Fig. 2.

Fig. 2

The topologies of HMASs.

Set the Markov process parameters $\Pi = [-2, 2; 0.8, -0.8]$ for the FO agents, and $p_{11} = 0.8$, $p_{12} = 0.2$, $p_{21} = 0.4$, $p_{22} = 0.6$ for the SO agents. By taking these parameters, the Markov process of the HMASs is shown in Fig. 3, where $\sigma _1 (t)$ indicates the Markov process of the SO agent, and the coordinate variable denotes the mode at the current moment of the SO agent. $\sigma _2 (t)$ depicts the Markov process for the FO agent, and the coordinate variable expresses the mode at the current moment of the FO agent.

Fig. 3

The considered Markov processes in the HAMSs.

Furthermore, the parameter of EMTa is set as: $\sigma _1=0.008$, $\sigma _2=0.015$, $\sigma _3=0.012$, $\Omega _1=[8.41,0.61;0.63,8.12]$, $\Omega _2=[5.38,0.45;0.42,5.21]$, $\Omega _3=[7.41,0.53;0.56,7.42]$, and the parameter of EMTb is set as: $\sigma _4=0.03$, $\sigma _5=0.05$, $\sigma _6=0.06$, $\Omega _4=[4.14,0.18;0.18,4.77]$, $\Omega _5=[5.64,0.16;0.16,5.56]$, $\Omega _6=[4.85,0.32;0.32,4.69]$. The sampling interval is set to $t_h = 0.1s$. In addition, in the proposed state observer and fault estimator, the gain matrix is chosen: $H_1=[0.69,0.06;0.04,0.62]$, $H_2=[0.15,0.02;0.03,0.66]$, $H_3=[0.58,0.18;0.17,0.56]$, $F_1=-[3.94,-0.15;0.08,2.24]$, $F_2=-[2.41,0.12;-0.25,4.12]$, $F_3=-[3.39,0.16;0.19,2.26]$, and the controller gain matrix is: $k_1=[1.21,0.16;0.11,1.84]$, $k_2=[2.52,0.11;0.16,2.23]$, $k_3=[1.96,0.18;0.19,1.88]$.

Due to the fact that external disturbances and nonlinearities are inevitable in real systems, it is assumed that the disturbances presented in each agent is $w = 0.1 sin (t)$, and the nonlinear function is $f (x_i) = 0.1 sin(x_i)$, $i = 1, 2$, $f (x_i, v_i) = -0.45 sin(x_i) - 0.2 v_i$, $i = 3, 4$. In addition, the states of different agents in the system are subject to partial loss of efficiency failures at different times, with a failure rate of $20\%$, as indicated below:

$$\begin{aligned} x_1 = \left\{ \begin{array}{l} {x_1}, {\hspace{13.0pt}} t< 0.8s,\\ 0.8 {x_1}, t \ge 0.8s, \end{array} \right. x_2 = \left\{ \begin{array}{l} {x_2}, {\hspace{13.0pt}} t< 0.5s,\\ 0.8 {x_2}, t \ge 0.5s, \end{array} \right. \\ x_3 = \left\{ \begin{array}{l} {x_3}, {\hspace{13.0pt}} t< 0.6s,\\ 0.8 {x_3}, t \ge 0.6s, \end{array} \right. x_4 = \left\{ \begin{array}{l} {x_4}, {\hspace{13.0pt}} t < 0.8s,\\ 0.8 {x_4}, t \ge 0.8s. \end{array} \right. \end{aligned}$$

Similarly, the controller is subjected to partial failure faults at times of 1s, 1.25s, 1.0s, 1.25s respectively.

Next, the initial state value is set for each agent : $x_1(0) = [3;-4]$, $x_2(0) = [2;-1.5]$, $x_3(0) = [-12;1]$, $x_4(0) = [3;-1]$, $v_3(0) = [-0.2;0.1]$, $v_4(0) = [0.4;0.7]$. By simulation, one can obtain Figs. 4, 5, 6, 7, 8, and 9. Figures 4 and 5 show the estimated values of fault and state information, respectively, from which it can be seen that the designed fault estimator and state observer are valid. Figure 6 illustrates the triggering moments of the position and velocity states under ETS-a and ETS-b, from which it is also seen that it is possible to reduce the data transmission. Table 3 shows the number of triggers for each agent between double ETS and single ETS.

Figures 7 and 8 demonstrate the trajectory evolution of the position and velocity states in the system, from which it can be seen that the states are able to reach consistency under the designed controller. Figure 9 represents the control inputs. Figure 10 shows the evolution curves of all agents following the same Markov process. Comparing Figs. 7, 8, and 10b–d, it can be seen that when following the same Markov process, the state values are relatively large at the first peak.

To further validate the effectiveness of the proposed double ETS, in this paper, quantitative analysis was conducted on convergence time, trigger times, and control cost, as well as compared with the single ETS. As shown in Table 4, the dual ETS significantly reduces communication overhead, that is, trigger times decreased by 37.1%, while shortening convergence time by 16.7% and achieving smoother control inputs, all while ensuring system consistency. These results demonstrate that the proposed strategy maintains robust control performance while conserving network resources.

Fig. 4

The estimation curve of the fault state.

Fig. 5

The estimation curve of the state.

Fig. 6

Trigger moments of ETS.

Table 3 Comparison of ETS.

Fig. 7

Evolution curves of position in HMASs.

Fig. 8

Evolution curves of velocity in HMASs.

Fig. 9

Control inputs.

Fig. 10

Evolution curves of HMASs under the same Markov.

Table 4 Performance comparison between double ETS and single ETS.

Conclusions

In this paper, the fault-tolerant control problem is investigated for the HMASs subject to inconsistent Markov, disturbances, nonlinear, sensor failures and actuator failures. Inconsistent Markov processes are introduced to characterize the different topological switching behaviors between FO and SO agents. In order to minimize the transmission of redundant information, a double ETS dependent on sampled-data is introduced. Based on this, a fault-tolerant observer and fault estimator are designed by utilizing the relative output estimation error. Then, based on the obtained estimation results, the relative output information is utilized to design fault-tolerant consensus controllers for each agent. Further, based on Lyapunov function method, Kronecker product and inequality techniques, criteria are obtained to achieve consensus for the system. Finally, the validity of the proposed method is verified by a simulation. Numerical simulations show that after a 20% performance loss fault occurs in the sensor/actuator, the proposed method can restore consistency within 15 seconds, with the position tracking error stabilizing within ±5%. At the same time, under the proposed double ETS, the number of triggers can be significantly reduced. In future work, it is proposed to combine deep reinforcement learning with double ETS to enhance real-time identification accuracy during concurrent actuator-sensor failures.