An optimization method for integrated demand response strategies for electricity and heat considering the uncertainty of user-side loads

Abstract

Optimizing the scheduling of integrated electric-heat systems (IEHS) is complex due to fluctuating user-side loads and their associated uncertainties. To address this, this paper proposes an integrated demand response (DR) optimization strategy for IEHS that accounts for load uncertainty. First, a probabilistic model leveraging Copula functions was formulated to capture the temporal correlation of load uncertainties. A non-parametric Kernel Density Estimation method was then employed to fit the load distribution, and randomized load fluctuation data were generated using Monte Carlo sampling to simulate uncertainty. Second, a DR model that incorporates the characteristics of the electric-heat system is introduced. The electrical and heating load are coordinated through distinct energy storage devices. Finally, the effectiveness of the strategy is validated through the application of an improved column-and-constraint generation algorithm. Simulation outcomes indicate that the presented optimization approach substantially improves the operational flexibility and performance of IEHS.

Introduction

Background

With the increasing integration of power systems and heating systems, “electricity substitution” has emerged as a key strategy for promoting the efficient use of clean energy¹. In this context, IEHS, as a novel form of integrated energy system, has been widely adopted in energy sector, offering a promising solution to facilitate the green and low-carbon transition². The integrated demand response for electricity and heat (IDR-EH) plays a crucial role in optimizing energy use, balancing electricity and heat demand, and enhancing system flexibility. However, as system scale continues to expand and user needs diversify, the dynamic changes and uncertainties of user-side loads have increasingly become critical factors influencing the dispatch optimization of electric-heat systems. Load uncertainty encompasses not only fluctuations in electrical load but also the time-varying nature of thermal load and the impact of external factors such as weather conditions. Therefore, addressing the uncertainty of user-side loads by proposing a targeted optimization method for demand response strategies in combined heat and power systems is of great significance for improving system scheduling efficiency, reducing operating costs, and ensuring the reliability of heat and power supply³.

Motivation for the research

As a typical multi-energy collaborative system, IEHS enhances the operating efficiency of the energy system and enables flexible energy distribution through the optimization of combined heat and power and energy storage. Literature⁴ applied IEHS to a building group to achieve globally optimal energy management for the integrated building cluster. Literature⁵ optimized a three-layer distributed robust optimization scheduling model for a multi-region interconnected IEHS, which significantly reduces the scheduling cost. Literature⁶ proposed a robust and proactive scheduling method for IEHS, introduced a wind power acceptance risk index, and considered both the operating cost and risk of the system to optimize its economy and safety. Literature⁷ developed a robust optimization scheduling model for IEHS conditional distributions, which enhances the safety and optimality of the scheduling results. Literature⁸ proposed an IEHS optimization planning method that considers the flexible configuration of heat storage as well as the hydraulic and thermal characteristics of the heat network, which effectively improves the economic efficiency of the planning scheme and promotes the consumption of wind power. Literature⁹ propose a comprehensive game-theoretic framework addressing electricity market bidding and generation scheduling, effectively capturing the complex dependencies and strategic behavior of market participants. Although the aforementioned studies provide relatively comprehensive discussions on the planning and scheduling of IEHS, they primarily focus on the optimization and scheduling of system equipment, without fully addressing the dispatchability of demand-side resources. To further enhance the flexibility and responsiveness of IEHS, it is crucial to strengthen the rational scheduling and management of demand-side resources.

DR is a critical mechanism that allows users to participate in system scheduling. Consumers modulate their load consumption based on market price signals and system demands, aiming to optimize economic returns. Although current DR research primarily focuses on regulating electricity loads, the increasing coupling of electricity and heat has made IDR-EH a crucial strategy for simultaneously balancing electricity and heat supply and demand. Literature¹⁰ proposed an AI- and blockchain-enabled framework for demand response management in smart EV charging networks, which leverages real-time prediction and dynamic load control to enhance flexibility and system resilience, offering a novel approach to scalable and decentralized DR implementation Literature¹¹ developed a comprehensive DR model applicable to both electrical and heating loads, enhancing energy efficiency and reducing operating costs. Literature¹² developed a framework for a retail-side bilateral competitive bidding energy market for combining electricity and heat, targeting winter electricity and heat demand from residents. This approach effectively optimizes the coordination of supply and demand resources, enhancing user energy conservation. Literature¹³ developed a stochastic multi-objective optimization framework that integrates demand response programs with mobile energy storage (EVs and E-Bikes) and green certificate markets, demonstrating significant improvements in the economic and environmental performance of microgrids under renewable energy uncertainty. In literature¹⁴, an economic dispatch approach was proposed for an Integrated Electric System (IES), emphasizing DR strategies for extensive electric heating applications. The model aims to mitigate the issue of limited carbon capture effectiveness during peak load times in the retrofitting process of thermal power plants for low-carbon operation. The aforementioned studies provide valuable insights into IDR-EH, but most fail to account for uncertainty in DR, which poses a challenge to the efficiency of DR optimization and the accuracy of system scheduling.

The successful implementation of DR on the user side relies on uncertainty modeling and the optimization of user behavior. Literature^15,16proposed an optimal energy storage capacity allocation method that accounts for flexibility and uncertainty in both source and load, enabling more reasonable allocation of energy storage and reducing system operating costs. Literature¹⁷ proposed a method for interval multi-objective optimal dispatch of IES in a multi-uncertainty environment, which effectively enhances the system’s ability to cope with uncertainties. Literature¹⁸ developed a novel flexible cluster regulation method for building clusters, which accounts for uncertainty and users’ dynamic electricity satisfaction, thereby enhancing the risk resilience of the building cluster grid and aggregator. In literature^19,20, an optimal configuration method for IES equipment is proposed that accounts for the uncertainty of DR. While enhancing risk resilience, it also integrates probability theory and interval theory. Existing stochastic MILP-based DR methods²¹ typically assume fixed scenarios and centralized coordination, which limits their ability to capture load correlations and user-side behavioral dynamics. Similarly, adaptive robust optimization approaches²² often rely on predefined uncertainty sets and do not explicitly model the nonlinear response characteristics of thermal loads or the strategic interactions among multiple stakeholders. However, existing research has not sufficiently addressed the impact of user load uncertainty on combined IDR-EH. Therefore, this study fills the gap by proposing a unified and probabilistically-informed optimization framework that explicitly considers user-side electric-thermal load uncertainty, incorporates dynamic behavioral characteristics, and enables multi-agent hierarchical decision-making for IDR-EH.

Research contributions

Building upon these identified gaps, the present study develops a novel dispatch optimization framework tailored for IEHS under user-side uncertainty. Unlike most existing studies that treat electric and thermal DR separately or neglect the temporal correlation of load uncertainty, this work proposes a unified and probabilistically-informed optimization framework for IEHS. By incorporating a Copula-based load uncertainty model with KDE and MC scenario generation, the proposed method captures both the randomness and the time correlation of user-side loads. Furthermore, the optimization framework considers the distinct dynamic behaviors of electric and heat loads, and improves the classic C&CG method by embedding Particle Swarm Optimization (PSO) to enhance global search efficiency. These integrated innovations contribute to a more realistic, flexible, and computationally efficient solution for dispatch optimization in the face of uncertainty. Specifically, the main contributions are as follows:

• (1) A Copula-based uncertainty model for load time correlation is proposed. The time correlation is modeled using the Copula function, and the uncertainty distribution of electric and heating load is fitted via KDE. MC sampling is employed to generate random scenarios within the load fluctuation range. This model more accurately reflects load fluctuations and uncertainties, providing more reliable data to support the dispatch optimization of the IEHS.

• (2) An optimal DR dispatch model based on electrical and heating uncertainty is developed, aimed at enhancing the dispatch capability of the IEHS under load fluctuations and uncertainty. In constructing the model, special consideration was given to the dynamic characteristics of the heat load and the random nature of fluctuations in the electrical load. By incorporating these key factors, the system’s adaptability to complex and uncertain environments is significantly enhanced, further improving its flexibility and scheduling accuracy.

• (3) The C&CG has been improved, MC sampling is employed to generate columns with uncertainty, and PSO is utilized to process the generated constraint columns. Its global search capability effectively avoids local optima, enhances global optimization, and complements global optimization with local constraint processing, providing a more efficient and accurate solution for the dispatch optimization of IEHS.

The proposed Copula-KDE-MC and PSO-C&CG combination represents a fundamental departure from prior models, establishing a new paradigm through its closed-loop synergy of high-fidelity uncertainty modeling and globally-enhanced robust optimization. Unlike conventional stochastic programming that often relies on simplistic parametric assumptions and fails to capture spatiotemporal load correlations²¹, or standard robust optimization that suffers from inherent conservatism and local optima convergence in non-convex settings^22,27, our framework creates a mutually reinforcing cycle. The Copula-KDE-MC component delivers a probabilistically rigorous and realistic input by capturing non-Gaussian margins and temporal dependencies of electro-thermal loads. This high-fidelity uncertainty representation, in turn, demands a solver that is both robust and globally conscious—a requirement uniquely met by the PSO-C&CG algorithm, which embeds PSO’s exploratory power into the C&CG framework to navigate the resulting complexity effectively. This integrated architecture systematically overcomes the classic trade-offs between uncertainty realism, computational tractability, and solution optimality, delivering a more unified, accurate, and reliable solution for IDR-EH dispatch. The distinct advantages of this integrated framework are quantitatively summarized in Table 1, which provides a comparative analysis against prior methodological approaches.

Table 1 Compare with other methods.

Organization of the paper

The remainder of this paper is organized as follows. Section “System structure and methodological framework” introduces the structure of the IEHS and the overall methodological framework, highlighting the coordination mechanisms among key system components. Section “DR optimization model based on user load uncertainty” details the proposed DR optimization model under load uncertainty, including the probabilistic load modeling, scenario generation process, and mathematical formulation of electrical and thermal DR strategies. Section “Improve the constraint generation algorithm to solve the model” presents the improved solution algorithm, which integrates the C&CG method with PSO to enhance computational efficiency. Section “Case analysis” discusses the simulation case studies, evaluates the performance of different DR strategies under typical scenarios, and compares the proposed method with benchmark approaches. Finally, Section “Conclusion” concludes the study with a summary of key findings.

System structure and methodological framework

Structure of the integrated electrothermal energy system

The electrical and heat load is decoupled through an energy storage device, with cogeneration achieved using an electric boiler (EB). The rational configuration and scheduling of electrical and heat energy storage devices can effectively manage the demand from the user side in IES.

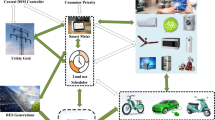
This paper presents an IEHS, the structural schematic of which is depicted in Fig. 1. The system consists of a distribution network, a heat and power plant, a controller, electric energy storage (EES), heat storage tank (HST), EB, and electrical and heat loads. The system is designed to transform externally supplied energy resources into multiple forms for both usage and storage. It receives input energy such as electricity from the power grid and thermal energy from a heat station, and it outputs electricity and heating. Internally, it comprises components like battery storage and thermal energy storage units.

Fig. 1

Structure of an integrated electrothermal energy system.

The system possesses flexible energy management capabilities that optimize operating costs and enhance efficiency. During off-peak hours, the system can purchase low-cost electricity for storage and utilize it during peak hours. Simultaneously, EB can convert electricity into heating to meet heat demands or store heat for later use. During peak electricity consumption, the EES unit can release electricity to supply the user’s electrical load or drive the EB to generate heat, thus ensuring user comfort and the economic operation of the system.

Method framework

This paper presents an optimal DR model that accounts for user-side load uncertainty. The model consists primarily of two components: user-side uncertainty analysis and DR optimization model, as shown in Fig. 2.

Fig. 2

Methodological framework.

In this paper, we analyze the uncertainty of the user-side load. Based on historical user load data, we construct a histogram from which the probability density function is derived. Subsequently, we perform KDE on the probability density function. To account for temporal correlations, we establish a Copula model. Finally, MC sampling is conducted to transform the originally uncertain load data into deterministic data.

In addition, in the model of IDR-EH, the system prioritizes the use of electric heat storage devices to regulate energy use, thereby smoothing fluctuations in electrical load and optimizing energy efficiency. EES units are charged with electricity during off-peak times and supply energy during peak periods, effectively contributing to the stabilization of the load profile. When the upper limit of energy storage capacity is reached, other loads (e.g., EB) are scheduled with fixed constraints. This strategy optimizes load scheduling by prioritizing energy storage resources, enhances system efficiency, reduces operating costs, and improves overall flexibility and economic performance.

DR optimization model based on user load uncertainty

Uncertainty analysis

The heat and electrical loads of the IES exhibit a high degree of uncertainty. Therefore, this paper employs KDE to statistically analyze the load forecast error, derive the probability density distribution curve, and perform random sampling based on this analysis.

This paper employs KDE with a Gaussian kernel to model load forecast error distributions without presuming parametric forms. The bandwidth parameter h is optimized via Least Squares Cross-Validation (LSCV) to minimize estimation error.

As a non-parametric technique, KDE derives the distributional properties from the data itself, avoiding the necessity of assuming any predefined distribution model²³.²⁴Assuming ${\text{z}}_{1} ,z_{2} ,...,z_{n}$ is an n-sample originating from an independent and identically distributed population F with the probability density function f, the corresponding KDE can be formulated as²⁴:

$$\hat{f}(x) = \frac{1}{nh}\sum\limits_{i = 1}^{n} {K\left( {\frac{{z - z_{i} }}{h}} \right)}$$

(1)

where, h is the bandwidth. n is the number of samples. $K(u)$ is the kernel function.

The Gaussian kernel function is utilized in this paper, and its mathematical expression is provided below:

$$K\left( u \right) = \frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{{u^{2} }}{2}}}$$

(2)

$$LSCV(\sigma ) = \frac{1}{{2\sqrt {\uppi } n\sigma }} + \frac{1}{n(n - 1)}\sum\nolimits_{j}^{N} {\left[ {K_{\sqrt 2 \sigma } (x_{i} - x_{j} ) - 2K_{\sigma } (x_{i} - x_{j} )} \right]}$$

(3)

The optimal bandwidth can be obtained by minimizing Eq. (3). This is an unconstrained minimization problem, which can be solved using an unconstrained nonlinear optimization solver. This method ensures that the bandwidth is selected based on minimizing the root mean square error (RMSE) of the density estimation, thereby improving the accuracy of the load uncertainty model.

To construct the time-dependent correlation of sampled user load values for each time period, the marginal probability distributions obtained via KDE must be transformed into a multivariate joint distribution. For this purpose, Copula theory provides a flexible and powerful framework, allowing separate modeling of marginal distributions and their dependence structure. At present, Copula-based modeling has become a mature and widely adopted method, with well-established construction logic and rigorous mathematical foundation. It is particularly effective in quantitative analyses involving inter-variable correlation, such as price modeling and multi-energy system uncertainty analysis.

In this study, Copula functions are employed to describe the temporal correlation among electric and thermal load values. Two main families of Copulas are typically used: elliptical Copulas (e.g., Gaussian and t-Copula), which assume symmetric dependence, and Archimedean Copulas (e.g., Frank, Gumbel, and Clayton), which offer greater flexibility in tail dependence modeling. Among them, the Frank-Copula is selected in this work due to its symmetric structure, broad applicability across correlation ranges, and analytical simplicity²⁵. Table 2 below presents the goodness-of-fit comparison for the candidate Copula models applied to the load time series, highlighting the Frank-Copula as the optimal choice based on the evaluation metrics.

Table 2 Goodness-of-fit evaluation of candidate copula models.

For a set of random variables (x₁, x₂, …, x_n), H is the joint distribution function and F₁,F₂, …, F_n are the marginal distribution functions. The connection between them is formulated using a Copula function C, such that:

$$H\left( {x_{1} ,x_{2} ,...,x_{n} } \right) = C\left( {F_{1} \left( {x_{1} } \right),F_{2} \left( {x_{2} } \right),...,F_{n} \left( {x_{n} } \right)} \right)$$

(4)

$$C\left( {u_{1} ,u_{2} ,...,u_{n} } \right) = H\left( {F_{1}^{ - 1} \left( {u_{1} } \right),F_{2}^{ - 2} \left( {u_{2} } \right),...,F_{n}^{ - n} \left( {u_{n} } \right)} \right)$$

(5)

When the joint probability density function h (x₁, x₂, …, x_n) of the random variables (x₁, x₂, …, x_n) and its marginal probability density function f₁, f₂, …, f_n exist, it can be introduced according to the law of chains:

$$\begin{aligned} h\left( {x_{1} ,x_{2} , \ldots ,{\mkern 1mu} x_{n} } \right) = & \frac{{\partial^{2} H\left( {x_{1} ,x_{2} , \ldots ,x_{n} } \right)}}{{\partial x_{1} x_{2} \ldots {\mkern 1mu} x_{n} }} = \frac{{\partial^{n} C(F_{1} (x_{1} ),(F_{2} (x_{2} ),...,(F_{n} (x_{n} )}}{{\partial x_{1} x_{2} \ldots {\mkern 1mu} x_{n} }} \\& = \frac{{\partial^{n} C(F_{1} (x_{1} ),(F_{2} (x_{2} ),...,(F_{n} (x_{n} )}}{{\partial F_{1} (x_{1} )\partial F_{2} (x_{2} )...\partial F_{n} (x_{n} )}} \cdot \frac{{\partial F_{1} (x_{1} )}}{{\partial x_{1} }} \cdot \frac{{\partial F_{2} (x_{2} )}}{{\partial x_{2} }}...\frac{{\partial F_{n} (x_{n} )}}{{\partial x_{n} }} \\ &= c(F_{1} (x_{1} ),(F_{2} (x_{2} ),...,(F_{n} (x_{n} ))f_{1} (x_{1} )f_{2} (x_{2} )...f_{n} (x_{n} ) \\ \end{aligned}$$

(6)

When describing the correlation of electric load and thermal load, $C( \cdot )$ is the two-dimensional Frank-Copula function with the expression as shown in Equation:

$$C(v_{1} ,v_{2} ,\theta_{1} ) = - \frac{1}{{\theta_{1} }}\ln \left[ {1 + \frac{{(\exp ( - \theta_{1} v_{1} ) - 1)(\exp ( - \theta_{1} v_{1} ) - 1)}}{{(\exp ( - \theta_{1} ) - 1)}}} \right]$$

(7)

where $v_{1}$ and $v_{2}$ represent the marginal distribution function of electric load and thermal load respectively. $\theta_{1}$ represents the parameter of the two-dimensional Frank-Copula function, which is estimated by the maximum likelihood estimation method.

Once the time-dependent joint probability distribution of electric and thermal loads is established using the Frank-Copula function, it becomes feasible to generate large-scale random scenarios that reflect real-world uncertainties in both marginal behavior and temporal correlation. The process of Copula function can be seen as Fig. 3.

Fig. 3

Flowchart of the copula-based uncertainty modeling process.

To this end, we employ a MC sampling method to generate multiple realizations of user-side load trajectories.

The MC sampling process starts with generating uniform random vectors over [0,1]n in the Copula space, which are then transformed into corresponding electric and thermal load values through the inverse cumulative distribution functions derived from the KDE-based marginal distributions. This process ensures the sampled data retains both empirical variability and modeled inter-temporal correlation.

In this study, 1,000 raw scenarios are generated to sufficiently represent the possible variations in load profiles. However, directly using all scenarios in optimization would lead to excessive computational overhead. Therefore, to reduce dimensionality while preserving diversity, we apply a K-means clustering algorithm to the sampled dataset. The number of clusters is empirically set to five, and the cluster centroids are used as typical representative scenarios. These typical scenarios are illustrated in Fig. 11 and used as input data for the robust dispatch optimization model in subsequent sections.

DR model

Objective function

$$\min f\left( u \right) + E\left[ {G\left( {x,\xi } \right)} \right]$$

(8)

$$f\left( u \right) = \sum\limits_{{t \in N_{T} }} {\left[ {a \cdot \left( {p_{t}^{da} } \right)^{2} + b \cdot p_{t}^{da} } \right]}$$

(9)

$$G\left( {x,\xi } \right) = \gamma^{vio} \cdot p_{s}^{vio} + \sum\limits_{{t \in N_{T} }} {\gamma^{rtp} } \cdot p_{t,s}^{rtp} + \sum\limits_{{t \in N_{T} }} {\sum\limits_{{i \in N_{N} }} {\left( {\alpha \cdot dis_{i,t,s}^{hvac} + \beta \cdot dis_{i,t,s}^{wh} } \right)} }$$

(10)

where, a/b is the electricity price factor. $p_{t}^{da}$ is the amount of electricity purchased from the day-ahead market. T is the total number of hours considered. $\gamma^{vio}$ is the peak load violation rate.$p_{s}^{vio}$ is the maximum load in excess of the agreed load limit. $\gamma^{rtp}$ is the real-time market purchase price. $p_{t,s}^{rtp}$ is the amount of electricity purchased from the real-time market. $dis_{i,t,s}^{hvac}$ is the user’s discomfort with the indoor temperature at time t (°C). $dis_{i,t,s}^{wh}$ is the user’s discomfort with the water temperature at time t (°C). $\alpha$/β is the weight factors.

DR constraints

The actual electrical load comprises replaceable load, transferable load, and cuttable load, with the replaceable load typically represented by heat, ventilation, and air conditioning (HVAC) systems and electric water heaters (EWH).

$$\left\{ {\begin{array}{*{20}l} {P_{i,t}^{le} = P_{i,t}^{rep} + P_{i,t}^{tran} - P_{i,t}^{cut} \, } \hfill \\ {\left| {P_{i,t}^{tran} } \right| \le P_{{\max^{tran} }} } \hfill \\ {\sum\limits_{t = 1}^{T} {P_{i,t}^{tran} } = 0} \hfill \\ {0 \le P_{i,t}^{cut} \le P_{{\max^{cut} }} } \hfill \\ {P_{i,t}^{rep} = P_{i,t}^{hvac} + P_{i,t}^{ewh} } \hfill \\ \end{array} } \right.$$

(11)

where, $P_{i,t}^{{{\text{le}}}}$ is the actual value of the electrical load. $P_{i,t}^{rep}$ is the replaceable value of the electrical load. $P_{i,t}^{{{\text{tran}}}}$ is the transferable value of the electrical load. $P_{i,t}^{{{\text{cut}}}}$ is the cuttable value of the electrical load. $P_{{{\text{max}}}}^{{{\text{tran}}}}$ is the upper limit of the transferable electrical load. $P_{{{\text{max}}}}^{{{\text{cut}}}}$ is the upper limit of the reducible electrical load.

Load model

DR model for electrical load

As illustrated in Fig. 4, user loads can be categorized according to their characteristics into cuttable loads, transferable loads, replaceable loads and fixed loads (e.g., lighting loads).

Fig. 4

Classification of electric loads for demand response.

• (1) Cuttable electrical load.

The load-dependent power supply times can be adjusted based on the schedule. Loads that require a reduction in their total demand and whose power supply times span multiple scheduling periods, such as washing machines, rice cookers, dishwashers, and microwave ovens, are considered. The reduction interval is defined as [t_cut1, t_cut2], and it must satisfy the continuity constraint of system operation.

$$\sum\limits_{t = \varepsilon }^{{\varepsilon + t_{c} - 1}} {y_{t} } = t_{c}$$

(12)

where, ε is the start time of the reduction. $t_{c}$ is the duration. $y_{t}$ is the reduction status, a 0–1 variable.

The cuttable load model is

$$F_{cut} = \sum\limits_{{t = t_{cut1} }}^{{t_{cut2} - t_{c} + 1}} {\frac{{P_{t}^{cut} }}{\Delta P(t)\psi }}$$

(13)

where, $P_{t}^{cut}$ is the actual power that can be reduced at time t after optimization. $\psi$ is the conversion factor for the magnitude of the electrical load of the regional power grid-community. ${\Delta }P(t)$ is the power deviation at time t between the typical daily load curve of the regional power grid user community and the typical daily load curve of the regional conventional minimum output curve in a typical day of a certain season.

• (2) Transferable electrical load.

The electricity consumption of transferable loads at various time periods can be adjusted flexibly; however, it is essential to ensure that the total load over the entire cycle remains unchanged after the transfer, such as electric vehicles, computers, and similar devices. Define the transferable interval as [t_tran1, t_tran2], ensuring that the total power consumption constraint is satisfied.

$$\sum\limits_{{t = t_{tran1} }}^{{t_{tran2} }} {L_{t}^{tran} } = \sum\limits_{{t = t_{tran} }}^{{t_{tran2} }} {P_{t}^{tran} }$$

(14)

where, $L_{t}^{{{\text{tran}}}}$ and $P_{t}^{tran}$ are the transferable load powers at time t before and after optimization.

The transferable load model is

$$F_{tran} = \sum\limits_{{t = t_{tran1} }}^{{t_{tran2} }} {\frac{{P_{t}^{tran} \nu_{t} }}{\Delta P(t)\psi }}$$

(15)

where, $\nu_{t}$ is a 0–1 variable that determines the load transfer status at time t. $\psi$ is the conversion factor for the magnitude of the electrical load of the regional power grid-community. ${\Delta }P(t)$ is the power deviation at time t between the typical daily load curve of the regional power grid user community and the typical daily load curve of the regional conventional minimum output curve in a typical day of a certain season.

• (3) Replaceable electrical load.

In this paper, HVAC and EWH are considered as the primary alternative loads, taking into account the effects of room and hot water temperatures on user comfort. The operating characteristics of HVAC systems and EWH primarily depend on factors such as indoor and outdoor temperatures, the equivalent thermal resistance of the building, and the specific heat capacities of air and water.

• (1) HVAC model²⁶

  $$T_{i,t,s}^{in} = T_{i,t - 1,s}^{in} + \left( {\frac{{T_{i,t,s}^{out} - T_{i,t - 1,s}^{in} }}{{R_{i}^{house} - b_{i,t}^{hvac} \cdot P_{i}^{hvac} }}} \right){\Delta }t/C_{i}^{house}$$

  (16)
  $$[\underline {T}_{i0}^{in} \sim \underline {T}_{i1}^{in} ] \le T_{i,t,s}^{in} \le [\overline{T}_{i0}^{in} \sim \overline{T}_{i1}^{in} ]$$

  (17)
  $$dis_{i,t,s}^{hvac} = \left| {\begin{array}{*{20}c} {T_{i,t,s}^{in} - T_{i}^{ins} } \\ \end{array} } \right|$$

  (18)

  where, $T_{i,t,s}^{in}$ is the room temperature preset point. $T_{i,t - 1,s}^{in}$ is the room temperature at the previous moment. $T_{i,t,s}^{out}$ is the outdoor temperature forecast. $R_{i}^{house}$ is the thermal resistance of the house. $b_{i,t}^{hvac}$ is the HVAC operating state of house i at time t. $P_{i}^{hvac}$ is the power of the HVAC. $C_{i}^{house}$ is the heat capacity of house i (J/°C). $\underline {T}_{i0}^{in} \sim \underline {T}_{i1}^{in}$/$\overline{T}_{i0}^{in} \sim \overline{T}_{i1}^{in}$ is the minimum/maximum indoor temperature limit of house i (°C). $T_{i}^{ins}$ is the indoor temperature setpoint of house i (°C).

• (2) EWH model

  $$\begin{aligned} T_{{i,t,s}}^{{wh}} = & T_{{i,t - 1,s}}^{{wh}} \\ & \quad + \frac{{T_{{i,t,s}}^{{in}} - T_{{i,t - 1,s}}^{{wh}} }}{{R_{i}^{{wh}} }}\Delta t/C_{i}^{{wh}} \\ & \quad - c^{{water}} \cdot m_{{i,t,s}}^{{water}} \left( {T_{{i,t - 1,s}}^{{wh}} - T_{{i,t,s}}^{{in}} } \right)\Delta t/C_{i}^{{wh}} \\ & \quad + b_{{i,t}}^{{wh}} \cdot P_{i}^{{wh}} \cdot \Delta t/C_{i}^{{wh}} \\ \end{aligned}$$

  (19)
  $$[\underline {T}_{i0}^{wh} \sim \underline {T}_{i1}^{wh} ] \le T_{i,t,s}^{wh} \le [\overline{T}_{i0}^{wh} \sim \overline{T}_{i1}^{wh} ]$$

  (20)
  $$dis_{i,t,s}^{wh} = \left| {\begin{array}{*{20}c} {T_{i,t,s}^{wh} - T_{i}^{whs} } \\ \end{array} } \right|$$

  (21)

  where, $T_{i,t,s}^{wh}$ is the predetermined water temperature. $T_{i,t - 1,s}^{wh}$ is the room temperature at the previous moment. $T_{i,t,s}^{in}$ is the predetermined room temperature. $R_{i}^{wh}$ is the thermal resistance of the house. $b_{i,t}^{wh}$ is the operating state of the EWH in house i at time t. $P_{i}^{wh}$ is the power of the EWH. $c^{water}$ is the heat capacity of water i (J/°C). $m_{i,t,s}^{water}$ is the hot water consumption of house i in scene s at time t (kg). $\underline {T}_{i0}^{wh} \sim \underline {T}_{i1}^{wh}$/$\overline{T}_{i0}^{wh} \sim \overline{T}_{i1}^{wh}$ is the minimum/maximum water temperature limit of the EWH in house i (°C). $T_{i}^{whs}$ is the hot water temperature setpoint of house i (°C).

DR model for heat load

The subjective nature of users’ heat temperature perception permits adjustments to heating output within a specified range. Additionally, the thermal inertia characteristic of heat transfer allows thermal loads to function as flexible participants in DR programs. During heat transfer, the specific heat capacity of water is c, and the heat supplied by the heat equipment in the time period t is $H_{HS,t}$ . Subsequently, the thermal change of water with mass $Q_{HS}$ as it passes through the heat source, transitioning from a return temperature $T_{h,t}$ to a supply temperature $T_{g,t}$ ,can be calculated as follows:

$$H_{HS,t} = cQ_{HS} \left( {T_{g,t} - T_{h,t} } \right)$$

(22)

For a load node with heat consumption $H_{load,t}$ in time period t, the resulting heat variation for water of mass $Q_{L}$ , transitioning from supply temperature $T_{g,t}$ to the return temperature $T_{h,t}$ is:

$$H_{load,t} = cQ_{L} \left( {T_{g,t} - T_{h,t} } \right)$$

(23)

To ensure user comfort in terms of temperature, the heat absorbed by the load node during period t should remain within a specified range:

$$H_{load}^{\min } \le H_{load,t} \le H_{load}^{\max }$$

(24)

Simultaneously, it must be ensured that the total heat consumption by the thermal load over T periods corresponds to the user’s intended heat requirement:

$$\sum\limits_{t = n}^{n + T\prime } {H_{load,t} } = \sum\limits_{t = n}^{n + T\prime } {H_{load,t}^{ideal} }$$

(25)

$$T^{{^{\prime } }} = m \times {\Delta }t$$

(26)

where, $T^{{^{\prime } }}$ is the maximum number of consecutive scheduling periods during the scheduling cycle.

The supply and return temperatures are constrained within the following limits:

$$T_{g}^{\min } \le T_{g,t} \le T_{g}^{\max }$$

(27)

$$T_{h}^{\min } \le T_{h,t} \le T_{h}^{\max }$$

(28)

where, $T_{h}^{\max }$$T_{h}^{\min }$ are the maximum and minimum return water temperatures. $T_{g}^{\max }$$T_{g}^{\min }$ are the maximum and minimum supply water temperatures.

Constraint

This paper comprehensively examines the role of user-side energy storage devices in DR. Energy storage systems (ESS) can absorb excess electricity and heating during periods of energy surplus and release stored energy during times of energy shortage, owing to their flexible scheduling capabilities and efficient energy supply characteristics, thus maintaining a balanced energy supply. IES devices significantly enhances the flexibility and stability of DR. The system prioritizes the use of energy storage devices during DR participation: energy is released during peak consumption periods to meet load demand. Once the energy storage device reaches its capacity limit, the system dispatches other loads participating in DR. This mechanism not only incentivizes users to participate in DR but also ensures energy comfort. Additionally, the flexible scheduling of energy storage enhances the adaptability and efficiency of DR strategies. The parameters of the energy storage device are presented in Table 2.

Model constraints for EES systems

The EES model comprises an energy state and associated constraints. To facilitate energy state modeling in a normalized and scalable manner, the EES system is described using the state-of-charge (SOC), which represents the ratio of the current stored energy to the rated energy capacity:

$$SOC_{t} = \frac{{E_{t} }}{{E_{\max }^{ES} }},SOC_{t} \in [SOC_{\min } ,SOC_{\max } ]$$

(29)

This normalized representation simplifies the formulation of energy-related constraints and improves computational tractability. The temporal evolution of the SOC is described in Eq. (30), which accounts for the cumulative effects of charging, discharging, and self-discharge losses over time. The operating range of the SOC is constrained between specified lower and upper bounds, as expressed in Eq. (31). Equation (32) ensures SOC consistency at the beginning and end of the scheduling cycle, which is important for cyclic dispatch planning. The charging and discharging power limits of the EES are enforced through Eqs. (33) and (34), while mutual exclusivity between charging and discharging is guaranteed by Eq. (35) using binary decision variables. Finally, Eq. (36) defines the net charging and discharging power variables used in the model.

$$SOC_{t} = (1 - \varepsilon )^{t} SOC_{0} + \sum\limits_{\tau = 1}^{t} {(\eta_{{{\text{ES}}}} \frac{{P_{\tau }^{{{\text{ES}},ch{\text{ar}}}} }}{{E_{{\text{n}}}^{{{\text{ES}}}} }} - \frac{{P_{\tau }^{{{\text{ES}},dis}} }}{{\eta_{{{\text{ES}}}} E_{{\text{n}}}^{{{\text{ES}}}} }})} \Delta t$$

(30)

$$SOC_{\min } \le SOC_{t} \le SOC_{\max }$$

(31)

$$\sum\limits_{\tau = 1}^{T} {(\eta_{ES} \frac{{P_{\tau }^{ES,char} }}{{E_{n}^{ES} }} - \frac{{P_{\tau }^{ES,dis} }}{{\eta_{ES} E_{n}^{ES} }})} \Delta t = 0$$

(32)

$$0 \le P_{t}^{ES,dis} \le z_{t}^{ES,dis} P_{n}^{ES}$$

(33)

$$0 \le P_{t}^{ES,char} \le z_{t}^{ES,char} P_{n}^{ES}$$

(34)

$$z_{t}^{ES,dis} + z_{t}^{ES,char} \le 1$$

(35)

$$P_{t}^{{{\text{ES}}}} = P_{t}^{{{\text{ES}},dis}} - P_{t}^{{{\text{ES}},char}}$$

(36)

where, ${\text{SOC}}_{t}$ is the energy state during the period of EES t. ε is the rate of self-energy loss. ${\text{SOC}}_{0}$, ${\text{SOC}}_{\max }$, ${\text{SOC}}_{\min }$ are the initial value, upper limit, and lower limit of the ESS. $\eta_{{{\text{ES}}}}$ is the energy storage charging and discharging efficiency. $E_{{\text{n}}}^{{{\text{ES}}}}$ is the rated energy storage capacity. $P_{\tau }^{{{\text{ES}},ch{\text{ar}} }}$ is the energy storage power during the period of τ. $z_{t}^{{{\text{ES}},dis}}$, $z_{t}^{{{\text{ES}},char}}$ are both binary variables that indicate the state of energy storage and discharge. If energy is being released, $z_{t}^{{{\text{ES}},dis}}$ is 1, if energy is being stored, $z_{t}^{{{\text{ES}},char}}$ is 1. $P_{{\text{n}}}^{{{\text{ES}}}}$ is the rated power of energy storage. $P_{t}^{{{\text{ES}}}}$ is the power of energy storage and discharge during the t period.

Model constraints for HST systems

The HST model comprises an energy state and associated constraints. Equation (37) represents the percentage of the HST state at each moment. Equation (38) represents the energy storage state constraint. Equation (39) ensures the consistency of the thermal energy storage state before and after the scheduling cycle. Additionally, the charging and discharging power of the HST cannot exceed its upper limit, as expressed in Eqs. (40, 41). The HST device cannot charge and discharge simultaneously, as described in Eq. (42). Equation (43) calculates the charging and discharging power of the HST.

$$V_{t} = (1 - \varepsilon )^{t} V_{0} + \mathop \sum \limits_{\tau = 1}^{t} (\eta_{HS} \frac{{P_{\tau }^{HS,char} }}{{E_{n}^{HS} }} - \frac{{P_{\tau }^{HS,dis} }}{{\eta_{HS} E_{n}^{HS} }})\Delta t$$

(37)

$$V_{\min } \le V_{t} \le V_{\max }$$

(38)

$$\mathop \sum \limits_{\tau = 1}^{T} (\eta_{HS} \frac{{P_{\tau }^{HS,char} }}{{E_{n}^{HS} }} - \frac{{P_{\tau }^{HS,dis} }}{{\eta_{HS} E_{n}^{HS} }})\Delta t = 0$$

(39)

$$0 \le P_{t}^{HS,dis} \le z_{t}^{HS,dis} P_{n}^{HS}$$

(40)

$$0 \le P_{t}^{HS,char} \le z_{t}^{HS,char} P_{n}^{HS}$$

(41)

$$z_{t}^{HS,dis} + z_{t}^{HS,char} \le 1$$

(42)

$$P_{t}^{{{\text{HS}}}} = P_{t}^{{{\text{HS}},dis}} - P_{t}^{{{\text{HS}},char}}$$

(43)

where, $V$ is the energy state of the heat energy storage for the time period t. ε is the energy self-dissipation rate. $V_{0}$ , $V_{\max }$ , $V_{\min }$ are the initial value, upper limit, and lower limit of the HST. $\eta_{{{\text{HS}}}}$ is the energy storage charging and discharging efficiency. $E_{{\text{n}}}^{{{\text{HS}}}}$ is the rated energy storage capacity. $P_{\tau }^{{{\text{HS}},ch{\text{ar}} }}$ is the energy storage power for the time period τ. $P_{\tau }^{{{\text{HS}},dis}}$ is the energy release power during the τ period. $z_{t}^{{{\text{HS}},dis}}$ ,$z_{t}^{{{\text{HS}},char}}$ are both binary variables that indicate the charging and discharging state of the energy storage, with $z_{t}^{{{\text{HS}},dis}}$ being 1 when energy is being released and $z_{t}^{{{\text{HS}},char}}$ being 1 when energy is being stored. $P_{{\text{n}}}^{{{\text{HS}}}}$ is the rated power of the energy storage. $P_{t}^{{{\text{HS}}}}$ is the charging and discharging power during the t period.

The parameters in Table 3, including storage efficiencies, SOC limits, and charging/discharging power constraints, are selected based on typical characteristics of commercial lithium-ion battery systems and insulated thermal storage tanks. For example, SOC bounds of 0.2–0.8 are commonly applied to avoid degradation due to deep cycling. Efficiency values of 0.9 (electric) and 0.8 (thermal) reflect average round-trip efficiency as reported in previous studies. These values are representative of medium-scale energy hubs such as community microgrids and building-level IES.

Table 3 Energy storage device parameters.

To ensure realistic operation of ESS, we impose a mutual exclusivity constraint between charging and discharging. This assumption is widely adopted in existing literature and reflects the physical and economic limitations of most electrochemical storage technologies, such as Li-ion batteries. Although certain advanced systems may technically allow concurrent operation, such behavior is generally suboptimal due to energy losses and cost implications, and is therefore avoided in practical dispatch scenarios. In this study, a symmetric efficiency assumption is adopted—specifically, both charging and discharging efficiencies are set to 0.9. This simplification facilitates model formulation and is consistent with commonly used assumptions in energy systems research. Although minor differences may exist between charging and discharging efficiencies due to hardware-level asymmetries, such differences are typically small (within 2–3%) for mainstream technologies such as lithium-ion batteries. Therefore, the symmetric efficiency assumption has negligible impact on dispatch outcomes, especially in aggregated, system-level analyses.

EB model constraint

This paper utilizes EB as the electric heat device. EB is a key component for achieving combined heat and power. It utilizes electricity as the energy source to heat water into steam within the heat furnace, which subsequently provides the required heat energy to the users. The output thermal power of EB is directly related to its inherent characteristics. The specific output power model is expressed as follows:

$$Q_{EB} = P_{EB} \cdot \eta_{EB}$$

(44)

$$0 \le P_{EB} \le P_{EB}^{{{\text{max}}}}$$

(45)

where, $Q_{EB}$ is the EB unit’s output thermal power. $P_{EB}$ is the EB unit’s power consumption. $P_{{{\text{eb}}}}^{{{\text{max}}}}$ is the upper limit of the electric boiler’s input power.

Other restrictions

• (1) Electric power balance constraint

  $$P_{E}^{load} = P_{ES}^{dis} - P_{ES}^{char} + P_{E}^{buy} - P_{EB}$$

  (46)

  where, $P_{E}^{load}$ is the electrical load. $P_{ES}^{dis}$ is the EES discharge power. $P_{ES}^{char}$ is the EES charge power. $P_{E}^{buy}$ is the grid purchased power. $P_{EB}$ is the EB power consumption.

• (2) Heat power balance constraint

  $$P_{H}^{load} = P_{HS}^{dis} - P_{HS}^{char} + P_{H}^{buy} + P_{EB}$$

  (47)

  where, $P_{H}^{load}$ is the heat load. $P_{HS}^{dis}$ is the HST discharge power. $P_{HS}^{char}$ is the HST charge power. $P_{H}^{buy}$ is the heat purchased from the heat station. $P_{EB}$ is the heat production power of the EB.

• (3) Power purchase constraints

  $$0 \le P_{E}^{buy} \le P_{buy}^{\max }$$

  (48)

  where, $P_{buy}^{\max }$ is the maximum electricity purchase.

Improve the constraint generation algorithm to solve the model

To solve the optimization model, this paper employs an improved C&CG algorithm²⁷. Like the Benders decomposition algorithm, the C&CG algorithm decomposes the original problem into a main problem and a subproblem, alternately solving both to obtain an optimal solution. After generating the constraint column, a PSO algorithm is employed for further optimization to avoid local optima. The algorithm progressively introduces variables and constraints related to the subproblem while solving the main problem, thus obtaining a tighter lower bound on the objective function and reducing the number of iterations.

To clearly illustrate the solution process, the following pseudocode outlines the improved hybrid optimization framework, where PSO is employed to solve the master problem and C&CG is embedded to evaluate robust performance under uncertain scenarios.

Parameter Settings:

The key parameters for the algorithm are set as follows, based on common practices in the literature and preliminary calibration to ensure a balance between exploration and exploitation: Population size N = 50, inertia weight linearly decreases from $\omega_{\max } = 0.9$ to $\omega_{\min } = 0.4$, cognitive and social factors c₁ = c₂ = 2.0, maximum iterations $MaxIter_{{{\text{PSO}}}} = 200$. The inner PSO loop terminates if the global best solution shows an improvement of less than 0.01% over 50 consecutive iterations. Convergence threshold $\varepsilon = 0.001$, maximum iterations $MaxCut = 25$. The detailed flowchart of the algorithm is shown in Fig. 5.

Fig. 5

Schematic diagram of the PSO-C&CG solution procedure.

This procedure enables the PSO to explore the solution space globally while the C&CG algorithm evaluates worst-case robustness by generating cuts for uncertain scenarios. The master problem (MP) determines scheduling decisions under a fixed uncertainty realization, and the subproblem (SP) identifies the most violated scenario based on the current solution. If convergence is not achieved, a new scenario and corresponding cut are introduced, and the process iterates until the gap between upper and lower bounds meets the defined tolerance ε.

In this study, the convergence threshold is set to ε = 0.001, which ensures high-precision convergence while maintaining a reasonable computational time. This value is chosen based on a sensitivity analysis, where ε = 0.001 demonstrates a favorable trade-off between solution quality and computational efficiency.

As shown in Table 4, tightening the convergence threshold from $10^{ - 2}$ to $10^{ - 4}$ results in slightly improved solution quality (0.3% improvement in the objective value), but with significantly increased computation time (over 60% longer). The difference in objective values between $10^{ - 3}$ and $10^{ - 4}$ is negligible (0.02%), suggesting diminishing returns beyond the default setting. Thus, $\varepsilon = 10^{ - 3}$ provides a well-balanced compromise between robustness and computational burden.

Table 4 Impact of convergence threshold ε on algorithm performance.

Decomposing the objective function gives the main problem in the form of:

$$\left\{ {\begin{array}{*{20}l} {\mathop {\min }\limits_{x} \alpha ,} \hfill \\ {s.t.\alpha \ge c^{T} y_{l} } \hfill \\ {Dy_{l} \ge d} \hfill \\ {Ky_{l} = 0} \hfill \\ {Fx + Gy_{l} \ge h} \hfill \\ {I_{u} y_{l} = u_{l}^{ * } } \hfill \\ {\forall l \le k} \hfill \\ \end{array} } \right.$$

(49)

Subproblems take the form of:

$$\mathop {\max }\limits_{u \in U} \mathop {\min }\limits_{y \in \Omega (x,u)} c^{T} y$$

(50)

The solution process is:

• (1) Set the initial scenario data as the value of the uncertain variable u₀, define the lower and upper bounds of the operating cost corresponding to the final scheduling plan, and initialize the number of iterations as k = 1.

• (2) Considering the uncertainty of the user-side load, solve the main problem to obtain the optimal solution. The value of the objective function of the main problem serves as the new lower bound.

• (3) Solve the subproblem based on the solution obtained from the master problem $x_{k}^{*}$ to determine the objective function value $f_{k}^{{}} (x_{k}^{*} )$ of the subproblem and the corresponding value $u_{k + 1}^{*}$ of the uncertain variable u, and update the upper bound $UB = \min \{ UB,f_{k}^{{}} (x_{k}^{*} )\}$;

• (4) Given the algorithm’s convergence threshold ε, if UB − LB ≤ ε, stop iteration and return the optimal solutions $x_{k}^{*}$ and $y_{k}^{*}$; otherwise, add the variable $y^{k + 1}$ and following constraints:

  $$\left\{ {\begin{array}{*{20}l} {\alpha \ge c^{{\text{T}}} y^{{k + 1}} } \hfill \\ {Dy^{{k + 1}} \ge d} \hfill \\ {Ky^{{k + 1}} = 0} \hfill \\ {Fx + Gy^{{k + 1}} \ge h} \hfill \\ {I_{u} y^{{k + 1}} = u_{{k + 1}}^{*} } \hfill \\ \end{array} } \right.$$

  (51)

If the stopping criterion is not met, the variable uₖ and the corresponding constraints are added to the master problem, and the algorithm proceeds to the next iteration (k = k + 1).

To rigorously evaluate the practical performance of the proposed PSO-C&CG algorithm, an extensive analysis was conducted to assess its convergence behavior and sensitivity to key parameters. Such an analysis is critical for verifying the robustness and reliability of the algorithm in practical applications. The algorithm was executed over 30 independent runs for each parameter configuration to ensure statistical significance of the results. The comprehensive findings, which integrate both sensitivity and convergence metrics, are summarized in Table 5.

Table 5 Consolidated performance analysis of the PSO-C&CG algorithm under varying population sizes.

The population size (N) of the PSO solver was identified as a critical parameter influencing the trade-off between solution quality and computational expense. The baseline configuration (N = 50) achieved the lowest mean operating cost among all tested setups, demonstrating its superior economic performance. While the large population configuration (N = 70) yielded a marginally improved solution stability, as indicated by the lowest standard deviation of the objective value, this came at the cost of a 26% increase in computation time compared to the baseline. Conversely, the small population configuration (N = 30), despite its computational speed, resulted in a significantly higher and more volatile operating cost. This behavior is characteristic of insufficient exploration of the solution space, leading to convergence to inferior local optima. Therefore, the baseline parameter N = 50 is justified as it optimally balances exploration and exploitation, ensuring high-quality, cost-effective dispatch decisions without prohibitive computational overhead.

A paramount finding is the 100% convergence success rate achieved across all 30 independent runs for every parameter configuration. This result unambiguously confirms the inherent numerical stability and reliability of the proposed PSO-C&CG framework, irrespective of the initial conditions or specific parameter tuning. Furthermore, the convergence process itself is highly predictable. The low standard deviation observed in the number of iterations required for convergence (particularly 1.2 for the baseline) indicates that the algorithm’s runtime behavior is consistent and repeatable. This predictability is a crucial attribute for the practical implementation of optimization algorithms in energy system scheduling, where reliable and timely decision-making is essential.

The computational complexity of the proposed hybrid PSO-C&CG algorithm exhibits favorable scaling properties for large-scale problems. The C&CG framework ensures that the number of iterations grows sub-linearly with problem size, as the decomposition structure effectively handles the min–max formulation through strategic scenario generation. Meanwhile, the PSO component maintains O(N) complexity per iteration, where N is the swarm size, which remains constant regardless of problem dimension.

Case analysis

Fitted estimate of uncertainty of the load

The probability distribution of the user load forecast error is represented by a histogram and a distribution curve, as shown in Figs. 6 and 7. The blue bars represent the histogram of the user load forecast error, with the left vertical axis indicating frequency, while the red curve represents the fitted probability density function, and the right vertical axis indicates the probability density. The horizontal axis represents the standard deviation of the user load forecast error. As discussed earlier, a probability distribution model for the load forecast error for each time period must be established. In this paper, 8:00 and 14:00 are selected as examples. The distribution of the 8:00 power load forecast error is shown in Fig. 6a. As shown in the figure, the normal distribution provides a poorer fit compared to the actual histogram distribution, whereas the KDE offers a better fit. The difference is primarily observed in the interval of ± [0.05, 0.1]. The RMSE of the two distribution fits are 3.52 × 10⁻³ and 5.45 × 10⁻³, respectively, indicating that KDE more accurately reflects the distribution characteristics of the user load forecast error. The distribution of the 14:00 power load forecast error is shown in Fig. 6b. The difference between the KDE and the normal distribution is primarily within the interval of ± [0.3, 0.25], with the RMSE of the two distribution fits being 2.89 × 10⁻³ and 8.76 × 10⁻³, respectively. The distribution of the heat load forecast error at 8:00 is shown in Fig. 7a, and the distribution at 14:00 is shown in Fig. 7b. It is evident that the KDE curve provides a significantly better fit for both the overall trend and local details.

Fig. 6

Comparison of forecasting error distributions for electrical load.

Fig. 7

Comparison of forecasting error distributions for heat load.

To assess the effectiveness of LSCV for bandwidth selection in KDE, we conducted a comparative study using three representative distributions: standard normal (light-tailed), t-distribution with 5 degrees of freedom (moderately heavy-tailed), and Cauchy distribution (strongly heavy-tailed). In each case, samples were drawn from the theoretical distribution, and its analytical probability density function (PDF) was taken as the True PDF for evaluation. Although the normal distribution is shown to be less accurate in modeling real-world load profiles, it is still adopted here as a representative light-tailed benchmark for validating the performance of bandwidth selection methods in KDE. For each case, KDE was performed using bandwidths determined by LSCV. Although the normal distribution is shown to be less accurate in modeling real-world load profiles, it is still adopted here as a representative light-tailed benchmark for validating the performance of bandwidth selection methods in KDE.

As illustrated in Fig. 8, the LSCV method enables accurate tail fitting while maintaining overall smoothness, especially under moderate and heavy-tailed distributions. Hence, LSCV demonstrates greater adaptability and robustness in modeling the uncertainty of electricity and thermal loads, especially in capturing marginal behavior.

Fig. 8

KDE performance evaluation under different theoretical distributions.

To compare the probability distributions of electric-heat load forecasting errors at different time periods, this paper takes electric load as an example and illustrates, as shown in Fig. 9, the comparison between the normal distribution and the kernel density distribution in terms of their RMSE over various time intervals. The results indicate that the normal distribution provides a poorer fit, particularly during certain time periods (e.g., 10:00–14:00 and 16:00–20:00), where the RMSE is significantly higher. In contrast, the kernel density distribution demonstrates lower RMSE for most time periods, suggesting that it more effectively captures the characteristics of the forecasting errors, especially in time intervals with considerable variability. Similarly, the kernel density distribution also exhibits advantages in the context of heat load forecasting errors. Therefore, the kernel density distribution model is better suited for modeling the forecasting errors of electric-heat loads, as it yields more accurate predictions and error analyses.

Fig. 9

Comparison of RMSE for different distribution functions.

Figure 10 illustrates the probability density distribution of load forecast errors across various time periods. The analysis reveals that near midday (e.g., 12:00), the forecast error distribution appears relatively “short and fat,” indicating that errors are concentrated during this period, corresponding to higher prediction accuracy. In contrast, during the morning (e.g., 10:00) and afternoon (e.g., 16:00) periods, the forecast error distribution becomes “tall and thin,” suggesting a broader error distribution with greater variability. Overall, the distribution of errors across the entire period exhibits a wide range, reflecting the high volatility of load forecast errors. Based on this analysis, using the distribution of all errors to generate scenarios may overlook significant differences between time periods, leading to less accurate forecast error scenarios. Therefore, a time-specific sampling generation method is more appropriate, as it can more accurately capture the characteristics of load forecast errors during different time periods, ultimately enhancing the accuracy and reliability of the forecast model.

Fig. 10

Probability density function curves for different time periods.

In this study, the joint statistical characteristics of electric and thermal load uncertainties are modeled using a Copula-based framework, which effectively captures the dependency structure among multiple correlated stochastic variables. A total of 1,000 joint scenarios are generated via MC simulation and subsequently reduced using the K-means clustering algorithm, with Euclidean distance adopted as the similarity metric. This method partitions the high-dimensional scenario space by minimizing the within-cluster sum of squared errors, and selects the centroid of each cluster as a representative scenario. The probability of each reduced scenario is then assigned proportionally to the size of its corresponding cluster, thereby preserving the statistical relevance and probabilistic weight of each realization.

To rigorously justify the selection of five representative scenarios and validate the efficacy of the K-means-based reduction technique, a comprehensive quantitative assessment was conducted. This assessment evaluates the statistical congruence between the reduced scenario set and the original 1,000 Monte Carlo samples through moment preservation analysis and distributional similarity measurement via the Wasserstein distance.

A critical criterion for effective scenario reduction is the preservation of key statistical moments. Table 6 compares the first four moments—mean, variance, skewness, and kurtosis—of the electrical and thermal load distributions between the original and reduced scenario sets. The results demonstrate that the relative errors for all moments remain below 5%, with errors for the central moments (mean and variance) within 2%. This indicates that the reduced set not only accurately captures the central tendency and dispersion of the original data but also effectively retains the shape characteristics, including asymmetry (skewness) and tail behavior (kurtosis).

Table 6 Statistical moment preservation between original and reduced scenario sets.

Beyond moment matching, the Wasserstein distance (also termed the Earth Mover’s Distance) was employed to quantify the overall distributional discrepancy. This metric provides a robust, non-parametric measure of the minimal cost required to transform one distribution into another. The computed distances are: Electric load: 4.72, Thermal load: 4.35.

A sensitivity analysis on the number of clusters revealed that using three clusters resulted in substantially larger Wasserstein distances (exceeding 12), indicating poor representation. In contrast, increasing the number of clusters to ten yielded only marginal improvements (distances ≈ 3.5) at a significant computational cost. The five-cluster configuration thus represents an optimal trade-off, achieving high distributional fidelity—as evidenced by the low Wasserstein metrics—while maintaining computational tractability for the subsequent optimization model.

The combined evidence from the moment preservation analysis and the distributional similarity assessment conclusively demonstrates that the five-cluster scenario set provides a statistically sound and computationally efficient representation of the original uncertainty space.

To determine an appropriate number of representative scenarios, a sensitivity analysis is conducted by comparing scenario sets of size 5, 10, and 20 in terms of operational fidelity and computational efficiency. As summarized in Table 7, selecting five scenarios achieves a favorable trade-off—limiting the economic deviation in operating cost to a mere 0.62% compared to the full-scenario benchmark, while significantly reducing the computational burden of the subsequent robust optimization problem.

Table 7 Comparison of optimization performance under different scenario quantities.

The resulting five typical scenarios are illustrated in Fig. 11, each representing a distinct temporal evolution pattern of electric and thermal loads along with their associated realization probability. As shown in the figure, the 24 h load profiles under these five scenarios exhibit two characteristic peaks: the first typically occurs between 10:00 and 12:00, and the second between 18:00 and 22:00. These peak periods correspond to higher daytime energy demand and align well with observed consumption patterns, underscoring the representativeness of the reduced scenario set. The final reduced scenarios are then used as inputs for robust scheduling optimization.

Fig. 11

Five representative scenarios of electrical load and heat load after K-means reduction.

Analysis of the operating results under different strategies

In order to rigorously evaluate the performance of the proposed PSO- C&CG algorithm, we conducted 30 independent runs under identical experimental settings and compared its results to the traditional C&CG method. The comparison focuses on two key aspects: computational efficiency and computational accuracy.

Computational efficiency is defined as the total average solving time per run, including the master problem and subproblem iterations. As shown in Fig. 12, the PSO- C&CG algorithm significantly reduces the average computation time from 139.6 s (traditional C&CG) to 95.8 s, achieving a 31.4% reduction in solving time. This improvement is attributed to the PSO component’s ability to accelerate convergence via parallel exploration of the solution space, particularly beneficial in large-scale stochastic optimization.

Fig. 12

Performance comparison with traditional algorithms.

Computational accuracy is defined as the relative reduction in objective function value compared to the baseline C&CG solution:

$$Accuracy Gain \left( \% \right) = \frac{{F_{CCG} - F_{PSO - CCG} }}{{F_{CCG} }} \times 100\%$$

(52)

where $F_{CCG}$ and $F_{PSO - CCG}$ are the objective values obtained by the traditional and proposed algorithms.

Strategy 1: Optimizes the output of supply-side equipment without accounting for DR.

Strategy 2: The thermoelectric coupling is decoupled by an energy storage device, and the user side participates solely in electric load DR to optimize the output of supply-side equipment.

Strategy 3: The thermoelectric coupling is decoupled by an energy storage device, and the user side participates solely in the selective response of the heat load to optimize the output of supply-side equipment.

Strategy 4: The thermoelectric coupling is decoupled by an energy storage device, and the user side participates in both electric load DR and thermal load supply selection response, optimizing the output of supply-side equipment.

Strategy 5: The thermoelectric coupling is decoupled by an energy storage device, and the user participates in both electric load DR and selective heat load supply response, considering the impact of load uncertainty.

The operating conditions for the five strategies are summarized in Table 8. Strategy 1 does not consider DR, with electricity and heat being operated independently. The system’s load demand is primarily met by purchasing electricity and heat, leading to a higher operating cost of 5,872.3 RMB. Strategy 2 incorporates demand-side management into the system’s economic operation. By regulating the power consumption of controllable and time-shifted loads during peak periods, the system reduces its electricity purchase cost, resulting in a reduced total operating cost of 5,615.9 RMB. Strategy 3 uses complementary load characteristics for replacement DR to reduce peak power purchases. However, the cost of operating the electric boiler increases, leading to a total operating cost of 5,603.4 RMB. Strategy 4 combines both DR methods from Strategies 2 and 3. While the boiler cost increases compared to the previous strategies, the peak-period electricity purchase is reduced, optimizing the total operating cost to 5,375.8 RMB. Strategy 5 builds upon Strategy 4 by factoring in the impact of load uncertainty. Due to the volatility in the load, both the boiler and exchange costs increase slightly, causing the total operating cost to rise to 5,468.3 RMB.

For a transparent interpretation of the results in Table 8, the derivation of the DR participation rate and carbon emission values is explicitly stated below:

Table 8 Operating results for different strategies.

DR Participation Rate: This metric was calculated to quantify the degree of demand-side flexibility utilized. It is defined as the ratio of the total flexible load actively dispatched by the optimization model (the sum of curtailed, shifted, and replaced loads during the scheduling horizon) to the total technical potential of flexible loads available from user-side devices (e.g., HVAC, EWH, shiftable appliances). The result is expressed as a percentage, providing a clear measure of resource engagement.

Carbon Emissions: The total carbon emissions were derived by combining the optimal dispatch results from the model with standardized emission factors. The calculation is primarily based on the equation:

$${\text{Total Emissions }} = \, \Sigma \, \left( {P_{E}^{{{\text{buy}}}} \times \eta \, + P_{EB} \times \mu } \right)$$

(53)

where, $\eta$ is grid emission factor, $\mu$ is fuel emission factor.

The grid emission factor corresponds to the average value for the regional power system. Consequently, the observed reduction in emissions under the proposed strategy (S5) is a direct outcome of the model’s decisions to minimize costly and carbon-intensive peak electricity purchases from the grid, leveraging instead local energy storage and flexible thermal loads.

Table 9 provides an economic comparison across five typical scenarios and their associated probabilities. Due to differences in scenario occurrence probabilities, the total costs vary accordingly. Therefore, the probability-weighted expected value of the total costs across these five typical scenarios is adopted in this paper to represent the total cost considering load uncertainty.

As shown in Tables 8 and 9, Strategy 5, which incorporates user-side load uncertainty, results in a slight increase in user cost by approximately 1.7% compared to other strategies. This cost increment primarily arises from the conservative scheduling adjustments designed to hedge against potential load fluctuations, thereby ensuring the system’s robustness and feasibility in practical operation. References^28,29,30 similarly indicate that robust optimization under uncertainty typically leads to moderate cost increases, which are widely regarded as a reasonable and acceptable trade-off in integrated energy systems. Specifically, this modest increase in cost yields enhanced system adaptability and improved operational reliability under uncertain conditions, effectively mitigating risks of violations or failures caused by unforeseen fluctuations. In real-world engineering applications, this slight economic burden is generally outweighed by the avoidance of potentially far greater losses due to system risks, thus providing significant practical and application value.

Table 9 Economic comparison under five representative scenarios.

The practical relevance of the identified 1–2% cost reduction, as evidenced by Strategy 5’s performance against the baseline (Strategy 1), extends beyond its nominal percentage. In the context of capital-intensive integrated energy systems with high annual operational expenditures, a 1.7% reduction translates into substantial absolute savings—approximately 100 RMB daily and over 36,500 RMB annually for the studied system. For utilities managing multiple such systems, these accumulated savings significantly enhance the economic viability and return on investment for deploying integrated demand response infrastructures. Furthermore, this cost efficiency is not achieved in isolation; it is concomitant with enhanced system flexibility and robustness against uncertainties, as quantified by the following uncertainty analysis. This combination of economic benefit and operational resilience underscores the strategic value of the proposed method for real-world applications.

To provide a more rigorous and quantitative assessment of the economic performance under uncertainty, Table 10 summarizes the statistical analysis of the total operating cost for Strategy 5, which explicitly incorporates load uncertainty. The expected cost is calculated as 5487.05 RMB, consistent with the weighted average cost presented in Table11. Furthermore, the standard deviation of 97.46 RMB indicates a moderate level of cost variability across scenarios.

Table 10 Statistical analysis of total cost under load uncertainty (Strategy 5).

Table 11 Comparative performance of proposed and benchmark strategies.

Importantly, the 95% confidence interval, computed based on the normal distribution approximation, ranges from 5297.03 RMB to 5677.07 RMB. This interval quantifies the uncertainty band within which the actual operating cost is likely to fall with high confidence, reflecting the system’s robustness against load fluctuations.

Such probabilistic evaluation enhances the reliability of the economic analysis by moving beyond deterministic single-point estimates and demonstrating that the proposed uncertainty-aware strategy maintains stable and cost-effective operation under realistic, stochastic conditions.

The provision of this 95% confidence interval for the expected operating cost (5487.05 ± 95.02 RMB) is critical for a comprehensive economic risk assessment. It quantifies the economic uncertainty inherent in the system due to load fluctuations, providing a bounded estimate rather than a single, potentially misleading, point value. The relatively narrow range, with a standard deviation of 97.46 RMB, indicates that while the day-to-day cost may vary, the long-term economic performance of Strategy 5 is predictable and stable. Decision-makers can therefore be highly confident that the operational cost will fall within this range, facilitating more reliable budgeting and risk management. This probabilistic assurance is a key advantage over deterministic optimization methods, which cannot characterize such economic risks.

Analysis of the results of the electrical energy operation

Figure 13 presents the results of the electrical energy operation for each strategy. The results indicate that, during the 22:00–6:00 tariff valley hours, when the electrical load is predominantly supplied by the grid, EB in all strategies are activated at 4:00, with the electrical storage devices operating in charging mode. In comparison to Strategy 3, Strategies 2 and 4 exhibit higher purchased power during the tariff valley period due to the shifting of part of the electric load to this period. During the peak tariff hours of 6:00–12:00, as both the electric load and tariff increase gradually, the system’s purchased power decreases correspondingly, and the electric storage equipment begins discharging. In comparison to Strategies 2 and 3, Strategy 4 notably reduces purchased power by curtailing and shifting some of the power usage, while guiding users to optimize their energy supply. Moreover, the electric storage discharge power in Strategy 4 is lower than that in Strategy 3 during this period, demonstrating superior energy management. During the 12:00–18:00 tariff flat period, the system’s purchased power increases as both the electric load and tariff decrease. During the 18:00–22:00 period, the second peak of the tariff, the system operates in a manner similar to the first peak period (6:00–12:00). However, in the latter half of the peak period, as the electrical load gradually decreases, the electrical storage discharge power and discharge frequency are significantly reduced across all strategies. Strategy 5 incorporates the uncertainty of the electrical load, which is supplied by the grid during the 22:00–6:00 tariff valley hours. The electrical storage device charges, and the electric boiler activates around 4:00 to provide thermal support. However, the purchased power and boiler power increase, thereby raising operating costs due to load fluctuations. During the 6:00–12:00 tariff peak hours, the purchased power gradually decreases as both the tariff and load rise, and the electric storage equipment begins discharging, though the discharge power fluctuates slightly. Between the 12:00 and 18:00 tariff hours, purchased power increases, system operation stabilizes, and both boiler and electrical energy exchange costs rise slightly due to fluctuations. During the second peak period (18:00–22:00), the operational mode mirrors that of the first peak period. Power purchase and discharge power are adjusted in response to load fluctuations, and the discharge power and equipment operation frequency are significantly reduced in the latter half as the load decreases.

Fig. 13

The results of the electrical energy operation.

Figure 14 illustrates the output characteristics of electric storage over a 24-h period under different strategies, with Strategy 5 representing the output under integrated DR that accounts for uncertainty. The figure reveals a significant difference in the temporal distribution of the output characteristics of EES across the various strategies (Strategies 2 to 5). During peak load hours (e.g., 7:00–11:00 and 18:00–22:00), EES supports the system by providing positive output, thereby alleviating peak load pressures. In contrast, during low load hours (e.g., 0:00–6:00 and 12:00–16:00), the EES operates in the negative direction, storing excess energy in preparation for the regulation of subsequent peak hours. Strategy 5, which incorporates integrated DR considering uncertainty, results in increased volatility in the output of electric storage, reflecting the system’s greater regulation task in response to load uncertainty.

Fig. 14

Electric energy storage operation patterns across different strategies.

Analysis of the results of the heat energy operation

The thermal performance results for each strategy are illustrated in Fig. 15. During the 22:00–6:00 tariff valley hours, thermal loads in each strategy are primarily supported by EB and HST. Compared to Strategies 2 and 3, Strategy 4 releases more thermal energy from storage, resulting in a smaller output from the EB. During the 6:00–12:00 period, Strategies 3 and 4 significantly reduce the power of electric heat equipment by optimizing its operation strategy, which increases the power of the heat load and further elevates the operating power of the EB. Additionally, Strategy 4 has a longer duration of heat storage compared to Strategy 3, thereby storing more thermal energy. During the 12:00–18:00 period, the heat output from the EB in each strategy decreases, while the HST begins to release heat. The 18:00–22:00 period represents the second tariff peak, during which the system operates similarly to the 6:00–12:00 period. Consequently, the heat load power increases, and the EB operate at higher power. During the 22:00–6:00 tariff valley hours, the thermal load in Strategy 5 is shared by EB and HST; however, the EB operating power fluctuates due to load variations, and the HST charging power also exhibits instability. During the 6:00–12:00 peak tariff hours, the EB operates at significantly higher power, while the HST’s heat storage duration is slightly shorter, leading to insufficient thermal energy reserves. During the 12:00–18:00 tariff period, the HST gradually releases heat to balance the load, although the release process is subject to fluctuations. During the second tariff peak (18:00–22:00), the EB operating power fluctuates slightly, the HST heat release power decreases, and the overall operating cost increases due to load uncertainty.

Fig. 15

The results of the heat energy operation.

Figure 16 illustrates the output characteristics of thermal storage over a 24-h period under different strategies, with Strategy 5 representing the output under integrated demand response that accounts for uncertainty. From the figure, it is evident that the thermal storage outputs in Strategies 2 to 5 exhibit significant temporal differences. During peak load hours (e.g., 0:00–6:00 and 18:00–24:00), the positive output of HST is higher, indicating that it releases heat to meet system demand. In contrast, during low load hours (e.g., 7:00–17:00), HST primarily functions by storing thermal energy through negative output. Specifically, Strategy 5 exhibits more significant output fluctuations, reflecting the ability of thermal storage to regulate output more flexibly in response to load fluctuations and system uncertainty under integrated DR that accounts for uncertainty.

Fig. 16

Heat energy storage operation patterns across different strategies.

Comparison with existing methods

To further verify the superiority of the proposed integrated DR strategy under uncertainty, this section conducts a comparative analysis with two representative benchmark methods from recent literature. Reference³¹ presents an electricity DR strategy based on a bilevel optimization model, which incorporates user participation and mixed response schemes. The model employs a Stackelberg game framework to coordinate demand flexibility in the electricity market. Reference³² proposes a robust load restoration model that accounts for uncertain dynamic loads, utilizing a stability-constrained polyhedral uncertainty set. This model represents a state-of-the-art framework for uncertainty-aware optimization.

These two methods are selected as benchmarks for advanced DR coordination and robust optimization under uncertainty. To ensure a fair comparison, both models are adapted to the same scenario dataset generated through Copula-KDE-based MC sampling, and applied to an identical multi-user IEHS structure.

Strategy 5: The proposed integrated DR framework.

Strategy 6: Two-layer power DR based on deterministic modeling³¹.

Strategy 7: Robust optimization and centralized dispatch based on box-type uncertainty sets³².

The comparative results are summarized in Table 11. The proposed Strategy 5 consistently outperforms both benchmark strategies across all performance indicators. Compared to Strategy 6, which focuses solely on electric DR, Strategy 5 reduces operating costs by 5.8%, boosts user participation by over 11%. This demonstrates the advantage of incorporating heat load flexibility. Compared to Strategy 7, which emphasizes uncertainty robustness but lacks flexibility due to its worst-case conservatism, the proposed model achieves better economic efficiency and demand-side responsiveness. Notably, the Copula-based joint distribution model captures both inter-variable dependency and temporal variability, allowing for a more realistic representation of user-side uncertainties than traditional box-type sets.

Scalability analysis

To comprehensively evaluate the scalability of the proposed PSO-C&CG algorithm, we conducted extensive numerical experiments on three systematically scaled test systems. Small-Scale System: The original case study presented in previous sections, serving as the baseline for comparison. Medium-Scale System: An expanded configuration with four times the number of users compared to the small-scale system. Large-Scale System: A significantly larger system with 900% more users, representing a challenging regional-scale integrated energy system.

The computational performance across different scales is summarized in Table 12, which includes the following key metrics.

Table 12 Scalability analysis of the proposed PSO-C&CG algorithm.

To evaluate the scalability of the proposed PSO-C&CG algorithm, its performance was rigorously tested across systems of varying user scales. The results demonstrate favorable scaling properties: firstly, the number of C&CG iterations exhibits a sub-linear increase, rising only from 15 to 22 as the user base scales up by a factor of ten (from 50 to 500 users). This indicates that the core logic of iteratively identifying critical worst-case scenarios remains highly efficient and does not deteriorate significantly with increasing problem dimensionality. Secondly, the total computation time grows predictably with the number of users, and the computational load maintains a consistent, near-equal split between the master problem and the subproblem (each consuming approximately 50% of the total time). This balanced profile confirms the robustness of the hybrid framework design, as neither component becomes a disproportionate bottleneck with increasing system size. Finally, for the large-scale system with 500 users, the total computation time remains at approximately 12 min, which is well within practical limits for day-ahead scheduling applications. This analysis confirms that, although the proposed framework is applied here at the community level, it possesses the computational tractability and reliability for problems of significantly larger scale, underscoring its potential for broader application.

Conclusion

This paper investigates the uncertainty of user-side load and develops an IDR-EH optimization model. To characterize the volatility and uncertainty inherent in multi-dimensional load data, a Copula-based load time-correlation uncertainty model was constructed, and the distribution of forecasting errors was fitted using the non-parametric KDE method. Subsequently, the MC sampling approach was utilized to obtain predictive fluctuations for each load, enabling the replacement of uncertain data with sampled datasets. Furthermore, by employing an EB as the electricity-heat coupling device and utilizing energy storage devices for decoupling, the proposed integrated DR optimization model comprehensively accounts for load uncertainties and coordinates electricity and heat demands. The major findings from the numerical analysis are summarized as follows:

Compared with the single electricity DR, the proposed IDR-EH yields an 81% increase in user compensation and a 0.7% reduction in total operating costs. In comparison with the single heat DR, user compensation improves by 99%, and the total operating costs decrease by 0.5%. Moreover, the IDR-EH demonstrates the most effective peak shaving and valley filling capability. After considering uncertainties, the operating costs are slightly higher than those under deterministic integrated demand response scenarios due to system fluctuations; however, the costs remain lower compared to scenarios without DR strategies.

The scalability analysis conducted in Section “Scalability analysis” demonstrates that the proposed PSO-C&CG framework maintains computational efficiency across systems of varying scales. While absolute computation time increases with problem size, the near-linear scaling relationship and stable convergence patterns confirm the method’s applicability to realistic large-scale integrated energy systems. For extremely large systems beyond those tested, potential enhancements such as parallel computing or hierarchical decomposition could be explored in future work.