Evaluating physics informed neural networks for water contamination risk prediction and environmental sustainability

Abstract

Growing pollution hazards in large watersheds, including Egypt’s Nile River, necessitate precise and effective monitoring of water quality indices. Although considerable efforts have been made to model individual parameters such as pH, Total Dissolved Solids (TDS), Electrical Conductivity (EC) and sodium (Na$^{+}$), the emphasis on isolated forecasts has often overlooked their interdependencies, thereby limiting estimation accuracy and practical applicability. Conventional machine learning methodologies further compound this issue, as they frequently lack adaptability and physical interpretability, resulting in inefficiencies for sustainable water management. To address these limitations, this study develops a physics-informed neural network (PINN) framework integrated with optimization boosting techniques to jointly predict pH, TDS (mg/L), EC ($\mu$S/cm), and Na$^{+}$ (mg/L) under three critical management strategies: industrial discharge regulation, salinity management and irrigation planning. The approach incorporates prior hydrodynamic and chemical knowledge to guide input categorization, employs adaptive weighting mechanisms to dynamically adjust feature relevance, and introduces a deep interaction module to capture intricate physicochemical couplings. A physics-constrained loss function ensures consistency with ecological processes. Field analysis revealed that while pH values (6.01–6.87) consistently met FAO standards, TDS, EC, and Na$^{+}$ frequently exceeded permissible thresholds, particularly during the dry season. Model evaluation showed that PINN outperformed conventional optimizers, achieving $\textrm{R}^{2}$ values of 0.945–0.999 and RMSE between 0.012–0.088. Cross-validation further confirmed its robustness, yielding consistently low RMSE and near-unity $\textrm{R}^{2}$ across folds. Interpretability analysis highlighted irrigation intensity, salinity loads, and industrial effluents as the dominant drivers of water quality dynamics. Overall, the proposed PINN not only advances predictive accuracy and computational efficiency but also provides a practical framework for supporting regulatory decision-making, optimizing salinity control, and guiding sustainable irrigation planning. Ultimately, this approach offers a viable pathway for mitigating contamination risks and ensuring the long-term sustainability of the Nile River ecosystem.

Introduction

Water is a naturally occurring resource, accessible to all, and a fundamental necessity for life. However, if not properly managed, it can become a conduit for harmful pathogens and toxic substances. Due to its wide range of applications, water plays a critical role in supporting societal health and economic growth. It is essential for domestic and industrial use, recreation, aquatic ecosystems, and agricultural production. However, the quality of water used for irrigation can be compromised by factors such as human activity, seasonal changes, soil pH, and improper waste disposal. The adverse effects of uncontrolled wastewater discharge into water sources intended for human use have prompted numerous studies on watershed contamination and its mitigation¹. To address these concerns, global regulatory frameworks such as the irrigation guidelines and standards established by the Food and Agriculture Organization (FAO) and the Egyptian Standard Organization have been implemented to ensure the preservation and safe use of water for upstream activities^2,3.

Furthermore, the condition of rivers and reservoirs is significantly influenced by pollution from domestic, regional, and agricultural sources. When such pollution renders water unsuitable for human consumption, commercial use, or agricultural purposes, it is classified as contaminated or polluted⁴. Water quality deterioration occurs when hazardous substances infiltrate water bodies or when the concentration of naturally occurring elements increases to levels that disrupt ecological balance and hinder the water’s natural self-purification processes. This degradation has caused extensive damage to aquatic ecosystems and poses serious threats to human health, including the spread of waterborne diseases prompting an urgent need for effective mitigation strategies⁵.

A healthy aquatic ecosystem is characterized by a balance of physical, chemical, and biological components, with water that is colorless, odorless, and tasteless. However, contamination disrupts these conditions, rendering the water unsuitable for domestic, industrial, or agricultural use. Both surface and groundwater sourced from communities exhibit varying levels of quality. While some rivers require only minimal treatment to meet safety standards, others necessitate intensive management and purification. Water quality is influenced by seasonal changes, geological structure, and the sources of pollution. For example, during the rainy season, increased rainfall can dilute contaminants, temporarily improving the physicochemical properties of water to resemble those of freshwater⁶.

Nonetheless, various pollutants ranging from human waste and food residues to mixed organic and inorganic compounds frequently enter river systems. Depending on the origin and tributaries, a river often serves as a major recipient of effluent from household and industrial activities. Therefore, effective pollution control and sustainable water management practices are essential for maintaining water quality and supporting safe usage across multiple sectors⁷.

Training datasets serve as the primary source of guidance for model selection and parameterization in the data-driven methodology of machine learning (ML). Within this framework, heuristic strategies, prior expertise, and trial-and-error procedures are commonly employed to determine an appropriate architecture, including the number of hidden layers, neurons per layer, and activation functions in a neural network (NN). Once the model structure is established, parameters are optimized by minimizing a loss function possibly subject to constraints which typically corresponds to reducing the prediction error on the training data. This procedure involves determining a parameter set $\theta ^{*}$ that minimizes the discrepancy between observed and predicted outcomes in supervised learning tasks, particularly in regression problems. In this context, the mean squared error (MSE) is commonly employed as the loss function:

$$\begin{aligned} \theta ^{*} = \arg \min _{\theta } \textrm{L}\big (\textrm{x}, \digamma (\textrm{y}; \theta )\big ), \end{aligned}$$

(1)

$$\begin{aligned} \textrm{L}\big (\textrm{x}, \digamma (\textrm{y}; \theta )\big ) = \mathbb {E}\Big [(\textrm{x}, \digamma (\textrm{y}; \theta ))^{2}\Big ], \end{aligned}$$

(2)

where $\textrm{y}$ denotes the input features, $\textrm{x}$ represents the corresponding observed or computed outputs, and $\digamma (\textrm{x}; \theta )$ is the ML model parameterized by $\theta$. Since it only measures the deviation of the predicted target values from the actual values for a given parameterization, the optimization using the loss function in (2) is entirely predictive in nature.

Determining the unknown conditional distribution $\textrm{p}(\textrm{y}\mid \textrm{x})$ is a central task in supervised ML, as it provides valuable insights into system structures and real-world phenomena. Given a training dataset $\mathcal {D}=(\textrm{x},\textrm{y})$ and a new input $\textrm{x}^{*}$, the objective of predictive tasks is to estimate the distribution $\textrm{p}(\textrm{y}^{*}|\textrm{y},\textrm{x}, \textrm{x}^{*})$. Numerous studies in ML and deep learning (DL) have demonstrated that statistical learning-based frameworks can be effectively applied across a wide range of scientific and engineering domains^8,9,10. Furthermore, research demonstrates that in DL, scaling both network size and dataset volume consistently improves the prediction of $\textrm{p}(\textrm{y}^{*}|\textrm{y}, \textrm{x}, \textrm{x}^{*})$, even in highly complex contexts. However, in data-scarce settings, incorporating prior knowledge about the system, such as $\pi (\textrm{y})$, provides an effective means of enhancing the generalization capacity of ML models.

ML is widely applied in ecological, scientific, and engineering domains to approximate the conditional distribution $\textrm{p}(\textrm{y}|\textrm{x})$, which typically represents a physical system governed by known laws^11,12,13. Although considerable prior knowledge about these complex systems often exists, it is rarely integrated into the modeling process due to the difficulty of embedding it systematically within the model structure. As a result, strategies that explicitly incorporate fundamental physical laws or domain-specific knowledge are generally preferred over purely data-driven approaches.

However, data-driven ML algorithms rely on numerous independent variables to capture the underlying complexity of the data, they pose significant challenges when applied to complex problems. Optimizing such high-dimensional parameter spaces typically requires massive amounts of training data, which is often impractical due to limited availability or the high cost of empirical acquisition^14,15. Moreover, models trained on small datasets may struggle to perform well on unseen data, rendering purely data-driven approaches vulnerable to issues of extrapolation and generalizability. Finally, when treated as “black boxes,” these models lack interpretability, making it difficult to understand the logic or mechanisms underlying their predictions.

By integrating knowledge of the physical principles governing a system into the design and training of ML models, Karniadakis et al.¹⁶ developed PI-ML to overcome the limitations of purely data-driven approaches. Specifically, Raissi et al.¹⁷ introduced the physics-based regularization into PINNs. This is achieved by incorporating terms that encode the underlying physical laws into the loss function, thereby constraining the parameter space of the model. A widely used strategy involves embedding the residuals of partial differential equations (PDEs) into the loss function, enabling simulations that are more consistent with the governing physics and thus more practically applicable.

Moreover, the training process generates simulations that minimize data-fit error while preserving consistency with the governing physics by employing loss functions that penalize predictions deviating from the underlying physical principles. Gradient propagation is maintained, allowing the predictive model to be trained in the usual manner, provided that the additional terms in the loss function are differentiable. This physics-informed learning paradigm has been effectively applied to numerous modeling challenges, particularly forward problems, where the objective is to predict latent solutions of systems governed by specified equations^18,19.

Recently, PINNs have gained recognition as an effective approach for solving complex computational problems¹⁶. By integrating DL algorithms with the mathematical frameworks of PDEs, ordinary differential equations (ODEs), and their associated boundary conditions (BCs), PINNs can significantly reduce or even eliminate the need for synthetic or empirical data. A typical PINN architecture consists of an input layer defined by spatial and/or temporal variables, multiple hidden layers with numerous neurons, and an output layer representing the target quantities of interest. This enables the formulation of a loss function that incorporates the residuals of the equations, along with relevant initial conditions (ICs) and BCs, thereby effectively guiding the training process¹⁷.

Spanning a wide range of configurations, parameters, and complexities, PINNs are highly effective for solving both ODEs and PDEs. A major advantage over traditional numerical methods is their mesh-free architecture, which enables training on randomly sampled points rather than structured grids significantly reducing computational cost and data dependency²⁰. The performance of PINNs is typically enhanced using optimization techniques, often based on gradient descent algorithms. Although the training phase may be longer than that of classical solvers, the resulting models allow for rapid and efficient solution evaluations. To ensure compliance with ICs and BCs, constraints are embedded into the loss function using appropriate scaling criteria. Because manual tuning of these parameters can be difficult, evolutionary strategies are being explored to automatically balance the contributions of each loss component during training. Furthermore, advanced network architectures such as Fourier feature networks have proven particularly effective in capturing high-frequency variations, especially in cases involving irregularities or complex geometries²¹.

However, industrial wastewater discharges from commercial zones along the banks have significantly polluted Egypt’s Nile River²². Many industries are strategically located near water bodies to facilitate the direct disposal of waste and agricultural runoff into the river²³. As a result, the water quality has deteriorated, reducing its suitability for irrigating adjacent farmlands. To evaluate the extent of degradation and identify optimal points for water recovery, key ecological indicators of the Nile were assessed using PINN algorithms. Based on common agricultural soil concerns, the parameters selected for analysis included pH (to assess overall water purity), sodium concentration (to evaluate ion toxicity), and both TDS and EC (to assess salinity)²⁴. Data were collected from several sampling points along the river and projections were generated over a one-year period (2019-2020)²⁵. The primary objective of this study is to assess the irrigation potential of the Nile River by forecasting the water quality index (WQI) across various temporal and spatial dimensions using artificial NN modeling^16,26.

Egypt’s farming industry has been significantly impacted by WP in the Nile River, primarily due to the accumulation of harmful ions in irrigation water²⁴. When crops are exposed to high concentrations of these ions, they often suffer biochemical damage, leading to substantial reductions in yield^23,24,25. In addition to ion toxicity, other pollutants introduce excessive nutrients into water sources, lowering crop productivity and leaving unsightly residues on fruits and leaves thereby reducing their market value. These contaminants also accelerate the corrosion of irrigation equipment, increasing maintenance and replacement costs²⁷.

Integrating aforesaid methods into the PINN architecture further enhances the capability to simulate and predict water pollution (WP) phenomena. Within this learning framework, PINNs embed the physical laws governing pollutant transport, such as PDEs. By incorporating these principles, PINNs can efficiently learn from limited but relevant data while maintaining consistency with established scientific laws. Leveraging both spatial and temporal features, PINNs can more accurately forecast WQIs along the Nile River, identify pollution hotspots, and evaluate the agricultural suitability of water^28,29. This integrated approach enables stakeholders to monitor contaminants, design effective mitigation strategies, and make informed decisions for water resource management by supporting sustainable and environmentally sound agriculture along the Nile River^30,31.

This study develops an interpretable PINN framework to assess water contamination risk and its implications for environmental sustainability in the Nile River using one-year data from 2019–2020. To overcome limitations of traditional approaches that treat all input variables equally, the PINN integrates optimization-boosting techniques to jointly predict key WQIs pH, TDS, EC, and Na$^{+}$ under irrigation planning, salinity management, and industrial discharge regulation (see Fig. 1).

Fig. 1

Graphical layout depicting the proposed WP system.

Field analysis was conducted at four stations to evaluate water contamination. The PINN employs categorized inputs informed by hydrochemical knowledge and a tanh-based activation mechanism to capture the varying influence of each parameter. A deep interaction module models complex physicochemical interactions among pollutants, and a hierarchical physics-constrained loss function ensures predictions remain consistent with governing water chemistry laws. Model interpretability is further evaluated by ablation studies, including models without the attention module and without the interaction module, enabling analysis of the spatiotemporal contributions of predictors and insights into factors driving water quality variations. For benchmarking, the PINN is compared with the Random Forest (RF) technique³², Residual Network (ResNet)³³, PI multi-task deep NN (PI-MTDNN)³⁴, and knowledge-informed NN (KI-NN)³⁵. The framework enables accurate mapping and analysis of water contamination risk across the Nile River, supporting informed water management, pollution mitigation, and sustainable agricultural practices. By rigorously analyzing the individual behaviors of pH, TDS, EC, and Na$^{+}$, and leveraging advanced methodologies such as PINNs, the entire procedure is illustrated in the flowchart presented in Fig. 2. This research emphasizes the importance of accurately predicting the water quality index for effective management, providing valuable insights into the model’s resilience and adaptability.

Fig. 2

Workflow depictions of the nonlinear WP system for Nile river.

Material and methods

Geographical scope

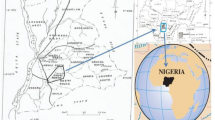
The research area is Egypt’s Nile River, a vital freshwater resource that supports domestic use, industrial activities, and agriculture across the country. Geographically, the study focuses on a section of the Nile in Lower Egypt, specifically the stretch flowing through and near Cairo, where urbanization and industrial development are highly concentrated. This region is approximately located between latitudes 29$^\circ$N and 31$^\circ$N, and longitudes 30$^\circ$E and 32$^\circ$E. It experiences a semi-arid to arid climate, having a mean yearly precipitation of roughly 200 mm and a mean temperature approximately 27$^\circ$C (Fig.3). Although seasonal temperature variations influence water quality and evaporation rates, the flow of the Nile remains relatively stable due to the regulatory effects of the Aswan High Dam.

Fig. 3

Thematic map showing pollution concentrations along the Nile River from Cairo to Helwan, Egypt. Map created by the authors using QGIS (3.28) and OpenStreetMap data (© OpenStreetMap contributors, licensed under ODbL). Pollution markers were visually added by the authors for illustration.

While the cooler months from November to February experience lower temperatures and reduced evaporation, the drier season from April to October is characterized by higher temperatures and increased evapotranspiration, potentially leading to concentrated pollution discharges. This seasonal meteorological pattern significantly influences contaminant transport and erosion processes within the river ecosystem.

In this region, the Nile River flows alongside several industrial zones, particularly in Greater Cairo and its surrounding areas. Notable industrial hubs such as Shubra El-Kheima, 10th of Ramadan City, and Helwan host a diverse range of factories, including those in the chemical, textile, and automotive sectors. The pollution load in the river is significantly intensified by the frequent discharge of wastewater and untreated effluents from these facilities (Fig. 4). Consequently, this area is well-suited for investigating the spatiotemporal dynamics of WP and its implications for environmental governance, sustainable agriculture, and public health.

Fig. 4

Map view of the Nile River in Egypt showing its main course, associated canals, lakes, and streams that contribute to pollution through the influx of industrial discharge and untreated domestic wastewater. Spatial distribution map of the study area. The map was created using QGIS (v3.28, QGIS Development Team, 2023, https://qgis.org) with OpenStreetMap as the base layer.

Geo-spatial sampling and evaluation

Based on a preliminary study, four sampling points were selected to evaluate WP in the Nile River during 2019–2020, focusing on areas affected by industrial discharges. These points, designated as $\textrm{G}_{1}$, $\textrm{G}_{2}$, $\textrm{G}_{3}$, and $\textrm{G}_{4}$, were strategically positioned to capture variations in contaminant levels along the waste water flow, taking into account ion dissolution and sediment transport processes. Sampling stations $\textrm{G}_{1}$ and $\textrm{G}_{2}$ were located upstream, while $\textrm{G}_{3}$ and $\textrm{G}_{4}$ were situated downstream. Water samples were collected in $1.5~\textrm{L}$ sterile plastic containers, with a distance of 20 meters maintained between each sampling point.

Routine water sampling was conducted monthly at each station from 2019-2020. Key WQIs including pH, TDS, EC, and Na$^{+}$ were analyzed. Each parameter was measured in duplicate, and the mean value was calculated as the final result. Samples were appropriately labeled and transported to the National Water Research Center (NWRC) in Cairo, Egypt³⁶ for preservation and further analysis. In-situ measurements of pH, TDS, and EC were also performed at each sampling location.

Physics-based characterization of WP dynamics

Let $\digamma (\textrm{y}_{1},\textrm{t})$ denote the hydrodynamic head, with $\textrm{y}_{1} \in \Omega \subset \mathbb {R}^d$. A general advection–diffusion–reaction balance with memory (storage) is

$$\begin{aligned} \textrm{X}_{\textrm{x}}\frac{\partial \digamma }{\partial \textrm{t}}(\textrm{y}_{1},\textrm{t}) + \nabla \cdot \big (-\mathcal {Q}_{\textrm{y}_{1}}(\textrm{y}_{1},\textrm{t})\nabla \digamma (\textrm{y}_{1},\textrm{t}) + \textrm{q}(\textrm{y}_{1},\textrm{t})\digamma (\textrm{y}_{1},\textrm{t})\big ) = \textrm{V}_{\textrm{a}}(\textrm{y}_{1},\textrm{t}) - \textrm{r}(\digamma ,\textrm{y}_{1},\textrm{t}), \end{aligned}$$

(3)

This formulation is highly relevant for studying the spread of WPs, where delayed contamination responses are represented, dispersive transport is captured by diffusion terms, and reaction terms account for natural attenuation or degradation. The variable $\textrm{x}$ represents simultaneous variations in hydrological forcing (the left-hand component of the equation). Consequently, the formulation (3) provides a direct link to assessing the risks of water quality deterioration and its implications for environmental sustainability. The physical interpretation of (3) is described as:

(i):

$\textrm{X}_{\textrm{x}}$ denotes the storage (capacity) or porosity-like coefficient, representing how much the domain stores/retains the hydraulic head per unit fractional derivative.

(ii):

$\mathcal {Q}_{\textrm{y}_{1}}(\textrm{y}_{1},\textrm{t})$ indicates the diffusion / hydraulic conductivity tensor, controlling pollutant dispersion in the Nile river or surface water.

(iii):

$\textrm{q}(\textrm{y}_{1},\textrm{t})$ is the advective or Darcy velocity, representing pollutant transport driven by flow fields.

(iv):

$\textrm{V}_{\textrm{a}}(\textrm{y}_{1},\textrm{t})$ constitutes the external pollutant sources/sinks (e.g., industrial discharge, agricultural runoff, injection/withdrawal).

(v):

$\textrm{r}(\digamma ,\textrm{y}_{1},\textrm{t})$ shows the reaction, attenuation, or sink term (e.g., biodegradation, sorption, evaporation).

Although, a pollutant spill at location ${\textrm{y}}_{0}$ and time $\textrm{t}_{0}$ with strength $\textrm{V}_{\textrm{a}}$ is considered as

$$\begin{aligned} \textrm{X}_{\textrm{x}}(\textrm{y}_{1},\textrm{t}) = \textrm{V}_{\textrm{a}}\,\wp (\textrm{y}_{1}-{\textrm{y}_{1}}_{0})\,\wp (\textrm{t}-\textrm{t}_{0}), \end{aligned}$$

(4)

which corresponds to the sudden release of contaminants into the system, a critical case for risk assessment in water resource management.

For $\textrm{y}_{1} \in \mathbb {R}$, with isotropic constant coefficients and no explicit advection term:

$$\begin{aligned} \textrm{X}_{\textrm{x}}\digamma _{\textrm{t}}(\textrm{y}_{1},\textrm{t}) = \mathcal {Q}_{\textrm{y}_{1}}\,\digamma _{\textrm{y}_{1}\textrm{y}_{1}}(\textrm{y}_{1},\textrm{t}) + \textrm{V}_{\textrm{a}}(\textrm{y}_{1},\textrm{t}) - \textrm{r}(\digamma ,\mathrm {y_{1}},\textrm{t}). \end{aligned}$$

(5)

For a single instantaneous point pollution event at $\textrm{y}_{1}=0, \textrm{t}=0$, we have

$$\begin{aligned} \textrm{X}_{\textrm{x}}(\mathrm {y_{1}},\textrm{t}) = \textrm{V}_{\textrm{a}}\,\wp (\textrm{t})\,\wp (\textrm{y}_{1}). \end{aligned}$$

(6)

If $\textrm{r} \equiv 0$, this corresponds to uncontrolled pollutant spread without natural attenuation, emphasizing long-term environmental risk. In different parameter regimes, (3) simplifies to:

• (i) Classical diffusion: $\textrm{X}=1$ gives the standard advection–diffusion–reaction PDE for pollutant transport.

• (ii) Diffusion with constant source: $\textrm{x}=0$, $\textrm{r}=0$, constant $\mathcal {Q}_{\textrm{y}_{1}}$ $\Rightarrow$ anomalous pollutant spreading with long memory, reflecting persistent contamination.

• (iii) Advection-dominated: $\Vert \textrm{x}\Vert \gg \mathcal {Q}_{\textrm{y}_{1}}/\mathcal {L}$, characterized by the Peclet number $Pe = \frac{\mathcal {L}\Vert \textrm{x}\Vert }{\mathcal {Q}_{\textrm{y}_{1}}},$ indicating rapid pollutant migration downstream.

For the standard diffusion equation, the fundamental solution can be expressed through a Green’s function approach³⁷:

$$\begin{aligned} \mathcal {G}_{\textrm{y}_{1}}(\textrm{y}_{1},\textrm{t}) = \frac{1}{\sqrt{4\pi (\mathcal {K}/\textrm{X}_{\textrm{x}})\textrm{t}}} \exp \Big (-\frac{\textrm{X}_{\textrm{x}}\textrm{y}_{1}^{2}}{4\mathcal {Q}_{\textrm{y}_{1}}\textrm{t}}\Big ), \end{aligned}$$

(7)

which describes pollutant concentration spreading in water bodies. In the standard diffusion case, the kernel is Gaussian, leading to normal decay and gradual dispersion of contamination. Thus, (3) subject to the ICs and BCs:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {Initial: } \digamma (\textrm{y}_{1},0)=\digamma _{0}(\textrm{y}_{1}) & \text {(initial pollutant concentration distribution)}, \\ \text {Dirichlet: } \digamma (\textrm{y}_{1},\textrm{t})=\textrm{g}_{\textrm{d}}(\textrm{y}_{1},\textrm{t}) \ \text {on } \partial \Omega _{\textrm{D}} & \text {(fixed concentration boundaries, e.g., clean water inflow)}, \\ \text {Neumann (flux): } \big (-\mathcal {Q}_{\textrm{y}_{1}}\nabla \digamma + \textrm{x}\digamma \big )\cdot n = \textrm{g}_{\textrm{N}} \ \text {on } \partial \Omega _{\textrm{N}} & \text {(pollutant flux boundaries)}, \\ \text {Far-field: } \digamma \rightarrow 0 \ \text {as } |\textrm{y}_{1}|\rightarrow \infty & \text {(pollutant concentration vanishes far away)}. \end{array}\right. } \end{aligned}$$

The central challenge addressed in this study is the accurate prediction of pollutant transport and persistence in river networks. Traditional advection–diffusion–reaction models often rely on idealized conditions, simplified reaction dynamics, and limited temporal representation. Such assumptions fail to capture delayed responses, long-term persistence, and nonlinear attenuation typical of real-world WP events. As a result, risk assessments based solely on classical models tend to underestimate contaminant spread, leading to inadequate management strategies for protecting water resources.

To overcome these limitations, an improved modeling approach is required that can:

• Represent realistic source terms for sudden pollutant spills;

• Account for heterogeneous diffusion and reaction mechanisms, including natural attenuation, sorption, and biodegradation;

• Incorporate temporal and spatial variability in hydrological forces affecting pollutant transport. To meet these needs, this study proposes a PINN framework, enhanced with analytical benchmarks and boosting techniques. The PINN integrates the governing physics of pollutant transport while reducing reliance on dense monitoring data, making it robust to sparse or noisy field measurements. Analytical benchmarks ensure physical consistency, while boosting techniques enhance predictive accuracy across diverse pollutant regimes. The benefits of this framework include:

• Capturing temporal dynamics for more reliable predictions of contaminant persistence;

• Modeling sudden spill events and downstream risks with greater accuracy;

• Reducing sensitivity to data scarcity, enabling practical application in data-limited river basins such as the Nile;

• Supporting environmental sustainability by quantifying risks of water quality deterioration under multiple scenarios;

• Providing a decision-support tool for policymakers to enable effective interventions that mitigate ecological and human health risks. In summary, the proposed PINN framework addresses the limitations of classical hydrodynamic models by coupling physics, data, and ML, delivering a sustainable, risk-aware approach for predicting WP dynamics in river systems.

PINN technique for WP dynamics

PINNs directly incorporate physiological regulations into the NN’s structure. This framework guarantees that the network’s effectiveness complies with these fundamental principles by integrating the governing equations of WP (3) into the network’s loss function, resulting in higher-quality and structurally consistent outcomes.

In particular, the parameters representing the residuals of the PDEs, as well as the ICs and BCs, contribute to the network’s loss function.

$$\begin{aligned} \textrm{L}=\varphi _{IC}\textrm{L}_{IC}+\varphi _{BC}\textrm{L}_{BC}+\varphi _{PDE}\textrm{L}_{PDE}, \end{aligned}$$

(8)

where every element is described as follows:

$$\begin{aligned} & \textrm{L}_{IC}=\frac{1}{\textrm{N}_{0}}\sum \limits _{\iota =1}^{\textrm{N}_{0}}\big \vert \digamma (0,{\textrm{y}_{1}}_{\iota },{\textrm{y}_{2}}_{\iota })-\digamma _{0}\big \vert ^{2},\nonumber \\ & \textrm{L}_{BC}=\frac{1}{\textrm{N}_{B}}\sum \limits _{\iota =1}^{\textrm{N}_{0}}\big \vert \digamma (\textrm{t}_{\iota },{\textrm{y}_{1}}_{\iota },{\textrm{y}_{2}}_{\iota })-\digamma _{BC}\big \vert ^{2},\nonumber \\ & \textrm{L}_{PDE}=\frac{1}{\textrm{N}}\sum \limits _{\iota =1}^{\textrm{N}_{0}}\big \vert \,^{ABC}\mathcal {D}_{\textrm{t}}^{\chi }\digamma (\textrm{t})-\mathcal {Q}\nabla ^{2}\digamma -\textrm{V}_{\textrm{a}}\wp _{\epsilon }(\textrm{t})\wp _{\epsilon }({\textrm{y}_{1}},{\textrm{y}_{2}})\big \vert ^{2}, \end{aligned}$$

(9)

Here, the total number of point collocations associated with the PDE, ICs and BCs are represented by the variables $\textrm{N}_{0}$, $\textrm{N}_{BC}$, and $\textrm{N}$, respectively.

We consider a NN $\mathcal {N}$ comprising $L_1$ layers, with $n_{1\iota }$ neurons in each layer $\kappa$. The $\kappa$-th layer’s scale of weight and biased field are represented by $\mathcal {W}_{\kappa }$ and $\textrm{c}_{\kappa }$, respectively. All hidden layers employ the same activation function, $\upsilon$, which will be addressed in a comprehensive way in the upcoming parts.

To assess the significance of $\digamma _{\kappa }$, the output of the $\kappa$-th layer can be articulated as:

$$\begin{aligned} \digamma _{\kappa }=\upsilon (\mathcal {W}_{\kappa }\digamma _{\kappa -1}+\textrm{c}_{\kappa }), \end{aligned}$$

(10)

where $\textrm{c}_{\kappa }$ constitutes the biased factor, $\mathcal {W}$ indicates a weighted framework, $\digamma _{\kappa -1}$ is the prior hidden state, and $\upsilon$ indicates the triggering functional. In this case, the supplied vector is represented by $\digamma _{0}=(\textrm{t},\textrm{y}_{1})$.

Neuron activation function

Given the vast scope of the research community, it is not feasible to provide a comprehensive review of stimulation mechanisms within the framework of computational neuroscience, especially from the perspective of PINNs based on a single academic article. Therefore, we limit our discussion in this section to existing foundational theories, primarily referencing Frederic et al.³⁸.

Activation functions play a crucial role in introducing nonlinearity into NNs. The behavior and performance of various network architectures are significantly influenced by the choice of activation function.

Among the widely utilized activation mechanisms are the sigmoid, linear, step, and piecewise-linear functions such as ReLU.

The applicability of linear functions is somewhat limited, as they are typically employed only in the output layer of multi-layer networks and are mainly suited for tasks such as regression or classification. Sigmoid functions, on the other hand, are widely favored due to their smoothness and ability to capture gradual transitions with high precision. This class of activation functions includes the hyperbolic tangent function (see Table 1). Recent studies have shown that, in the construction of deep NNs, the hyperbolic tangent often outperforms the logistic function. In this investigation, we explore the use of the activation operator $\tanh (\beta \textrm{y}_{1})$ in the concealed phases, with particular focus on tuning the parameter $\beta$. Further descriptions on activation mechanisms, readers are referred to Frederic et al. ³⁸.

Table 1 Strategic formulation of standard activation processes

Architectural intricacy of the NN

To assess the intricacy of a NN involving three hidden layers employing the $\tanh \beta$ function as its stimulation mechanism in modeling WP dynamics, three key measures are considered: the Rademacher complexity, the VC (Vapnik–Chervonenkis) dimension, and the total number of trainable parameters³⁹.

Let $\textrm{m}_{0}$ symbolize the overall amount of inputs processed by synapses and $\textrm{m}_{1},$ $\textrm{m}_{2}$ and $\textrm{m}_{3}$ indicate the value of neuron in each of the three hidden layers, respectively, corresponding to the total quantity of factors. Suppose the total count of output neurons equal $\textrm{m}_{4}$. The procedure that follows can be used to figure out the aggregate amount of criteria, represented by the symbol $\textrm{Q}_\textrm{m}$:

$$\begin{aligned} \textrm{Q}_\textrm{m}=\sum \limits _{\iota =0}^{3}(\textrm{m}_{\iota }.\textrm{m}_{\iota +1}+\textrm{m}_{\iota +1}). \end{aligned}$$

(11)

The expression can be expanded, and specific components can be rearranged as

$$\begin{aligned} \textrm{Q}_\textrm{m}=(\textrm{m}_{0}.\textrm{m}_{1}+\textrm{m}_{1})+(\textrm{m}_{1}.\textrm{m}_{2}+\textrm{m}_{2})+(\textrm{m}_{2}.\textrm{m}_{3}+\textrm{m}_{3})+(\textrm{m}_{3}.\textrm{m}_{4}+\textrm{m}_{4}). \end{aligned}$$

(12)

Additionally, rearranging one gets

$$\begin{aligned} \textrm{Q}_\textrm{m}=\textrm{m}_{0}.\textrm{m}_{1}+\textrm{m}_{1}.\textrm{m}_{2}+\textrm{m}_{2}.\textrm{m}_{3}+\textrm{m}_{3}.\textrm{m}_{4}+\mathcal {Q}+\textrm{m}_{4}, \end{aligned}$$

(13)

Here, the weakest restriction in this case is denoted by $\mathcal {Q}$, which stands for the aggregate amount of neurotransmitters that are located solely within the hidden layers as $\mathcal {Q}=\textrm{m}_{1}+\textrm{m}_{2}+\textrm{m}_{3}.$

The system’s capability to fully distinguish and categorize various features in the data entered region is gauged by the $\textrm{V}\textrm{C}$ dimension. The NN’s $\textrm{Q}_\textrm{m}$ dimension $\textrm{V}\textrm{C}$ is potentially limited by:

$$\begin{aligned} \textrm{d}_{\textrm{V}\textrm{C}}\le \textrm{Q}_\textrm{m}\ln _{2}(\textrm{Q}_\textrm{m}). \end{aligned}$$

(14)

The ability of the proposed category to identify and describe random fluctuations is determined by Rademacher intricacy $\textrm{R}_\textrm{m}(\textrm{Q})$. A mathematical class’s Rademacher intricacy $\textrm{F}$ is determined by

$$\begin{aligned} \textrm{R}_\textrm{m}(\textrm{F})=\textrm{E}\bigg [\sup \limits _{f_{1}\in \textrm{Q}}\frac{1}{\textrm{m}}\sum \limits _{\iota =1}^\textrm{m}\upsilon _{\iota }f_{1}({\textrm{y}_{1}}_{\iota })\bigg ]. \end{aligned}$$

(15)

In this case the Rademacher factors are indicated by $\upsilon _{\iota }$.

The Rademacher structure of a NN containing quad weighting arrays ($\textrm{W}_{\jmath },~(\jmath =1,...,4)$) is potentially limited by assuming the Lipschitz value $\mathfrak {L}$ underlying the $\tanh$ stimulation functional in addition to the weighted matrix parameters. The Rademacher intricacy can be accurately determined as follows:

$$\begin{aligned} \textrm{R}_\textrm{m}(\textrm{F})\le \frac{\mathfrak {L}}{\sqrt{\textrm{m}}}\big (\Vert \mathcal {W}_{1}\Vert _{\textrm{F}}\Vert \mathcal {W}_{2}\Vert _{\textrm{F}}\Vert \mathcal {W}_{3}\Vert _{\textrm{F}}\Vert \mathcal {W}_{4}\Vert _{\textrm{F}}\big ). \end{aligned}$$

(16)

The Frobenius norm regarding the weighted matrix $\mathcal {W}_{\jmath }$ is indicated in this scenario by $\Vert \mathcal {W}_{\jmath }\Vert _{\textrm{F}}$, where $\mathfrak {L}$ constitutes a fixed value and $\textrm{m}$ indicates the total quantity of observations (collocation nodes). A quantitative basis for comprehending the intricacy involved in NN design is provided by these equations.

Predictive function class

Every matrix of weights and sensitivity arrays is included within the NN’s feature value $\vartheta$. The complete factor vector is capable of being written as follows, assuming that the biased vectors are represented as $\textrm{c}_{1},\textrm{c}_{2},\textrm{c}_{3}$ and $\textrm{c}_{4}$. Also,

$$\begin{aligned} \vartheta =\big \{\mathcal {W}_{1},\textrm{c}_{1},\mathcal {W}_{2},\textrm{c}_{2},\mathcal {W}_{3},\textrm{c}_{3},\mathcal {W}_{4},\textrm{c}_{4}\big \}. \end{aligned}$$

(17)

The set of operations that NNs can estimate is referred to as the hypothesis category $\textrm{H}$. Proper generalization of the predictive network, while avoiding overfitting, depends on the breadth and diversity of this category. For a NN with factor $\vartheta$, the hypothesis within the category $\textrm{H}$ can be described as follows:

$$\begin{aligned} \textrm{H}=\big \{\digamma _{\vartheta }(\textrm{y}_{1}):\vartheta \in \Theta \big \}, \end{aligned}$$

(18)

where $\Theta$ denotes the network’s feature region. The NN with a specific parameter configuration $\vartheta$ produces the predicted output $\digamma _{\vartheta }$, which serves as an estimate of the true response $\digamma _{\textit{true}}$. The decision involving the trade-off between the probability of overfitting and the network’s approximation capability is influenced by the complexity level of $\digamma$.

Error characterization

The PINN framework accounts for three categories of inefficiencies: estimation errors, adaptation inaccuracies, and optimization faults. Analyzing these error types offers valuable insights into the limitations and potential enhancements of the PINN architecture. While expanding the hypothesis space can improve predictive accuracy, it also increases the risk of overfitting, which hampers the model’s generalization capability. For a more in-depth discussion on training error (optimization), prediction error (generalization), and estimation error related to representational capacity, we recommend the insightful work by Poggio et al.⁴⁰.

Optimization failure occurs when the loss function is not fully minimized during training. Given the available training data, this type of error is primarily influenced by the mathematical method employed to optimize the NN parameters:

$$\begin{aligned} \tilde{\textrm{E}}=\textrm{E}\Big \{\big (\digamma _{true}(\textrm{y}_{1},\textrm{t})-\digamma _{\vartheta }^{*}(\textrm{y}_{1},\textrm{t})\big )^{2}\Big \}-\min \limits _{\vartheta \in \Theta }\textrm{E}\Big \{\big (\digamma _{true}(\textrm{y}_{1},\textrm{t})-\digamma _{\vartheta }(\textrm{y}_{1},\textrm{t})\big )^{2}\Big \}, \end{aligned}$$

(19)

where $\digamma _{\vartheta }^{*}$ stands for a representation that was acquired following training.

The discrepancy between the performance of a WP system (3) on learning data and its effectiveness across the entire spatiotemporal regime is referred to as the generalization error.

$$\begin{aligned} \hat{\textrm{E}}=\textrm{E}_{\textrm{y}_{1},\textrm{t}}\Big \{\big (\digamma _{true}(\textrm{y}_{1},\textrm{t})-\digamma _\textrm{m}(\textrm{y}_{1},\textrm{t})\big )^{2}\Big \}. \end{aligned}$$

(20)

An estimation error occurs when the NN fails to closely match the exact solution within the prescribed hypothesis class $\textrm{H}$:

$$\begin{aligned} \bar{\textrm{E}}=\inf \limits _{\theta \in \Theta }\textrm{E}_{\textrm{y}_{1},\textrm{t}}\Big \{\big (\digamma _{true}(\textrm{y}_{1},\textrm{t})-\digamma _{\vartheta }(\textrm{y}_{1},\textrm{t})\big )^{2}\Big \}. \end{aligned}$$

(21)

We focus on the best possible approximation of the exact solution, denoted as $\digamma _{\text {true}}$, that can be obtained within the hypothesis category $\textrm{H}$. It is essential to highlight that as the overall capacity of the hypothesis set $\textrm{H}$ increases, the estimation error tends to decrease⁴⁰.

Attention module

Key WQIs, such as pH, TDS, EC, and Na$^{+}$, are influenced by a variety of hydrological, chemical, and ecological factors that vary across space and time. Conventional separate estimation methods often incorporate hydrodynamic factors (e.g., flow rate, temperature, turbidity) and spatiotemporal indicators (e.g., sampling location coordinates and day of the year) to predict each pollutant independently. However, the effects of these shared factors differ for each water quality metric. For example, high water temperatures can accelerate ionic reactions, increasing EC, while simultaneously promoting Na$^{+}$ mobilization through enhanced salt dissolution. Similarly, in low-flow conditions, natural alkalinity and sediment interactions may buffer the impact of TDS and Na$^{+}$ on pH.

The PINN framework incorporates a self-attention (SA) mechanism to dynamically estimate the influence of shared environmental factors on each pollutant, thereby accounting for these variations. Unlike conventional softmax-based attention, a tanh activation function is employed to capture both positive and negative effects of these factors, ensuring a more nuanced representation of pollutant-specific impacts:

$$\begin{aligned} \text {SA} = \tanh \left( \frac{\mathcal {U} \mathcal {K}^\mathcal {T}}{\sqrt{\textrm{d}_\textrm{F}}}\right) \mathcal {V},\end{aligned}$$

(22)

$$\begin{aligned} \mathcal {U}, \mathcal {K}, \mathcal {V} = \mathcal {W}_\mathcal {U} \textrm{F}_\text {share}, \mathcal {W}_\mathcal {K} \mathcal {F}_\text {share}, \mathcal {W}_\mathcal {V} \mathcal {F}_\text {share}, \end{aligned}$$

(23)

where $\textrm{d}_\textrm{F}$ is the dimension of shared features $\mathcal {F}_\text {share}$, and $\mathcal {W}_\mathcal {U}, \mathcal {W}_\mathcal {K}, \mathcal {W}_\mathcal {V}$ are learnable weights mapping $\mathcal {F}_\text {share}$ into query ($\mathcal {U}$), key ($\mathcal {K}$) and value ($\mathcal {V}$) representations, respectively. The calibrated shared features are then integrated into pollutant-specific deep NN modules to produce first-level estimations for pH, TDS, EC, and Na$^{+}$.

Each deep NN module consists of three hidden layers, each containing 512 neurons. The output layer of the pH module has a single neuron, while the output layers of the TDS, EC, and Na$^{+}$ modules correspond to their respective pollutants. The framework’s attention-based structure enables dynamic adjustment of the contributions of shared factors based on their distinct influences on each WQI, allowing for realistic and interpretable predictions of contamination risk across the Nile River.

Interaction module

The transport and transformation of contaminants are strongly influenced by various chemical and biological processes, in addition to hydrological and ecological factors that affect WQIs across different locations. Contaminants such as TDS, EC, and Na$^{+}$ interact with each other and with natural constituents through complex physicochemical processes, resulting in fluctuations in their concentrations. For example, dissolution, precipitation, and adsorption of dispersed salts and ions affect both Na$^{+}$ mobilization and overall EC levels. Similarly, natural buffering by carbonates and sediments can cause variations in pH, while interactions among ions, sediments, and organic matter influence TDS.

To account for these interactions and reduce estimation biases, the PINN framework incorporates a deep interaction module. The outputs of the pollutant-specific deep NN modules’ final hidden layers contain sufficient information on pH, TDS, EC, and Na$^{+}$. These outputs are concatenated with an abstract interaction feature $\mathcal {F}_\text {Int}$ to represent relationships among the pollutants. A deep NN with three hidden layers of 512 neurons and an output layer of four neurons corresponding to pH, TDS, EC, and Na$^{+},$ then captures the complex interdependencies among WQIs, producing the final integrated predictions of contamination risk along the Nile River.

Physics-constrained multi-tier loss function

By quantifying the difference between predicted and observed WQIs, the loss function allows the PINN model to optimize its weights and parameters through backpropagation. For joint estimation of multiple pollutants, the basic loss function is defined as the weighted sum of mean squared errors (MSE) across all tasks:

$$\begin{aligned} \text {Loss} = \sum _\textrm{i} w_\textrm{i} \, \text {MSE}_\textrm{i}, \quad \textrm{i} \in \{\text {pH, TDS, EC, Na}^+\} \end{aligned}$$

(24)

$$\begin{aligned} \text {MSE}_\textrm{i} = \frac{1}{\textrm{N}} \sum _{\jmath =1}^{\textrm{N}} \big ( \hat{u}_{\textrm{i},\jmath } - u_{\textrm{i},\jmath } \big )^2. \end{aligned}$$

(25)

Here, $w_\textrm{i}$ denotes the weight of pollutant $\textrm{i}$ (set to 1, giving equal importance), $\textrm{N}$ is the total number of samples, and $\hat{u}_{\textrm{i},\jmath }$ and $u_{\textrm{i},\jmath }$ are the predicted and observed concentrations of the pollutant.

Constraints based on water chemistry are incorporated to ensure physically consistent predictions. For example, due to natural ionic interactions, the concentration of Na$^{+}$ cannot exceed the corresponding TDS level. Limiting the loss function to the final outputs alone can lead to poor convergence and increased sensitivity to noise. To mitigate this, preliminary outputs from the attention module are included as an early-stage evaluation, providing intermediate feedback that enhances model stability and improves learning. The final hierarchical physics-constrained loss function is formulated as:

$$\begin{aligned} \text {Loss} = \sum _\textrm{i} \text {MSE}_{\textrm{i}}^{L_{1}} + \sum _\textrm{i} \text {MSE}_{\textrm{i}}^{L_{2}} + \alpha \big ( \text {ReLU}_{L_{1}} + \text {ReLU}_{L_{2}} \big ), \quad \textrm{i} \in \{\text {pH, TDS, EC, Na}^+\} \end{aligned}$$

(26)

$$\begin{aligned} \text {ReLU}_{L} = \sum _{\jmath =1}^{\textrm{n}} \max \big (0, \text {Na}^+_{L,\jmath } - \text {TDS}_{L,\jmath } - \epsilon \big ), \quad L \in \{L_{1}, L_{2}\} \end{aligned}$$

(27)

where $L_{1}$ and $L_{2}$ correspond to the first-level (attention module) and second-level (interaction module) outputs, $\alpha$ is the weight of the physics constraint (set to 0.01), and $\epsilon$ is a small tolerance.

The Adam optimizer is implemented for training, using 200 epochs and an initial learning rate of 0.01. To guarantee consistent convergence, the learning rate is decreased in half after 50 consecutive epochs if the validation loss fails to increase. Comprehensive water contamination risk estimation in the Nile River is made possible by the PINN’s ability to generate reliable, scientifically accurate, and precise forecasts of pH, TDS, EC and Na$^{+}$ levels thanks to its hierarchical, physics-informed loss structure.

Formulated approach

This subsection presents the mathematical approaches and techniques used to model WP flow, including formalization strategies and PINNs. The physical model governing WP dynamics (3) is incorporated into the loss function of the PINNs in this study, ensuring that the network’s predictions align with fundamental scientific principles.

PINN implementation

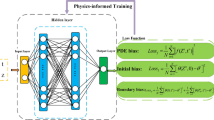
To assess the performance of the PINN system in solving the WP system (3), we conducted computational tests. The experiment focused on the transport dynamics in a one-dimensional setting, with the NN configured as described in Table 2. The NN model (3) includes three hidden layers with tanh activation functions to enhance nonlinearity and learning capability, as illustrated in Fig. 5.

Table 2 Key hyperparameters.

Fig. 5

Schematic representation of the NN architecture for the model (3) consists of three hidden layers, each featuring the $\tanh$ activation function to exhibit nonlinearity and enhance learning capacity.

Gradient-based optimization methods, particularly the Adam optimizer, were employed to train the NN. The learning rate was set to $3 \times 10^{-3}$. To effectively minimize the loss function $\mathfrak {L}(\vartheta )$, the backpropagation algorithm continuously updates the system’s parameters $\vartheta$ during the training phase. The following weights were assigned to the different components of the cumulative loss function: $\Phi _{pde} = 1$, $\Phi _{BC} = 100$, and $\Phi _{IC} = 100$. As shown in Fig. 6, we used Chebyshev nodes in the $\textrm{y}_{1}$-direction and a geometrically decreasing measure in the $\textrm{t}$-direction to generate the collocation node arrangement, which we referred to as the Cheb-Ex configuration. The advantages of this setup have been extensively analyzed in⁴¹. Mathematical challenges⁴² arise due to the peculiarities introduced by the DDF $\wp (\textrm{y}_{1})$ in the WP model (3). As a solution, we have decided to employ the following trigonometric estimation:

$$\begin{aligned} \wp _{cosine}(\textrm{y}_{1})={\left\{ \begin{array}{ll} \frac{1+\cos (\pi \textrm{y}_{1})}{2}~~~~if ~~\vert {\textrm{y}_{1}}\vert \le 1\\ 0~~~~~~~~~~~~~~eleswhere. \end{array}\right. } \end{aligned}$$

(5.1)

The following evaluation metrics were used to assess the efficacy of the PINN technique:

• Training objective evaluation: Monitored the model’s performance during training by tracking the loss function value.

• The coefficient of multiple determination ($\textrm{R}^{2}$): A statistical metric that quantifies how well a regression model explains the variability of the dependent variable based on the independent variables.

• Mean squared error (MSE): Measured the discrepancy between estimated outputs and true results by calculating the squared differences.

• Mean absolute error (MAE): Assessed prediction accuracy by averaging the absolute differences from the true results.

As shown in Fig. 7, we created a reference error grid (REG) to evaluate various error measures. A zoomed-in view of the network, enlarged by 25%, is also provided for clarity. The REG was designed to enhance error estimation accuracy, particularly in regions near the temporal space sector where an abrupt source/sink, described by DDF, was applied. A broader distribution of $\digamma _{large} = 0.5$ was used for the remaining area, while a denser distribution of $\digamma _{dense} = 0.009$ was employed for this critical section.

Fig. 6

The implementation of the Adam optimization technique to create a NN with a $3\times 10^{-3}$ learning rate is demonstrated in Fig. 6. The reverse transmission approach uses weightings $\Phi _{pde} = 1$, $\Phi _{BC} = 100$, and $\Phi _{IC} = 100$ to update the system’s parameters in order to minimize the loss function. The Cheb-Ex setup uses a dynamically declining criterion and Chebyshev distribution for collocation node ordering.

Fig. 7

A REG for assessing localized oversights is constructed with a 25% zoomed-in version for clarification. Accuracy is improved close to temporal domains where impulsive Dirac delta dynamics are present thanks to the REG. While a broader distribution $\digamma _{large}=0.5$ covers the remaining domain, a tighter panel spacing $\digamma _{dense}=0.009$ is applied close to crucial spots.

Neural activation method selection

As previously mentioned, selecting an appropriate activation function is critical in NN design, particularly for PI simulations. Table 1 provides the computational descriptions of several commonly used activation functions, including the $\tanh$, sigmoidal, softplus and rectified linear unit function. To assess their influence on training performance and explore potential enhancements, special attention was given to the parameter $\beta$ in the hyperbolic tangent function, expressed as $\tanh (\beta \textrm{y}_{1})$, within the encoded regions.

Instead of relying solely on conventional activation functions such as sigmoid, softplus, or ReLU, this study explored a range of $\beta$ values using customized implementations of the $\tanh (\beta \textrm{y}_{1})$ function. As illustrated in Fig. 8, we compared the performance of traditional activation functions with ten different configurations of $\tanh (\beta \textrm{y}_{1})$. The computational experiments confirmed the effectiveness of the $\tanh (\beta \textrm{y}_{1})$ function. The accompanying graphic highlights how $\tanh (\beta \textrm{y}_{1})$ increasingly resembles a step function as $\beta$ approaches infinity.

DL architecture

In this scenario, let $\textrm{N}$ denote a NN with five layers, where each layer $\kappa$ contains $\textrm{m}_{\kappa }$ synapses. The weight matrix and bias vector for the $\kappa$-th layer are denoted by $\mathcal {W}_{\kappa }$ and ${\textrm{c}}_{\kappa }$, respectively. The output of the $\kappa$-th layer is computed using the following formula: $\digamma _{\kappa }=\tanh (\mathcal {W}_{\kappa }\digamma _{\kappa -1}+{\textrm{c}}_{\kappa }),$ where $\tanh$ is applied element-wise to the resulting vector. The input to the system is given by $\digamma _{0} = (\textrm{y}_{1}, \textrm{t})$, representing the initial input array.

For a case involving multiple inputs and a single output, the dimensionality or the set of adjustable parameters-$\textrm{y}_{1}$ can be determined using the following procedure:

$$\begin{aligned} \textrm{y}_{1}=2.{\textrm{y}_{1}}+\textrm{y}_{2}.\textrm{y}_{3}+\textrm{y}_{3}.1+\textrm{y}_{1}+\textrm{y}_{2}+\textrm{y}_{3}+1. \end{aligned}$$

(29)

Considering the design of the unseen phase:

$$\begin{aligned} \mathcal {Q}=\textrm{y}_{1}+\textrm{y}_{2}+\textrm{y}_{3}. \end{aligned}$$

(30)

Here, $\mathcal {Q}$ represents the overall of synapses in the hidden layer of the NN, which can be computed using Eq. (30). The term ${\textrm{y}_{1}}{\jmath }$ denotes the number of synapses in the $\jmath$-th hidden layer and is treated as a weak constraint in our design.

To analyze how the architecture of hidden layers affects the performance of the PINN, we varied the number of localization indicators, the initialization points, and the overall trainable parameters ($\textrm{y}_{1}$). According to overall neurons and their adjustable features, we examined nine different configurations, which were categorized into three groups. Each configuration was evaluated using 30 distinct random initializations to ensure robustness (see Table 3).

Table 3 Trainable parameter sizes for various hidden layer structures

The relationship between MAE and the cumulative loss was examined across various permutations of layer configurations. As shown in Table 3, different setups varied in the number of hyperparameters and layer dimensions, while keeping the total synapse count constant (in our analysis, $\mathcal {Q}=64$). Assuming $\textrm{y}_{1}$ remains constant in (29), we explored topologies with similar dimensions for a more comprehensive analysis, categorizing the results into different subgroups as shown in Table 3. Additionally, certain limitations had to be considered in order to properly address the problem, which motivated the introduction of $\mathcal {Q}$. As a result, the final architecture is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum \limits _{\jmath =1}^{3}{\textrm{y}_{1}}_{\jmath }=\mathcal {Q}=fixed;\\ \textrm{y}_{1}=2.{\textrm{y}_{1}}+\textrm{y}_{2}.\textrm{y}_{3}+\textrm{y}_{3}.1+\textrm{y}_{1}+\textrm{y}_{2}+\textrm{y}_{3}+1;\end{array}\right. } \end{aligned}$$

(31)

By selecting hidden layer configurations based on Problem (31), Table 3 was generated. Notably, for the configuration with dimensions 1136, we restricted ourselves to a specific subset of all possible topologies for that particular dimension. This approach paves the way for further mathematical research into these categories and their connection to analyzing formulas as functional approximations.

Performance metric

The PDE based on WP dynamics (3), incorporated into the PINN framework, uses $\textrm{X}_{\textrm{x}}$ as the effective storage or retardation coefficient of the porous medium (units: $1/\textrm{L}$), while $\digamma (\textrm{y}_{1},\textrm{t})$ represents the pollutant concentration at position $\textrm{y}_{1}$ and time $\textrm{t}$ (units: $\delta /\textrm{L}^{3}$). The dispersion coefficient in the $\textrm{y}_{1}$-direction is denoted by $\mathcal {Q}{\textrm{y}_{1}}$ (units: $\textrm{L}^2/\mathcal {T}$), and $\wp (\textrm{y}_{1})\wp (\textrm{t})$ indicates a point source or sink of contamination (units: $\delta /(\textrm{L}^{3}\mathcal {T})$). The pollutant mass or volume introduced or removed per unit area is represented by $\textrm{V}_{\textrm{a}}$ (units: $\delta /\textrm{L}^{2}$). The term $\digamma _{\textrm{t}}(\textrm{y}_{1},\textrm{t})$ denotes the temporal change in contaminant concentration due to accumulation or depletion in the porous medium. The diffusion term, $\mathcal {Q}{\textrm{y}_{1}}\digamma {\textrm{y}_{1}\textrm{y}_{1}}$, characterizes the spatial spreading of the pollutant due to concentration gradients. Lastly, the source term, $\textrm{V}_{\textrm{a}} \wp (\textrm{y}_{1})\wp (\textrm{t})$, captures the instantaneous introduction or removal of pollutant mass at a specific location and time.

Specific physical parameters were applied in the simulations for the WP model (3), including a storage coefficient of $\textrm{X}_{\textrm{x}} = 1.0$, a dispersion coefficient of $\mathcal {Q}{\textrm{y}_{1}} = 0.001$, and a transient contaminated source/sink intensity of $\textrm{V}_{\textrm{a}} = 1.0$. To ensure that the network’s estimates align with the empirical constraints of pollutant logistics, PINNs incorporate the mathematical framework of WP phenomena directly into the NN’s loss function. The loss function $\textrm{L}(\vartheta )$ includes terms that account for the underlying interactions of the WP system, along with the ICs and BCs, as follows:

$$\begin{aligned} \textrm{L}(\vartheta )= \varphi _{IC}\textrm{L}_{IC}+ \varphi _{BC}\textrm{L}_{BC} + \varphi _{\mathcal {F}}\textrm{L}_{\mathcal {F}}. \end{aligned}$$

(32)

The IC loss ensures that the NN’s prediction of pollutant concentration matches the known initial concentration, $\digamma _{0}$, at time $\textrm{t} = 0$:

$$\begin{aligned} \textrm{L}_{IC}(\vartheta ) = \frac{1}{\textrm{N}_{IC}} \sum _{\iota =1}^{\textrm{N}_{IC}} \left\| \digamma _\vartheta (0, {\textrm{y}_{1}}_\iota ) - \digamma _{0} \right\| ^2, \end{aligned}$$

(33)

where $\textrm{N}_{IC}$ represents the number of points at which the initial concentrations are specified, and $\digamma _{\vartheta }$ denotes the predicted pollutant concentration. The BC loss ensures that the model’s predictions satisfy the pollutant concentration values, $\digamma _{BC}$, at the domain boundaries:

$$\begin{aligned} \textrm{L}_{BC}(\vartheta ) = \frac{1}{\textrm{N}_{BC}} \sum _{\iota =1}^{\textrm{N}_{BC}} \left\| \digamma _\vartheta (\textrm{t}_{\iota }, {\textrm{y}_{1}}_\iota ) - \digamma _{BC} \right\| ^2, \end{aligned}$$

(34)

where $\textrm{N}_{BC}$ is the number of BC points.

The advection-diffusion equation governing the propagation of contaminants in water is satisfied by the NN’s estimations, thanks to the physics-informed loss. This expression corresponds to the residual of the PDE, which quantifies the deviation between the prevailing pollutant characteristics and the expected behavior.

$$\begin{aligned} \textrm{L}_{\mathcal {F}}(\vartheta ) = \frac{1}{\textrm{N}} \sum _{\iota =1}^{\textrm{N}} \left\| {\digamma _{\textrm{t}}(\textrm{t}_{\iota },{\textrm{y}_{1}}_{\iota })}- \nabla \cdot \big (\mathcal {Q}_{\textrm{y}_{1}}(\textrm{y}_{1},\textrm{t})\nabla \digamma (\textrm{y}_{1},\textrm{t}) + \textrm{q}(\textrm{y}_{1},\textrm{t})\digamma (\textrm{y}_{1},\textrm{t})\big ) \right\| ^2, \end{aligned}$$

(35)

where the total quantity of localization nodes utilized for implementing the PDE is $\textrm{N}$.

Numerical simulations

The numerical results for the WP dynamics predictions, based on the previously described approaches, are presented in this subsection.

Activation function sensitivity analysis

The training efficiency and predictive accuracy of NNs used to model WP variability are strongly influenced by the choice of activation functions. In this study, several formulations of the scaled hyperbolic tangent activation function, $\tanh (\beta \textrm{y}_{1})$, were examined by varying the gradient scaling factor $\beta$. Figure 8 illustrates various versions of the scaled hyperbolic tangent function, along with standard activation functions for comparison.

Figure 9 provides a detailed analysis of the error metrics and loss values corresponding to each variant of the activation function. A consistent trend emerged when using a fixed number of training epochs and a standardized NN architecture: increasing $\beta$ results in steeper gradients, enhancing the network’s sensitivity to localized features, such as the influence of a Dirac delta source in the pollutant transport equation. However, excessively steep gradients (e.g., $\tanh (10 \textrm{y}_{1})$) were found to increase both total and boundary losses, indicating that overly large values of $\beta$ may negatively impact the model’s overall performance.

Among the tested configurations, $\tanh (2\textrm{y}_{1})$ yielded the lowest MAE and MSE, indicating an optimized trade-off between training efficiency and forecasting precision. Consequently, this activation function was adopted for all subsequent simulations.

As shown in Fig. 10, while $\tanh (2\textrm{y}_{1})$ did not always outperform $\tanh (\textrm{y}_{1})$ in individual runs, it consistently achieved a lower mean MAE across multiple trials, demonstrating its robustness and effectiveness. Future work could involve finer tuning of $\beta$, such as using incremental steps of $\Delta \beta = 0.5$, to further refine performance.

Fig. 8

Ten versions of the $\tanh \beta$ of the type $\tanh (\beta \textrm{y}_{1})$, assessed spanning a variety of $\beta$ values, are compared with conventional activation functions (sigmoid, softplus, and ReLU). Considering $\tanh (\beta \textrm{y}_{1})$ asymptotically approaching a step function as $\beta \mapsto \infty$, the animation demonstrates how increasing $\beta$ strengthens the nonlinearity and provides greater control over gradient dynamics in PINN training.

Fig. 9

Using a set range of learning epochs and a uniform NN topology, the $\beta$-scaled $\tanh \beta$ activation function is used to compare loss functions and error measures. Mean boundary and total loss with 15th–85th percentile ranges, are displayed in the left panel. The mean values of MAE and MSE, together with the 15th–95th percentile intervals, are displayed in the right panel.

Fig. 10

Spatial distribution of population density under varying toxin fields and activation sensitivities. Columns represent different activation functions’ analytical solution, $\tanh (\textrm{y}_1)$, $\tanh (2\textrm{y}_1)$, and $\tanh (10\textrm{y}_1),$ while rows correspond to different toxin configurations. The color intensity indicates population density, with higher values representing stronger survival. This visualization supports the observation that $\tanh (2\textrm{y}_1)$ yields more consistent performance across toxin environments.

Model evaluation

The sample-based and grid-based cross-validation (CV) results for pH, TDS, EC, and Na$^{+}$ in the Nile River during 2019–2020 are summarized in Fig. 11. The density scatter plots indicate that the proposed PINN model achieved high overall prediction accuracy. Among the four WQIs, the model performed best in estimating pH levels. Specifically, the sample-based CV yielded $\textrm{R}^{2}$, RMSE, and MAE values of 0.999, 0.256, and 0.204, respectively, for pH. The fitting line, with a slope of 0.999, closely matched the 1:1 line, highlighting strong agreement between predicted and observed values. Although the grid-based CV results were slightly lower, the $\textrm{R}^{2}$ value remained high at 0.999, confirming the model’s reliability.

The estimations for TDS and EC were also satisfactory. For TDS, the sample-based (grid-based) CV results showed $\textrm{R}^{2}$ of 0.990, RMSE of 64.145 mg/L (56.807 mg/L), and MAE of 47.856 mg/L (47.856 mg/L). EC predictions demonstrated comparable performance, with sample-based CV $\textrm{R}^{2}$, RMSE, and MAE values of 0.98, 74.502 $\mu$S/cm, and 63.906 $\mu$S/cm, respectively. Grid-based CV results exhibited a minor decrease, with an $\textrm{R}^{2}$ reduction of 0.001, yet remained consistent with the sample-based trend. The fitting slopes for TDS and EC exceeded 0.999, indicating minimal estimation bias. The model’s performance on the 2019 data was similar to that observed in 2020, with comparable $\textrm{R}^{2}$, RMSE, and MAE values. Detailed results are provided in the supporting information.

To evaluate the spatial robustness of the model, site-specific assessment results were analyzed across monitoring locations. Similar to pH, TDS, EC, and Na$^{+}$ predictions exhibited strong performance at most sites. For pH, over 84% of sites achieved $\textrm{R}^{2}$ values above 0.90, while 85% and 78% of sites exceeded $\textrm{R}^{2}=0.990$ for TDS and EC, respectively. Spatial performance was generally higher in regions with denser monitoring coverage, where sufficient data enabled the PINN to effectively learn complex nonlinear relationships among water quality parameters (see Ruan et al.⁴³). In contrast, sites with sparse observations or highly variable hydrological conditions showed slightly higher estimation errors.

Temporal variations in model performance were also analyzed (see Fig. 12). Monthly bias boxplots (observed minus predicted values) revealed median values near zero for all four pollutants, demonstrating accurate daily predictions. The largest biases occurred in December, with median values of $-0.12$ for pH, 1.5 mg/L for TDS, 1.8 $\mu$S/cm for EC, and 0.05 mg/L for Na$^{+}$. Residual ranges were smallest for pH during this period, whereas TDS and EC exhibited smaller residuals in summer months. Monthly mean relative errors (MREs) showed stable trends, with pH averaging 8.5% across the year, and TDS, EC, and Na$^{+}$ remaining around 18–20%. Seasonal variations in concentrations contributed to minor fluctuations in MRE. Overall, the PINN model reliably captured both spatial and temporal variability in Nile River water quality, demonstrating robust predictive capability for pH, TDS, EC, and Na$^{+}$.

Fig. 11

CV results of the proposed model for pH, TDS, EC, and Na$^{+}$ in 2020.

Fig. 12

Monthly model estimation errors for pH, TSD, EC and Na$^{+}$ in 2020.

Boosting the impact of modules and loss functions

The application of a cascade structure with an attention module and an interaction module to capture the intricate coupling among categorized factors in the joint estimation of pH, TDS, EC, and Na$^{+}$ formed the core innovation of the proposed model. Ablation analysis was performed to evaluate the effectiveness of each module (Table 4). The baseline model WP directly used all factors as inputs to estimate pH, TDS, EC, and Na$^{+}$ without specific treatment of shared or interacting variables. In contrast, the model without the attention module (Model_wa) could not differentiate the varying impacts of shared drivers on individual indicators, focusing only on their interrelationships. Similarly, the model without the interaction module (Model_wi) ignored the mutual influences among water quality parameters, thereby reducing its ability to perform residual corrections.

Evaluation results highlighted the contribution of each module. The baseline model yielded the lowest performance, with $\textrm{R}^{2}$ values of 0.87, 0.82, 0.76, and 0.74 for pH, TDS, EC, and Na$^{+}$, respectively. Model_wa, benefiting from the interaction module that accounted for parameter interdependencies, improved estimation accuracy by 0.03–0.07 across all indicators. Model_wi, which retained the attention mechanism, performed even better, with $\textrm{R}^{2}$ values of 0.91, 0.89, 0.86, and 0.84, demonstrating the importance of distinguishing the impact of shared drivers. Overall, both modules made complementary contributions, and their combination achieved the most accurate joint predictions.

Figure 13 presents the ablation analysis results for different model configurations (Model_base, Model_wa, Model_wi, and the proposed PINN) in the joint estimation of pH, TDS, EC, and Na$^{+}$. The comparison of $\textrm{R}^{2}$, RMSE, and MAE across models highlights the contributions of the attention and interaction modules. The proposed PINN consistently achieves superior predictive accuracy by effectively integrating both modules.

Table 4 Ablation analysis for the models with different modules.

Fig. 13

Spider plots of $\textrm{R}^{2}$, RMSE, and MAE from ablation analysis, illustrating the impact of attention and interaction modules on the estimation of pH, TDS, EC, and Na$^{+}$. The Proposed PINN shows the best overall performance.

Furthermore, leveraging the multi-level hierarchical outputs of the model and the principles of hydrological and physicochemical processes, a hierarchical physics-constrained loss function (Loss_all) was designed. Additional experiments were conducted to investigate the contribution of each component of this loss function (Table 5). The baseline loss (Loss_base) considered only final outputs, while Loss_$L_{1}$ incorporated intermediate outputs from the attention module. Loss_phy further integrated physical constraints related to contaminant transport. Compared with Loss_base, incorporating intermediate results (Loss_$L_{1}$) provided modest improvements in pH and Na$^{+}$ estimation, while physics constraints (Loss_phy) led to substantial gains in TDS and EC prediction accuracy ($\textrm{R}^{2}$ reaching 0.90 and 0.87, respectively). Ablation analysis of different loss functions across WQIs are presented in Fig. 14. The results show that incorporating intermediate outputs (Loss_L1) modestly enhances pH and Na$^{+}$ predictions, while physics constraints (Loss_phy) provide marked improvements in TDS and EC estimation. The combined loss function (Loss_all) balances accuracy across all indicators, confirming that multi-level outputs and physics-based constraints jointly improve predictive performance.

Fig. 14

Performance comparison of ablation loss functions across pH, TDS, EC, and Na$^{+}$.

Table 5 Ablation analysis for the different loss functions.

In summary, the integration of attention and interaction modules, along with physics-informed constraints, enabled robust estimation of pH, TDS, EC, and Na$^{+}$, thereby providing a reliable framework for assessing water contamination risks and supporting sustainable river management.

Comparison with separate estimation

To assess the effectiveness of the proposed PINN framework in evaluating water contamination risks in the Nile River, Egypt, separate estimation models were developed for pH, TDS, EC, and Na$^{+}$. These models retained the same structural components as the PINN feature encoder, attention module, and interaction module to ensure fair comparison. The estimation performance and efficiency are summarized in Table 6. For pH, the separate model achieved $\textrm{R}^{2}$, RMSE, and MAE values of 0.92, 11.67, and 8.42, respectively. TDS and EC yielded $\textrm{R}^{2}$ values of 0.88 and 0.84, with RMSE/MAE values of 8.72/5.63 and 15.95/10.59, respectively, while Na$^{+}$ showed the lowest performance. Overall, the separate models followed similar patterns to PINN, with pH performing best and Na$^{+}$ worst (see Wu et al.⁴⁴). However, PINN improved joint estimation accuracy for TDS, EC, and Na$^{+}$, with $\textrm{R}^{2}$ gains of up to 0.03, and slightly reduced RMSE and MAE for pH. By incorporating interactions among WQIs and environmental constraints, PINN enhanced estimation accuracy while reducing redundancy. Efficiency gains were also significant: the joint model required only 3.98M parameters nearly half of the combined separate models and reduced training time per epoch on an NVIDIA GeForce RTX 4090D GPU from 5.17s to 2.06s (see Jiang et al.⁴⁵). Figure 15 presents the estimation performance of separate models, highlighting that pH achieved the highest accuracy and Na$^{+}$ the lowest. Compared to these results, PINN demonstrated clear advantages in accuracy, efficiency, and sustainability, underscoring its potential for advancing water quality monitoring and resource management in the Nile River basin.

Table 6 Comparison of the proposed model and separate models.

Fig. 15

Performance of separate estimation models for pH, TDS, EC, and Na$^{+}$ in evaluating Nile River water contamination risks. pH achieved the highest accuracy ($\textrm{R}^{2}$ = 0.92), while Na$^{+}$ showed the lowest. Compared to these models, the proposed PINN framework enhances joint estimation accuracy and efficiency, supporting sustainable water quality monitoring.

Comparison with other ML models

Four advanced ML models were evaluated to benchmark their performance against the proposed PINN framework (Table 7). These included the RF³², the ResNet³³, the PI-MTDNN proposed by Mu et al.³⁴, and the KI-NN developed by Wu et al.³⁵. Among these, the RF model exhibited the weakest performance, yielding sample-based CV $\textrm{R}^{2}$ (RMSE) values of 0.87 (14.21) for pH, 0.84 (10.25) for TDS, 0.80 (18.17) for EC, and slightly lower accuracy for Na$^{+}$. In contrast, the ResNet and PI-MTDNN models showed improved performance, with both achieving sample-based CV $\textrm{R}^{2}$ values of 0.91 for pH and 0.88 for TDS. For EC, the PI-MTDNN model reached an $\textrm{R}^{2}$ of 0.85, slightly outperforming ResNet ($\textrm{R}^{2}$ = 0.84). The KI-NN model demonstrated balanced results, with sample-based CV $\textrm{R}^{2}$ and RMSE (MAE) values of 0.90 and 12.64 (9.08) for pH, and $\textrm{R}^{2}$ values of 0.87 and 0.84 for TDS and EC, respectively, while also providing reliable predictions for Na$^{+}$.

Overall, the proposed PINN model outperformed all compared models, achieving the highest $\textrm{R}^{2}$ values and the lowest RMSE and MAE across all WQIs. Both sample-based and grid-based CV results consistently confirmed the robustness of the PINN framework. These findings highlight that the PINN framework’s specialized feature encoder, attention mechanism, and interaction module make it particularly effective for joint estimations of pH, TDS, EC, and Na$^{+}$, thereby offering a more reliable approach to assessing water contamination risks and supporting environmental sustainability in the Nile River, Egypt.

To visually assess the performance and variability of the models, violin plots were constructed for each water quality parameter (pH, TDS, EC, and Na$^{+}$), as shown in Fig. 16. Each Taylor’s plot represents the distribution of sample-based CV metrics $\textrm{R}^{2}$, RMSE, and MAE for the five evaluated models: RF, ResNet, PI-MTDNN, KI-NN, and the proposed PINN. The width of each violin corresponds to the density of the simulated values around the observed metric, providing an intuitive depiction of both central tendency and variability.

From the Taylor’s plots Fig. 16, it is evident that the RF model exhibited the widest RMSE and MAE distributions and lower $\textrm{R}^{2}$ values, confirming its weaker performance relative to the other models. The ResNet and PI-MTDNN models showed narrower distributions and higher $\textrm{R}^{2}$ values for pH and TDS, indicating more consistent predictions. The KI-NN model achieved balanced performance across all metrics, with moderate spread in RMSE and MAE, while the proposed PINN consistently produced the narrowest violins with the highest $\textrm{R}^{2}$ values and lowest RMSE and MAE.

These violin plots not only reinforce the quantitative results reported in Table 7 but also provide a more comprehensive view of model reliability, illustrating that the PINN framework is robust and stable across multiple WQIs. The plots further underscore the advantage of PINN’s feature encoder, attention mechanism, and interaction module in achieving precise and reproducible predictions for assessing water contamination risks in the Nile River.

Table 7 Comparison of the proposed model and other ML models for water contamination risk in the Nile River, Egypt.

Fig. 16

Taylor plot of the models’ performances in predicting the distribution of $\textrm{R}^{2}$, RMSE, and MAE for different ML models across water quality parameters, highlighting the superior performance and consistency of the proposed PINN framework in Nile river.

Difference between predictions and observed data

To demonstrate the effectiveness of the proposed PINN framework for the Nile River in Egypt, the differences between predicted and observed WQIs are illustrated in Fig. 17. The predicted and actual curves exhibit closely aligned trends, confirming the capability of PINN to accurately capture variations in contamination levels. This reliable prediction performance highlights the framework’s potential for assessing water contamination risks in the Nile River and underscores its broader implications for promoting environmentally sustainable water resource management.

Fig. 17

Predicted versus observed WQIs (pH, TDS, EC, and Na$^{+}$) for the Nile River in Egypt using the PINN framework. The close alignment confirms accurate contamination risk assessment and supports sustainable water management.

Model training loss and validation loss

We trained the PINN framework with fixed hyperparameters to evaluate water contamination risks in the Nile River, focusing on key sediment-related parameters (pH, TDS, EC, and Na$^{+}$). As shown in Fig. 18, the curves of training loss and validation loss for the PINN model converge after about ten epochs, indicating stable learning performance. This convergence highlights the model’s robustness in capturing contamination dynamics and its potential contribution to environmentally sustainable water resource management.

Fig. 18

Predicted versus observed WQIs (pH, TDS, EC, and Na$^{+}$) for the Nile River in Egypt using the PINN framework. The close alignment confirms accurate contamination risk assessment and supports sustainable water management.

Assessment of latent layer architectures

To evaluate the performance of different latent phase architectures in simulating water contamination variability, the relationship between the MAE and the Total Loss was analyzed. As shown in Table 3, each network configuration maintained a uniform total neuron count ($\mathcal {Q}=64$); however, the distribution of neurons across the hidden layers varied. This variation led to differences in network complexity often referred to as model dimensionality or the total number of trainable parameters.

To enable a fair comparison, architectures with identical total parameter counts were grouped separately, allowing the effect of neuron distribution across layers to be isolated. These groupings are presented in Table 3. Using various hidden layer configurations each with distinct structural implications–the scatter plots in Fig. 19 illustrate the dependency between the cumulative error metric and MAE. Notably, the 32-16-16 configuration exhibited a significant drop in MAE as the cumulative error metric decreased. This suggests that allocating more neurons to the first hidden layer enhances the model’s predictive performance in capturing water contamination dynamics. Furthermore, this configuration demonstrated greater consistency, as evidenced by its closer adherence to the regression line and a reduced number of outliers.

A more detailed analysis was conducted on network topologies with varying layer structures but an identical total number of neurons. The configurations, spanning multiple architecture families, are presented in Figs. 20 and 21. Within each category, certain layouts consistently outperform others as the overall parameter count increases. Notably, even when the total number of training epochs is kept constant, the configurations highlighted in blue demonstrate a more substantial reduction in MAE and MSE for a given decrease in total loss. This suggests that even subtle variations in neuron distribution across layers can significantly impact model performance. For example, although the 16-32-16 and 16-31-17 architectures have nearly identical neuron counts, their predictive accuracies differ markedly.

Based on this analysis, we conclude that optimal performance is achieved when the number of neurons in each hidden layer follows the pattern $2^{\textrm{p}}$, as long as the overall count neurons and latent phases (as defined by the weak constraint $\mathcal {Q}$) remain constant. Additionally, configurations that allocate more neurons to the first hidden layer departing from the strict $2^{\textrm{p}}$ pattern consistently outperform others when the stricter constraint of maintaining the same hyperparameters is relaxed, as shown in Fig. 22. This suggests that increasing the representational capacity of the initial layer is particularly effective in capturing the complex spatiotemporal dynamics of WP transmission.

Fig. 19

Using three topologies with various hallmarks but exactly identical overall numbers of hidden layer neurons (expressed as powers of 2), scattered graphs displaying (left) MAE versus cumulative loss and (right) MSE versus cumulative loss are displayed. The inter-quartile range is shown by the outlined region surrounding each mean line, emphasizing how this pattern changes throughout the information presented.

Fig. 20

Scatter plots evaluating three NN designs with different layer significance but a similar overall amount of hidden neurons, represented as powers of two, show (left) MAE versus cumulative loss and (right) MSE versus cumulative loss. The inter-quartile range, which captures variation among attempts, is represented by the outlined region surrounding every tendency curve. The importance of neuron dispersion on model precision is illustrated by the superior results of blue-highlighted layouts, which show greater declines in MAE and MSE for similar reductions in total loss.

Fig. 21

Scatter plots illustrating the performance of three NN configurations with differing layer distributions but an equal total number of hidden neurons, expressed as powers of two. The left panel shows MAE vs. total loss, and the right shows MSE vs. total loss. The shaded bands around each trend line indicate the inter-quartile range, reflecting variability across runs. Blue-highlighted architectures demonstrate more pronounced reductions in MAE and MSE for comparable decreases in total loss, emphasizing the critical role of neuron allocation in determining model accuracy.

Fig. 22

Comparing the efficiency of neural network designs with different hidden layer neuron allocations, assuming a fixed total neuron count determined by the weak constraint $\mathcal {Q}$. The $2^p$ distribution topologies function best when the overall count of neurons and latent phases are fixed. The significance of improving the figurative capabilities of the initial layer for demonstrating the intricate spatiotemporal variations in WP the emission is highlighted by the fact that frameworks that allocate further neurons to the first hidden layer frequently entertain better than others when the restriction on the number of hyperparameters is loosened.

WP management performance

The CV results presented in Table 8 and visually illustrated in Fig. 23 provide a comprehensive evaluation of three key management strategies including industrial discharge regulation, salinity management, and irrigation planning on the major water quality parameters of the Nile River, namely pH, TDS, EC, and Na$^{+}$. Motivated by the urgent need to safeguard the Nile against escalating industrial effluents, increasing salinity pressures, and intensive irrigation demands, the study compares multiple ML models, including RF, ResNet, PI-MTDNN, KI-NN, and the proposed PINN, with predictive accuracy assessed through CV RMSE and $\textrm{R}^{2}$ metrics. The use of CV ensures that the reported performance values reflect not only model fit but also robustness and generalizability, thereby offering a reliable benchmark for decision-making under uncertain environmental conditions.

However, the results reveal clear performance differences across models. RF consistently exhibits higher RMSE and lower $\textrm{R}^{2}$ values across all strategies, underscoring its limited ability to capture the nonlinear and interdependent nature of water quality dynamics. ResNet, PI-MTDNN, and KI-NN achieve intermediate performance, demonstrating some ability to model complex relationships but lacking the stability and precision of the proposed framework. In contrast, PINN consistently delivers the lowest RMSE and near-unity $\textrm{R}^{2}$ across folds, confirming its superior capability to capture intricate parameter interactions while maintaining robustness under rigorous validation.

Collectively, these findings highlight the pivotal role of advanced ML frameworks, particularly PINN, in strengthening water resource management. By providing accurate and generalizable predictions, PINN offers a reliable foundation for regulating industrial discharges, improving salinity control, and guiding irrigation planning. Beyond methodological advancement, this predictive strength represents a practical pathway toward sustainable water governance and long-term environmental protection of the Nile River system.

Table 8 Performance comparison of different methods under three strategies for pH, TDS, EC, and Na$^{+}$.

Fig. 23

CV performance of five ML models under three water management strategies (industrial discharge regulation, salinity management, and irrigation planning) for key Nile River parameters: pH, TDS, EC, and Na$^{+}$. The proposed PINN model consistently achieves the lowest RMSE and highest $\textrm{R}^{2}$, demonstrating superior predictive accuracy and robustness.

Field analysis

Characterization data, WQI outcomes, and the NN model’s predictive performance form the three main components of the research results. Statistical summaries for all four field stations ($\textrm{G}_{1}$–$\textrm{G}_{4}$) are presented in Table 9, providing key metrics including mean, median, maximum, minimum, and standard deviation (SD) to capture the variability and central tendencies of the water quality parameters.

The analysis of water quality parameters across the four field stations revealed notable spatial and temporal variations. Average values ranged from 6.27–6.36 for pH, 1902–2503 mg/L for TDS, 3.41–7.52 $\mu$S/cm for EC, and 38.72–52.18 mg/L for Na$^{+}$, with low standard deviations (pH: 0.07–0.14; TDS: 110–210 mg/L; EC: 3–7.5 $\mu$S/cm; Na$^{+}$: 7.5–12 mg/L), indicating that measurements were closely clustered around the means (Table 9). The highest values observed were pH 6.45–6.60, TDS 2250–2700 mg/L, EC 2.40–5.50 $\mu$S/cm, and Na$^{+}$ 62–85 mg/L, while the lowest were pH 6.05–6.10, TDS 1300–2150 mg/L, EC 2.05–3.00 $\mu$S/cm, and Na$^{+}$ 20.50–41 mg/L.

WQI assessment showed that stations $\textrm{G}_{1}$-$\textrm{G}_{4}$ consistently exceeded FAO irrigation standards (TDS: 0–2000 mg/L, EC: 0–3 $\mu$S/cm, Na$^{+}$: 0–40 mg/L), particularly during dry periods when TDS ranged 2075–2680 mg/L, EC 3.12–5.70 $\mu$S/cm, and Na$^{+}$ 42–84.9 mg/L. In contrast, station G4 remained within permissible limits (TDS: 1015–1980 mg/L, EC: 2.05–2.90 $\mu$S/cm, Na$^{+}$: 30.1–38.6 mg/L). Beeswarm plots (Fig. 24) visually illustrate the distribution and density of individual measurements for each parameter across the four stations, highlighting outliers, clustering, and variability within and between stations. These results underscore the impact of anthropogenic activities such as urban waste, industrial effluents, and agricultural runoff, while indicating that pollution levels decrease downstream. The PINN model effectively captured WQI fluctuations, showing high predictive performance across stations ($\textrm{R}^{2}$: 0.947–0.971; MSE: 0.025–0.085), with TDS predictions demonstrating the most consistency, thus validating its reliability for data-driven water management strategies.

Fig. 24

Beeswarm plots showing the distribution of water quality parameters (pH, TDS, EC, Na$^{+}$) across the four field stations ($\textrm{G}_{1}$–$\textrm{G}_{4}$) of the Nile River. The plots highlight the variability, clustering, and presence of outliers for each parameter across stations.

The WQI results reveal the levels of TDS, EC, and Na$^{+}$ in the Nile River, Egypt. According to FAO^2,3 irrigation water supply criteria, acceptable ranges are 0–2000 mg/L for TDS, 0–3 $\mu$S/cm for EC, and 0–40 mg/L for Na$^{+}$. Across all seasons, pH levels ranged from 6.05 to 6.80, remaining within FAO standards at every sampling location.

At stations 1 through 3, measured levels of TDS, EC, and Na$^{+}$ ranged from 2050–2600 mg/L, 3.10–5.65 $\mu$S/cm, and 41.50–76.30 mg/L, respectively, exceeding FAO limits. In contrast, station 4 remained within permissible limits (TDS: 1015–1980 mg/L, EC: 2.05–2.90 $\mu$S/cm, Na$^{+}$: 30.10–38.60 mg/L). During the dry period, concentrations increased across all stations (TDS: 2075–2680 mg/L, EC: 3.12–5.70 $\mu$S/cm, Na$^{+}$: 42.00–84.90 mg/L), highlighting the increasing impact of human activities and environmental pressures on water quality, which continue to affect the river’s ecological health. Effective management measures are essential to prevent long-term detrimental effects. The investigation indicated that pollution levels decrease downstream. Although pH remained within recommended thresholds, values could still contribute to agricultural toxicity or nutritional disorders (see Fig. 25 and Table 10). Excessive TDS can reduce oxygen saturation, alter taste, and increase water acidity, while elevated ion levels increase EC, limiting nutrient and moisture uptake by plant roots and complicating cultivation (see⁴⁶). The WQI was accurately modeled using the PINN approach, which captured periodic fluctuations with minimal divergence from observed data, effectively tracking and forecasting changes in water quality.

However, the PINN model (3), integrating data-driven learning with statistical principles of water quality dynamics, was evaluated using $\textrm{R}^{2}$ and MSE metrics during training, testing, and prediction phases. The $\textrm{R}^{2}$ values for pH, TDS, EC, and Na$^{+}$ (0.088–0.095, 0.016–0.087, 0.015–0.086, and 0.017–0.085, respectively) demonstrate its ability to capture complex relationships under physical constraints. During training, the model showed exceptionally high alignment with experimental data and physical laws ($\textrm{R}^{2}$: pH 0.982–0.991, TDS 0.983–0.989, EC 0.982–0.990, Na$^{+}$ 0.982–0.990). Evaluation performance remained excellent ($\textrm{R}^{2}$: pH 0.954–0.969, TDS 0.955–0.972, EC 0.953–0.968, Na$^{+}$ 0.956–0.970), with TDS predictions showing the most consistency. Prediction results further confirmed reliability ($\textrm{R}^{2}$ 0.947–0.971; MSE 0.025–0.085), validating PINN’s ability to capture realistic water quality dynamics while accounting for mass-balance and compositional constraints. System performance was most consistent during training, followed by testing and prediction.

Table 9 Characteristic statistics for selected WQI parameters across groups $\textrm{G}_{1}$ to $\textrm{G}_{4}$.

Table 10 Statistical metrics for the training, testing, and forecasting performance of the model (3) for pH, TDS, EC, and Na$^+$.

Fig. 25

Statistical assessment of the PINN model’s capability to simulate the concentrations of pH, TDS, EC, and Na$^{+}$ across various Nile River regions. The model demonstrated strong predictive reliability, consistently maintaining high $\textrm{R}^{2}$ values and low MSE during training, testing, and forecasting stages. Pollutant levels followed seasonal patterns, with peak concentrations observed during dry periods. These findings validate the model’s effectiveness in capturing WQI dynamics for accurate prediction.

Conclusion

This study developed a PINN framework to jointly predict key water quality indices (pH, TDS, EC, and Na$^{+}$) in Egypt’s Nile River under critical management strategies, including industrial discharge regulation, salinity management, and irrigation planning. By integrating hydrochemical knowledge, an adaptive attention mechanism, a deep interaction module, and a physics-constrained loss function, the proposed PINN effectively addressed the limitations of conventional ML approaches that often overlook parameter interdependencies and physical interpretability.

Comprehensive evaluations demonstrated that PINN consistently outperformed benchmark models such as RF, ResNet, PI-MTDNN, and KI-NN, achieving superior accuracy, robustness, and computational efficiency. CV confirmed its stability across temporal and spatial domains, while ablation studies highlighted the complementary contributions of the attention and interaction modules. Field validation further revealed that although pH values largely complied with FAO standards, TDS, EC, and Na$^{+}$ frequently exceeded permissible thresholds, emphasizing the urgency of effective water quality management.

Beyond predictive accuracy, the PINN framework provides interpretability by identifying irrigation intensity, salinity loads, and industrial effluents as the dominant drivers of water quality dynamics. This capacity to combine accurate forecasting with physical interpretability positions PINN as a practical and sustainable decision-support tool.

Finally, the proposed PINN offers a reliable pathway for monitoring and mitigating water contamination risks in the Nile River. Its predictive strength and interpretability not only support regulatory decision-making and pollution control but also contribute to long-term environmental sustainability and resilient water governance in large river basins.

Limitations:

Although the proposed PINN framework demonstrates strong predictive performance and interpretability, several limitations remain. First, the model relies on the availability and quality of monitoring data, and its accuracy decreases in regions with sparse measurements or high hydrological variability. Second, the current study focused primarily on four key water quality indicators (pH, TDS, EC, and Na$^{+}$), while other important parameters such as dissolved oxygen, heavy metals, and nutrients were not included. Expanding the model to capture a wider spectrum of physicochemical variables would provide a more comprehensive understanding of ecosystem health. Third, while the framework incorporates domain knowledge through physics-informed constraints, it does not fully account for dynamic processes such as seasonal flow changes, sediment transport, or long-term climate variability, which may influence prediction robustness.

Future research:

Future work can address these challenges by integrating remote sensing data and high-resolution hydrological simulations to improve spatial generalization. Incorporating additional WQIs and biological indicators would enhance the ecological relevance of the predictions. Moreover, extending the PINN to hybrid models that combine physical process-based simulations with data-driven learning may further improve both accuracy and interpretability. Finally, deploying the model in real-time monitoring systems and decision-support platforms will help translate research findings into actionable strategies for sustainable water resource management.