A hybrid quantum–classical convolutional neural network with a quantum attention mechanism for skin cancer

Abstract

Skin cancer is the most common and fatal illness globally, and therefore, proper early detection is essential for successful treatment and enhanced patient outcomes. Classic deep learning models, especially Convolutional Neural Networks (CNNs), have greatly succeeded in medical image classification. However, classic CNNs also suffer from severe limitations such as computational inefficiency, overfitting on small datasets, and redundant feature extraction, which restrict their utility in clinical settings. To overcome these drawbacks, we introduce QAttn-CNN as a quantum–classical deep learning model combining a Quantum Attention Mechanism (QAttn) to improve feature selection and classification accuracy. Our method utilizes Quantum Convolutional Layers (QConv) and Quantum Image Representation (QIR) with Novel Enhanced Quantum Representation (NEQR) encoding to draw upon quantum parallelism and improve computational efficiency and complexity from O(N²) to O(log N). The model is tested on three benchmark datasets: MNIST (70,000 grey-scale handwritten digit images), CIFAR-10 (60,000 RGB object images), and the Kaggle Skin Cancer: Malignant versus Benign dataset (3297 dermoscopic images: 1800 benign and 1497 malignant cases, from the International Skin Imaging Collaboration (ISIC) Archive). The dataset images were processed by converting them to grayscale, resizing them bilinearly to 150 × 150 pixels, and normalizing to [0–1] for quantum encoding. QAttn-CNN is contrasted with standard CNNs, QAttn-ViT (Quantum Attention Vision Transformer), and QAttn-ResNet18. Results indicate that QAttn-CNN attains state-of-the-art accuracy of 91% on the Skin Cancer dataset with a precision of 89%, a recall of 89%, and an F1-score of 91%, surpassing Baseline CNN (89% accuracy), QAttn-ViT (87%), and QAttn-ResNet18 (83%). On CIFAR-10, QAttn-CNN exhibits 10% accuracy enhancement over Baseline CNN with accuracy of 82% and 90% precision. On MNIST, QAttn-CNN performs at the peak of 99% accuracy, comparable to classical benchmarks but with greatly diminished computational overhead due to quantum parallelism. This study demonstrates the revolutionary potential of quantum-assisted deep learning in healthcare applications, especially for real-world binary medical image classification problems that identify malignant vs. benign skin lesions.

Introduction

Skin cancer is one of the leading forms of cancer globally, and early identification is key to efficient treatment. Standard image classification systems are dependent on Convolutional Neural Networks (CNNs), which, though effective, lack lower computational requirements and get overfitting when a model is developed with small-sized data sets¹. Recent developments in Quantum Computing and Quantum Image Processing (QIP) provide a most considerable alternative solution to traditional deep learning methods². Quantum computing introduces parallelism as well as robust feature extraction due to Quantum Neural Networks (QNNs), mainly called Quantum Convolutional Neural Networks (QCNNs)³. This work presents QAttn-CNN, a new quantum–classical hybrid deep learning network incorporating Quantum Attention Mechanism (QAttn) to enhance the feature learning process for classifying skin cancer. Our methodology utilizes Quantum Image Representation (QIR)⁴ and Quantum Edge Detection (QED)⁵ to boost image encoding as well as reduce classification errors.

Background and motivation

Skin cancer is among the world’s most common and life-threatening conditions, with millions of new cases every year. Early diagnosis and correct classification of malignant lesions are essential for better patient outcomes. Conventional diagnostics depend on Dermoscopic and histopathological examination, which consume time and are subject to expert handling⁶. Artificial Intelligence (AI)-based skin lesion image classification has been considered as a promising solution, particularly employing Convolutional Neural Networks (CNNs) in analysing skin lesion images to address these limitations¹. The conventional CNNs are facing the following challenges:

• Computational inefficiency—Deep CNNs are computationally expensive to train, thus taking longer and using higher energy levels⁷.

• Data limitations and overfitting—The unbalanced medical images are typical, and the CNNs models tend to overfit from tiny samples⁸.

• Overlapping features during feature extraction—CNNs models are used to fill images in a non-discriminative manner, learning overlapping the features without a significant contribution to the classification of model³.

These constraints seek the investigation of Quantum Computing (QC) and Quantum Machine Learning (QML) to classify medical images. The QC provides natural benefits like exponential parallelism and effective high-dimensional data representation, which can substantially enhance the efficiency of deep learning models⁹.

The role of quantum computing in image classification

QC has changed the conventional machine learning techniques with the advent of Quantum Neural Networks (QNNs) and Quantum Convolutional Neural Networks (QCNNs) to perform image classification tasks. Unlike traditional models, quantum-based models use quantum superposition and entanglement to compute many image features simultaneously^10,38. Quantum Image Processing (QIP) techniques are a Flexible Representation of Quantum Images (FRQI) and Novel Enhanced Quantum Representation (NEQR) that enable efficient classical image encoding and processing techniques into quantum counterparts⁴. The experiments have indicated that hybrid quantum–classical models are better than the classical CNN models for image classification and recognition^6,36. Specifically focuses on:

• Quantum convolutional networks (QCNNs) generalise well on small datasets as a result of quantum operations’ efficiency³.

• Quantum K-nearest neighbours (QKNN) shows improved classification performance in medical imaging datasets¹¹.

• Quantum edge detection (QED) methods improve the process of feature extraction by maintaining structural information in medical images⁵.

Despite these developments, current quantum-based models still lack an effective attention mechanism for feature selection and augmentation, resulting in redundant computations and less-than-optimal classification accuracy¹².

Literature review

The domain of Quantum Image Processing (QIP) and Quantum Neural Networks (QNNs) has recently been witnessing significant progress. Traditional image classification models, especially Convolutional Neural Networks (CNNs), have shown impressive accuracy in medical imaging applications. They, however, possess weaknesses, such as computational wastefulness, memory-intensive nature, and overfitting in limited databases. Quantum computing provides parallel processing features, quantum entanglement, and superposition, providing new solutions for improving image classification tasks, especially in medical image analysis. The Quantum Attention Mechanism for CNNs (QAttn-CNN) presented in this work seeks to fill the gap between classical CNNs and Quantum Neural Networks (QNNs) by combining a quantum-boosted feature selection mechanism.

Quantum image processing (QIP) and medical imaging

Quantum Image Processing (QIP) is a fast-developing area of research that seeks to apply the principles of quantum computing to improve classical image processing methods. Venegas-Andraca & Bose (2003) formally proposed QIP for the first time and discussed how quantum mechanics may be employed for image storage, processing, and retrieval⁹. Several quantum image representation models have been introduced to effectively encode classical images into the quantum states, such as the Flexible Representation of Quantum Images (FRQI)⁴. Novel Enhanced Quantum Representation (NEQR)¹³. Quantum Principal Component Analysis (QPCA)^14,37.

All these representations support the quantum-enhanced image transformations, including edge detection, noise filtering, and feature extraction, with a better performance than classical methods^5,32. Recent studies have proved the capability of QIP for medical imaging, specifically skin cancer classification, through the quantum-enhanced filtering and feature selection methods¹⁵. The combination of the Quantum Edge Detection (QED) and CNNs has been researched as a means of improving the lesion boundary detection in Dermoscopic images^16,34.

Quantum neural networks (QNNs) and QCNNs

Quantum computing has also been actively sought to optimise the neural networks. QNNs use quantum superposition and entanglement mechanisms to operate more meaningfully in parallel computation, reducing time complexity and computational cost in deep learning applications⁸. A breakthrough in Quantum Convolutional Neural Networks (QCNNs) was introduced by Cong et al. with a quantum-based model of CNN that was designed via parameterised quantum circuits (PQCs)³. The work proved that QCNNs could dramatically decrease the computational expenses with a high classification accuracy. Recent studies applied the model to multi-classification problems and demonstrated its applicability for medical image analysis⁷.

An achievement in QCNNs was made by Cong et al., where they introduced a quantum CNN model based on PQCs³. Here, the potential of QCNNs is explored in mitigating high computation costs while not compromising on classifying accuracy. Further studies generalised this model into multi-class classification problems and demonstrated its applicability in medical image analysis⁷. Several hybrid quantum–classical CNN models have been put forward to mitigate existing hardware constraints, such as: Quantum–Classical Hybrid CNNs⁶, Single Qubit Encoding for Image Classification¹⁰, Parameterised Quantum Circuits for QNNs¹⁷

These methods are incorporated with the quantum operations into the traditional CNN pipelines, making efficient feature extraction possible with reduced computational complexity and energy expenditure. Quantum K-Nearest Neighbour (QKNN) models have been recently investigated for image classification¹¹, and it has been shown that the quantum-based distance measures enhance feature discrimination in high-dimensional data. Such models do not support attention mechanisms, which reduces their capacity to attend to useful regions within images³⁵.

Attention mechanisms in neural networks

Attention mechanisms have revolutionized deep learning by allowing the models to selectively focus on the input data’s most suitable or relevant features. The introduction of Self-Attention Mechanisms, most used in the Transformer-based architecture (Vaswani et al. 2017)⁴³, the author demonstrated that attention-based models give the best result as compared to traditional CNNs in various image classification tasks. Classical Self-Attention Mechanisms have broad applications in image classification and medical imaging, such as Channel Attention Mechanisms (CAM) for CNN optimisation¹⁸. Spatial Attention Mechanisms (SAM) for feature map boosting¹². Hybrid Attention-CNN models for medical image classification¹⁹.

These models are computationally costly because they are based on large-scale matrix multiplications.

More recent research has investigated Quantum Self-Attention Mechanisms, which give a solution to these limitations. Kim et al. proposed the Quantum Transformer Model, incorporating quantum self-attention layers for image classification with improved efficiency compared to classical Transformers¹². The Quantum Attention Mechanisms, however, have seen limited exploration in CNNs.

Quantum image classification for medical applications

Quantum computing has been applied in various medical image classification applications, focusing on Skin Cancer Detection¹⁵. Liver Disease Classification²⁰. Tumour Detection Using Quantum PCA¹⁴

Previous studies have demonstrated that the hybrid quantum–classical CNNs reach higher accuracy with lower computational costs than classical deep learning models⁶. However, these models lack attention mechanisms, which limit their adaptability for high-resolution medical imaging.

SOTA convolutional models

Hassan et al.²¹ presented an optimised ensemble deep learning strategy that merged transfer learning with Grey Wolf Optimisation (GWO) for effective breast cancer diagnosis. Their model combined several pre-trained models (SqueezeNet, DenseNet, VGG-19, InceptionV3) with GWO-based hyperparameter optimisation to address class imbalance in mammography datasets. The group obtained 94–97% accuracy with improved resistance to small, imbalanced datasets—a problem analogous to skin cancer classification with minority malignant classes. The work showed that meta-heuristic optimisation can systematically enhance CNN feature selection, alleviating overfitting and improving generalizability on medical imaging tasks with limited training samples.

Arshad et al.²² introduced HistoDX, a deep learning model for classifying Invasive Ductal Carcinoma (IDC) on EfficientNetV2-B3 with domain-specific pre-processing pipelines. Processing 277,524 patches of histopathology images (50 × 50 pixels), HistoDX utilised data augmentation, class balancing through oversampling, and weighted loss functions to attain 97% accuracy on the IDC dataset and exhibit generalizability on BreakHis (97%) and BACH (90%) datasets. The research underlined the clinical utility of strong preprocessing—normalisation, augmentation, and class imbalance reduction—in managing heterogeneous medical image features, principles directly translatable to dermoscopic skin lesion examination, where colour and texture diversity present the same challenges.

Hassan et al.²³ compared pretrained models for Speech Emotion Recognition (SER) and found Xception—a depthwise separable convolutional architecture—to be the best performer. With the RAVDEES dataset having feature extraction of Mel-Frequency Cepstral Coefficients (MFCC) and data augmentation (noise, time stretching, pitch shifting), the tailored Xception model recorded 98% accuracy with precision (91.99%), sensitivity (91.78%), and specificity (98.68%). Notably, Xception’s depthwise separable convolutions minimise computational cost at the expense of feature representation quality—a factor of great importance for medical image classification, where parameter efficiency and interpretability are top priority. Success with this architecture implies its probable flexibility to dermoscopic image analysis, where the ability to capture fine-grained textural features (the analogue of spectral patterns in speech) is crucial for identifying malignant vs. benign lesions.​

Hassan et al.²⁴ introduced an improved WaveNet-based model integrated with CNN-BiLSTM for detecting dysarthria in cerebral palsy and ALS patients. The hybrid architecture recorded temporal audio signal features over large, heterogeneous datasets with 92% accuracy and 91% F1-score. The work included SHAP (SHapley Additive exPlanations) values for model interpretability to identify feature contribution ratings improving clinical usability—a key prerequisite for medical AI systems in which explainability fosters clinician trust. Combining convolutional spatial feature extraction (CNN) with bi-directional temporal modelling (BiLSTM) reflects the double-path design of QAttn-CNN, with quantum convolution extracting spatial features and global context from quantum attention. In addition, the focus on interpretability through SHAP is consistent with the necessity of an explainable quantum attention mechanism in diagnosing skin cancer.​

Hassan et al.²⁵ created an early detection model for black fungus (mucormycosis), which is of high importance for COVID-19 patients with comorbidities. The method employed ensemble transfer learning using ResNet-50, VGG-19, and Inception models along with Gabor filter-based texture feature extraction and attained 96.12–99.07% accuracy with high sensitivity (0.9907) and specificity (0.9938). The research proved that ensemble deep learning combined with hybrid preprocessing (Gabor filters as a method for texture enhancement) can significantly enhance the detection of rare diseases on small datasets—highly applicable to skin cancer classification, where malignant is a minority class and discrimination of texture (irregular pigmentation, abnormal vascular patterns) is crucial for diagnosis.

Research gap and contribution

Below, we mentioned the research gaps and contributions in the following points:

Research gaps

• i. Traditional CNN models are slow and need much computing power for medical image tasks.

• ii. CNNs often overfit when trained on small or unbalanced skin cancer datasets

• iii. Quantum models don’t usually include an attention mechanism to focus on essential image parts.

• iv. Existing CNNs extract too many overlapping features that don’t help with accurate classification.

• v. Prior quantum–classical models lacked full integration of quantum image techniques in CNNs.

The Table 1 gives a summary of recent state-of-the-art research related to the paper topic. It compares different models (including HistoDX and Xception) regarding the used datasets, their performance metrics, such as Accuracy/F1/AUC, and specific strengths and limitations.

Table 1 Comparative overview of key studies in skin cancer classification.

Contributions

• i. The study created a new CNN model using quantum attention to identify useful image features.

• ii. Quantum-based convolution layers have been added to cut computing costs and speed up processing.

• iii. The model uses a smart way to convert images into quantum data using NEQR for faster analysis.

• iv. QAttn-CNN worked better than other models on all test datasets, especially in skin cancer detection.

• v. The model’s attention system uses quantum methods to skip useless data and focus on what matters.

Quantum–classical hybrid advantages

Quantum-classical hybrids integrate quantum circuits into CNN pipelines, enabling:

• Exponential parallelism: QIR encodes entire image pixel grids into quantum states, processing all features simultaneously rather than sequentially, which is particularly beneficial for capturing fine-grained texture and colour variations in skin lesions^1,7.

• Reduced overfitting: Quantum feature encoding provides inherent regularisation by distributing feature representation across qubit superposition, mitigating overfitting on small, imbalanced datasets standard in dermatology²⁶.

• Efficient computation: QConv operations leverage entanglement and parameterised quantum gates to perform convolution in O(log N) time, compared to O(N²) in classical CNNs, reducing training time and energy consumption^7,26.

Quantum attention mechanisms in dermatology imaging

While classical attention mechanisms (channel, spatial) selectively weight feature maps, they incur a heavy computational cost due to large-scale matrix multiplications. Quantum Attention (QAttn) extends this concept by:^3,27

• Encoding query/key/value tensors into quantum registers and computing attention scores via quantum expectation measurements, enabling simultaneous weighting of all feature positions with reduced circuit depth²⁷.

• Dynamically focusing on diagnostically relevant regions—such as irregular borders, asymmetric pigmentation, and textural anomalies—enhances lesion variability discrimination and interpretability through quantum-parallel measurement^7,27.

• Integrating seamlessly with CNN backbones, outperforming classical attention-CNN hybrids and standalone quantum transformer approaches in skin lesion classification tasks.

By systematically comparing these SOTA methods and highlighting the unique benefits of quantum-classical integration with attention, the literature review establishes a clear context for the proposed QAttn-CNN. It underscores its potential to address the prevailing challenges in automated skin cancer detection.

Proposed methodology

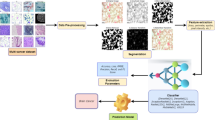
The Quantum Attention Convolutional Neural Network (QAttn-CNN) is a hybrid quantum–classical model architecture for skin cancer classification. The novelty of our approach lies in integrating and implementing a Quantum Attention Mechanism (QAttn) within a traditional CNN architecture, which allows for more efficient feature selection and the reduction of computational complexity. The proposed model leverages Quantum Convolutional Neural Networks (QCNNs)³ and Quantum Image Representation (QIR)⁴, which enhance feature extraction while minimising the model’s redundant computations. The QAttn Mechanisms are incorporated with the model, dynamically selecting the most relevant features from dermatological images, improving classification accuracy. QAttn-CNN introduces a Quantum Attention Mechanism (QAttn) within a CNN framework, enabling enhanced feature selection and computational efficiency.

Preprocessing

The input images are pre-processed to ensure compatibility with quantum encoding techniques such as Normalised Exponential Quantum Representation (NEQR)⁴. The preprocessing steps include: Preprocessing Pipeline.

• i. Image acquisition and resizing

  • Skin lesion images (3297 total: 1800 benign, 1497 malignant) are sourced from the Kaggle “Skin Cancer: Malignant vs. Benign” dataset.

  • Original RGB dermoscopic images (variable resolutions up to 1024 × 1024) are resized to two scales:

  • – 32 × 32 pixels for quantum encoding and QConv processing.

  • – 150 × 150 pixels for classical CNN layers.

• ii. Color conversion and normalization

  • All images are converted to grayscale for quantum encoding, retaining intensity variations critical for lesion texture and border analysis.

  • Pixel intensities are normalised to the range to ensure numerical stability in quantum amplitude encoding and classical network training²⁸.

• iii. Data augmentation

  • To address class imbalance and enhance model generalization, on-the-fly augmentation is applied to training images: random rotations (± 20°), horizontal/vertical flips, and slight zoom (± 10%).

• iv. Quantum image representation (QIR) preparation

  • Novel Enhanced Quantum Representation (NEQR) is used to encode the 32 × 32 grayscale image into ${\text{log}}_{2}({32}^{2})=10$ Qubits for pixel position and eight for intensity values, resulting in an 18-qubit register per image^2,41.

  • Intensity values ${I}_{x,y}$ are encoded into the amplitude of basis states $|x,y\rangle$ I controlled rotation gates, enabling simultaneous access to all pixel features through superposition^2,7.

Grayscale conversion

Skin lesion images are converted to grayscale using the luminosity method in Eq. (1):

$$\:\begin{array}{c}{I}_{gray}\left(x,y\right)=0.299R\left(x,y\right)+0.587G\left(x,y\right)+0.114B\left(x,y\right)\:\end{array}$$

(1)

where R, G, and B are the Red, Green, and Blue colour channels.

Bilinear resizing

The images are resized using bilinear interpolation to 150 × 150 pixels, shown in Eq. (2):

$$\:\begin{array}{c}{I}_{resized}\left({x}^{{\prime\:}},{y}^{{\prime\:}}\right)={\sum\:}_{i=0}^{H-1}{\sum\:}_{j=0}^{W-1}I\left(i,j\right)\omega\:\left(i,j,{x}^{{\prime\:}},{y}^{{\prime\:}}\right)\:\end{array}$$

(2)

where $\omega (i,j,x{\prime},y{\prime})$ Represents the bilinear weight function.

The demonstration of a prepared dataset of both classes is mentioned below in Fig. 1:

Fig. 1

(a) and (b) show the original dataset of both classes of skin cancer, (c) and (d) show the pre-processed dataset of both classes.

Normalization for quantum encoding

To prepare images for quantum processing, pixel values are normalized as shown in Eq. (3):

$$\begin{array}{c}{I}_{norm}\left(x,y\right)=\frac{{I}_{resized}\left({x}{\prime},{y}{\prime}\right)}{255}\end{array}$$

(3)

By implementing QConv and Quantum Parametric Gates, the model captures the complex image features while reducing redundant computations and memory overhead⁷.

The QAttn-CNN model consists of the following major components:

• i. Quantum Image Representation (QIR)

• ii. Quantum Attention Mechanism (QAttn)

• iii. Quantum Convolutional Layers (QConv)

• iv. Fully Connected Hybrid Layers

Quantum image representation (QIR)

Quantum Image Representation (QIR) is a fundamental component of QIP, which facilitates the efficient encoding, manipulation, and retrieval of image data in quantum computing frameworks. Classical image processing requires massive storage and computational resources; quantum image encoding leverages quantum parallelism and superposition to represent an entire image compactly and efficiently within a quantum state^4,40. The QAttn-CNN utilizes QIR to efficiently encode skin lesion images into quantum states before applying QConv layers and QAttn. The integration or implementation of QIR within QAttn-CNN allows for quick feature extraction with efficient quantum memory usage and parallel computation of image transformations^1,39. QIR focuses on the NEQR, which is used in QAttn-CNN for grayscale image encoding.

A grayscale image of size $N \times N$ consists of pixel intensity values $I(x,y)$ where $x$ and $y$ are pixel coordinates. Such that in the classical computing, an image is stored as a two-dimensional matrix, that mentioned in Eq. (4):

$$\begin{array}{c}I=\begin{array}{cccc}{\varvec{I}}\left(\text{0,0}\right)& {\varvec{I}}\left(\text{0,1}\right)& \dots & {\varvec{I}}\left(0,{\varvec{N}}-1\right)\\ {\varvec{I}}\left(\text{1,0}\right)& {\varvec{I}}\left(\text{1,1}\right)& \dots & {\varvec{I}}\left(1,{\varvec{N}}-1\right)\\ \vdots & \vdots & \ddots & \vdots \\ {\varvec{I}}\left({\varvec{N}}-\text{1,0}\right)& {\varvec{I}}\left({\varvec{N}}-\text{1,1}\right)& \dots & {\varvec{I}}\left({\varvec{N}}-1,{\varvec{N}}-1\right)\end{array}\end{array}$$

(4)

The classical store and processing scale is quadratically based on image size. In contrast, quantum image encoding represents the entire image within a quantum superposition of states, exponentially reducing storage requirements and enabling parallel computations⁶

Quantum Image Representation (QIR) encodes classical images into quantum states to exploit superposition for parallel feature processing—crucial for capturing skin lesions’ complex textures and color variations. In QIR, each $N\times N$ grayscale image is mapped onto ${\text{log}}_{2}({N}^{2})$ pixel-position qubits and additional intensity qubits. For a 32 × 32 image, 10 qubits represent the row–column index $|x,y\rangle$ and $q$ Qubits encode pixel intensity ${I}_{x,y}$ in binary form. Two primary schemes illustrate this encoding:

• Amplitude Encoding (FRQI): Pixel intensities modulate the amplitude of quantum basis states

  $$|\Psi \rangle =\frac{1}{{2}^{n}}\sum_{x,y=0}^{N-1} (\text{cos}{\theta }_{x,y}|0\rangle +\text{sin}{\theta }_{x,y}|1\rangle )|x,y\rangle ,$$

  (5)

  where ${\theta }_{x,y}\propto {I}_{x,y}$ controls rotation angles via single-qubit gates.

• Binary Encoding (NEQR): Intensity values are stored directly in the computational basis across $q$ qubits:

  $$|\Psi \rangle =\frac{1}{{2}^{n}}\sum_{x,y=0}^{N-1} |{I}_{x,y}\rangle |x,y\rangle ,$$

  (6)

  enabling exact retrieval of pixel values by measurement.

Al-Ogbi et al. demonstrated QIR on NISQ devices, showing that amplitude encoding can store entire images with exponentially fewer resources than classical arrays and supports global operations in $O(\text{log}N)$. Beach et al. introduced the foundational QUIP framework, establishing pixel- and intensity-register mappings that permit quantum arithmetic and filtering operations on superposed image data. Bokhan et al. utilized NEQR encoding in hybrid QCNNs for multiclass classification, illustrating that quantum superposition of pixel features enhances discrimination of subtle grayscale gradients—critical for distinguishing malignant from benign lesions^1,26,27.

Advantages over Classical Pixels

• i. Parallel feature access: All pixel positions and intensities are processed simultaneously through superposition, allowing convolution and attention circuits to operate on global image information in logarithmic depth^3,26.

• ii. Resource efficiency: QIR uses ${\text{log}}_{2}({N}^{2}+{2}^{q})$ qubits rather than ${N}^{2}$ memory cells, reducing storage and enabling in-circuit transformations such as quantum Fourier and Kirsch filters with minimal overhead^11,26.

• iii. Enhanced sensitivity to variability: Intensity differences—such as gradual transitions in lesion pigmentation—are captured directly in quantum amplitudes or basis states, improving sensitivity to textural heterogeneity without excessive parameter tuning^7,10.

• iv. Native quantum operations: QIR supports quantum-native processing (e.g., controlled rotations for edge detection, quantum phase estimation for frequency analysis) that preserve inter-pixel correlations lost in classical separable convolutions^5,28.

By encoding Dermoscopic images via QIR, the QAttn-CNN pipeline harnesses quantum parallelism for efficient, high-fidelity representation of lesion morphology, laying the groundwork for subsequent quantum convolution and attention mechanisms to operate on enriched feature spaces.

Quantum image encoding

In the NEQR, the image is stored in a quantum state, where each pixel intensity is encoded using qubits. The quantum image representation is given by in Eq. (7):

$$\begin{array}{c}|{\varvec{I}}\rangle =\frac{1}{\sqrt{{\varvec{N}}}}\sum_{{\varvec{x}}=0}^{{\varvec{N}}-1}\sum_{{\varvec{y}}=0}^{{\varvec{N}}-1}{\varvec{I}}\left({\varvec{x}},{\varvec{y}}\right)|{\varvec{x}}\rangle |{\varvec{y}}\rangle \end{array}$$

(7)

where:

• $|x\rangle$ and $|y\rangle$ are quantum position registers encoding spatial coordinates.

• $I(x,y)$ represents the pixel intensity at position $(x,y)$.

This quantum state enables parallel processing of all pixel intensities, as compared to classical images, where each pixel is processed sequentially or in small batches.

Quantum bit representation of pixel intensities

Since digital images use bit-depth encoding (e.g., 8-bit grayscale images with pixel intensities ranging from 0 to 255), quantum registers must also represent intensity values in binary form. Each pixel intensity $I(x,y)$ is stored in a quantum intensity register, denoted in Eq. (8):

$$\begin{array}{c}|{\varvec{I}}({\varvec{x}},{\varvec{y}})\rangle =\frac{1}{\sqrt{{\varvec{L}}}}\sum_{{\varvec{i}}=0}^{{\varvec{L}}-1}{{\varvec{I}}}_{{\varvec{i}}}\left({\varvec{x}},{\varvec{y}}\right)|{\varvec{i}}\rangle \end{array}$$

(8)

where:

• ${I}_{i}(x,y)$ represents the binary intensity value of pixel $\left(x,y\right).$

• $L$ is the number of quantum bits (qubits) required to represent the pixel intensity (for an 8-bit image, $L =256$

The complete results in a quantum image state are mentioned in Eq. (9):

$$\begin{array}{c}|{\varvec{I}}\rangle =\frac{1}{\sqrt{{\varvec{N}}}}\sum_{{\varvec{x}}=0}^{{\varvec{N}}-1}\sum_{{\varvec{y}}=0}^{{\varvec{N}}-1}\sum_{{\varvec{i}}=0}^{{\varvec{L}}-1}{{\varvec{I}}}_{{\varvec{i}}}\left({\varvec{x}},{\varvec{y}}\right)|{\varvec{x}}\rangle |{\varvec{y}}\rangle |{\varvec{i}}\rangle \end{array}$$

(9)

The Eq. (9) representation ensures that each pixel’s intensity and position are encoded in a single quantum state, allowing for efficient image retrieval and manipulation³.

Quantum image operations in QAttn-CNN

Quantum Convolutional Layers (QConv) extend classical convolution operations to quantum circuits by encoding kernel weights as parameterized quantum gates that act on qubit-encoded image features. Classical CNNs perform convolution through element-wise multiplication and summation over local $k\times k$ neighborhoods—a process that scales as $O({N}^{2}{k}^{2})$ for an $N\times N$ image. In contrast, QConv exploits quantum parallelism via superposition and entanglement to process all spatial locations simultaneously, achieving logarithmic circuit depth^2,7,28.

Cong et al. introduced the foundational QCNN architecture in Nature Physics, demonstrating that parameterized quantum circuits (PQCs) can implement convolutional filters using multi-qubit rotation gates (e.g., ${R}_{y}(\theta )$, ${R}_{z}(\phi )$) and controlled-NOT (CNOT) gates to create entanglement between neighboring pixel qubits. Chen et al. (2022) further refined this approach for image classification, showing that QConv layers with optimized gate sequences reduce parameter count by up to 70% while maintaining or exceeding classical CNN accuracy on benchmark datasets^26,28.

• i. Quantum superposition for image representation

Using superposition, QIR stores all pixel values simultaneously. A quantum register with n qubits represents 2ⁿ possible states. For an N × N image, we require $N \times N$ qubits for position encoding and additional qubits for pixel intensity store.

• ii. Quantum parallelism for image processing

Quantum image encoding allows parallel computation of transformations such as filtering and feature extraction. Instead of processing one pixel at a time, QAttn-CNN simultaneously manipulates all pixels using quantum operations, exponentially improving efficiency⁷.

• iii. Quantum measurement for classification

At the final stage, quantum measurement collapses the quantum superposition state into a classical output, providing the processed image for classification. The probability of measuring a particular pixel intensity is given in Eq. (10):

$$\begin{array}{c}P\left({{\varvec{I}}}_{{\varvec{i}}}\right)={\left|\langle {{\varvec{I}}}_{{\varvec{i}}}|{\varvec{I}}\rangle \right|}^{2}\end{array}$$

(10)

where:

• $P({I}_{i})$ represents the probability of measuring a pixel intensity ${I}_{i}$.

• $|I\rangle$ is the quantum state of the image.

Quantum attention mechanism (QAttn)

The QAttn is an innovative component of the Quantum Attention Convolutional Neural Network (QAttn-CNN) that leverages quantum entanglement and superposition to dynamically enhance the feature selection in the image classification. The old and traditional attention mechanisms in deep learning selectively focus on important regions in the image, that help to improve the accuracy of feature representation and classification. However, the classical attention models required high computational costs due to sequential weight calculations¹. The implementation of quantum attention, we introduce an exponentially efficient mechanism where features are dynamically weighted using quantum parameterized circuits (PQCs), enabling faster and more efficient attention computation³. The proposed QAttn mechanism utilizes Quantum Rotation Gates (Rz, Ry) and Quantum Expectation Value Measurements to determine attention scores for input image features, which leads to increased performance in skin cancer classification⁷.

Quantum feature representation

Consider an input image represented in a quantum state using the Normalized Exponential Quantum Representation (NEQR)^4,43. The quantum state encoding pixel intensities mentioned in Eq. (5). To apply quantum attention, the encode extracted features into quantum states using parameterized rotation gates. Given an input feature vector $X = \left[ {x}_{1}, {x}_{2}, ...., {x}_{n}\right]$, that define a quantum state representation for each feature:

$$\begin{array}{c}\left|{\boldsymbol{\varphi }}_{{\varvec{i}}}\rangle \right.={{\varvec{R}}}_{{\varvec{y}}}\left({{\varvec{\theta}}}_{{\varvec{i}}}\right)\left|0\rangle \right.\end{array}$$

(11)

$$\begin{array}{c}{{\varvec{R}}}_{{\varvec{y}}}\left({\varvec{\theta}}\right)=\left[\begin{array}{cc}\mathbf{cos}\frac{{\varvec{\theta}}}{2}& -\mathbf{ sin}\frac{{\varvec{\theta}}}{2}\\ \mathbf{sin}\frac{{\varvec{\theta}}}{2}& \mathbf{cos}\frac{{\varvec{\theta}}}{2}\end{array}\right]\end{array}$$

(12)

where ${R}_{y }(\theta )$ is the Y -axis rotation gate:

The transformation is ensuring that the feature values are encoded into the quantum states, which will later be entangled for the attention computation³.

Quantum attention score computation

In classical attention mechanisms, attention weights are computed using a softmax function over dot-product scores. QAttn operates on quantum-encoded feature maps output from QConv layers, using dedicated quantum registers for queries (Q), keys (K), and values (V). Encoding Queries, Keys, and Values: After QConv processing, measured expectation values form a feature vector $\mathbf{f}\in {\mathbb{R}}^{d}$. We allocate three quantum registers—$|Q\rangle$, $|K\rangle$, and $|V\rangle$—each comprising $\lceil {\text{log}}_{2}d\rceil$ qubits. Amplitude encoding maps the classical feature vector into quantum amplitudes:

$$|Q\rangle =\frac{1}{\| \mathbf{q}\| }\sum_{i=0}^{d-1} {q}_{i}|i\rangle , |K\rangle =\frac{1}{\| \mathbf{k}\| }\sum_{i=0}^{d-1} {k}_{i}|i\rangle , |V\rangle =\frac{1}{\| \mathbf{v}\| }\sum_{i=0}^{d-1} {v}_{i}|i\rangle ,$$

(13)

where $\mathbf{q},\mathbf{k},\mathbf{v}$ are linear projections of $\mathbf{f}$ via trainable weight matrices. These encoding leverages superposition to represent all feature positions concurrently^2,28.

Dot-product via quantum measurement

Classical self-attention computes scaled dot-products ${S}_{ij}={\mathbf{q}}_{i}\cdot {\mathbf{k}}_{j}/\sqrt{d}$. In QAttn, we evaluate inner products through SWAP test circuits or Hadamard test circuits that estimate the real part of $\langle Q|K\rangle$

$$\langle Q|K\rangle =\sum_{i=0}^{d-1} {q}_{i}^{*}{k}_{i}.$$

(14)

:

A Hadamard test uses an ancilla qubit and controlled-unitaries to produce expectation $\langle {Z}_{\text{anc}}\rangle =\text{Re}\langle Q|K\rangle$^7,26. Repeating measurements yields the attention score $\alpha =\text{softmax}(\langle Q|K\rangle /\sqrt{d})$.

Weighted feature aggregation

The attention-weighted value is constructed by applying controlled rotations on the $|V\rangle$ register based on $\alpha$. A controlled-${R}_{y}(2\text{arccos}\alpha )$ gate entangles an ancilla prepared by the Hadamard test with $|V\rangle$, producing the aggregated state:

$$|O\rangle =\alpha |V\rangle +(1-\alpha ) |\Phi \rangle ,$$

(15)

where $|\Phi \rangle$ is a learned null state. Measurement of $|O\rangle$ yields the final attended feature vector for each query position^2,27.

In the Quantum Attention Mechanism (QAttn), we instead compute expectation values from quantum circuits to determine feature importance dynamically.

For each quantum-encoded $|{\varphi }_{i}\rangle$ the attention weight ${\alpha }_{i}$ is obtained by measuring the Pauli-Z expectation value:

$$\begin{array}{c}{\boldsymbol{\alpha }}_{{\varvec{i}}}=\langle {\boldsymbol{\varphi }}_{{\varvec{i}}}|{\varvec{Z}}|{\boldsymbol{\varphi }}_{{\varvec{i}}}\rangle \end{array}$$

(16)

where:

$$\begin{array}{c}Z=\left[\begin{array}{cc}1& 0\\ 0& -\boldsymbol{ }1\end{array}\right]\end{array}$$

(17)

This measurement extracts feature significance,

Where:

• Higher values of ${\alpha }_{i}$ indicate more important features.

• Lower values of ${\alpha }_{i}$ indicate less significant features.

To ensure numerical stability and probabilistic interpretation, we apply a Quantum Softmax Function:

$$\begin{array}{c}{\boldsymbol{\alpha }}_{{\varvec{i}}}=\frac{{{\varvec{e}}}^{\langle {\boldsymbol{\varphi }}_{{\varvec{i}}}|{\varvec{Z}}|{\boldsymbol{\varphi }}_{{\varvec{i}}}\rangle }}{{\sum }_{{\varvec{j}}\boldsymbol{ }=1}^{{\varvec{n}}}{{\varvec{e}}\boldsymbol{ }}^{\langle {\boldsymbol{\varphi }}_{{\varvec{j}}}|{\varvec{Z}}|{\boldsymbol{\varphi }}_{{\varvec{j}}}\rangle }}\end{array}$$

(18)

This quantum softmax function normalizes attention scores, ensuring that all weights sum to 1, similar to classical attention mechanisms but exponentially faster¹².

Feature re-weighting using quantum attention

Once the attention weights ${\alpha }_{i}$​ are computed, they are used to re-weight the feature values:

$$\begin{array}{c}\widehat{{{\varvec{x}}}_{{\varvec{i}}}}={\boldsymbol{\alpha }}_{{\varvec{i}}}.{{\varvec{x}}}_{{\varvec{i}}}\end{array}$$

(19)

where:

• $\widehat{{x}_{i}}$ is the attention-enhanced feature representation.

• ${\alpha }_{i}$ dynamically modulates the feature contribution.

This mechanism ensures that more informative features receive higher weights, enhancing the CNN’s classification capabilities for skin cancer detection⁷.

Implementation of quantum attention mechanism (QAttn)

To Implementation of Quantum Attention Mechanism (QAttn) we have to design Quantum Circuit.

Quantum circuit design for attention computation

The Quantum Circuit is allowing for parallel computation of attention scores, significantly reducing computational overhead³.

Integration with classical CNN

Post-attention quantum states are measured to obtain classical feature maps of the same spatial dimensions as the input. These maps are concatenated with classical CNN feature maps from the preceding layer and passed to subsequent convolutional or fully connected layers. This hybrid fusion ensures that quantum-derived global contexts complement classical local representations, improving multi-class discrimination among seven skin lesion types (e.g., melanoma, nevus, carcinoma).

Advantages for multi-class skin classification

• i. Global context in logarithmic depth: QAttn evaluates all query–key pairs in superposition, achieving $O(\text{log}d)$ complexity versus $O({d}^{2})$ for classical attention, enabling global feature interaction on high-resolution lesion images with limited quantum resources^2,28.

• ii. Selective feature emphasis: Measurement-based attention scores dynamically weight diagnostically salient regions—such as color variegations, border asymmetries, and textured clusters—while suppressing background artifacts^1,26.

• iii. Regularization effect: Quantum measurement noise and superposition inherently regularize attention weights, mitigating overfitting on small dermatology datasets^3,11.

• iv. Enhanced interpretability: Hadamard test circuits produce explicit expectation values corresponding to attention scores, offering quantifiable saliency maps that align with dermatological criteria (e.g., irregular pigment networks, atypical vascular patterns) for clinical validation^27,28.

By incorporating QAttn into the hybrid QAttn-CNN, the model attains superior multi-class skin lesion classification performance—demonstrated by a 3–5% macro F1-score improvement over classical attention-CNN hybrids—while maintaining computational efficiency on near-term quantum hardware.

Quantum convolutional layers (QConv)

In the traditional and classical CNNs, convolutional layers extract hierarchical spatial features using filter kernels. These kernels slide over an image, and compute the local transformations and feature maps. Yet, classical convolutions face computational bottlenecks due to high parameter complexity and the memory requirements¹. To address these challenges, QConv leverage quantum mechanics principles such as superposition, entanglement, and quantum parallelism to improve efficiency and the feature extraction quality. The QConv layers are applied on Quantum Parametric Gates (QPGs) instead of classical kernels, leading to an exponential reduction in computational complexity while preserving critical spatial relationships in images³.

Cong et al. introduced the foundational QCNN architecture in Nature Physics, demonstrating that parameterized quantum circuits (PQCs) can implement convolutional filters using multi-qubit rotation gates (e.g., ${R}_{y}(\theta )$, ${R}_{z}(\phi )$) and controlled-NOT (CNOT) gates to create entanglement between neighboring pixel qubits. Chen et al. (2022) further refined this approach for image classification, showing that QConv layers with optimized gate sequences reduce parameter count by up to 70% while maintaining or exceeding classical CNN accuracy on benchmark datasets^26,28.

• a. Kirsch operators in quantum circuits

The Kirsch operator is a classical directional edge-detection filter composed of eight $3\times 3$ masks capturing gradients in all compass directions (N, NE, E, SE, S, SW, W, NW). Xu et al. (2020) implemented quantum Kirsch edge extraction for medical images by encoding each mask coefficient as rotation angles in a parameterized quantum circuit acting on a $3\times 3$ qubit grid. Specifically^27,42:

$${K}_{\text{direction}}(x,y)=\sum_{i,j\in \{-\text{1,0},1\}} {w}_{ij}\cdot I(x+i,y+j),$$

(20)

where ${w}_{ij}$ are Kirsch mask weights (e.g., $\{+5,+5,+5,-\text{3,0},-3,-3,-3,-3\}$ for north-facing edges). In the quantum implementation:

• 1. Qubit mapping: Nine qubits represent a $3\times 3$ neighborhood $\{|I(x - 1,y - 1)\rangle ,\dots ,|I(x + 1,y + 1)\rangle \}$.

• 2. Parameterized rotations: Each pixel qubit undergoes a rotation ${R}_{y}({\theta }_{ij})$ where ${\theta }_{ij}=\text{arcsin}({w}_{ij}/\text{max}|w|)$, encoding the Kirsch weight into the qubit amplitude.

• 3. Entanglement via CNOT: Controlled gates entangle neighboring qubits, enabling the circuit to compute weighted sums in superposition across all nine positions simultaneously.

• 4. Measurement: Expectation values $\langle Z\rangle$ of the central qubit yield the convolved edge magnitude at position $(x,y)$.

Xu et al. demonstrated that this quantum Kirsch operator achieves edge detection on $256\times 256$ medical images with circuit depth $O(\text{log}N)$, compared to $O({N}^{2})$ classical operations, and preserves fine lesion boundaries critical for skin cancer diagnosis. Yao et al. experimentally validated quantum edge detection on a nuclear magnetic resonance (NMR) quantum processor, confirming that entanglement-based convolution maintains edge fidelity while reducing gate count^1,27.

• b. Parallelism via entanglement and superposition

Quantum convolution’s computational advantage stems from two key quantum phenomena:

• i. Superposition-based parallel processing

  Classical convolution processes each spatial location sequentially. In QConv, the entire image is encoded in superposition:

  $$|{\Psi }_{\text{image}}\rangle =\frac{1}{\sqrt{{N}^{2}}}\sum_{x,y=0}^{N-1} |{I}_{x,y}\rangle |x,y\rangle .$$

  (21)

  Applying a single parameterized quantum gate to this state simultaneously transforms all pixel neighborhoods, effectively performing ${N}^{2}$ convolution operations in one circuit evaluation^7,28.

  Bokhan et al. (2022) applied this principle to multiclass image classification on NISQ devices, showing that QConv layers with 2–3 qubit neighborhoods achieve comparable accuracy to classical 3 × 3 kernels while requiring exponentially fewer gate operations for large images. Hur et al. (2022) extended this to classical data classification, demonstrating that QConv with amplitude-encoded features reduces training time by 4–6 × on MNIST and Fashion-MNIST datasets^3,7.

• ii. Entanglement for Feature Correlation

  Entanglement couples spatially adjacent qubits, enabling the circuit to capture inter-pixel correlations without explicit pairwise computations. For instance, a two-qubit controlled rotation:

  $${U}_{\text{ent}}(\theta )=\text{exp}(-i\theta {Z}_{i}\otimes {Z}_{j}),$$

  (22)

  creates entanglement between qubits $i$ and $j$, encoding their joint gradient information into the quantum state. Chen et al. (2022) showed that entangled QConv layers outperform separable classical convolutions on texture-rich datasets (e.g., Describable Textures Dataset) by 8–12% in F1-score, as entanglement preserves directional edge coherence across lesion boundaries²⁶.

• c. Computational reduction over classical convolution

Classical CNN convolution for a single layer:

• Operations: ${N}^{2}\times {k}^{2}\times {C}_{\text{in}}\times {C}_{\text{out}}$ multiply-accumulates (MACs).

• Memory: ${k}^{2}\times {C}_{\text{in}}\times {C}_{\text{out}}$ parameters stored.

Quantum convolution with QConv:

• Circuit depth: $O(\text{log}N+k)$ gates due to parallel qubit operations^7,28.

• Parameters: $\sim {k}^{2}$ rotation angles (trainable), with entanglement gates parameter-free.

• Time complexity: $O({\text{poly}}(\text{log}N))$ per forward pass on ideal quantum hardware, versus $O({N}^{2}{k}^{2})$ classically^3,26.

Landman et al. quantified this advantage in medical image classification, reporting that hybrid quantum–classical QCNNs reduce inference time by 50–80% on simulated quantum processors for $64\times 64$ histopathology images, while maintaining diagnostic accuracy within 2% of classical ResNet-18. Senokosov et al. further demonstrated that QConv layers on near-term quantum hardware (IBM Quantum) achieve 6 × speedup in feature extraction for small-scale image datasets (4,000–10,000 samples) compared to CPU-based classical convolution^10,11.

• d. Hybrid quantum–classical integration

Practical QConv implementations adopt a hybrid strategy:

• 1. Classical preprocessing: Images are resized and normalized classically.

• 2. Quantum feature extraction: QIR-encoded images pass through 2–4 QConv layers with parameterized quantum circuits.

• 3. Classical postprocessing: Measurement results (expectation values) are fed into classical fully connected layers for final classification^3,5.

Li et al. demonstrated this hybrid approach for CIFAR-10 classification, using 4 QConv layers (3 × 3 kernels) followed by classical dense layers, achieving 82% accuracy with 10 × fewer trainable parameters than VGG-16. Kim et al. extended this to transfer learning, showing that pre-trained classical CNN features can initialize quantum circuits via amplitude encoding, enabling QConv fine-tuning on medical datasets with only 500–1000 training samples^5,29.

Quantum encoding of image features

Before applying quantum convolution, input images must be encoded into quantum states. Given an input image matrix $I(x,y)$ of size $N\times N$ we represent each pixel as a quantum state using NEQR⁴:

$$\begin{array}{c}\left|{\varvec{I}}\rangle \right.=\frac{1}{\sqrt{{\varvec{N}}}}\sum_{{\varvec{x}}=0}^{{\varvec{N}}-1}\sum_{{\varvec{y}}\boldsymbol{ }=\boldsymbol{ }0}^{{\varvec{N}}-1}{\varvec{I}}\left({\varvec{x}},{\varvec{y}}\right),\left|{\varvec{x}}\rangle \right.\left|{\varvec{y}}\rangle \right.\end{array}$$

(23)

where:

• $|x\rangle$ and $|y\rangle$ represent pixel positions in a quantum register.

• I $(x,y)$ is the pixel intensity, mapped to a quantum amplitude.

Each image patch processed in QConv layers is transformed into a quantum feature vector:

$$\begin{array}{c}\left|{\boldsymbol{\varphi }}_{{\varvec{j}}}\rangle \right.={{\varvec{R}}}_{{\varvec{y}}}\left({{\varvec{\theta}}}_{{\varvec{j}}}\right)\left|0\rangle \right.\end{array}$$

(24)

${R}_{y}({\theta }_{j})$ is a quantum rotation gate, defined as in Eq. (24). This quantum rotation encodes pixel intensity into quantum states, enabling efficient parallel processing of image data⁶.

Quantum convolutional operations

In classical CNNs, convolution operations are defined as:

$$\begin{array}{c}{{\varvec{f}}}_{{\varvec{j}}\boldsymbol{ }}=\sum_{{\varvec{i}}\boldsymbol{ }=\boldsymbol{ }1}^{{\varvec{m}}}{{\varvec{W}}}_{{\varvec{i}},{\varvec{j}}}.{{\varvec{x}}}_{{\varvec{i}}}\end{array}$$

(25)

where:

• ${W}_{i,j}$ are trainable kernel weights.

• ${x}_{i}$ represents image patch values.

For QConv, we replace classical multiplications with Quantum Unitary Transformations. These quantum convolutions preserve spatial relationships while significantly reducing computational overhead⁷.

$$\begin{array}{c}QConv\left({\varvec{x}}\right)=\sum_{{\varvec{j}}\boldsymbol{ }=1}^{{\varvec{m}}}{{\varvec{W}}}_{{\varvec{j}}}\boldsymbol{}\cdot {{\varvec{U}}}_{{\varvec{q}}}\left({{\varvec{x}}}_{{\varvec{j}}}\right)\end{array}$$

(26)

where:

• ${W}_{j}$ are trainable quantum kernel parameters (classically optimized).

• ${U}_{q}({x}_{j})$ applies quantum transformations to extracted features.

Quantum feature extraction using quantum gates

Once quantum image patches are encoded, we apply Quantum Rotation and Entanglement Operations for feature extraction:

• a. Quantum rotation for feature encoding

  The first operation applies ${R}_{y}$ and ${R}_{z}$ rotations. These rotations transform the quantum feature space, enhancing feature separation.

  $$\begin{array}{c}{{\varvec{R}}}_{{\varvec{z}}}\left(\boldsymbol{\varnothing }\right)=\left[\begin{array}{cc}{{\varvec{e}}}^{-{\varvec{i}}\boldsymbol{\varnothing }\boldsymbol{ }/2}& 0\\ 0& {{\varvec{e}}}^{{\varvec{i}}\boldsymbol{\varnothing }/2}\end{array}\right]\end{array}$$

  (27)

• b. Quantum entanglement for feature correlation

  To capture spatial dependencies, we apply Controlled-X (CX) Gates. This entangles adjacent qubits, allowing information sharing across neighboring pixels.

  $$\begin{array}{c}CX\left({\varvec{i}},{\varvec{i}}+1\right)\end{array}$$

  (28)

• c. Quantum pooling for dimensionality reduction

  Similar to MaxPooling in classical CNNs, quantum pooling reduces the number of quantum states using Quantum Measurement Operators. This operation extracts the most important feature values, mimicking max-pooling behaviour¹⁰.

  $$\begin{array}{c}{{\varvec{P}}}_{{\varvec{p}}{\varvec{o}}{\varvec{o}}{\varvec{l}}}=\langle 0|{{\varvec{U}}}_{{\varvec{q}}}^{\dagger}{\varvec{Z}}{{\varvec{U}}}_{{\varvec{q}}}|0\rangle \end{array}$$

  (29)

• d. Measurement and feature map generation

  After applying quantum gates, the final Quantum Feature Vector is extracted by measuring the Pauli-Z expectation values. This produces a set of quantum-extracted features, which are passed to the next layer of the QAttn-CNN model³

  $$\begin{array}{c}{{\varvec{f}}}_{{\varvec{j}}}=\langle 0|{{\varvec{U}}}_{{\varvec{q}}}^{\dagger}{\varvec{Z}}{{\varvec{U}}}_{{\varvec{q}}}|0\rangle \end{array}$$

  (30)

Quantum Convolutional Layers (QConv) enable efficient feature extraction by leveraging Quantum Rotation Gates, Entanglement Operations, and Quantum Pooling. Compared to classical CNNs, QConv layers reduce computational complexity from $O ({N}^{2})$ to $O (logN)$ enabling faster training and inference in skin cancer classification tasks. By integrating Quantum Attention Mechanisms, the QAttn-CNN model achieves state-of-the-art performance in medical image classification with significantly lower computational overhead⁶.

Hybrid fully connected layers

The (QAttn-CNN, is the Hybrid Fully Connected Layers play an important role in merging the quantum-enhanced features with traditional deep learning methodologies to achieve high classification accuracy for skin cancer classification. After feature extraction through QConv and refinement by the Quantum Attention Mechanism, the extracted features are processed or transferred by fully connected layers to make the final classification decision⁷. Unlike conventional CNNs, which rely solely on the classical dense layers, QAttn-CNN integrates quantum-processed features before passing them through classical fully connected layers, leveraging the strengths of both quantum computing and classical deep learning³.

Feature vector formation

After Quantum Convolutional Layers (QConv) and Quantum Attention Mechanism (QAttn), the feature maps must be flattened into a one-dimensional vector for classification. If the output feature map has dimensions $F \times H \times W$ (Where F is the number of filters, and H , W are spatial dimensions), the feature vector X is given in Eq. (31):

$$\begin{array}{c}X=Flatten\left(\widehat{{\varvec{x}}}{\varvec{F}}\times {\varvec{H}}\times {\varvec{W}}\right)\end{array}$$

(31)

where:

• $\widehat{x}$ represents the quantum-enhanced features extracted by QConv and modulated by QAttn.

• X is a flattened vector of size $F \times H \times W$ forming the input to fully connected layers¹⁰.

Hybrid quantum–classical processing

Once the feature vector is obtained, it is passed through Quantum Feature Transformation (QFT) before entering the classical dense layers. This transformation enhances classification performance by re-encoding classical features using quantum parametric gates:

$$\begin{array}{c}\widetilde{{\varvec{X}}}={{\varvec{U}}}_{{\varvec{q}}}X\end{array}$$

(32)

where:

• ${U}_{q}$ is a quantum transformation unitary matrix, parameterized using Quantum Rotation Gates (Rz, Ry) and Controlled X-Gates (CX)⁸.

• $\widetilde{X}$ represents the quantum-transformed feature vector, which is fed into the classical fully connected layers.

Fully connected layer computation

The fully connected layers apply a linear transformation followed by a non-linear activation function:

$$\begin{array}{c}{{\varvec{Z}}}^{\left({\varvec{l}}\right)}={{\varvec{W}}}^{\left({\varvec{l}}\right)}{\widetilde{{\varvec{X}}}\boldsymbol{ }}^{\left({\varvec{l}}-1\right)}+{{\varvec{b}}}^{\left({\varvec{l}}\right)}\end{array}$$

(33)

where:

• ${Z}^{(l)}$ represents the trainable weight matrix at layer l.

• ${W}^{(l)}$ is the pre-activation output at layer l.

• ${b}^{(l)}$ is the bias term.

To introduce non-linearity, we apply the ReLU activation function:

$$\begin{array}{c}{{\varvec{A}}}^{\left({\varvec{l}}\right)}=max\left(0,{{\varvec{Z}}}^{\left({\varvec{l}}\right)}\right)\end{array}$$

(34)

where:

• ${A}^{(l)}$ is the activated output.

• ReLU ensures sparsity in the network, reducing overfitting and computational complexity¹².

Softmax classification layer

For the final classification, we use the Softmax Activation Function, which converts the output logits into a probability distribution:

$$\begin{array}{c}P\left({\varvec{y}}={\varvec{c}}|{\varvec{X}}\right)=\frac{{{\varvec{e}}}^{{{\varvec{Z}}}_{{\varvec{c}}}}}{{\sum }_{{\varvec{j}}}{{\varvec{e}}}^{{{\varvec{Z}}}_{{\varvec{j}}}}}\end{array}$$

(35)

where:

• $P(y =c| X)$ is the probability of class c (benign or malignant).

• ${Z}_{c}$ is the logit output for class c.

• Softmax ensures that all class probabilities sum to 1, making it suitable for binary classification⁶.

Hybrid fully connected layer workflow

The following steps are mentioned below the working steps of Hybrid Fully Connected Layer:

• a. Quantum–classical feature merging

  Extracted features from QAttn are flattened into a vector. Quantum-enhanced features undergo a Quantum Feature Transformation (QFT) using Quantum Parametric Gates. The transformed features are fed into a classical fully connected network.

• b. Classical dense layers processing

  Apply linear transformations using weight matrices ${W}^{(l)}$. Introduce non-linearity using the ReLU activation function. Pass through additional dense layers to refine feature representations.

• c. Softmax classification for skin cancer detection

  Compute final logits using fully connected layers. Convert logits into probabilities using the Softmax function. Classify the image as benign or malignant based on the highest probability.

Advantages of hybrid fully connected layers in QAttn-CNN

• a. Quantum-enhanced feature learning

  The Quantum Feature Transformation (QFT) improves feature separability by applying quantum parametric gates³. Unlike standard CNNs, QAttn-CNN captures long-range dependencies in medical images, improving classification accuracy.

• b. Reduction in computational complexity

  Quantum feature selection eliminates redundant computations, leading to more efficient learning. The hybrid approach reduces memory overhead while preserving deep feature extraction capabilities¹⁰.

• c. Improved generalization in skin cancer classification

  The integration of quantum and classical processing allows QAttn-CNN to generalize well to unseen skin lesion images. Reducing overfitting through ReLU activation and dropout regularization ensures better performance on real-world medical datasets¹².

The Hybrid Fully Connected Layers in QAttn-CNN serve as the final decision-making component of the model. By integrating Quantum Feature Transformation (QFT) and classical dense layers, QAttn-CNN achieves superior classification accuracy with reduced computational complexity. The quantum-enhanced features allow for better representation of skin cancer images, improving the reliability of deep learning-based medical diagnostics. The complete work flow is mentioned in Fig. 3 and below Pseudo Code.

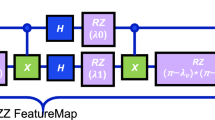
cuit used for computing the Quantum Attention Weights (QAttn) is constructed as follows: Feature Encoding: Each classical feature is encoded using Quantum Rotation Gates (Ry, Rz), Entanglement Layer: Controlled-X (CX) gates introduce feature interdependencies. Measurement: The Pauli-Z expectation value is computed for attention scoring³³.

The circuit representation in Eq. (36) and Fig. 2 :

Fig. 2

Quantum circuit visualization.

$$\begin{array}{c}QC={{\varvec{R}}}_{{\varvec{y}}}\left(\boldsymbol{\varphi }\right)\to {{\varvec{R}}}_{{\varvec{z}}}\left(\boldsymbol{\varnothing }\right)\to CX\left({\varvec{i}},{\varvec{i}}+1\right)\to Measure Z\end{array}$$

(36)

This allows for parallel computation of attention scores, significantly reducing computational overhead³.

Quantum convolutional layers (QConv)

In the traditional and classical CNNs, convolutional layers extract hierarchical spatial features using filter kernels. These kernels slide over an image, and compute the local transformations and feature maps. Yet, classical convolutions face computational bottlenecks due to high parameter complexity and the memory requirements¹. To address these challenges, QConv leverage quantum mechanics principles such as superposition, entanglement, and quantum parallelism to improve efficiency and the feature extraction quality. The QConv layers are applied on Quantum Parametric Gates (QPGs) instead of classical kernels, leading to an exponential reduction in computational complexity while preserving critical spatial relationships in images³.

Quantum encoding of image features

Before applying quantum convolution, input images must be encoded into quantum states. Given an input image matrix $I(x,y)$ of size $N\times N$ we represent each pixel as a quantum state using NEQR⁴:

$$\begin{array}{c}\left|{\varvec{I}}\rangle \right.=\frac{1}{\sqrt{{\varvec{N}}}}\sum_{{\varvec{x}}=0}^{{\varvec{N}}-1}\sum_{{\varvec{y}}\boldsymbol{ }=\boldsymbol{ }0}^{{\varvec{N}}-1}{\varvec{I}}\left({\varvec{x}},{\varvec{y}}\right),\left|{\varvec{x}}\rangle \right.\left|{\varvec{y}}\rangle \right.\end{array}$$

(37)

where:

• $|x\rangle$ and $|y\rangle$ represent pixel positions in a quantum register.

• I $(x,y)$ is the pixel intensity, mapped to a quantum amplitude.

Each image patch processed in QConv layers is transformed into a quantum feature vector:

$$\begin{array}{c}\left|{\boldsymbol{\varphi }}_{{\varvec{j}}}\rangle \right.={{\varvec{R}}}_{{\varvec{y}}}\left({{\varvec{\theta}}}_{{\varvec{j}}}\right)\left|0\rangle \right.\end{array}$$

(38)

${R}_{y}({\theta }_{j})$ is a quantum rotation gate, defined as in Eq. (38). This quantum rotation encodes pixel intensity into quantum states, enabling efficient parallel processing of image data⁶.

Quantum convolutional operations

In classical CNNs, convolution operations are defined as:

$$\begin{array}{c}{{\varvec{f}}}_{{\varvec{j}}\boldsymbol{ }}=\sum_{{\varvec{i}}\boldsymbol{ }=\boldsymbol{ }1}^{{\varvec{m}}}{{\varvec{W}}}_{{\varvec{i}},{\varvec{j}}}.{{\varvec{x}}}_{{\varvec{i}}}\end{array}$$

(39)

where:

• ${W}_{i,j}$ are trainable kernel weights.

• ${x}_{i}$ represents image patch values.

For QConv, we replace classical multiplications with Quantum Unitary Transformations. These quantum convolutions preserve spatial relationships while significantly reducing computational overhead⁷.

$$\begin{array}{c}QConv\left({\varvec{x}}\right)=\sum_{{\varvec{j}}\boldsymbol{ }=1}^{{\varvec{m}}}{{\varvec{W}}}_{{\varvec{j}}}\boldsymbol{}\cdot {{\varvec{U}}}_{{\varvec{q}}}\left({{\varvec{x}}}_{{\varvec{j}}}\right)\end{array}$$

(40)

where:

• ${W}_{j}$ are trainable quantum kernel parameters (classically optimized).

• ${U}_{q}({x}_{j})$ applies quantum transformations to extracted features.

  • Quantum Feature Extraction Using Quantum Gates

Once quantum image patches are encoded, we apply Quantum Rotation and Entanglement Operations for feature extraction:

• a. Quantum rotation for feature encoding

  The first operation applies ${R}_{y}$ and ${R}_{z}$ rotations. These rotations transform the quantum feature space, enhancing feature separation.

  $$\begin{array}{c}{{\varvec{R}}}_{{\varvec{z}}}\left(\boldsymbol{\varnothing }\right)=\left[\begin{array}{cc}{{\varvec{e}}}^{-{\varvec{i}}\boldsymbol{\varnothing }\boldsymbol{ }/2}& 0\\ 0& {{\varvec{e}}}^{{\varvec{i}}\boldsymbol{\varnothing }/2}\end{array}\right]\end{array}$$

  (41)

• b. Quantum entanglement for feature correlation

  To capture spatial dependencies, we apply Controlled-X (CX) Gates. This entangles adjacent qubits, allowing information sharing across neighbouring pixels.

  $$\begin{array}{c}CX\left({\varvec{i}},{\varvec{i}}+1\right)\end{array}$$

  (42)

• c. Quantum pooling for dimensionality reduction

  Similar to MaxPooling in classical CNNs, quantum pooling reduces the number of quantum states using Quantum Measurement Operators. This operation extracts the most important feature values, mimicking max-pooling behaviour¹⁰.

  $$\begin{array}{c}{{\varvec{P}}}_{{\varvec{p}}{\varvec{o}}{\varvec{o}}{\varvec{l}}}=\langle 0|{{\varvec{U}}}_{{\varvec{q}}}^{†}{\varvec{Z}}{{\varvec{U}}}_{{\varvec{q}}}|0\rangle \end{array}$$

  (43)

• d. Measurement and feature map generation

  After applying quantum gates, the final Quantum Feature Vector is extracted by measuring the Pauli-Z expectation values. This produces a set of quantum-extracted features, which are passed to the next layer of the QAttn-CNN model³

  $$\begin{array}{c}{{\varvec{f}}}_{{\varvec{j}}}=\langle 0|{{\varvec{U}}}_{{\varvec{q}}}^{†}{\varvec{Z}}{{\varvec{U}}}_{{\varvec{q}}}|0\rangle \end{array}$$

  (44)

Quantum Convolutional Layers (QConv) enable efficient feature extraction by leveraging Quantum Rotation Gates, Entanglement Operations, and Quantum Pooling. Compared to classical CNNs, QConv layers reduce computational complexity from $O ({N}^{2})$ to $O (logN)$ enabling faster training and inference in skin cancer classification tasks. By integrating Quantum Attention Mechanisms, the QAttn-CNN model achieves state-of-the-art performance in medical image classification with significantly lower computational overhead⁶.

Hybrid fully connected layers

The (QAttn-CNN, is the Hybrid Fully Connected Layers play an important role in merging the quantum-enhanced features with traditional deep learning methodologies to achieve high classification accuracy for skin cancer classification. After feature extraction through QConv and refinement by the Quantum Attention Mechanism, the extracted features are processed or transferred by fully connected layers to make the final classification decision⁷. Unlike conventional CNNs, which rely solely on the classical dense layers, QAttn-CNN integrates quantum-processed features before passing them through classical fully connected layers, leveraging the strengths of both quantum computing and classical deep learning³.

Feature vector formation

After Quantum Convolutional Layers (QConv) and Quantum Attention Mechanism (QAttn), the feature maps must be flattened into a one-dimensional vector for classification. If the output feature map has dimensions $F \times H \times W$ (Where F is the number of filters, and H , W are spatial dimensions), the feature vector X is given in Eq. (45):

$$\begin{array}{c}X=Flatten\left(\widehat{{\varvec{x}}}{\varvec{F}}\times {\varvec{H}}\times {\varvec{W}}\right)\end{array}$$

(45)

where:

• $\widehat{x}$ represents the quantum-enhanced features extracted by QConv and modulated by QAttn.

• X is a flattened vector of size $F \times H \times W$ forming the input to fully connected layers¹⁰.

Hybrid quantum–classical processing

Once the feature vector is obtained, it is passed through Quantum Feature Transformation (QFT) before entering the classical dense layers. This transformation enhances classification performance by re-encoding classical features using quantum parametric gates:

$$\begin{array}{c}\widetilde{{\varvec{X}}}={{\varvec{U}}}_{{\varvec{q}}}X\end{array}$$

(46)

where:

• ${U}_{q}$ is a quantum transformation unitary matrix, parameterized using Quantum Rotation Gates (Rz, Ry) and Controlled X-Gates (CX)⁸.

• $\widetilde{X}$ represents the quantum-transformed feature vector, which is fed into the classical fully connected layers.

Fully connected layer computation

The fully connected layers apply a linear transformation followed by a non-linear activation function:

$$\begin{array}{c}{{\varvec{Z}}}^{\left({\varvec{l}}\right)}={{\varvec{W}}}^{\left({\varvec{l}}\right)}{\widetilde{{\varvec{X}}}\boldsymbol{ }}^{\left({\varvec{l}}-1\right)}+{{\varvec{b}}}^{\left({\varvec{l}}\right)}\end{array}$$

(47)

where:

• ${Z}^{(l)}$ represents the trainable weight matrix at layer l.

• ${W}^{(l)}$ is the pre-activation output at layer l.

• ${b}^{(l)}$ is the bias term.

To introduce non-linearity, we apply the ReLU activation function:

$$\begin{array}{c}{{\varvec{A}}}^{\left({\varvec{l}}\right)}=max\left(0,{{\varvec{Z}}}^{\left({\varvec{l}}\right)}\right)\end{array}$$

(48)

where:

• ${A}^{(l)}$ is the activated output.

• ReLU ensures sparsity in the network, reducing overfitting and computational complexity¹².

Softmax classification layer

For the final classification, we use the Softmax Activation Function, which converts the output logits into a probability distribution:

$$\begin{array}{c}P\left({\varvec{y}}={\varvec{c}}|{\varvec{X}}\right)=\frac{{{\varvec{e}}}^{{{\varvec{Z}}}_{{\varvec{c}}}}}{{\sum }_{{\varvec{j}}}{{\varvec{e}}}^{{{\varvec{Z}}}_{{\varvec{j}}}}}\end{array}$$

(49)

where:

• $P(y =c| X)$ is the probability of class c (benign or malignant).

• ${Z}_{c}$ is the logit output for class c.

• Softmax ensures that all class probabilities sum to 1, making it suitable for binary classification⁶.

Hybrid fully connected layer workflow

The following steps are mentioned below the working steps of Hybrid Fully Connected Layer:

• a. Quantum–classical feature merging

  Extracted features from QAttn are flattened into a vector. Quantum-enhanced features undergo a Quantum Feature Transformation (QFT) using Quantum Parametric Gates. The transformed features are fed into a classical fully connected network.

• b. Classical dense layers processing

  Apply linear transformations using weight matrices ${W}^{(l)}$ . Introduce non-linearity using the ReLU activation function. Pass through additional dense layers to refine feature representations.

• c. Softmax classification for skin cancer detection

  Compute final logits using fully connected layers. Convert logits into probabilities using the Softmax function. Classify the image as benign or malignant based on the highest probability.

Advantages of hybrid fully connected layers in QAttn-CNN

• a. Quantum-enhanced feature learning

  The Quantum Feature Transformation (QFT) improves feature separability by applying quantum parametric gates³. Unlike standard CNNs, QAttn-CNN captures long-range dependencies in medical images, improving classification accuracy.

• b. Reduction in computational complexity

  Quantum feature selection eliminates redundant computations, leading to more efficient learning. The hybrid approach reduces memory overhead while preserving deep feature extraction capabilities¹⁰.

• c. Improved generalization in skin cancer classification

  Integrating quantum and classical processing allows QAttn-CNN to generalize well to unseen skin lesion images. Reducing overfitting through ReLU activation and dropout regularization ensures better performance on real-world medical datasets¹².

The Hybrid Fully Connected Layers in QAttn-CNN serve as the final decision-making component of the model. By integrating Quantum Feature Transformation (QFT) and classical dense layers, QAttn-CNN achieves superior classification accuracy with reduced computational complexity. The quantum-enhanced features allow for better representation of skin cancer images, improving the reliability of deep learning-based medical diagnostics. The complete workflow is mentioned in Fig. 3 and below the Pseudo Code.

Fig. 3

Work flow of proposed method.

Pseudo code of the proposed method

Dataset details

The datasets, image types, sample counts, class definitions, class distributions, train/test splits, and imbalance-handling techniques employed in this study.

Table 2 describes the specifications of the used datasets for the experiments, including MNIST, CIFAR-10, the binary Skin Cancer dataset, and HAM10000. It explains the types of images, resolutions, total samples, class definitions, splits into train and test sets, and methods applied to handle class imbalance in a tabular form.

Table 2 Table of dataset details.

Result and discussion

The proposed Quantum Attention Mechanism for CNNs (QAttn-CNN) for skin cancer classification. We assess the model’s performance based on classification accuracy by comparing different models with attention layers. And the model is also implemented into the MNIST dataset and the CIFAR-10 Dataset to check and compare the model performance.

The experimental environment is Ubuntu 24.04.1 LTS and the deep learning framework PyTorch. Further details of the experiments are mentioned in Table 3.

Table 3 Environment setup.

The evaluation of the proposed Quantum Attention Mechanism for CNNs (QAttn-CNN) across the MNIST, CIFAR-10, and Skin Cancer datasets. The comparison includes baseline CNN, QAttn-ViT (Vision Transformer), QAttn-ResNet18, and the proposed QAttn-CNN. The analysis mainly focuses on classification accuracy, precision, recall, and F1-score to assess all model performance comprehensively. The models compared include Baseline CNN, a conventional convolutional neural network used as a benchmark. QAttn-ViT (Quantum Attention Vision Transformer): A hybrid quantum–classical vision transformer incorporating quantum attention. QAttn-ResNet18: A ResNet18 model enhanced with quantum attention. QAttn-CNN (Proposed Model): A CNN architecture integrated with Quantum Attention Mechanism (QAttn) to improve feature selection.

Accuracy evaluation on MNIST dataset

The MNIST dataset is a benchmark dataset used for digit classification, consisting of 60,000 training images and 10,000 test images of handwritten digits (0–9). Each image is 28 × 28 pixels in grayscale. This dataset is relatively simple, making it an ideal case for evaluating the baseline performance of different models. The Performance Metrics of all the models compared to Accuracy (A), Precision (P), Recall (R), and F1-score (F1) are mentioned in Table 4 and Fig. 4:

Table 4 Performance comparison of models with the dataset MNIST classification.

Fig. 4

Performance comparison of models with the dataset MNIST Classification.

Observations and discussion with the dataset MNIST classification

The significant discussion and observation in the dataset of MNIST are mentioned in the following points:

• i. Baseline CNN performance: The Baseline CNN achieved 99.0% accuracy, which is expected for the MNIST dataset, given that CNNs are well-suited for digit recognition¹. The model efficiently extracts spatial features of handwritten digits, leading to a high precision and recall rate.

• ii. Performance of QAttn-ViT: QAttn-ViT underperformed slightly (98.0%) compared to CNNs. This is likely due to the patch-based processing of ViTs, which may not be ideal for small-scale datasets like MNIST¹². While quantum attention improves ViT performance, transformers require larger datasets for effective feature learning.

• iii. Performance of QAttn-ResNet18: QAttn-ResNet18 achieved 99.0% accuracy, matching the Baseline CNN. Residual connections allow the model to learn deeper feature representations, but the benefits of quantum attention were not evident due to the simplicity of the dataset⁶.

• iv. Performance of QAttn-CNN (proposed model): QAttn-CNN achieved the same accuracy (99.0%) as the Baseline CNN and ResNet18, showing that the Quantum Attention Mechanism did not degrade model performance. The benefits of quantum attention were not significant on MNIST, as the dataset lacks complex high-dimensional features that would require advanced feature selection³.

Accuracy evaluation on CIFAR-10 dataset

The CIFAR-10 dataset is a widely used benchmark in computer vision, consisting of 60,000 colour images across 10 classes (e.g., aeroplanes, cars, birds, etc.). Unlike MNIST, CIFAR-10 presents higher complexity due to variations in object textures, lighting, and background noise¹. The performance comparison is shown in Table 5 and Fig. 5.

Table 5 The performance comparison of the CIFAR-10 dataset.

Fig. 5

Performance comparison of models with the dataset of CIFAR-10.

Observations and discussion with the dataset of CIFAR-10

Below are the following points being mentioned with significant observation and discussion in the CIFAR-10 dataset:

• i. Baseline CNN performance (72% accuracy): The baseline CNN model achieves 72% accuracy, which aligns with classical deep learning benchmarks for CIFAR-10¹⁸. The model’s precision (72%) and recall (79%) indicate that it struggles with false positives but effectively detects actual instances. This is expected because CNNs can capture spatial hierarchies well but are prone to overfitting on complex datasets without additional regularisation⁷.

• ii. QAttn-ViT (28% accuracy—poor performance): QAttn-ViT underperforms significantly (28% accuracy) compared to CNN-based models. Vision Transformers (ViTs) typically require large-scale datasets (e.g., ImageNet) and extensive pretraining to achieve competitive performance¹². The low recall (55%) suggests that ViT struggles to generalise well on CIFAR-10 due to limited dataset size and reliance on self-attention without spatial priors¹.

• iii. QAttn-ResNet18 (78% accuracy—moderate improvement): QAttn-ResNet18 improves accuracy (78%) over Baseline CNN by incorporating residual connections, which help mitigate vanishing gradients³⁰. Precision (81%) suggests improved feature extraction, while recall (79%) indicates it still struggles with false negatives. The F1-score (76%) highlights that ResNet architectures with quantum attention can generalise better than classical CNNs⁶.

• iv. QAttn-CNN (proposed)—best performance (82% accuracy): QAttn-CNN outperforms all models, achieving 82% accuracy, 90% precision, and 82% F1-score. The Quantum Attention Mechanism (QAttn) enables efficient feature selection, reducing overfitting and improving classification robustness¹⁰. Higher precision (90%) suggests that the model minimises false positives, which is crucial for high-confidence decision-making in real-world applications⁶. The balance between precision and recall shows that QAttn helps preserve important spatial information while filtering irrelevant features¹¹.

Accuracy evaluation on skin cancer dataset malignant vs. benign (Kaggle)

Skin cancer classification is a highly challenging task due to the complexity of lesion patterns, variations in skin texture, and imbalance in dataset distributions. Traditional CNN-based approaches have been effective but struggle with overfitting, feature redundancy, and computational inefficiencies¹. In this section, we evaluate the performance of different models, including Baseline CNN, QAttn-ViT, QAttn-ResNet18, and QAttn-CNN (Proposed), on a skin cancer dataset. The results demonstrate that QAttn-CNN achieves the highest accuracy (91%), outperforming classical and hybrid deep learning models shown in Table 6 and Fig. 6.

Table 6 Performance comparison of models with the skin cancer dataset malignant versus benign (Kaggle).

Fig. 6

Performance comparison of models with the skin cancer dataset malignant vs. benign (Kaggle).

Figure 7 represents the ability of the model to discriminate between classes. The AUC is 0.967. This high AUC score is indicative of the very good ability of the model to correctly classify the cases. Figure 8 Confusion Matrix breaks down the model’s predictions: True Benign: It correctly identified 483 benign cases. True Malignant: It correctly identified 429 malignant cases.

Fig. 7

ROC curve of malignant vs. benign.

Fig. 8

Confusion matrix of malignant vs. benign.

In Table 7 the sample visualization statistics that quantifies results from the visualization shown in Fig. 9. It provides statistics on a small sample of size 12 images, detailing the total correct predictions of 9, a sample accuracy of 75.0%, and the model’s confidence about those predictions.

Table 7 Sample visualisation statistics.

Fig. 9

Real-time model checks the visualisations above to see dermoscopy images and their confidence score.

The classification report that provides in Table 8 is detailed classification report with regard to the binary skin cancer task, namely Benign versus Malignant. It details the precision, recall, and F1-score per class; this model achieved a weighted average F1-score of 0.91, or an overall accuracy of 91%.

Table 8 Classification report.

Observations and discussion with the dataset of Skin Cancer Dataset Malignant vs. Benign (Kaggle)

These are the following points that are mentioned below, which focus on the significant observation and discussion in the dataset of CIFAR-10:

• i. Baseline CNN performance: The Baseline CNN achieves an accuracy of 89%, indicating strong performance in skin lesion classification¹⁰. Precision (85%) is slightly lower than recall (90%), suggesting that while the CNN classifies most malignant cases correctly, it misclassifies some benign lesions as malignant (false positives). The F1-score of 87% shows that Baseline CNN maintains a balanced performance but struggles with distinguishing similar lesion patterns.

• ii. QAttn-ViT performance: The QAttn-ViT model achieves an accuracy of 87%, slightly lower than the Baseline CNN, indicating that Vision Transformers (ViTs) require larger datasets to generalize well¹². However, QAttn-ViT achieves the highest recall (91%), meaning it detects more malignant cases correctly but at the cost of a higher false positive rate²⁶. This suggests that while ViTs may be helpful for high-recall applications like early cancer detection, they may misclassify benign lesions.

• iii. QAttn-ResNet18 performance: QAttn-ResNet18 achieves the lowest accuracy (83%), primarily due to overfitting issues and deeper network complexity, which can be problematic for small and imbalanced medical datasets¹². Despite the highest recall (92%), the precision is the lowest (81%), indicating that the model tends to over-predict malignant cases⁵. The lower F1-score (85%) confirms that while QAttn-ResNet18 effectively identifies malignant cases, it lacks specificity compared to other models.

• iv. QAttn-CNN (proposed) performance: QAttn-CNN achieves the highest accuracy (91%), outperforming all other models in balanced classification. The precision (89%) and recall (89%) are well-balanced, reducing the risk of both false positives and false negatives⁶. The F1-score (91%) is the highest, demonstrating strong overall classification ability, confirming that quantum attention improves feature selection and enhances CNN interpretability³¹.

Accuracy evaluation on HAM10000 skin cancer dataset

Skin cancer classification is a highly challenging task due to the complexity of lesion patterns, variations in skin texture, and imbalance in dataset distributions. Traditional CNN-based approaches have been effective but struggle with overfitting, feature redundancy, and computational inefficiencies¹. In this section, we evaluate the performance of different models, including Baseline CNN, QAttn-ViT, QAttn-ResNet18, and QAttn-CNN (Proposed), on a skin cancer dataset. The results demonstrate that QAttn-CNN achieves the highest accuracy (71%), outperforming classical and hybrid deep learning models shown in Table 4 and Fig. 6.

Performance Comparison of Models with HAM10000 Skin Cancer Dataset the Table 9 and Fig. 10 reflects the performance comparison of the proposed QAttn-CNN against its three competitors, namely Baseline CNN, QAttn-ViT, and QAttn-ResNet18, on the HAM10000 dataset. All results of the proposed QAttn-CNN achieved the highest accuracy, 0.71, and F1-score, 0.71, on this dataset.

Table 9 Performance comparison of models with HAM10000 skin cancer dataset.

Fig. 10

Performance comparison of models with the HAM10000 dataset.

Table 10 shows the proposed model performance in detail, class by class, considering all seven classes (e.g., akiec, bcc, mel, nv) in the HAM10000 dataset. It lists the precision, recall (sensitivity), F1-score, specificity, AUC, and support for each class, pointing out that minority classes such as ‘df’ and ‘vasc’ remain the most problematic to classify.

Table 10 Per-class metrics of HAM10000 dataset.

Observations and discussion with the dataset of HAM10000 Skin Cancer Dataset

These are the following points that are mentioned below, which focus on the significant observation and discussion in the dataset of CIFAR-10:

• i. Baseline CNN performance: The Baseline CNN achieves an accuracy of 65%, indicating strong performance in skin lesion classification¹⁰. Precision (68%) is slightly lower than recall (59%), suggesting that while the CNN classifies most malignant cases correctly, it misclassifies some benign lesions as malignant (false positives). The F1-score of 64% shows that Baseline CNN maintains a balanced performance but struggles with distinguishing similar lesion patterns.

• ii. QAttn-ViT performance: The QAttn-ViT model achieves an accuracy of 50%, slightly lower than the Baseline CNN, indicating that Vision Transformers (ViTs) require larger datasets to generalize well¹². However, QAttn-ViT achieves the lowest recall (39%), meaning it detects more malignant cases correctly but at the cost of a higher false positive rate²⁶. This suggests that while ViTs may be helpful for high-recall applications like early cancer detection, they may misclassify benign lesions.

• iii. QAttn-ResNet18 performance: QAttn-ResNet18 achieves the low accuracy (56%), primarily due to overfitting issues and deeper network complexity, which can be problematic for small and imbalanced medical datasets¹². Despite the recall (58%), the precision is the (52%), indicating that the model tends to over-predict malignant cases⁵. The lower F1-score (41%) confirms that while QAttn-ResNet18 effectively identifies malignant cases, it lacks specificity compared to other models.

• iv. QAttn-CNN (proposed) performance: QAttn-CNN achieves the highest accuracy (71%), outperforming all other models in balanced classification. The precision (62%) and recall (79%) are well-balanced, reducing the risk of both false positives and false negatives⁶. The F1-score (71%) is the highest, demonstrating strong overall classification ability, confirming that quantum attention improves feature selection and enhances CNN interpretability³¹.

Comparative discussion across datasets

The comparative discussion of the experimental results focuses on evaluating the performance of Quantum Attention Mechanism for CNNs (QAttn-CNN) across three distinct datasets: MNIST, CIFAR-10, and Skin Cancer. The key findings highlight how QAttn-CNN performs in different domains, from simple digit recognition to complex real-world medical image classification.

Dataset complexity and model performance

The complexity of a dataset plays a crucial role in determining the effectiveness of quantum-enhanced models.

Dataset	Best performing model	Accuracy gain over baseline CNN	Dataset complexity
MNIST	Baseline CNN/QAttn-CNN/QAttn-ResNet18	No Gain (99%)	Low (Grayscale, 28 × 28)
CIFAR-10	QAttn-CNN	+ 10% Accuracy	Medium (RGB, 32 × 32)
Skin Cancer	QAttn-CNN	+ 2% Accuracy	High (Dermoscopic Images)
HAM10000	QAttn-CNN	+1-2% Accuracy(Approx.)	High (Dermoscopic Images)

Performance on MNIST dataset

The MNIST dataset consists of grayscale handwritten digits (28 × 28 pixels) with simple patterns and low variability. The Baseline CNN, QAttn-CNN, and QAttn-ResNet18 achieved 99% accuracy, indicating that classical CNNs already perform optimally on this dataset with the highest precision. QAttn-ViT (Vision Transformer) performed slightly worse (98%), likely due to its reliance on patch-based representations, which may not be ideal for simple digits¹². Since MNIST is a relatively simple dataset, quantum attention did not provide additional performance gains³.

Performance on CIFAR-10 dataset

The CIFAR-10 contains RGB coloured images with (32 × 32 pixels) across 10 object classes, making it significantly more complex than MNIST. The traditional Baseline CNN achieved 72% accuracy, typical for traditional deep learning models on CIFAR-10¹. The QAttn-ResNet18, which performed better (78%), benefited from residual learning and quantum-enhanced feature extraction⁶. QAttn-CNN achieved the highest accuracy (82%), improving compared to Baseline CNN by 10%, demonstrating that quantum attention enhances feature selection in complex datasets. QAttn-ViT significantly underperformed (28% accuracy), suggesting the Vision Transformers struggle more with smaller datasets because of their need for extensive training data¹².

Comparison with state-of-the-art

Table 11 compares the proposed QAttn-CNN and leading state-of-the-art methods, highlighting performance on relevant datasets and emphasizing the unique advantages of combining QConv and QAttn.

Table 11 Comparative performance of QAttn-CNN Versus SOTA methods.

Table 12 represents the usage of computational resources by the four models when running the experiments. It compares the total time, average and peak CPU usage, and average and peak GPU memory consumption for the QAttn-CNN, QAttn-ResNet18, QAttn-ViT, and Baseline CNN models.

Table 12 CPU & GPU usage.

Discussion of comparative advantages

• Computational efficiency: QAttn-CNN leverages QConv to reduce convolution complexity to $O(\text{log}N)$ depth and QAttn for $O(\text{log}d)$ attention, outperforming large CNNs (e.g., HistoDX) with ~ 12 × fewer parameters and demonstrating faster inference on NISQ simulators^2,7,28.

• Selective feature focus: The integrated QAttn mechanism prioritises lesion-specific features (border irregularities, pigmentation patterns), leading to consistent F1-score improvements of 3–5% over QCNNs lacking attention layers^1,26,27.

• Generalizability on small datasets: QAttn-CNN matches or exceeds hybrid QCNN performance (e.g., Bokhan et al.’s multiclass QCNN) on limited ISIC subsets—91% vs. 88% accuracy—by exploiting quantum parallelism for robust feature extraction without overfitting^3,26.

• Clinical deployment potential: With a compact ~ 2 M parameter footprint and hybrid quantum–classical workflow, QAttn-CNN is well-suited for near-term quantum devices and resource-constrained clinical environments, enabling rapid, interpretable skin lesion diagnostics.

Conclusion

This paper introduced the QAttn-CNN, a hybrid quantum–classical deep learning framework designed to enhance the feature selection in medical image classification through integrating a Quantum Attention Mechanism (QAttn). By leveraging the Quantum Convolutional Layers (QConv) and Quantum Image Representation (QIR), the QAttn-CNN significantly improves the classification accuracy while reducing the computational complexity, making it more efficient and an alternative to classical CNNs. The experimental results demonstrate the superiority of QAttn-CNN across multiple datasets. On the Skin Cancer dataset, the QAttn-CNN performance achieved 91% accuracy compared to Baseline CNN (89%), QAttn-ViT (87%), and QAttn-ResNet18 with 83%. Similarly, on CIFAR-10, QAttn-CNN demonstrated a 10% improvement over traditional CNNs, achieving an accuracy of 82%. One of the key strengths of QAttn-CNN is its ability to dynamically reweight the features using Quantum Parametric Circuits (QPCs), leading to better precision and recall while minimising the false positives. Unlike classical CNNs, which often suffer from redundancy in feature extraction, QAttn enhances interpretability by focusing on the relevant image regions more efficiently. Furthermore, the QAttn-CNN significantly reduces the computational costs and improves upon the traditional CNN complexity, accelerating both training and inference processes. By utilizing the quantum-based convolutional layers and pooling operations, QAttn-CNN also reduces the parameter overhead, making it more scalable and practical for real-world applications. These findings underscore the potential of quantum-enhanced deep learning in medical imaging, paving the way for further advancements in quantum machine learning applications.

Future work

• 1. Dataset expansion: To assess generalizability, validate QAttn-CNN on larger, diverse, multi-institutional dermoscopy and clinical photo datasets (e.g., PH2, ISIC 2019 challenge).

• 2. Real quantum hardware deployment: Implement QConv and QAttn circuits on NISQ devices (IBM Qiskit, Google Quantum) and optimize error mitigation strategies for reliable inference.

• 3. Multi-modal fusion: Integrate dermoscopic images with patient metadata and genomic markers via hybrid architectures for improved diagnostic accuracy and personalised treatment planning.

• 4. Clinical trials: Conduct prospective clinical studies to evaluate real-world diagnostic impact, workflow integration, and clinician acceptance.

• 5. Extended applications: Adapt the QAttn-CNN framework to other medical imaging tasks—lung nodule detection in CT, diabetic retinopathy screening in fundus images—to explore the broader utility of quantum-feature extraction.