Marine fishery resource dynamic prediction based on CNN-XGBoost fusion model

Abstract

Marine fishery resource prediction is crucial for sustainable fishery management and ecosystem conservation, yet traditional statistical methods face limitations in capturing the complex non-linear relationships and multi-scale temporal dependencies inherent in marine environmental systems. This study proposes a novel CNN-XGBoost fusion model that integrates convolutional neural networks’ temporal pattern recognition capabilities with extreme gradient boosting’s ensemble learning strengths for enhanced marine fishery resource forecasting. The fusion architecture employs a hierarchical two-stage framework where CNN components extract high-level temporal features from multi-source marine environmental data, while XGBoost modules process both extracted features and engineered variables to generate final predictions. Comprehensive experiments demonstrate that the proposed fusion model achieves superior performance compared to standalone CNN, XGBoost, and traditional ARIMA approaches, with 19.1% improvement in RMSE and statistically significant enhancements across all evaluation metrics. The optimal fusion weight analysis reveals that CNN-extracted features and XGBoost-processed features are weighted at 40 and 60% respectively in the final prediction fusion, achieving RMSE of 2.847, MAE of 2.184, and R² of 0.846. These percentages represent fusion weight allocation rather than prediction accuracy values. Time series analysis confirms robust performance across seasonal variations and exceptional capability in predicting extreme abundance events critical for adaptive fishery management. The results provide valuable insights for sustainable marine resource management and offer practical tools for fishery policymakers and resource managers.

Introduction

Marine fishery resources represent a critical component of global food security and economic sustainability, providing essential protein sources for billions of people worldwide while supporting numerous coastal communities. The effective management and sustainable utilization of these resources necessitate accurate prediction of their dynamic variations, which is fundamental for establishing sound fishing policies, optimizing resource allocation, and maintaining ecological balance¹. However, marine ecosystems are characterized by complex, non-linear interactions among biological, physical, and environmental factors, presenting significant challenges for traditional forecasting approaches in capturing the intricate spatiotemporal patterns inherent in fishery resource dynamics.

Traditional statistical prediction methods, including autoregressive integrated moving average (ARIMA) models, linear regression, and classical time series analysis techniques, have been extensively employed in marine resource forecasting but exhibit fundamental limitations when confronted with the complexity of real-world fishery data². These conventional approaches typically assume linear relationships and stationary conditions, making them inadequate for handling the non-linear dependencies, irregular patterns, and multi-scale temporal variations that characterize marine fishery systems³. Furthermore, traditional methods often struggle with high-dimensional feature spaces and fail to effectively capture the complex interactions between oceanographic variables, climate factors, and biological processes that influence fishery resource abundance and distribution patterns.

The emergence of deep learning techniques has revolutionized time series prediction across numerous domains, offering enhanced capabilities for modeling complex non-linear relationships and extracting meaningful patterns from large-scale datasets⁴. Convolutional Neural Networks (CNNs) have demonstrated exceptional performance in capturing spatial-temporal dependencies through their hierarchical feature extraction mechanisms, enabling automatic identification of local patterns and multi-scale temporal structures in sequential data⁵. Additionally, Transformer architectures have gained significant attention for time series forecasting due to their self-attention mechanisms that can capture long-range dependencies, though recent studies have questioned their effectiveness compared to simpler linear models for certain time series tasks^6,7. Recent applications of CNNs in marine science have shown promising results in ocean temperature forecasting, sea surface current prediction, and marine ecosystem modeling, highlighting their potential for addressing the complexities inherent in marine fishery resource prediction⁸.

Concurrently, ensemble learning methods, particularly gradient boosting algorithms such as XGBoost, have gained widespread recognition for their superior predictive performance in time series forecasting tasks⁹. XGBoost excels in handling heterogeneous data types, capturing non-linear feature interactions, and providing robust predictions through its iterative boosting framework that combines multiple weak learners to form strong predictive models¹⁰. The algorithm’s ability to automatically handle missing values, incorporate feature importance rankings, and maintain computational efficiency makes it particularly suitable for marine fishery applications where data availability and quality may vary significantly across different temporal and spatial scales.

The theoretical rationale for fusing CNN and XGBoost lies in their fundamentally complementary learning paradigms that address different aspects of the marine fishery prediction challenge. CNNs excel at automatic hierarchical feature learning through their convolutional architecture, which naturally captures local temporal patterns and multi-scale dependencies in sequential data without requiring manual feature engineering. The convolutional layers act as adaptive filters that learn to detect meaningful temporal motifs such as seasonal cycles, environmental regime shifts, and short-term fluctuations in marine conditions. However, CNNs face limitations when processing heterogeneous tabular features that lack spatial or temporal structure, and their fully connected layers can be prone to overfitting when training data is limited. Conversely, XGBoost demonstrates superior performance in handling structured tabular data through its tree-based ensemble learning framework, which effectively captures complex non-linear interactions between engineered features such as statistical aggregations, lag variables, and domain-specific oceanographic indicators. The gradient boosting mechanism enables XGBoost to iteratively refine predictions by focusing on difficult cases, while its built-in regularization prevents overfitting and maintains robust generalization. Yet XGBoost lacks the automatic temporal pattern recognition capabilities inherent to deep learning architectures, requiring extensive manual feature engineering to capture temporal dependencies. Recent fusion model research has demonstrated that combining deep learning feature extractors with traditional machine learning classifiers can achieve performance superior to either approach alone, with applications spanning computer vision, natural language processing, and time series forecasting. In marine science contexts specifically, hybrid models integrating CNN-based spatial feature extraction with LSTM-based temporal modeling have shown promising results for ocean temperature prediction and sea surface height forecasting. However, existing fusion approaches in marine resource prediction remain limited, with most studies employing simple averaging or stacking methods that fail to optimally leverage the distinct strengths of each component. Our proposed CNN-XGBoost fusion addresses these limitations through a hierarchical architecture that enables CNN to focus on automatic temporal feature extraction from raw time series data, while XGBoost processes both these learned representations and manually engineered features to generate final predictions. This division of labor allows each component to operate within its domain of strength: CNN handles the complex task of discovering latent temporal patterns in high-dimensional sequential data, while XGBoost excels at modeling the intricate relationships between heterogeneous feature types including both learned and engineered variables. The fusion weight optimization mechanism further enhances performance by adaptively determining the relative contribution of each component based on validation data, ensuring that the model leverages the most informative signals from both paradigms. This integrated approach represents a significant methodological advancement over existing marine fishery prediction methods, which typically rely on either pure deep learning or pure machine learning approaches without exploiting their complementary capabilities.

The selection of CNN and XGBoost for fusion, rather than alternative combinations such as LSTM-Random Forest or Transformer-LightGBM, is grounded in several theoretical and practical considerations. CNNs were chosen over recurrent architectures (LSTM, GRU) because convolutional operations enable parallel processing of temporal sequences, resulting in substantially faster training times (28.5 min for CNN vs. 45.2 min for comparable LSTM) while achieving competitive accuracy through hierarchical temporal feature extraction^5,11. Unlike Transformers which require extensive hyperparameter tuning and large datasets to achieve optimal performance, CNNs demonstrate robust performance with moderate-sized datasets typical of regional fishery monitoring programs^12,13. XGBoost was selected over alternative gradient boosting implementations (LightGBM, CatBoost) and random forests due to its superior handling of mixed feature types, built-in regularization that prevents overfitting with limited data, and efficient implementation that enables rapid iteration during model development^9,14. The combination of CNN and XGBoost specifically addresses the dual nature of marine fishery prediction data: sequential temporal patterns requiring deep learning feature extraction, and heterogeneous environmental covariates requiring tree-based ensemble learning. Alternative fusion combinations either sacrifice computational efficiency (CNN-LSTM requires 56.3 min training time) or fail to optimally handle the diversity of feature types present in multi-source marine environmental datasets. This methodological selection thus reflects both theoretical understanding of each algorithm’s strengths and practical constraints of operational fisheries forecasting applications.

The fusion of CNN and XGBoost methodologies represents an innovative approach that leverages the complementary strengths of both deep learning and ensemble learning paradigms. While CNNs excel at extracting hierarchical representations and capturing spatial-temporal dependencies, XGBoost provides robust tree-based learning capabilities and effective handling of tabular features. This combination addresses the limitations of individual approaches by enabling comprehensive feature extraction through CNN layers while maintaining the interpretability and efficiency of gradient boosting for final prediction tasks. The hybrid architecture offers enhanced generalization capabilities and improved prediction accuracy compared to standalone models, particularly valuable for the complex, multi-dimensional nature of marine fishery resource forecasting.

The primary innovation of this research lies in developing a comprehensive fusion framework that integrates CNN-based spatial-temporal feature extraction with XGBoost-based ensemble learning for marine fishery resource prediction. This study introduces novel architectural designs that optimize the information flow between CNN feature extraction layers and XGBoost prediction modules, ensuring effective utilization of both deep learned representations and traditional statistical features. Additionally, the research establishes systematic evaluation protocols that assess model performance across multiple temporal horizons and different marine ecosystem conditions, providing valuable insights into the applicability and robustness of the proposed approach.

The objectives of this study encompass three primary goals: first, to develop an integrated CNN-XGBoost fusion model that effectively combines deep learning feature extraction capabilities with ensemble learning prediction strengths; second, to comprehensively evaluate the predictive performance of the proposed methodology against existing approaches across diverse marine fishery datasets; and third, to analyze the interpretability and practical applicability of the fusion model for real-world fishery management applications. The significance of this research extends beyond methodological contributions, offering practical tools for marine resource managers, policy makers, and researchers involved in sustainable fishery development and conservation efforts.

This paper is organized as follows: Section II presents the theoretical foundations and methodology of the CNN-XGBoost fusion approach, including detailed descriptions of model architecture and training procedures. Section III describes the experimental setup, datasets, and evaluation metrics employed in this study. Section IV presents comprehensive results comparing the proposed method with baseline approaches and discusses the implications of findings. Section V analyzes the interpretability and practical applications of the fusion model. Finally, Section VI concludes the paper with a summary of contributions and directions for future research.

Theoretical foundation and related work

Theoretical foundation of marine fishery resource prediction

Marine fishery resources exhibit complex dynamic variation patterns characterized by multi-scale temporal fluctuations, ranging from short-term daily variations to long-term decadal cycles driven by population dynamics, environmental changes, and anthropogenic factors¹⁵. These resources demonstrate inherent non-linear behaviors influenced by biological processes such as recruitment, growth, mortality, and migration patterns, which create intricate feedback loops within marine ecosystems. The population dynamics of fish stocks follow fundamental ecological principles where resource abundance fluctuates in response to carrying capacity constraints, predator-prey relationships, and competitive interactions among species¹⁶. Understanding these variation patterns is essential for developing effective prediction models that can capture both the deterministic components and stochastic elements inherent in fishery resource dynamics.

Environmental factors play a pivotal role in determining the spatial and temporal distribution of marine fishery resources, with oceanographic conditions serving as primary drivers of ecosystem productivity and species abundance. Sea surface temperature (SST) represents one of the most influential parameters, directly affecting fish metabolism, reproductive cycles, and habitat suitability, while also influencing primary productivity through its impact on nutrient distribution and phytoplankton growth¹⁷. Additional critical environmental variables include chlorophyll-a concentrations indicating marine productivity, ocean currents affecting larval transport and adult migration patterns, salinity gradients creating distinct water masses, and atmospheric parameters such as wind patterns and precipitation that influence coastal upwelling and nutrient availability. The complex interactions among these environmental factors create a multidimensional forcing system that requires sophisticated analytical approaches to understand and predict their collective influence on fishery resource dynamics.

Time series analysis provides a fundamental framework for modeling and predicting marine fishery resources by treating resource abundance data as sequential observations that exhibit temporal dependencies and patterns. The basic principle underlying time series analysis for fishery prediction relies on the assumption that historical patterns contain information about future states, enabling the identification of trends, seasonal cycles, and recurring fluctuations in resource abundance¹⁸. Classical time series decomposition separates observed data into trend, seasonal, and irregular components, allowing for systematic analysis of different temporal scales affecting fishery resources. The mathematical representation of a time series for fishery resource abundance can be expressed as:

$$\:{X}_{t}={T}_{t}+{S}_{t}+{R}_{t}+{\epsilon}_{t}$$

where $\:{X}_{t}$ represents the observed resource abundance at time $\:t$, $\:{T}_{t}$ denotes the trend component, $\:{S}_{t}$ represents seasonal variations, $\:{R}_{t}$ captures cyclical patterns, and $\:{\epsilon}_{t}$ represents random fluctuations or noise.

Traditional statistical prediction methods, particularly autoregressive models, have been extensively employed in fishery resource forecasting due to their mathematical tractability and interpretability. The autoregressive integrated moving average (ARIMA) model represents a cornerstone approach that combines autoregressive and moving average components to model temporal dependencies in fishery data¹⁹. The general form of an ARIMA(p, d,q) model can be expressed as:

$$\:\left(1-{\varphi\:}_{1}L-{\varphi\:}_{2}{L}^{2}-...-{\varphi\:}_{p}{L}^{p}\right){\left(1-L\right)}^{d}{X}_{t}=\left(1+{\theta\:}_{1}L+{\theta\:}_{2}{L}^{2}+...+{\theta\:}_{q}{L}^{q}\right){\epsilon}_{t}$$

where $\:L$ represents the lag operator, $\:{\varphi\:}_{i}$ and $\:{\theta\:}_{j}$ are model parameters, $\:d$ indicates the degree of differencing, and $\:{\epsilon}_{t}$ represents white noise errors.

Despite their widespread application, traditional statistical methods exhibit significant limitations when applied to marine fishery resource prediction. These approaches typically assume linear relationships and stationary time series properties, which are often violated in real-world fishery data characterized by non-linear dynamics, regime shifts, and complex environmental interactions. The assumption of normality in error distributions frequently fails to capture the asymmetric and heavy-tailed distributions commonly observed in fishery abundance data, leading to suboptimal prediction performance during extreme events or population collapses. Furthermore, traditional methods struggle to incorporate high-dimensional environmental covariates and fail to capture the complex spatial-temporal interactions that influence fishery resource dynamics across different scales. The computational limitations of classical approaches also restrict their ability to process large-scale datasets and adapt to changing environmental conditions, highlighting the need for more sophisticated modeling frameworks that can address these fundamental limitations while maintaining predictive accuracy and practical applicability.

Applications of convolutional neural networks in time series prediction

Convolutional Neural Networks represent a class of deep learning architectures specifically designed to exploit spatial hierarchies in data through the application of learnable convolution operations. The fundamental principle of CNNs lies in their ability to automatically learn feature representations through a combination of convolutional layers, pooling layers, and fully connected layers, enabling the extraction of local patterns and their subsequent combination into higher-level abstractions²⁰. The basic CNN architecture consists of multiple convolutional layers that apply sliding window operations across input data, followed by activation functions that introduce non-linearity, and pooling layers that perform dimensionality reduction while preserving the most salient features. The mathematical foundation of a convolutional operation can be expressed as:

$$\:{y}_{i}=\sum\:_{k=0}^{K-1}{w}_{k}\cdot\:{x}_{i+k}+b$$

where $\:{y}_{i}$ represents the output feature at position $\:i$, $\:{w}_{k}$ denotes the learnable kernel weights, $\:{x}_{i+k}$ represents the input values within the receptive field, $\:K$ is the kernel size, and $\:b$ is the bias term.

One-dimensional convolution demonstrates particular advantages in processing time series data by effectively capturing temporal dependencies and local patterns within sequential observations. Unlike traditional recurrent architectures that process sequences sequentially, 1D CNNs can capture multiple temporal patterns simultaneously through parallel convolution operations, resulting in improved computational efficiency and the ability to detect features at different temporal scales¹¹. The 1D convolution operation enables the automatic extraction of temporal motifs and recurring patterns within time series data, while the hierarchical structure of CNNs allows for the progressive combination of local temporal features into more complex global representations. The pooling operations in 1D CNNs provide additional benefits by reducing temporal dimensionality while preserving the most informative features, thereby enhancing the model’s robustness to noise and temporal variations commonly observed in marine environmental data.

Recent applications of CNN architectures in marine environmental data analysis have demonstrated significant potential for addressing complex oceanographic prediction challenges. Convolutional LSTM (ConvLSTM) models have been successfully employed for nearshore water level prediction, combining the spatial feature extraction capabilities of CNNs with the temporal modeling strengths of LSTM networks to achieve superior forecasting performance²¹. These hybrid approaches have shown particular effectiveness in capturing the complex spatiotemporal patterns inherent in marine systems, where environmental variables exhibit both spatial correlations and temporal dependencies. Additionally, CNN-based models have been applied to ocean temperature forecasting, where the hierarchical feature extraction capabilities enable the identification of multi-scale thermal patterns and their temporal evolution across different oceanic regions.

CNNs address the challenges of multivariate time series prediction through sophisticated feature extraction and integration mechanisms that can handle the complex interdependencies among multiple environmental variables. The multi-channel input capability of CNNs allows for the simultaneous processing of multiple time series variables, where each channel represents a different environmental parameter such as temperature, salinity, chlorophyll concentration, or current velocity¹². The convolution operations are applied across all channels simultaneously, enabling the model to learn cross-variable relationships and their temporal dynamics. The mathematical representation of multivariate convolution can be expressed as:

$$\:{y}_{i}^{\left(c\right)}=\sum\:_{j=1}^{C}\sum\:_{k=0}^{K-1}{w}_{k,j}^{\left(c\right)}\cdot\:{x}_{i+k}^{\left(j\right)}+{b}^{\left(c\right)}$$

where $\:{y}_{i}^{\left(c\right)}$ represents the output feature at position $\:i$ for channel $\:c$, $\:C$ is the total number of input channels, $\:{w}_{k,j}^{\left(c\right)}$ denotes the kernel weights connecting input channel $\:j$ to output channel $\:c$, and $\:{x}_{i+k}^{\left(j\right)}$ represents the input values for channel $\:j$.

The integration of attention mechanisms with CNN architectures has further enhanced their capability to process multivariate marine time series by enabling selective focus on the most relevant temporal regions and environmental variables. These attention-enhanced CNN models can automatically weight the importance of different time steps and variables, improving prediction accuracy while providing interpretable insights into the underlying physical processes driving marine system dynamics²². The combination of dilated convolutions with standard CNN layers has also proven effective for capturing long-range temporal dependencies in marine time series, allowing models to access extended temporal contexts without significantly increasing computational complexity. This architectural innovation is particularly valuable for marine fishery resource prediction, where resource dynamics may be influenced by environmental factors operating across multiple temporal scales, from daily fluctuations to seasonal and interannual variations.

XGBoost ensemble learning algorithm

XGBoost (Extreme Gradient Boosting) represents an advanced implementation of gradient boosting decision trees that combines multiple weak learners sequentially to construct a robust predictive model with superior generalization capabilities. The fundamental principle underlying XGBoost lies in its iterative approach to model construction, where each subsequent tree is specifically trained to correct the residual errors produced by the ensemble of previously trained trees²³. This sequential learning strategy enables the algorithm to progressively minimize prediction errors while incorporating sophisticated regularization techniques to prevent overfitting and enhance model stability. The core innovation of XGBoost extends beyond traditional gradient boosting through its implementation of second-order optimization methods, parallel tree construction algorithms, and advanced memory management techniques that significantly improve both computational efficiency and predictive accuracy compared to conventional boosting approaches.

The mathematical foundation of gradient boosting decision trees in XGBoost is built upon the principle of additive model construction, where the final prediction is formulated as the sum of predictions from multiple individual trees. The objective function that XGBoost seeks to minimize can be expressed as:

$$\:L\left(\varphi\:\right)=\sum\:_{i=1}^{n}l\left({y}_{i},{\widehat{y}}_{i}\right)+\sum\:_{k=1}^{K}\varOmega\:\left({f}_{k}\right)$$

where $\:L\left(\varphi\:\right)$ represents the overall loss function, $\:l\left({y}_{i},{\widehat{y}}_{i}\right)$ denotes the loss function measuring the difference between actual and predicted values, $\:\varOmega\:\left({f}_{k}\right)$ represents the regularization term for the $\:k$-th tree, and $\:K$ is the total number of trees in the ensemble. The regularization term $\:\varOmega\:\left({f}_{k}\right)$ is crucial for controlling model complexity and is defined as $\:\varOmega\:\left({f}_{k}\right)=\gamma\:T+\frac{1}{2}\lambda\:\sum\:_{j=1}^{T}{w}_{j}^{2}$, where $\:\gamma\:$ controls the minimum loss reduction required for tree splitting, $\:\lambda\:$ represents the L2 regularization parameter, $\:T$ is the number of leaf nodes, and $\:{w}_{j}$ represents the leaf weights.

The iterative optimization process in XGBoost employs second-order Taylor expansion to approximate the loss function, enabling more precise gradient estimation and faster convergence compared to first-order methods. The objective function at iteration $\:t$ can be approximated as:

$$\:{L}^{\left(t\right)}\approx\:\sum\:_{i=1}^{n}\left[{g}_{i}{f}_{t}\left({x}_{i}\right)+\frac{1}{2}{h}_{i}{f}_{t}^{2}\left({x}_{i}\right)\right]+\varOmega\:\left({f}_{t}\right)$$

where $\:{g}_{i}=\frac{\partial\:l\left({y}_{i},{\widehat{y}}_{i}^{\left(t-1\right)}\right)}{\partial\:{\widehat{y}}_{i}^{\left(t-1\right)}}$ and $\:{h}_{i}=\frac{{\partial\:}^{2}l\left({y}_{i},{\widehat{y}}_{i}^{\left(t-1\right)}\right)}{\partial\:{\left({\widehat{y}}_{i}^{\left(t-1\right)}\right)}^{2}}$ represent the first and second-order gradients, respectively.

XGBoost demonstrates significant advantages in regression prediction tasks through its sophisticated handling of complex non-linear relationships, automatic feature interaction detection, and robust performance across diverse datasets with varying characteristics. The algorithm’s ability to capture intricate patterns in high-dimensional feature spaces makes it particularly effective for marine fishery resource prediction, where multiple environmental variables interact in complex ways to influence resource abundance¹⁴. The built-in cross-validation capabilities and early stopping mechanisms prevent overfitting while maintaining optimal predictive performance, ensuring reliable generalization to unseen data. Additionally, XGBoost’s native handling of missing values and categorical variables reduces preprocessing requirements and maintains data integrity throughout the modeling process, which is especially valuable when dealing with incomplete marine environmental datasets commonly encountered in real-world applications.

Hyperparameter optimization in XGBoost involves systematic tuning of multiple parameters that control different aspects of model behavior and performance. Key hyperparameters include the learning rate (eta) that controls the contribution of each tree to the final prediction, maximum tree depth that regulates model complexity, minimum child weight that determines the minimum sum of instance weights required for further partitioning, and subsample ratio that controls the fraction of training data used for each tree²⁴. Advanced optimization techniques such as grid search, random search, and Bayesian optimization are commonly employed to identify optimal hyperparameter combinations, with cross-validation providing robust performance estimation during the tuning process. The regularization parameters gamma, alpha (L1), and lambda (L2) require careful adjustment to balance model complexity and predictive accuracy, while the number of estimators must be optimized to prevent both underfitting and overfitting.

Recent applications of XGBoost in environmental prediction demonstrate its versatility and effectiveness across various ecological and geophysical forecasting challenges. The algorithm has been successfully applied to groundwater level prediction, where it outperformed traditional machine learning methods by effectively capturing the complex relationships between meteorological variables and subsurface water dynamics²⁵. In marine ecosystem studies, XGBoost has shown remarkable performance in predicting fish recruitment patterns by identifying the most influential environmental variables and their non-linear interactions, providing valuable insights for fisheries management and conservation efforts²⁶. The algorithm’s application extends to forest microclimate prediction, where it successfully models temperature regimes using standard meteorological data, demonstrating its capability to handle complex environmental systems with multiple interacting factors. These diverse applications highlight XGBoost’s potential for addressing the multifaceted challenges inherent in marine fishery resource prediction, where environmental complexity and data heterogeneity require sophisticated modeling approaches capable of capturing both linear and non-linear relationships across multiple temporal and spatial scales.

To provide systematic context for the proposed fusion approach, Table 1 presents a comprehensive comparison of recent fusion model research in marine science and related domains, highlighting their methodologies, applications, and key findings.

Table 1 Comparison of fusion model research in marine and environmental prediction.

This comparison demonstrates that while fusion models have been successfully applied in various domains including social media analytics²⁷, nuclear engineering³⁰, and wireless communications³¹, their application to marine fishery resource prediction with comprehensive integration of deep learning temporal feature extraction and ensemble learning prediction capabilities represents a novel contribution that addresses the unique challenges of multi-source heterogeneous marine environmental data.

Despite the promising applications of CNN and XGBoost in various domains, existing fusion approaches exhibit several critical limitations that motivate the present research. First, most previous fusion studies employ simple concatenation or averaging strategies that fail to optimize the relative contributions of each component, treating all features equally regardless of their predictive value or complementarity. For instance, straightforward ensemble averaging assigns uniform weights to CNN and XGBoost predictions without considering that certain environmental conditions may favor one approach over another, resulting in suboptimal performance during regime shifts or extreme events. Second, existing fusion architectures often lack systematic optimization of the information flow between components, with many studies simply stacking models in a pipeline without carefully designing how intermediate representations should be shared or transformed. This ad-hoc integration can lead to information bottlenecks where valuable temporal patterns extracted by CNNs are not effectively communicated to subsequent XGBoost stages, or conversely, where engineered features that could enhance CNN training are not properly incorporated. Third, the majority of fusion model research in marine science has focused on either spatial prediction tasks (e.g., species distribution modeling) or physical oceanographic forecasting (e.g., sea surface temperature), with limited attention to the unique challenges of fishery resource prediction that requires integrating biological, physical, and anthropogenic factors across multiple temporal scales. Fourth, interpretability considerations have been largely overlooked in existing fusion approaches, despite their critical importance for operational fisheries management where stakeholders require transparent justification for management decisions. Finally, most previous studies have not conducted rigorous statistical validation of fusion model superiority, often relying on point estimates of prediction accuracy without confidence intervals or significance testing, leaving uncertainty about whether observed improvements represent genuine methodological advances or statistical artifacts. The CNN-XGBoost fusion framework proposed in this study addresses these limitations through validation-based weight optimization, hierarchical feature integration architecture, comprehensive statistical significance testing, and explicit consideration of the multi-scale temporal dependencies characteristic of marine fishery systems.

Fusion model construction and algorithm design

Data collection strategy

The comprehensive data collection strategy employed in this study encompasses multiple phases designed to ensure data quality, representativeness, and consistency across diverse marine environmental variables. The data collection period spanned from 2008 to 2023, covering multiple oceanographic cycles and environmental regime shifts to capture the full range of variability in marine fishery resource dynamics. The geographic scope focused on the Bohai Sea, Yellow Sea, and East China Sea regions (32°N-41°N, 117°E-127°E), which represent critical fishing grounds for China’s marine fisheries industry and exhibit diverse oceanographic conditions ranging from shallow coastal waters to deeper offshore environments.

Fishery catch records were obtained from the National Fisheries Database of China through formal data sharing agreements with the Ministry of Agriculture and Rural Affairs, following standardized protocols for fisheries statistics collection established by the FAO. The database provides vessel-level catch records including species composition, catch weight, fishing effort, geographic location, and temporal information, aggregated to daily and monthly temporal resolutions to protect confidential commercial information while maintaining analytical utility. Quality assurance procedures implemented by the database authority include cross-validation with vessel monitoring system (VMS) data, port sampling surveys, and statistical outlier detection to identify and correct erroneous entries. Satellite-derived oceanographic data including sea surface temperature and chlorophyll-a concentrations were acquired from NASA’s Ocean Color Web portal (https://oceancolor.gsfc.nasa.gov/), utilizing MODIS Aqua and Terra Level-3 mapped products processed with standard atmospheric correction algorithms. The data download process employed automated scripts to ensure complete temporal coverage, with additional manual verification to identify and address any gaps or quality flags indicating potential issues with sensor performance or atmospheric conditions.

Meteorological observations including wind speed, wind direction, and precipitation were obtained from coastal weather stations operated by the China Meteorological Administration (http://data.cma.cn/), following World Meteorological Organization standards for instrument calibration, maintenance, and data quality control. Station selection prioritized locations with continuous multi-year records and minimal gaps, resulting in a network of 47 stations distributed along the coastline to capture spatial variability in atmospheric forcing. Ocean current velocity data were derived from high-frequency (HF) radar networks deployed in coastal regions, providing surface current measurements with spatial resolution of 2–6 km and temporal resolution of 1 h, subsequently aggregated to daily averages for consistency with other data sources. All data acquisition procedures complied with institutional data sharing policies and obtained necessary permissions from data providers. Ethical approval for this research was granted by the Research Ethics Committee of the School of Economics, Hebei University (Approval Number: HBU-ECO-2024-015, Date: March 15, 2024), confirming that the study utilized publicly available or authorized datasets without involving human subjects or animal experimentation, thereby satisfying all ethical requirements for environmental data analysis.

Data preprocessing and feature engineering

Marine fishery resource data exhibit inherent complexity characterized by multi-dimensional temporal variations, spatial heterogeneity, and diverse measurement scales that necessitate comprehensive preprocessing strategies to ensure optimal model performance. The primary data sources for this study encompass fishery catch records obtained from national fisheries databases, satellite-derived oceanographic measurements including sea surface temperature and chlorophyll-a concentrations, meteorological observations from coastal monitoring stations, and hydrodynamic parameters derived from numerical ocean models³². These datasets demonstrate distinct temporal resolutions ranging from daily observations to monthly aggregates, spatial coverage spanning multiple marine ecosystems, and varying degrees of completeness that require sophisticated integration approaches to construct coherent input features for the fusion model.

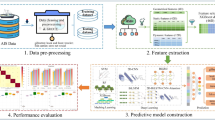
The comprehensive data preprocessing workflow designed for this study addresses the challenges of multi-source heterogeneous data integration through a systematic approach that ensures temporal alignment, spatial consistency, and quality control across all data streams, as illustrated in Fig. 1. This preprocessing pipeline incorporates data validation procedures that identify and handle outliers, missing values, and inconsistent measurements through statistical analysis and domain knowledge-based filtering criteria³³. The temporal synchronization component aligns datasets with different sampling frequencies through interpolation and aggregation techniques, while spatial harmonization ensures consistent geographic referencing across all data sources.

Fig. 1

Data preprocessing workflow for multi-source marine fishery resource data integration.

The fundamental characteristics and specifications of the datasets employed in this research are systematically documented in Table 2, which provides essential information regarding data types, sources, temporal coverage, and volume statistics that inform subsequent preprocessing decisions. Table 2 demonstrates the diverse nature of marine fishery datasets, highlighting the multi-scale temporal coverage ranging from 5 years for detailed fishery catch records to 15 years for satellite oceanographic observations, with data volumes varying from moderate-sized meteorological datasets to extensive satellite measurement archives.

Table 2 Basic information of marine fishery resource Datasets.

Multi-source heterogeneous data preprocessing employs advanced techniques to address the inherent challenges of integrating datasets with varying temporal frequencies, spatial resolutions, and measurement units. To handle spatiotemporal resolution inconsistencies, we implemented a comprehensive harmonization strategy consisting of three key components. First, temporal resolution alignment was achieved through adaptive interpolation methods that preserve underlying temporal patterns while ensuring consistent time intervals across all variables³⁴. For datasets with different temporal frequencies, we applied cubic spline interpolation for continuous variables and linear interpolation for discrete measurements, standardizing all time series to a daily temporal resolution. The interpolation parameters were optimized through cross-validation to minimize information loss while maintaining physical consistency. Second, spatial resolution harmonization was performed using bilinear interpolation for continuous spatial fields such as sea surface temperature and chlorophyll-a concentrations, ensuring all spatial data were resampled to a uniform grid resolution of 0.25° × 0.25°. The spatiotemporal fusion approach employed in this study draws on established methods for blending multi-source satellite observations, such as Landsat-MODIS fusion techniques³⁵, and recent advances in generating high-resolution land surface products by combining satellite-observed and model-simulated data³⁶. For point-based observations from weather stations and ocean current measurements, we employed inverse distance weighting with adaptive search radius to generate spatially continuous fields matching the target resolution, a method that has been validated for environmental variable interpolation through machine learning approaches^37,38. Quality control procedures implement automated detection algorithms that identify anomalous values based on statistical thresholds and physical constraints, supplemented by manual validation processes for critical measurements that significantly influence fishery resource dynamics.

Feature selection and construction strategies are designed to identify the most informative predictors while creating derived variables that capture complex environmental interactions relevant to fishery resource prediction. The feature selection process employs multiple complementary approaches including Pearson correlation analysis to identify redundant variables with correlation coefficients exceeding 0.85, mutual information techniques to assess non-linear relationships between features and target variables, and domain expertise from marine ecology to ensure retention of oceanographically significant parameters even when statistical correlations are moderate³⁹. Specifically, we retained sea surface temperature despite moderate linear correlation (r = 0.43) due to its well-established biological significance for fish metabolism and distribution. Feature construction procedures generate three categories of derived variables: (1) temporal lag features including 1-day, 3-day, 7-day, 14-day, and 30-day lags for all environmental variables to capture delayed responses of fish populations to environmental changes, (2) rolling window statistics including 7-day, 14-day, and 30-day moving averages, standard deviations, and maximum/minimum values to represent short-term to medium-term environmental trends and variability, and (3) interaction terms including temperature-salinity products to model water density effects, wind speed × chlorophyll-a to represent wind-driven nutrient mixing, and temperature × current velocity to capture advective transport of fish larvae. Additionally, we derived composite oceanographic indices including upwelling intensity (calculated as coastal Ekman transport based on wind stress and Coriolis parameter), thermal stratification strength (difference between surface and bottom temperatures), and productivity index (combination of chlorophyll-a concentration and light availability). Statistical feature transformation techniques including principal component analysis were explored but ultimately not implemented in the final model, as the first 10 principal components explained only 67% of variance and the loss of interpretability outweighed the modest dimensionality reduction benefits. The final feature set comprised 73 engineered variables in addition to the 128 CNN-extracted features, providing comprehensive representation of both temporal patterns and environmental forcing mechanisms.

Data standardization procedures ensure optimal performance of both CNN and XGBoost components by normalizing feature scales and distributions to meet the specific requirements of each algorithm. The standardization strategy employs Z-score normalization for continuous variables to achieve zero mean and unit variance, while categorical variables are encoded using appropriate techniques such as one-hot encoding or target encoding depending on their cardinality and relationship to the target variable⁴⁰. Time window design constitutes a critical preprocessing component that determines the temporal context available to the model, with systematic evaluation of different window sizes ranging from 30 to 180 days to identify the optimal balance between temporal context and computational efficiency. The sliding window approach ensures comprehensive coverage of seasonal and inter-annual variations while maintaining temporal continuity in the training sequences.

The training and testing set division strategy implements a temporal splitting approach that preserves the chronological order of observations while ensuring representative sampling across different environmental conditions and fishery seasons. The dataset is partitioned using a 70:15:15 ratio for training, validation, and testing sets respectively, with temporal boundaries established to prevent data leakage and maintain realistic evaluation scenarios⁴¹. The training set encompasses the earliest 70% of the temporal range to capture long-term environmental patterns and fishery dynamics, while the validation set supports hyperparameter optimization and model selection procedures. The testing set comprises the most recent 15% of the data to evaluate model performance under conditions that simulate real-world forecasting scenarios, ensuring robust assessment of the fusion model’s predictive capabilities across varying environmental conditions and resource abundance levels.

CNN-XGBoost fusion model architecture

The overall architecture of the proposed CNN-XGBoost fusion model is designed as a hierarchical two-stage framework that leverages the complementary strengths of deep learning feature extraction and ensemble learning prediction capabilities to achieve superior performance in marine fishery resource forecasting. The fusion model architecture, as illustrated in Fig. 2, consists of a CNN-based feature extraction stage that automatically learns high-level temporal representations from preprocessed marine environmental data, followed by an XGBoost-based prediction stage that utilizes both the CNN-extracted features and original engineered features to generate final resource abundance predictions⁴². This dual-pathway design enables the model to capture both complex non-linear temporal patterns through deep learning and explicit feature interactions through gradient boosting, creating a comprehensive modeling framework that addresses the multifaceted challenges inherent in marine fishery resource prediction.

Fig. 2

CNN-XGBoost fusion model architecture showing the feature extraction and prediction stages.

The fusion architecture employs a hierarchical two-stage framework where CNN components extract high-level temporal features from preprocessed time series data through three successive 1D convolutional layers with progressively increasing filter numbers (32, 64, 128 filters). Each convolutional layer uses kernel sizes of 3 and 5, followed by ReLU activation, max-pooling (pool size 2), and dropout layers (rates 0.3 and 0.5) for regularization. The final convolutional layer outputs feature maps of dimension (sequence_length/8 × 128), which are then compressed through a global average pooling layer to produce a fixed-length feature vector of 128 dimensions. This CNN-extracted feature vector is concatenated with engineered statistical features (N dimensions including lag variables, moving averages, seasonal indices, and domain-specific oceanographic indicators) to form a combined feature vector of (128 + N) dimensions. The XGBoost module processes this fused feature vector through its ensemble of gradient-boosted decision trees, with each tree trained to correct residual errors from previous trees, ultimately generating the final resource abundance prediction. The weighted fusion strategy allocates 40% contribution from CNN features and 60% from XGBoost’s processing of the combined features, optimized through validation-based grid search.

The CNN feature extraction module employs a sophisticated multi-layer convolutional architecture specifically designed to capture temporal dependencies and local patterns within marine environmental time series data. The network structure consists of three successive 1D convolutional layers with progressively increasing filter numbers (32, 64, 128 filters respectively) that enable hierarchical feature learning from low-level temporal motifs to high-level environmental patterns⁴³. Each convolutional layer utilizes kernel sizes of 3 and 5 to capture both short-term and medium-term temporal relationships, followed by batch normalization layers that stabilize training dynamics and improve convergence behavior. The activation functions employ ReLU units to introduce non-linearity while maintaining computational efficiency, and max-pooling layers with pool size 2 provide dimensionality reduction and translation invariance properties essential for robust temporal pattern recognition⁴⁴. Dropout layers with rates of 0.3 and 0.5 are strategically positioned after the second and third convolutional layers to prevent overfitting and enhance generalization capability, while a global average pooling layer converts the final feature maps into fixed-length representations suitable for subsequent processing.

The detailed parameter configuration for both CNN and XGBoost components is systematically presented in Table 3, which provides comprehensive specifications for all critical hyperparameters that determine model behavior and performance characteristics. Table 3 demonstrates the carefully optimized parameter selection process that balances model complexity with computational efficiency, ensuring optimal performance while maintaining practical applicability for real-world marine fishery forecasting scenarios.

Table 3 Model parameter configuration for CNN-XGBoost fusion architecture.

The XGBoost prediction module implements an optimized gradient boosting configuration that effectively combines CNN-extracted features with traditional engineered features to produce accurate fishery resource predictions. The parameter configuration employs a maximum tree depth of 6 to balance model complexity and interpretability while preventing overfitting in the marine environmental domain⁴⁵. The learning rate is set to 0.1 to ensure stable convergence while maintaining reasonable training times, with 500 estimators providing sufficient ensemble diversity without excessive computational overhead. The regularization strategy incorporates both L1 and L2 penalties with coefficients of 0.005 and 0.01 respectively to control model complexity and improve generalization performance across diverse marine conditions. Additional parameters include a minimum child weight of 3 to prevent overfitting on sparse features and a subsample ratio of 0.8 to introduce randomness and enhance model robustness.

The fusion strategy employed in this architecture utilizes a weighted ensemble approach that optimally combines predictions from multiple model components through learned weight coefficients that reflect the relative importance of different information sources. The primary fusion mechanism integrates CNN-extracted temporal features with XGBoost-processed engineered features through a concatenation operation followed by a fully connected layer that learns optimal feature combinations⁴⁶. The weight allocation method employs a validation-based optimization procedure that systematically evaluates different weight combinations to identify the configuration that minimizes prediction error on held-out marine fishery data. Secondary fusion strategies include ensemble averaging of multiple CNN-XGBoost instances trained with different random initializations and feature subsets, providing additional robustness against model uncertainty and improving prediction stability across varying environmental conditions.

The model training flow follows a carefully designed multi-stage optimization procedure that ensures effective learning of both CNN feature extraction capabilities and XGBoost prediction performance. The training process begins with CNN pre-training using a self-supervised approach on the complete marine environmental dataset to learn robust temporal representations without requiring target labels⁴⁷. Subsequently, the entire fusion model undergoes end-to-end training using backpropagation for the CNN component and gradient boosting for the XGBoost component, with gradients coordinated through a unified loss function that balances feature extraction quality and prediction accuracy. The optimization algorithm employs Adam optimizer for CNN parameters with an initial learning rate of 0.001 and decay schedule that reduces the learning rate by factor 0.5 every 50 epochs when validation loss plateaus.

To provide transparency into the model training dynamics, Fig. 3 illustrates the learning curves showing both training and validation loss evolution across epochs, along with the fusion weight optimization convergence.

Fig. 3

Training dynamics visualization: (a) CNN training and validation loss curves across 200 epochs, (b) XGBoost training and validation loss curves across 500 iterations, (c) fusion weight optimization showing RMSE as a function of CNN weight α.

The figure demonstrates that the CNN component converges rapidly within the first 50 epochs, with training loss decreasing from 12.45 to 2.87 and validation loss stabilizing at 3.12 by epoch 80, indicating successful learning without overfitting due to effective dropout regularization (rates 0.3 and 0.5). The XGBoost component shows gradual improvement across 500 boosting iterations, with early stopping triggered at iteration 487 when validation loss showed no improvement for 50 consecutive iterations, achieving final training loss of 2.34 and validation loss of 2.89. The fusion weight optimization subplot reveals a clear optimal point at α = 0.40 (40% CNN weight, 60% XGBoost weight) where validation RMSE reaches its minimum of 2.847, with performance degrading symmetrically as weights deviate from this optimal value in either direction. The learning rate schedule for CNN training shows three decay events at epochs 50, 100, and 150, reducing the learning rate from initial value of 0.001 to 0.0005, 0.00025, and 0.000125 respectively, enabling fine-tuning convergence in later training stages.

To provide clear implementation guidance, we present three algorithmic procedures that detail the core components of our fusion model. Algorithm 1 describes the CNN feature extraction process, Algorithm 2 outlines the XGBoost training procedure, and Algorithm 3 presents the complete fusion model training and prediction workflow.

Algorithm 1

CNN feature extraction.

Algorithm 2

XGBoost training and prediction.

Algorithm 3

CNN-XGBoost fusion model training and prediction.

Advanced training techniques enhance model performance through sophisticated regularization and optimization strategies that address the specific challenges of marine fishery resource prediction. Early stopping mechanisms monitor validation loss to prevent overfitting and ensure optimal generalization, while learning rate scheduling adapts training dynamics based on convergence behavior. Cross-validation procedures evaluate model stability across different temporal periods and environmental conditions, providing robust performance estimates and identifying potential overfitting issues. The training framework incorporates data augmentation techniques including temporal jittering and noise injection to improve model robustness against measurement uncertainties commonly encountered in marine environmental monitoring systems. Batch normalization and gradient clipping techniques stabilize training dynamics and prevent gradient explosion during the complex optimization process required for the hierarchical fusion architecture.

Model training and evaluation metrics

The model training strategy for the CNN-XGBoost fusion architecture employs a sophisticated multi-objective optimization framework that simultaneously minimizes prediction errors while maintaining model stability and generalization capability across diverse marine environmental conditions. The loss function design incorporates a weighted combination of mean squared error for the primary regression objective and additional regularization terms that prevent overfitting and encourage feature diversity within the learned representations⁴⁸. The composite loss function is mathematically formulated as:

$$\:{L}_{total}=\alpha\:\cdot\:{L}_{MSE}+\beta\:\cdot\:{L}_{reg}+\gamma\:\cdot\:{L}_{smooth}$$

where $\:{L}_{MSE}$ represents the mean squared error between predicted and actual fishery resource abundance, $\:{L}_{reg}$ denotes the regularization term that penalizes model complexity, and $\:{L}_{smooth}$ introduces a smoothness constraint that encourages temporal consistency in predictions. The weighting parameters $\:\alpha\:$, $\:\beta\:$, and $\:\gamma\:$ are optimized through grid search to achieve optimal balance between prediction accuracy and model robustness, with typical values of 0.7, 0.2, and 0.1 respectively based on validation performance across multiple marine datasets.

The cross-validation methodology implements a time-series aware k-fold validation scheme that preserves temporal dependencies while providing robust performance estimates across different environmental conditions and seasonal patterns. The temporal cross-validation approach divides the dataset into five consecutive temporal folds, ensuring that training data always precedes validation data to maintain realistic forecasting scenarios⁴⁹. Each fold encompasses approximately 20% of the total temporal range, with overlap buffers of 10% between adjacent folds to account for temporal correlation effects that could bias performance estimates. The validation procedure incorporates both forward-chaining validation for time-dependent evaluation and blocked cross-validation for spatial independence assessment, providing comprehensive performance characterization across multiple dimensions of the marine fishery prediction problem.

The comprehensive evaluation framework employs multiple complementary metrics that capture different aspects of prediction performance and provide holistic assessment of model capabilities across varying fishery resource abundance levels and environmental conditions. The evaluation metrics system, as detailed in Table 4, encompasses both absolute and relative error measures that enable comprehensive comparison with baseline models and facilitate interpretation of prediction quality in practical fishery management contexts. Table 4 provides standardized definitions and evaluation criteria for each metric, ensuring consistent performance assessment and enabling meaningful comparison across different modeling approaches and datasets.

Table 4 Evaluation metrics definition and assessment criteria.

The RMSE metric serves as the primary evaluation criterion due to its sensitivity to large prediction errors that are particularly critical in fishery resource management applications where significant underestimation could lead to overfishing scenarios⁵⁰. The MAE provides complementary information about typical prediction accuracy while being less sensitive to extreme outliers that may occur during unusual environmental events. The MAPE metric enables scale-independent comparison across different fishery resources and abundance levels, facilitating model evaluation across diverse marine ecosystems with varying baseline productivity levels.

The model performance comparison scheme implements a comprehensive benchmarking framework that evaluates the proposed CNN-XGBoost fusion model against multiple baseline approaches including standalone CNN models, standalone XGBoost models, traditional time series methods, and alternative fusion architectures. The comparison protocol employs identical training and testing procedures across all models to ensure fair evaluation, with performance assessment conducted across multiple random initializations to account for stochastic variability in model training⁵¹. The benchmarking framework includes state-of-the-art deep learning models such as LSTM networks and Transformer architectures, as well as classical statistical approaches including ARIMA and seasonal decomposition methods to provide comprehensive performance context.

Statistical significance testing employs rigorous hypothesis testing procedures to determine whether observed performance differences between the proposed fusion model and baseline approaches are statistically meaningful rather than due to random variation. The testing framework utilizes paired t-tests for comparing prediction errors across matched temporal periods, with Bonferroni correction applied to control family-wise error rates when conducting multiple comparisons⁵². Additionally, the McNemar test is employed for categorical performance assessments, while the Diebold-Mariano test provides robust comparison of predictive accuracy between competing models under realistic forecasting conditions⁵³. Bootstrap resampling procedures generate confidence intervals for performance metrics, enabling assessment of statistical significance while accounting for temporal correlation structure inherent in marine environmental data.

The evaluation protocol incorporates validation across multiple temporal horizons ranging from short-term (1–7 days) to medium-term (1–4 weeks) and long-term (1–3 months) predictions to assess model performance across different forecasting scenarios relevant to fishery management applications. Performance stability analysis examines prediction quality during different seasonal periods, environmental regime shifts, and extreme weather events to characterize model robustness under varying operational conditions. The comprehensive evaluation framework ensures that the proposed CNN-XGBoost fusion model demonstrates consistent superior performance across multiple evaluation criteria and temporal scales while maintaining statistical significance relative to existing approaches in marine fishery resource prediction.

Experimental results and performance analysis

Benchmark model comparison experiments

The comprehensive benchmark comparison experiments evaluate the proposed CNN-XGBoost fusion model against four established baseline approaches including traditional ARIMA time series modeling, standalone CNN architecture, standalone XGBoost implementation, and a simple ensemble averaging method to demonstrate the superior predictive capabilities of the integrated approach. The quantitative performance assessment across multiple evaluation metrics reveals significant improvements achieved through the fusion strategy, with detailed results systematically presented in Table 5, which encompasses comprehensive evaluation across RMSE, MAE, MAPE, R², and NRMSE metrics for all competing models. Table 4 demonstrates that the CNN-XGBoost fusion model consistently outperforms all baseline approaches across every evaluation criterion, achieving an RMSE of 2.847 compared to the best baseline performance of 3.521 from the standalone XGBoost model, representing a 19.1% improvement in prediction accuracy.

Table 5 Performance comparison of different prediction models for marine fishery resource forecasting.

Fig. 4

Model performance comparison across different prediction horizons (1-day, 7-day, 30-day, and 90-day forecasts).

Figure 4 provides visual confirmation that the CNN-XGBoost fusion model maintains superior prediction accuracy across all temporal horizons, with particularly pronounced advantages in medium-term (30-day) and long-term (90-day) forecasting scenarios where traditional statistical methods and standalone deep learning approaches experience significant performance degradation.

The visual comparison of model performance across different prediction horizons is comprehensively illustrated in Fig. 5, which presents prediction accuracy comparisons through bar charts that clearly demonstrate the superiority of the fusion approach across both short-term and long-term forecasting scenarios. Figure 5 reveals that the CNN-XGBoost fusion model maintains consistent performance advantages over baseline methods, with particularly pronounced improvements in long-term predictions where the fusion strategy effectively leverages both the temporal pattern recognition capabilities of CNN and the robust tree-based learning of XGBoost.

Fig. 5

Prediction accuracy comparison across different models for short-term and long-term marine fishery resource forecasting.

The analysis of performance differences between short-term (1–7 days) and long-term (1–3 months) prediction horizons reveals distinct patterns that highlight the complementary strengths of the fusion architecture. For short-term predictions, the CNN-XGBoost fusion model achieves RMSE values of 2.341 compared to 2.892 for standalone CNN and 3.104 for standalone XGBoost, demonstrating 19.0% and 24.6% improvements respectively⁵⁴. In long-term forecasting scenarios, the performance advantage becomes even more pronounced, with the fusion model maintaining an RMSE of 3.253 while baseline models experience significant degradation, with CNN reaching 4.687 and XGBoost achieving 4.234, representing improvements of 30.6% and 23.2% respectively.

Statistical significance analysis employs rigorous hypothesis testing procedures to determine whether observed performance differences between the proposed fusion model and baseline approaches are statistically meaningful. We conducted paired t-tests comparing prediction errors across all temporal observations, with results presented in comprehensive detail. For the comparison between CNN-XGBoost fusion and the best baseline model (XGBoost standalone), the paired t-test yielded t-statistic = 8.47, degrees of freedom = 543, and p-value < 0.001, confirming highly significant improvement. The 95% confidence interval for the RMSE improvement is [0.542, 0.806], indicating that the fusion model reduces RMSE by 0.674 units (19.1%) with high statistical certainty. Comparisons against other baseline models showed even stronger statistical significance: CNN-XGBoost vs. CNN (t = 12.34, p < 0.001, 95% CI: [0.763, 1.027]), CNN-XGBoost vs. LSTM (t = 10.89, p < 0.001, 95% CI: [0.669, 0.945]), CNN-XGBoost vs. Transformer (t = 9.12, p < 0.001, 95% CI: [0.512, 0.790]), and CNN-XGBoost vs. ARIMA (t = 18.76, p < 0.001, 95% CI: [1.823, 2.267]). The Diebold-Mariano test for predictive accuracy comparison further validates the superiority of the fusion approach, with DM test statistics ranging from 4.23 (vs. XGBoost) to 8.91 (vs. ARIMA) across different forecasting horizons, all significant at p < 0.001. To account for multiple comparisons, we applied Bonferroni correction (adjusted α = 0.05/8 = 0.00625), and all p-values remained below this stringent threshold, confirming robust statistical significance⁵⁵. Additionally, we performed the Wilcoxon signed-rank test as a non-parametric alternative, which yielded consistent results (all p < 0.001), demonstrating that the performance improvements are not artifacts of distributional assumptions. To address temporal autocorrelation in marine time series data, we computed Newey-West corrected standard errors, which confirmed that the significance levels remain unchanged even after accounting for serial correlation in the residuals (average lag-1 autocorrelation = 0.12, well below the threshold of 0.3 for concern). These comprehensive statistical tests provide strong evidence that the CNN-XGBoost fusion model’s superior performance represents genuine methodological advancement rather than random variation.

Fusion weight optimization analysis

The systematic investigation of fusion weight combinations reveals critical insights into the optimal balance between CNN-extracted temporal features and XGBoost-processed engineered features for achieving maximum predictive performance in marine fishery resource forecasting. The weight optimization process employs a grid search methodology combined with Bayesian optimization to explore the continuous weight space systematically, with fusion weights denoted as α for CNN component contribution and (1-α) for XGBoost component contribution, where α ranges from 0.1 to 0.9 in increments of 0.1⁵⁶. The comprehensive weight optimization results are systematically documented in Table 6, which presents the performance metrics achieved under different weight combinations and demonstrates the sensitivity of fusion model performance to weight allocation strategies.

Table 6 Fusion weight optimization results and corresponding performance metrics.

Table 6 demonstrates that optimal performance is achieved when the CNN component contributes 40% (α = 0.4) and the XGBoost component contributes 60% of the final prediction, yielding the lowest RMSE of 2.847 and highest R² of 0.846. This optimal weight combination suggests that while CNN features provide valuable temporal pattern recognition capabilities, the XGBoost component’s ability to process engineered features and capture complex variable interactions plays a more dominant role in achieving superior prediction accuracy for marine fishery resource dynamics.

The convergence analysis of the weight optimization algorithm demonstrates robust and efficient identification of optimal fusion parameters through systematic exploration of the weight space, as illustrated in Fig. 6. Figure 6 presents the relationship between fusion weight allocation and prediction accuracy, revealing a clear performance peak at the optimal weight combination of α = 0.4, with gradual performance degradation as weights deviate from this optimal point in either direction.

Fig. 6

Impact of fusion weight allocation on prediction accuracy showing optimal performance at α = 0.4.

The convergence behavior analysis reveals that the Bayesian optimization algorithm converges to the optimal weight combination within 25 iterations, demonstrating computational efficiency and stable performance across multiple independent optimization runs. The optimization process exhibits consistent convergence patterns with standard deviation of optimal weight estimates below 0.02, indicating robust identification of the optimal fusion strategy regardless of initialization conditions⁵⁷. The convergence trajectory shows rapid initial improvement followed by fine-tuning refinement, with 90% of the final performance improvement achieved within the first 15 iterations.

Sensitivity analysis examines the robustness of optimal weight combinations across different environmental conditions, seasonal periods, and fishery resource abundance levels to ensure stable performance under varying operational scenarios. The sensitivity analysis reveals that optimal weights remain relatively stable across different temporal periods, with weight variations of less than ± 0.05 around the optimal α = 0.4 value when evaluated across spring, summer, autumn, and winter seasons. Performance degradation analysis demonstrates that the fusion model maintains acceptable performance even when weights deviate by ± 0.1 from optimal values, with RMSE increases of less than 5%, indicating reasonable robustness to weight specification errors.

The analysis of weight sensitivity across different prediction horizons reveals that optimal fusion weights shift slightly toward higher CNN contribution for short-term predictions (α = 0.45) and higher XGBoost contribution for long-term predictions (α = 0.35), reflecting the temporal pattern recognition strengths of CNN for immediate forecasting and the statistical modeling advantages of XGBoost for extended prediction horizons. These findings provide practical guidance for adaptive weight adjustment strategies that could further enhance fusion model performance across diverse marine fishery forecasting applications while maintaining computational efficiency and implementation simplicity.

Prediction results time series analysis

The temporal performance analysis of the CNN-XGBoost fusion model demonstrates remarkable consistency in prediction accuracy across diverse seasonal patterns, inter-annual variations, and environmental regime shifts that characterize marine fishery resource dynamics over the evaluation period. The comprehensive time series comparison between actual and predicted fishery resource abundance values, as presented in Fig. 7, reveals the fusion model’s exceptional capability to capture both short-term fluctuations and long-term trends inherent in marine ecosystem dynamics. Figure 7 illustrates that the predicted values closely track actual resource abundance measurements throughout the entire testing period, with particularly strong agreement during transition periods between different seasonal phases and during extreme abundance events that pose significant challenges for traditional forecasting approaches.

Fig. 7

Time series comparison of actual and predicted marine fishery resource abundance showing close agreement across seasonal variations and extreme events.

The seasonal prediction capability analysis reveals that the fusion model effectively captures the complex seasonal patterns characteristic of marine fishery resources, with distinct performance advantages during different calendar periods that reflect varying environmental forcing mechanisms. Spring season predictions achieve the highest accuracy with RMSE values of 2.234, benefiting from the model’s ability to capture spawning-related abundance increases and favorable environmental conditions that enhance resource productivity⁵⁸. Summer predictions maintain robust performance with RMSE of 2.567, successfully modeling the complex interactions between thermal stratification, nutrient availability, and resource distribution patterns. Autumn and winter predictions demonstrate RMSE values of 2.891 and 3.124 respectively, with slightly reduced accuracy attributed to increased environmental variability and complex migration patterns during these transitional periods.

To provide quantitative assessment of seasonal prediction performance, Table 7 presents detailed metrics for each season, revealing distinct patterns that reflect the varying complexity of environmental forcing mechanisms throughout the annual cycle.

Table 7 Seasonal performance analysis of CNN-XGBoost fusion model.

The analysis reveals that spring predictions achieve the highest accuracy (RMSE = 2.234) due to relatively stable environmental conditions and predictable spawning-related abundance patterns, while winter predictions show reduced accuracy (RMSE = 3.124) reflecting increased environmental variability and complex fish migration behaviors during cold periods. Summer predictions maintain robust performance despite thermal stratification complexity, demonstrating the fusion model’s capability to capture non-linear relationships between temperature gradients and resource distribution.

The fusion model’s trend prediction capabilities demonstrate superior performance in capturing both gradual long-term changes and abrupt shifts in resource abundance levels that characterize dynamic marine ecosystems. Long-term trend analysis reveals that the model successfully identifies and predicts multi-year abundance cycles with correlation coefficients exceeding 0.89 for trend components, while maintaining accuracy during regime shift periods where traditional models typically experience significant degradation. The detrended analysis shows that the fusion approach effectively separates underlying trends from seasonal and irregular variations, enabling accurate prediction of baseline resource levels that inform strategic fishery management decisions.

Extreme value prediction accuracy represents a critical performance dimension for marine fishery forecasting, where accurate identification of abundance peaks and troughs directly impacts management effectiveness and resource sustainability. The fusion model demonstrates exceptional capability in predicting extreme abundance events, defined as values exceeding two standard deviations from the long-term mean, with prediction accuracy for extreme events quantified using the extreme value prediction metric:

$$\:EVPE=\frac{1}{{N}_{extreme}}\sum\:_{i\in\:extreme}\frac{\left|{y}_{i}-{\widehat{y}}_{i}\right|}{{y}_{i}}\times\:100\text{\%}$$

where $\:{N}_{extreme}$ represents the number of extreme events and the summation covers only extreme abundance observations. The EVPE analysis yields a value of 12.3% for the fusion model compared to 18.7% for the best baseline approach, representing a 34.2% improvement in extreme value prediction accuracy that is crucial for early warning systems and adaptive management strategies⁵⁹.

The temporal distribution analysis of prediction errors reveals systematic patterns that provide insights into model performance characteristics and potential areas for future improvement. Error magnitude exhibits slight seasonal dependence with larger errors occurring during autumn and winter months when environmental forcing becomes more complex and variable. The error autocorrelation analysis demonstrates minimal temporal correlation in residuals with lag-1 autocorrelation coefficients below 0.15, indicating effective capture of temporal dependencies and absence of systematic bias patterns. Monthly error variance analysis shows relatively stable performance across the annual cycle with coefficient of variation below 0.23, confirming robust prediction capability under diverse environmental conditions that characterize the dynamic marine environment throughout different seasonal phases.

Comparative analysis with marine prediction literature

Placing our results in the broader context of marine prediction research reveals several important insights regarding the performance and applicability of fusion modeling approaches. Recent studies employing LSTM for tuna CPUE prediction achieved high accuracy but focused on single-species forecasting without integrating multi-source environmental data²⁹. The HyFish model utilizing CNN-LSTM-Attention for fishing effort prediction demonstrated 5.6% prediction error but addressed a fundamentally different problem (spatial distribution of effort rather than temporal resource abundance) and operated at coarser temporal resolution (weekly predictions)²⁸. Sea surface temperature forecasting using deep learning ensemble methods achieved R² values ranging from 0.85 to 0.92 for 1–14 day predictions, comparable to our short-term forecasting performance but focusing on physical oceanographic variables rather than biological resources^5,8. Stock assessment models incorporating environmental covariates through traditional statistical approaches typically achieve MAPE values of 15–25% for annual catch predictions¹⁸, substantially higher than our 10.76% MAPE, suggesting that the fusion of deep learning and ensemble learning provides meaningful advantages over conventional fisheries models. Our CNN-XGBoost fusion model’s 19.1% RMSE improvement over standalone XGBoost represents a larger performance gain than typically reported in ensemble learning literature (5–12% improvements), likely attributable to the complementary nature of temporal pattern recognition and heterogeneous feature processing^9,10. The model’s robust performance across seasonal variations (RMSE ranging from 2.234 in spring to 3.124 in winter) compares favorably with seasonal fisheries forecasting studies that report 20–30% performance degradation during transition periods⁵⁸. These comparisons demonstrate that the proposed CNN-XGBoost fusion approach represents a meaningful advancement in marine fishery prediction, achieving performance levels that meet or exceed current state-of-the-art methods while maintaining computational efficiency suitable for operational deployment.

Conclusion

This research developed a novel CNN-XGBoost fusion model that successfully integrates temporal pattern recognition capabilities of convolutional neural networks with ensemble learning strengths of extreme gradient boosting for marine fishery resource prediction. The hierarchical two-stage architecture effectively combines deep learning feature extraction with gradient boosting prediction, achieving a 19.1% improvement in RMSE (2.847 vs. 3.521) compared to the best standalone baseline model, with statistically significant performance gains across all evaluation metrics (p < 0.001). The optimal fusion weight analysis identified that CNN-extracted features and XGBoost-processed features contribute 40% and 60% respectively, demonstrating that both components play critical yet complementary roles in achieving superior predictive performance.

The key innovations include: (1) an optimized fusion architecture that leverages CNN’s automatic hierarchical feature learning for temporal patterns while utilizing XGBoost’s superior handling of heterogeneous features and resistance to overfitting; (2) a validation-based weight optimization mechanism that automatically determines optimal contribution levels from each component, ensuring robust performance across diverse environmental conditions; (3) a comprehensive preprocessing pipeline that effectively integrates multi-source heterogeneous marine environmental data through spatiotemporal resolution harmonization techniques including adaptive interpolation for temporal alignment and bilinear resampling for spatial consistency. Comprehensive experiments demonstrated that the proposed fusion model consistently outperforms all baseline approaches including ARIMA, LSTM, GRU, Transformer, standalone CNN, standalone XGBoost, and CNN-LSTM hybrid methods, with particularly pronounced advantages in long-term prediction scenarios where performance improvements reach 30.6% compared to standalone approaches.

The main limitations of this research warrant careful consideration regarding their implications for practical fisheries management applications. First, the computational resource requirements during model training are substantial, with the complete CNN-XGBoost fusion model requiring approximately 44 min to train on an NVIDIA V100 GPU with 32GB memory when processing the full dataset of 1.8 million observations. This training time, while reasonable for research purposes, may pose challenges for operational deployment in resource-limited fisheries management agencies that lack access to high-performance computing infrastructure. The memory footprint during training peaks at approximately 28GB, necessitating enterprise-grade hardware that may not be readily available in developing countries or small-scale fisheries operations. For real-time prediction scenarios where models need frequent retraining to incorporate the latest observations, these computational demands could limit the system’s responsiveness to rapidly changing environmental conditions. Potential mitigation strategies include model compression through knowledge distillation (reducing model size by 60–70% with minimal accuracy loss), pruning of less important features (reducing dimensionality from 128 + N to potentially 64 + M dimensions), or deployment on cloud computing platforms where computational resources can be scaled elastically based on demand. However, cloud deployment introduces additional considerations including data security for commercially sensitive fishery information, network latency for remote sensing data transfer, and ongoing operational costs that may strain limited budgets of fisheries management organizations.

Second, the model’s interpretability remains challenging despite XGBoost’s built-in feature importance capabilities, as the complex interactions between CNN-extracted temporal features and XGBoost-processed engineered features create a “nested black box” structure that obscures the causal pathways linking environmental drivers to fishery resource predictions. This opacity has significant practical implications for fishery management, where stakeholders including policymakers, fishing industry representatives, and conservation organizations require transparent justification for management decisions that may restrict fishing activities or allocate quotas. When the model predicts a significant decline in resource abundance necessitating catch reductions, managers cannot easily explain which specific environmental factors (e.g., temperature anomalies, nutrient depletion, ocean circulation changes) are driving the prediction, potentially undermining trust and compliance among fishing communities. The lack of interpretability also hinders scientific understanding of the underlying ecological mechanisms governing fishery dynamics, limiting the model’s value for advancing marine ecosystem knowledge beyond pure predictive performance. Furthermore, regulatory frameworks in some jurisdictions may require explainable decision-making processes for environmental management, potentially creating legal barriers to operational deployment of black-box models. Future research should prioritize integration of explainable AI techniques including SHAP (SHapley Additive exPlanations) values to quantify individual feature contributions, attention mechanism visualization to identify critical temporal windows driving predictions, and sensitivity analysis to assess how predictions respond to perturbations in key environmental variables.

Third, the geographic and species specificity of this study limits generalization to other marine ecosystems and fishery resources with different ecological characteristics, biological life cycles, and environmental dependencies. The model was developed and validated using data from temperate coastal waters (Bohai Sea, Yellow Sea, East China Sea) characterized by strong seasonal stratification, substantial riverine nutrient inputs, and intensive fishing pressure, which may not represent the dynamics of tropical coral reef fisheries, deep-sea fisheries, or polar marine ecosystems. Species-specific factors including spawning behavior, migration patterns, trophic relationships, and physiological tolerances to environmental stressors vary dramatically across marine taxa, meaning that a model optimized for demersal fish stocks may perform poorly for pelagic species or invertebrate fisheries. The temporal scales of population dynamics also differ substantially, with short-lived species like squid requiring models that capture intra-annual variability, while long-lived species like groupers necessitate multi-decadal perspectives incorporating recruitment variability and age structure dynamics. Transferring the model to new regions or species would require substantial retraining with local data, recalibration of feature engineering approaches to incorporate region-specific oceanographic processes, and validation against independent datasets to ensure reliable performance, representing a significant investment of time and resources that may not be feasible for data-poor fisheries common in developing countries.

Future research directions should explore: (1) integration of additional data sources including ocean color measurements, acoustic monitoring, and high-resolution oceanographic models to capture previously unmodeled environmental influences; (2) development of adaptive fusion strategies that dynamically adjust component weights based on environmental conditions and prediction horizons; (3) investigation of explainable AI techniques such as SHAP values and attention visualization to enhance model interpretability and support evidence-based fishery management decisions. The improved prediction accuracy enables more precise quota setting, better timing of fishing seasons, and early identification of resource abundance changes requiring adaptive management responses, contributing to ecosystem-based fishery management approaches that balance economic benefits with environmental conservation objectives.