Introduction

Research background and motivations

Childhood is the key stage of physical development and healthy growth, and physical quality has a far-reaching impact on the future health of individuals during this period. Good physical fitness can improve children’s immunity and ability to resist diseases while promoting the healthy development of their psychological and social abilities1,2,3. Therefore, it is significant for parents, educational institutions, and relevant government departments to accurately and scientifically evaluate children’s physical fitness accurately and scientifically. With the rapid development of artificial intelligence (AI) technology, data mining and machine learning methods provide new means for analyzing and modeling complex data4. self-organizing maps (SOM) neural network is an unsupervised learning algorithm, which can reduce and classify data in high-dimensional space, and better extract potential patterns from data through cluster analysis. This method provides a new idea for evaluating children’s physical fitness.

Traditional evaluation methods cannot fully deal with complex multidimensional data. However, the SOM neural network combined with cluster analysis can improve the accuracy of classification and evaluation while maintaining data characteristics. Through the analysis of a large number of children’s physical fitness data, this study hopes to provide reliable data support for individualized evaluation and intervention.

Research objectives

  1. (1)

    An evaluation model of children’s physical fitness is constructed based on the SOM neural network.

  2. (2)

    Classification and characteristic analysis of children’s physical fitness combined with cluster analysis.

  3. (3)

    The evaluation method of children’s physical fitness is optimized, improving the comprehensiveness and accuracy of the evaluation.

In short, this study intends to explore a more effective evaluation method of children’s physical fitness by combining SOM neural networks with cluster analysis. Meanwhile, it improves the accuracy and comprehensiveness of the evaluation results, promoting the scientific process of children’s health evaluation and management.

Literature review

In previous studies, Johnstone et al.5 found that the traditional evaluation methods of children’s physical fitness mainly focused on single indicators such as strength, speed, and flexibility, and often ignored the integrity of physical fitness. They put forward a comprehensive evaluation system based on multi-dimensional indicators. Still, this system had shortcomings in complex data processing5. Aubert et al. (2022) argued that there were regional and individual differences in the evaluation criteria of children’s physical fitness, and it was difficult to capture the diversity of children’s groups by a single statistical analysis method. They suggested that more multivariate statistical models should be used to improve the comprehensiveness of evaluation6. Conger et al.7 found that the SOM neural network had strong dimensionality reduction and classification ability in medical and health data analysis, and could effectively identify potential structures in high-dimensional data. They used the SOM network to group patients’ data, proving its superiority in classification7. Chan et al.8 pointed out that the application of the SOM neural network in children’s health assessment was limited, but it had great potential in nonlinear data modeling and processing. Through experiments, the SOM neural network was successfully applied to the classification of children’s health data, and satisfactory results were achieved8. Wunsch et al.9 discovered that cluster analysis technology could be effectively applied to analyze children’s health data. By clustering children’s data, the characteristics of different health groups were found, and corresponding health intervention measures were proposed9. Rhodes et al. (2022) found that combining cluster analysis could better reveal the health characteristics of different groups of children. Furthermore, through hierarchical cluster analysis technology, a large number of children’s physical fitness data were processed, and a clear group classification result was obtained, which provided data support for personalized health guidance10.

Compared to previous studies, this study introduces innovations in both methodology and evaluation systems. Most past studies have relied on traditional linear statistical methods or single-dimensional fitness evaluation indicators, such as strength, speed, and flexibility. While these methods may apply to specific dimensions, they fail to provide a comprehensive reflection of children’s overall health, overlooking the importance of multidimensional evaluation. Moreover, relying on single indicators can lead to a one-sided and static understanding of children’s physical fitness, making it difficult to reveal individual differences and diversity. In contrast, this study not only focuses on individual dimensions of physical fitness but also incorporates factors closely related to children’s growth, such as mental health and nutritional status, into the evaluation system. It develops a multidimensional and dynamic health evaluation framework. Furthermore, by combining SOM neural networks with cluster analysis and other data mining techniques, this study overcomes the limitations of traditional linear methods. It achieves dimensionality reduction and refined classification analysis of high-dimensional health data. This method is more effective in uncovering hidden patterns in children’s health data, offering a more scientific, comprehensive, and personalized physical fitness evaluation.

In summary, this study surpasses traditional research in evaluation dimensions, methodological choices, and result refinement. It provides new ideas and tools for dynamic monitoring and comprehensive intervention of children’s physical fitness, with significant theoretical and practical value.

Research methodology

Application of SOM neural network in data dimension reduction and classification

SOM is a neural network algorithm based on unsupervised learning, which maps high-dimensional input data into low-dimensional space through the self-organization characteristics of data, forming a mapping relationship with topological structure11,12,13. Its core goal is to preserve the topological relationship between input data. In other words, similar data points should be as close as possible in the mapped space, thus revealing the potential structure and mode of data. The SOM neural network has powerful data dimensionality reduction and classification ability, especially when dealing with high-dimensional data, it can effectively reduce the data dimensionality to two-dimensional (2D) or three-dimensional space by topology preservation, and show the potential structure of the data by visual means14,15. Its specific application is exhibited in (Table 1):

Table 1 Application of SOM in data dimension reduction and classification.
Full size table

In one word, applying the SOM neural network in data dimension reduction and classification has important theoretical and practical value. Especially, when handling complex high-dimensional data, it provides an effective way to reveal the potential patterns of data, and it is easy to understand and analyze through visual means. This makes the SOM neural network widely used in many fields, including health management, image processing, and market analysis18,19,20.

Application of cluster analysis in health data

Cluster analysis is an unsupervised learning method that aims to group samples in a dataset based on their similarity, thus forming multiple categories or “clusters”. In cluster analysis, similarity is usually judged through a distance measure that maximizes the similarity between samples within a cluster and minimizes the similarity between different clusters. Specifically, the goal of cluster analysis is:

  1. (1)

    Intra-class compactness: Samples within a cluster are close to each other and have a high degree of similarity.

  2. (2)

    Inter-class separability: Samples from different clusters have significant differences and are separated from each other.

Cluster analysis does not require prior provision of data labels or category information, and is suitable for discovering potential structures, patterns, or distributions of data. Common clustering methods include K-means, density peak clustering, and hierarchical clustering21. Within a cluster, the similarity of data objects is high, while the data objects between different clusters are quite different. Cluster analysis does not depend on prior labels or classification, and it realizes automatic classification of data by mining the internal structure and pattern of data22. Cluster analysis is widely used in health data analysis, especially in individual health assessment, disease classification, patient grouping, and medical service optimization. Clustering technology can help identify potential patterns and heterogeneity in health data, thus supporting medical decision-making. For example, in health management, cluster analysis can divide patients into different groups according to their health status, lifestyle, or sign data23,24. For example, based on multidimensional health data, patients can be classified into healthy, high-risk, and disease patient populations. This can provide personalized health management plans for different groups, optimize the allocation of medical resources, and improve the efficiency of health intervention25.

Cluster analysis also plays a key role in disease classification, especially in subtype identification of complex diseases. For example, in cancer research, clustering based on patients’ gene expression profiles and pathological data can identify different subtypes of diseases and provide a basis for accurate treatment26,27,28. In addition, cluster analysis can identify the differences between patients with the same disease, thus offering data support for making personalized treatment plans29.

Therefore, the application of cluster analysis in health data provides a powerful tool for personalized health management, disease classification, and public health research. By identifying the patterns and potential groups in health data, cluster analysis can promote the accuracy and efficiency of medical services and improve overall health management levels30.

Construction of children’s physical fitness evaluation model based on SOM neural network and cluster analysis

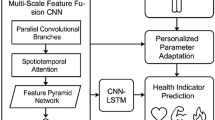
Unlike traditional linear dimensionality reduction methods, the SOM neural network can effectively reduce data dimensions in nonlinear, high-dimensional spaces. Children’s physical fitness data typically exhibit characteristics of nonlinearity, multidimensionality, and complexity. SOM can map high-dimensional data into a lower-dimensional space through adaptive learning while preserving the topological structure of the original data. This helps uncover the inherent distribution and potential patterns within the data. SOM is an unsupervised learning algorithm, meaning it can learn and classify data without requiring label information. This feature is critical in evaluating children’s physical fitness, as some health data lack explicit category labels. SOM can achieve adaptive dimensionality reduction and cluster analysis by learning the intrinsic structure of the data. This makes SOM particularly suited for preliminary exploratory analysis and the processing of high-dimensional data. In addition to dimensionality reduction, SOM can visualize data by creating grid mappings, projecting high-dimensional data onto a 2D space, and forming intuitive cluster maps. This visualization advantage helps to better understand the distribution structure and classification results of the data, making it more interpretable and valuable for application in children’s physical fitness evaluation. The evaluation of children’s physical fitness requires both scientific rigor and practicality. SOM, with its low computational cost and strong generalization ability, can efficiently handle high-dimensional health data in real-world scenarios, making it especially suitable for dynamic analysis and detailed classification of large-scale children’s health data. The optimized model’ architecture is displayed in (Fig. 1):

Fig. 1
figure 1

Architecture of the optimized model.

Full size image

Before inputting data into the SOM neural network, a series of rigorous data preprocessing steps is required to ensure data quality and improve the model’s performance and stability. First, data cleaning is performed, which involves handling missing values and detecting outliers to remove incomplete or severely abnormal data. This helps to avoid noise that could interfere with the model’s learning process. Next, the data undergoes normalization. Since SOM is sensitive to the numerical range of input data, Z-score normalization or Min-Max scaling is applied to bring all feature data to the same scale, preventing features with larger values from dominating the model. Based on this, feature selection and dimensionality reduction are conducted. The importance of features is assessed through correlation analysis or random forest (RF) algorithms, and irrelevant or redundant features are removed to reduce data complexity. Additionally, dimensionality reduction techniques such as principal component analysis (PCA) are applied to retain key information while reducing the computational load on the model. For class imbalance issues, data balancing techniques such as under-sampling of the majority class are used to equalize the data distribution and prevent the model from being biased toward the majority class during training. Furthermore, categorical data are transformed into numerical format to meet the input format requirements of the SOM network. For example, one-hot encoding is used to convert categorical features into numeric vectors, ensuring that all sample data structures are consistent, with irrelevant columns and features excluded. Finally, the processed data are split into training, validation, and testing sets, typically using 70% of the data for training, 15% for validation, and 15% for testing. This ensures that model training and evaluation are representative, while random sampling helps avoid data bias.

After data preprocessing, the data is input into the architecture of the SOM neural network. SOM maps high-dimensional data to low-dimensional space through its unsupervised learning characteristics. Thus, it generates preliminary clustering results and lays a foundation for further analysis. Based on the preliminary clustering results, the model introduces the refined clustering module of the traditional clustering algorithm to classify and optimize the clustering results generated by SOM to improve the model’s accuracy and refined analysis abilities. On this basis, the model is verified by the performance evaluation module, and the model’s performance is comprehensively evaluated by using various indicators (such as accuracy, recall, and F1 score) to ensure its superiority in classification and clustering tasks. At the same time, the visualization module visually presents the final clustering and classification results, which is convenient for researchers to intuitively analyze the data distribution and supports subsequent decision-making. In addition, the model designs personalized optimization and automatic parameter adjustment modules. It dynamically optimizes the parameters and clustering strategy of the model according to the evaluation results to ensure its adaptability and robustness in different application scenarios. Finally, the model applies the analysis results to the actual scene through the application and feedback module and iteratively optimizes the model combined with user feedback, thus continuously improving the performance and application effect of the model. The design and integration of this series of modules make the proposed model have great significance in improving the scientific, accurate, and personalized analysis ability of children’s physical fitness evaluation.

To ensure the effectiveness and stability of the clustering results produced by the model, this study has optimized both data preparation and model design. It ensures that the input data are free from missing values and outliers, and undergoes standardization to eliminate the impact of varying data dimensions on clustering outcomes. Meanwhile, it handles imbalanced data through over-sampling or under-sampling to prevent the clustering results from being biased toward certain classes. Moreover, features highly correlated with the clustering target are selected through correlation analysis, PCA, etc., and redundant information is removed to enhance clustering accuracy. In terms of model design, appropriate distance metrics (such as Euclidean distance, cosine similarity, or Manhattan distance) are chosen based on the data characteristics to ensure that similarity calculations align with the actual data distribution. The optimal number of clusters is determined automatically using metrics such as silhouette score and the elbow method, ensuring that the model can reasonably partition the dataset. The model then adjusts key parameters automatically to achieve the best clustering performance, enhancing both stability and the reproducibility of results.

Experimental design and performance evaluation

Datasets collection, experimental environment, and parameters setting

The dataset used in this study comes from the National Population Health Science Data Center, a professional institution under the China Academy of Medical Sciences; It is dedicated to collecting, sorting out, and sharing population health-related data nationwide. The dataset covers about 10,000 children’s health records, with a total of about 200,000 pieces of data, covering many aspects such as body shape, function, and quality. Its main features include basic information about children (such as age, gender, height, and weight), and physical fitness (such as the measurement data of key dimensions like strength, flexibility, and endurance). Meanwhile, it encompasses health assessment indicators (such as body mass indicator BMI and cardiopulmonary function test results). In addition, the dataset also contains information about environmental factors, such as living area, eating habits, and exercise frequency. To ensure the scientificity and validity of the data, this study has conducted strict preprocessing on the data, including data cleaning, data standardization, and dimensionality reduction. Data cleaning mainly deletes samples with too many missing or significant abnormal values. Data standardization adopts the Z-score method to normalize feature data. The dimension reduction process extracts the most representative features through PCA. Finally, the dataset is divided into training set (70%), verification set (15%), and test set (15%) to ensure that the training and evaluation of the model are representative. The dataset is downloaded through the National Population Health Science Data Center (https://www.ncmi.cn/).

The health and growth database of children and adolescents in China is led by the China Center for Disease Control and Prevention (China CDC). This dataset covers the physical health and growth data of 15,000 children and adolescents nationwide, with a total of about 300,000 records. Data features include basic information (e.g., height, weight, age, and gender), physical fitness (e.g., muscle strength, flexibility, and cardiopulmonary function), and behavior and living habits (e.g., diet frequency, sleep duration, and daily exercise). In the data preprocessing, this study uses the Interquartile Range (IQR) method to detect and remove abnormal values that deviate from the normal range. At the same time, it fills a few missing values by nearest neighbor interpolation. Then, the RF algorithm is employed to select features, and the key features that have a significant impact on the model are screened out, and the category data are sampled to balance the category distribution. The multidimensional characteristics of this dataset can provide rich information support for this study. The dataset can be obtained from the official website of China CDC (https://www.chinacdc.cn/).

The National Health and Nutrition Inspection Survey (NHANES) dataset is provided by the US Centers for Disease Control and Prevention, which is an open dataset focusing on health and nutrition surveys. This study selects the data from 1999 to now, of which the annual sample size is about 10,000, and the total data volume is huge. Its characteristics encompass physical health information (e.g., height, weight, and body fat percentage), health indicators (e.g., heart rate, vital capacity, and blood test results), and behavioral data (e.g., exercise frequency and dietary intake type). In data preprocessing, the data formats of different years are unified and integrated, and the numerical features are standardized by the Min-Max normalization method. Moreover, interactive features are constructed based on the original features, and noise data are removed by low-pass filtering. The diversity and scale of NHANES datasets provide reliable reference data for the study. The dataset is obtained through the NHANES official website (https://www.cdc.gov/nchs/nhanes/).

The European Adolescent Health Survey dataset is provided by the EU Health Data Sharing Program, covering more than 20 European countries and containing the health and behavior records of about 12,000 adolescents. The characteristics of this dataset include physical health data (height, weight, and BMI), physical activity records (weekly exercise time and exercise type), and mental health status (stress level and life satisfaction assessed by questionnaire). In the data preprocessing, this study codes and cleans up the abnormal values in the questionnaire records, and uses multiple interpolations to deal with the missing data. Then, the dimension of the data is reduced by factor analysis to reduce redundant information, and the feature dimension is unified for clustering and classification analysis. This dataset’s international perspective and multidimensional characteristics provide important supplementary data support for this study. Datasets are available through Eurostat (https://ec.europa.eu/eurostat).

In the experiment, the processor is Intel Core i9-12900 K, and the memory is Corsair Vengeance 64 GB DDR 5 4800 MHz. The graphics card is NVIDIA GeForce RTX 3090, and the hard disk is Samsung 980 Pro NVMe 1 TB SSD. The version of the operating system is Ubuntu 22.04 LTS 64-bit. The programming language version is Python 3.10, the deep learning framework version is TensorFlow 2.10, and the SOM library version is MiniSom 2.2.9. The mesh size of the optimized model is 30 × 30, the initial learning rate is 0.5, then gradually decays to 0.01, and the initial radius of the neighborhood radius is 5. With the training, it gradually shrinks to 1, the number of training iterations is 1000, and the distance metric is Euclidean distance. The contrast models of the experiment are T-distributed stochastic neighbor embedding (T-SNE), density peak clustering (DPC), and deep embedded clustering (DEC).

Performance evaluation

Comparative analysis of model performance

The comparison indicators selected in the performance comparison experiment are accuracy, precision, recall, F1 score, area under the receiver operating characteristic curve (AUC-ROC), and model training time. Firstly, the public dataset provided by the National Population Health Science Data Center is selected. The experimental data are indicated in (Fig. 2):

Fig. 2
figure 2

Performance comparison experiment ((a): Accuracy; (b): Precision; (c): Recall; (d): F1 Score; (e): AUC-ROC; (f): Training time).

Full size image

Figure 2 illustrates that in the proposed optimized model, the accuracy is 0.934 for strength, 0.851 for flexibility, and 0.863 for endurance, respectively, showing that the classification effect is superior to other models in all variables. In contrast, the DEC model’s accuracy is also excellent, especially in the strength dimension of 0.917. The DPC model’s flexibility is less than 0.799, and the T-SNE model’s strength is 0.876. The proposed model has the best precision in the strength dimension, which is 0.844, while the flexibility and endurance are 0.782 and 0.787 respectively, which has obvious advantages compared with other models. The precision of DEC in strength is 0.827, while the flexibility of T-SNE is weak, only 0.714. The proposed optimized model’s recall is still ahead in strength, flexibility, and endurance, which are 0.881, 0.803, and 0.809. The recall of DEC is also close to the optimized model, especially 0.865 in the strength dimension, and 0.749 in the flexibility of DPC, which is slightly lower than the optimized model. The F1 score of strength dimension, flexibility, and endurance of the optimized model are 0.862, 0.797, and 0.798, all of which are at the highest level. The DEC model has a score of 0.846 in F1 in the strength dimension, while T-SNE scores 0.722 in the flexibility dimension. The AUC-ROC reveals that the AUC values of the optimized model in strength, flexibility, and endurance are 0.944, 0.859, and 0.875, respectively, which shows a high classification ability. The AUC of the DEC model is 0.927 in the strength dimension, and the flexibility of DPC is 0.812, slightly lower than that of the optimized model. Finally, in the training time, the performance of the optimized model is significantly better than other models, with a training time of 6.729 s in the strength dimension, followed by 7.663 s in the DEC model. The training time of T-SNE and DPC is longer. Especially, the training time of the DPC model is 10.123 s in the endurance dimension. To further verify the performance of the optimized model on different datasets, this study selects four indicators: mean squared error (MSE), silhouette coefficient, model reasoning time, and classification balance. The experimental results are presented in (Fig. 3):

Fig. 3
figure 3

Performance comparison under different datasets ((a): MSE; (b): Silhouette coefficient; (c): Reasoning time; (d): Class balance ratio).

Full size image

The results in Fig. 3 show that, in the MSE comparison, the optimized model performs best on the database of children and adolescents’ health and growth in China, with an MSE of 0.742, while the MSE of T-SNE and DPC models are 0.456 and 0.382. On NHANES and European adolescent health survey datasets, the optimized model reaches 0.765 and 0.753 respectively, significantly exceeding other models. In comparing silhouette coefficients, the optimized model performs best on the China dataset, with 0.552, while the DPC model is only 0.294. On the NHANES dataset, the optimized model reaches 0.575, which is better than DEC’s 0.389. The silhouette coefficient of the European dataset is 0.563, which continues to lead. The reasoning time of the optimized model is the lowest, and the China dataset is 0.293 s. In contrast, the reasoning time of DEC and T-SNE is 0.584 and 0.745 s, respectively. On NHANES and European datasets, the time to optimize the model is still the shortest, at 0.312 and 0.305 s, respectively. In the classification balance, the performance of the optimized model on the three datasets significantly outperforms other models. It reaches 0.718 on the China dataset, much higher than T-SNE’s 0.423 and DPC’s 0.381. The performance on NHANES and European datasets is 0.732 and 0.724 respectively, which is better than all other models.

Sensitivity analysis

To study the parameters of the model, the experiment also set up sensitivity analysis, and the experimental objectives are as follows:

  1. (1)

    The impact of two core parameters, grid size, and learning rate, on the performance of the optimized model, is evaluated.

  2. (2)

    It is necessary to verify whether the parameter changes significantly affect the classification performance, clustering effect, and operating efficiency.

  3. (3)

    The best parameter configuration is found through sensitivity analysis to ensure a balance between model performance and efficiency.

The experimental grid size is set to 5 × 5, 10 × 10, 15 × 15 and 20 × 20 to evaluate the impact of mapping resolution of the SOM neural network. The learning rate is set to 0.01, 0.03, 0.05, 0.07, and 0.10, and the influence of the learning rate on the convergence speed and classification performance of the model is tested. The experiment uses the China database of children and adolescents’ health and growth. Each group of parameters is repeated 10 times to reduce the interference of randomness on the results. The experimental results of grid size are outlined in (Table 2):

Table 2 Sensitivity analysis results of grid size.
Full size table

In Table 2, with the increase of the grid size from 5 × 5 to 20 × 20, the performance indicator of the model has changed. Regarding accuracy and F1 score, the grid size reaches the highest value of 0.88 and 0.87 respectively when it is 15 × 15. However, it drops slightly when it is 20 × 20, indicating that the mapping accuracy may decrease if the grid size is too large. As grid size increases, the training time increases significantly, from 10.23 s to 25.34 s, illustrating that higher resolution brought about an increase in computational cost. In terms of the silhouette coefficient, the peak value is 0.58 when the grid size is 15 × 15, which indicates that the clustering effect is the best under this configuration. The experimental results of the learning rate are shown in (Table 3):

Table 3 Sensitivity analysis results of learning rate.
Full size table

The results in Table 3 indicate that when the learning rate is 0.07, the accuracy and F1 score reach the highest values of 0.88 and 0.87, respectively, but too high learning rate (such as 0.1) leads to a slight decline in the model performance. In terms of training time, when the learning rate is high, the model converges faster, from 18.12 s of 0.01 to 15.67 s of 0.1, which shows the influence of the learning rate on calculation efficiency. When the learning rate is 0.07, the silhouette coefficient reaches the highest value of 0.57, suggesting that a moderate learning rate can better balance the convergence speed and clustering effect.

Cluster analysis experiment

The study also sets up a cluster analysis experiment to further analyze the model’s validity. The comparison indicators are silhouette coefficient, intra-class distance, inter-class distance, weighted average contour score, class distribution uniformity, and cluster number selection. The experimental results are suggested in (Fig. 4):

Fig. 4
figure 4

Cluster analysis experiment ((a): Silhouette coefficient; (b): Intra-class distance; (c): Inter-class distance; (d): Weighted average contour score; (e): Uniformity of class distribution; (f): Number of clusters selection).

Full size image

The results of Fig. 4 show that the proposed optimized model performs best in the silhouette coefficient, with the scores of strengths, flexibility, and endurance of 0.655, 0.559, and 0.601 respectively, indicating that the clustering effect is significantly improved. In contrast, the silhouette coefficient of the DEC model in the strength dimension is 0.632, while the score of T-SNE in flexibility is low, only 0.481. In terms of intra-class distance, the performance of the optimized model is also superior, and the intra-class distances of strength, flexibility, and endurance are 3.201, 3.824, and 3.511 respectively. The DEC model’s intra-class distance reaches 3.312 in the strength dimension, which is slightly higher than that of the optimized model, and the flexibility of T-SNE is the worst, at 4.212. For the inter-class distance, the optimized model has the highest value in each dimension, and the inter-class distances of strength, flexibility, and endurance are 6.821, 6.012, and 6.421 respectively. The inter-class distance of DEC in the strength dimension is close to the optimized model, reaching 6.679, and that of DPC in flexibility is 5.671. The weighted average contour score also shows the leading performance of the optimized model, with a strength dimension of 0.629, flexibility of 0.542, and endurance of 0.584, which are higher than other models. DEC scored 0.603 in strength dimension, while T-SNE scored only 0.463 in flexibility. In the uniformity of category distribution, the uniformity scores of strengths, flexibility, and endurance of the optimized model are 0.859, 0.789, and 0.827, respectively, showing a relatively balanced distribution. The score of DEC in the strength dimension is 0.834, while the flexibility of T-SNE is 0.722. For the number selection of clusters, the optimized model selects 9 clusters in the strength dimension, with a flexibility of 7 and endurance of 8, all of which are more than other models. DEC chose 8 clusters in the strength dimension, while T-SNE chose fewer clusters in the flexibility and endurance dimensions.

Discussion

From the results of performance comparison experiments, the proposed optimized model performs well in many indicators, especially in the three dimensions of strength, flexibility, and endurance, which show high accuracy and stability. This reveals that the optimized model has obvious advantages in data dimensionality reduction and clustering effect while showing stronger robustness in classification performance. Although the DEC model is close to the optimized model in some indicators, its overall performance is slightly inferior, particularly in the flexibility and endurance dimensions, and its performance has not been fully surpassed. However, the performance of T-SNE and DPC models is insufficient, especially in training time and accuracy. This reflects that the traditional dimensionality reduction and clustering methods may have some limitations in effect and efficiency when handling complex health data. The advantage of the optimized model in training time is also very significant, especially when dealing with high-dimensional data, the training speed is remarkably faster than other models through reasonable parameter setting and optimization. This characteristic makes it have higher practical application value when processing large-scale data. At the same time, the comparison results of different datasets further verify the excellent performance of the optimized model in terms of MSE, silhouette coefficient, and classification balance. Among them, the performance of the optimized model in classification accuracy and balance exhibits its ability to solve the problem of uneven distribution of categories in health data analysis. In addition, in the efficiency indicator of reasoning time, the rapid response of the optimized model improves its practicability and provides feasibility for real-time analysis of health data.

From the results of cluster analysis experiments, the optimized model is outstanding in key indicators such as intra-class distance, silhouette coefficient, and inter-class distance. This shows that the model can effectively identify the differences between different categories. Meanwhile, it ensures the compactness of intra-class data and the separation of inter-class data, which reflects the strong clustering effect. Especially in the inter-class distance and the weighted average contour score, the numerical value of the optimized model is higher than other models, illustrating that it can distinguish different clustering categories more effectively. In contrast, the DEC model is close to the optimized model in silhouette coefficient and intra-class distance. However, it is insufficient in terms of inter-class distance and weighted contour score, especially in flexibility and endurance. However, the performance of T-SNE and DPC models lags the optimized model in many dimensions, especially in the intra-class distance and the balance of class distribution, and the effect of T-SNE is weak. In addition, the optimized model shows higher flexibility and adaptability in selecting cluster numbers, which can choose reasonable cluster numbers according to data characteristics and ensure the classification appropriateness of data with different dimensions. Generally speaking, the proposed optimized model has remarkable advantages in the clustering effect. It can effectively meet the analysis needs of high-dimensional and complex health data, and provide a scientific and efficient solution for evaluating children’s physical fitness.

Conclusion

Research contribution

This study innovatively combines SOM neural networks with cluster analysis techniques to construct a model for evaluating children’s physical fitness. Unlike traditional linear statistical analyses and unidimensional evaluation methods, this model effectively handles high-dimensional, complex data through the nonlinear dimensionality reduction capability of SOM. Concurrently, it utilizes optimized cluster analysis techniques for fine-grained classification of children’s physical fitness. This approach breaks through the limitations of traditional methods in both dimensionality reduction and clustering. Thus, it significantly enhances the model’s adaptability and robustness when processing children’s health data with nonlinear and heterogeneous characteristics. Furthermore, the optimization of the SOM neural network algorithm markedly improves clustering performance, as reflected in key indicators such as silhouette score, intra-cluster distance, and inter-cluster distance. The optimized model demonstrates higher clustering accuracy and data interpretability in three core dimensions—strength, flexibility, and endurance—providing more precise data support for subsequent health interventions. Additionally, this study proposes a children’s physical fitness evaluation framework based on the three key dimensions of flexibility, strength, and endurance. It overcomes the limitations of traditional single-indicator evaluations and constructing a more comprehensive, dynamic evaluation system. This system helps parents and educators more intuitively and accurately understand the physical fitness status of children, providing a scientific basis for developing personalized health education and intervention strategies.

In conclusion, the optimized model proposed in this study holds significant importance in terms of technical innovation, application breadth, and practical value. It offers a scientific tool for evaluating children’s physical fitness and opens up new directions and methodological support for the research on health education and intervention systems.

Future works and research limitations

Firstly, the dataset used in this study mainly comes from a specific regional group of children, which introduces certain limitations regarding the regional applicability of the research findings. Children in different regions may exhibit significant differences in physical fitness development, influenced by various factors such as geography, socioeconomic background, and cultural environment. As a result, the model’s cross-regional applicability and generalizability may be restricted. Secondly, although the combination of the SOM neural network and cluster analysis has been optimized in this study, the complexity of the model may incur high computational costs in practical applications. In particular, when dealing with large-scale datasets, the time and computational resources required for model training increase significantly, posing challenges for resource-limited application scenarios, such as real-time health monitoring systems in schools and communities. Additionally, the physical fitness evaluation in this study primarily focuses on three core dimensions—strength, flexibility, and endurance. While these three indicators are essential components of children’s physical fitness, they do not fully encompass all relevant factors in children’s health assessment. For example, factors such as mental health, nutritional status, and lifestyle habits also remarkably influence children’s physical fitness development. However, these variables have not been included in the evaluation framework, which may lead to some incompleteness in the model’s evaluation results.

Future research could focus on several directions to enhance the model’s performance and practical application value. Firstly, future studies aim to collect a larger, more diverse dataset of children’s physical fitness, covering different regions, socioeconomic backgrounds, and cultural factors to ensure the data’s representativeness and generalizability. This helps improve the model’s ability to generalize and apply across different contexts, particularly through cross-cultural and cross-regional validation of the model’s effectiveness and robustness. It also explores the commonalities and differences in children’s physical fitness across diverse environments. Secondly, to address the computational challenges in large-scale data processing, future research could optimize the model structure and explore more efficient algorithms and parameter optimization methods to reduce computational costs and improve analysis speed. Additionally, distributed computing techniques or cloud computing resources may be introduced to enable distributed data processing and task parallelization, significantly enhancing the model’s operational efficiency and scalability, especially in large-scale health data analysis scenarios. Furthermore, future studies could explore integrating the model with real-time data acquisition technologies, such as wearable devices and health monitoring sensors, to enable dynamic monitoring and continuous analysis of children’s physical fitness. This transitions the model from offline analysis to real-time evaluation, further enhancing its practicality in health interventions and personalized recommendations. Lastly, future research could concentrate on the interaction between health data and psychological and environmental factors, building a more comprehensive children’s health evaluation framework. By integrating multimodal data (such as physical fitness, mental state, nutritional intake, and environmental variables), the mechanisms by which multiple factors influence children’s health should be explored. This can provide scientific support for the development of more accurate health interventions.

In conclusion, future research could delve into areas such as data scale, computational efficiency, real-time monitoring, and multimodal data integration. This it can construct a more forward-looking, practical, and comprehensive children’s physical fitness evaluation system, offering strong support for children’s health development.