Balanced dung beetle optimization algorithm based on parameter substitution and escape strategy

Abstract

Dung Beetle algorithm is an intelligent optimization algorithm with advantages in exploitation ability. However, due to the high randomness of parameters, premature convergence and other reasons, there is an imbalance between exploration and exploitation ability, and it is easy to fall into the problem of local optimal solution. The purpose of this study is to improve the optimization performance of dung beetle algorithm and explore its engineering application value. A balanced dung beetle optimization algorithm was proposed, and parabolic adaptive parameter $R$ was introduced to broaden the exploration range and slow down premature convergence. Gaussian distributed phase parameter $\beta$ is introduced to reduce the randomness of parameters and stimulate the potential of algorithm exploitation. Levy flight escape strategy is introduced to balance the global exploration ability of the algorithm and fully explore the solution space. The effectiveness of the improved strategy is verified by comparing the CEC2017 benchmark function with the single strategy variant. The experimental results show that BDBO algorithm is superior to other algorithms in terms of convergence accuracy and generalization ability, and the accuracy improvement percentage is 35.29% compared with DBO algorithm. Wilcoxon rank sum test was used to evaluate the experimental results, which proved that the improvement strategy was statistically significant. Finally, the BDBO algorithm is applied to the tracking technology of the maximum power point of the photovoltaic system, and the experimental results show that the application effect of the BDBO algorithm is better and has more engineering application value.

Introduction

Meta-heuristic algorithm is a class of methods for solving global optimization problems¹. Because it is easy to understand and implement, and has high optimization efficiency, it is widely used in computer science, medicine, artificial intelligence, engineering optimization and other fields to solve various optimization problems². Classical meta-heuristic algorithms such as PSO, DE, GA, etc. provide inspiration for the subsequent research and development of many optimization algorithms. According to the No Free Lunch (NFL) theorem, many meta-heuristic algorithms based on animal group behavior have been proposed. Erik and Miguel et al. proposed a social spider optimization algorithm (SSO) based on the cooperative behavior of social spiders, which can alleviate the problems of premature convergence and unbalanced exploration and exploitation ability through gender-specific search agent mechanisms³. Hector et al. proposed a hybrid metaheuristic algorithm using metaheuristic operators from unstructured evolutionary game theory and fusing Cheetah Optimizer and Particle Swarm Optimization to solve continuous optimization problems⁴. Xue and Shen proposed the Dung Beetle Optimizer (DBO) algorithm based on the group cooperation mechanism of dung beetle population⁵. DBO algorithm has the characteristics of fast convergence⁶ and strong exploitation ability⁷.

The generalization ability is reflected by the transfer performance of the algorithm between different problems and the adaptability on datasets with similar characteristics but different distributions. DBO algorithm has strong generalization ability because of its group search characteristics, which is very suitable for complex dynamic optimization problems. Therefore, this study chooses to further explore the potential of DBO algorithm. DBO algorithm has problems such as unbalanced exploration and exploitation ability, easy to fall into local optimal solution⁸ and premature convergence⁹ due to excessive parameter randomness and premature convergence. In order to explore better optimization performance, convergence speed and accuracy of DBO algorithm, some scholars have carried out improvement research on DBO algorithm. He et al. initialized the population by Chebyshev chaotic mapping, and used curve-adaptive Gold Sinusoids strategy and Levy flights with Cauchy-t mutation strategy to replace the position updating equation of some dung beetles, so as to improve the exploration power of search and the generalization ability of the algorithm¹⁰. Xiao and Cui et al. used the good point set initialization strategy and greedy strategy to improve the population quality, and introduced differential evolution strategy and Dynamic Lens Opposition-Based Learning (DLOBL) to improve the convergence accuracy of the algorithm¹¹. Adegboye et al. used dynamic pinhole imaging technology (DGS-SCSO) to enhance the global exploration ability of the algorithm, and used the golden sine algorithm strategy to improve the convergence speed of the algorithm¹². Farah et al. used auxiliary function pairs to correct the mean position to solve the problem that the algorithm is easy to fall into local optimum, and introduced nonlinear equations to coordinate the exploration and exploitation stages of the traditional SCA algorithm¹³. Ülker et al. used Gaussian mutation specular reflection learning (GS) and local escape operator (LEO) to prevent local optima and improve convergence speed¹⁴. In addition, some scholars have developed new algorithms to solve the problem of unbalanced exploration and exploitation capabilities. Erik et al. proposed a state of matter search algorithm (SMS) based on natural phenomena. SMS algorithm can modify the intensity of exploration and exploitation in different stages to improve the balance between exploration and exploitation, while retaining the good search ability of evolutionary algorithm¹⁵. Cao et al. proposed an Enhanced WOA algorithm (EWOA). EWOA adopts Improved Dynamic Inverse Learning (IDOL) to adaptively adjust the exploitation and exploration mode, and uses adaptive weights to prevent falling into local optimal solutions¹⁶. Zhao et al. proposed an improved shuffled frog leaping algorithm with inertia weight (MSFLA)¹⁷. The inertia weight a was introduced to increase the exploration range, so as to balance the exploration and exploitation ability of the algorithm. Erik et al. proposed a new metaheuristic optimization algorithm based on search strategy and social strategy, which used counters to determine the exploration mode of search agents to improve the diversity of search patterns¹⁸.It can be seen that the use of strategies such as initialization mapping and adaptive weights can improve the performance of the algorithm to a certain extent and balance the exploration and exploitation ability of the algorithm, but there are also certain shortcomings. For example, the initialization mapping method has certain limitations, and it is difficult to effectively improve the adaptability and flexibility of the algorithm in dealing with different problems. The location update alternative method cannot fully tap the local exploitation potential of the original algorithm, resulting in a waste of computational resources¹⁹. The Cuckoo Search (CS) and refraction learning (RL) methods adopted by Adegboye et al. can stimulate the local development potential of the algorithm²⁰. Therefore, the DBO algorithm still has a large space to explore, which is the main motivation to study it and introduce it into engineering applications in this paper.

MPPT controller is an important part of photovoltaic system and an important control device to ensure the efficient use of photovoltaic energy²¹. The output power of solar panels is affected by many factors, which in turn affect the utilization of light energy. At present, most photovoltaic power stations use MPPT technology, combined with intelligent optimization algorithms to adjust the operating point to ensure that it is always at the maximum power point to make full use of available solar energy²². Therefore, it is crucial to precisely regulate the maximum power point so that the photovoltaic system can output at maximum power²³. In recent years, many scholars have introduced different swarm intelligence optimization algorithms into the MPPT technology of photovoltaic systems²⁴ and conducted in-depth studies. Such as genetic algorithm²⁵, differential evolution algorithm²⁶, particle swarm optimization algorithm²⁷, Bat algorithm²⁸, Gray Wolf algorithm²⁹, simulated annealing algorithm³⁰, gravity search algorithm³¹, Henry Gas solubility optimization algorithm³², etc. However, these algorithms have their own advantages, but they also have problems such as premature convergence and easy to fall into local optimal solutions, especially in variable and complex application problems. Therefore, it is necessary to introduce a more adaptive and flexible optimization algorithm into the MPPT control system.

The local exploitation potential is reflected in the improvable space of the algorithm’s ability to explore the global optimal solution in the best exploration region. In order to balance the exploration and exploitation ability of DBO algorithm and fully tap its local exploitation potential, a balanced dung beetle optimization algorithm is proposed and applied to MPPT control of photovoltaic system. Firstly, a parabolic curve is used to replace the linear change of $R$ parameter to broaden the area search range and slow down the premature convergence. The independent random vectors $b1$, $b2$, $C2$ are replaced by random numbers obediently normal distribution to reduce the randomness of parameters and stimulate the exploitation ability potential of the algorithm. In addition, the Levy flight escape mechanism is introduced to balance the global exploration ability of the algorithm and fully explore the solution space³³. Different from the previous single strategy improvement, the parabolic $R$ parameter and Levy flight can slow down the slow convergence of the single strategy variant with Gaussian distribution parameters, and realize the complementary advantages of strategies. In order to verify the performance of BDBO algorithm, we use the CEC2017 benchmark function to conduct a series of comparative experiments to evaluate the optimization ability of the algorithm, and the Wilcoxon rank sum test is used to evaluate the experimental results to analyze their statistical significance. Finally, the BDBO algorithm is applied to the MPPT technology to verify the practical application potential of the algorithm³⁴.

The main contributions of this paper are summarized as follows:

• 1. In BDBO, DBO is the main body of the algorithm. The Gaussian distributed parameter $\beta$ strategy was used to reduce the randomness of the parameters and further stimulate the exploitation ability potential of the algorithm.

• 2. The Levy flight escape mechanism was introduced to balance the global exploration ability of the algorithm. The parabolic $R$ parameter strategy was used to slow down the premature convergence, and the Gaussian distributed parameter $\beta$ strategy variant was used to slow down the slow convergence speed.

• 3. Through the benchmark function test, it is verified that the improved Dung beetle optimization algorithm is more superior in generalization ability and convergence accuracy. The Wilcoxon rank sum test was used to prove the significant difference between the experimental results of the improved strategy, especially the Gaussian distributed parameter $\beta$ strategy variant, and the original DBO algorithm.

• 4. The improved dung beetle optimization algorithm is applied to MPPT optimization example of photovoltaic system, and its practical application value is verified by circuit simulation experiment compared with other optimization algorithms.

The rest of this paper is organized as follows: The second section mainly introduces the basic principle of the dung beetle algorithm, and explains the shortcomings of the algorithm. Section 3 describes the BDBO algorithm in detail and analyzes the complexity of the algorithm. In the fourth section, the CEC2017 benchmark functions are selected to evaluate the performance of the BDBO algorithm, and the Wilcoxon rank-sum test is used to evaluate the experimental results. In the fifth part, the application potential of BDBO is verified by using MPPT technology. Section 6 summarizes the conclusions of this study.

Overview of the DBO algorithm

Basic DBO algorithm

The DBO algorithm is inspired by the rolling, dancing, foraging, stealing and reproduction behaviors of dung beetle populations in nature, and simulates the competition phenomenon of dung beetles through group cooperation. DBO algorithm has the advantages of strong evolutionary ability, fast search speed and strong exploitation ability. The algorithm searches for the global optimal solution through the specific behaviors of four types of dung beetles. There are four types of rolling dung beetles, nursing dung beetles, foraging dung beetles and stealing dung beetles, among which rolling dung beetles can perform two kinds of behaviors: rolling dung beetles and dancing, and the general proportion distribution is set at 20%, 20%, 25% and 35%.

Ball rolling dung beetle

In nature, dung beetles use light to navigate, making sure they move in a straight line. In the optimization process, the rolling dung beetle explores the solution space according to its fitness and historical movement direction, and its position update mode is shown in Eq. (1).

$$x_{i}^{t + 1} = x_{i}^{t} + \alpha \times k \times x_{i}^{t - 1} + b \times \Delta x$$

(1)

where, ${x}_{i}^{t}$ represents the position of the i dung beetle at the t step, k ∈ (0,0.2) represents the constant value of the deflection coefficient, which is generally set to 0.1, and b ∈ (0,1) represents the constant term, which is generally set to 0.3. $\Delta x$ is used to simulate changes in light intensity, and its calculation equation is shown in Eq. (2).

$$\Delta x = \left| {x_{i}^{t} - x_{{{\text{worst}}}} } \right|$$

(2)

where, ${x}_{\text{worst}}$ indicates the global worst position information. $\alpha$ ∈(−1,1) is used to simulate the direction deviation under natural factors, and the renewal equation of $\alpha$ is shown in Eq. (3).

$$\alpha = \left\{ {\begin{array}{*{20}c} 1 & {\eta > \lambda } \\ { - 1} & {\eta < \lambda } \\ \end{array} } \right.$$

(3)

where $\eta$∈(0,1) represents a random number and $\lambda$ represents the probability that the beetle will not be able to move forward when it encounters an obstacle. $\alpha =1$ indicates straight line movement in the current direction, $\alpha =-1$ indicates deviation from the original direction.

When dung beetles encounter obstacles, they change direction by dancing. In the DBO algorithm, when the rolling dung beetle encounters a boundary, it changes its direction of movement through the tangent function. The updated dance behavior calculation equation is shown in Eq. (4).

$$x_{i}^{t + 1} = x_{i}^{t} + \tan \left( \theta \right)\left| {x_{i}^{t} - x_{i}^{t - 1} } \right|$$

(4)

where $\theta$ ∈[0, π] represents the deviation coefficient, $\theta$ ∈{0, π/2, π} does not update the position. Thus, directional changes in rolling dung beetles are closely related to historical location information.

Raising dung beetles

In nature, dung beetles will roll the dung ball to a safe place to lay eggs, providing a safe feeding environment for young dung beetles. In the DBO algorithm, dung beetles use boundary selection strategy to restrict the spawning area in order to find the best solution in the local optimal area. The spawning area definition equation is shown in Eq. (5).

$$\left\{ {\begin{array}{*{20}c} {Lb^{*} = max\left( {X^{*} \times \left( {1 - R} \right),Lb} \right)} \\ {Ub^{*} = min\left( {X^{*} \times \left( {1 + R} \right),Ub} \right)} \\ \end{array} } \right.$$

(5)

where, $L{b}^{*}$ is the lower boundary of the spawning area and $U{b}^{*}$ is the upper boundary of the spawning area. $R=1-t/T$ is used to control the boundary change of the spawning area, where T represents the maximum number of iterations and ${X}^{*}$ is the local optimal solution. In the DBO algorithm, dung beetles breed in the local optimal area to produce a new generation of candidate solutions. The position update equation of the oosphere is shown in Eq. (6).

$$B_{i}^{t + 1} = X^{*} + b_{1} \times \left( {B_{i}^{t} - Lb^{*} } \right) + b_{2} \times \left( {B_{i}^{t} - Ub^{*} } \right)$$

(6)

where, $b1$ and $b2$ are independent random vectors of 1 × D, ${B}_{i}^{t}$ is the position of the i feeder beetle at the t iteration, and D is the dimension. The use of mutation operation to update the location is conducive to improving the local exploitation ability.

Dung beetles on the prowl

The young beetles will be guided by the best feeding areas. The optimal feeding area is affected by the global optimal solution, and the boundary definition equation of the optimal feeding area is shown in Eq. (7).

$$\left\{ {\begin{array}{*{20}c} {Lb^{b} = max\left( {X^{b} \times \left( {1 - R} \right),Lb^{b} } \right)} \\ {Ub^{b} = min\left( {X^{b} \times \left( {1 + R} \right),Ub^{b} } \right)} \\ \end{array} } \right.$$

(7)

where ${X}^{b}$ is the global optimal location, $L{b}^{b}$ is the lower bound of the best foraging region, $U{b}^{b}$ is the upper bound of the best foraging region, and $R$ parameter is used to control the proximity of the foraging region boundary to the global optimal solution. The foraging dung beetle will search for the optimal solution in the optimal feeding area, and the position renewal equation of the foraging dung beetle is shown in Eq. (8).

$${x}_{i}^{t+1}={x}_{i}^{t}+{C}_{1}\times \left({x}_{i}^{t}-L{b}^{b}\right)+{C}_{2}\times \left({x}_{i}^{t}-U{b}^{b}\right)$$

(8)

where ${C}_{1}$ represents a random number subject to normal distribution, and ${C}_{2}$ ∈ (0,1) represents a random vector of size 1 × D. Using the normal distribution of parameter ${C}_{1}$ to guide the searching behavior of dung beetles is conducive to improving the local exploitation ability.

The thieving dung beetle

The theft mimics what some dung beetles do when they steal dung balls. Interspecies collaboration and information sharing are facilitated by cross-operation of dung beetle. The replacement equation for stealing dung beetles is shown in Eq. (9).

$${x}_{i}^{t+1}={X}^{b}+S\times g\times \left(\left|{x}_{i}^{t}-{X}^{*}\right|+\left|{x}_{i}^{t}-{X}^{b}\right|\right)$$

(9)

where S is a constant term, g represents a random vector of size 1 × D that follows a normal distribution, ${X}^{*}$ is the current local optimal solution, and ${X}^{b}$ is the global optimal solution.

Algorithmic inadequacy

Premature convergence

Dung beetle optimization algorithm has strong generalization ability and exploitation ability, but it also has some defects in algorithm accuracy. The algorithm tends to employ a greedy search strategy throughout the entire search process. Based on Eqs. (5) and (7), both brooding dung beetles and foraging dung beetles utilize the optimal solution ${X}^{*}$、${X}^{b}$ to determine the most favorable search area, subsequently updating their positions using information from the optimal solution and the identified best search area. However, the multiple utilization of the optimal solution may accelerate the premature convergence between the local best region and the local optimal solution. The dynamic boundary equation of the best search region is given in Eq. (10).

$$\left\{ {\begin{array}{*{20}c} {Lb = max\left( {X \times \left( {1 - R} \right),Lb} \right)} \\ {Ub = = min\left( {X \times \left( {1 + R} \right),Ub} \right)} \\ \end{array} } \right.$$

(10)

According to the equation, the positions of brooding and foraging dung beetles are strictly restricted to the optimal region, and the optimal search region is affected by the $R$ parameter. $R=1-t/T$ is linearly decreasing, and the dynamic boundary and range of the best region gradually decrease with the number of iterations. Reducing the search region prematurely is easy to cause the algorithm to fall into the local optimal solution.

Imbalanced exploration

The exploration ability of the dung beetle determines the exploration range and convergence speed of the algorithm. According to Eq. (1), the dung beetle uses ${x}_{i}^{t}$, ${x}_{i}^{t-1}$ and light intensity $\Delta x$ to update its position. However, the number of ball-rolling dung beetles is small and the migration range is small, which makes it difficult to fully explore the solution space or escape from the local optimal solution. Secondly, the light intensity $\Delta x$ is affected by the global worst position ${x}_{\text{worst}}$, which may affect the quality of new solutions. It is difficult to effectively explore the new best search area by only rolling ball behavior and dancing behavior, which affects the balance between exploration and exploitation ability, and makes the algorithm easy to fall into local optimal solutions ³⁵.

High randomness of parameters

Brooding dung beetles and foraging dung beetles can provide superior exploitation ability by exploring the optimal solution in the best search area. According to Eqs. (6) and (8), the two dung beetles exploit locally by using the best search area boundary information, and the utilization degree of the search area boundary information is affected by the random weights ${b}_{1}$, ${b}_{2}$, ${C}_{1}$ and ${C}_{2}$. However, the randomness of the weight parameter is too high. In the exploitation stage, the random parameter is too high to limit the local exploitation ability of dung beetles, affect the quality of new solutions, and it is difficult to fully tap the exploitation potential of the algorithm³⁶.

The proposed algorithm

Dung Beetle Optimization Algorithm (DBO) has strong exploitation ability, but it still needs to solve the problems of premature convergence, unbalanced exploration ability and high randomness of parameters. The proposed Balanced Dung beetle optimization algorithm (BDBO) reduced the randomness of parameters, enhanced the exploration ability and escape ability, and further explored the exploitation potential of the algorithm.

Parabolic R parameter substitution

In the DBO algorithm, ball-rolling dung beetles are responsible for global exploration, while brooding dung beetles, foraging dung beetles, and stealing dung beetles collaborate for local exploitation. The exploitation dung beetle uses the boundary information of the search area to update its position. The local optimal search area is affected by the parameter $R$, and the premature convergence of the search area is easy to cause the algorithm to fall into the local optimal solution. The reduction speed of the search area can be slowed down by adjusting the $R$ parameter. Equation (11) is the update equation of the $R$ parameter.

$$R = 1 - \frac{t}{T}$$

(11)

According to literature³⁷, nonlinear control parameters are conducive to balancing exploration and exploitation capabilities. Literature³⁸ proposes an inverted S-type control parameter, which proves that nonlinear control parameters play a coordinating role. The optimal search area shrinks with the linear decrease of the parameter $R$, and the search area shrinks too fast, which is not conducive to the algorithm to explore the global optimal solution. Therefore, the parabolic shape parameter is proposed to replace the parameter $R$ in order to broaden the local optimal region. The update equation for the parabolic adaptive control parameter $R$ is as shown in Eq. (12).

$$R = 1 - \frac{{0.5 \times 10 \times \left( {\frac{t}{{\sqrt {5T} }}} \right)^{2} }}{T}$$

(12)

where R is used to control the local optimal region change, and t is the current number of iterations. The change curve of parabolic adaptive parameter $R$ is shown in Fig. 1.

Fig. 1

A parabolic curve.

It can be seen from Fig. 1 that the updated control parameter $R$ presents a parabolic linear change. The adaptive parameters can change dynamically according to the number of iterations, and the value of the parabolic control parameters under the same number of steps is larger, and the local optimal area is more extensive, which can prevent the algorithm from falling into the local optimal solution due to premature convergence, balance the exploration and exploitation ability.

Gaussian distributed parameter substitution

Disturbance factor is a technique that uses random parameters to improve the performance of the algorithm. Using disturbance factor to control the population search behavior can prevent the algorithm from falling into local optimal solution. However, if the randomness of the disturbance factor is too strong, the search performance of the algorithm will be limited. The position update of brooding dung beetles and foraging dung beetles is affected by random parameters, and controlling individual update by random parameters can increase the diversity of population³⁹. However, in the exploitation phase, the high randomness of the parameters will affect the quality of the updated solution and limit the exploitation ability of the algorithm. The location renewal mode of dung beetles rearing and foraging is shown in Eq. (13).

$$\left\{ {\begin{array}{*{20}c} {B_{i}^{t + 1} = X^{*} + b_{1} \times \left( {B_{i}^{t} - Lb^{*} } \right) + b_{2} \times \left( {B_{i}^{t} - Ub^{*} } \right)} \\ {x_{i}^{t + 1} = x_{i}^{t} + C_{1} \times \left( {x_{i}^{t} - Lb^{b} } \right) + C_{2} \times \left( {x_{i}^{t} - Ub^{b} } \right)} \\ \end{array} } \right.$$

(13)

where the control parameters $b1$, $b2$ and $C2$ are random vectors. To solve the above problems, Gaussian distributed random parameters were used to replace random vectors to reduce the randomness of parameters⁴⁰. The standard deviation of the normal distributed parameters has a significant impact on the parameter randomness. Therefore, the normal distribution parameters are used to control the random parameters by a small standard deviation, and then the fine disturbance of local search is generated to stimulate the development potential of the algorithm. In addition, the phased parameter control strategy is used to improve the convergence speed of $b1$ and other parameters in different stages. In the early stage of exploration, random vector parameters were used to achieve variation operations and increase population diversity. In the later stage of exploitation, Gaussian distributed random numbers are used to control the population search behavior and realize the fine exploitation of local areas. The corresponding form of the control parameter $\beta$ at different stages is shown in Eq. (14).

$$\begin{array}{*{20}c} {\beta = } \\ \end{array} \left\{ {\begin{array}{*{20}c} {\beta_{0} \sim rand} & {t \le \frac{T}{10}} \\ {\beta_{0} \sim {\mathcal{N}}\left( {mean,std} \right)} & {t > \frac{T}{10}} \\ \end{array} } \right.$$

(14)

where $\beta$ represents the three control parameters $b1$, $b2$ and $C2$, and the Gaussian distribution parameter $\mathcal{N}(mean,std)$ can be regulated according to the actual situation. The distribution state is set as $\mathcal{N}(0,0.1)$ in the simulation experiment. The change process of control parameter $\beta$ is shown in Fig. 2.

Fig. 2

Parameter control strategy presented.

The blue trajectory represents the early exploration stage, where the degree of variation of random parameters is large, while the red trajectory represents the exploitation stage, where parameters are generated in a Gaussian distributed way, guiding the detailed exploitation of local areas. Gaussian distributed parameter control strategy can improve the utilization of local optimal solutions and stimulate the exploitation potential of algorithms.

Levy flight escape strategy

The escape ability is reflected in the ability of the algorithm to jump out of the local optimal solution by using long-distance migration. Random walk, Levy flight and other methods can help the algorithm jump out of the current search area, dynamically adjust the search range and direction, and prevent it from falling into the local optimal solution. The number of rolling dung beetles is small and the migration range is small, so it is difficult to effectively explore the new best search area or escape from the local optimal solution, which affects the balance between exploration and exploitation ability, and makes the algorithm easy to fall into the local optimal solution. In order to solve the above problems, Levy flight is used to travel long distances to fully explore the solution space. Levy flight⁴¹ was first proposed by Paul Pierre Lévy and applied to Cuckoo Search Algorithm by Xin-She Yang and Suas Deb⁴². Levy flight combines the characteristics of short-range dense search and long-distance accidental jump, which can realize multi-scale exploration in the search space and provide a mechanism for the algorithm to jump out of local optimum. Many scholars⁴³ will use Levy flight to carry out long-distance travel to enhance the optimization performance of the algorithm. Its calculation equation is shown in Eq. (15).

$$x_{i}^{\prime } \left( t \right) = x_{i} \left( t \right) + l \oplus Levy\left( \lambda \right)$$

(15)

where ${x}_{i}(t)$ represents the current position, $\oplus$ represents the point-to-point product, $Levy(\lambda )$ represents the Levy step size, and $l$ is the step scale coefficient. In order to improve the exploration ability and escape ability of the algorithm, a Levy flight escape strategy was proposed to help the algorithm escape from the local optimal solution. Its pseudocode is shown in Table 1.

Table 1 Levy flight strategy pseudocode.

When the global optimal solution is not updated for K consecutive times, the algorithm is regarded as having local stagnation, and Levy flight is used to update the position information of the rolling dung beetle. Related literature⁴⁴ shows that the algorithm performs well when K = 10. The process of escaping the local optimal solution using levy flight is shown in Fig. 3.

Fig. 3

Escape route presentation.

where the sphere range represents the local optimal region and the cyan straight line is the position change path of the global optimal solution. It can be seen from the Fig. 3 that Levy flight has good global exploration ability, which can balance the exploration ability of the algorithm and help the algorithm effectively escape from the local optimal solution.

BDBO algorithm flow

Using parameter substitution strategy and Levy flight escape strategy can effectively improve the optimization performance of the algorithm. The implementation process of balanced dung Beetle Optimization algorithm (BDBO) is shown in Fig. 4.

Fig. 4

Flowchart of BDBO algorithm.

The BDBO algorithm generates dung beetle populations through random initialization and evaluates the location information of dung beetles according to the fitness function. In each iteration, the rolling dung beetle updated its position by rolling and dancing. The optimal local renewal area was determined by the substituted $R$ parameter, and the breeding dung beetles and foraging dung beetles updated according to the stage changes of $\beta$ parameter. Thieving dung beetles update their location by stealing. In addition, when the global optimal solution is not updated for K consecutive times, dung beetles will migrate through Levy flight to escape the local optimal solution.

The complexity of population initialization in the original DBO algorithm is $O(n\cdot d)$, where $d$ represents the dimension and $n$ represents the population number. The algorithm runs $t$ times, and the complexity of the update operation of the four types of dung beetles under each iteration is $O(0.25n\times d)$, so the total time complexity is $O(t\cdot (n\cdot d+f))$, where $f$ represents the cost of fitness function evaluation. In the improved BDBO algorithm, the computational complexity of $R$ parameter updating $t$ times is $O(t\cdot 1)$. Breeding and foraging dung beetles need to randomly sample the parameters of Gaussian distribution, and the computational complexity is about $O(\frac{9}{10}\cdot \frac{n}{2}\cdot d)$. The computational complexity of generating the $Levy$ flight step is about $O(\frac{n}{4}\cdot d)$, which is negligible since the $Levy$ flight strategy is only executed when the global optimal solution has not been updated many times. Therefore, the time complexity of BDBO is about $O(t\cdot (\frac{29}{20}\cdot n\cdot d+f+1))$, which does not significantly increase the complexity of the original DBO algorithm.

Experimental evaluation and results

Experiment preparation

In the research of optimization algorithm, CEC test set is the recognized benchmark function test set. In order to verify the optimization performance of the proposed BDBO algorithm, part of the CEC-2017 benchmark function test set was used to compare the BDBO algorithm with excellent metaheuristic optimization algorithms. F1 to F12 are unimodal functions as shown in Table 2, and F13 to F24 are multi-modal functions as shown in Table 3. In addition, the study analyzed the statistical significance of the improved strategy by performing a Wilcoxon rank-sum test with a significance level of 5% to evaluate the results of the single strategy variant comparison experiment.

Table 2 Test functions 1.

Table 3 Test functions 2.

The experiment uses $Matlab$ R2023a software under Windows 11 operating system to execute the code, and the simulation experiments are all run in the computer equipment configured as 7950X–14,900K, and the computing memory is 64G. The initial population is set to 100, the upper and lower bounds are set to [100, −100], the dimensions are set to 30 and 100 dimensions, the number of independent runs is set to 10, and the random seed value is set to 123–132. The number of iterations of the traditional algorithm comparison experiment is set to 1000, and each iteration is evaluated, and the function test is carried out in 30 dimensions and 100 dimensions. The number of iterations of the comparison experiment of the improved algorithm is set to 30,000, and the dimension is set to 100. The number of iterations for the comparison experiment of the variant algorithm is set to 1000, and the dimension is set to 100. The optimization performance of BDBO algorithm is verified by the above comparison tests.

Traditional algorithm comparison

In order to verify the improvement effect of the proposed BDBO algorithm, dung Beetle Optimization algorithm, firefly optimization algorithm, particle swarm optimization algorithm, Cuckoo optimization algorithm and fireworks optimization algorithm were selected for comparison experiments. In addition, the BDBO algorithm is compared with the DBO algorithm improved by single policy to verify the effectiveness of the improved strategy.

• 1. Firefly Algorithm (FA) is a global optimization algorithm based on natural selection and evolution⁴⁵. Inspired by the bright light behavior of fireflies, the algorithm is easy to implement and can make full use of the parallel computing performance of computers to speed up optimization.

• 2. Particle swarm optimization (PSO) is one of the most classic swarm intelligence algorithms⁴⁶, inspired by the phenomenon of bird predation and fish foraging. PSO algorithm has strong optimization performance for non-convex optimization problems.

• 3. Cuckoo Search Algorithm (CSA) is a global optimization algorithm based on Levy flight⁴⁷, inspired by cuckoo’s breeding strategy. Cuckoo optimization algorithm, which combines stochastic search and deterministic search, is one of the early optimization algorithms that introduced Levy flight into applied mathematics.

• 4. Fireworks Algorithm (FWA) has a strong adaptive ability, and its inspiration comes from the blooming of fireworks⁴⁸. Because of its adaptive characteristics, fireworks algorithm can show strong global exploration ability and adapt to various continuous and discrete optimization problems.

The test results from F1 to F8 are shown in Table 4. The test results from F9 to F16 are shown in Table 5. The test results from F17 to F24 are shown in Table 6. By comparing the mean value, standard deviation, minimum fitness value and convergence curve of the operation results, the actual optimization effect of the BDBO algorithm can be intuitively understood.

Table 4 Experimental results of traditional algorithm 1.

Table 5 Experimental results of traditional algorithm 2.

Table 6 Experimental results of traditional algorithm 3.

It can be seen from Table 4 that in the unimodal test function, the BDBO algorithm is very competitive in both 30 and 100 dimensions. As can be seen from the table, in the 30-dimensional unimodal function test, FA and FWA algorithms have problems of premature convergence and falling into local optimal solutions, but BDBO algorithm can constantly jump out of local optimal solutions through Levy flight and carry out local fine exploitation. The convergence curve in 30 dimensions is shown in Fig. 5.

Fig. 5

30-dimensional convergence curve.

As can be seen from the Fig. 5, in the test functions F4 and F5, the escape and exploitation ability of BDBO algorithm is the most obvious, and the optimization effect of the algorithm is the best, indicating that the improved strategy effectively improves the ability of DBO algorithm to escape the local optimal solution. In addition, in the multi-modal test function, BDBO algorithm is more superior than other algorithms, which indicates that BDBO algorithm has stronger adaptability and flexibility. The convergence curve in 100 dimensions is shown in Fig. 6.

Fig. 6

100-dimensional convergence curve.

As can be seen from the Fig. 6, in the high-dimensional multimodal test function, the algorithm will face problems such as dimensional disaster and local optimal solution, and other algorithms are trapped in local optimal solutions, but BDBO algorithm shows excellent optimization performance. In addition, in the benchmark function, the optimization performance of BDBO is significantly better than the original DBO algorithm, and has more advantages over other algorithms. Therefore, the proposed improvement strategy plays a substantial role in improving the performance of DBO algorithm.

Improved algorithm comparison

The choice is to utilize the latest Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion (QHDBO) and the improved sine-guided Dung Beetle Optimization (IDBO) algorithm were compared with BDBO algorithm to verify the improved effect of the algorithm^49,50, and the experiment was carried out under the condition of 100 dimensions. The comparative experimental results show that the BDBO algorithm is significantly better than QHDBO and IDBO in terms of optimization accuracy, especially in the multimodal test functions, the optimization accuracy of BDBO algorithm is always in the leading position. The benchmark function test results are shown in Table 7.

Table 7 Experimental results of improved algorithm 1.

It is known from Table 8 that the BDBO algorithm has good optimization performance in high-dimensional multimodal benchmark functions. Secondly, the standard deviation of the experimental results of BDBO algorithm is significantly higher, which indicates that the algorithm is highly sensitive to random parameters, and the fine disturbance of parameters has a significant impact on the optimization performance of the algorithm. However, its stability and time complexity still need to be improved. There are many disturbance factors in BDBO algorithm, and Gaussian distributed parameters effectively reduce the randomness of parameters, but also enhance the sensitivity of the algorithm to parameters. Secondly, the running time of BDBO is relatively long, which indicates that there is still much room for improvement in its computational complexity. The convergence curve of the variant algorithm intuitively shows the advantages of BDBO algorithm over QHDBO and IDBO improved algorithms. The convergence curve of the variant algorithm is shown in Fig. 7.

Table 8 Experimental results of improved algorithm 2.

Fig. 7

Convergence curve of the variant algorithm.

The observation of Fig. 7 shows that BDBO algorithm has good convergence speed and optimization accuracy, which is significantly better than the other two algorithms. The optimization effect of BDBO algorithm is more dependent on the number of evaluations, and the fitness value steadily decreases with the increase of the number of evaluations. Secondly, the optimization ability of BDBO algorithm becomes more and more prominent with the increase of dimension and mode, indicating that BDBO algorithm is more suitable for complex optimization problems.

Single strategy variant comparison

In order to verify the effect of the improved strategy, the BDBO algorithm is compared with the single strategy variant, and the experiment was conducted under the condition of 100 dimensions. The test results from f1 to f16 are shown in Table 9, the test results from f17 to f21 are shown in Table 10, in which BDBO represents the balanced dung beetle optimization algorithm, DPO-R represents the parabolic adaptive parameter $R$ strategy, DPO-G represents the Gaussian distributed parameter $\beta$ strategy, and DPO-L represents the Levy flight escape strategy.

Table 9 Results of single strategy variation comparison 1.

Table 10 Results of single strategy variation comparison 2.

The observational results show that, the single strategy variants have their own advantages in the benchmark experiment. Levy flight speed can explore the optimal solution interval, and continuously escape the local optimal solution through long-distance walking. Using Gaussian distributed parameter $\beta$ to greatly enhance the utilization of the global optimal solution can further stimulate the exploitation potential of the algorithm. The parabolic adaptive parameter $R$ can be used to broaden the exploration scope of dung beetles, balance the exploration and exploitation capabilities of the algorithm, quickly converge to the optimal solution interval in the early stage, and significantly improve the optimization performance of the algorithm by combining the parameter $\beta$ and Levy flight strategy. The experimental convergence curve of the single strategy variant is shown in Fig. 8.

Fig. 8

Single strategy variant convergence curve.

As can be seen from Fig. 8, the effect of the DPO-G variant and the BDBO algorithm is relatively better under the single mode scenario of F1–F9, indicating that the Gaussian distributed parameter $\beta$ strategy is the main reason for the improved algorithm accuracy. And compared with DPO-G, BDBO algorithm in the early exploration stage has stronger exploration ability and can quickly converge to the local optimal region. In addition, the BDBO algorithm also has obvious advantages in the late iteration. Therefore, the proposed BDBO algorithm has practical significance.

The study used the Wilcoxon rank-sum test method to test the results of the single strategy variant comparison test. The Wilcoxon rank sum test is a nonparametric test method to test for significant differences between the two algorithms⁵¹. Using statistical tests to avoid the chance of experimental results is a common method for algorithm testing experiments. The p-value results of the Wilcoxon rank sum test are shown in Table 11.

Table 11 Wilcoxon rank sum test p-values.

Table 11 shows that the BDBO algorithm has significant advantages over the original DBO algorithm, and the experimental results of 17 test functions out of 21 have significant differences, indicating that the proposed improvement strategy is statistically significant. The single strategy variants DBO-R, DBO-L and DBO-G have great advantages over the original DBO, and can significantly improve the optimization performance of the algorithm. In addition, the percentage of accuracy improvement calculated by BDBO algorithm over DBO algorithm is 35.29%, and the optimization accuracy is significantly improved. Therefore, the improved strategy can significantly improve the optimization performance of the algorithm. It is worth noting that the test results of the DBO-G variant show that the p-value in the 17 test functions is less than 0.05, which is a significant difference, indicating that the random parameter $\beta$ has a great influence on the optimization performance of the DBO algorithm. In addition, it can be seen from Fig. 7 that the parabolic $R$ parameter and Levy flight escape strategy can slow down the slow convergence of DBO-G variant, and the optimization performance of DBO algorithm can be significantly improved with the Gaussian distribution parameter $\beta$ strategy.

MPPT application based on BDBO algorithm

In order to verify the practical application effect of BDBO algorithm, the particle swarm optimization algorithm and gravity search algorithm (GSA) are applied to MPPT module to compare the experiment, and the power point tracking efficiency of the three algorithms is compared by observing the output power convergence curve. In the working circuit of photovoltaic system, it is crucial to accurately build function components for power point optimization to improve the conversion rate of light energy⁵². Using the $simulink$ tool to simulate the photovoltaic circuit, as shown in Fig. 9, the optimization algorithm call exists in the form of components in the circuit. The experiment set up the same circuit simulation conditions to control the influence of irrelevant variables. In addition, dynamic parameter acquisition is accepted through an online algorithm to ensure real-time power point optimization.

Fig. 9

Photovoltaic circuit simulation.

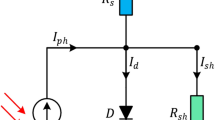
The Boost circuit is constructed based on the I-U characteristics of photovoltaic cells. In practical application engineering, the photovoltaic circuit is composed of multiple photovoltaic cells in series and parallel, and its I–U characteristics are affected by the number of series and parallel cells. The I–U characteristic expression of the combined circuit is shown in Eq. (16)⁵³.

$${I}_{PV}={N}_{p}{I}_{ph}-{N}_{p}{I}_{d}\left\{\text{exp}\left[\frac{q\left({V}_{PV}+{I}_{PV}{R}_{s}\right)}{{N}_{s}AKT}\right]-1\right\}-{N}_{p}\frac{{V}_{PV}+{R}_{s}{I}_{PV}}{{N}_{s}{R}_{p}}$$

(16)

where ${I}_{PV}$ is the output current of the photovoltaic cell, ${I}_{ph}$ is the photogenerated current, ${I}_{d}$ is the saturation current, ${V}_{PV}$ is the output voltage of the solar cell, $A$ is the ideal factor, $K$ is the Boltzmann constant, $T$ is the immediate temperature, $q$ is the amount of electronic charge, ${R}_{s}$ is the series resistance, ${R}_{p}$ is the parallel resistance, ${N}_{p}$ is the number of parallel cells, and the number of parallel cells is the following: ${N}_{s}$ Indicates the number of batteries in series. The calculation equation of photogenerated current ${I}_{ph}$ is shown in Eq. (17).

$${I}_{ph}=\left(\frac{G}{{G}_{n}}\right)\left[{I}_{scr}+{k}_{i}\left(T-{T}_{r}\right)\right]$$

(17)

where, ${I}_{ph}$ represents the photogenerated current, $G$ represents the actual light intensity, ${G}_{n}$ represents the nominal light intensity, ${I}_{scr}$ represents the short circuit current under nominal conditions, and ${k}_{i}$ represents the current temperature coefficient.

The engineering application of MPPT is a dynamic optimization problem. The photovoltaic system obtains the best operating point by calling the optimization algorithm component to improve the efficiency of the system. The optimization algorithm uses online learning programming to output the global optimal solution for the next time based on the information state of the system at the current time. The workflow of the MPPT online learning optimization component is shown in Fig. 10.

Fig. 10

Online algorithm workflow.

Figure 10 shows that the algorithm calculates the fitness value of the individual at the current time by updating the system dynamic parameter information, and outputs the best operating point information at the next time for the system. A period of time is discretized into enough time periods, and each time period can be approximately regarded as a moment. Finally, the algorithm decided to update the solution vector iteratively according to the system running time. The actual application effect of BDBO algorithm is shown in Fig. 11.

Fig. 11

BDBO output power change curve.

The simulation results show that the BDBO algorithm can control the maximum power output stably when the light intensity changes. The ultimate power data and the index ranking of sensitivity and stability of the three algorithms are studied and counted, and the final results are shown in Table 12.

Table 12 Experimental result.

The smaller the ranking value, the better the performance of the algorithm. According to Table 10, the output power of BDBO in the application environment reaches up to 32,14, which has a significant advantage over the other two algorithms, indicating that BDBO algorithm has stronger adaptability to the change of environmental factors. The experimental results show that the stability of BDBO algorithm is poor, but the comprehensive performance is good. The comparative experimental results of the three algorithms are shown in Fig. 12.

Fig. 12

Comparison of output power change curves.

The fluctuation degree of the output power change curve under the application of PSO and GSA algorithms is low, but the saturation degree of the curve is also low, indicating that the algorithm falls into the local optimal solution. The output power saturation degree of BDBO algorithm is obviously higher, and the final output power exceeds 30W, far exceeding the limit output power of PSO algorithm and GSA algorithm. Therefore, BDBO algorithm has better effect in engineering application, higher adaptability and sensitivity, and the proposed BDBO algorithm has practical application value.

Conclusion

A balanced BDBO algorithm is proposed, which effectively balances the exploration and exploitation capabilities of DBO algorithm by reducing the randomness of parameters and enhancing the exploration ability of the algorithm, and improves the convergence accuracy and escape ability of the algorithm. The experimental results of CEC-2017 benchmark function show that the convergence accuracy of BDBO algorithm is higher than that of DBO, FA, PSO, CSA and FWA algorithms. From the convergence curve, it can be seen that the exploration ability and escape ability of BDBO algorithm are significantly improved, and it has significant advantages over QHDBO and IDBO variant algorithms in terms of convergence speed and accuracy. In addition, the results of Wilcoxon rank sum test show that all strategy variants have significant advantages over the original DBO algorithm, and the P values are basically less than 0.05, which is statistically significant. For MPPT engineering application problems, BDBO algorithm performs well, and the optimization effect is obviously better than PSO and GSA algorithm, which verifies the optimization performance and practical application value of BDBO algorithm. The parameters R and $\beta$ of the original algorithm are optimized and adjusted, which provides a new idea for the improvement of DBO algorithm. In the future research, the stability of BDBO algorithm, the sensitivity to random parameters and the improvement of its computational complexity will further improve its optimization performance, making the algorithm better suitable for large-scale optimization problems with complexity. In addition, the performance of the algorithm is verified by MPPT application, which proves that the BDBO algorithm is suitable for complex engineering applications and can be further studied.