Introduction

With the rapid development of autonomous driving technology and the automobile manufacturing industry, lane detection as one of the core functions of autonomous driving has been paid more and more attention, and great achievements have been achieved1,2,3,4. During the driving process of the autonomous vehicle, the lane line could help the autonomous vehicle to accurately determine the current position and direction on the road, so that the vehicle’s driving trajectory can be automatically adjusted if necessary to ensure the safe driving of the autonomous vehicle5,6. Therefore, it is crucial to accurately identify the location of the lane line. Although traditional CNN-based lane detection algorithms have addressed this problem to a certain extent and can achieve detection results in simple scenarios, lane detection in complex environments still faces many challenges. In real-world autonomous driving scenarios, lane markings are easily obscured by complex conditions such as rain, snow, extreme lighting (e.g., glare, low light), and traffic congestion, making accurate lane detection challenging. For example, factors such as rain and fog may cause the algorithm to fail to detect lane markings, and the detection speed may fall below 60 FPS7. These issues have long been challenges in the field of autonomous driving. Therefore, it is very important to improve the accuracy of lane detection and reduce detection time in complex environments.

In recent years, owing to the continuous advancements in deep learning, the Transformer model has exhibited remarkable performance in the field of natural language processing (NLP) and has proven its applicability in various other domains8. Therefore, we tried to resolve the lane detection trouble with the Transformer. In contrast to conventional lane detection algorithms based on convolutional neural networks, the proposed lane detection approach in this study departs from the use of convolutional frameworks and instead adopts the Transformer model as the fundamental architecture9. Diverging from convolutional neural networks, the Transformer can better process sequence data and capture long-distance relationships in the sequence, helping to improve the accuracy of lane detection, which is especially important for lane detection problems10. Additionally, the Transformer’s capability for parallel data processing contributes significantly to reducing detection time, which is a crucial factor for real-time applications.

In real-world driving scenarios, lane detection is often affected by various factors such as, weather conditions, lighting, and obstruction from other vehicles, which can result in suboptimal detection performance. Additionally, the high complexity of existing algorithms leads to slow detection speeds11. In this paper, we propose a lane detection method for complex road environments. Compared to the Transformer-based LSTR algorithm, our method improves detection accuracy by 4.17% on the complex scene lane dataset CULane, while achieving a detection speed of 78 FPS. It demonstrates broad applicability in practical driving scenarios. In summary, the contributions of this paper are as follows: It demonstrates broad applicability in practical driving scenarios. In summary, the contributions of this paper are as follows:

  1. (1)

    We propose a lane detection model for complex road environments based on pure Transformer architecture, which eliminates the need for manually designing convolutional kernels or filters, making it more flexible. Furthermore, the model iteratively employs attention mechanisms to capture contextual information. This understanding of the global environment enables the model to adapt to various weather conditions and types of roads.

  2. (2)

    To solve the problem of high computational complexity when implementing global attention by multi-head attention mechanism, a separable lane multi-head attention mechanism based on window self-attention is proposed. This mechanism uses a single window to mark the core information of each window, which can more quickly and effectively establish attention relationships between different windows, thereby reducing computational costs and improving detection speed.

  3. (3)

    To address the issue of insufficient information interaction between two adjacent windows in the multi-head attention mechanism, we propose an extended and overlapping strategy, which expands the size of input features and uses larger and overlapping windows to segment the expanded features. This strategy effectively enhances detection accuracy in complex road environments by facilitating information transfer among adjacent pixels.

The rest of this paper is organized as follows. First, the proposed lane detection model is introduced in detail. Next, the proposed lane detection method is tested on multiple datasets, and the experimental results are analyzed. Finally, a summary of the paper is provided.

Related work

In the field of automatic driving, lane detection technology plays a crucial role in enabling vehicles to achieve functions such as autonomous driving and automatic parking. Therefore, research on lane detection technology has become a hot topicin the field of autonomous driving technology. Over the past decade, lane detection technologies have mainly been divided into two categories: traditional lane detection methods and deep learning-based lane detection methods.

Traditional method

Traditional lane detection methods first preprocess the image to obtain the region of interest through smoothing, denoising, and other techniques. Then, they extract edge information from the lane markings using manually designed features and fit the extracted features to obtain lane information.

Early lane detection is usually based on image brightness and color changes through pixel-level operations to detect lane lines. To improve the accuracy of lane detection, many scholars have started to concentrate on feature extraction methods. In12, a multi-channel threshold fusion method based on gradient and background difference is proposed. This method combines the HSV (Hue Saturation Value) feature of the lane line to detect the lane line. A fast method for lane line extraction is proposed in13, which improves the detection accuracy by improving the fire-fly edge detection algorithm. In14, a lane detection algorithm named LANA is introduced. LANA utilizes frequency domain features for lane detection and overcomes some drawbacks of previous algorithms, such as interference at distant edges. However, these methods are less accurate in detecting lane markings. In15, a quadratic min-valued segmentation method based on the Otsu method is proposed. This method obtains lane line feature points by progressive scanning on road images that have been binarized with lane area and background area, and then filters and fits the feature point clustering. In16, a method for linear prediction of lane lines using the local gradient feature of grayscale images is proposed. This method utilizes the vertical gradient image instead of employing a threshold for binary conversion. Consequently, it is not affected by changes in lighting and shadows.

The traditional lane detection methods typically involve using feature extractors to extract lane features and then performing post-processing to fit curves. However, this approach is susceptible to various sources of interference, which can result in lower detection accuracy. Moreover, the post-processing steps in these methods increase computational overhead, which affects real-time performance.

Deep learning-based method

With the continuous development of graphics processing hardware, deep learning has shown the advantages of high performance and efficiency in many challenging fields. By building artificial neural networks and using massive data sets to train neural network, the network can learn features independently and have good robustness to complex environments.

With the rise of deep learning, a large number of scholars are interested in using deep learning to solve the problem of image lane detection. By using specially designed network structures, such as convolutional layers and pooling layers, convolutional neural networks can automatically learn features from images and detect lane lines. Some of the earliest works used basic CNN structures, such as LeNet17 and AlexNet18. The advantages of the above methods are that features can be directly extracted from images, thus reducing the complexity of manual feature design. However, due to the limitation of the number of semantic segmentation categories, these methods are often difficult to accurately detect lane lines in complex environments. In complex environments, lane line detection results are susceptible to the following impacts: under adverse weather conditions or insufficient lighting, the algorithm may mistakenly identify non-lane features as lane lines, resulting in false positives; lane lines may be obscured by rain, snow, or obstacles, leading to false negatives, especially in low-light or foggy conditions; moreover, environmental factors may increase detection processing time, particularly when poor image quality necessitates additional preprocessing steps, leading to detection delays. In19, a robust lane detection algorithm adapted to various challenging situations is proposed. This method uses a fuzzy image enhancement generation adversarial network to enhance the fuzzy lane features, thereby improving the precision rate of lane detection and reducing the detection time. An improved large-field model for lane detection is proposed in20, which can be used to detect lane lines in harsh environments. In21, a lane detection algorithm based on deep learning is proposed. The algorithm utilizes multi-scale spatial convolution and multi-task learning to effectively handle complex road conditions, such as obstructions, lighting variations, and road surface wear, among others. In22, a lane detection method based on the VGG16 network is proposed, which combines self-attention distillation models and Spatial Convolutional Neural Network (SCNN) models to some extent, addressing the issue of low detection accuracy in complex road scenarios.

The remarkable success of the Transformer model in the field of natural language processing has attracted researchers to explore its adaptability to computer vision. Researchers have confirmed that the Transformer model outperforms CNN-based backbone networks in lane line detection tasks23,24,25,26. CNN has a small receptive field and needs to stack multiple convolutional layers to achieve a larger receptive field, which leads to higher spatial complexity in image processing and requires more computing resources. On the other hand, the Transformer uses a self-attention mechanism to acquire features in the image and does not need to expand the receptive field through overlapping convolutional layers. As a result, it is more computationally efficient. In27, a Transformer network is utilized to detect lane lines and employ a self-attention mechanism to capture the long and narrow structure, as well as the global context information of the lane lines. This approach resulted in an enhancement in the overall detection speed. A lane detection method based on a perspective transformer layer and a spatial converter network28. The process of inverse perspective mapping is decomposed into several differentiable homologous transformation layers, and subsequent convolution layers are used to refine the interpolation feature map to reduce artifacts and improve detection accuracy. In29, a lane detection Transformer based on multi-frame input is proposed. The Visual Transformer module is used to obtain the interaction information with lane instances, to return the parameters of the lane under the lane shape model. Polynomial regression is combined with the Transformer to capture global context information through the self-attention mechanism, and the global-local training strategy is used to capture multi-scale features to capture richer lane information involving structure and context30. In31, a HW-Transformer model based on row-column self-attention is proposed, which significantly outperforms traditional CNN-based segmentation methods in lane line detection tasks by restricting the attention range and introducing a self-attention knowledge distillation mechanism. A Transformer architecture named CondFormer is proposed, which achieves independent detection of each lane by generating conditional convolution kernels. It strikes an excellent balance between accuracy and speed by combining global modeling capability with detailed feature extraction32. Although the methods using Transformer for lane detection have achieved good results in simple scenarios, their accuracy and speed still need improvement in complex conditions. Therefore, it is necessary to improve both the accuracy and speed of lane detection in complex environments.

Proposed method

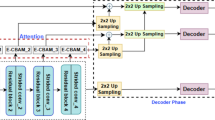
This paper aims to establish a lane detection model designed for complex scenarios. The model structure is displayed in Fig. 1. In this section, we provide a detailed overview of our proposed lane detection method, including the establishment of the lane model, the definition of the loss function, and a comprehensive explanation of the network architecture of the model.

Fig. 1
figure 1

The network architecture diagram.

Full size image

Lane representation

Lane model

The lane model is defined as a polynomial structure:

$$\begin{aligned} X = {\sum _{n=0}^N \alpha _{n} Y^n} + b \end{aligned}$$
(1)

where \(\left( X,Y \right)\) represents the points of the lane lines on the ground. N is the degree of polynomial X. b and \(\alpha _{n}\) are the coefficients in the lane polynomial function.

In real driving environments, the shape of lanes is not usually complicated. Therefore, a commonly used cubic polynomial is used to approximate the shape of the lanes on the flat ground:

$$\begin{aligned} X = \alpha _1 Y^3 + \alpha _2 Y^2 + \alpha _3 Y + b \end{aligned}$$
(2)

The cubic polynomial of a flat road is transformed into a “bird’s-eye view” to avoid the influence of uneven roads. The transformation formula is as follows:

$$\begin{aligned} \left\{ \begin{aligned} X&= x \times f_x \times Y \\ Y&= \frac{H}{y \times {f_y}} \end{aligned} \right. \end{aligned}$$
(3)

where \(\left( x,y \right)\) represents the corresponding pixel point on the transformed bird’s-eye view perspective, \(f_x\) represents the width of a pixel on the focal plane divided by the focal length, \(f_y\) represents the height of a pixel on the focal plane divided by the focal length, and H represents the height of the camera installation.

Considering that the camera may tilt due to the bumps during driving, assuming that the tilt angle is \(\theta\), the transformation before and after the tilt is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x = x' \\ {\left[ \begin{array}{l} f \\ y \end{array}\right] =\left[ \begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right] \left[ \begin{array}{l} f' \\ y' \end{array}\right] } \end{array} \right. \end{aligned}$$
(4)

where f represents the focal length of the camera. \(f'\) represents the focal length of the camera after pitch transformation, and \(\left( x',y' \right)\) are the corresponding pixel points after pitch transformation. In combination with Eqs. (2)–(4), it can be obtained:

$$\begin{aligned} x' = \frac{\alpha _{1}'}{(y' - f'')^2} + \frac{\alpha _{2}'}{(y' - f'')} + \alpha _{3}' + b' \times y' -b'' \end{aligned}$$
(5)

where \(f'' = f \sin \theta\), \(\alpha _{1}'=\alpha _{1} \cos ^2 \theta \times H^2 / f_x \times {f_y}^2\), \(\alpha _{2}'=\alpha _{2} \cos \theta \times H / f_x \times {f_y}\), \(\alpha _{3}'=\alpha _{3} / f_x\), \(b' = b \times f_y / f_x \cos \theta \times H\) and \(b'' = b \times f_y \times f \tan \theta / f_x \times H\). Additionally, the model also considers the confidence score \(c_{i} \in {[0,1]}\) of the lane marking (0 represents the background, and 1 represents the lane marking).

Therefore, the output of the i lane marking is parameterized as \(p_{i}\) based on the above analysis:

$$\begin{aligned} p_{i} = \left( c_{i}, \alpha _{1}', \alpha _{2}',\alpha _{3}', f'', b', b'' \right) \end{aligned}$$
(6)

where \(i \in \{1,\ldots ,M\}\), The value of M corresponds to the total number of lanes.

Lane prediction loss

The algorithm proposed in this paper uses the Hungarian matching loss to perform a bipartite graph matching between the predicted lane line parameters and the actual lane lines. The regression loss for a specific lane is optimized based on the matching results.

Firstly, the predicted set of lane line parameters is defined as:

$$\begin{aligned} \mathscr {P} = \{p_{i}\}^M _{i=1} \end{aligned}$$
(7)

where M is defined as being greater than the number of lanes that commonly occur. Then, the set of real lane line markers is represented as:

$$\begin{aligned} \mathscr {S} = \{(c_{i}, x'_{i},y'_{i})\}^M _{i=1} \end{aligned}$$
(8)

Next, by searching for the optimal injection function: \(l:\mathscr {S}\rightarrow \mathscr {P}\), the bipartite matching problem between the predicted set of lane line parameters and the set of real lane line markers is defined as a minimal cost problem:

$$\begin{aligned} \hat{l} = \mathop {\arg \min }\limits _{l} \sum _{i}^M \mathscr {L}_{bmc}(\mathscr {P}_{l_{i}},\mathscr {S}_i), \end{aligned}$$
(9)

where \(\mathscr {L}_{bmc}\) is the matching cost between the i-th real lane line and the predicted parameter set with index \(l_{i}\). The matching cost takes into account both category prediction and the similarity between the predicted parameter set and the real lane.

Finally, the regression loss function is defined as:

$$\begin{aligned} \begin{aligned} \mathscr {L} = \sum _{i=0}^M -\mu _{1}\log {g\left( c_{i}\right) }+\mathbbm {Z}\left( c_{i}=1\right) \mu _{2} L_{mae}\left( S_i, \mathscr {S}_{\hat{l}(i)}\right) \end{aligned} \end{aligned}$$
(10)

where \(g\left( c_{i}\right)\) is the probability of category i, \(\mathscr {S}_{\hat{l}(i)}\) is the fitted lane line sequence, \(\mu _{1}\) and \(\mu _{2}\) are the coefficients of the loss function, \(L_{mae}\) represents the mean absolute error, and \(\mathbbm {Z}(\cdot )\) represents the indicator function.

Separable lane detection block

The multi-head attention mechanism proposed by Transformer models the relationships between all pixels when processing two-dimensional feature maps, which increases the computational complexity and slows down the speed of lane detection. In this paper, we propose a separable lane multiple attention mechanism (Sep-LMSA) based on window self-attention, which employs a single window to label the core information of each window, enabling a prompt and efficient establishment of attentional relationships between different windows. This mechanism includes a Depthwise Self-Attention (DSA) module, which can capture spatial information within individual sub-windows. Additionally, DSA is combined with a Pointwise Self-Attention (PSA) module to integrate spatial information from different sub-windows and enable global information interaction.

Based on this mechanism, we construct a Separable Lane Detection Block (SepLDT Block), as illustrated in Fig. 1, that consists of two residual structures. The first residual structure consists of a Sep-LMSA and a Layer Normalization (LN), while the second residual structure consists of a Multilayer Perceptron (MLP) and an LN.

Depthwise self-attention

Firstly, for a given input \(x \in \mathbb {R}^{B \times C \times H \times W}\), where B is the batch size, C is the number of channels, H is the height, and W is the width, the feature map of the input is divided into:

$$\begin{aligned} x' = \mathbb {R}^{(n_{windows} \times B)\times C \times N} \end{aligned}$$
(11)

where \(n_{windows}\) is the number of segmented windows, \(N=H_{window} \times W_{window}\), \(H_{window}\) is the height of the segmented sub-window, and \(W_{window}\) is the width of the segmented sub-window.

Then, for the window token \(W_t \in \mathbb {R}^{(n_{windows} \times B) \times C \times 1}\) generated for each sub-window, the window mark is concatenated with the feature of the sub-window to generate the feature representation of each sub-window:

$$\begin{aligned} z = \text {Concat}(W_t, x') = W_t + x' \end{aligned}$$
(12)

Secondly, the feature representation of each sub-window obtained is mapped to query (q), key (k), and value (v), where \(Q, K,V \in \mathbb {R}^{(n_{windows \times B}) \times C \times (N + 1)}\). The obtained q, k, and v are split into multi-head forms:

$$\begin{aligned} {Q, K, V} \in \mathbb {R}^{(n_{windows} \times B) \times n_{heads} \times (N + 1) \times C_{head}} \end{aligned}$$
(13)

where \(n_{heads}\) represents the number of multi-head formats and \(C_{head}\) represents the number of channels in the multi-head format.

Finally, all pixels in each sub-window and their corresponding window tokens are integrated. The query, key, and value are used to calculate the attention function separately and form the matrices Q, K, and V. This produces the output of the DSA:

$$\begin{aligned} \text {DSA}(z) = \text {Attetion} (z\cdot W_Q, z\cdot W_K, z\cdot W_V) \end{aligned}$$
(14)

where \(W_Q\), \(W_K\), and \(W_V\) represent three linear layers used for query, key, and value calculation, and the attention mechanism is a standard self-attention mechanism.

After normalization using LN, the output is obtained as:

$$\begin{aligned} z' = \text {DSA} (\text {LN}(z)) \end{aligned}$$
(15)

Pointwise self-attention

The DSA is a local operation and needs to merge the spatial information of each sub-window to establish attention relationships between all windows and form global attention. This paper proposes a PSA module to integrate the spatial information of different windows and achieve global information interaction, thus obtaining the feature output of the input feature.

The feature map \(\dot{z} \in \mathbb {R}^{B \times n_{heads} \times n_{windows} \times N \times C_{head}}\) and window token \(w_t \in \mathbb {R}^{B \times n_{heads} \times n_{windows} \times C_{head}}\) are extracted from the output of the DSA by the PSA module. Then, using the window token, PSA models the attention relationship between different windows. Combined with Layer Normalization and GeLu activation function, the window token is mapped to query branch and key branch using a \(1 \times 1\) convolution to generate the attention map. Meanwhile, the feature map is used as the value branch. This enables the attention calculation between windows and achieves global information exchange, generating an attention map as output:

$$\begin{aligned} \begin{aligned} \text {PSA}(\dot{z}, w_t) = \text {Attetion} (&\text {GeLu}(\text {LN}(w_t))\cdot {W_Q}, \text {GeLu}(\text {LN}(w_t)) \cdot W_K, \dot{z}) \end{aligned} \end{aligned}$$
(16)
Fig. 2
figure 2

Extended and overlapping strategy.

Full size image

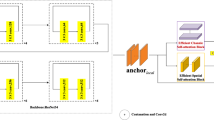
Multi-resolution overlapping feature aggregation block

Expand and overlap strategy

To address the insufficient information interaction between adjacent windows in the multi-head attention mechanism, resulting in challenges recognizing lane markings in complex road environments, we propose an extended and overlapping strategy. The strategy expands the size of input features and uses larger and overlapping windows to segment the expanded features. By promoting information transfer among neighboring pixels, this strategy enhances detection accuracy in complex road environments, thereby significantly elevating the performance of lane detection models. Figure 2 shows a feature size of 9×9 without an overlapping strategy and a feature size of 13×13 with overlapping strategy, where the 13×13 overlapping strategy includes an edge padding operation with a padding value of 3.

Based on the extended and overlapping strategy, a Multi-resolution Overlapping Feature Aggregation Block (MO Feature Aggregation Block) using standard multi-head attention architecture is designed. The multi-resolution overlapping feature aggregation module is added in each stage to obtain a larger receptive field and enhance the accuracy of lane detection. The structure of the multi-resolution overlapping feature aggregation module is shown in Fig. 3.

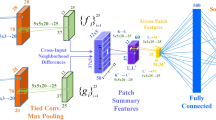
Scale cosine muti-head self-attention

In the standard self-attention calculation process, the similarity term of pixel pairs is obtained by the dot product calculation between query vectors and key vectors. When attention networks are used to train computer vision models, especially on large-scale datasets, some modules and head modules of the attention map may be dominated by a small number of pixel pairs, resulting in unsatisfactory results. To solve this problem, this paper designs a Scale Cosine multi-head Self-attention (SCMHSA) method to replace the dot product calculation method in self-attention.

Fig. 3
figure 3

The structure diagram of multi-resolution overlapping feature aggregation block.

Full size image
$$\begin{aligned} \text {sim}(q_i, k_j) = \frac{\cos (q_i, k_j)}{\lambda } + B_{ij} \end{aligned}$$
(17)

where \(B_{ij}\) is the relative positional deviation between pixel i and pixel j, and \(\lambda\) is a learnable parameter set to 0.01.

Due to the lower resolution of the training dataset compared to the higher resolution of the vehicle’s front-facing camera, the pre-trained model’s performance in detecting lane markings in real-world environments remains suboptimal. To address this issue, this paper introduces the Log-spaced Continuous Position Bias (Log-CPB) method, which effectively transfers a pre-trained model using low-resolution images to downstream tasks with high-resolution inputs, and smoothly interacts with information between windows of different resolutions. For the continuous position bias, this method does not directly optimize parameterized bias, but uses a small meta-network to deal with irregular data points based on relative coordinates:

$$\begin{aligned} C(\Delta {x}, \Delta {y}) = G(\Delta {x}, \Delta {y}) \end{aligned}$$
(18)

where G is a small network structure consisting of two MLPs and a ReLU activation function. The meta-network G generates a bias value for any relative coordinates, so it can be naturally transferred to fine-tuning tasks with windows of different resolutions.

When processing windows with a large resolution span, relative position bias requires large computational costs. To address this problem, logarithmically spaced coordinates are used instead of linearly spaced coordinates for relative position encoding:

$$\begin{aligned} \left\{ \begin{aligned} \Delta {\hat{x}}&= \text {sign(x)} \cdot \log (1+ \left| \Delta {x} \right| ) \\ \Delta {\hat{y}}&= \text {sign(y)} \cdot \log (1+ \left| \Delta {y} \right| ) \end{aligned} \right. \end{aligned}$$
(19)

where \(\Delta {x}\) and \(\Delta {y}\) are linear scaling coordinates, while \(\Delta {\hat{x}}\) and \(\Delta {\hat{x}}\) are logarithmically spaced coordinates.

Prediction FFNs

As the prediction head, the FFN Prediction can directly output the predicted lane parameters. A linear operation projects the output of the network’s final stage into \(2\times M\). Then, a softmax layer is employed to obtain the predicted class \(c_{i} \in\) [0, 1], \(i\in 1,\dots ,M\), where 0 denotes the background, 1 represents the lane, and M is typically much larger than the actual number of lanes in normal scenarios. Simultaneously, a three-layer perceptron with a ReLU activation function projects the output of the network’s final stage into the dimension of \(4\times M\), where the parameter 4 represents the four sets of lane models. Finally, another three-layer perceptron obtains the shared parameters.

Experiments

Dataset

The CULane dataset encompasses more intricate urban driving scenarios, incorporating challenges such as shadows, extreme lighting conditions, and road congestion. LLAMAS is a newly established extensive dataset, without a publicly available test set. Detailed information regarding these datasets is presented in Table 1.

Table 1 Details of datasets.
Full size table

Evaluation metrics

To fairly compare various advanced methods, we follow the evaluation metrics provided by the official of each dataset.

For the TuSimple dataset, three metrics are officially provided: Accuracy, False Positive (FP), and False Negative (FN). Accuracy refers to the ratio of correctly predicted lane points to the total number of annotated lane points. FP refers to the ratio of incorrectly predicted lane lines to the total number of correctly predicted lane lines. FN refers to the ratio of undetected lane lines to the total number of annotated lane lines. Frames Per Second (FPS) is a measure of the number of images a system can process in one second. In lane detection or other real-time applications, FPS is often used to indicate how smoothly and quickly the algorithm operates. Accuracy ranges from 0 to 1, and the real-time performance standard is that the FPS value should be greater than or equal to 30. Higher values of Accuracy and FPS indicate better detection results, while a lower value of FP and FN indicate better detection results. Accuracy is defined as follows:

$$\begin{aligned} Accuracy=\frac{\sum _{i}{N_{pred}}_{i}}{\sum _{i}{N_{gt}}_{i}} \end{aligned}$$
(20)

where \({N_{gt}}_{i}\) represents the number of ground truth points for the i-th lane and \({N_{pred}}_{i}\) represents the number of correctly predicted lane points for the i-th lane.

The metrics of FP and FN are defined as follows:

$$\begin{aligned} \begin{aligned} FP&= \frac{F_{pred}}{N_{pred}} \\ FN&= \frac{M_{pred}}{N_{gt}} \end{aligned} \end{aligned}$$
(21)

where \(F_{pred}\) stands for the number of incorrectly predicted lanes, and \(N_{pred}\) represents the total predicted lane count. \(M_{pred}\) signifies the count of predicted missed ground truth channels, and \(N_{gt}\) is the count of all ground truth channels. According to the TuSimple benchmark, we have set the allowed deviation distance to 20 pixels. A point is considered true if the distance between it and its corresponding marker is within the allowable deviation range.

For the CULane and LLAMAS dataset, three metrics are officially provided: F1, Precision, and Recall. F1-score is a commonly used evaluation metric for lane detection, as it combines both precision and recall. It is commonly used in binary or multi-class classification tasks. The value of the F1-score ranges from 0 to 1, with a value closer to 1 indicating better model performance. In a lane line classification task, which is a binary classification task, Precision refers to the proportion of samples that are truly positive among those classified as positive. Recall refers to the proportion of positive samples that are correctly classified as positive. Higher values of F1, Precision, and Recall indicate better detection results. The definition of F1 score is as follows:

$$\begin{aligned} F1 = \frac{2 \cdot {Precision} \cdot {Recall}}{{Precision} + {Recall}} \end{aligned}$$
(22)

where \({Precision} = \frac{TP}{TP + FP}\) and \({Recall} = \frac{TP}{TP + FN}\). Lanes are assumed to be 30 pixels wide. If the pixel Intersection over Union (IoU) between the predicted and ground truth lanes is over 0.5, the lane segments are considered to be matched.

Implementation details

In this study, we conduct experiments on three different datasets: TuSimple, CULane, and LLAMAS. Our model is trained for the task of lane detection using a single RTX 2080 Ti. We use 500K iterations for training all datasets, without using a validation set during training, and only adjusting hyperparameters on the validation set. The initial learning rate is set to 1e-1, with a decay of 10 times every 450,000 iterations. The coefficients of the loss function are set to 3 and 2, while the fixed number of predicted curves is set to 7. The batch size is set to 1633. The input resolution for TuSimple and LLAMAS is set to 360x640, while for CULane it is set to 288x800. We also apply a cosine annealing learning rate schedule to optimize performance.

Additionally, we apply various data augmentation techniques to the training process, including random affine transforms, random horizontal flipping, and color jittering.

SOTA methods comparison

In this section, we conduct experiments and perform result analysis on three datasets: TuSimple, CULane34, and LLAMAS44. In the TuSimple dataset experiments, nine algorithms are compared: SCNN, RESA, UFLD, FastDraw, ENet-SAD, Line-CNN, PINet, PolyLane-Net, and LSTR. In the CULane dataset experiments, seven algorithms, including SCNN, RESA, UFLD, CurveLanes-NAS, FastDraw, ENet-SAD, and LSTR, are compared. In the LLAMAS dataset experiments, four algorithms, including SCNN, RESA, PolyLane-Net, and LaneATT, are compared.

Experimental results of TuSimple

The experimental results on the TuSimple dataset are shown in Table 2 The TuSimple dataset does not include complex weather conditions such as fog and rain, so the detection of near and far lane markers is the main factor for comparison. SCNN, RESA, UFLD, FastDraw, ENet-SAD, Line-CNN, and PINet are all point detection-based methods, while PolyLane-Net and LSTR, like the proposed method in this chapter, are curve prediction-based methods.

Table 2 Comparison experiment results on TuSimple. bold, italic, and bolditalic indicate the first, second, and third scores, respectively.
Full size table

Among the point detection-based methods, Line-CNN has the highest detection accuracy of 96.87%, but its detection speed is only 30 frames per-second. Compared to Line-CNN, the method proposed in this chapter has a 0.45% lower detection accuracy, but its detection speed is 2.6 times faster than Line-CNN. Compared to the fastest detection algorithm UFLD, the proposed method has a 0.81% higher detection accuracy, but there is a large difference in detection speed. However, the proposed lane detection method already meets the real-time requirement.

Among curve prediction-based methods, the detection accuracy of the proposed method is improved by 3.06% than PolyLane-Net and a 0.24% higher detection accuracy than LSTR.

In order to more intuitively show the superiority of the lane detection method in this paper, three algorithms, LSTR, SCNN, and RESA, are selected for visual result comparison. The visualization results are shown in Fig. 4, where the first column is the original image, the second column is the detection results of the proposed method, the third column is the detection results of the LSTR algorithm, the fourth column is the detection results of the SCNN network, and the fifth column is the detection results of the RESA algorithm. The visualization result comparison on the TuSimple dataset mainly focuses on the detection performance of near and far lane markings in common driving environments, as well as the detection performance when lane markings are occluded. The first and second rows show the detection results in the ideal driving environment on straight and curved roads. For distant lane lines, the method proposed in this paper exhibits significantly better detection performance compared to the other three methods. The three detected lane markings extend to the disappearing point of the far end, forming a vanishing point. The third, fourth, and fifth rows show the detection performance in the presence of occluded lane markings. Since SCNN and RESA are point-based detection algorithms, they cannot accurately mark the obscured lane markings when other vehicles are present in the image. LSTR is better than SCNN and RESA, but there are still shortcomings in the detection performance of the far-end lane markings, and in the fourth row of the detection result, the leftmost lane marking of the image is missed.

Experimental results of CULane

The experimental results of the CULane dataset comparison are shown in Table 3. The CULane dataset contains nine driving scenarios, so the F1 scores for each scenario and the total F1 score for all scenarios need to be calculated separately. The numbers in the ’No lane’ column represent the count of false positives. This is because there are no lanes in the images of the crossroad driving scenario. A lower number indicates better model performance.

Fig. 4
figure 4

Comparison of visualization results of TuSimple.

Full size image
Table 3 Comparison experiment results on CULane.
Full size table

The visual comparison of the CULane dataset is illustrated in Fig. 5. Figure 5 provides a visual contrast of the detection results in the common straight driving environment (first, second, and third rows), strong light interference driving environment when exiting the tunnel (fourth row), normal strong light interference driving environment (fifth row), dusk driving environment (sixth and seventh rows), raining at night driving environment (eighth row), and night driving environment with light interference (ninth row). From the comprehensive visual comparison results, it is evident that the detection performance of the method proposed in this chapter is significantly superior to the other three algorithms. The detection accuracy of SCNN and RESA is lower than that of our algorithm under complex conditions such as occlusion, external interference, and poor lighting. In nighttime driving environments, they are almost unable to detect lane markings. The detection performance of LSTR is better than SCNN and RESA, but there are still cases of missed detection.

Fig. 5
figure 5

Comparison of visualization results of CULane.

Full size image

Experimental results of LLAMAS

The experimental results of the LLAMAS dataset comparison are shown in Table 4. In the LLAMAS dataset comparison results, the F1 score of the proposed method is the highest compared to all other methods, including SCNN which has the highest score among point-based detection methods. The proposed method outperforms PolyLaneNet, which is also a curve-based prediction method, by 5.97%.

The visualization results of the LLAMAS dataset comparison are shown in Fig. 6. Since the LLAMAS dataset mainly consists of urban and highway driving environments, the visualization comparison result mainly considers whether there are false negatives and false positives in the detection results and the detection performance of the far-end lane markings.

Table 4 Comparison experiment results on LLAMAS.
Full size table
Fig. 6
figure 6

Comparison of visualization results of LLAMAS.

Full size image

Visual comparison results of BDD100K

The trained model on the TuSimple dataset is directly used for transfer detection on the BDD100K dataset to verify the generalization and transferability of the proposed method. The results are compared with LSTR, SCNN, and RESA in terms of visualization. The visualization comparison results of the BDD100K dataset are shown in Fig. 7.

Fig. 7
figure 7

Comparison of visualization results of BDD100K.

Full size image

Ablation study

In this experiment, the ablation experiments mainly verify the improvement of the proposed method and examine the real-time performance of the method. Therefore, ablation experiments were conducted on the TuSimple and CULane.

Analysis of the inffluence of separable lane detection block

The lane detection model proposed in this paper is based on a pure Transformer architecture, which means that the pure Transformer model introduces a significant computational cost. Therefore, a SepLDT block is introduced to address this issue. To validate the effectiveness of the SepLDT block, the separable lane detection block was split and replaced with a window-based multi-head self-attention mechanism, and the accuracy, parameters, training time, and inference speed (Frames Per Second, FPS) of the original complete algorithm were compared. The comparison results are shown in Table 5.

Table 5 Comparison results of the model with and without the SepLDT block on the TuSimple and CULane datasets.
Full size table

After the SepLDT blocks are dismantled and replaced with a window-based multi-head self-attention mechanism, the network model is still based on the pure Transformer architecture. As shown in Table 5, the inference speed of the model significantly decreases. This is due to the fact that the window-based multi-head self-attention mechanism models the relationship between each pixel in the two-dimensional feature map, generating a large amount of calculation that slows down the speed of the model’s inference. The final accuracy of the model after splitting was not as good as the original complete algorithm because using multi-head self-attention mechanism makes it difficult for the model to converge quickly during training, and the loss value continues to oscillate downward, which affects the performance of the model, while the model’s parameter size and training time significantly increased.

Figure 8 shows the comparison of the accuracy improvement during model training between the separable lane detection block split and the original complete algorithm without splitting. From the figure, it can be seen that although the two models have similar final accuracy, the separable lane detection block has a slower and smaller improvement rate and amplitude in accuracy compared to the original complete algorithm without splitting.

Fig. 8
figure 8

The comparison of accuracy of separable lane detection block on the TuSimple.

Full size image

Figure 9 shows the comparison of the loss value improvement during model training between the separable lane detection block split and the original complete algorithm without splitting. The result shows that after splitting the separable lane detection block, the loss value during the training process is difficult to maintain a stable downward trend, and the loss value fluctuates continuously with a large amplitude, which can affect the final accuracy of the model. After adding the separable lane detection block, the loss value of the network is quickly maintained at a low level.

Fig. 9
figure 9

The comparison of loss of separable lane detection block on the TuSimple.

Full size image

Analysis of the inffluence of multi-resolution overlapping feature aggregation block

The experiment directly split the multi-resolution overlapping feature aggregation block and passed the output of the previous layer network directly as input to the next layer network. The accuracy, parameter, training time, and FPS of the original complete algorithm were compared. The comparison result is shown in Table 6.

Table 6 Comparison results of the model with and without the MOFA block on the TuSimple and CULane datasets.
Full size table

From the comparison results, it can be observed that after splitting the MOFA block, the model’s parameter count and training time were reduced accordingly, and the FPS increased. This is because, after dismantling the MOFA block, it was not replaced with any other module and the output of the previous layer was directly passed to the next layer. Furthermore, the accuracy of the model after dismantling the MOFA block dropped significantly on the TuSimple and CULane datasets, which validates the effectiveness of the MOFA block.

Figure 10 shows the comparison of the accuracy improvement during model training after directly splitting the multi-resolution overlapping feature aggregation block. It can be seen from the experimental results that after splitting the multi-resolution overlapping feature aggregation block, the model’s accuracy during training shows a significant continuous decline, while the original complete algorithm only experienced a single decrease in accuracy at the beginning of training and then maintained a steady upward trend.

Fig. 10
figure 10

The comparison of accuracy of MO feature aggregation block on the TuSimple.

Full size image

Figure 11 shows the comparison of the loss value during model training after directly splitting the multi-resolution overlapping feature aggregation block. It can be seen from the experimental results that the original complete algorithm without splitting the multi-resolution overlapping feature aggregation block is significantly better than the algorithm after splitting the module.

Fig. 11
figure 11

The comparison of loss of MO feature aggregation block on the TuSimple.

Full size image

Figure 12 shows the attention map of the last layer output of the encoder. Several points were tested on lane markings with different conditions. Among them, the points (300, 467) and (310, 750) are clear lane markings, and their attention maps display a clear, long and narrow lane structure. The neighborhood near the point (360, 530) lacks lane markings, but the encoder still recognizes a unique, narrow structure by learning global context. The right half of the point (280, 813)’s lane marking is completely occluded, so the encoder pays more attention to the lane marking features without obstruction to the left of the point. The point (280, 959) is a mark at the far end of the field of view. Although the lane markings at the far end of the point are small in pixels, the encoder still has excellent feature capture performance for remote lane markings and captures clear lane marking information.

Figure 13 shows the attention map of the last layer output of the decoder. Like the encoder, the attention map of each lane output in the decoder is analyzed. The decoder is able to concentrate attention on the narrow structure of the lane, which can help the proposed method to use instance segmentation to separate the specific lane without requiring additional operations such as non-maximum suppression.

Fig. 12
figure 12

The diagram of encoder attention map.

Full size image
Fig. 13
figure 13

The diagram of decoder attention map.

Full size image

Evaluation on self-collected images

To demonstrate the versatility and robustness of our lane detection model in real-world scenarios, the Apollo platform was used to collect lane line images in real-world scenarios. The Apollo driving platform is shown in the Fig. 14. Since it is difficult to collect lane line images in complex real-world scenarios such as fog, snow, and traffic accidents, lane line images were collected under conditions of low light, post-rain, and occlusion. The trained lane detection model was used to detect the lane line images we collected, and the detection results are shown in the Fig. 14. As shown in Fig. 14, the performance of lane line detection is satisfactory, with no false negatives. This validates the versatility and robustness of the algorithm in real-world scenarios.

Fig. 14
figure 14

The experimental results on the self-collected images.

Full size image

Conclution

This paper proposes an end-to-end complex road environment lane detection model with a pure Transformer architecture. Firstly, a separable lane multi-head attention mechanism based on window self-attention is proposed. This mechanism can establish the attention relationship between each window faster and more effectively, reducing the computational cost and improving the detection speed. Then, an extended and overlapping strategy is designed, which solves the problem of insufficient information interaction between two adjacent windows of the standard multi-head attention mechanism, thereby obtaining more global information and effectively improving the detection accuracy in complex road environments. Finally, extensive experimental analysis is carried out on three datasets, TuSimple, CULane, and LLAMAS. The results are compared with other advanced methods, achieving competitive accuracy and real-time performance.