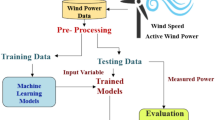
Abstract
Predicting wind speed simultaneously at multiple heights, particularly at 10 and 100 metres (m), presents unique challenges due to diverse influences. At lower altitudes, wind speed is significantly affected by surface factors including roughness, vegetation, and man-made structures, causing sharp fluctuations, while at higher altitudes, it is primarily influenced by atmospheric conditions, resulting in smoother flow patterns. Traditional models often require separate systems for each altitude, limiting their efficiency and accuracy. This study introduces the brain emotional learning based on basic and functional memories (BELBFM) model, inspired by adaptive emotional learning mechanisms in the mammalian brain, to predict wind speeds at both altitudes simultaneously. Using ERA5 reanalysis data, BELBFM effectively captures the nonlinear dynamics of wind behavior. Evaluation with data from the Persian Gulf demonstrates BELBFM’s high accuracy, enhancing predictive capabilities for applications in renewable energy and structural engineering. This unified model provides a robust and efficient solution for adaptive wind forecasting.
Similar content being viewed by others
Introduction
Wind speed modeling is crucial in meteorology, with significant applications in optimizing renewable energy, designing robust structures, and improving weather forecasting models1,2. Accurate prediction of wind speeds at altitudes of 10 and 100 m is essential for optimizing wind turbine performance, designing robust structures, and enhancing weather prediction models3,4.Despite advancements in the field, simultaneously predicting wind speeds at these two heights remains a challenging problem due to the distinct atmospheric dynamics involved5,6.
At 10 m, wind speed is heavily influenced by surface roughness and obstacles like buildings, trees, and terrain7. These factors create localized turbulence and variability, resulting in less predictable wind patterns. Conversely, at 100 m, wind speed is less affected by surface obstructions, leading to a more stable and consistent profile8,9. The differences in atmospheric conditions at these altitudes necessitate a modeling approach that considers the unique dynamics of each altitude.
Wind speed modeling at various heights has been explored using diverse methodologies, ranging from traditional numerical weather prediction (NWP) models to advanced machine learning techniques.
NWP models rely on physical principles and mathematical equations to simulate atmospheric processes10. Examples include widely used models such as WRF and ECMWF11,12. NWP models provide detailed and accurate forecasts but are computationally intensive, requiring extensive data sets and high computational power13,14. Despite their success in predicting wind speeds, their high computational cost limits flexibility and accessibility12,15.
Computational fluid dynamics (CFD) models are physics-based models simulate fluid flows and their interaction with surfaces, making them effective for studying wind behavior around complex structures like buildings and turbines16. While CFD models can capture detailed flow patterns and turbulence, they are computationally demanding and require specialized resources. They are typically limited to localized studies or specific scenarios17,18.
Machine learning (ML) techniques, such as artificial neural networks (ANN), support vector machines (SVM), and deep learning models, have gained popularity for modeling complex, nonlinear relationships in large datasets19,20. Deep learning models like CNNs and RNNs are particularly effective in identifying patterns in wind speed data21,22. These ML models can adapt and improve over time, but they are computationally intensive and difficult to interpret23,24.
Hybrid approaches combining physics-based models with machine learning are also being explored. These models leverage the detailed understanding from NWP and CFD models along with the adaptability of ML techniques. While hybrid models can improve forecasting accuracy and reduce computational demands, they present challenges in integrating and balancing the different modeling approaches25,26.
Despite advancements in traditional and machine learning methods, predicting wind speeds at multiple heights continues to pose challenges. Traditional models like NWP and CFD are effective but computationally demanding and inflexible17,18.ML models, while promising, struggle to provide simultaneous predictions at multiple altitudes and often lack interpretability23,24. Hybrid models, which combine data-driven27 and physics-based approaches, offer improved accuracy but still face challenges in efficiency and generalization across various conditions25,26. Thus, there is a need for a unified model capable of predicting wind speeds at both 10 and 100 m, leveraging advanced computing while addressing the limitations of current models.
To address these challenges, this study introduces the brain emotional learning based on basic and functional memories (BELBFM) model, inspired by the emotional learning mechanisms of the mammalian brain. BELBFM leverages basic and functional memories to create an adaptive framework for modeling wind behavior. By integrating inputs from sensory, thalamic, cortical, amygdala, and orbitofrontal components, the model captures the complexities of wind speed dynamics with enhanced accuracy and computational efficiency.
The contributions of this study are as follows:
-
Unified dual-height modeling: BELBFM predicts wind speeds at both 10 and 100 m, addressing the distinct atmospheric dynamics at these heights.
-
Innovative methodology: The model employs an ensemble learning framework, combining outputs from various memory units trained on layered wind speed data, optimized for performance.
-
Efficient training: A correlation-based data pruning technique significantly reduces the training dataset, enhancing computational efficiency without compromising accuracy.
-
Real-world applicability: The model demonstrates potential for applications in renewable energy management, weather forecasting, and disaster preparedness.
By addressing the limitations of existing methods, BELBFM provides a novel solution for simultaneous wind speed prediction at multiple altitudes. The rest of the paper is structured as follows: Sect. 2 introduces the proposed model, Sect. 3 details its implementation, Sect. 4 presents the results, and Sect. 5 discusses the findings and concludes the study.
Methodology: brain emotional learning based on basic and functional memories (BELBFM)
Over the past three decades, a novel approach inspired by the mammalian brain’s emotional learning mechanisms has been developed for modeling and forecasting complex nonlinear systems28. Brain Emotional Learning-Based Models (BELMs) stem from neuroscience, psychology, AI, and computational modeling29. Psychologists like John Watson and neuroscientists such as Joseph LeDoux, who studied the amygdala’s role in fear conditioning, laid the groundwork for this field30. In 2001, Balkenius and Morén introduced a computational model of the interaction between the amygdala and orbitofrontal cortex in emotional conditioning as the first BELM31. This model laid the foundation for further advancements. In 2004, Lucas and his team introduced BELBIC (brain emotional learning-based intelligent controller)32, which was applied to domains such as washing machine control33 and dynamic system prediction34. Subsequent improvements enabled applications in intelligent control, prediction, and emotional learning. For instance, BELMs have been used for DC motor speed control35, earthquake prediction36, emotion recognition37,38, and Alzheimer’s diagnosis39. BELMs have also been integrated with other intelligent methods, such as fuzzy neural networks to enhance performance40. Recent developments include applications in humanoid robots41, active noise cancellation systems42, and time-series prediction43. Hybrid models combining BELMs with deep learning and fuzzy techniques have further expanded their real-world applicability38,44. From simulating brain processes to addressing complex systems, BELMs have evolved into powerful tools for tackling increasingly sophisticated challenges when combined with modern AI techniques.
As mentioned before, various computational models have been inspired by the human brain. One of these important models is the amygdala-orbitofrontal subsystem model45. The amygdala-orbitofrontal subsystem, which is the main basis of many computational models, has a simple structure. As shown in Fig. 1, this subsystem consists of four interconnected components: the sensory cortex, thalamus, amygdala, and orbitofrontal cortex. Sensory inputs are processed through the thalamus and sensory cortex before reaching the amygdala and orbitofrontal cortex. The amygdala generates emotional responses (E), while the orbitofrontal cortex modulates these responses based on feedback (REW) to refine decision-making and control in dynamic environments. Various architectures of the amygdala-orbitofrontal subsystem have been presented and used in above mentioned applications.
The graphical description of amygdala orbitofrontal subsystem45.
BELMs and their advancements represent a significant evolution in computational modeling, offering robust solutions for addressing complex, real-world challenges.
Building on BELM advancements, this paper suggests Brain Emotional Learning Based on Basic and Functional Memories (BELBFM) as a novel approach to the amygdala-orbitofrontal subsystem along with specialized memory for amygdala and orbitofrontal parts to model wind speeds simultaneously at 10 and 100 m. The architecture of the proposed model (depicted in Fig. 2) consists of five main components: Sensory input (SI), Thalamus (TH), Sensory cortex (SC), Amygdala (AMIG), and Orbitofrontal cortex (OFC).
-
SI: Receives and labels input signals (wind components u and v) for wind speeds at both 10 and 100 m.
-
TH: Calculates wind speeds at both altitudes, then passes these results to the SC block. Additionally, it sends an output indicating the wind speed type (10 or 100 m) to the F unit in the AMIG.
-
SC: Generates input-target vectors required for training, evaluation, and exploitation phases and sends them to both the OFC and AMIG blocks.
-
OFC: Includes two basic memory units (O1 and O2) and two functional memory units (WO1 and WO2).
-
AMIG: Contains a basic memory unit (A), a functional memory unit (WA), and a fusion unit (F). Basic memory units are trained with data from the SC block, while functional memory units store performance history based on error rates. The F unit integrates the results from the basic and functional memory units.
Architecture of the proposed BELBFM model, illustrating the five main components: Sensory input (SI), Thalamus (TH), Sensory cortex (SC), Amygdala (AMIG), and Orbitofrontal cortex (OFC). Each component is designed to process and integrate input data for wind speed prediction at multiple altitudes by utilizing both basic and functional memories. This architecture leverages emotional learning mechanisms to enhance prediction accuracy and adaptability.
This architecture emulates emotional learning processes and aims to enhance wind speed prediction accuracy by combining diverse memory types and leveraging past performance.
BELBFM implementation
Main dataset
This study relies on atmospheric data obtained from the ERA5 reanalysis dataset. The ERA5 dataset, developed by the European centre for medium-range weather forecasts (ECMWF), provides a detailed picture of Earth’s atmosphere since 1940. This dataset, with a high resolution of 0.25 degrees and hourly updates, provides detailed atmospheric data that captures even small-scale wind variations, which are critical for precise forecasting. In the equatorial region, each grid cell represents an area of approximately 29 × 29 km46. The focus is on the u-component and v-component of wind speed at 10 and 100 m above ground level, measured in meters per second, to calculate surface wind speed.
Feature selection
In this study, a neighborhood-based approach for feature selection was employed, considering the influence of neighboring cells on wind speed at specific locations. The neighborhood-based pattern (NBP) ensures systematic data collection across the entire area, providing comprehensive spatial coverage of wind speeds.
To extract relevant features from the wind speed data, an effective NBP must be defined. As shown in Fig. 3, various cellular patterns, such as 3 × 3, 5 × 5, and 7 × 7, can be used to identify the appropriate features. Wind patterns often undergo significant variations over short distances due to topographical features such as mountains and valleys. Using larger cellular patterns (e.g., 7 × 7) gathers more information from neighboring points, enabling the model to better capture complex and extensive wind patterns that may influence wind speed at the central point. However, larger cellular patterns incur higher computational costs and longer processing times. Conversely, modeling with smaller grids (e.g., 3 × 3) offers lower computational costs and requires less processing time and resources. However, it may fail to capture spatial details effectively, reducing prediction accuracy.
To balance accuracy, complexity, and computational efficiency, larger grids can be utilized in a pruned manner. With a simple argument, it can be assumed that the cellular layers closer to the center of the pattern have the greatest effect on the central cell of the pattern. The cells located in the farther layers of the cellular network can be pruned alternately. This selection method ensures that the wind effect in this layer is distributed evenly, with a gradual decrease from the cells closer to the center to the more distant cells, while the information from the neighboring cells closer to the center, which have a stronger wind effect, remains prioritized.
In this study, a pruned 5 × 5 grid pattern is employed, as illustrated in (Fig. 4). While a regular 5 × 5 pattern includes 25 features, the pruned version reduces this number to 17. Feature vectors based on this pruned pattern are constructed according to Eq. (1). In this equation, \(\:{C1}_{\left(t\right)}^{\left(i\right)}\) indicates the value of wind speed in the middle cell at time t. The i indicates the position of \(\:{C1}_{\left(t\right)}^{\left(i\right)}\) in the grid of database. \(\:{C2}_{\left(t\right)}^{\left(i\right)}\) to \(\:{CX}_{\left(t\right)}^{\left(i\right)}\) represent the values of wind speed in the neighboring cells of \(\:{C1}_{\left(t\right)}^{\left(i\right)}\) in the neighborhood-based pattern. \(\:{C1}_{(t+1)}^{\left(i\right)}\) indicates the value of wind speed in the middle cell at time t + 1 as the target.
Region and time range selection
The Persian Gulf (PG) is a shallow sea bordered by the mountainous coastlines of Iran and the flat shores of the Arabian Peninsula, with an average depth of only 35 m, reaching up to 180 m in the Northern part47. Positioned in a subtropical high-pressure zone, the PG experiences a dry climate characterized by low rainfall and high evaporation, making it particularly vulnerable to the impacts of climate change48. The PG’s climate is influenced by Mediterranean weather systems and the Indian monsoon, with two main seasons (summer and winter) and brief spring and fall transitions49,50.
One of the key climatic features of the PG is the presence of shamal winds. Shamal winds are a strong northwesterly wind that blows year-round, significantly affecting the region’s weather. These winds exhibit distinct patterns in summer and winter51. During late spring, low-pressure thermal systems form over southern Iran and Saudi Arabia, while a high-pressure ridge extends from the Mediterranean eastward, creating a pressure gradient that generates shamal winds. In winter (November to March), these winds, linked to mid-latitude weather systems, are stronger, reaching speeds of 15–20 m per second, leading to dust storms and reduced visibility. Winter shamal winds are more intense than those in summer, influencing the region’s precipitation-evaporation balance50,52.
Given the distinct seasonal patterns of shamal winds and their significant climatic impact, the PG serves as an ideal location for this research. Figure 5 shows the PG region. Data from 2001 to 2020 for the PG region (23° to 31°N, 47° to 59°E) were used for training and testing sets, while data from 2021 to 2023 were employed to evaluate the model’s performance across different time periods and locations.
Train and test datasets generation
We retrieved U and V wind component data from the ERA5 dataset to calculate wind speed in meters per second. Using the neighborhood model described in the “Feature Selection” section, input-target vector pairs were extracted from the wind speed data. The initial training dataset consisted of approximately 350 million records for the PG region, spanning the years 2001 to 2020.
The large size of the training dataset presents a significant challenge for the modeling process. Record pruning is a technique designed to reduce the size of large training datasets by removing redundant records53. This approach involves analyzing feature vectors to identify and eliminate those that are highly correlated. Highly correlated feature vectors can introduce redundancy and provide little to no additional information to the model. By pruning these vectors, the dataset is refined to retain only the most informative and unique features.
In this study, a correlation-based pruning approach was employed, utilizing the Spearman correlation coefficient. This coefficient measures both the strength and direction of monotonic relationships between records, making it particularly suitable for identifying highly representative records within the dataset. The process is as follows:
-
a)
A threshold value between 0 and 1 is determined.
-
b)
The Spearman correlation coefficient of each record is calculated against the entire dataset.
-
c)
Records with a maximum absolute correlation coefficient value less than or equal to the threshold are retained as training records, while the remaining records are designated as testing records.
To apply the record pruning technique, a threshold value of 0.55 for the Spearman correlation coefficient was determined through a trial-and-error approach. After the pruning process, the number of records in the training dataset was reduced from approximately 350 million to 242,628 records—less than 0.07% of the original dataset size. The reduced dataset was then used as the training dataset, while the remaining records were designated as the test dataset.
Additionally, to ensure the model’s robustness and generalizability, a separate test dataset was created using data from a different time period (2021 to 2023) that was excluded from the training dataset. Detailed descriptions of the training and test datasets are provided in (Table 1).
Model generation
Input labeling
Input signals are received in the SI block and labeled based on Eq. (2), where \(\:{SI}_{\left(t\right)}^{S}\) represents the wind components (u and v) corresponding to 10-meter and 100-meter speeds at time t.
Wind speed calculation in TH block
In the TH block, using Eqs. (3), 10 and 100 m wind speeds are calculated from the labeled wind components.
Input-target vector generation
The SC block generates the input-target vectors needed for training and evaluation based on Fig. 4 and Eq. (4) to (6). Subsequently, \(\:{SC}_{\left(t\right)}^{O1}\) and \(\:{SC}_{\left(t\right)}^{O2}\) are sent to the OFC, and \(\:{SC}_{\left(t\right)}^{A}\) is sent to the AMIG block. In these equations, the values of \(\:{C}_{t}^{\text{i}}\) are equivalent to the wind speeds at the positions specified in (Fig. 4).
Basic memory units generation
Multilayer neural network models were used to create the basic memory units, labeled O1, O2, and A. These models were trained with Train 1, Train 2, and Train 3 datasets, respectively (see Table 1). To achieve the best models, a range of hyperparameters was explored according to (Table 2). Additionally, Table 2 shows the hyperparameters of the best models for basic memories O1, O2, and A.
Generation of functional memory units
Evaluating the performance of machine learning models is essential. In this research, we use several error metrics: Standard deviation of error (SDE), Mean square error (MSE), Root mean square error (RMSE), Mean absolute error (MAE), Mean absolute percentage error (MAPE), and coefficient of determination (R-squared, or R2). SDE measures the dispersion of errors between predicted and actual values. A lower SDE indicates better model accuracy and stability54. MSE is the average of squared differences between predicted and actual values, with smaller values indicating better accuracy. It is sensitive to outliers due to the squaring of errors55. RMSE is similar to MSE but represents the error in the same units as the data. It penalizes larger errors more heavily and provides an average measure of error56. MAE measures the average absolute difference between predicted and actual values. It is easy to interpret but less sensitive to large errors compared to RMSE57. MAPE expresses forecast accuracy as a percentage, which makes it easy to understand. A lower MAPE indicates better accuracy. It does not account for the direction of errors (over or under predictions)54,55. R2 is a statistical measure that represents the proportion of the variance in the dependent variable that can be predicted from the independent variables in a regression model. In other words, it indicates how well the independent variables explain the variability of the dependent variable. While a high R2 suggests a good fit, it does not necessarily mean the model is perfect or the best one. It is possible for a model to have a high R2 but still not be ideal due to overfitting, where the model becomes too complex for the data. For this reason, R2 alone is usually not sufficient to evaluate models58.
To evaluate the performance of basic memory units, these metrics (SDE, MAE, MSE, RMSE, and MAPE) are applied to wind speed data at heights of 10 m and 100 m. Performance coefficients (W) are calculated for each basic memory unit (O1, O2, and A) and are updated as the error metrics change, reflecting the predictive ability of each unit.
To calculate the values of the performance coefficients in the functional memory units WO1, WO2, and WA, the trained models {X} were evaluated with the data from the Test 1 and Test 2 datasets (see Table 1). Finally, the performance coefficients of the functional memories are calculated using Eq. (7) to (9), where \(\:{Z}_{X}^{S}\) is the value of the error metric {Z} for the basic memory unit {X} and wind speed {S}.
According to equations (10) to (12), each functional memory unit holds ten performance coefficients. Table 5 shows the values of the performance coefficients for functional memory units.
Fusion of the results
In Eq. (9), each performance coefficient is constrained between zero and one, and the sum of the performance coefficients for each error metric {Z} and wind speed {S} equals one. This approach allows for separately calculating the combined outputs of the basic and functional memory units based on each error metric and wind speed. The model’s final output, represented by the F unit in the AMIG block, for each input with wind speed {S} at time t is calculated by averaging these combined outputs, as shown in equations (13) through (18).
The process outlined in equations (13) through (18) to generate the final model output is summarized in Eq. (19):
Model exploitation
After the training phase, the model advances to deployment. During deployment, similar to training, the input signal passes through the SI and TH blocks before reaching the SC block. However, with new data for predictions, the SC block processes a single feature vector, as described in Eq. (20).
The feature vector \(\:{SC}_{t}\) is then sent to the basic memory units O1, O2, and A, and the outputs of these units are forwarded to the F unit. In the F unit, the final result is computed using Eq. (18) or Eq. (19).
Brief overview of the BELBFM components and interactions
Table 3 provides a brief description of the BELBFM blocks and units, along with their role, inputs and outputs. Furthermore, to better understand how the BELBFM model works, the following pseudo-code is provided:
-
Input: U10, V10, U100, V100 (wind components at 10 and 100 m heights).
-
Output: Predicted wind speeds (S10, S100).
Initial preparation
-
a)
Define the study region and time range.
-
b)
Select the grid-based database with wind speed data (e.g., ERA5 with hourly updates).
-
c)
Define a neighborhood-based pattern to generate feature vectors (e.g., a 5 × 5 grid).
Feature extraction
-
a)
Load the ERA5 reanalysis dataset.
-
b)
Extract the U and V wind components at 10 and 100 m heights.
-
c)
Generate labeled input signals in SI block (U10, V10, U100, V100).
-
d)
Calculate wind speed at both altitudes in TH block.
-
e)
Extract input-target vectors based on defined neighborhood-based pattern in SC block.
Model training
-
a)
Split input-target vectors to generate train and test datasets:
-
i.
Create train and test datasets based on a correlation-based pruning approach.
-
ii.
Generate extra test datasets for evaluation of the final model.
-
b)
Train basic memory units:
-
i.
O1: Train on 10 m wind speed data (S10).
-
ii.
O2: Train on 100 m wind speed data (S100).
-
iii.
A: Train on combined wind speed data from both heights (S10 and S100).
-
c)
Optimize hyperparameters for each unit model (e.g., layer size, activation functions).
Evaluate basic memory units and update functional memory weights
-
a)
Calculate performance using error metrics (e.g., SDE, MAE, and MAPE) for O1, O2, and A.
-
b)
Update functional memory weights (WO1, WO2, WA) based on error metrics.
Fusion of results
-
a)
Combine outputs from the basic and functional memory units using:
-
i.
Weighted sum (preferred method).
-
ii.
Simple mean (optional).
Model exploitation
-
a)
Process new input data through SI, TH, and SC blocks and O1, O2, and A units.
-
b)
Predict final wind speeds (S10, S100) using the fusion mechanism (F unit).
Output results
-
a)
Validate model predictions against the test dataset.
-
b)
Evaluate performance using error metrics to ensure accuracy and reliability.
Results
The modeling and testing processes were performed on a desktop computer with specifications outlined in (Table 4). Hyperparameter optimization took approximately 5 h, while the final model training completed in just 3 min.
During the training phase, three basic memory units, O1, O2, and A, were trained using data from the Train 1, Train 2, and Train 3 datasets, respectively. The trained models were evaluated on the Test 1 and Test 2 datasets to determine the performance coefficients of functional memories WO1, WO2, and WA, as shown in (Table 5). The final model was created by combining the outputs of the basic memory units and functional memories.
To assess the effectiveness of functional memories in the final model, the F unit used both weighted and simple mean methods, as shown in Eq. (21).
During deployment, the final model was tested using data from Test 3, Test 4, Test 5, and Test 6. Table 6 displays results from tests with the basic memory units (O1, O2, and A) using Test 1, Test 2, Test 4, and Test 5.
Key findings include the following:
-
Model O1, trained on 10-meter wind speed data, demonstrates cross-height predictive capability by effectively predicting 100 m wind speed. Similarly, O2, trained on 100-meter data, performs well in predicting 10-meter wind speed.
-
Model A, trained on both 10-meter and 100-meter data, shows better accuracy in predicting 10 m speeds.
-
The models generally exhibit lower error metrics with recent data (2021–2023) compared to earlier periods (2001–2020), suggesting improved performance with newer data.
-
O1 consistently outperforms O2 and A, indicating that predicting wind speeds at higher altitudes (100 m) is more complex than at lower altitudes (10 m), requiring advanced data integration.
Table 7 evaluates the performance of the BELBFM model in predicting wind speeds at both 10 and 100 m, using six statistical error metrics (SDE, MAE, MSE, RMSE, MAPE, and R2) across two time periods: 2001–2020 and 2021–2023. The analysis includes three basic memory units (O1, O2, A) and two combination methods (Simple Mean and Weighted Sum).
Key insights:
-
Training phase (2001–2020, Train 3): Model A, trained on both heights, achieves the lowest MAPE (27.841), indicating superior accuracy over models O1 and O2.
-
Test phase (2001–2020, Test 3): The Weighted Sum method outperforms the Simple Mean across all error metrics, indicating enhanced accuracy by leveraging additional information from the base models.
-
Test phase (2021–2023, Test 6): In this recent data period, the Weighted Sum method once again outperforms the Simple Mean, demonstrating lower error metrics across the board and confirming the model’s adaptability to recent data and consistency in predictive accuracy.
Furthermore, to evaluate the performance of the BELBFM model, its results were compared with those of other regression models. For this purpose, several regression models were trained using the Train 3 dataset (2001–2020) and evaluated with the Test 6 dataset (2021–2023) using the Regression Learner Toolbox in MATLAB R2023R software. Table 8 compares the performance of BELBFM with that of these models. An analysis of the table highlights the superior performance of BELBFM compared to the alternative models. Notably, BELBFM achieves the lowest RMSE (0.6002) and MAE (0.4480), along with the highest R2 value (0.9506), indicating its exceptional ability to explain variance in wind speed data. In contrast, models such as Neural Networks and Gaussian Process Regression show comparatively higher error rates and lower predictive accuracy.
Discussion and conclusion
The BELBFM model represents a significant advancement in wind speed prediction, utilizing an innovative ensemble learning methodology that outperforms traditional approaches such as numerical weather prediction (NWP) and computational fluid dynamics (CFD). By integrating outputs from memory units trained on distinct wind speed data layers with optimized performance coefficients, BELBFM achieves superior predictive accuracy. Its emotionally-inspired learning principles effectively capture the inherent nonlinearities of atmospheric processes, facilitating reliable wind speed forecasts across diverse conditions.
A notable contribution of this study is BELBFM’s dual-height wind speed modeling capability, predicting wind speeds at both 10 and 100 m. This feature provides a comprehensive understanding of wind behavior across critical altitudes, crucial for applications in renewable energy optimization, climate modeling, and weather forecasting. The model’s flexible regression approach, based on a neighborhood feature set, minimizes computational demands and improves accuracy by prioritizing the most relevant data points, setting it apart from conventional time series models.
Performance metrics underscore the model’s predictive power. Despite the challenges of predicting wind speeds at 100 m due to numerous influencing factors, BELBFM’s dual-height modeling effectively utilizes 10-meter data for accurate 100-meter predictions, and vice versa. Model A, which integrates data from both heights, demonstrates high accuracy in predicting 10-meter wind speeds. Its consistent performance across two periods (2001–2020 and 2021–2023) suggests strong adaptability to new data while mitigating concerns about overfitting. Furthermore, the Weighted Sum method consistently outperforms the Simple Mean method, enhancing predictive accuracy across diverse datasets.
Comparative analysis with other well-known regression models, as detailed in Table 8, highlights BELBFM’s superiority. It achieves the lowest RMSE and MAE values and the highest R2, underscoring its exceptional ability to explain variance in wind speed data effectively.
BELBFM’s correlation-based data pruning technique is another valuable feature, reducing the training dataset to less than 0.07% of its original size while retaining representative samples. This efficient process accelerates the modeling workflow without compromising prediction quality, making the model particularly suitable for real-time applications in renewable energy management, weather forecasting, and disaster preparedness.
The model also demonstrates computational efficiency. By leveraging a pruned 5 × 5 grid during feature selection, BELBFM significantly reduces the number of processed features. The feature selection phase has a time complexity of O(n·k), while the training phase for each memory unit’s multilayer perceptron (MLP) has a complexity of O(T·L·N2), where n is the number of data points, k the neighboring cells, T the number of iterations, L the number of layers, and N the neurons per layer. Spearman correlation-based pruning further reduces computational demands, achieving a complexity of O(n2), thereby drastically reducing the dataset size to 0.07%. These optimizations ensure both accuracy and efficiency, completing hyperparameter tuning within five hours and model training in under three minutes on standard hardware.
Despite its strengths, the model’s reliance on ERA5 data may introduce variability in performance, contingent upon the quality and resolution of the input data. Further research is needed to validate BELBFM’s effectiveness across diverse regions and incorporate additional atmospheric variables for refined predictions. Enhancing adaptability to real-time data and changing weather conditions could further expand its utility.
The novelty of BELBFM lies in its innovative architecture and methodological advancements. By integrating basic and functional memory units with adaptive emotional learning mechanisms, the model effectively captures the nonlinear and dynamic nature of atmospheric processes. Its dual-height predictive capability addresses a critical gap in simultaneous wind speed modeling at varying altitudes, providing enhanced utility for renewable energy optimization and climate modeling. The incorporation of correlation-based data pruning ensures computational efficiency, setting BELBFM apart as a practical solution for real-time applications. This framework underscores the transformative potential of brain-inspired learning methods in advancing wind speed prediction and related meteorological applications.
In conclusion, BELBFM exemplifies the potential of emotionally-inspired learning models to advance meteorological research. Its performance, adaptability, and efficiency open promising opportunities for deployment across wind energy forecasting and broader environmental fields.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Amiridis, V. et al. Aeolus winds impact on volcanic ash early warning systems for aviation. Sci. Rep. 13, 1–14 (2023).
Ren, Y., Wen, Y., Liu, F., Zhang, Y. & zhang, Z. Deep convolution IT2 fuzzy system with adaptive variable selection method for ultra-short-term wind speed prediction. Energy Convers. Manag. 309, (2024).
Porté-Agel, F., Bastankhah, M. & Shamsoddin, S. Wind-turbine and wind-farm flows: a review. Bound. Layer. Meteorol. 174, 1–59 (2020).
de Souza Ferreira, G. W. et al. Assessment of the wind power density over South America simulated by CMIP6 models in the present and future climate. Clim. Dyn. 62, 1729–1763 (2023).
Blougouras, G., Philippopoulos, K. & Tzanis, C. G. An extreme wind speed climatology—Atmospheric driver identification using neural networks. Sci. Total Environ. 875, (2023).
Tar, K. Some statistical characteristics of monthly average wind speed at various heights. Renew. Sustain. Energy Rev. 12, 1712–1724 (2008).
Stull, R. An Introduction to Boundary Layer Meteorology. (2012).
Cichowicz, R. & Dobrzański, M. Impact of building types and CHP plants on air quality (2019–2021) in central-eastern European monocentric agglomeration. Sci. Total Environ. 878, (2023).
Zhao, Z. et al. Observations of boundary layer wind and turbulence of a landfalling tropical cyclone. Sci. Rep. 12, (2022).
Kunić, Z., Ženko, B. & Boshkoska, B. M. FOCUSED–short-term wind speed forecast correction algorithm based on successive NWP forecasts for use in traffic control decision support systems. Sensors 21, 3405 (2021).
Frnda, J. et al. A weather forecast model accuracy analysis and ECMWF enhancement proposal by neural network. Sens. (Basel) 19, (2019).
Wang, H., Yin, S., Yue, T., Chen, X. & Chen, D. Developing a dynamic-statistical downscaling framework for wind speed prediction for the Beijing 2022 winter olympics. Clim. Dyn. 1–19. https://doi.org/10.1007/S00382-024-07282-3/FIGURES/14 (2024).
Chen, H., Birkelund, Y., Anfinsen, S. N., Staupe-Delgado, R. & Yuan, F. Assessing probabilistic modelling for wind speed from numerical weather prediction model and observation in the Arctic. Sci. Rep. 11, 1–11 (2021).
Gaidai, O. et al. Novel methods for wind speeds prediction across multiple locations. Sci. Rep. 12, 1–9 (2022).
Prieto-Herráez, D. et al. Local wind speed forecasting based on WRF-HDWind coupling. Atmos. Res. 248, 105219 (2021).
Weerasuriya, A. U. et al. New inflow boundary conditions for modeling twisted wind profiles in CFD simulation for evaluating the pedestrian-level wind field near an isolated building. Build. Environ. 132, 303–318 (2018).
Wijesooriya, K., Mohotti, D., Lee, C. K. & Mendis, P. A technical review of computational fluid dynamics (CFD) applications on wind design of tall buildings and structures: past, present and future. J. Build. Eng. 74, 106828 (2023).
Zehtabiyan-Rezaie, N., Iosifidis, A. & Abkar, M. Data-driven fluid mechanics of wind farms: a review. J. Renew. Sustain. Energy 14, (2022).
Ponnusamy, V., Nallarasan, V., Rajasegar, R. S., Arivazhagan, N. & Gouthaman, P. Modern real-world applications using data analytics and machine learning. Stud. Big Data 145, 215–235 (2024).
Hua, L., Zhang, C., Peng, T. & Ji, C. & Shahzad Nazir, M. Integrated framework of extreme learning machine (ELM) based on improved atom search optimization for short-term wind speed prediction. Energy Convers. Manag. 252, (2022).
Mulia, I. E., Ueda, N., Miyoshi, T., Iwamoto, T. & Heidarzadeh, M. A novel deep learning approach for typhoon-induced storm surge modeling through efficient emulation of wind and pressure fields. Sci. Rep. 13, (2023).
Zhang, Z. & Yin, J. Spatial-temporal offshore wind speed characteristics prediction based on an improved purely 2D CNN approach in a large-scale perspective using reanalysis dataset. Energy Convers. Manag. 299, (2024).
Sun, P., Liu, Z., Wang, J. & Zhao, W. Interval forecasting for wind speed using a combination model based on multiobjective artificial hummingbird algorithm. Appl. Soft Comput. 150, 111090 (2024).
Li, W., Gao, X., Hao, Z. & Sun, R. Using deep learning for precipitation forecasting based on spatio-temporal information: a case study. Clim. Dyn. 58, 443–457 (2022).
Liu, M., De, Ding, L. & Bai, Y. L. Application of hybrid model based on empirical mode decomposition, novel recurrent neural networks and the ARIMA to wind speed prediction. Energy Convers. Manag. 233, (2021).
Bommidi, B. S. & Teeparthi, K. A hybrid wind speed prediction model using improved CEEMDAN and autoformer model with auto-correlation mechanism. Sustain. Energy Technol. Assess 64, (2024).
Hakimi, A., Monadjemi, S. A. & Setayeshi, S. An introduction of a reward-based time-series forecasting model and its application in predicting the dynamic and complicated behavior of the earth rotation (Delta-T values) [Formula presented]. Appl. Soft Comput. 113, (2021).
Fakhrmoosavy, S. H., Setayeshi, S. & Sharifi, A. A modified brain emotional learning model for earthquake magnitude and fear prediction. Eng. Comput. 34, 261–276 (2018).
Kumar, M., Gangadharan, S. M. P. & Choudhury, N. Machine learning model for teaching and emotional intelligence. Emotion. AI Human-AI Interact. Soc. Netw. 147–168 https://doi.org/10.1016/B978-0-443-19096-4.00014-6 (2024).
LeDoux, J. The Emotional Brain: The Mysterious Underpinnings of Emotional Life. (1998).
Balkenius, C. & Morén, J. Emotional learning: a computational model of the amygdala. Cybern Syst. 32, 611–636 (2001).
Lucas, C., Shahmirzadi, D. & Sheikholeslami, N. Introducing BELBIC: brain emotional learning based intelligent controller. Intell. Autom. Soft Comput. 10, 11–21 (2004).
Lucas, C., Milasi, R. M. & Araabi, B. N. Intelligent modeling and control of washing machine using locally linear neuro-fuzzy (llnf) modeling and modified brain emotional learning based intelligent controller (BELBIC). Asian J. Control 8, 393–400 (2006).
Parsapoor, M. & Lucas, C. Modifying brain emotional learning model for adaptive prediction of chaotic systems with limited data training samples. Lect. Notes Manag. Sci. 1, 328–341 (2008).
Chung, J. & Kim, H. Brain Emotional Learning Based Intelligent Controller Design for DC Motor Speed Control. in IEEE International Work Conference on Bioinspired Intelligence (IWOBI) 69–74 (2019).
Fakhrmoosavy, S. H., Setayeshi, S. & Sharifi, A. An intelligent method for generating artificial earthquake records based on hybrid PSO–parallel brain emotional learning inspired model. Eng. Comput. 34, 449–463 (2018).
Farhoudi, Z., Setayeshi, S. & Rabiee, A. Using learning automata in brain emotional learning for speech emotion recognition. Int. J. Speech Technol. 20, 553–562 (2017).
Farhoudi, Z., Setayeshi, S., Razazi, F. & Rabiee, A. Emotion recognition based on multimodal fusion using mixture of brain emotional learning. Adv. Cogn. Sci. 21, 113–127 (2020).
Emami, S. B., Nourafza, N. & Fekri-Ershad, S. A method for diagnosing of Alzheimer’s disease using the brain emotional learning algorithm and wavelet feature. J. Intell. Proc. Electr. Technol. 13, 65–78 (2021).
Zhao, J., Lin, C. M. & Chao, F. Wavelet fuzzy brain emotional learning control system design for MIMO uncertain nonlinear systems. Front. Neurosci. 12, 918 (2019).
Fang, W. et al. An improved fuzzy brain emotional learning model network controller for humanoid robots. Front. Neurorobot. (2019).
Le, T. L., Huynh, T. T. & Lin, C. M. Adaptive filter design for active noise cancellation using recurrent type-2 fuzzy brain emotional learning neural network. Neural Comput. Appl. 32, 8725–8734 (2020).
Milad, H. S. A. & Gu, J. Expanded neo-fuzzy adaptive decayed brain emotional learning network for online time series predication. IEEE Access 9, 65758–65770 (2021).
Golshan, M., Teshnehlab, M., Sharii, A. & Sharifi, A. Brain-inspired emotional learning algorithm enhanced with type-one and interval type-two fuzzy extreme learning machine in noisy data. https://doi.org/10.21203/RS.3.RS-3206470/V1 (2023).
Hakimi, A., Monadjemi, S. A. & Setayeshi, S. Modeling of the earth’s rotation variations using a novel approach inspired by the brain emotional learning. AUT J. Model. Simul. 54, 173–184 (2022).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Cavalcante, G. H., Feary, D. A. & Burt, J. A. The influence of extreme winds on coastal oceanography and its implications for coral population connectivity in the southern Arabian Gulf. Mar. Pollut. Bull. 105, 489–497 (2016).
Privett, D. W. Monthly charts of evaporation from the N. Indian Ocean (including the Red sea and the Persian Gulf). Q. J. R. Meteorol. Soc. 85, 424–428 (1959).
Pourkerman, M. et al. The impacts of Persian Gulf water and ocean-atmosphere interactions on tropical cyclone intensification in the Arabian sea. Mar. Pollut Bull. 188, 114553 (2023).
Ghafarian, P., Kabiri, K., Delju, A. H. & Fallahi, M. Spatio-temporal variability of dust events in the Northern Persian Gulf from 1991 to 2020. Atmos. Pollut Res. 13, 101357 (2022).
Perrone, T. J. Winter Shamal in the Persian Gulf (Naval Environmental Prediction Research Facility Monterey, 1979).
Owlad, E., Stoffelen, A., Ghafarian, P. & Gholami, S. Wind field and gust climatology of the Persian Gulf during 1988–2010 using in-situ, reanalysis and satellite sea surface winds. Reg. Stud. Mar. Sci. 52, 102255 (2022).
Li, K. et al. Exploiting redundancy in large materials datasets for efficient machine learning with less data. Nat. Commun. 14, 1–10 (2023).
Abdul-Rahman, A. Time series analysis in forecasting mental addition and summation performance. Front. Psychol. 11, (2020).
Mohammed, N. A. & Al-Bazi, A. An adaptive backpropagation algorithm for long-term electricity load forecasting. Neural Comput. Appl. 34, 477–491 (2022).
Huang, Y. et al. Image-based features in machine learning to identify delivery errors and predict error magnitude for patient-specific IMRT quality assurance. Strahlenther. Onkol. 199, 498–510 (2023).
Mohamed, J., Mohamed, A. I. & Daud, E. I. Evaluation of prediction models for the malaria incidence in Marodijeh Region, Somaliland. J. Parasit. Dis. 46, 395–408 (2022).
Cameron, A. C. & Windmeijer, F. A. G. An R-squared measure of goodness of fit for some common nonlinear regression models. J. Econom. 77, 329–342 (1997).
Acknowledgements
We would like to thank the European Centre for Medium-Range Weather Forecasts (ECMWF) for providing free access to the ERA5 data. Additionally, we are grateful to Dr. Hossein Farjami from INIOAS for his assistance in preparing (Fig. 5).
Author information
Authors and Affiliations
Contributions
AH Contributed to resources, methodology, investigation, data curation, visualization, formal analysis, validation, and software development. He also prepared the original draft and contributed to reviewing and editing. PG Contributed to conceptualization, supervision, project administration, and validation. All authors reviewed and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hakimi, A., Ghafarian, P. Simultaneous prediction of 10m and 100m wind speeds using a model inspired by brain emotional learning. Sci Rep 15, 4304 (2025). https://doi.org/10.1038/s41598-025-88295-8
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-88295-8
Keywords
This article is cited by
-
Enhanced significant wave height prediction in the Southern Ocean using an ANFIS model optimized with subtractive clustering
Scientific Reports (2025)
-
Analyzing the cyclical impact of sunspot activity and ENSO on precipitation patterns in Gilan province: a wavelet-based approach
Scientific Reports (2025)