A novel fixed-time prescribed performance sliding mode control for uncertain wheeled mobile robots

Abstract

This paper proposes a novel fixed-time prescribed performance sliding mode control method, specifically designed to address trajectory tracking issues in wheeled mobile robots (WMRs) affected by wheel slipping, skidding (WSS), and external disturbances. A new prescribed performance sliding surface is first introduced based on a prescribed performance function (PPF) and a non-singular fast terminal sliding function (NFTSF). This design ensures that tracking errors converge to zero within a fixed time while maintaining stability by keeping error states within predefined limits. A novel fixed-time prescribed performance non-singular fast terminal sliding mode control (FPP-NFTSMC) algorithm is proposed based on the sliding function. The control method integrates a uniform second-order sliding mode (USOSM) algorithm to provide a continuous control signal, effectively reducing the chattering effect. This method combines the benefits of PPF, NFTSMC, and USOSM algorithm to achieve high-precision position tracking, minimize chattering, guarantee fixed-time convergence, ensure tracking errors remain within bounds, and maintain robustness against WSS, and external disturbances. The fixed-time stability of the WMR systems is demonstrated by the Lyapunov stability theory. The effectiveness of the proposed method is validated through simulations of tracking straight-line and U-shaped trajectories.

Introduction

Recently, wheeled mobile robots (WMRs) have increasingly been utilized in various fields, including industrial automation, logistics, healthcare, household tasks, and hazardous environments with limited human access^1,2,3,4,5,6. These versatile robots offer unparalleled flexibility and efficiency, capable of performing tasks either autonomously or with human oversight. Effective control is vital for their efficient operation and safety, allowing them to navigate, interact with their surroundings, and complete tasks accurately and efficiently. However, achieving precise and robust control is challenging due to the complex dynamics of WMRs and environmental uncertainties. Robustness is crucial for managing diverse operating conditions like WSS. These factors are key considerations in designing and controlling of WMRs, requiring robust control strategies to minimize their impact and enhance overall performance and safety.

In literature, many dynamics model-based control methods have been investigated to enhance robot tracking performance like computed torque control^7,8, adaptive control^9,10, fuzzy logic control¹¹, neural network-based control^12,13, and sliding mode control (SMC)^14,15,16. Compared to other methods, SMC is often considered an effective control approach, particularly valued for its robustness in handling uncertainties, and external disturbances in nonlinear dynamic systems. SMC has been successfully applied to WMRs, ensuring system stability by driving it toward a desired trajectory or state¹⁷. Especially, it offers excellent tracking performance and stability with a relatively simple design process. Despite these advantages, SMC is not without its drawbacks. One of the primary limitations is that it only guarantees asymptotic stability due to utilizing the linear sliding function, meaning that the system’s state variables will eventually converge to the desired equilibrium point, it may take an indefinite amount of time to do so. This gradual convergence can be a significant limitation in applications where rapid stabilization is critical. Additionally, SMC is known for causing the chattering phenomenon, which involves rapid oscillations around the sliding surface due to high-frequency switching control actions.

Finite-time control is widely recognized as an effective control strategy, especially appreciated for its ability to stabilize the systems. Unlike traditional control methods, which typically guarantee asymptotic stability, where the system state approaches to desired equilibrium point as time goes to infinity, finite-time control ensures that the convergence occurs within a finite period of time. This characteristic is crucial for applications that require rapid stabilization and precise timing, such as robotics^18,19, aerospace systems^20,21, and electrical circuits²². In the SMC family, finite-time convergence and stability can be obtained by using non-linear sliding functions instead of linear one; for example, terminal sliding mode control (TSMC)²³, fast TSMC^24,25, non-singular TSMC^26,27, and non-singular fast TSMC (NFTSMC)^28,29,30. Besides its advantages, the convergence speed of finite-time control approaches can be notably influenced by the system’s initial conditions. In many practical scenarios, when the initial conditions deviate significantly from the nominal values for which the controller was designed, the system may experience slower convergence rates or fail to achieve the desired state within the specified finite time. To overtake the problem, fixed-time stability has been developed, which guarantees that system states reach a desired equilibrium within a predetermined, fixed amount of time regardless of the initial state³¹. By providing reliable and predictable convergence times, fixed-time stability continues to play a vital role in increasing the safety, performance, and reliability of modern control systems, such as spacecraft³², underwater vehicle³³, robot manipulators^34,35, and mobile robots³⁶.

In order to minimize the chattering phenomenon, a common approach is to replace the discontinuous signum function in switching control law by a continuous one. In this approach, the most popular method is the boundary layer technique^37,38. While this approach decreases the chattering of the control input, it results in the system state not being exactly on the sliding surface but rather within a region around it, which reduces the tracking accuracy of the controlled systems. Another approach involves using high-order sliding mode (HOSM) that transfers the discontinuity to a higher-order derivative, effectively reducing chattering^39,40. The super-twisting algorithm (STA) is a second-order sliding mode control method widely used in control systems to ensure robust and precise performance despite uncertainties and disturbances^41,42. Moreover, it can bring the system state to the sliding surface in finite time, ensuring rapid response and stability. Unfortunately, the convergence time of STA still depends on system’s initial conditions.

To ensure robot stability, the essential is to maintain state errors within a defined boundary. The prescribed-performance control (PPC) strategy is an advanced control method that focuses on setting measurable outputs for a system and designing a control method to meet specific operational goals. This includes ensuring fast transient response, accurate steady-state performance, robustness against disturbances, and limiting overshoot^43,44,45. PPC is especially useful for managing complex and uncertain systems, in which conventional control methods may fall short. In this approach, a prescribed performance function (PPF) and an error transformation function (ETF) are applied to achieve specific control objectives. The PPF plays a vital role in maintaining tracking errors within specified bounds over time, which can be critical in safety-critical applications. The ETF is a technique used in control systems to modify the error signal before it is processed by the control algorithm. The transformed error can improve the overall control performance, leading to faster convergence, increased robustness, and better stability of the controlled system. By explicitly defining desired performance criteria, PPC can enhance a system’s robustness against dynamic uncertainties and external disturbances, leading to superior performance^46,47,48.

In light of the aforementioned motivations, a novel fixed-time prescribed-performance NFTSMC (FPP-NFTSMC) algorithm, specifically designed for WMRs, is presented in this article. The proposed controller aims to achieve control objectives despite the presence of WSS and external disturbances, including high tracking accuracy, fast convergence, reduced chattering, singularity elimination, fixed-time convergence, and a bounded range of tracking errors. To the best of the authors’ knowledge, this is the first application of fixed-time prescribed performance SMC for mobile robots. To demonstrate the efficiency of the designed controller, two simulation examples are conducted: tracking a simple straight trajectory and navigating a U-shaped trajectory. The following briefly describes the primary contributions of this paper:

• Introduce a novel prescribed-performance NFTSF by integrating transformed errors, which effectively addresses the singularity problem,

• Propose a novel FPP-NFTSMC approach using the proposed sliding surface and USOSM algorithm to improve WMRs tracking accuracy under total impacts of WSS, and external disturbances,

• Attain high control performance with low tracking errors, rapid convergence, no singularity problem, and constrained tracking errors within a prescribed boundary,

• Mitigate chattering effect in control input by applying the USOSM method,

• Achieve stability and ensure fixed-time convergence of the WMR system using Lyapunov stability theory.

The organization of this study is presented as following:

• Section II presents the kinematic and dynamic models of a four-WMR and covers some foundational concepts necessary for understanding the control methodologies.

• Section III presents the design of the proposed prescribed-performance sliding surface and the proposed FPP-NFTSMC. This section includes a detailed stability analysis and fixed-time convergence of the four-WMR.

• Section IV showcases the simulation results conducted to evaluate the designed control algorithm in two different working examples.

• Section V concludes the paper, summarizing the findings and contributions.

Problem formulation

Preliminaries

Throughout the paper, the notation $\lfloor {x}\rceil ^\alpha = \left| x\right| ^\alpha \textrm{sign}(x)$ is used, where $x\in {\mathbb {R}}$, $\forall \alpha \ge 0$, and $\textrm{sign}(\cdot )$ represents signum function. When $\alpha = 0$, $\lfloor {x}\rceil ^0= \textrm{sign}(x)$.

Lemma 1

⁴⁹:

Consider the system

$$\begin{aligned} \begin{aligned} {\dot{x}}_1&= -K_1 \Gamma _1({x}_1) + {x}_2\\ {\dot{x}}_2&= -K_2 \Gamma _2({x}_1) - \dot{d} \end{aligned} \end{aligned}$$

(1)

with

$$\begin{aligned} \begin{aligned} \Gamma _1({x}_1)&= \lfloor {{x}_1}\rceil ^{1/2} + \gamma \lfloor {{x}_1}\rceil ^{3/2} \\ \Gamma _2({x}_1)&= \frac{3}{2} \gamma ^2 \lfloor {{x}_1}\rceil ^{2} + 2 \gamma {x}_1 + \frac{1}{2} \lfloor {{x}_1}\rceil ^{0} \end{aligned} \end{aligned}$$

(2)

where $\gamma> 0$, $|\dot{d}| \le d_{max}$, and $d_{max}> 0$.

If $K_1, K_2$ are selected to satisfy the conditions

$K = \left\{ (K_1, K_2) \in {\mathbb {R}}^2 \mid 0<K_1 \le 2\sqrt{d_{max}}, K_2> \frac{K_1^2}{4} + \frac{4 d_{max}^2}{K_1^2} \right\} \cup \left\{ (K_1, K_2) \in {\mathbb {R}}^2 \mid K_1> 2\sqrt{d_{max}}, K_2> 2 d_{max} \right\}$, the system states $x_1$ and $x_2$ will converge to zero within fixed time $T_0$⁴⁹.

Kinematic model of four-WMR

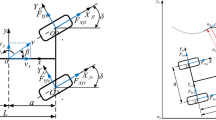
In this section, a four-WMR with framework as shown in Fig. 1is considered. In order to design an effective control method, the kinematic model of the four-WMR is introduced following the methodology outlined in¹³. Parameters of the four-WMR and their notations are described in Table. 1.

Table 1 Four-WMR parameter notations.

Fig. 1

Four-WMR.

The robot’s kinematic model is derived from the constraints imposed by the velocity components that can be determined as follows

$$\begin{aligned} \begin{aligned} u&=\frac{1}{2}\ (u_l+u_r\ )\\ v&=\frac{d}{b}\ (u_l-u_r )+v^s\\ r&=\frac{1}{2b}\ (u_l-u_r )\\ u_l&=R\omega _l-u_l^s\\ u_r&=R\omega _r-u_r^s \end{aligned} \end{aligned}$$

(3)

The trajectory of the four-WMR in global Cartesian coordinate is represented as

$$\begin{aligned} \begin{aligned} {\dot{X}}&=u\cos (\theta )-(v+lr)\sin (\theta )\\ {\dot{Y}}&=u\sin (\theta )+(v+lr)\cos (\theta )\\ \dot{\theta }&=r \end{aligned} \end{aligned}$$

(4)

Dynamic model of four-WMR

For a four-WMR, the total of the external forces and moments acting on the robot body-centered lead to the motion equations as following

$$\begin{aligned} \begin{aligned} {\dot{u}}&= \frac{1}{m}(F_{xr}+F_{xl}+P_x)+vr\\ {\dot{v}}&= \frac{1}{m}(F_{yr}+F_{yl}+P_y)-ur\\ {\dot{r}}&= \frac{1}{I_z}\left[ (F_{xl}-F_{xr})b-(F_{yl}+F_{yr})d-M_d\right] \\ \dot{\omega }_r&= \frac{1}{I_e}(n\tau _R - F_{xr}R)\\ \dot{\omega }_l&= \frac{1}{I_e}(n\tau _L - F_{xl}R) \end{aligned} \end{aligned}$$

(5)

where m represents the mass; $I_z$ denotes the moment of inertia (MoI) about the z-axis; $I_e = I_t + n^2I_m$, $I_t$, and $I_m$ denote the effective MoI, MoI of wheel, and MoI of motor, respectively; $\tau _L$ and $\tau _R$ denotes the control torque at left and right wheel, respectively; and $n>1$ is the gear ratio.

Accurate modeling of the friction forces between the tires and the ground is crucial for developing a precise dynamics model for a WMR. Each tire of the WMR experiences two primary friction components as illustrated in Fig. 1. The longitudinal friction force acts in the direction of the tire’s rotation and is influenced by the slip ratio. The lateral friction force, on the other hand, acts perpendicular to the direction of the tire’s rotation and is influenced by the slip angle.

By eliminating the friction forces and reorganizing the dynamics equation of (5) and combining it with the kinematic models from (3) and (4), the dynamics model of the four-WMR can be described as:

$$\begin{aligned} \left[ \begin{matrix} {\dot{X}}\\ {\dot{Y}}\\ \dot{\theta }\\ {\dot{u}}\\ {\dot{r}}\\ \end{matrix}\right] = \left[ \begin{matrix} u\cos (\theta )-(d+l)r\sin (\theta )\\ u\sin (\theta )+(d+l)r\cos (\theta )\\ r\\ \frac{mdR^2r^2}{\Omega _u}\\ -\frac{mdR^2ur}{\Omega _r}\\ \end{matrix}\right] + \left[ \begin{matrix} 0 & 0\\ 0 & 0\\ 0 & 0\\ \frac{nR}{\Omega _u} & 0\\ 0 & \frac{nbR}{\Omega _r}\\ \end{matrix}\right] \left[ \begin{matrix} \tau _u\\ \tau _r\\ \end{matrix}\right] + \left[ \begin{matrix} \delta _x\\ \delta _y\\ 0\\ \delta _u\\ \delta _r\\ \end{matrix}\right] \end{aligned}$$

(6)

where $\Omega _u=mR^2+2I_e; \Omega _r=2b^2I_e+R^2(I_z+md^2); \tau _u= \frac{1}{2}(\tau _L+\tau _R); \tau _r= \frac{1}{2}(\tau _L-\tau _R); \delta _u=\frac{1}{\Omega _u}\left[ R^2P_x+mR^2rv^s-I_e({\dot{u}}_l^s+{\dot{u}}_r^s)\right] ;$

$\delta _r=\frac{1}{\Omega _r}\left[ dR^2P_y-M_dR^2-mdR^2{\dot{v}}^s-bI_e({\dot{u}}_l^s-{\dot{u}}_r^s)\right] ;\delta _x=-v^s\sin (\theta ); \delta _y=v^s\cos (\theta ).$ 

In (6), the third component of left side represents the lumped uncertainties, including WSS, and external disturbances and is denoted as $\delta _m = \left[ \begin{matrix}\delta _x\,\, \delta _y\,\, 0\,\, \delta _u\,\, \delta _r \end{matrix}\right] ^T$.

Taking time derivative of the dynamics model (6) and substituting the kinematic equations, the robot dynamics model in state space form can be obtained as following

$$\begin{aligned} \begin{aligned} {\dot{x}}_1&= {x}_2\\ {\dot{x}}_2&= M(\theta )\left[ \tau + \Upsilon ({x}_2, \theta , \delta _m)+\Xi ({x}_2, \theta , \delta _m)\right] \\ \dot{\theta }&= r({x}_2, \theta , \delta _m) \end{aligned} \end{aligned}$$

(7)

where $x_1 = \left[ \begin{matrix} X&Y \end{matrix}\right] ^T$, $x_2 = \left[ \begin{matrix}{\dot{X}}&{\dot{Y}} \end{matrix}\right] ^T$, $M(\theta )$ is a positive definite matrix, $M(\theta ) = \left[ \begin{array}{ll} \frac{nR}{\Omega _u}\cos (\theta ) & -\frac{nRb(d+l)}{\Omega _r}\sin (\theta )\\ \frac{nR}{\Omega _u}\sin (\theta ) & \frac{nRb(d+l)}{\Omega _r}\cos (\theta )\\ \end{array}\right] ,$ $\Upsilon ({x}_2, \theta , \delta _m) = \left[ \begin{array}{ll} -\frac{lmR^2+2(d+l)I_e}{nR}r^2\\ \frac{2b^2I_e+R^2(I_e-mdl)}{nbR(d+l)}ur\\ \end{array}\right] ,$ $\Xi ({x}_2, \theta , \delta _m) = \left[ \begin{array}{ll} -\frac{\Omega _u}{nR}(\delta _u-v^sr)\\ \frac{\Omega _r}{nbR(d+l)}((b+l)\delta _r-{\dot{v}}^s)\\ \end{array}\right] ,$ and $r({x}_2, \theta , \delta _m) = \frac{1}{d+l}\left[ -({\dot{X}}-\delta _x)\sin \theta + ({\dot{Y}}-\delta _y)\cos \theta \right] .$

In simple operation conditions, it can be assumed that WSS and external disturbances are zero, the dynamics model can be rewritten as

$$\begin{aligned} \begin{aligned} {\dot{x}}_1&= {x}_2\\ {\dot{x}}_2&= M_0(\theta )\left[ \tau + \Upsilon _0({x}_2, \theta )\right] \\ \dot{\theta }&= r({x}_2, \theta ) \end{aligned} \end{aligned}$$

(8)

where $\Upsilon _0({x}_2, \theta ) = \left[ \begin{matrix} -\frac{lmR^2+2(d+l)I_e}{nR}r^2_{({x}_2, \theta )}\\ \frac{2b^2I_e+R^2(I_e-mdl)}{nbR(d+l)}u_{({x}_2, \theta )}r_{({x}_2, \theta )}\\ \end{matrix}\right] ,\ \text {and}\; r({x}_2, \theta ) = \frac{1}{d+l}(-{\dot{X}}\sin \theta + {\dot{Y}}\cos \theta ).$

By combining (7) and (8), the robot dynamics model can be transformed as

$$\begin{aligned} \begin{aligned} {\dot{x}}_1&= {x}_2\\ {\dot{x}}_2&= M_0(\theta )\left[ \tau + \Upsilon _0\right] +D \end{aligned} \end{aligned}$$

(9)

where $D = (M-M_0)(\theta )\left[ \tau + \Upsilon + \Xi ({x}_2, \theta , \delta _m)\right] + M(\theta )\left[ \Upsilon -\Upsilon _0 +\Xi ({x}_2, \theta , \delta _m)\right]$ denotes the lumped of WSS and external disturbances.

Error dynamics model

By defining position tracking errors $e_1$ and velocity tracking errors $e_2$ as

$$\begin{aligned} \begin{aligned} e_1&= x_1 - x_d\\ e_2&= \dot{e}_1 = x_2 - {\dot{x}}_d \end{aligned} \end{aligned}$$

(10)

where $x_d$ denotes assumed trajectory and ${\dot{x}}_d$ denotes assumed velocity, the four-WMR system in (9) is transferred to error dynamics as

$$\begin{aligned} \begin{aligned} {\dot{e}}_1&= {e}_2\\ {\dot{e}}_2&= M_0(\theta )\left[ \tau + \Upsilon _0\right] +D-\ddot{x}_d \end{aligned} \end{aligned}$$

(11)

The principal purpose of this article is to develop a control approach that effectively mitigates the adverse influences of WSS, and external disturbances in WMRs with precise tracking ability. In addition, the control method aims to keep the tracking error within predefined bounds. Without the requirement of a state observer or estimator, this novel proposed control strategy is constructed under the assumption that the position and velocity in the system are always available.

Control algorithm design

Prescribed-performance function

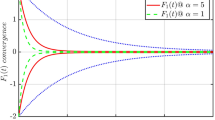
The PPF facilitates tracking errors within specified bounds over time. An illustration of PPC is shown in Fig. 2. Generally, PPF, $P\left( t\right)$, relates to the tracking error and is chosen based on the following conditions

• $P\left( t\right)$ is a smooth function.

• ${lim}_{t\rightarrow \infty }\ P\left( t\right) \ =\ p_\infty>0$.

• $P\left( t\right)$ is decreasing and positive.

The PPF is selected as⁴⁵

$$\begin{aligned} P(t) = (p_0 - p_\infty )\textrm{exp}(-\lambda t) + p_\infty \end{aligned}$$

(12)

where $p_0$, $p_\infty$ satisfy $p_0> p_\infty> 0$, $p_0> |e_1(0)|$, and $\lambda>0$.

Fig. 2

An illustration of PPC.

The ETF is a technique used in control systems to modify the error signal before it is processed by the control algorithm. Through suitable transformation function design, the system’s disturbances, uncertainties, and nonlinearities may be reduced, leading to faster convergence, improved robustness, and better stability of the controlled system. The ETF, $\Psi \left( \xi _1\right)$ is selected based on the following conditions

• $\Psi \left( \xi _1\right)$ is a smooth and strictly increasing function.

• $-1<\Psi \left( \xi _1\right) <1$.

• $\Psi \left( \xi _1\right) =0\ \text {when}\ \xi _1=0$.

• $\left\{ \begin{matrix} {lim}_{\xi _1\rightarrow -\infty } \Psi (\xi _1)\ & =& -1\\ {lim}_{\xi _1\rightarrow +\infty } \Psi (\xi _1)\ & =& 1\\ \end{matrix} \right.$.

where $\xi _1$ represents transformed error.

The specific ETF for this study is chosen as⁴³

$$\begin{aligned} e_1 = P(t)\Psi (\xi _1) \end{aligned}$$

(13)

where

$$\begin{aligned} \Psi (\xi _1) = \frac{2}{\pi }\arctan (\xi _1) \end{aligned}$$

(14)

From the ETF (14), transformed error is produced as follows

$$\begin{aligned} \begin{aligned} \xi _1&= \Psi ^{-1}\left( \frac{e_1}{P(t)}\right) \\&=\tan \left( \frac{\pi }{2} \times \frac{e_1}{P(t)}\right) \end{aligned} \end{aligned}$$

(15)

Taking time derivative of (13), yields

$$\begin{aligned} \begin{aligned} {\dot{e}}_1&= {\dot{P}}(t)\Psi (\xi _1) + P(t)\dot{\Psi }(\xi _1) \\&={\dot{P}}(t)\frac{2}{\pi }\arctan (\xi _1) + P(t)\frac{2}{\pi }\frac{d}{dt}\arctan (\xi _1)\\&={\dot{P}}(t)\frac{2}{\pi }\arctan (\xi _1) + P(t)\frac{2}{\pi }\frac{\dot{\xi _1}}{1+\xi _1^2} \end{aligned} \end{aligned}$$

(16)

where ${\dot{P}}(t) = -\lambda (p_0 - p_\infty )\textrm{exp}(-\lambda t).$

From (16), the derivative of transformed error with respect to time is obtained as

$$\begin{aligned} \dot{\xi _1} = \frac{\pi (1+{\xi _1}^2)}{2P(t)}\left( {\dot{e}}_1-\frac{2{\dot{P}}(t)}{\pi }\arctan (\xi _1)\right) \end{aligned}$$

(17)

Taking time derivative of (16), yields

$$\begin{aligned} \begin{aligned} \ddot{e}_1&= {\ddot{P}}(t)\Psi (\xi _1) + 2{\dot{P}}(t)\dot{\Psi }(\xi _1) + P(t)\ddot{\Psi }(\xi _1) \\&= {\ddot{P}}(t) \frac{2}{\pi } \arctan (\xi _1) + 2 {\dot{P}}(t) \frac{2}{\pi } \frac{\dot{\xi _1}}{1+\xi _1^2} + P(t) \frac{2}{\pi } \frac{\ddot{\xi _1}(1+{\xi _1}^2)-2\xi _1\dot{\xi _1}^2}{\left( 1+{\xi _1}^2\right) ^2} \\&=\frac{2}{\pi } \left( {\ddot{P}}(t)\arctan (\xi _1)+ \frac{2{\dot{P}}(t)\dot{\xi _1}}{1+{\xi _1}^2}- \frac{2P(t)\xi _1\dot{\xi _1}^2}{\left( 1+{\xi _1}^2\right) ^2} \right) + \frac{2}{\pi } P(t) \frac{\ddot{\xi _1}}{1+\xi _1^2} \end{aligned} \end{aligned}$$

(18)

where ${\ddot{P}}(t)= \lambda ^2(p_0 - p_\infty )\textrm{exp}(-\lambda t).$

From (18), the second-order derivative of transformed error with respect to time is obtained as

$$\begin{aligned} \ddot{\xi _1} = \frac{\pi (1+{\xi _1}^2)}{2P(t)}\left( \ddot{e}_1- \Sigma \right) \end{aligned}$$

(19)

where $\Sigma =\frac{2}{\pi } \left( {\ddot{P}}(t)\arctan (\xi _1)+ \frac{2{\dot{P}}(t)\dot{\xi _1}}{1+{\xi _1}^2} - \frac{2P(t)\xi _1\dot{\xi _1}^2}{\left( 1+{\xi _1}^2\right) ^2} \right) .$

Combining (17), (19), and (11), the dynamics model of four-WMR is transferred into

$$\begin{aligned} \begin{aligned} \dot{\xi }_1&= {\xi }_2\\ \dot{\xi }_2&= \chi \left[ M_0(\theta )\left[ \tau + \Upsilon _0\right] +D-\ddot{x}_d - \Sigma \right] \end{aligned} \end{aligned}$$

(20)

where $\chi = \frac{\pi (1+{\xi _1}^2)}{2P(t)}>0$.

Prescribed-performance NFTSF design

To design an effective control signal, a novel prescribed-performance NFTSF is proposed based on the transformed error as follows

$$\begin{aligned} \sigma = \xi _2 + \Pi (\xi _1) + \varkappa _3 \Omega (\xi _1) \end{aligned}$$

(21)

The term $\Pi (\xi _1)$ is expressed as

$$\begin{aligned} \Pi (\xi _1) = \varkappa _1 \xi _1 + \varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2}, \end{aligned}$$

(22)

and the term $\Omega (\xi _1)$ is used to handle the singularity problem that is expressed as

$$\begin{aligned} \Omega (\xi _1) = \left\{ \begin{matrix} \lfloor {\xi _1}\rceil ^{\alpha _3} & if & \left| \xi _1 \right| \geqslant \epsilon \\ \epsilon ^{\alpha _3-1} \xi _1 & if & \left| \xi _1 \right| < \epsilon \\ \end{matrix}\right. \end{aligned}$$

(23)

where parameters $\varkappa _1, \varkappa _2, \varkappa _3$ are positive constants, $\alpha _2> 1, 0< \alpha _3 < 1$, and $\epsilon> 0$ denote a small constant.

From the SMC theory⁵⁰, when the system reaches sliding mode, the following property is obtained:

$$\begin{aligned} \sigma = 0, \text { and } \dot{\sigma }= 0 \end{aligned}$$

(24)

Combining (21) and (24), yields

$$\begin{aligned} \xi _2 = - \Pi (\xi _1) - \varkappa _3 \Omega (\xi _1) \end{aligned}$$

(25)

Remark 1

The term $\lfloor {\xi _1}\rceil ^{\alpha _3}$ with $0< \alpha _3 < 1$ may produce singularity problem because its derivative, $\alpha _3\left| {\xi _1}\right| ^{\alpha _3-1}\xi _2$, includes negative power of $\xi _1$. When $\xi _1 = 0$ and $\xi _2 \ne 0$, this will be infinity. Thus, the use of $\Omega (\xi _1)$ in (23) helps to avoid the singularity.

Theorem 1

Consider the sliding mode dynamics described in (25), the origin ${\xi }$ is determined as a stable equilibrium point, and the state trajectories of the system reach an arbitrarily small range, $\epsilon$, in a limited convergence time and then converge zero exponentially.

Proof 1

To analyze the convergence of the system, we consider two cases as follows

Case 1: When $\left| \xi _1 \right| \geqslant \epsilon$, the sliding function in (21) is represented as

$$\begin{aligned} \sigma = \xi _2 + \varkappa _1 \xi _1 + \varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2} + \varkappa _3 \lfloor {\xi _1}\rceil ^{\alpha _3} \end{aligned}$$

(26)

The sliding mode dynamics (25) will be expressed as

$$\begin{aligned} \xi _2 = - \varkappa _1 \xi _1 - \varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2} - \varkappa _3 \lfloor {\xi _1}\rceil ^{\alpha _3} \end{aligned}$$

(27)

Consider a Lyapunov function as following

$$\begin{aligned} V_1 = \frac{1}{2} \xi _1^T \xi _1 \end{aligned}$$

(28)

Taking time derivative of (28) and substituting (27), yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_1&= \xi _1^T \xi _2\\&= \xi _1^T (- \varkappa _1 \xi _1 - \varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2} - \varkappa _3 \lfloor {\xi _1}\rceil ^{\alpha _3})\\&= - \varkappa _1 \xi _1^2 - \varkappa _2 \left| \xi _1 \right| ^{\alpha _2+1} - \varkappa _3 \left| \xi _1 \right| ^{\alpha _3+1}\\&= - 2\varkappa _1 V_1 - \varkappa _2 2^\frac{\alpha _2+1}{2} V_1^\frac{\alpha _2+1}{2} - \varkappa _3 2^\frac{\alpha _3+1}{2} V_1^\frac{\alpha _3+1}{2} \end{aligned} \end{aligned}$$

(29)

Denoting $k_1 = 2\varkappa _1, k_2 = \varkappa _2 2^\frac{\alpha _2+1}{2}, \text {and} \ k_3 = \varkappa _3 2^\frac{\alpha _3+1}{2}$

In the following, the differential (29) will be solved as

$$\begin{aligned} \begin{aligned} T_1&\le \displaystyle \lim _{V_1(\xi _1(0))\rightarrow \infty } \int _{0}^{V_1(\xi _1(0))} \frac{V_1}{k_1 V_1 + k_2 V_1^\frac{\alpha _2+1}{2} + k_3 V_1^\frac{\alpha _3+1}{2}}\\&\le \int _{0}^{1} \frac{V_1}{k_1 V_1 + k_3 V_1^\frac{\alpha _3+1}{2}} + \lim _{V_1(\xi _1(0))\rightarrow \infty } \int _{1}^{V_1(\xi _1(0))} \frac{V_1}{k_1 V_1 + k_2 V_1^\frac{\alpha _2+1}{2}}\\&\le \int _{0}^{1} \frac{V_1}{k_1 V_1 + k_3 V_1^\frac{\alpha _3+1}{2}} + \lim _{V_1(\xi _1(0))\rightarrow \infty } \int _{1}^{V_1(\xi _1(0))} \frac{V_1}{k_2 V_1^\frac{\alpha _2+1}{2}}\\&= \frac{2}{k_1(1-\alpha _3)}ln\left( 1+ \frac{k_1}{k_3} \right) + \frac{2}{k_2(\alpha _2 - 1)} \end{aligned} \end{aligned}$$

(30)

The above analysis shows that the state trajectories of the sliding mode system (25) reach a predetermined small set, $\epsilon$, within a limited convergence time $T_1$.

Case 2: When $\left| \xi _1 \right| < \epsilon$, the sliding function in (21) is represented as

$$\begin{aligned} \sigma = \xi _2 + \varkappa _1 \xi _1 + \varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2} + \varkappa _3 \epsilon ^{\alpha _3-1} \xi _1 \end{aligned}$$

(31)

The sliding mode dynamics (25) will be expressed as

$$\begin{aligned} \xi _2 = - \varkappa _1 \xi _1 - \varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2} - \varkappa _3 \epsilon ^{\alpha _3-1} \xi _1 \end{aligned}$$

(32)

Using the same Lyapunov function $V_1$ as in (28), taking its derivative and substituting (32), yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_1&= \xi _1^T (- \varkappa _1 \xi _1 - \varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2} - \varkappa _3 \epsilon ^{\alpha _3-1} \xi _1)\\&= - (\varkappa _1 + \varkappa _3 \epsilon ^{\alpha _3-1}) \xi _1^2 - \varkappa _2 \left| \xi _1 \right| ^{\alpha _2+1}\\&= - 2(\varkappa _1 + \varkappa _3 \epsilon ^{\alpha _3-1}) V_1 - \varkappa _2 2^\frac{\alpha _2+1}{2} V_1^\frac{\alpha _2+1}{2}\\&\le - 2(\varkappa _1 + \varkappa _3 \epsilon ^{\alpha _3-1}) V_1 \end{aligned} \end{aligned}$$

(33)

Based on the Lyapunov stability theory, it can be concluded that the state trajectories converge to zero exponentially. Consequently, the Theorem 1 is completely demonstrated.

$\square$

Remark 2

The ETF in (14) is defined by $\arctan (\xi _1)$ function, which guarantees that the position tracking error, $e_1$, will be zero if the transformed error, $\xi _1$, converges to zero.

Remark 3

It is noted that the linear term $\varkappa _1 \xi _1$ in (22) helps the system to converge faster when the state of the system is very far away from the origin and weaker when the state of the system is near the origin than two nonlinear terms $\varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2}$ in (22) and $\varkappa _3 \lfloor {\xi _1}\rceil ^{\alpha _3}$ in (23). When the state of the system remains at a distance from equilibrium, $\varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2}$ dominates over $\varkappa _3 \lfloor {\xi _1}\rceil ^{\alpha _3}$. In contrast, when the state of the system is close to the origin, $\varkappa _3 \lfloor {\xi _1}\rceil ^{\alpha _3}$ dominates over $\varkappa _2 \lfloor {\xi _1}\rceil ^{\alpha _2}$. Combining of these terms guarantees a high convergence rate in the whole sliding function.

Fixed-time prescribed-performance NFTSMC design

Based on the prescribed-performance NFTSF (21), a novel FPP-NFTSMC signal is proposed as following

$$\begin{aligned} \tau = -M_0^{-1}\left( \tau _{eq} + \tau _{sw}\right) \end{aligned}$$

(34)

where $\tau _{eq}$ represents equivalent control

$$\begin{aligned} \tau _{eq} = \left[ -\ddot{x}_d - \Sigma + \chi ^{-1}\left( \dot{\Pi }(\xi _1) + \varkappa _3 \dot{\Omega }(\xi _1)\right) \right] +M_0\Upsilon _0, \end{aligned}$$

(35)

and $\tau _{sw}$ represents switching control, which is designed based on the USOSM as following

$$\begin{aligned} \begin{aligned} \tau _{sw}&= \beta _1 \Gamma _1(\sigma ) + \vartheta \\ \dot{\vartheta }&= \beta _2 \Gamma _2(\sigma ) \end{aligned} \end{aligned}$$

(36)

with $\dot{\Pi }(\xi _1) = \varkappa _1 \xi _2 + \varkappa _2 \alpha _2 \left| {\xi _1}\right| ^{\alpha _2 - 1}\xi _2$; $\dot{\Omega }(\xi _1) = \left\{ \begin{matrix} \alpha _3\left| {\xi _1}\right| ^{\alpha _3-1}\xi _2 & if & \left| \xi _1 \right| \geqslant \epsilon \\ \epsilon ^{\alpha _3-1} \xi _2 & if & \left| \xi _1 \right| < \epsilon \\ \end{matrix}\right.$; $\beta _1$, and $\beta _2$ denote positive constants and are selected based on Lemma 1. The functions $\Gamma _1(\sigma )$, and $\Gamma _2(\sigma )$ are described as

$$\begin{aligned} \begin{aligned} \Gamma _1(\sigma )&= \lfloor {\sigma }\rceil ^{1/2} + \gamma \lfloor {\sigma }\rceil ^{3/2} \\ \Gamma _2(\sigma )&= \frac{3}{2} \gamma ^2 \lfloor {\sigma }\rceil ^{2} + 2 \gamma \sigma + \frac{1}{2} \lfloor {\sigma }\rceil ^{0} \end{aligned} \end{aligned}$$

(37)

where $\gamma> 0$ represents a constant.

Theorem 2

Suppose that the derivative of lumped of WSS and external disturbances D in the four-WMR (9) is bounded as

$$\begin{aligned} |\dot{D}|\le D_{max} \end{aligned}$$

(38)

where $D_{max}$ is a positive constant.Then, if the control input is designed as in (34), (35), and (36) with suitably chosen parameters, the stability of the robot system is guaranteed and the sliding surface converges to zero within fixed-time.

Proof 2

Taking time derivative of the proposed sliding function (21), yields

$$\begin{aligned} \dot{\sigma } = \dot{\xi }_2 +\dot{\Pi }(\xi _1) + \varkappa _3 \dot{\Omega }(\xi _1) \end{aligned}$$

(39)

Combining the transformed error dynamics (20), with control signals in ((34), (35), and (36)) and substituting into (39), yields

$$\begin{aligned} \begin{aligned} \dot{\sigma }&= -\beta _1 \Gamma _1(\sigma ) + \vartheta + D \\ \dot{\vartheta }&= -\beta _2 \Gamma _2(\sigma ) \end{aligned} \end{aligned}$$

(40)

By denoting $\vartheta _1 = \vartheta + D$, the system (40) can be rewritten as

$$\begin{aligned} \begin{aligned} \dot{\sigma }&= -\beta _1 \Gamma _1(\sigma ) + \vartheta _1 \\ \dot{\vartheta _1 }&= -\beta _2 \Gamma _2(\sigma ) - \dot{D} \end{aligned} \end{aligned}$$

(41)

The form of (41) is in the same form of (1) in Lemma 1; accordingly, it can be concluded that the sliding surface $\sigma$ will converge to zero within fixed-time $T_0$⁴⁹. Thus, the Theorem 2 is fully proven. $\square$

Therefore, the settling time is determined as $T_s = T_0 + T_1$.

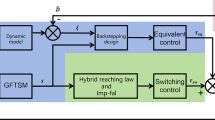
The block diagram of the proposed FPP-NFTSMC is presented in Fig. 3.

Fig. 3

Block diagram of the proposed FPP-NFTSMC.

Results and discussions

Simulation setup

To validate the powerfulness of the proposed algorithm, simulations are performed to manage the WMR system under two operational scenarios: 1) following a straight trajectory and 2) following a U-shaped path. By simulating various scenarios and disturbances, we aim to thoroughly evaluate the tracking ability and robustness of the WMR. For computer simulations, MATLAB/Simulink is used where the sampling time is 1 ms. The WMR’s parameters are detailed in Table 2. The control parameters are selected by the trial-and-error approach to obtain suitable performance and their values are outlined in Table 3 ( with ${\bar{D}}$ is defined in Appendices).

Table 2 Four-WMR parameter values.

Table 3 Control parameter values.

Case 1: In this case, the WMR is tasked with tracking a straight trajectory, depicted in Fig. 8. The trajectory consists of three separate phases that follow a predetermined velocity profile:

• The WMR undergoes a phase of constant acceleration, steadily increasing its velocity from an initial value to a specified maximum velocity,

• The WMR maintains the constant maximum velocity,

• The WMR enters a phase of constant deceleration, gradually reducing the velocity to zero.

According to the three operation phases, the trajectory of the WMR is assumed as:

$$\begin{aligned} \left\{ \begin{array}{ll} \begin{aligned} x_d & = \left\{ \begin{array}{lll} & 1 + \frac{8}{90}t^2 & 0 \le t< 3\\ & 1 + \frac{8}{15}(t-1.5) & 3 \le t< 7\\ & -\frac{187}{45} + \frac{80}{45}t - \frac{4}{45}t^2 & 7 \le t \le 10 \end{array}\right. \\ y_d & = \left\{ \begin{array}{lll} & 1 + \frac{2}{18}t^2 & 0 \le t< 3\\ & 1 + \frac{2}{3}(t-1.5) & 3 \le t < 7\\ & -\frac{49}{9} + \frac{20}{9}t - \frac{1}{9}t^2 & 7 \le t \le 10 \end{array}\right. \end{aligned} \end{array} \right. \end{aligned}$$

(42)

The initial position is assumed as $\left[ \begin{matrix}x&y&\theta \end{matrix}\right] ^T = \left[ \begin{matrix}1.1&1.1&0 \end{matrix}\right] ^T$. In the context of tracking a straight-line trajectory, the robot’s wheel skidding is not considered a significant factor, which implies that the skidding velocity $v^s$ is effectively zero $(0\ \mathrm {m/s})$. The wheel slipping is assumed as simple sinusoidal function

$$\begin{aligned} \begin{aligned} u_r^s&= 0.15 + 0.25 \sin (3t)\\ u_l^s&= 0.15 + 0.25 \sin (3t) \end{aligned} \end{aligned}$$

(43)

The expected external disturbances are as $P_x=10 (\textrm{N})$, and $P_y=10 (\textrm{N})$.

Case 2: The objective of this scenario is to assess how well the suggested control approach compensates for WSS and external disturbances while following a difficult U-shaped trajectory, as shown in Fig. 14. The trajectory poses a challenging situation where abrupt wheel sliding motion could happen, requiring strong control systems to keep tracking accuracy and stability.

The trajectory is divided into three separate phases:

• In the first stage, the four-WMR accelerates to reach a set velocity along a straight line; therefore, only the influences of wheel slipping on the robot are under consideration.

• When WMR reaches the turning spot, it makes a U-turn to follow the trajectory’s curving course. WSS effects are taken into account since this phase necessitates synchronized motion control to safely handle the steep turn while preserving stability and adherence to the intended trajectory.

• The robot executes a U-turn, then slows down and travels straight ahead to the intended location. Like the first phase, only the effects of wheel slipping are taken into account.

The expected trajectory is as follows

$$\begin{aligned} \left\{ \begin{array}{ll} \begin{aligned} x_d & = \left\{ \begin{array}{ll} 1 + 2.5\frac{\pi }{100}t^2 & 0 \le t< 5\\ 1 + \frac{5\pi }{8} + 2.5\cos (\frac{\pi }{10}(t-5)-\frac{\pi }{2}) & 5 \le t< 15\\ 1 + \frac{35\pi }{8} - 2.5\frac{\pi }{10}t + 2.5\frac{\pi }{100}(t-15)^2 & 15 \le t \le 20 \end{array}\right. \\ y_d & = \left\{ \begin{array}{ll} 1 & 0 \le t< 5\\ 3.5 + 2.5\sin (\frac{\pi }{10}(t-5)-\frac{\pi }{2}) & 5 \le t < 15\\ 6 & 15 \le t \le 20 \end{array}\right. \end{aligned} \end{array} \right. \end{aligned}$$

(44)

The WMR’s initial position is assumed as $\left[ \begin{matrix}x&y&\theta \end{matrix}\right] ^T = \left[ \begin{matrix}1.1&1.1&0 \end{matrix}\right] ^T$.

The assumed wheel skidding of WMR is

$$\begin{aligned} \begin{aligned} v^s&= \left\{ \begin{matrix} 0 & 0 \le t< 5\\ 0.35 + 0.1\cos (\frac{\pi }{5}t) & 5 \le t < 15\\ 0 & 15 \le t \le 20 \end{matrix}\right. \end{aligned} \end{aligned}$$

(45)

The assumed WMR’s wheel slipping is

$$\begin{aligned} \begin{aligned} u_r^s&= 0.15 + 0.25 \sin (3t)\\ u_l^s&= 0.15 + 0.25 \sin (3t) \end{aligned} \end{aligned}$$

(46)

The expected external disturbances are as

$$\begin{aligned} \begin{aligned} P_x, P_y&= \left\{ \begin{matrix} 30 & \text {if} \ 5 \le t < 15,\\ 10 & else. \end{matrix}\right. \end{aligned} \end{aligned}$$

(47)

Simulation results

To verify the control performance of the proposed FPP-NFTSMC, a comparison to three other controllers: 1) the conventional SMC, which is designed in (50); 2) an NFTSMC with selected sliding function as in²⁹ and the control signal is described in (55); and 3) a fixed-time NFTSMC with selected sliding function as in⁵¹ and the control signal is described in (60); is performed.

In Case 1, the position tracking errors are illustrated in Fig. 4. Overall, all four control methods provide good tracking performance when the robot is under the influence of wheel slipping. The result shows that the convergence speeds of SMC and NFTSMC are slower than those of fixed-time NFTSMC and the proposed FPP-NFTSMC. Further, the proposed FPP-NFTSMC provides tracking errors with the fastest convergence rate. Regarding the tracking performance, the chattering phenomenon, which will be shown in Fig. 7, affects the tracking results of SMC, NFTSMC, and fixed-time NFTSMC; specifically, they appear with a little chattering effect. Among the controllers, the conventional SMC provides the lowest tracking performance and the fixed-time NFTSMC provides the closest result to the proposed FPP-NFTSMC. The proposed FPP-NFTSMC, in the red solid line, obtains a smooth tracking error with the highest tracking performance. The results of velocity tracking are presented in Fig. 5. Unlike position tracking, the velocity tracking errors of SMC, NFTSMC, and fixed-time NFTSMC are highly affected by the chattering phenomenon in the control signals (see Fig. 7). Thanks to the application of the USOSM algorithm in switching control law, the proposed FPP-NFTSMC provides smooth control input; therefore, it achieves the highest velocity tracking results. To simplify the comparison, in terms of sliding function and control input, we focus on comparing the results of the proposed FPP-NFTSMC and fixed-time NFTSMC. As shown in Fig. 6, the proposed prescribed performance NFTSF reaches the convergence stage quickly with a low chattering effect. Results of control input signals are illustrated in Fig. 7. As in Fig. 7a, the control input of fixed-time NFTSMC has a high chattering phenomenon. On the contrary, the proposed FPP-NFTSMC in Fig. 7b, with a smooth switching control law, provides control input with a low chattering effect. In Fig. 8, the assumed trajectory and tracking results are presented.

Fig. 4

Position tracking errors of four-WMR in case 1.

Fig. 5

Velocity tracking errors of four-WMR in case 1.

Fig. 6

Sliding surface in case 1.

Fig. 7

Control input torque of four-WMR in case 1.

Fig. 8

Trajectory of four-WMR in case 1.

In Case 2, Fig. 9 shows the result of position tracking error. Similar to Case 1, the proposed FPP-NFTSMC provides the best control performance with the highest tracking performance and fastest convergence speed. Especially, the proposed control algorithm maintains the tracking ability when wheel skidding occurs, demonstrating robustness. In this part, a small comparison with different initial values is added to show the fast convergence characteristic of the proposed FPP-NFTSMC. In Fig. 9, with the initial value $\left[ \begin{matrix}x&y&\theta \end{matrix}\right] ^T = \left[ \begin{matrix}1.1&1.1&0 \end{matrix}\right] ^T$, the convergence time is around 0.73 seconds. In Fig. 10, when changing the initial value to $\left[ \begin{matrix}x&y&\theta \end{matrix}\right] ^T = \left[ \begin{matrix}1.4&1.4&0 \end{matrix}\right] ^T$, the convergence time of SMC and NFTSMC become bigger and exceed 2 seconds. In contrast, the proposed FPP-NFTSMC maintains the convergence process and reaches the convergence state after 0.94 seconds. Fig. 11 illustrates the velocity tracking performance. As shown in the result, the velocity tracking errors of the SMC, NFTSMC, and fixed-time NFTSMC are influenced by the chattering issues of the control signal. On the other side, the proposed FPP-NFTSMC offers the highest velocity tracking accuracy with a low chattering phenomenon. The results sliding surface is shown in Fig. 12, where the proposed prescribed performance NFTSF can reach the convergence stage rapidly at both the initial time and the time that wheel skidding occurs. According to the control input signal results, the fixed-time NFTSMC provides control input with a high chattering phenomenon as in Fig. 13a. Otherwise, by using the USOSM algorithm, the proposed FPP-NFTSMC offers the control signal with low chattering phenomenon as in Fig. 13b. Fig. 14 shows the results of tracking the assumed U-shaped trajectory. The results in both cases are similar, showing the effectiveness of the proposed FPP-NFTSMC and adaptability to various working conditions.

Fig. 9

Position tracking errors of four-WMR in case 2 with the initial value $\left[ \begin{matrix}x&y&\theta \end{matrix}\right] ^T = \left[ \begin{matrix}1.1&1.1&0 \end{matrix}\right] ^T$.

Fig. 10

Position tracking errors of four-WMR in case 2 with the initial value $\left[ \begin{matrix}x&y&\theta \end{matrix}\right] ^T = \left[ \begin{matrix}1.4&1.4&0 \end{matrix}\right] ^T$.

Fig. 11

Velocity tracking errors of four-WMR in case 2.

Fig. 12

Sliding surface in case 2.

Fig. 13

Control input torque of four-WMR in case 2.

Fig. 14

Trajectory of four-WMR in case 2.

Conclusions

This paper proposed a novel SMC tactic for WMRs under the influence of WSS, and external disturbances. Using the advantages of each technique, a unique prescribed-performance NFTSF is first presented by combining the NFTSMC and transformed error. The proposed prescribed-performance NFTSF and the USOSM algorithm serve as the foundation for the proposal of a novel FPP-NFTSMC. Thanks to the utilizing of the USOSM algorithm, the proposed FPP-NFTSMC provides a smooth control signal, thereby overcoming the common chattering problem in SMC. The suggested approach provides remarkable tracking performance, including low tracking error, quick convergence, robustness against WSS and external disturbances, decreased chattering phenomenon, and ensuring tracking errors remain within bounds. The stability and fixed-time convergence of the overall system are demonstrated using the Lyapunov function. Finally, the efficiency of the suggested FPP-NFTSMC is validated through simulations.