Introduction

The usage of technology in the classroom has resulted in a large amount of data that may be used to improve the modern educational system. EDM, which use data mining techniques to analyze large amount of academic and personal information, developed as a result of data growth. These include data about teachers, students, courses, syllabuses, test questions, and circulars. This large data set gives a significant opportunity to improve educational systems through machine learning and student performance prediction1. In this the environment, predicting student performance is crucial to educational interventions. Learning experiences also boost success2. Accurate student performance prediction helps schools provide individualized learning experiences and assist students to reach their academic potential2. Data’s dynamic nature makes algorithms inefficient1,2,3,4,5. Information gain, chi-square, and correlation matrix analysis with heat maps cannot adapt to changing data patterns2,3,4,5,6. Because of this constraint, education and prediction improvements are limited. We aim to correctly predict student success in these instances.

Standard feature selection algorithms cannot adapt to these changing data patterns. Our DE-FS algorithm combines classic feature selection with an ensemble approach that adjusts dynamically to changing data patterns to overcome these constraints6. This study helps three ways. DE-FS, an improved feature selection approach, combines established tactics to improve accuracy. We also provide dynamic and adaptive thresholding to effectively choose features across many datasets. To conclude, we evaluate DE-FS’s forecasting abilities for student accomplishment to help educators and data analysts make recommendations. We use student demographics, grades, and other information. Different educational contexts’ data is validated and tested7. We found that DE-FS outperforms the state-of-the-art in dynamic educational contexts and fluctuating data patterns. Greater flexibility improves precision and efficiency. The gains we found require dynamic thresholds and adaptive thresholding. De-FS ensures accurate and flexible student performance estimates in the ever-changing educational situation8.

The key contributions of our research are as follows:

  • We propose a novel feature selection model, “Dynamic Feature Ensemble Evolution for Enhanced Feature Selection” (DE-FS), which integrates traditional techniques like correlation matrix analysis, information gain, and Chi-square with heat maps to improve feature selection.

  • Our study introduces a dynamic and adaptive thresholding mechanism in DE-FS, allowing the model to adjust to evolving data patterns. This overcomes the limitations of static feature selection methods and prevents issues like overfitting and underfitting.

  • The DE-FS model demonstrates superior predictive accuracy for student performance, enabling more effective personalized learning interventions and better allocation of educational resources.

  • We validate the DE-FS model across diverse educational datasets, showcasing its adaptability to fluctuating data patterns and dynamic educational contexts.

Related works

Many studies on educational data mining have employed data-driven methods to predict and improve student performance. This section reviews existing publications to reveal the many ways and methods utilized to address this crucial educational topic. While previous works9,10,11,12,13,14,15,16,17 have made major contributions, DF-FS algorithm offers new perspectives and ways to better educational data mining.

Several studies have examined demographic, school, psychological, and socioeconomic factors that may affect children’ academic success11,18,19,20. Additionally, several models predict student achievement21,22. For instance10, improved student pass/fail prediction accuracy and success rates using KNN, decision trees, naive Bayes classification, and linear regression. A framework was developed to predict student performance by considering variables such as personal history, age, gender, educational background, mental well-being, and social activities. The model also identifies risk factors linked to critical values of key characteristics. In another study9, conducted an experiment aimed at early identification of high-risk students in a specific course using predictive techniques. By applying correlation analysis, they identified 14 key factors and achieved an 86.2% recognition rate for high-risk students using the Naive Bayes classifier.

The model also made datasets more accessible by precisely measuring true positives, true negatives, false positives, and false negatives11. described a decision tree method for estimating how well students will do in school, focusing on techniques for choosing features, like combining, cleaning, and normalizing data. The researchers carefully chose significant features and trained the system with filter-based approaches, resulting in a precision of 90.13%. However, their inability to access critical data, such as quiz questions, assignments, and midterm exams, delayed their capacity to develop the model even further12. Employed sequential minimum optimization (SMO)-based support vector machines (SVM) and logistic regression to predict students’ future behavior and classify their academic performance as outstanding, average, or substandard. The logistic regression model achieved 73% accuracy using the WEKA tool, but the SVM (SMO) model did better, at 79%. The models were assessed using criteria such as recall, precision, F1-score, and accuracy13. sought to improve student satisfaction by soliciting comments on academic performance, social activities, and interest in technical technologies using social networking sites. The study used a meta-heuristic wrapper technique and a stacked ensemble machine learning algorithm to identify key features and minimize data dimensionality, yielding an ensemble model with a Root Mean Square Error (RMSE) of 0.373, exceeding previous techniques14. Used data analysis and business intelligence approaches, such as decision trees and artificial neural networks (ANN), to estimate secondary school student performance in school. The study used grades from the second period of in-person instruction to forecast grades in courses such as mathematics and Portuguese. Although the decision tree and ANN algorithms achieved accuracies of 94% and 72%, respectively, incorporating internet data and additional attributes could improve real-time prediction capabilities15. proposed Support Vector Machines (SVM) and k-Nearest Neighbors (KNN) for predicting students’ exam results.

The study, which used various algorithms, achieved accuracies of 91% for SVM and 92% for KNN. KNN outperformed SVM with a correlation coefficient of 0.96 compared to 0.95. The proposed methodology combined decision-making, correlation analysis, and quantitative techniques, utilizing a data warehouse and tools like Python for diverse analyses and future predictions16,17. Developed a dual-phase machine learning approach combining supervised and unsupervised algorithms to improve recommendation accuracy compared to other methods. The author suggested that including more information from faculty members, such as evaluations of academic advisers, could enhance performance predictions21. used clustering and classification methods to predict students’ technical evaluation results. The dataset was split into training and testing groups, each with 50% of the instances. The decision tree method outperformed K-means clustering and naive Bayes, achieving the highest accuracy of 81%22. Established a student database and categorized instructors into low-risk, medium-risk, and high-risk groups based on in-class assignments, training participation, and final exam grades23. Recommended assessing student behavior during the early years after graduation to predict future achievements. Additionally24, developed a system to identify at-risk student’s early using classification methods. Table 1 gives the Summary of related works.

Table 1 Summary of related works.
Full size table

Prior research has highlighted several deficiencies, including limitations in classifier methods, feature selection techniques, ensemble methods, evaluation metrics, adaptability to changing data patterns, data source diversity, real-time prediction capabilities, and data comprehensiveness. Studies often used a narrow range of classifier methods and feature selection techniques, with limited exploration of ensemble techniques.

Evaluation measures were usually poor, focusing solely on accuracy rather than a broader range of metrics. Furthermore, there was no correction for shifting data patterns, which is critical for educational datasets that evolve over time. Many research23,25,26,27 only used historical campus data, ignoring the integration of internet data and the investigation of real-time prediction skills. The DF-FS algorithm solves these challenges by using a diverse set of classifiers, three feature selection strategies, a stacking ensemble method, and a thorough evaluation strategy.

Although previous research28,29,30,31,32 has made significant progress in predicting student success, our analysis fills several gaps in the existing works. These include a lack of variety in classifier algorithms and feature selection techniques, resulting in lower predicted accuracy. Additionally, there is an absence of research on ensemble methodologies and comprehensive evaluation metrics. Many present models are unable to adapt to changing data patterns in dynamic educational environments and rely on previous data, ignoring the possibility of adding data for real-time predictions. Previous research has also failed to address the timeliness of predictions and the need for additional data such as curriculum information33,34,35. By identifying these drawbacks, we establish the necessity of our proposed technique. The DE-FS algorithm developed in our research aims to address these gaps by offering more accurate and adaptive forecasts of student performance in ever-changing educational environments.

Sarker et al.36 employed Educational Data Mining (EDM) to examine Bangladeshi higher secondary students’ academic performance. Four major areas were studied: forecasting students’ final exam performance based on internal exam results, determining subjects’ effects on classifier performance, assessing students’ performance growth, and finding consistent performance trends from past exams. Internal examination scores predicted academic performance better than board GPA, according to the study. English, ICT, and Bangla were also identified as performance-affecting subjects. Sarker identified at-risk and high-performing subjects by tracking student performance. The study showed the ability to identify consistent performers, letting college officials adjust strategies for failing and outstanding students. Okoye et al.37 developed RG-DMML to predict student retention and graduation. The CRISP-DM model used Bagging and Wrapper feature selection with K-Nearest Neighbor (KNN) for supervised learning. Both retention and graduation had good precision, recall, accuracy, and F1-scores, with retention predicting more efficiently. The study also examined how these predictions could identify at-risk kids and enable timely interventions, counseling, and decision-making to improve educational results. Priyambada et al.38 suggested a two-layer ensemble learning system to predict student performance using learning behavior data and domain knowledge. SVM, KNN, and Random Forest algorithms are used in the ensemble prediction layer and the ensemble progressive prediction layer, which incorporates past and present predictions. A vertically coherent curriculum’s tight course-taking norms are considered, and students’ behavior and subject knowledge are used to predict whether they will graduate on time or late in eight semesters. Academic stakeholders can intervene sooner to assure on-time graduation due to enhanced student performance prediction. Lam et al.39 reviewed multiple machine learning models to predict student performance using data from 253 undergraduate students in five classrooms in three VnCodelab courses, an interactive learning management system. The study analyzed engagement patterns, exercise time, and progress tracking to predict student grades. This study examined five base classifiers (Random Forest, Logistic Regression, Support Vector Machine, Naïve Bayes, k-Nearest Neighbor) and a Stacking Classifier on a dataset with 13 characteristics. The Stacking Classifier predicted students’ final course scores better than individual models, demonstrating the importance of attendance and prior academic performance. The study identified attendance as an important predictor, proposing focused actions to boost student success. A predictive model to help instructors monitor and intervene with student progress is available, with plans to refine models and explore more data sources. Niyogisubizo al40 proposed a stacking ensemble method to predict university course dropout, a major education issue. Random Forest (RF), Extreme Gradient Boosting (XGBoost), Gradient Boosting (GB), and Feed-forward Neural Networks were used on a 2016–2020 Constantine the Philosopher University in Nitra dataset. The proposed model outperformed base models in accuracy and AUC. Early intervention can reduce dropout rates by identifying students at risk based on social welfare, learning conditions, and family status, according to research. Ensemble learning improved dropout predictions and suggested further research into deep learning models and other factors. Results showed that accurate prediction and early intervention can significantly reduce student dropout.

Bhuyan et al. addressed challenges in data privacy, feature selection, and cancer diagnosis. A novel privacy framework balanced computational cost and user-defined anonymity using multi-objective optimization. A robust feature selection algorithm enhanced classification accuracy by reducing irrelevant features. Additionally, a deep learning-based diagnostic framework integrated YOLO, FrCN, and CNN for precise cancer detection, outperforming conventional methods across datasets41,42,43.

Paper44 explores advanced ML and DL techniques for critical applications, including early cardiovascular disease (CVD) detection, intrusion detection systems (IDS), and Android malware detection. For CVD prediction, a voting ensemble model combined with chi-square feature selection achieved 92.11% accuracy. For IDS, feature selection using PCA and SVD improved classification accuracy, with Ridge Regression reaching 99.85% for binary classification. Lastly, the DL-AMDet deep learning framework effectively detected Android malware, achieving 99.935% accuracy by combining CNN-BiLSTM and Deep Autoencoders for static and dynamic analysis45,46.

Hussain et al.47 emphasized the significance of feature selection in predictive modeling in a foundational survey on data mining techniques. Punitha et al.48 introduced a high-ranking ensemble network with advanced feature selection strategies to enhance student performance prediction. Gaftandzhieva et al.49 explored student satisfaction in blended learning environments, emphasizing the need for adaptive models that consider evolving educational contexts. Hybrid optimization models have effectively enhanced decision-making processes in real-world scenarios50. AI-driven optimization frameworks have shown promising results in improving computational efficiency and predictive accuracy across various domains51. Evolutionary computation methods dynamically adapt to complex problem spaces, contributing to optimization strategies52. Machine learning-based student performance prediction has been extensively explored in education, providing data-driven insights for academic success and early intervention53,54.

The motivation for this study arises from the limitations and gaps identified in previous works on predicting student performance using educational data mining techniques. Existing studies have primarily focused on static feature selection methods, such as correlation analysis, information gain, and Chi-square, which fail to adapt to the dynamic nature of educational data. Many approaches lack diversity in classifier algorithms and ensemble methods, which hinders their ability to provide accurate and flexible predictions in fluctuating educational contexts. Additionally, most studies prioritize accuracy as the sole evaluation metric, neglecting other important measures such as precision, recall, and F1-score.

Another significant drawback is the reliance on historical campus data, with limited efforts to integrate diverse data sources, such as real-time internet-based information, which could enhance prediction capabilities. Previous methods often suffer from an inability to adapt to evolving data patterns, leading to overfitting or underfitting, and fail to incorporate dynamic thresholds for feature selection. The timeliness of predictions and the inclusion of critical data, such as curriculum content and continuous assessment, are also frequently overlooked. Furthermore, the absence of robust ensemble techniques and adaptive models has limited the scalability and effectiveness of prior methods in handling large and complex datasets.

These deficiencies motivated our development of the DE-FS algorithm, which integrates traditional and ensemble feature selection techniques with a dynamic and adaptive thresholding mechanism. By addressing these gaps, our study aims to provide a more accurate, adaptive, and comprehensive solution for predicting student performance, enabling real-time interventions and better decision-making in dynamic educational environments.

The manuscript is presented as follows: “Related works” section: discusses related works. “Problem statement” section discusses the problem statement, “Preliminaries” section discusses the fundamental concepts. “Proposed system” section explains the proposed methodology. “Experimental setup” section describes the hardware, software, datasets, evaluation metrics and methodologies used to conduct and validate the experiments and “Result and Discussion” section presents the experimental findings.

Problem statement

In the field of educational data mining, the precise prediction of student performance is essential for effective teaching strategies. Although traditional feature selection methods have demonstrated potential, they encounter difficulties in adjusting to the diverse educational data. With the constant evolution and diversification of educational data, there is an increasing need for a feature selection technique that can adapt dynamically and consistently enhance the accuracy of the model55. DF-FS tackles this issue by methodically and astutely choosing the most pertinent characteristics from datasets with diverse attributes. Choosing features is critical for enhancing ML models. DF-FS dynamically selects the best collection of features for a classification model based on data attributes.

The goal is to enhance accuracy, stability, and accessibility so educators and researchers can anticipate student outcomes. It solves feature dependency, data type differences, and model-specific feature selection.

Given a dataset D = {(x1, y1), (x2, y2)… (xn, yn)}, where xi denotes the feature vector for the ith student and yi is the corresponding performance label, the objective is to discover the optimal feature subset F* that maximizes a chosen evaluation metric E. This can be expressed as follows:

$$Maximize\,E{\left(F\right)}^{*}$$
(1)

Subject to:

  • |F*| <= k (where k represents a predefined maximum number of features). This constraint ensures that the selected feature subset remains within practical limits.

  • F* exhibits dynamic adaptability to changing data patterns.

Preliminaries

Chi-square

Feature selection for categorical datasets was performed using the Chi-Square test, which assesses the relationship between features and the target variable56. This method helps identify the most relevant features by measuring statistical dependence. Features with higher Chi-Square values indicate a stronger association with the target variable, making them suitable for further analysis. Proper encoding of categorical variables is essential to ensure accurate results.

Information gain

Information Gain was employed to assess feature importance by measuring the reduction in uncertainty when splitting data, particularly in decision tree models57. Features with higher Information Gain were prioritized for improving prediction accuracy, ensuring the selection of the most relevant attributes while minimizing overfitting.

Correlation matrix

Pearson correlation was used in the Correlation Matrix with a Heat Map to identify features with significant linear relationships to student performance58. Along with Chi-Square and Information Gain, Correlation Analysis was incorporated into the DE-FS framework to enhance feature selection by addressing interdependencies, information gain, and linear correlations, ensuring an efficient and comprehensive approach to educational data analysis.

Dynamic thresholding

It is specifically the Mean and Standard Deviation-Based methodology, helps the DF-FS method uncover relevant features that adapt to changing data patterns7. The mean and standard deviation of feature values are used to calculate a dynamic threshold, a specified number of standard deviations from the mean. Data patterns change; thus, the mean and standard deviation are reassessed to alter the threshold. Features inside this threshold are kept; those outside may be removed. This dynamic technique was chosen for its ability to maintain feature selection precision while adapting to changing data patterns, making it ideal for educational data mining7,47.

Adaptive thresholding

For educational data mining, the DF-FS algorithm requires adaptive thresholding8. For feature value central tendency and dispersion, Mean and Standard Deviation-Based Thresholds is used. This adaptive threshold helps educational datasets that change over time by adapting dynamically to data distributions. Setting the threshold to a specified number of standard deviations from the mean matches the data distribution, retaining only important features for analysis. This versatility makes it a powerful and reliable tool for sustaining feature quality as data patterns change. Feature selection and prediction accuracy improve. Thus, this method is appropriate for data qualities that change often59.

Proposed system

Rationale

The DE-FS algorithm has several strong justifications. Firstly, it improves at feature selection by identifying the most important features, hence improving the prediction results. DE-FS is particularly useful in dynamic environments such as education, where data is always changing. The approach significantly improves prediction accuracy, which is crucial when predicting student progress. Furthermore, DE-FS lowers information overload by removing unnecessary features, which improves model efficiency and accessibility. Its adaptive thresholding function ensures that the parameters used to choose features are consistent with how the data develops, which is useful as educational data evolves. DE-FS contributes to the development of data-driven educational approaches and interventions, resulting in improved educational outcomes. DE-FS can be used to solve problems in educational data mining because it can work with different datasets and areas and can be used over and over again.

The use of chi-square, information gain, and correlation analysis in DE-FS is a calculated decision that builds on each method’s capabilities. The chi-square test detects statistical mutual dependence, information gain determines the relevance of features and correlation analysis investigates feature interaction. DE-FS combines these fundamental methods to create a robust ensemble capable of handling a wide range of patterns in educational data. Despite its potential difficulty, DE-FS’s adaptability overcomes this by tailoring feature selection algorithms to changing educational environments. This adaptability ensures that DE-FS remains successful in managing the challenges of combining multiple methods and accurately predicting student performance in changing educational conditions.

DE-FS offers many convincing reasons. First, it enhances feature selection by detecting key features, increasing prediction outcomes. DE-FS works well in dynamic situations like schooling where data changes frequently. It greatly improves forecast accuracy, which is critical for student development prediction. DE-FS also reduces information overload by reducing unneeded elements, improving model efficiency and accessibility. As educational data evolves, its adaptive thresholding algorithm guarantees that feature selection parameters match data development. DE-FS improves educational results by developing data-driven educational approaches and solutions. DE-FS can be reused and used across datasets and fields to solve educational data mining problems.

DE-FS uses chi-square, information gain, and correlation analysis to maximize their strengths. The chi-square test detects statistical mutual dependency, information gain determines feature relevance, and correlation analysis examines feature interaction. DE-FS uses these essential principles to produce a strong ensemble that can handle many educational data patterns. DE-FS adapts feature selection algorithms to changing educational contexts, overcoming its potential difficulty. DE-FS’s versatility helps it combine several methodologies and effectively forecast student performance under shifting educational situations.

Algorithm

DE-FS iteratively picks the best dataset characteristics. First, it selects a subset of features and evaluates performance using a dynamic threshold. Each feature’s relevance is assessed using several selection methods. Performance is measured using a metric and thresholds are modified accordingly. Repeat until a stopping point, such as iterations or performance, is achieved. The algorithm continuously examines the best-performing feature subset to find the best set depending on the criteria.

The complete description of the algorithm can be found in Algorithm 1.

Algorithm 1
figure a

DE-FS (dynamic feature ensemble evolution for enhanced feature selection) algorithm.

Full size image
Fig. 1
figure 1

Workflow of DF-FS.

Full size image

DE-FS for dynamic feature selection employs a systematic approach (Fig. 1). It uses traditional feature selection techniques such as Chi-square, Information Gain, and correlation analysis to perform dynamic selection. The main loop evaluates the relevance of each feature. Features that exceed the thresholds are included in the candidate subset. It controls execution by applying defined stopping criteria. DE-FS tracks the highest performing feature subset (F*) in each cycle. This subset is optimized and validated using tenfold cross-validation. DE-FS was evaluated to ensure its durability and effectiveness with educational datasets, with the boosting feature quality and prediction accuracy while addressing challenges posed by changing data patterns. The algorithm is distinguished by its use of adaptive and dynamic thresholding methods. They allow us to change the feature selection criterion in response to changing data patterns. It detects significant characteristics by responding to changing educational datasets. It ensures that the algorithm is successful and responsive to data variability. Our methodology is unusual in that it combines traditional feature selection approaches (Chi-square, Information Gain, and correlation analysis) with a dynamic threshold mechanism. This combination allows us to address the difficulties more effectively. The performance assessment reveals that the proposed strategy improves prediction accuracy in educational data mining.

Algorithm selection and synergy

Our research improves performance by combining feature selection methods with classification algorithm. Feature selection techniques are chosen based on their relevance to data features. We use Chi-Square to evaluate categorical variables like gender and school60. Information Gain evaluated the role of each attribute in generating pass/fail results60. The Correlation Matrix with Heat Map looks at the relationships between continuous and ordinal properties. Random Forest was chosen for classification because of its ability to handle complex, non-linear interactions and generate feature significance ratings. Decision trees are chosen because of their accessibility and ability to handle many attribute types. Neural Networks provided insights into attribute influence and linear correlations, whereas Support Vector Machines handled high-dimensional data and class imbalances.

Algorithmic combination and advantages

Our methodology for constructing algorithmic combinations61 aims to maximize the benefits of each feature selection and classification algorithm in order to develop a high-accuracy model62.

These algorithms are chosen for their specific advantages, resulting in an integrated effect that addresses the challenges experienced by current forecasting educational performance approaches. Algorithmic combinations are formed by combining feature selection and classification algorithms63. Our dataset has a different range of attributes with increasing importance. Feature selection strategies are chosen based on how well they match the properties of the features. We evaluate classification algorithms based on their ability to manage complicated interactions, nonlinear patterns, and class imbalances while maintaining dataset properties and aims62. For instance, we use Information Gain using Random Forest, a classifier known for its ensemble approach and complex relationship capturing. The suggested method improves prediction by identifying key traits and deleting irrelevant data. It decreases class gaps and gives a comprehensive overview of student success prediction by studying attribute-student success relationships. The method enhances model accuracy and usability. Using feature selection with classification algorithms improves individual benefits and addresses dimensionality reduction, nonlinear correlations, and class imbalances. It produces a model that outperforms its individual components.

Fig. 2
figure 2

Synergy of feature selection and classification.

Full size image

Figure 2 depicts the use of feature selection approaches and classification algorithms in predictive modelling for student achievement in educational data analysis. It depicts how these aspects interact and collaborate to improve their efficiency and solve challenges.

Feature Selection Methods: Fig. 2 shows three feature selection strategies utilized in the study: Chi-Square, Information Gain, and Correlation Matrix. These methods find the most relevant attributes in a dataset. The numerical values (3, 1, 2) next to each technique denote the number of properties it assesses. Chi-Square, for example, analyzes three attributes, Information Gain one, and Correlation Matrix two.

Classification Algorithm: Fig. 2 shows many classifying methods that are necessary for generating predictions based on the selected attributes. Random Forest, Decision Trees, Neural Network, Support Vector Machine, J48, and Naive Bayes are some of the techniques used. The numerical values next to each algorithm indicate the number of attributes used for prediction.

Enhancing Strengths: Fig. 2 shows how combining feature selection approaches and classification algorithms strengthens each component. For example, Decision Trees with “2” attributes are combined with Information Gain, which concentrates on a particular attribute. This combination improves both feature significance and prediction accuracy. Different combinations provide specific benefits while improving overall performance.

Addressing issues: Fig. 2 also demonstrates how various combinations address different problems in the dataset and prediction purpose. Some combinations reduce dimensionality, deal with non-linear relationships, correct class imbalances, and manage variability, whereas others maximize hyperparameter settings.

Interaction and Synergy: Fig. 2 illustrates the interconnections between feature selection approaches and classification algorithms, demonstrating their collaborative function. The linkages show how each element complements and strengthens the others, indicating an integrated approach to enhancing predictive modeling.

Figure 2 emphasizes the significance of using the best combination of feature selection approaches and classification algorithms to improve forecast accuracy for student performance61.

It shows how effective feature selection reduces noise while identifying relevant qualities, hence improving classification algorithm performance62. The graph shows a number of classification methods, each of which is suitable for particular elements of the prediction task63. Overlapping areas in the diagram imply successful strategy integration and effectiveness. This method solves educational data analysis issues such complex relationships and unequal class distributions60. A mixed predictive modeling strategy for educational data is shown in the diagram. Features selection and categorization can be used to create a more accurate and useful predictive model62. In future work, we plan to incorporate advanced optimization algorithms64,65,66 to further enhance the feature selection process, ensuring even more precise identification of relevant features. This will allow for continuous refinement of the dynamic thresholds, improving the model’s accuracy and adaptability to large-scale, evolving educational datasets.

Experimental setup

Python and scikit-learn were used to construct the DF-FS algorithm2. The experiment used a system with an Intel Core i7 processor, NVIDIA GeForce GTX 1650 GPU, and 16 GB DDR4 RAM. The model was trained and tested using two public Portuguese high school datasets11. Several approaches were used for feature selection and classification, including Decision Trees, Random Forests, Support Vector Machines, Neural Networks, Naïve Bayes, and J4812,13,14,15,16,17. Humans and machines set hyperparameters. Performance was measured by accuracy, F1-score, and CV-score21.

Dataset used

The analysis predicted student progress using two public datasets. The records from two Portuguese schools included academic success, socio-demographic data, and school attributes. The data came from questionnaires and school reports. One dataset has 33 parameters for pupils’ math skills and the other for Portuguese language training. Student success trends may have been investigated with longitudinal data. This improved analysis and prediction. The extensive use of these datasets in earlier studies makes them relevant to our research goals. Because they are relevant to the research’s goals, these datasets allow for an in-depth investigation of the complexity of forecasting student performance by considering multiple aspects. The files explain research on how demographic, socioeconomic, and academic factors affect student achievement. Their widespread use in educational data mining shows their importance in solving student achievement prediction research issues. The dataset’s many features make it ideal for testing feature selection, classification, and model combining methods.

Data preprocessing

Missing values were imputed depending on the data, and categorical variables were encoded for numerical processing. Outlier management and data normalization were employed to reduce the impact of unexpected results. Data quality checks found duplicates and formatting mistakes. Feature engineering improved model prediction. To evaluate models properly, datasets were split into training and testing subsets.

Machine learning approaches

We applied various machine learning techniques to enhance feature selection and classification. Decision Trees and Random Forest simplified data patterns and improved prediction accuracy, while SVM handled high-dimensional, imbalanced data effectively. Neural Networks provided probabilistic insights, Naïve Bayes efficiently addressed class imbalances, and J48 excelled in large dataset classification.

Performance evaluation

  1. 1.

    The performance is assessed using a confusion matrix. In the objective of the proposed work, the four alternative outcomes of a binary classification problem are specified as follows:

  2. 2.

    True Positive (TP): The number of occurrences where the actual class and predicted class are both positive.

  3. 3.

    True Negative (TN): The number of occurrences in which the actual and expected classes are both negative.

  4. 4.

    False Positive (FP): The number of times in which the true category is negative while the predicted category is positive.

  5. 5.

    False Negative (FN): The number of occurrences where the true category is positive while the predicted category is negative. This study evaluates the performance of the suggested models using accuracy, f-score, and CV-score metrics.

  1. 1.

    Accuracy: This is the number of correctly predicted observations divided by the total number of observations. It measures how well the model works overall and is worked out like this67:

    $$Accuracy=\frac{TP+TN}{(TP+TN+FP+FN)}$$
    (2)

    where TP = True Positive, TN = True Negative, FP = False Positive, FN = False Negative.

  2. 2.

    The F1-score is the average of recall and precision. It is useful when the data is not balanced and we must find a balance between precision and recall. Here’s how to calculate your F1 score4,67:

    $$Precision=\frac{TP}{TP+FP}$$
    (3)
    $$Recall=\frac{TP}{TP+FN}$$
    (4)
    $$F1-score=\frac{2*Precision*Recall}{Precision+Recall}$$
    (5)
  3. 3.

    The cross-validation score (CV-score) evaluates a machine learning model’s performance on untrained data. Cross-validation is a resampling strategy that involves separating data into training and validation sets and repeating the process several times. The cross-validation score is generated by averaging the performance across each validation set. Its objective is to examine if the model is overfitting or underfitting67.

    $$CV-Score=\frac{\left(SumofvalidationScores\right)}{\left(Numberofiterations\right)}$$
    (6)

    The performance of the proposed model was evaluated using these metrics, and the results were compared with previous studies to determine the effectiveness of the proposed approach.

Result and discussion

Analyzing results: DF-FS for predicting student performance

Three experiments were carried out to predict student performance. In the first experiment, the chi-square feature selection method was applied to the student data subset from the UCI Machine Repository to identify the most important attributes. In the second experiment, the information gain method was used, and in the third, the correlation matrix with heat map was employed. Table 2 shows the features chosen by each feature selection technique, with G3 (the final grade) as the target feature.

Table 2 Optimal feature set selected by three feature selection techniques.
Full size table
Fig. 3
figure 3

Traditional Feature selection techniques-Mathematics dataset.

Full size image
Fig. 4
figure 4

Traditional Feature selection techniques- Portuguese dataset.

Full size image

Among these, the correlation matrix with heat map performed best, as it not only captured features highly correlated with student performance but also minimized redundancy. The distribution of attribute values is visualized in bar charts, as depicted in Figs. 3 and 4, showing the distribution for each attribute.

Table 3 Performance of six different machine learning algorithms on a mathematics dataset.
Full size table

Table 3 presents the performance of six machine learning algorithms using three feature selection methods: Chi-Square, Information Gain, and Correlation Heat Map. The performance is evaluated using accuracy and F1-score. Neural Networks (NN) and Random Forest (RF) are the top performers in terms of accuracy, both achieving over 91% across all feature selection methods. Notably, NN achieves an accuracy of 92.43% with Correlation Heat Map.

RF exceeds all other feature selection approaches, with Information Gain being the most successful. In terms of F1-score, Neural Network and Naive Bayes outperform. It takes Correlation Heat Map to get an F1-score of 92.55% for NN and Information Gain to get the same score for Naive Bayes. Support Vector Machine (SVM) and RF both do well, but RF gets the best F1-score (92.91%) when Information Gain is used. In comparison, Decision Trees (DT) and J48 perform poorly. From 88.98 to 90.68%, DT’s accuracy and F1-score range, while J48’s varies from 87.29 to 91.53%. Naive Bayes performs well with Information Gain, scoring 92.91% in both accuracy and F1-score, but its performance suffers while utilizing Correlation Heat Map. When Information Gain is used, RF gets an accuracy of 92.43% and an F1-score of 92.55%, but when Correlation Heat Map is used, it drops to 86.44% accuracy and an F1-score of 86.89%.

Table 4 Performance of six different machine learning algorithms on a Portuguese dataset.
Full size table

Table 4 provides a comparison of different algorithms on the Portuguese dataset, using three feature selection methods: Chi-Square, Information Gain, and Correlation Heat Map. There are two measures used for the evaluation: accuracy and F1-score. Three algorithms—Neural Networks (NN), Random Forest (RF), and Naive Bayes (NB)—are the most accurate. All three get above 90% accuracy across all feature selection methods. NN works best, with a 92.82% success rate, which can be reached with both the Chi-Square and Correlation Heat Map feature selection methods. RF and NB perform well with all of the feature selection methods, with Chi-Square being the best for both of them. When examining F1-score, NB and RF take the lead, with NB achieving the greatest F1-score of 92.20% utilizing Correlation Heat Maps. The NN method also does well, with an F1-score of 89.23%, which is the second-highest of all the methods. Meanwhile, Support Vector Machine (SVM) and J48 work less well.

SVM achieves accuracy and F1-score values ranging from 90.23 to 92.30%, while J48 falls between 90.05% and 92.28%. The performance of each algorithm is influenced by the feature selection method. RF performs consistently well but achieves its highest accuracy and F1-score with Chi-Square. NB performs best with Correlation Heat Map, achieving 94.30% accuracy and a 92.20% F1-score. Decision Trees (DT) perform lowest with Chi-Square but improve when using Correlation Heat Map, where they reach their highest accuracy and F1-score.

Table 5 Performance of classifiers using ensemble stacking methods on a Portuguese dataset.
Full size table

Table 5 compares ensemble stacking performance of six machine learning algorithms using a Portuguese dataset. The algorithms’ accuracy and cross-validation (CV) scores are assessed. Chi-Square, Information Gain, and Correlation Heat Map stack. We found that Random Forest (RF) and Support Vector Machine (SVM) have the highest accuracy, ranging from 93.61 to 95.36%. The maximum accuracy for RF is 94.67% with Correlation Heat Map stacking, while SVM is 95.36% with Information Gain stacking.

Decision Trees (DT), Naive Bayes (NB), and Neural Networks (NN) all have good accuracy ranging from 92.93 to 94.39%. Information Gain stacking provides DT the good accuracy (96.03%), whereas Chi-Square stacking gives NB the highest accuracy (94.39%). In terms of cross-validation (CV) score, RF and NB perform good, with CV values ranging from 89.74 to 94.36%. The best Information Gain stacking score for RF is 93.33%, while for NB it is 94.36%.

Neural Networks (NN) and J48 perform relatively poorly in both accuracy and CV score, with accuracy values ranging from 86.17 to 94.05% and CV scores between 83.33% and 91.28%. The performance of each algorithm is influenced by the stacking method used. RF performs well across all stacking methods but achieves its best results with Correlation Heat Map stacking. DT and NB excel with Information Gain stacking, while SVM reaches its peak performance with Information Gain stacking for both accuracy and CV score.

Table 6 Performance of classifiers using ensemble stacking methods on a mathematics dataset.
Full size table

The comparison of different algorithms on Mathematics dataset is given in Table 6. In the comparison we observed that Decision Trees (DT) perform consistently across all three stacking methods, with particularly strong results using Information Gain. Random Forest (RF) shows strong performance across all methods, especially with the Chi-Square method. Support Vector Machine (SVM) has lower performance across all methods, particularly with Correlation Heat Map. Neural Networks (NN) perform well with Chi-Square and Information Gain but show reduced performance with Correlation Heat Map. Naive Bayes (NB) performs best with Information Gain but poorly with Chi-Square and Correlation Heat Map. J48 performs well with Chi-Square and Information Gain but performs less effectively with Correlation Heat Map.

Table 7 Performance of ensemble stacking methods on a mathematics dataset and Portuguese dataset.
Full size table

Table 7 compares the performance of different ensemble stacking methods on Mathematics and Portuguese datasets using Accuracy and F1-Score metrics. For the Mathematics dataset, the Chi-Square ensemble stacking approach achieved the accuracy of 95.80 and F1-Score of 96.91, while the Correlation Heat Map method achieved 95.36. The Chi-Square approach achieved the F1-Score of 91.80 for the Portuguese dataset. The ensemble stacking approaches performed well on both datasets, with accuracy ranging from 94.17 to 95.80 and F1-Scores ranging from 90.91 to 96.91.

Fig. 5
figure 5

Proposed ensemble staking method evaluation on Mathematics dataset using (a) chi-square staking method Information gain staking method and correlation heat map staking method.

Full size image
Fig. 6
figure 6

Proposed ensemble staking method evaluation on Portuguese dataset using chi-square staking method (b) Information gain staking method and correlation heat map staking method.

Full size image

Figure 5 illustrates the performance of different ensemble stacking methods (Chi-Square, Information Gain, and Correlation Heat Map) on the Mathematics dataset, where the model shows strong predictions for both “Pass” and “Fail” categories. Figure 6 shows the results for the Portuguese dataset, emphasizing the model’s ability to make accurate predictions, with 61 correct predictions and only 10 incorrect ones.

Fig. 7
figure 7

The comparison analysis of the proposed work and base classifiers for Mathematics and Portuguese datasets.

Full size image

Figure 7 compares the accuracy of the proposed ensemble model against six base classifiers (DT, RF, SVM, NN, NB, and J48). The proposed model achieved the highest accuracy of 95.8% on the Mathematics dataset, significantly outperforming the base models, with Neural Networks (NN) coming second at 93.22%. Random Forest (RF) and Naive Bayes (NB) showed accuracies of 91.53% and 92.37%, respectively. These results underscore the strength of the ensemble approach, particularly for predicting student performance.

Figure 8 figure presents the mean computation time in seconds for different algorithms on the Mathematics and Portuguese datasets. The proposed “DF-FS” model demonstrates the fastest computation times (32.3 s for Mathematics and 41.5 s for Portuguese), indicating its efficiency compared to other base classifiers such as NN and NB, which take significantly longer. This suggests that the proposed model not only delivers superior performance but also operates more efficiently.

Fig. 8
figure 8

Computation time analysis of the proposed work and base classifiers for Mathematics and Portuguese datasets.

Full size image

Enhancing predictive models with DE-FS

This section explores the results of our study in predicting student performance. Our analysis of 18 carefully chosen combinations reveals how predictive model performance is affected by data distribution, feature attributes, and class imbalances. The effectiveness of algorithms is notably influenced by the data distribution, with certain algorithms performing exceptionally well based on dataset attributes such as categorical, ordinal, or continuous features. Table 8 summarizes the effectiveness of different feature selection and classification algorithm combinations on the Mathematics and Portuguese datasets. The combinations are tailored to specific dataset characteristics, such as handling categorical, ordinal, or continuous features. Key insights include the ability of Chi-Square with Random Forest to effectively handle categorical attributes and class imbalances, while Information Gain with Decision Trees excels in identifying predictive attributes, leading to high performance in ensemble models.

Table 8 Summary of feature selection and classification algorithm combinations.
Full size table

Results on mathematics dataset

For the Mathematics dataset, “Chi-Square + Random Forest” pairing excels due to its ability to handle categorical attributes and class imbalances, making it effective for complex, non-linear data patterns as shown in Table 9. The “Information Gain + Decision Trees” combination improves in collecting important attributes, resulting in high recall and balanced performance. Meanwhile, “Correlation Heat Map + J48” uses its ability to detect linear correlations, resulting in good models with balanced precision and recall.

Table 9 Performance evaluation of different feature selection and classification algorithm combinations on mathematics dataset.
Full size table
Fig. 9
figure 9

Performance of chi-square on mathematics dataset.

Full size image
Fig. 10
figure 10

Performance of Information gain on mathematics dataset.

Full size image
Fig. 11
figure 11

Performance of correlation heat map on mathematics dataset.

Full size image

The differences in performance across the various combinations are determined by how effectively the feature selection methods correspond to the dataset’s features and are compatible with the classification algorithms. Combinations that are properly customized to the dataset’s features, distribution, and class imbalance management often produce better results. Choosing the right combination requires adapting it to the dataset’s particular features, ensuring a smooth interplay between feature selection and classification methodologies for successful predictive modeling in educational data analysis (Figs. 9, 10 and 11). Table 10 gives the performance Evaluation of Different Feature Selection and Classification Algorithm Combinations on Portuguese dataset.

Table 10 Performance evaluation of different feature selection and classification algorithm combinations on Portuguese dataset.
Full size table
Fig. 12
figure 12

Performance of chi-square on portuguese dataset.

Full size image
Fig. 13
figure 13

Performance of correlation heat map on mathematics datasets.

Full size image
Fig. 14
figure 14

Performance of correlation heat map on Portuguese dataset.

Full size image

Results on Portuguese dataset

The “Chi-Square” method is also effective, and the “Correlation Heat Map” method works well in some situations (Figs. 12, 13 and 14). Notable combinations include “Information Gain + Decision Tree” and “Information Gain + Random Forest,” both of which perform well as seen in Table 10. The “Information Gain + Decision Tree” combination performs better in terms of accuracy, precision, and recall. In contrast, “Information Gain + J48” demonstrates low accuracy and precision. The “Correlation Heat Map + SVM” combo provides good accuracy and precision. Several important features were used for evaluating combinations in both the mathematics and Portuguese datasets, including:

  1. 1.

    Data Type: For datasets with mostly categorical features and strong connections, such as those addressed by “Chi-Square” approaches, these techniques can effectively capture and use these associations to improve performance. On the other hand, “Information Gain” is better suited to datasets with a large number of predictive attributes, allowing DT, RF, and Support Vector Machines (SVM) to focus on the most informative features.

  2. 2.

    Interdependencies: Feature selection algorithms should take into account the interrelationships between variables. Techniques like the “Correlation Heat Map,” which highlight linear correlations, are useful for classifiers like SVMs.

  3. 3.

    Classification Models: Decision trees are prized for their interpretability and ability to handle a wide range of data types, making them ideal for methods such as “Chi-Square” and “Information Gain.” SVMs, on the other hand, perform better when dealing with large amounts of data and complex decision boundaries.

Fig. 15
figure 15

Pareto font of combinations on mathematics dataset.

Full size image
Fig. 16
figure 16

Pareto font of combinations on Portuguese dataset.

Full size image

Based on the data in Fig. 15, Combination 8 is the most effective for the Mathematics dataset. It uses “Information Gain” to choose the features and Random Forest (RF) as the classification method.

This combination is the best on all three criteria, as shown by its Pareto front position. Due to its accuracy and low false positives and negatives, Random Forest is best for mathematics datasets due to its adaptability and “Information Gain” impact. Figure 16 shows the Pareto front analysis for the Portuguese dataset, showing that “Information Gain” and SVM work well. This combination balances Accuracy, Precision, and Recall on the Pareto front, in the upper right corner. This indicates balanced assessment elements, making it a good choice for Portuguese dataset.

The study analyzes how datasets and feature selection and classification algorithms can predict student performance. The research uses 18 combinations of these strategies to show how data distribution, feature characteristics, and class imbalances affect model performance. The results show that feature selection approaches must match dataset attributes for optimal predictions. Since Random Forest can handle class imbalances, “Chi-Square + RF” works well with group qualities and strong relationships. Furthermore, “Information Gain” functions well in several contexts, making it a solid choice. It improves educational data prediction by explaining how feature selection and classification algorithms interact. It informs academics and practitioners on how to construct predictive models that match the dataset’s properties, improving student performance projections.

Fig. 17
figure 17

Distribution of misclassification rates on Mathematics dataset.

Full size image

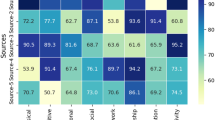
Misclassification rates for different feature selection and classification method combinations from Table 9 are shown in Fig. 17. The most effective model is Chi-Square + Random Forest (RF), which has the lowest error rate of 4.20%. Information Gain + Naïve Bayes (NB) has the greatest error rate (11.24%), 167.6% greater than the best-performing model. Figure 17 shows that Chi-Square-based feature selection, especially with RF, offers the best classification performance. However, Naïve Bayes models tend to have higher misclassification rates, independent of feature selection method. The histogram shows error rates, helping choose the best student performance prediction models.

Fig. 18
figure 18

Distribution of misclassification rates on Portuguese dataset.

Full size image

Misclassification rates for different feature selection and classification method combinations from Table 10 are shown in Fig. 18. Information Gain + DT has the lowest error rate, 96.03% accuracy, 3.97% error rate. The highest error rate is 13.83% for Information Gain + J48, which has an accuracy of 86.17%. Feature selection approaches affect classification results, as seen by the 9.86% gap between the best and worst algorithms. Information Gain-based models outperform the other three feature selection approaches, with three out of six combinations achieving 94% accuracy. Chi-Square and Correlation Heat Map models are less accurate in some classifiers. Selecting the best feature selection and classification pair is important since several combinations around 92–95% accuracy reflect a concentration of models within a restricted performance range.

Fig. 19
figure 19

Average computation time of different models across Mathematics dataset.

Full size image

Figure 19 shows the average calculation time for classification models and feature selection approaches, with a red dashed line. This lets you compare model efficiency. The fastest model, “Chi-Square + DT,” computes 78% faster than the slowest, “Information Gain + RF,” which takes 75% longer. Computationally cheaper than Information Gain or Correlation Heat Map, Chi-Square feature selection models run faster. Complex classifiers like Random Forest (RF) and Neural Networks (NN) take longer to compute since they use many decision trees and matrix computations. Decision Tree (DT) and Naïve Bayes (NB) are the most efficient classifiers, with calculation speeds 40–60% faster than slower models. The J48 classifier, a decision tree variant, balances performance by keeping calculation time within 5–15% of the average. This analysis says “Chi-Square + DT” or “Chi-Square + NB” are optimal for speed.

Fig. 20
figure 20

Average computation time of different models across Portuguese dataset.

Full size image

The Fig. 20 compares classification models’ average calculation time with Chi-Square, Information Gain, and Correlation Heat Map feature selection methods. Model computation times vary, with more classifiers like Neural Networks (NN) and Random Forest (RF) taking longer than simpler models like Decision Trees (DT) and Naïve Bayes (NB). Information Gain + NN has the largest calculation time, 25% more than other models. Chi-Square + NB has the lowest computation time, 30% lower than average. The computing time trade-off shows model complexity versus efficiency. Neural Networks and Random Forests are accurate but need more processing resources, making them unsuitable for time-sensitive applications. However, Decision Trees and Naïve Bayes may have slightly lower classification performance but faster computations. The confusion matrices in Figs. 21 and 22 provide a visual representation of classification performance for different feature selection and classification algorithm combinations.

Fig. 21
figure 21

Confusion Matrix of different models across Mathematics dataset.

Full size image
Fig. 22
figure 22

Confusion Matrix of different models across Portuguese dataset.

Full size image

Comparative analysis

Table 11 presents the results of many machine learning studies that predicted student performance. Different studies employed different models. For 32 features, Random Forest (RF) and Support Vector Machine (SVM) classifiers with Recursive Feature Elimination (RFE) and Boruta algorithms performed 86.55% in Mathematics and 89.74% in Portuguese. In a combined filtering technique, Naïve Bayes (NB), Decision Tree (DT), and RF classifiers achieved 93% accuracy in Mathematics and 94% accuracy in Portuguese for 15 features. Using 10 features, XGBoost, Gradient Boosting (GB), and Light GBM models with ensemble modeling achieved 96.63% accuracy for Mathematics and 94.28% for Portuguese.

An SVM using a combined filter-wrapper technique had 92.91% mathematics accuracy and 93.91% Portuguese accuracy with 15 features. The suggested study used 12 features, NB, DT, SVM, KNN, and NN classifiers, chi-square, information gain, and correlation heat map approaches to achieve 95.8% mathematics precision and 95.3% Portuguese precision. Results reveal that the suggested strategy is more accurate than earlier research.

Table 11 Comparison of proposed work with existing works.
Full size table

Discussion

DE-FS technology is a breakthrough in educational data mining since it combines standard feature selection methods with an adaptable ensemble approach to maintain accuracy as educational data changes. DE-FS outperformed “Chi-Square + Random Forest.” in a Mathematics dataset study. The 95.80% success percentage is much higher than previous methods. This shows how it can enhance student performance predictions and target interventions in real-world schooling. DE-FS is an innovative tool that helps schools improve learning, allocate resources, and forecast accurately. It could improve things, but further research is needed to make it more adaptable and evaluate its performance in other educational situations. More meaningful data and better student achievement will ensue.

The DF-FS method outperforms previous methods for altering datasets and data patterns. It does this by combining feature selection and classification. DF-FS employ adaptive thresholding to select the optimal group by continuously monitoring how significant each feature is, unlike older systems, which often encounter feature relevance issues and overfit or underfit. By showing how judgments are made, weighting the most essential variables enhances prediction accuracy and clarity. The DF-FS technique is good at resolving class imbalances and providing fair and accurate predictions since it focuses on minority classes. It can manage linear and nonlinear interactions with Random Forest and Neural Network methods, improving prediction accuracy. DF-FS makes prediction modeling more flexible, accurate, class imbalance-tolerant, and understandable for educational data analysis.

Significance and contribution

A major advancement in Educational Data Mining (EDM) and ICT is Dynamic Ensemble Feature Selection (DE-FS). Data-driven strategies boost student performance and resource allocation in the DE-FS, improving education. Its versatility allows it to quickly adapt to changing trends in modern educational environments, making it perfect for dynamic educational data. As ICT grows and provides more data, DE-FS must give students rapid, individualized aid to study better. Combining DE-FS with ICT shows how data and technology are becoming more significant in education, improving student performance and making teaching easier.

Limitations

DE-FS is improving despite its difficulties. Its performance depends on training data accuracy and quality because complete or skewed datasets lower its effectiveness. DE-FS requires a lot of computational power, which could be a concern for schools with poor tech. It is also important for the features to be well-defined, so datasets with poorly defined attributes may make the method less effective. Also, universities that don’t have data science tools find it hard to adopt DE-FS because they need people who know how to analyze and look at data. There needs to be work done to improve the quality of the data, make the best use of resources, and train teachers so that DE-FS can keep working well in school data mining.

Future work

Future research will focus on enhancing the adaptability and scalability of the DE-FS framework to accommodate larger and more diverse educational datasets. This includes exploring real-time implementation to enable instantaneous predictions and interventions, as well as incorporating additional data sources such as behavioral and social interactions to improve prediction accuracy further. Efforts will also be directed toward optimizing computational efficiency to make DE-FS more accessible for institutions with limited resources. Additionally, expanding the framework to evaluate its performance across various educational contexts and integrating advanced machine learning techniques, such as deep learning, will help address the evolving challenges in educational data mining.

Conclusion

This study shows that data-driven decision-making improves student performance prediction in dynamic educational environments. DE-FS, our feature selection model, combines Chi-square, information gain, correlation heat maps, ensemble stacking, and dynamic thresholding to achieve 95.8% accuracy while reducing the feature set to 12 attributes, a significant improvement over static feature selection methods. DE-FS improves predictive accuracy and computational efficiency by minimizing feature redundancy, making it ideal for dropout prediction, academic interventions, and personalized learning pathways. However, scalability for huge educational datasets and feature interpretability for educators and decision-makers remain issues. Further study will improve DE-FS to handle multi-modal learning analytics, integrate it with deep learning models for feature extraction, and optimize it for real-time adaptive learning applications. DE-FS improves Educational Data Mining by combining accuracy, flexibility, and reduced computational complexity, overcoming static approaches’ drawbacks and improving educational outcomes.