Sub pico-second pulses in mono-mode optical fibers with Triki-Biswas model

Abstract

This study explores the Triki-Biswas (TB) model, a novel model describing soliton dynamics in monomodal optical fibers with non-Kerr dispersion, to obtain optical solitons. Optical bright and singular solitons were derived using the generalized Jacobi elliptic function (gJEF) method and the $\tan \left( \frac{V(\eta )}{2}\right) -$expansion method. Trigonometric, hyperbolic, exponential, polynomial, and rational functions are obtained. The physical dynamics of the obtained solutions confirmed the existence of known complex structures, such as shock waves, dark solitons, periodic waves, and singular periodic solutions. The simulations generated in Mathematica 11.3 are graphically presented to depict the nature of the acquired solutions. These results are novel and have not been reported previously in the literature.

Introduction

Solitons^1,2 play a pivotal role in soliton transmission technology^{3,4,5,6,7,8,9,10,11}, particularly in applications involving optical fibers^12,13,14,15, telecommunications, and data transmission^16,17,18,19 across transcontinental and transoceanic distances. Numerous mathematical models^{20,21,22,23,24,25}, including but not limited to the complex Ginzburg-Landau model, Fokas-Lenells equation, Radhakrishnan-Kundu-Lakshmanan equation, Lakshmanan-Porsezian-Daniel model, Kundu-Eckhaus model, Kaup-Newell equation, nonlinear Schrödinger’s equation, and Gerdjikov-Ivanov equation, contribute to the comprehension and manipulation of solitons in these optical contexts^{26,27,28,29,30,31,32,33,34,35,36,37} and many others^{38,39,40,41,42}. The TB equation is another crucial governing model employed in various techniques, such as chirped soliton solutions, the exp$(V(\eta ))$-expansion technique, conservation laws, first integral technique, and traveling wave hypothesis^43,44,45. Numerous^46,47,48 other studies exist in the literature irrespective of conservation laws.

The TB equation represents a significant advancement and serves as a generalized form of the derivative nonlinear Schrödinger equation. This equation is specifically tailored to govern the dynamics of subpicosecond pulse propagation. Notably, the TB model is a promising candidate for describing the propagation of ultrashort pulses in optical fiber systems, particularly in scenarios where the Kerr effect imposes limitations. The incorporation of derivative quintic non-Kerr nonlinearity terms within this model plays a pivotal role, especially in facilitating the transmission of extremely brief pulses with widths of the order of sub-10 fs in highly nonlinear optical fibers. Given the challenges faced by the telecommunications industry, the TB equation has emerged as a valuable asset that significantly contributes to the generation of essential optical solitons. Numerous studies have been conducted on the TB model^49,50,51.

The TB model is investigated by employing the generalized Jacobi elliptic function method^52,53,54 and $\tan \left( \frac{V(\eta )}{2}\right)$-expansion method^55,56. The primary objective is to recover subpicosecond optical soliton solutions and ascertain the conditions that govern their existence. Additionally, the adopted methods led to the discovery of supplementary solutions, including shock waves, double periodic waves, and singular periodic solutions, facilitated by the reverse formulation of the constraints. A comprehensive analysis of the model’s intricacies is presented in subsequent sections of this article. None of the ansatz methods are so strong that they can deal with all types of solutions for each NLPDE. The generalized Jacobi elliptic function method does not apply to nonlinear problems/PDEs, where the product of the even and odd terms appears as a single term. This section covers the remaining cases. In addition, it is very difficult to deal with some classes of variable coefficient NLPDEs using both techniques.

The remainder of this paper is organized as follows. In "Coordinated strategies" section, comprehensive methodologies for the gJEF method and $\tan \left( \frac{V(\eta )}{2}\right)$-expansion method are presented. The application of these techniques to the TB equation is described in "Solitary wave solutions in the TB model (1)" section. In addition to the mathematical derivations, "Analysis of the physical implications of the obtainedresults" section provides a graphical representation of the outcomes, aiding the interpretation of their physical significance.Thee paper concludes with a discussion and concluding remarks in "Discussion and conclusions" section.

Formulation of the regulatory model

The model proposed by Triki and Biswas^43,44,45 is presented as follows

$$\begin{aligned} Q_t+\textit{ia} Q_{\textrm{xx}}+\textit{b}\left( |Q|^{2 n} Q\right) _x=0. \end{aligned}$$

(1)

The initial term in the equation governs the temporal evolution of pulses with the coefficient ‘$\textit{a}$, ensuring the presence of group velocity dispersion in the model. The profile of subpicosecond optical solitons is represented by the complex-valued function Q(x, t). The non-Kerr dispersion effect is counteracted by coefficient ‘$\textit{b}$’ when $n>2$. When the nonlinearity parameter takes the value of $n=1$, the model aligns with the Kaup-Newell model. Conversely, when $n=2$, the significance of the derivative quintic non-Kerr nonlinearity terms becomes pronounced in the transmission of extremely short pulses, characterized by widths around sub-10 fs, within highly nonlinear optical fibers.

Coordinated strategies

Examine the nonlinear PDE expressed in the following form

$$\begin{aligned} E\left( Q, Q_x, Q_t, Q_{\textrm{xx}}, Q_{\textrm{xt}}, \ldots \right) =0, \end{aligned}$$

(2)

where $Q = Q(x, t)$ denotes the solution of the nonlinear PDE (2). Using this transformation, we obtain

$$\begin{aligned} Q(x,t)=Z(\eta )e^{i\phi },\,\,\,\,\,\, \eta =x\pm ct,\,\,\,\,\,\, \phi =\mu _1 x-\mu _2 t+\mu _3, \end{aligned}$$

(3)

where the parameters $\mu _{1}$ represent the soliton frequency, $\mu _{2}$ denotes the soliton wave, $\mu _{3}$ signifies the soliton phase, and c represents the speed of the wave. Then the nonlinear PDE (2) can be transformed into an ordinary differential equation (ODE) as follows

$$\begin{aligned} W(Z,Z',Z'',...)=0, \end{aligned}$$

(4)

where $Z'=\frac{dZ}{d \eta }\cdot$

General procedure to the gJEF method.

In this scenario, the gJEF method was detailed using the following approach: To arrive at waveform solutions for Eq (2), it is essential to follow these specified steps;

Step 1: Take into account the subsequent structure as the solution for Eq (4);

$$\begin{aligned} Z(\eta )=\sum _{p=0}^{N}a_{p}V^p(\eta ), \end{aligned}$$

(5)

where, the identification of the real parameters $a_p (p=1, 2, \cdots , N)$ is necessary and the function $V(\eta )$ satisfies the solution

$$\begin{aligned} V'(\eta )=\sqrt{s_1+s_2V^2(\eta )+\frac{s_3}{2}V^4(\eta )}, \end{aligned}$$

(6)

where $s_1,\,\,s_2$ and $s_3$ are parameters.

Step 2: The parameter N can be determined by using the homogeneous balancing principle.

Step 3: Upon substituting Eq (5) into Eq (4) and then using Eq (6), we derive an associated system of equations featuring various $V(\eta )$ monomials. Solving this system yields a set of values for the required parameters.

Step 4: The constants $s_1$, $s_2$, and $s_3$ values presented in Table 1 can be employed to deduce solutions for Eq (6).

As stated earlier, the elliptic functions $\operatorname {sn}(\eta )$, $\operatorname {cn}(\eta )$, and $\operatorname {dn}(\eta )$ conform to the prescribed relationships

$$\begin{aligned} \begin{aligned}&\operatorname {sn}^{2}(\eta )+\operatorname {cn}^{2}(\eta )=1,~\operatorname {dn}^{2}(\eta )+\Upsilon ^{2}\operatorname {sn}^{2}(\eta )=1, ~(\operatorname {sn}(\eta ))^\prime=\operatorname {cn}(\eta )\operatorname {dn}(\eta ), \\&(\operatorname {cn}(\eta ))^\prime=-\operatorname {sn}(\eta )\operatorname {dn}(\eta ),~~(\operatorname {dn}(\eta ))^\prime =-\Upsilon ^{2}\operatorname {sn}(\eta )\operatorname {cn}(\eta ). \end{aligned} \end{aligned}$$

(7)

When $\Upsilon \longrightarrow 0$, the Jacobi elliptic function degenerate to the triangular functions,

$$\begin{aligned} \begin{array}{lll} \operatorname {sn}(\eta ) \rightarrow \sin (\eta ), & \operatorname {cn}(\eta ) \rightarrow \cos (\eta ), \\ \operatorname {cs}(\eta ) \rightarrow \cot (\eta ), & d s(\eta ) \rightarrow \csc (\eta ). \end{array} \end{aligned}$$

When $\Upsilon \longrightarrow 1$, the Jacobi elliptic function degenerate to the hyperbolic functions,

$$\begin{aligned} \begin{aligned}&\operatorname {sn}(\eta ) \rightarrow \tanh (\eta ), \quad \operatorname {cn}(\eta ) \rightarrow \operatorname {sech}(\eta ), \quad d n(\eta ) \rightarrow \operatorname {sech}(\eta ), \\&\operatorname {cs}(\eta ) \rightarrow \operatorname {csch}(\eta ), \quad d s(\eta ) \rightarrow \operatorname {csch}(\eta ). \end{aligned} \end{aligned}$$

In this context, the elliptic functions approach trigonometric functions as $\Upsilon \rightarrow 0$ and the hyperbolic functions for $\Upsilon \rightarrow 1$ are detailed in Table 2.

Table 1 Types of solutions of (6).

Table 2 When $\Upsilon \mapsto 1$.

$\tan \left( \frac{V(\eta )}{2}\right)$-expansion method

The procedure is elucidated through the following steps;

Step: 1 Following this scheme, we posit the solution for ODE (4) as follows:

$$\begin{aligned} Z\left( \eta \right) =\sum _{p=0}^{N}a_p\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^p+ \sum _{p=1}^{N}b_p\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^{-p}, \end{aligned}$$

(8)

where the constants $a_p$ (where $0 \le p \le N$) and $b_p$ (where $1 \le p \le N$) have yet to be determined. Function $V(\eta )$ complies with the ODE:

$$\begin{aligned} V^\prime =\theta _1 \sin (V(\eta ))+\theta _2 \cos (V(\eta )) +\theta _3. \end{aligned}$$

(9)

The following are the specific solutions to (9).

Case (1) For $\theta _1^2+\theta _2^2-\theta _3^2<0$ and $\theta _2-\theta _3\ne 0$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2} (\eta +C)\bigg )\bigg ], \end{aligned}$$

(10)

Case (2) For $\theta _1^2+\theta _2^2-\theta _3^2>0$ and $\theta _2-\theta _3\ne 0$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]. \end{aligned}$$

(11)

Case (3) For $\theta _1^2+\theta _2^2-\theta _3^2>0$, $\theta _2\ne 0$ and $\theta _3=0$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2}\tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]. \end{aligned}$$

(12)

Case (4) For $\theta _1^2+\theta _2^2-\theta _3^2<0$, $\theta _3\ne 0$ and $\theta _2=0$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]. \end{aligned}$$

(13)

Case (5) For $\theta _1^2+\theta _2^2-\theta _3^2>0$, $\theta _2-\theta _3\ne 0$ and $\theta _1=0$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]. \end{aligned}$$

(14)

Case (6) For $\theta _1=0$ and $\theta _3=0$,

$$\begin{aligned} V(\eta )=\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1},\frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]. \end{aligned}$$

(15)

Case (7) For $\theta _2=0$ and $\theta _3=0$,

$$\begin{aligned} V(\eta )=\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1},\frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]. \end{aligned}$$

(16)

Case (8) For $\theta _1^2+\theta _2^2=\theta _3^2$,

$$\begin{aligned} V(\eta )=-2\tan ^{-1}\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ]. \end{aligned}$$

(17)

Case (9) For $\theta _1=\theta _2=\theta _3=ic_0$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [e^{ic_0(\eta +C)}-1\bigg ]. \end{aligned}$$

(18)

Case (10) For $\theta _1=\theta _3=ic_0$ and $\theta _2=-ic_0$,

$$\begin{aligned} V(\eta )=-2\tan ^{-1}\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ]. \end{aligned}$$

(19)

Case (11) For $\theta _3=\theta _1$,

$$\begin{aligned} V(\eta )=-2\tan ^{-1}\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ]. \end{aligned}$$

(20)

Case (12) For $\theta _1=\theta _3$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ]. \end{aligned}$$

(21)

Case (13) For $\theta _3=-\theta _1$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ], \end{aligned}$$

(22)

Case (14) For $\theta _2=-\theta _3$,

$$\begin{aligned} V(\eta )=-2\tan ^{-1}\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]. \end{aligned}$$

(23)

Case (15) For $\theta _2=0,~\theta _1=\theta _3$,

$$\begin{aligned} V(\eta )=-2\tan ^{-1}\bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]. \end{aligned}$$

(24)

Case (16) For $\theta _1=0$ and $\theta _2=\theta _3$,

$$\begin{aligned} V(\eta )=2\tan ^{-1}\bigg [\theta _3(\eta +C)\bigg ]. \end{aligned}$$

(25)

Case (17) For $\theta _1=0$ and $\theta _2=-\theta _3$,

$$\begin{aligned} V(\eta )=-2\tan ^{-1}\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ]. \end{aligned}$$

(26)

Case (18) For $\theta _1=0$ and $\theta _2=0$,

$$\begin{aligned} V(\eta )=\theta _3(\eta +C). \end{aligned}$$

(27)

Balance index N can be determined using the homogeneous balance principle.

Step: 3 Upon obtaining the value of N in the previous step, substitute Eq (4), and the coefficients of $\tan \bigg (\frac{V(\eta )}{2}\bigg )^p$ and $\tan \bigg (\frac{V(\eta )}{2}\bigg )^{-p}$. A system of algebraic equations was derived by setting each coefficient to zero. When solved using Mathematica software, these equations allow for the determination of the values of $a_0$, $a_p$, $b_p$ $(p=1,2,\cdots ,N)$, $\theta _1$, $\theta _2$, and $\theta _3$.

Step: 4 Substitute the values of $a_0$, $a_1$, $b_1$, ..., $a_p$, $b_p$, and c into Eq (8), the solution for ODE (4) is obtained. The solution for PDE (2) follows by using the transformation (3).

Solitary wave solutions in the TB model (1)

The model proposed by TB is presented as follows

$$\begin{aligned} Q_t+i\textit{a} Q_{\textrm{xx}}+b\left( |Q|^{2 n} Q\right) _x=0. \end{aligned}$$

In order to obtain exact solution to Eq (1), we apply the traveling wave transformation (3), and subsequently separating real and imaginary parts results

$$\begin{aligned} & -Z'c -aZ'\mu _{1}-aZ'+2nbZ'Z^{2n}+bZ'Z^{2n}=0, \end{aligned}$$

(28)

$$\begin{aligned} & -Z' +aZ'-a\mu _{1}Z'+2nb\mu _{1}Z^{2n+1}+\mu _{1}bZ^{2n+1}=0. \end{aligned}$$

(29)

Both the real and imaginary components describe the speed of the model through the medium by the relation $Z=X^{\frac{1}{2n}}$, so one can get

$$\begin{aligned} -4n^2X^{2}(\mu _{2}+\mu _{1}^2a)+a(1-2n)(X')^{2}+4n^2 aXX'' +4n^2 b\mu _{1}X^3=0. \end{aligned}$$

(30)

The homogeneous balancing principle suggests the index for Eq (30)

$$\begin{aligned} N=2. \end{aligned}$$

(31)

Soliton solutions using the gJEF method

In this section, the solitary wave and periodic solutions for the TB model (1) are calculated. We employ the gJEF method to handle these waveform solutions. For $N=2$, the Eq (5) suggests

$$\begin{aligned} X(\eta )=a_0+a_1 V(\eta )+a_2V^2(\eta ). \end{aligned}$$

(32)

We insert the values in (30) and subsequently use (6) to arrive at the system of equations. We solve this system using Mathematica and follow the results

$$\begin{aligned} \begin{aligned} b&=-\frac{1}{2}\frac{as_{3}}{\mu _{1} a_{2}},~\mu _{2}=-a\mu _{1}^2+2as_{2},~a_0=-\frac{a_2s_2}{s_3},~a_1=2\sqrt{-\frac{s_{2}}{s_{3}}},~a_2=a_2. \end{aligned} \end{aligned}$$

(33)

By substituting the values of parameters, the solution (32) becomes as

$$\begin{aligned} X(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}V(\eta )+a_2V^2(\eta ). \end{aligned}$$

(34)

For different values of function $V^2(\eta )$, (34) ascertains diverse soliton solutions.

Family: 1

When $s_{1}=-(1+\Upsilon ^2),\,\,\,s_{2}=2\Upsilon ^2, \,\,\,s_{3}=1$.

We derive the periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )= \text {sn}(\eta ,\Upsilon )$.

$$\begin{aligned} X_1(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {sn}(\eta ,\Upsilon )+a_2\text {sn}^2(\eta ,\Upsilon ), \end{aligned}$$

(35)

and by the relationship, $Z=X^\frac{1}{2n}$, we follow

$$\begin{aligned} Z_1(\eta )=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {sn}(\eta ,\Upsilon )+a_2\text {sn}^2(\eta ,\Upsilon )\bigg )^\frac{1}{2n}. \end{aligned}$$

(36)

In the scenario where $\Upsilon$ tends to 1, Eq (36) transforms into the shock wave solution for Eq (1) as indicated by

$$\begin{aligned} Q_{1}(x,t)=\bigg (- \frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\tanh (x-c t)+a_2\tanh ^2(x-c t)\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(37)

Family: 2

When $s_{1}=2\Upsilon ^2-1,\,\,\,s_{2}=2, \,\,\,s_{3}=-\Upsilon ^2(1-\Upsilon ^2)$.

We derive the periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )= \text {ds}(\eta ,\Upsilon )$.

$$\begin{aligned} X_2(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {ds}(\eta ,\Upsilon )+a_2\text {ds}^2(\eta ,\Upsilon ), \end{aligned}$$

(38)

and

$$\begin{aligned} Z_2(\eta )=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {ds}(\eta ,\Upsilon )+a_2\text {ds}^2(\eta ,\Upsilon )\bigg )^\frac{1}{2n}. \end{aligned}$$

(39)

In the scenario where $\Upsilon$ tends to 1, Eq (39) transforms into the singular soliton wave solution for Eq (1) as indicated by

$$\begin{aligned} Q_{2}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {csch}(x-c t)+a_2\text {csch}^2(x-c t)\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(40)

Family: 3

When $s_{1}=2-\Upsilon ^2,\,\,\,s_{2}=2, \,\,\,s_{3}=1-\Upsilon ^2$.

We derive the periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )= \text {cs}(\eta ,\Upsilon )$.

$$\begin{aligned} X_3(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {cs}(\eta ,\Upsilon )+a_2\text {cs}^2(\eta ,\Upsilon ), \end{aligned}$$

(41)

and

$$\begin{aligned} Z_3(\eta )=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {cs}(\eta ,\Upsilon )+a_2\text {cs}^2(\eta ,\Upsilon )\bigg )^\frac{1}{2n}. \end{aligned}$$

(42)

In the scenario where $\Upsilon$ tends to 0, Eq (42) transforms into the singular soliton wave solution for Eq (1) as indicated by

$$\begin{aligned} Q_{3}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\coth (x-c t) +a_2\coth ^2(x-c t)\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(43)

Likewise, as $\Upsilon$ approaches 1, we obtain a singular soliton solution for Eq (1) given by

$$\begin{aligned} Q^*_{3}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {csch}(x-c t)+a_2\text {csch}^2(x-c t)\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(44)

Family: 4

When $s_{1}=2\Upsilon ^2-1,\,\,\,s_{2}=-2\Upsilon ^2, \,\,\,s_{3}=1-\Upsilon ^2$.

We derive the periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )= \text {cn}(\eta ,\Upsilon )$.

$$\begin{aligned} X_4(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {cn}(\eta ,\Upsilon )+a_2\text {cn}^2(\eta ,\Upsilon ), \end{aligned}$$

(45)

and

$$\begin{aligned} Z_4(\eta )=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {cn}(\eta ,\Upsilon )+a_2\text {cn}^2(\eta ,\Upsilon )\bigg )^\frac{1}{2n}. \end{aligned}$$

(46)

In the scenario where $\Upsilon$ tends to 1, Eq (46) transforms into the optical bright soliton wave for Eq (1) as indicated by

$$\begin{aligned} Q_{4}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {sech}(x-c t)+a_2\text {sech}^2(x-c t)\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(47)

Family: 5

When $s_{1}=2-\Upsilon ^2,\,\,\,s_{2}=-2, \,\,\,s_{3}=\Upsilon ^2-1$.

We derive the periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )= \text {dn}(\eta ,\Upsilon )$.

$$\begin{aligned} X_5(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {dn}^2(\eta ,\Upsilon )+a_2\text {dn}^2(\eta ,\Upsilon ), \end{aligned}$$

(48)

and

$$\begin{aligned} Z_{5}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {dn}^2(\eta ,\Upsilon )+a_2\text {dn}^2(\eta ,\Upsilon )\bigg )^\frac{1}{2n}. \end{aligned}$$

(49)

In the scenario where $\Upsilon$ tends to 1, Eq (49) transforms into optical bright soliton solution for Eq (1) as indicated by

$$\begin{aligned} Q_{5}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\text {sech}(x-c t) +a_2\text {sech}^2(x-c t)\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(50)

Family: 6

When $s_{1}=\frac{\Upsilon ^2-2}{2},\,\,\,s_{2}=\frac{\Upsilon ^2}{2}, \,\,\,s_{3}=\frac{1}{4}$.

We derive the double periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )= \frac{\text {sn}(\eta ,\Upsilon )}{1\pm \text {dn}(\eta ,\Upsilon )}$.

$$\begin{aligned} X_6(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\frac{\text {sn}(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))}+a_2\frac{\text {sn}^2(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))^2}, \end{aligned}$$

(51)

and

$$\begin{aligned} Z_{6}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\frac{\text {sn}(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))}+a_2\frac{\text {sn}^2(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))^2}\bigg )^\frac{1}{2n}. \end{aligned}$$

(52)

In the scenario where $\Upsilon$ tends to 1, Eq (52) transforms into

$$\begin{aligned} Q_{6}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\frac{\tanh (x-c t)}{(1\pm \text {sech}(x-c t))}+a_2\frac{\tanh ^2(x-c t)}{(1\pm \text {sech}(x-c t))^2}\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(53)

Family: 7

When $s_{1}=\frac{\Upsilon ^2-2}{2},\,\,\,s_{2}=\frac{\Upsilon ^2}{2}, \,\,\,s_{3}=\frac{\Upsilon ^2}{4}$.

We derive the double periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )=\frac{\text {sn}(\eta ,\Upsilon )}{1\pm \text {dn}(\eta ,\Upsilon )}$.

$$\begin{aligned} X_7(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\frac{\text {sn}(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))}+a_2\frac{\text {sn}^2(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))^2}, \end{aligned}$$

(54)

and

$$\begin{aligned} Z_{7}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\frac{\text {sn}(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))}+a_2\frac{\text {sn}^2(\eta ,\Upsilon )}{(1\pm \text {dn}(\eta ,\Upsilon ))^2}\bigg )^\frac{1}{2n}. \end{aligned}$$

(55)

In the scenario where $\Upsilon$ tends to 1, Eq (55) transforms into

$$\begin{aligned} Q_{7}(x,t)=\left( -\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\frac{\tanh (x-{sps})}{(1\pm \text {sech}(x-c t))}+a_2\frac{\tanh ^2(x-c t)}{(1\pm \text {sech}(x-c t))^2}\right) ^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(56)

Family: 8

When $s_{1}=\frac{\Upsilon ^2+1}{2},\,\,\,s_{2}=-\frac{1}{2}, \,\,\,s_{3}=-\frac{(1-\Upsilon ^2)^2}{4}$.

We derive the double periodic wave solution for (30) by adopting the Jacobi amplitude function as $V(\eta )=\Upsilon \text {cn}(\eta ,\Upsilon )\pm \text {dn}(\eta ,\Upsilon )$.

$$\begin{aligned} X_8(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\Upsilon \text {cn}(\eta ,\Upsilon )\pm \text {dn}(\eta ,\Upsilon )+a_2(\Upsilon \text {cn}(\eta ,\Upsilon )\pm \text {dn}(\eta ,\Upsilon ))^2, \end{aligned}$$

(57)

along with

$$\begin{aligned} Z_{8}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\Upsilon \text {cn}(\eta ,\Upsilon )\pm \text {dn}(\eta ,\Upsilon )+a_2(\Upsilon \text {cn}(\eta ,\Upsilon )\pm \text {dn}(\eta ,\Upsilon ))^2\bigg )^\frac{1}{2n}. \end{aligned}$$

(58)

In the scenario where $\Upsilon$ tends to 1, Eq (58) transforms into

$$\begin{aligned} Q_{8}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}(\text {sech}(x-c t)\pm \text {sech}(x-c t))+a_2(\text {sech}(x-c t)\pm \text {sech}(x-c t))^2\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(59)

Family: 9

When $s_{1}=0,\,\,\,s_{2}=2, \,\,\,s_{3}=0$.

We derive a rational solution for (30) by adopting the amplitude function as $V(\eta )=\frac{F}{\eta }$.

$$\begin{aligned} X_9(\eta )=-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\bigg (\frac{D}{\eta }\bigg )+a_2\bigg (\frac{F}{\eta }\bigg )^2, \end{aligned}$$

(60)

and

$$\begin{aligned} Z_{9}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\bigg (\frac{F}{\eta }\bigg )+a_2\bigg (\frac{F}{\eta }\bigg )^2\bigg )^\frac{1}{2n}. \end{aligned}$$

(61)

In the scenario where $\Upsilon$ tends to 0, Eq (61) transforms into

$$\begin{aligned} Q_{9}(x,t)=\bigg (-\frac{a_2s_2}{s_3}+2\sqrt{-\frac{s_{2}}{s_{3}}}\bigg (\frac{F}{x-c t}\bigg )+a_2\bigg (\frac{F}{x-c t}\bigg )^2\bigg )^\frac{1}{2n}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned}$$

(62)

Soliton solutions for TB model (1) using $\tan \left( \frac{V(\eta )}{2}\right) -$expansion method

The solution (8) assumes the following mathematical expression

$$\begin{aligned} X\left( \eta \right) =a_0+a_1\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]+ b_1\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^{-1}+a_2\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^2+ b_2\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^{-2}. \end{aligned}$$

(63)

We substitute Eq (63) into Eq (30), and then compare the polynomials of the type $\tan \bigg (\frac{V(\eta )}{2}\bigg )$ results in the following system

$$\begin{aligned} \begin{aligned} \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{0}&:3b_{2}\theta _2^2 r-3b_{2}\theta _2^2\Upsilon +6b_{2}\theta _2\theta _3 r-6b_{2}\theta _2\theta _3\Upsilon +3b_2 \theta _3^2 r -3b_2 \theta _3^2 \Upsilon +2b_2 p=0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{1}&:b_1 \theta _2^2 r-b_1 \theta _2^2 \Upsilon +2b_1 \theta _2\theta _3 r-2b_1\theta _2\theta _3\Upsilon +b_1 \theta _3^2 r-b_1 \theta _3^2 \Upsilon +10b_2 \theta _1\theta _2 r-10b_2 \theta _1 \theta _2\Upsilon +\\&10b_2 \theta _1 \theta _3 r-10b_2 \theta _1 \theta _3 \Upsilon +4b_1 b_2 p =0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{2}&: 3b_1\theta _1\theta _2 r-3b_1\theta _1\theta _2 \Upsilon +3b_1\theta _1\theta _3 r -3b_1\theta _1\theta _3\Upsilon +8b_2 \theta _1^2 r-8b_2\theta _1^2 \Upsilon +2b_2 \theta _2^2 r-2b_2 \theta _2^2\Upsilon \\&+12b_2\theta _2\theta _3 r-12b_2\theta _2\theta _3\Upsilon +10b_2\theta _3^2 r-10b_2\theta _3^2\Upsilon +4a_{0}b_2 p+2b_{1}^2 p+4b_2^2 p\\&+2b_2\gamma ^2-2b_2k^2 -2b_2 w=0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{3}&: 2b_1\theta _1^2 r- 2b_1\theta _1^2\Upsilon +b_1\theta _2^2 r-b_1 \theta _2^2 \Upsilon +4b_1\theta _2\theta _3 r-4b_1\theta _2\theta _3\Upsilon +3b_1 \theta _3^2 r-3b_1\theta _3^2\Upsilon \\&+14b_2 \theta _1\theta _2 r-14b_2\theta _1\theta _2\Upsilon +26b_2\theta _1\theta _3 r-26b_2\theta _1\theta _3\Upsilon +4a_0 b_1 p+4a_1b_2p\\&+8b_1b_2p+2b_1\gamma ^2-2b_1k^2-2b_1w=0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{4}&:a_1\theta _1\theta _2 r-a_1\theta _1\theta _2 \Upsilon +a_1\theta _1\theta _3 r-a_1\theta _1\theta _3\Upsilon +a_2\theta _2^2r-a_2\theta _2^2\Upsilon +2a_2\theta _2\theta _3 r-2a_2\theta _2\theta _3\Upsilon \\&+a_2\theta _3^2 r-a_2\theta _3^2\Upsilon +5b_1\theta _1\theta _2 r-5b_1\theta _1\theta _2 \Upsilon +7b_1\theta _1\theta _3 \Upsilon -7b_1\theta _1\theta _3\Upsilon +16b_2\theta _1^2 r\\&-16b_2\theta _1^2\Upsilon -4b_2\theta _2^2 r+4b_2\theta _2^2\Upsilon +4b_2\theta _2\theta _3 r-4b_2\theta _2\theta _3\Upsilon +12b_2\theta _3^2 r-12b_2\theta _3^2\Upsilon \\&+2a_0^2 p+8a_0b_2p+2a_0\gamma ^2-2a_0k^2+4a_1b_1p+4a_2b_2p+4b_1^2p\\&+4b_2^2p+4b_2\gamma ^2-4b_2k^2-2a_0w-4b_2w=0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{5}&:2a_1\theta _1^2r-2a_1\theta _1^2\Upsilon -a_1\theta _2^2r +a_1\theta _2^2\Upsilon +a_1\theta _3^2r-a_1\theta _3^2\Upsilon +6a_2\theta _1\theta _2 r\\&-6a_2\theta _1\theta _2 \Upsilon +6a_2\theta _1\theta _3 r-6a_2\theta _1\theta _3 \Upsilon +4b_1\theta _1^2r-4b_1\theta _1^2\Upsilon -b_1\theta _2^2r+b_1\theta _2^2\Upsilon +2b_1\theta _2\theta _3 r\\&-2b_1\theta _2\theta _3\Upsilon +3b_1\theta _3^2r-3b_1\theta _3^2\Upsilon -2b_2\theta _1\theta _2 r+2b_2\theta _1\theta _2 \Upsilon +22b_2\theta _1\theta _3 r-22b_2\theta _1\theta _3 \Upsilon \\&+4a_0a_1p+8a_0b_1p+8a_1b_2p+2a_1\gamma ^2-2a_1k^2+4a_2b_1p+4b_1b_2p+4b_1\gamma ^2\\&-4b_1k^2-2a_1w-4b_1w=0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{6}&:-a_1\theta _1\theta _2 r+a_1\theta _1\theta _2 \Upsilon +5a_1\theta _1\theta _3 r-5a_1\theta _1\theta _3\Upsilon +8a_2\theta _1^2r-8a_2\theta _1^2\Upsilon -2a_2\theta _2^2 r+2a_2\theta _2^2\Upsilon \\&+4a_2\theta _2\theta _3 r-4a_2\theta _2\theta _3\Upsilon +6a_2\theta _3^2 r-6a_2\theta _3^2 \Upsilon +b_1\theta _1\theta _2 r-b_1\theta _1\theta _2\Upsilon +5b_1\theta _1\theta _3 r-5b_1\theta _1\theta _3\Upsilon \\&+8b_2\theta _1^2 r-8b_2\theta _1^2 \Upsilon -2b_2\theta _2^2 r+2b_2\theta _2^2\Upsilon -4b_2\theta _2\theta _3 r+4b_2\theta _2\theta _3\Upsilon +6b_2\theta _3^2 r-6b_2\theta _3^2 \Upsilon \\&+4a_0^2p+4a_0a_2p+4a_0b_2p+4a_0\gamma ^2-4a_0k^2+2a_1^2p+8a_1b_1p+8a_2b_2p+2a_2\gamma ^2\\&-2a_2k^2+2b_1^2p+2b_2\gamma ^2-2b_2k^2-4a_0w -2a_2w-2b_2w=0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{7}&:4a_1\theta _1^2r-4a_1\theta _1^2\Upsilon -a_1\theta _2^2r+a_1\theta _2^2\Upsilon -2a_1\theta _2\theta _3 r+2a_1\theta _2\theta _3\Upsilon +3a_1\theta _3^2r-3a_1\theta _3^2\Upsilon \\&+2a_2\theta _1\theta _2 r-2a_2\theta _1\theta _3\Upsilon +22a_2\theta _1\theta _3 r-22a_2\theta _1\theta _3\ \Upsilon +2b_1\theta _1^2r-2b_1\theta _1^2\Upsilon -b_1\theta _2^2r+b_1\theta _2^2\Upsilon \\&+b_1\theta _3^2r-b_1\theta _3^2\Upsilon -6b_2\theta _1\theta _2 r+6b_2\theta _1\theta _2\Upsilon +6b_2\theta _1\theta _3 r-6b_2\theta _1\theta _3\Upsilon +8a_0a_1p+4a_0b_1p\\&+4a_1a_2p+4a_1b_2p+4a_1\gamma ^2-4a_1k^2+8a_2b_1p+2b_1\gamma ^2-2b_1k^2-4a_1w-2b_1w =0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{8}&:-5a_1\theta _1\theta _2 r+5a_1\theta _1\theta _2\Upsilon +7a_1\theta _1\theta _3 r-7a_1\theta _1\theta _3\Upsilon +16a_2\theta _1^2r-16a_2\theta _1^2\Upsilon -4a_2\theta _2^2r\\&+4a_2\theta _2^2\Upsilon -4a_2\theta _2\theta _3 r+4a_2\theta _2\theta _3\Upsilon +12a_2\theta _3^2 r-12a_2\theta _3^2\Upsilon -b_1\theta _1\theta _2 r+b_1\theta _1\theta _2\Upsilon \\&+b_1\theta _1\theta _3 r-b_1\theta _1\theta _3\Upsilon +b_2\theta _2^2 r-b_2\theta _2^2\Upsilon -2b_2\theta _2\theta _3 r+2b_2\theta _2\theta _3\Upsilon +b_2\theta _3^2 r-b_2\theta _3^2\Upsilon \\&+2a_0^2 p+8a_0a_2p+2a_0\gamma ^2-2a_0k^2+4a_1^2p+4a_1b_1p+2a_2^2p+4a_2b_2p+4a_2\gamma ^2\\&-4a_2k^2-2a_0w-4a_2w=0,\\ \end{aligned} \end{aligned}$$

(64)

$$\begin{aligned} \begin{aligned} \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{9}&:2a_1\theta _1^2 r-2a_1\theta _1^2\Upsilon +a_1\theta _2^2r -a_1\theta _2^2\Upsilon -4a_1\theta _2\theta _3 r+4a_1\theta _2\theta _3\Upsilon +3a_1\theta _3^2 r-3a_1\theta _3^2\Upsilon \\&-14a_2\theta _1\theta _2 r+14a_2\theta _1\theta _2\Upsilon +26a_2\theta _1\theta _3 r-26a_2\theta _1\theta _3\Upsilon +4a_0a_1p+8a_1a_2p\\&+2a_1\gamma ^2-2a_1k^2+4a_2b_1p-2a_1w=0,\\ \bigg (\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg )^{10}&:-3a_1\theta _1\theta _2 r+3a_1\theta _1\theta _2 \Upsilon +3a_1\theta _1\theta _3 r -3a_1\theta _1\theta _3\Upsilon +8a_2 \theta _1^2 r-8a_2\theta _1^2 \Upsilon +2a_2 \theta _2^2 r-2a_2 \theta _2^2\Upsilon \\&-12a_2\theta _2\theta _3 r+12a_2\theta _2\theta _3\Upsilon +10a_2\theta _3^2 r-10b_2\theta _3^2\Upsilon +4a_{0}a_2 p+2a_{1}^2 p+4a_2^2 p\\&+2a_2\gamma ^2-2a_2k^2 -2a_2 w=0. \end{aligned} \end{aligned}$$

(65)

The following outcomes were acquired through the utilization of the Mathematica software

Set: 1 $\eta =\frac{1}{5}(1+2i)$, $\theta _2=\theta _2$, $a_0=a_0$, $a_1=\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}$, $a_2=a_2$, $b_1=0$, $b_2=0$, $b=\frac{a(\theta _2^2-2\theta _2\theta _3+\theta _3^2)}{-4a_2 k}$, $\mu _2=\frac{3a_0\theta _2^2-6a_0\theta _2\theta _3+3a_0\theta _3^2-8a_2k^2+3a_2\theta _2^2-3a_2\theta _3^2)}{8a_2}\cdot$

$$\begin{aligned} X\left( \eta \right) =a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]+a_2\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^2, \end{aligned}$$

(66)

where $\theta _1,\theta _2$, and $\theta _3$ represent arbitrary constants and $\eta =x\pm ct$. By considering families $1-18$ following solution families are obtained

$$\begin{aligned} & \begin{aligned} Q_{10}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}} \bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}\\&(\eta +C)\bigg )\bigg ]+a_2\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(67)

$$\begin{aligned} & \begin{aligned} Q_{11}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}\\&(\eta +C)\bigg )\bigg ]+a_2\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(68)

$$\begin{aligned} & \begin{aligned} Q_{12}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2}\tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]\\&+a_2\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2}\tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(69)

$$\begin{aligned} & \begin{aligned} Q_{13}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]\\&+a_2\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(70)

$$\begin{aligned} & \begin{aligned} Q_{14}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]\\&+a_2\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(71)

$$\begin{aligned} & \begin{aligned} Q_{15}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\\&+a_2\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\bigg )^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(72)

$$\begin{aligned} & \begin{aligned} Q_{16}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1}, \frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\\&+a_2\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1},\frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\bigg )^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(73)

$$\begin{aligned} & \begin{aligned} Q_{17}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ]\\&+a_2\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(74)

$$\begin{aligned} & \begin{aligned} Q_{18}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [e^{ic_0(\eta +C)}-1\bigg ] \\&+a_2\bigg [e^{ic_0(\eta +C)}-1\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(75)

$$\begin{aligned} & \begin{aligned} Q_{19}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ] \\&+a_2\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(76)

$$\begin{aligned} & \begin{aligned} Q_{20}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ] \\&+a_2\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(77)

$$\begin{aligned} & \begin{aligned} Q_{21}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ] \\&+a_2\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(78)

$$\begin{aligned} & \begin{aligned} Q_{22}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ] \\&+a_2\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(79)

$$\begin{aligned} & \begin{aligned} Q_{23}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]\\&+a_2\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(80)

$$\begin{aligned} & \begin{aligned} Q_{24}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ] \\&+a_2\bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(81)

$$\begin{aligned} & \begin{aligned} Q_{25}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\theta _3(\eta +C)\bigg ]+a_2\bigg [\theta _3(\eta +C)\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(82)

$$\begin{aligned} & \begin{aligned} Q_{26}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ] +a_2\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ]^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(83)

$$\begin{aligned} & \begin{aligned} Q_{27}\left( x,t\right) =&\bigg [a_0+\sqrt{\frac{6a_0 a_2\theta _2-6a_0 a_2\theta _3+2a_2^2\theta _2+2a_2^2\theta _3}{\theta _2-\theta _3}}\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg ) \\&+a_2\bigg (\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )\bigg )^2\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(84)

Set: 2 $\theta _1=-2\sqrt{2}\theta _2$, $b=\frac{\sqrt{2}\theta _2^2a}{2a_1k}$, $\theta _3=0$, $a_0=\sqrt{2}a_1$, $a_1=a_1$, $a_2=0$, $b_1=-a_1$, $b_2=0$, $n=\frac{1}{8}(1+\sqrt{7}i)$, $\mu _2=-ak^2$.

$$\begin{aligned} X\left( \eta \right) =\sqrt{2}a_1+a_1\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]-a_1\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^{-1}, \end{aligned}$$

(85)

where $\theta _1,\theta _2$, and $\theta _3$ represent arbitrary constants and $\eta =x\pm ct$. By considering families $1-18$ one can the following solutions can be obtained:

$$\begin{aligned} \begin{aligned} Q_{28}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&-a_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(86)

$$\begin{aligned} & \begin{aligned} Q_{29}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&-a_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(87)

$$\begin{aligned} & \begin{aligned} Q_{30}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2}\tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]\\&-a_1\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2}\tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(88)

$$\begin{aligned} & \begin{aligned} Q_{31}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]\\&-a_1\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2} (\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(89)

$$\begin{aligned} & \begin{aligned} Q_{32}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]\\&-a_1\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(90)

$$\begin{aligned} & \begin{aligned} Q_{33}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\\&-a_1\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(91)

$$\begin{aligned} & \begin{aligned} Q_{34}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1}, \frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\\&-a_1\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1},\frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(92)

$$\begin{aligned} & \begin{aligned} Q_{35}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ] -a_1\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(93)

$$\begin{aligned} & \begin{aligned} Q_{36}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [e^{ic_0(\eta +C)}-1\bigg ]-a_1\bigg [e^{ic_0(\eta +C)}-1\bigg ]^{-1} \bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(94)

$$\begin{aligned} & \begin{aligned} Q_{37}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ] -a_1\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(95)

$$\begin{aligned} & \begin{aligned} Q_{38}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ] -a_1\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(96)

$$\begin{aligned} & \begin{aligned} Q_{39}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ] -a_1\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(97)

$$\begin{aligned} & \begin{aligned} Q_{40}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ] -a_1\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(98)

$$\begin{aligned} & \begin{aligned} Q_{41}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]-a_1\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(99)

$$\begin{aligned} & \begin{aligned} Q_{42}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]- a_1\bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(100)

$$\begin{aligned} & \begin{aligned} Q_{43}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\theta _3(\eta +C)\bigg ]- a_1\bigg [\theta _3(\eta +C)\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(101)

$$\begin{aligned} & \begin{aligned} Q_{44}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ]- a_1\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(102)

$$\begin{aligned} & \begin{aligned} Q_{45}\left( x,t\right) =&\bigg [\sqrt{2}a_1+a_1\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )- a_1\bigg (\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(103)

Set: 3 $\theta _1=\frac{(\theta _2+\theta _3)a_0}{b_1}$, $b=-\frac{(\theta _2^2+2\theta _2\theta _3+\theta _3^2)aa_0}{b_1^2k}$, $a_0=a_0$, $a_1=-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}$, $a_2=0$, $b_1=b_1$, $b_2=0$, $c=0$.

$$\begin{aligned} X\left( \eta \right) =a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]+b_1\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^{-1}, \end{aligned}$$

(104)

where, $\theta _1,\theta _2$, and $\theta _3$ represent arbitrary constants, and $\eta =x\pm ct$. We consider families $1-18$ leading to

$$\begin{aligned} & \begin{aligned} Q_{46}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(105)

$$\begin{aligned} & \begin{aligned} Q_{47}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(106)

$$\begin{aligned} & \begin{aligned} Q_{48}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2} \tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2} \tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(107)

$$\begin{aligned} & \begin{aligned} Q_{49}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(108)

$$\begin{aligned} & \begin{aligned} Q_{50}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(109)

$$\begin{aligned} & \begin{aligned} Q_{51}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\\&+b_1\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(110)

$$\begin{aligned} & \begin{aligned} Q_{52}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1}, \frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\\&+b_1\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1},\frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(111)

$$\begin{aligned} & \begin{aligned} Q_{53}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ] +b_1\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(112)

$$\begin{aligned} & \begin{aligned} Q_{54}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [e^{ic_0(\eta +C)}-1\bigg ]+b_1\bigg [e^{ic_0(\eta +C)}-1\bigg ]^{-1} \bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(113)

$$\begin{aligned} & \begin{aligned} Q_{55}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ] +b_1\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(114)

$$\begin{aligned} & \begin{aligned} Q_{56}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ] +b_1\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(115)

$$\begin{aligned} & \begin{aligned} Q_{57}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ] +b_1\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(116)

$$\begin{aligned} & \begin{aligned} Q_{58}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ] +b_1\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(117)

$$\begin{aligned} & \begin{aligned} Q_{59}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]+b_1\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(118)

$$\begin{aligned} & \begin{aligned} Q_{60}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]+b_1 \bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(119)

$$\begin{aligned} & \begin{aligned} Q_{61}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\theta _3(\eta +C)\bigg ]+b_1 \bigg [\theta _3(\eta +C)\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(120)

$$\begin{aligned} & \begin{aligned} Q_{62}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ] +b_1\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(121)

$$\begin{aligned} & \begin{aligned} Q_{63}\left( x,t\right) =&\bigg [a_0-\frac{b_1(\theta _2-\theta _3)}{\theta _2+\theta _3}\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )+b_1\bigg (\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(122)

Set: 4 $\theta _1=\theta _1$, $b=-\frac{2a\theta _1\theta _3}{b_1k}$, $a_0=\frac{b_1\theta _1}{2\theta _3}$, $a_1=-\frac{b_1}{2}$, $a_2=0$, $b_1=b_1$, $b_2=0$, $c=0$, $k=k$, $\theta _2=3\theta _3$, $\mu _2=-a(k^2+\theta _1^2+8\theta _3^2)$.

$$\begin{aligned} X\left( \eta \right) =\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2}\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]+b_1\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^{-1}, \end{aligned}$$

(123)

where, $\theta _1,\theta _2$, and $\theta _3$ represent arbitrary constants, and $\eta =x\pm ct$. By considering families $1-18$ leads to following results

$$\begin{aligned} & \begin{aligned} Q_{64}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2}\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(124)

$$\begin{aligned} & \begin{aligned} Q_{65}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2}\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(125)

$$\begin{aligned} & \begin{aligned} Q_{66}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2} \tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2} \tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(126)

$$\begin{aligned} & \begin{aligned} Q_{67}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+b_1\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(127)

$$\begin{aligned} & \begin{aligned} Q_{68}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2}\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]\\&+b_1\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(128)

$$\begin{aligned} & \begin{aligned} Q_{69}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\\&+b_1\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(129)

$$\begin{aligned} & \begin{aligned} Q_{70}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1}, \frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\\&+b_1\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1},\frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(130)

$$\begin{aligned} & \begin{aligned} Q_{71}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ] +b_1\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(131)

$$\begin{aligned} & \begin{aligned} Q_{72}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [e^{ic_0(\eta +C)}-1\bigg ]+b_1\bigg [e^{ic_0(\eta +C)}-1\bigg ]^{-1} \bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(132)

$$\begin{aligned} & \begin{aligned} Q_{73}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ] +b_1\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(133)

$$\begin{aligned} & \begin{aligned} Q_{74}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ] +b_1\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(134)

$$\begin{aligned} & \begin{aligned} Q_{75}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ] +b_1\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(135)

$$\begin{aligned} & \begin{aligned} Q_{76}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ] +b_1\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(136)

$$\begin{aligned} & \begin{aligned} Q_{77}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]+b_1\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(137)

$$\begin{aligned} & \begin{aligned} Q_{78}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]+b_1 \bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(138)

$$\begin{aligned} & \begin{aligned} Q_{79}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\theta _3(\eta +C)\bigg ]+b_1 \bigg [\theta _3(\eta +C)\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(139)

$$\begin{aligned} & \begin{aligned} Q_{80}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \bigg [\frac{1}{\theta _3(\eta +C)}\bigg ] +b_1\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ]^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(140)

$$\begin{aligned} & \begin{aligned} Q_{81}\left( x,t\right) =&\bigg [\frac{b_1\theta _1}{2\theta _3}-\frac{b_1}{2} \tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )+b_1 \bigg (\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )\bigg )^{-1}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(141)

Set: 5 $\theta _1=-\frac{(\theta _2+\theta _3)a_1}{a_2}$, $b=-\frac{a(\theta _2^2-2\theta _2\theta _3+\theta _3^2)}{4a_2k}$, $a_0=-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}$, $a_1=a_1$, $a_2=a_2$, $b_1=0$, $b_2=0$, $c=0$, $n=\frac{1}{5}(1+2i)$.

$$\begin{aligned} X\left( \eta \right) =-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ] +a_2\bigg [\tan \bigg (\frac{V(\eta )}{2}\bigg )\bigg ]^{2}, \end{aligned}$$

(142)

where, $\theta _1,\theta _2$, and $\theta _3$ represent arbitrary constants, and $\eta =x\pm ct$. By considering families $1-18$ leads to

$$\begin{aligned} & \begin{aligned} Q_{82}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+a_2\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(143)

$$\begin{aligned} & \begin{aligned} Q_{83}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3} \tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+a_2\bigg [\frac{\theta _1}{\theta _2-\theta _3}-\frac{\sqrt{\theta _3^2+\theta _2^2-\theta _1^2}}{\theta _2-\theta _3}\tanh \bigg (\frac{\sqrt{\theta _3^2-\theta _2^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(144)

$$\begin{aligned} & \begin{aligned} Q_{84}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2} \tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+a_2\bigg [\frac{\theta _1}{\theta _2}-\frac{\sqrt{\theta _2^2+\theta _1^2}}{\theta _2} \tanh \bigg (\frac{\sqrt{\theta _2^2+\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(145)

$$\begin{aligned} & \begin{aligned} Q_{85}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3} \tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]\\&+a_2\bigg [-\frac{\theta _1}{\theta _3}+\frac{\sqrt{\theta _3^2-\theta _1^2}}{\theta _3}\tan \bigg (\frac{\sqrt{\theta _3^2-\theta _1^2}}{2}(\eta +C)\bigg )\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(146)

$$\begin{aligned} & \begin{aligned} Q_{86}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]\\&+a_2\bigg [\sqrt{\frac{\theta _2+\theta _3}{\theta _2-\theta _3}}\tanh \bigg (\frac{\sqrt{\theta _2^2-\theta _3^2}}{2} (\eta +C)\bigg )\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(147)

$$\begin{aligned} & \begin{aligned} Q_{87}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\\&+a_2\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _2(\eta +C)}-1}{e^{2\theta _2(\eta +C)}+1}, \frac{e^{2\theta _2(\eta +C)}}{e^{2\theta _2(\eta +C)}+1}\bigg ]\bigg )\bigg )^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(148)

$$\begin{aligned} & \begin{aligned} Q_{88}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1}, \frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\\&+a_2\bigg (\tan \bigg (\frac{1}{2}\tan ^{-1}\bigg [\frac{e^{2\theta _1(\eta +C)}}{e^{2\theta _1(\eta +C)}+1},\frac{e^{2\theta _1(\eta +C)}-1}{e^{2\theta _1(\eta +C)}+1}\bigg ]\bigg )\bigg )^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(149)

$$\begin{aligned} & \begin{aligned} Q_{89}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ] +a_2\bigg [\frac{(\theta _2+\theta _3)(\theta _1(\eta +C)+2)}{\theta _1^2(\eta +C)}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(150)

$$\begin{aligned} & \begin{aligned} Q_{90}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [e^{ic_0(\eta +C)}-1\bigg ]+a_2\bigg [e^{ic_0(\eta +C)}-1\bigg ]^{2} \bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(151)

$$\begin{aligned} & \begin{aligned} Q_{91}\left( x,t\right) =&\bigg [ -\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ] +a_2\bigg [\frac{e^{ic_0(\eta +C)}}{e^{ic_0(\eta +C)}-1}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(152)

$$\begin{aligned} & \begin{aligned} Q_{92}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ] +a_2\bigg [\frac{(\theta _1+\theta _2)e^{\theta _2(\eta +C)}-1}{(\theta _1-\theta _2)e^{\theta _2(\eta +C)}-1}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(153)

$$\begin{aligned} & \begin{aligned} Q_{93}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ] +a_2\bigg [\frac{(\theta _2+\theta _3)e^{\theta _2(\eta +C)}+1}{(\theta _2-\theta _3)e^{\theta _2(\eta +C)}-1}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(154)

$$\begin{aligned} & \begin{aligned} Q_{94}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ] +a_2\bigg [\frac{e^{\theta _2(\eta +C)}+\theta _2-\theta _1}{e^{\theta _2(\eta +C)}-\theta _2-\theta _1}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(155)

$$\begin{aligned} & \begin{aligned} Q_{95}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]+a_2\bigg [\frac{\theta _1 e^{\theta _1(\eta +C)}}{\theta _3 e^{\theta _1(\eta +C)}}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(156)

$$\begin{aligned} & \begin{aligned} Q_{96}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1\bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]+a_2 \bigg [\frac{\theta _3(\eta +C)+2}{\theta _3(\eta +C)}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(157)

$$\begin{aligned} & \begin{aligned} Q_{97}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [\theta _3(\eta +C)\bigg ]+a_2 \bigg [\theta _3(\eta +C)\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(158)

$$\begin{aligned} \begin{aligned} Q_{98}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \bigg [\frac{1}{\theta _3(\eta +C)}\bigg ] +a_2\bigg [\frac{1}{\theta _3(\eta +C)}\bigg ]^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})} \end{aligned} \end{aligned}$$

(159)

$$\begin{aligned} \begin{aligned} Q_{99}\left( x,t\right) =&\bigg [-\frac{(\theta _2+\theta _3)a_2}{\theta _2-\theta _3}+a_1 \tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )+a_2 \bigg (\tan \bigg (\frac{1}{2}\theta _3(\eta +C)\bigg )\bigg )^{2}\bigg ]^{\frac{1}{2n}}e^{\iota (\mu _{1}x-\mu _{2} t+\mu _{3})}. \end{aligned} \end{aligned}$$

(160)

Analysis of the physical implications of the obtained results

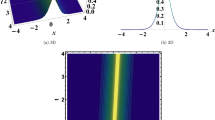
This section provides a concise summary of the outcomes derived in the preceding sections. The theory of periodic and soliton solutions constitutes a fundamental and well-established domain in the modern theory of differential equations. These solutions play a crucial role in the analysis of dynamical systems and find applications across various fields, including mathematical biology, social sciences, and other nonlinear sciences, where phenomena are modeled with diverse parameters. Hence, it is essential to explore the conditions associated with these arbitrary parameters that give rise to periodic wave and soliton solutions. Graphical representations were used to elucidate the physical characteristics of the obtained solutions. In Fig. 1, the 3D and 2D plots illustrate the solution $Q_1(x,t)$, featuring both real and imaginary components. This solution portrays a sub-picosecond shock wave within the intervals $-10\le x \le 10$ and $-5 \le t \le 5$, with the parameter values set as $s_2=-1$, $n=2$, and all other arbitrary parameters set to unity. Figure 2 depicts the 3D and 2D plots of the solution $Q_2(x,t)$, showing both real and imaginary aspects. These graphs illustrate a singular soliton solution within the intervals $-10 \le x \le 20$ and $-10 \le t \le 10$, where the parameter values are specified as $s_2=-1$ and $n=2$, and all other arbitrary parameters are set to unity. Figure 3 displays the profiles of the solution $Q_3(x,t)$, illustrating sub-picosecond singular wave solutions with ranges $-10 \le x \le 20$ and $-10 \le t \le 10$. The parameter values were set as $s_2=-1$ and $n=2$, and all other arbitrary parameters were assigned a value of unity. Figure 4 illustrates the 3D and 2D plots of the solution $Q_4(x,t)$, showing a sub-picosecond bright soliton solution over the spatial and temporal intervals $-10 \le x \le 20$ and $-10 \le t \le 10$. The parameters are specified as $s_2=-1$ and $n=2$, and the remaining units. The plots in Fig. 5 correspond to the solution $Q_6(x,t)$, depicting a double periodic wave solution within the intervals $-10 \le x \le 20$ and $-10 \le t \le 10$. The parameters were set as $s_2=-1$ and $n=2$, and all other parameters were assigned a value of unity. Figure 6 illustrates the periodic wave solutions over the ranges $-10 \le x \le 10$ and $-5 t \le 5$, derived from the solution $Q_{27}(x,t)$. The parameters were set to $n=2,~\theta _2=2$, and all other arbitrary elements were set to unity.

Fig. 1

Profile of sub-pico-second shock wave solution $Q_1(x,t)$ by setting parameters $s_3=\theta _1=\theta _2=\theta _3=a_2=c=1,~n=2$ and $s_2=-1$.

Fig. 2

Profile of singular soliton solution $Q_2(x,t)$ by setting parameters $s_3=\theta _1=\theta _2=\theta _3=a_2=c=1,~n=2$ and $s_2=-1$.

Fig. 3

Profile of sub-pico-second singular soliton waves $Q_3(x,t)$ by setting parameters $s_3=\theta _1=\theta _2=\theta _3=a_2=c=1,~n=2$ and $s_2=-1$.

Fig. 4

Profile of sub-pico-second bright soliton $Q_4(x,t)$ by setting parameters $s_3=\theta _1=\theta _2=\theta _3=a_2=c=1,~n=2$ and $s_2=-1$.

Fig. 5

Profile of double periodic waves $Q_6(x,t)$ by setting parameters $s_3=\theta _1=\theta _2=\theta _3=a_2=c=1,~n=2$ and $s_2=-1$.

Fig. 6

Profile of periodic wave solution $Q_{27}(x,t)$ by setting parameters $a_0=a_2=s_3=\theta _1=\theta _2=\theta _3=\theta _3=c=C=1,~n=2$ and $\theta _2=2$.

Discussion and conclusions

This study explored subpicosecond optical soliton solutions within the TB model. By leveraging advanced techniques, specifically the gJEF method and the $\tan \left( \frac{V(\eta )}{2}\right)$-expansion method, a diverse range of wave solutions, including sub-picosecond shock wave solitons, sub-picosecond optical bright and singular solitons, and double periodic waves, were systematically derived. Distinct from previous works by Yıldırım⁵⁰ and Ghazala and Sayed⁵¹, our results introduce novel solution classes such as shock waves and double periodic wave solutions.

Furthermore, for the sake of novelty, a rigorous exploration of periodic wave solutions for the TB model (1) was undertaken. Nine periodic wave solutions, expressed in terms of Jacobi amplitude symbols and others, were obtained using the $\tan \left( \frac{V(\eta )}{2}\right)$-expansion method. This novel contribution enriches our theoretical understanding of the TB model (1). The outcomes of this study underscore the necessity for a more intricate examination of the model. Future investigations may extend the TB equation relevant to birefringent fibers and Dense Wavelength Division Multiplexing (DWDM) technology, employing robust methodologies such as extended Kudryashov’s methodology, trial equation procedures, and Lie symmetry analysis. The comprehensive findings of these studies will be presented in subsequent publications.