Introduction

The heart is the most vital organ in the human body as it is responsible for supplying blood to the entire body. Among the various heart diseases, CVDs are the most prevalent, and they can lead to sudden and severe health complications, including death1,2. It is typically caused by the accumulation of plaque along the inner walls of the coronary arteries. In severe cases, this build-up of plaque can significantly obstruct blood flow to the heart muscle3. Therefore, early prediction and detection of these conditions are imperative4. The analysis of physiological signals, such as ECG5,6, PCG and EEG7,8 helps to understand various health conditions. Nowadays, machine learning (ML) and deep learning (DL) are the advanced technologies used to detect and classify diseases automatically9,10. Existing works11,12 classified heart disease either by using ECG or PCG alone. Reliance solely on ECG or PCG in the cardiovascular disease classification, particularly in CVD and CAD, poses significant limitations to unique diagnostic insights provided by each modality. Solely reliance on ECG will miss characteristic murmurs associated with aortic stenosis, tricuspid regurgitation, and mitral stenosis, and murmurs associated with complications like valve regurgitation due to ischemic damage. AF, characterized by irregular heart rhythms and the absence of P waves on ECG, is challenging to detect solely with PCG13 due to its focus on heart sounds rather than electrical activity. Similarly, the ischemic changes indicative of IHD, such as ST-segment elevation or depression on ECG, would be overlooked with PCG alone. The ECG captures the electrical activity by which the function of the heart chamber during a heartbeat is analyzed. So, heart diseases that are related to heart muscle functioning and improper electrical activity alone are detected by the ECG. Thus, it could not be able to recognize the valvular heart disorder and the other mechanical irregularities of the heart function. On the other hand, the PCG effectively detects valvular heart diseases along with the disorder that occurs around the heart region but not electrical functioning-based heart diseases. Therefore, in this work, the efficient heart disease detection system is presented by integrating both ECG and PCG signals in this paper. Reference14 proposed the automated cardiac prosthetic valve dysfunction detection model using PCG signals. Although the model demonstrates promising results, its performance exhibits variability in the leave-one-subject-out cross-validation (90.64%),indicates challenges in generalization. Reference15 developed the machine learning models to classify rhythm and morphology problems in 12-lead ECGs. Reference16 utilized ML models to predict CVD by extracting features from ECG and PCG signals using the Convolutional layer-LSTM with ECG and PCG Net. Despite employing a genetic AI algorithm to reduce feature dimensionality, the model’s accuracy was hindered by LSTM’s poor performance with noisy data. Reference17 proposed Dual-Scale Deep Residual Network (DDR-Net) for detecting cardiovascular diseases (CVDs) using both ECG and PCG signals. The study employs the SVM-RFECV method for feature selection.The model is limited to classifying outputs as “normal” or “abnormal,” without identifying specific diseases, which restricts its clinical utility for detailed diagnosis. Additionally, the lack of explicitly addressed preprocessing techniques may reduce the model’s robustness in handling noisy data. Reference18 developed PCTMF-Net for heart sound classification, employing a Multi-Head Transformer Encoder, but faced misclassification issues due to reliance solely on heart sound signals. Reference19 introduced a time-adaptive ECG-driven CVD prediction model using bidirectional LSTM and Short Time Fourier Transform, yet it lacked identification of arrhythmia-related heart diseases. Reference20 proposed a coronary heart disease detection model based on a Hybrid Convolution-Transformer Neural Network (HCTNN) using PCG signals. It combines a pruned Vision Transformer (ViT) for global feature encoding and a CNN for local feature extraction with an adaptive feature fusion module. Though the model achieved an accuracy of 94.24%, it has high computational complexity and preprocessing overhead with CWT spectrograms.21 proposed a tensor decomposition-based model for diagnosing and recognizing heart sounds. Reference22 proposed GAN-LSTM for heart disease detection, achieving high accuracy but sensitive to hyperparameters. Reference23 implemented 1D-CAD CapsNet for coronary artery disease detection, showing effectiveness despite high computation costs. Reference24 developed the Gabor CNN model for the automatic detection of CAD, myocardial infarction, and congestive heart failure. However, it’s important to note that the model required a larger dataset for proper training of the system. Reference25 employed a hybrid CNN-based classification of heartbeats to identify heart disease. The model utilized the DWT to reduce the noise and segment the ECG signal. However, the model had time complexity while training the CNN. Reference26 described the recognition of cardiac abnormalities through the synchronized analysis of ECG and PCG signals. This approach detected the QRS complex using the PTA algorithm. However, during signal synchronization, the misalignment of signals had a detrimental effect on the classification process. Reference27 explored the CNN-based heart sound classification by using the Local Binary and Ternary Pattern features (LBP, LTP). However, the LBP method became complex when dealing with noise, which led to the misclassification of heart sounds. Reference28 explained the detection of coronary artery stenosis by using the ECG and PCG signal with entropy calculation using SVM and XGboost model. The presence of nonstationary data sequences in the sample raised the possibility of overfitting, which could potentially influence the reliability of statistical testing. Reference29 developed an automated 2oo2 safety-related heart health monitoring system.The model addresses challenges like noise interference and equipment malfunctions, ensuring more accurate detection of cardiac abnormalities. In the future, a heart health monitoring system can be incorporated as an extension of the proposed model to enhance robustness and reliability for clinical studies.

Problem statement

The previous work of ECG-PCG-based heart disease detection has some drawbacks, and it is described below,

  • Solely relying on ECG might miss subtle high-frequency murmurs caused by narrowed coronary arteries and lead to missed diagnoses of myocardial ischemia or infarction. similarly depending solely on PCG subtle changes in the electrical activity of the heart are missed and result in incomplete evaluation of heart abnormalities Li et al. (2021)30.

  • For detecting the peak signals, only the signals that meet the amplitude threshold are taken into consideration, while all other signals are disregarded. So, it leads to a loss of information and energy, which might contain valuable data.

  • The heartbeat localization is an important step in classifying heart disease, which provides information about the heart abnormality. Energy-based heartbeat localization has been performed in previous work, which provides irrelevant information about the heart.

The main objective of the proposed methodology is described as,

  • Perform fusion of ECG and PCG signals to capture both mechanical and electrical activity of the heart.

  • Improve the accuracy of peak detection, which acquires valuable information from the signal.

  • Prevent information loss from the signal through Algebraic Integer-quantized Stationary Wavelet Transform (AI-SWT) localization.

  • Improve classification accuracy by selecting highly correlated features using the Heming Wayed Polar Bear Optimization (HeWaPBO) algorithm.

Research novelty

In most of the prevailing works, including19,24,30, either ECG or PCG signal source is adopted for the heart disease classification. The model proposed by Ref.31 classifies cardiovascular valvular diseases into five categories using only the PCG signal. Building upon this, ECG and PCG signals are utilized and fused to categorize multiple heart disorders in the proposed work. Relying solely on PCG hampers the classification of multiple cardiac conditions. The diagnostic approach can be improved by utilizing both modalities for classification. Further, the amplitude threshold used for the peak detection caused signal information loss and resulted in the misclassification of heart diseases. So, the waveform is localized using the improved SWT named AI-SWT to analyze the heartbeat, and the peak signal is detected using the Bayesian decision technique. Moreover, the disease classification in Ref.28 caused an overfitting issue, which affected the data learning and produced incorrect disease classification. To suppress this issue, the CP-SBI method is adopted in the proposed model, which minimizes the spatial dimension of the signal and triggers the neuron’s learning efficiency. Moreover, the selection of significant features and the correlation analysis of fused signals further enhanced the disease classification performance of the proposed methodology.

Methods

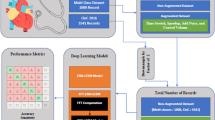
In this section, the CP-SBI-DCNN-based CVD classifier is proposed by using both ECG and PCG signals and is depicted in Fig. 1. The workflow initiates from the accessing of ECG and PCG signals. Then, the ECG signals are pre-processed to remove the signal artifacts and improve the signal quality. Here, the denoising, Baseline wander removal, and Isoelectric line correction are performed to remove the noisy components, discard the baseline deviations, and attain the exact signal amplitudes, respectively. Further, the PCG signal is pre-processed through windowing, variation evaluation, and denoising to retrieve accurate signal information. Thus, the signal discontinuities, signal point variation, and noisy factors are eliminated from the PCG signal. Subsequently, both the pre-processed ECG and PCG signals are fused for analyzing the waves, heartbeats, and signal features in time series. From the fused signal, the wave detection is carried out by using PTA to analyze the ventricular depolarization of the heart. Then, the waveforms of Systole, Diastole, S1, and S2 are localized by examining the signal patterns using the proposed AI-SWT. Here, the complexity of analyzing patterns while using SWT is resolved by introducing the AI method along with the SWT. Afterward, the heart rate is extracted by using the Sum slope technique from the localized waveforms to determine the signal amplitude. At the same time, the peak signal of the heart rate is identified by employing the Bayesian decision method.Thereafter, both the extracted heart rate and the detected peak signals are given to the clustering process, which groups the normal and abnormal signal characteristics using the LK-DBSCAN algorithm. Here, the LK technique is included in the DBSCAN to properly cluster the similar dense signal values. Further, the features are extracted from the abnormal signal cluster and then the optimal features from the extracted features are selected by using the HeWaBPO algorithm. Here, the HeWa measure is utilized for calculating the bear movement accurately without scale invariance during exploration. Thus, the optimal solution is attained for feature selection. Meanwhile, the correlation signal patterns between the fused signals are identified by formulating the correlation matrix. Finally, the correlated patterns, extracted heart rate, and the selected abnormal signal features are fed to the introduced CP-SBI-DCNN to categorize the multiple classes, such as AV, TV, MV PV, AF, and Ischemic of the heart disease.

Fig. 1
figure 1

Block diagram of the multi-class heart disease classification model by utilizing Noise Filtering (NF), Moving Average Filter (MAF), Pan Tompkins Algorithm (PTA), Algebraic Integer quantized Stationary Wavelet Transform (AI-SWT), Low-rank Kernelized Density-Based Spatial Clustering of Applications with Noise (LK-DBSCAN), Heming Wayed Polar Bear Optimization (HeWaPBO), and C squared Pool Sign BI-power-activated Deep Convolutional Neural Network (CP-SBI-DCNN) techniques.

Full size image

Signal fusion

The fusion is accomplished by identifying common reference points, such as R peaks in the ECG signal and the onset of heart sounds in the PCG signal, to establish a consistent time scale for both signals followed by feature concatenation. In this phase, both pre-processed ECG \((\chi _p)\) and PCG \((\beta _p)\) signals are fused based on the time series of the signals, waves, and heartbeats of the ECG and PCG signals. Then, the fused signal \(S_F(t)\) is determined by,

$$\begin{aligned} S_F(t)=\chi _p(PQRST)+\beta _p(S_1,S_2,S_3,S_4)+\gamma (\chi _p,\beta _p) \end{aligned}$$
(1)

Here, PQRST represents the waves present in the ECG signal,\(S_1,S_2,S_3,S_4\) denotes the recorded heartbeats in \((\beta _p)\) , and \(\gamma\) denotes the other components present in both \((\beta _p)\),\((\chi _p)\) signals.

Wave detection

In this phase, \(S_F(t)\) input signals undergo wave detection, particularly focusing on identifying the QRS complex using the Pan Tompkins Algorithm (PTA), which signifies the ventricular depolarization in the heart. It is computed as follows,

$$\begin{aligned} W(I)=\frac{\lambda (T)}{NS} \end{aligned}$$
(2)

Here, \(\lambda\) denotes the windowing function, which is multiplied by the signal waveform feature (T) and NS represents the number of samples in the width of the integration window.

R peak detection

After the window integration, two thresholds are chosen: a higher threshold is employed to detect the R peaks, and a lower threshold is set for a search-back process. The R peak detection rate \(\Re\) is determined by,

$$\begin{aligned} \Re =\frac{F_p+D_f}{NR} \end{aligned}$$
(3)

Here,\(F_p\) represents the false peak detection, \(D_f\) denotes the failure detection, and NR is the total number of R peaks. Finally, R peak detected signals \((\Re _{sig})\) are obtained.

Localization

Following the wave detection process, the Systole, Diastole, S1, and S2 waveforms are precisely located from the \((\Re _{sig})\) signal by using the AI-SWT technique to identify the pattern of the signal. The AI-SWT solves the shift-invariance and non-redundancy issues in the signal. The conventional SWT calculated the length of the signal by calculating the length of both the approximation and detailed coefficients at each level of analysis32. However, the random length calculation leads to an increase in the complexity of the process. Therefore, Algebraic Integer Quantization is introduced to calculate the approximation and detail coefficients. The AI-SWT is derived by,

$$\begin{aligned} SW(\Re _{sig})=TF(\Re _{sig}*L_{sig}*WT) \end{aligned}$$
(4)

Where, \(SW(\Re _{sig})\) represents the wavelet transformation of the signal, TF denotes the transformation function, \(L_{sig}\) represents the length of the signal at each level, and WT is the applied wavelet. The Length of the signal is determined by,

$$\begin{aligned} L_{sig}=A_K *d_k \end{aligned}$$
(5)

Where, \(A_k\) represents the approximate coefficient of the signal and \(d_K\) represents the detail coefficient of the signal. The heart sound localized signals\((\lambda _l)\) are obtained, and it is expressed by,

$$\begin{aligned} \lambda _l=(\lambda _{S1},\lambda _{S2},\lambda _{SS},\lambda _{DS}) \end{aligned}$$
(6)

Where, \(\lambda _{S1},\lambda _{S2},\lambda _{SS},\lambda _{DS}\) represents the S1, S2, Systole, and Diastole heart sound localized signal, respectively.

Consider the two valvular conditions, AV and PV. In Aortic Valve (AV) illness, increasing pressure on the left side of the heart causes ECG alterations such as left ventricular hypertrophy or left atrial enlargement. Pulmonary Valve (PV) disease affects the right side of the heart and can induce right ventricular overload and right atrial hypertrophy, which can influence the PCG signal. This physiological variance is reflected in the ECG and PCG signals’ waveform timing (e.g., QRS complex or heart sounds like S1, S2). The novel heartbeat localization technique, AI-SWT is implemented to analyze these signal deviations for efficient classification using the CP-SBI-DCNN classifier.

Heart rate extraction

After localizing the heart sounds \((\lambda _l)\), the heart rate can be extracted using the Sum Slope technique. This method involves analyzing the signal to determine the rate of change in amplitude, often by measuring the slope of certain features related to the heartbeats. The heart rate \(H_{RE}\) is extracted by,

$$\begin{aligned} H_{RE}=\Gamma (\lambda _l) \Gamma =\sum \limits _{q=w}^n\Delta (\lambda _l)_q \end{aligned}$$
(7)

Where, \(\Gamma\) represents the Sum Slope Function,\(\Delta (\lambda _l)_q\) represents the slope of the signal, and w represents the window of the signal.

Peak signal detection

The peak of the signal is detected from \((\lambda _l)\) by employing the Bayesian decision technique. Peak detection involves the identification of the positions of peaks within a signal. The \(S_p\) number of peak detected signals \(S_{peak}\) is obtained as,

$$\begin{aligned} s_{peak}=(S_1,S_2,S_3,...S_p) \end{aligned}$$
(8)

where, \((S_1,S_2,S_3,...S_p)\) denotes the p number of peak signals present in the localized heartbeat sound.

Clustering

In the clustering phase, both the \(H_{RE}\) and \(S_{peak}\) are clustered into two distinct groups: normal, and abnormal using the Low-rank Kernelized Density-Based Spatial Clustering of Applications with Noise (LK-DBSCAN) technique. The algorithm operates by identifying regions of high data point density and extracting neighbouring points within a certain distance. This process is repeated iteratively until all the relevant neighbourhood points are grouped together, effectively forming distinct clusters33. The LK-DBSCAN-based clustering model initializes the data points of the signal and is expressed by,

$$\begin{aligned} DP(H_{RE},S_{peak})=({D_1,D_2,D_3,...D_{np}}) \end{aligned}$$
(9)

Where,np represents the number of data points in the signal. At first, a randomly selected data point is referred to as an unvisited data point \((DP)_\upsilon\). Then, find the all neighboring points by,

$$\begin{aligned} ND=\varepsilon (DP(H_{RE}),S_{peak}) \varepsilon =\sum \limits _{j=1}^{np}\phi _jK_{pq} \end{aligned}$$
(10)

Here, ND represents the neighboring data points, \(\varepsilon\) represents the radius of the particular density of the data point area, Meanwhile, \(\varepsilon\) is estimated by multiplying the \(\phi _j\) (weight parameter) with a low-rank kernel matrix \(K_{pq}\) , which is determined by,

$$\begin{aligned} K_{pq}=K(y_i,y_j) \end{aligned}$$
(11)

Here \(y_i,y_j\) represents the data point coordinates. Next, the minimum number of neighboring points Minpts is defined by,

$$\begin{aligned} \textit{Minpts}=\sum \limits _{j=1}^{np}\rho _j \end{aligned}$$
(12)

Where,\(\rho _j\) represents the \(j^{th}\)value of the density measured in a specific data point. The distance \((\textit{dist})\) between the neighboring points (u,v) is calculated by,

$$\begin{aligned} \textit{dist}=\sum \limits _{j=1}^{np}(u_j-v_j)^2 \end{aligned}$$
(13)

Where,\(u_j\) and \(v_j\) indicate the two neighbouring data points having j density value in the fused signal. After that, when the distance between the two neighbouring points among the fused ECG and PCG signal is equal or less than \(\varepsilon\) , these points are considered as neighbours; otherwise, it is denoted as noise. If the visited data point is not assigned to the cluster, then it is created in the new cluster. This process is repeated until all visited data points move on to the cluster or noise. Finally, the data points of the signals are clustered \(DP_{cluster}\) into normal \((N_{signal})\) and abnormal \((CD_{signal})\) signals. Then, it is expressed as,

$$\begin{aligned} DP_{cluster}=(N_{sig},DP_{sig}) \end{aligned}$$
(14)

The Low-rank Kernelized Density-Based Spatial Clustering (LK-DBSC) plays a pivotal role in distinguishing between normal and abnormal signals, which is critical for effective cardiovascular disease classification. Here’s a detailed clarification of its role and impact:

  • Separation of Normal and Abnormal Signals: LK-DBSC is employed to analyze the density and spatial distribution of signal data points. By utilizing kernelized techniques, it captures non-linear relationships in the feature space, enabling more precise clustering of signals. Low-rank approximations reduce computational complexity while preserving essential features, enhancing the clustering process.

  • Noise Reduction and Signal Purification: This method effectively isolates outliers and noise within the signal data, which often interfere with accurate classification. The separation ensures that only high-quality signal features are used for downstream processing.

  • Feature Enhancement for Classification: By segregating normal and abnormal signals, LK-DBSC ensures that the subsequent classification models operate on more homogeneous and well-defined data groups. This separation improves the accuracy of identifying specific disease categories, such as valvular diseases, atrial fibrillation, and coronary artery diseases.

  • Impact on Overall Performance: Improved classification accuracy, efficiency in processing, enhanced interpretability

Feature extraction

From the \((CD_{sig})\) signals, important features are extracted. Here, the PCG signal features, such as Mean Absolute Deviation (MAD), Inter Quartile Range (IQR), skewness, Shannon’s entropy, maximum frequency, dynamic range, total harmonic distortion, maximum amplitude, power, mean, variance, root mean square error, bandwidth, mid-frequency, average frequency, Cepstrum peak amplitude, Mel-frequency cepstral coefficients (MFCCs), and kurtosis are extracted from the signals. These features provide valuable information about the characteristics of the phonocardiogram signals. Then, the ECG signal features like interval measurement, morphology features, standard deviation, mean, correlation, and temporal features were also extracted.

Feature selection

From the extracted features \(( \vartheta )\), the important features are selected by using the HeWaPBO algorithm. The conventional PBO algorithm is based on the Polar Bear’s (PB) food searching and hunting behaviour. This algorithm effectively selects the features, and the bear motion is calculated based on the Euclidean distance measure, which causes a sudden change in the direction of the bear and leads to a scale-invariant problem. To address this issue, the model includes the Heming Way distance calculation instead of the Euclidean distance calculation, which solves the sudden change in the direction issue. The HeWaPBO is derived by, The population of the PB (features \(( \vartheta )\) ) is initialized and the optimum solution is found in the global and local search space. The population of a number of PB \((\partial\)B) is expressed by,

$$\begin{aligned} \partial B=(\partial B_1,\partial B_2,......\partial B_s) \end{aligned}$$
(15)

The PB’s nature to glide on an iceberg in the exploration of food in the global search space is expressed by,

$$\begin{aligned} \partial B_M=\partial B^{I}_{s,r}+\tau *\gamma _1+\gamma _2 \end{aligned}$$
(16)

Where, \(\partial B_M\) is the movement of the PB,\(\partial B^{I}_{s,r}\) represents the \(s^{th}\) PB in the \(r^{th}\) coordinate within the \(I^{th}\) iteration,\(\tau\) denotes the distance between the current PB and the optimum PB, and \(\gamma _1,\gamma _2\) represents the random number. The distance \(\tau\) is calculated by using the Heming Way distance calculation, and it is determined by,

$$\begin{aligned} \tau =\sum \limits _{r=1}^{n+1}\sigma (\partial B_{s,r},\partial B_{b,r}) \end{aligned}$$
(17)

Here, \(\partial B_{b,r}\) represents the best PB, \(\sigma\) represents the Hemingway function parameter, and n+1 represents the last coordinate of the position of the bear. In the local search space, the polar bears are surrounded by prey and it is characterized by two parameters, such as the distance vision parameter and the angle of tumbling \((\phi )\) parameter. The distance vision radius is determined by,

$$\begin{aligned} R=4vcos(\phi )sin(\phi ) \end{aligned}$$
(18)

The local search space of each PB is identified by using the vision radius, and the position is updated by,

$$\begin{aligned} \partial B^{new}_s=\partial B^{actual}_s \pm \left[ \sum \limits _{g=1}^s R sin(\phi _g)+R cos(\phi _g)\right] \end{aligned}$$
(19)

Where, \((\partial B^{new}_s)\) represents the new position of the bear, \((\partial B^{actual}_s)\) denotes the actual position of the bear, and g represents the number of bears. Then, the fitness (high classification accuracy) of the population \(\textit{fit}(\partial B)\) is defined as,

$$\begin{aligned} \textit{fit}(\partial B)=\textit{acc}_{max} \end{aligned}$$
(20)

Here, \(\textit{acc}_{max}\) denotes the maximum classification accuracy. The population growth of the bear depends on the reproduction of the best and starvation of the worst among the population. The dynamic population is controlled based on the random constant \(\psi\), and it is expressed by,

$$\begin{aligned} \left\{ \begin{array}{ll} \partial B_{Re\text {production}} & \psi > 0.75 \\ \partial B_{\text {Death}} & \psi < 0.25 \\ \end{array} \right\} . \end{aligned}$$
(21)

Where, \(\partial B_{Re\text {production}}\) denotes the reproduction rate of the bear, and \(\partial B_{\text {Death}}\) is the death rate of the bear. The newly reproduced population \(\partial B_{Re\text {p}}\) is determined by,

$$\begin{aligned} \partial B_{Re\text {p}}=\frac{ \partial B_{\text {best}}+\partial B_{\text {s}}}{2} \end{aligned}$$
(22)

Here,\(\partial B_{\text {s}}\) implies the \(s^{th}\) PB and \(\partial B_{\text {best}}\) denotes the best polar bear in the \(I^{th}\) iteration. This process is reiterated until the best solution is achieved. After executing all steps,17 features are chosen as the optimum feature \((\vartheta _\textit{best})\) based on fitness function. The pseudocode for HeWaPBO algorithm is given in algorithm 1.

Algorithm 1
figure a

.

Full size image

In the proposed model, the HeWaPBO algorithm uses Hamming weighted distance instead of Euclidean distance. The Hamming distance is scale-invariant and improves feature selection by avoiding erratic movements and local traps in the optimization process. It enhances the stability and efficiency of the model by accurately selecting critical features from ECG and PCG signals. The key hyperparameters of PBO are a) Population size-50 b) Number of iterations-100. c) Learning parameters: Exploration parameter-0.8 and Exploitation parameter-0.5 d)Hamming distance weight-0.5.

Trial-and-error experiments were conducted to determine the optimal values for these parameters. Various population sizes (30, 40,80), iterations (50, 75,120), exploration parameters (0.2, 0.5, 1), exploitation parameters (0.2, 0.5, 0.8), and Hamming distance weights (0.4, 0.6, 0.8) were tested. Among these, the above-mentioned values provided the best solution for the model’s performance.

Correlation matrix generation

Generating a correlation matrix from \(S_F(t)\) is a common technique to identify patterns and relationships within the data. Each entry in the correlation matrix represents the correlation coefficient between two variables. The variables are referred to as different data points or time series values within the fused signal. The correlation coefficient \(\upsilon (S_F(t))\) is determined by,

$$\begin{aligned} \upsilon (S_F(t)) = \frac{N\sum (bc) - (\sum b)(\sum c)}{\sqrt{[N\sum b^2 - (\sum b)^2][N\sum c^2 - (\sum c)^2]}} \end{aligned}$$
(23)

Where, N denotes the number of data points in \((S_F(t))\) and b,c is the data point coordinate of \((S_F(t))\) . Based on \(\upsilon (S_F(t))\), the nc number of correlation matrices \((CR_{b,c})\) is generated, and it is defined by,

$$\begin{aligned} \begin{aligned} (CR_{b,c}) = \begin{bmatrix} CR_1 & CR_2 & CR_3\\ CR_4 & CR_5 & CR_6\\ CR_7 & \dots & CR_{nc} \end{bmatrix} \end{aligned} \end{aligned}$$
(24)

Classification

In this section,\((\vartheta _\textit{best})\) ,(\(CR_{b,c}\)) ,and \((H_{RE})\) are inputted to the CP-SBI-DCNN classifier for classifying the types of CVDs into Valvular diseases {AV, TV, MV, PV}, Arrhythmia AF, and CAD {Ischemic heart disorder}. The traditional DCNN effectively minimized computation while achieving accurate disease classification within the extensive dataset34. However, the DCNN model required more time due to maxpool operation. To overcome this issue, the proposed model modified the max pool layer into a Csquared pool layer and also included the Sign BI-Power activation function to trigger the neurons more efficiently.The Pseudocode for heart diseases classification is given in algorithm 2.

Algorithm 2
figure b

.

Full size image

The input layer in a neural network receives the best features of the abnormal signal \((\vartheta _\textit{best})\), the correlation matrix of the fused ECG and PCG signal (\(CR_{b,c}\)), and the heart rate that is analyzed from the localized waveforms of the fused signal \((H_{RE})\) . Then, the input layer transmits this input to the convolutional layer (CL). Here, the parameters, such as weights, biases, the maximum number of iterations, and the number of input layers, are initialized. The input layer is responsible for learning and extracting relevant signal features through a set of convolutional filters.

Csquared pooling layer

The Csquared pooling layer performed the downsampling operation. It reduces the spatial dimensions of the feature maps, helping the neural network focus on the most important information while reducing the computational load. The Csquared pooling layer output \((CS_L)\) is defined by,

$$\begin{aligned} CS_L=\Phi [CL*\omega *bs] \end{aligned}$$
(25)

Here,\(\Phi\) represents the Csquared pooling operation. The spatial dimension is reduced by using the flattening operation\((FL_{op})\) , and it is expressed by,

$$\begin{aligned} FL_{op}=FL(CS_L) \end{aligned}$$
(26)

Output layer

The output layer executes the final classification based on the Sign BI- Power activation function, and it is expressed by,

$$Op = \bar{\lambda} \left[ {FC_{L} } \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \bar{\lambda} \left( {FC_{L} } \right) = \frac{1}{2}sig^{r} \left( {FC_{L} } \right) + \frac{1}{2}sig^{r} \left( {FC_{L} } \right)$$
(27)

Where \(\bar{\lambda}\)represents the Sign BI-Power activation function, and \(sig^r\) represents the function parameter. Finally, this output classified both ECG-PCG signals into six classes, such as (AV), (TV), (MV), (PV), (AF), and Ischemic heart disorder.

Results and discussion

Database description

The PCG signals are considered from the CirCor DigiScope Phonocardiogram Dataset35 and ECG signals from PTB-XL36. For effective validation of the proposed model, the other dataset sources related to the heart disease classes are collected from the openly available Physionet database. This database also consists of six types of heart disease classes: AV, TV, MV, PV, AF, and Ischemic. In this work, the performance of the proposed ECG-PCG-based multi-classifier for the classification of heart diseases are presented.

Fig. 2
figure 2

Peak and heart rate extraction from ECG and PCG signals.

Full size image
Fig. 3
figure 3

(a) Cross-validation of the proposed model (b) ROC curve analysis of the CP-SBI-DCNN model.

Full size image

Figure 2 depicts the ECG and PCG signals and respective waveforms obtained during the experiment.The cross-validation based on K-Fold data splitting for the proposed classifier is represented in Fig. 3a. The higher accuracy attained for both the training and validation by the proposed model depicts its learning tendency over different data values. Figure 3b illustrates the Receiver Operating Characteristic Curve (ROC) analysis for the proposed CP-SBI-DCNN model. It has a high TPR of 0.96 and maintains a low FPR of 0.01. This substantiates its effectiveness as a superior classification model for heart disease detection. Table 1 provides the evaluation statistics of the proposed model for the heart disease classes.

Table 1 Statistics of the proposed CP-SBI-DCNN model.
Full size table

Discussions

Figure 4a shows the performance analysis of the proposed CP-SBI-DCNN and existing models, such as DCNN, CNN, RBN, and DNN. The computation details of the used metrics for the performance evaluation are listed by li et al.[16].The average classification metrics are accuracy of 97%, precision of 95%, recall of 96%, F-measure of 96%, and sensitivity of 98%. For analysis, the proposed classifier named CP-SBI-DCNN is compared with the simple relevant existing methods, such as Deep Convolutional Neural Network (DCNN), Convolutional neural Network (CNN), Radial Basis Neural Network (RBN), and Deep Neural Network (DNN). However, the existing methods attained comparatively low accuracy, precision, recall, F-Measure, and sensitivity in the average of 89%, 86%, 87%, 87%, and 96%. The model is a lesser error-prone model as it attains a minimal error rate of 0.0307. This is because of fusing both the ECG and PCG signals and performing careful pre-processing and heartbeat analysis by the proposed method. Figure 4b and c comparative analysis of the proposed model with the existing techniques with respect to clustering time.

Fig. 4
figure 4

(a) Performance analysis of the proposed CP-SBI-DCNN (b) Comparision analysis of FPR vs FNR (c) Comparative analysis of the proposed LK-DBSCAN.

Full size image

Therefore, the CP-SBI-DCNN achieved a high TPR of 0.966, and TNR of 0.988. Further, the model obtained a low False Positive Rate (FPR) of 0.011 and FNR of 0.033, which shows that the proposed model classified the disease accurately. Meanwhile, the existing techniques obtained an average TPR of 0.87 and TNR of 0.96, which is relatively lower than the proposed technique. These existing techniques also attained a higher average FPR of 0.03 and FNR of 0.12. As the correlation of two different signals, Heartbeat rate, and optimal features of abnormal signal are considered, the proposed model attained enhanced performance over the conventional approaches. However, the aforementioned factors were not focused on by the existing methods, thus obtaining lower performance when compared to the proposed technique

The utilization of the LK function for effectively grouping the low-density data points of the signal prevents biased clustering. Thus, the proposed algorithm efficiently categorizes signals into normal and abnormal groups based on high-density data points. So, the proposed algorithm consumed 1349 ms for the clustering signal. In the meantime, the existing DBSCAN, K-Means, FCM, and PAM consumed 1882ms, 2505ms, 2914ms, and 3146ms, respectively, which is more than the proposed algorithm. The lack of analysis of the low-density data points and the inadequate signal analysis before the clustering in the existing methods degrades their clustering performance. Table 2 analyzes the performance of the proposed classifier regarding statistical measures, such as Variance (Var) and Standard Deviation (SD) for varying epochs. Here, the proposed model attained a minimum Var of 0.03 and SD of 0.16 compared to existing methods.

Table 2 Statistical analysis of the proposed classifier.
Full size table

The validation process in the proposed model employs a rigorous approach through 5-fold cross-validation, ensuring that the model is evaluated on diverse subsets of the data to minimize bias and overfitting. Additionally, performance analysis using statistical measures such as Variance (Var) and Standard Deviation (SD) for varying epochs demonstrates the model’s stability and reliability. The proposed model achieved a minimal Var of 0.03 and SD of 0.16, outperforming existing methods. These metrics highlight the robustness of the validation method.

Table 3 gives the comparative analysis of proposed model.

Table 3 Comparative analysis of the proposed LK-DBSCAN.
Full size table

LK-DBSCAN exhibits superior performance with minimal RMSE (0.35341), MSE (0.12497), and MAE (0.15497) compared to existing algorithms. Table 4 presents a comparative analysis of the proposed multi-heart disease classification system utilizing the CP-SBI-DCNN classifier against related approaches.

Table 4 Comparison analysis with state-of-art approaches.
Full size table

This fusion enhances the depth of information extracted from both signals, capturing complementary aspects of heart function. The correlation matrix, by quantifying the relationship between ECG and PCG signals, provides valuable insights into their interdependencies, aiding in feature extraction and enhancing the model’s discriminative power. Consequently, the CP-SBI-DCNN classifier receives a refined input, enabling a more accurate classification of heart diseases. This integration of signal fusion and correlation matrix analysis not only optimizes the utilization of available data but also improves the model’s robustness and generalization capabilities. Overall, the incorporation of these techniques underscores the sophistication and effectiveness of the proposed multi-heart disease classification system, offering superior performance compared to existing methods. The challenges encountered during the experiment are: (a) The leftover noise from outside factors (such as patient movement, ambient noise, or inaccurate sensors). (b) Variation in ECG and PCG signal properties brought on by age, gender, body composition, and comorbidities. The proposed work can be extended by incorporating additional biomarkers such as biochemical biomarkers such as Troponin and Lipid profiles to improve categorization and diagnostics. Furthermore, investigation using advanced neural networks can be inculcated to make the model more clinically applicable.

Conclusion

This study introduced a comprehensive approach leveraging novel methodologies, such as CP-SBI-DCNN, Bayesian distribution techniques, AI-SWT, and HeWaPBO algorithm for accurate classification and peak detection in cardiovascular diseases (CVDs). Irrespective of the previous works, the fusion of ECG and PCG signals, proper pre-processing, the localization of waveforms, and the clustering of signals enhanced the effectiveness of the proposed heart disease detection system. The usage of the Bayesian technique and AI-SWT localization method returned the peak signal identification and also tackled the loss of signal information respectively, which was noticed in the previous works. Furthermore, the correlation matrix analysis of the fused ECG and PCG signals significantly enhanced the accuracy of CVD classification, such as AV, PV, MV, TV, Ischemic, and AF, thus addressing a crucial gap in current diagnostic approaches. The utilization of the HeWaPBO algorithm optimized the feature selection, thus improving the classification performance. Through the integration of deep learning and critical signal information, a remarkable accuracy of 97% and a minimal error rate of 0.037 were achieved by the proposed model. Therefore, an enhanced system for the multi-class heart disease classification was provided by the proposed methodology.