Hierarchical multi step Gray Wolf optimization algorithm for energy systems optimization

Abstract

Gray Wolf Optimization (GWO), inspired by the social hierarchy and cooperative hunting behavior of gray wolves, is a widely used metaheuristic algorithm for solving complex optimization problems in various domains, including engineering design, image processing, and machine learning. However, standard GWO can suffer from premature convergence and sensitivity to parameter settings. To address these limitations, this paper introduces the Hierarchical Multi-Step Gray Wolf Optimization (HMS-GWO) algorithm. HMS-GWO incorporates a novel hierarchical decision-making framework that more closely mimics the observed hierarchical behavior of wolf packs, enabling each wolf type (Alpha, Beta, Delta, and Omega) to execute a structured multi-step search process. This hierarchical approach enhances exploration and exploitation, improves solution diversity, and prevents stagnation. The performance of HMS-GWO is evaluated on a benchmark suite of 23 functions, showing a 99% accuracy, with a computational time of 3 s and a stability score of 0.9. Compared to other advanced optimization techniques such as standard GA, PSO, MMSCC-GWO, WCA, and CCS-GWO, HMS-GWO demonstrates significantly better performance, including faster convergence and improved solution accuracy. While standard GWO suffers from premature convergence, HMS-GWO mitigates this issue by employing a multi-step search process and better solution diversity. These results confirm that HMS-GWO outperforms other techniques in terms of both convergence speed and solution quality, making it a promising approach for solving complex optimization problems across various domains with enhanced robustness and efficiency.

Introduction

Meta-heuristic algorithms (MHA) represent sophisticated methods that systematically investigate the search space of optimization problems, aiming to discover near-optimal solutions¹. These algorithms are broadly classified into two categories: local search techniques (LST) and population-based techniques (PBT)^2,3. Furthermore, they can be categorized based on their foundational concepts, such as evolutionary, physical, chemical, human-based, and swarm intelligence methodologies^4,5. Local search techniques (LST) initiate with an initial solution and iteratively refine it by examining neighboring solutions. This process continues either until a predefined number of iterations is completed or the algorithm converges to a local optimal solution. Notable examples of local search algorithms include simulated annealing⁶, tabu search⁷, greedy randomized adaptive search procedure (GRASP)⁸, variable neighborhood search⁹, iterated local search¹¹, β-hill climbing¹², and the vortex search technique¹³. Evolutionary-based techniques, a subset of population-based techniques (PBT), involve the initial generation of a population of solutions, which are progressively improved through iterative processes such as reproduction, mutation, and natural selection. Examples of these techniques include the genetic algorithm¹⁴, evolutionary programming¹⁵, genetic programming¹⁶, differential evolution¹⁷, biogeography-based optimization¹⁸, and probability-based incremental learning (PBIL)¹⁹. Physically- and chemically-inspired techniques derive their principles from physical laws and chemical interactions. Among these are methods such as plasma generation optimization²⁰, ray optimization²¹, solar system algorithm²², equilibrium optimizer²³, gravitational search algorithm²⁴, billiards-inspired optimization²⁵, Henry gas solubility optimization²⁶, simulated annealing⁶, vortex search algorithm¹², and chemical reaction optimization²⁷. Social or human-inspired techniques are largely modeled after societal behaviors and human actions. Notable examples include harmony search²⁸, brainstorm optimization²⁹, heap-based optimizer³⁰, teaching-learning-based optimization³¹, political optimizer³², Ali Baba and the forty thieves algorithm³³, group teaching optimization algorithm³⁴, Ebola optimization search algorithm³⁵, football game-inspired algorithm³⁶, coronavirus herd immunity optimizer³⁷, arithmetic optimization algorithm³⁸, stock exchange trading optimization³⁹, and poor and rich optimization. Swarm intelligence (SI) algorithms are often modeled after the collective behaviors found in various animal species, such as birds, frogs, bats, rats, bees, ants, and other organisms⁴⁰. These algorithms typically replicate the process by which swarms search for food, with individual members relying on their interactions with each other or indirect environmental cues (known as stigmergy) to guide the search⁴¹. This leads to a self-organizing system where cooperation occurs without central control. The algorithm usually begins with an initial swarm of potential solutions, which can be categorized into leaders and followers. The leaders guide the search, while the followers adjust their positions based on the leaders’ movements. Through these interactions, the swarm moves collectively toward finding an optimal solution. The most widely used swarm intelligence (SI) algorithms include Ant Colony Optimization⁴², Particle Swarm Optimization⁴³, Krill Herd Optimization⁴⁴, Cuckoo Search⁴⁵, Firefly Algorithm⁴⁶, White Shark Optimizer⁴⁷, Chicken Swarm Optimization⁴⁹, Snake Optimizer⁵⁰, Ant Lion Optimizer⁵¹, Elephant Herding Optimization⁵², Sparrow Search Algorithm⁵³, Horse Herd Optimization⁵⁴, Dragonfly Algorithm⁵⁵, Moth-Flame Optimization⁵⁶, Whale Optimization Algorithm⁵⁷, Komodo Mlipir Algorithm⁵⁸, Chimp Optimization Algorithm⁵⁹, Dwarf Mongoose Optimization Algorithm⁶⁰, Lemurs Optimizer⁶¹, and Grey Wolf Optimizer (GWO)⁶², along with many other SI-based techniques. The fastest-growing SI algorithm, the Grey Wolf Optimizer (GWO), was presented by Mirjalili et al.⁶³, to mimic the hunting habits of natural grey pack populations⁶⁴. Because of its many remarkable qualities, which include flexibility, soundness and completeness, memory lessness, derivative freedom, parameter and derivative freedom, and ease of adaptation, the GWO is a very potent optimizer. When the GWO first begins searching, it focuses heavily on the exploration phase. However, throughout the final run, it gradually shifts the positions of the top three leaders to give the exploitation phase more emphasis. As a result, GWO can handle many optimization issues from several research domains, including image processing, networking and communication, engineering, and more⁶⁵. Much work has been done on the core architecture of the Grey Wolf Optimizer (GWO) to address the intricate search space properties of real-world and combinatorial optimization problems, especially those with highly limited, non-convex, and nonlinear features. It can now successfully handle scenarios with severe constraints and multi-objective issues thanks to these enhancements. In addition, GWO has been improved by adding components from several optimization techniques to improve its efficiency. Hybridization with additional optimization algorithms has also been used to improve the quality of GWO-generated solutions by striking a balance between exploration and exploitation capabilities. Several examples of GWO have been proposed in the literature, and each one is appropriate for a particular use in research^65,66,67,68. The Grey Wolf Optimizer (GWO) begins by initializing a random population of grey wolves, which are organized into four hierarchical tiers: Alpha, Beta, Delta, and Omega. These tiers reflect the wolves’ roles within the hunting process, with the Alpha being the best solution, followed by the Beta and Delta wolves. The Omega wolves serve as the followers, guided by their attraction to the top three wolves—Alpha, Beta, and Delta. In the optimization phase, GWO calculates the distances between the Omega wolves and the leading wolves, using this information to adjust the wolves’ positions through behaviors such as tracking, encircling, and chasing prey. The algorithm leverages two key parameters to maintain a balance between exploration (searching for new solutions) and exploitation (refining existing solutions), ensuring an effective optimization process⁶⁴. In recent years, the Grey Wolf Optimizer (GWO) has garnered considerable interest from researchers, with its applications spanning a wide range of optimization problems in fields such as science, engineering, and industry. However, GWO has certain limitations, particularly its tendency to become stagnant during the exploitation phase and its slow convergence rate in the later stages of optimization. To address these issues, we revisited the natural hunting behaviors of grey wolves. In real-world scenarios, frequent interactions between the leader wolves and the Omega wolves occur throughout the hunting process, a behavior known as “judging prey.” This interaction can be leveraged to enhance GWO’s performance. Building on this observation, we propose incorporating this behavior into the GWO framework, leading to the development of an improved optimization algorithm called the Hierarchical Multi-Step Grey Wolf Optimizer (HMS-GWO).

The study presents a novel approach for system identification of small-scale fixed-wing Unmanned Aerial Vehicles (UAVs) using metaheuristic optimization techniques¹⁰⁷. Thirteen widely used optimization algorithms are evaluated over ten independent runs, with their performance statistically ranked using Friedman’s test based on fitness values¹⁰⁸. The results reveal the superior performance of the L-SHADE algorithm, achieving mean R-squared errors of 0.5465 and 0.0487 for longitudinal and lateral dynamics, respectively, surpassing other algorithms¹⁰⁹. Additionally, the study explores the application of the Grey Wolf Optimizer (GWO), Stochastic Fractal Search (SFS), and Adaptive Differential Evolution with Optional External Archive (JADE) for optimizing planar frames under AISC-LRFD standards¹¹⁰. It also introduces the 2-Archive Multi-Objective Cuckoo Search (MOCS2arc) algorithm, an enhanced version of the Multi-Objective Cuckoo Search (MOCS), designed to optimize eight truss structures and six ZDT test functions while balancing mass and compliance. MOCS2arc incorporates a dual-archive strategy to enhance solution diversity and optimization efficiency¹¹¹. Comparative evaluations against MOSCA, MODA, MOWHO, MOMFO, MOMPA, NSGA-II, DEMO, and MOCS demonstrate MOCS2arc’s dominance in generating diverse and optimal solutions, supported by Friedman’s and Wilcoxon’s statistical tests. Beyond UAV system identification, the study proposes a meta-learning-based alternating minimization (MLAM) technique for addressing nonconvex optimization problems, particularly bilinear inverse and nonlinear Gaussian mixture model challenges. Unlike traditional alternating minimization (AM) strategies, MLAM employs meta-learning to adaptively minimize global losses, enhancing performance while maintaining algorithmic interpretability. In the context of network function virtualization (NFV), the study introduces an SFC deployment optimization (SFCDO) algorithm based on breadth-first search (BFS), which optimizes virtual network function (VNF) performance¹¹¹. SFCDO prioritizes minimal-hop paths to improve network resource utilization and reduce end-to-end latency, outperforming greedy and simulated annealing algorithms. Another key contribution is a mobile robot-based thermal comfort monitoring system for indoor environments. By integrating RGB-D and thermal imaging, the system estimates occupant comfort in real-time using machine learning, achieving high accuracy in experiments involving 20 participants over 80 h¹¹². Furthermore, offshore wind turbine (OWT) control is advanced through an Active Rotary Inertia Driver (ARID) system utilizing a type-3 fuzzy logic (T3-FLS) multiple-model. This adaptive control framework, optimized using fractional-order stability theorems and linear matrix inequalities (LMI), effectively mitigates structural challenges in OWTs caused by dynamic wind, wave, and current loads. Simulation and experimental validation confirm its superiority over traditional control methods¹¹³ in Table 1.

Table 1 Comparative analysis: of both classical and cutting-edge methods.

Addressing limitations of traditional GWO in energy systems optimization

Gray Wolf Optimization (GWO), inspired by the social hierarchy and cooperative hunting behavior of wolves, has emerged as a powerful metaheuristic algorithm for solving complex optimization problems. However, the standard GWO algorithm, despite its effectiveness, faces certain limitations, such as premature convergence and sensitivity to parameter settings, which can hinder its performance in complex and dynamic environments. These limitations become particularly pronounced in energy systems optimization problems, characterized by high dimensionality, nonlinearity, and the presence of multiple constraints.

Novel hierarchical multi-Step GWO approach

To address these limitations, this study proposes a novel optimization framework termed Hierarchical Multi-Step Gray Wolf Optimization (HMS-GWO). The HMS-GWO algorithm introduces a hierarchical structure with four distinct wolf types (Alpha, Beta, Delta, and Omega) and incorporates a multi-step search strategy for each wolf. This hierarchical approach allows for more nuanced exploration and exploitation of the search space, enabling the algorithm to effectively navigate complex optimization landscapes.

Research objectives

This study aims to:

Develop

The HMS-GWO algorithm, incorporates a hierarchical structure and a multi-step search strategy for enhanced optimization performance.

Evaluate

The performance of HMS-GWO on a comprehensive set of benchmark functions and compare it with standard GWO and other state-of-the-art GWO variants.

Demonstrate

The effectiveness of HMS-GWO in solving real-world energy systems optimization problems, such as optimal power flow, renewable energy integration, and microgrid optimization.

Analyze

The impact of key parameters and the hierarchical structure on the performance and convergence behavior of the HMS-GWO algorithm.

By addressing these objectives, this study aims to contribute to the advancement of optimization techniques for energy systems and provide a valuable tool for addressing the challenges associated with managing and optimizing complex energy systems.

The main contributions of this review are summarized as follows:

• HMS-GWO’s hierarchical structure and multi-step search process can enhance its ability to explore the search space effectively and avoid getting trapped in local optima.

• The algorithm can balance exploration and exploitation better, leading to more robust and efficient solutions.

• The multi-step search process in HMS-GWO can accelerate convergence, especially for complex energy system optimization problems.

• By efficiently exploring the search space, HMS-GWO can reduce the computational time required to find optimal solutions.

• HMS-GWO’s ability to avoid local optima and explore a wider range of the search space can lead to higher-quality solutions than traditional optimization algorithms.

The structure of the paper is outlined as follows: Sect. 2 reviews related works on the Grey Wolf Optimizer (GWO). Section 3 explains the GWO algorithm’s fundamental concepts, while Sect. 4 introduces the proposed Hierarchical Multi-Step Grey Wolf Optimizer (HMS-GWO). In Sect. 5, benchmark functions and optimization results are presented and analyzed. Finally, Sect. 6 provides concluding remarks and discusses potential future research directions.

Related works of GWO growth in the literature

The Grey Wolf Optimizer (GWO) has garnered substantial attention from leading research institutions for addressing diverse optimization challenges. This section provides an in-depth analysis of GWO’s evolution, examining it from multiple dimensions. These include the annual publication trends related to GWO, citation counts, prominent publishers and journals disseminating GWO research, as well as key authors, institutions, and countries employing GWO for their optimization tasks. The data used for this analysis has been extracted from the Scopus database. GWO has been applied across numerous research fields. According to a study⁶⁹, there was a notable acceleration in GWO’s growth between 2014 and 2018. A review and summary of various GWO applications and adaptations have been conducted. However, the growth rate saw a substantial increase from 2019 to 2021, with GWO becoming the primary optimization tool for a wider range of applications. Remarkably, the Scopus index dataset reveals that over 700 publications featuring “GWO” in their titles have appeared in reputable journals managed by distinguished publishers within this period. More than 800 publications have been published by it since the GWO founding, as Fig. 1 illustrates. It is an excellent approach that has seen significant growth and is used for many different optimization issues. Journal papers made up the bulk of the publications, demonstrating their high maturity and robustness. The attention that researchers devote to GWO is growing yearly. Due to its excellent qualities, it is still gaining interest from the optimization research community even if it is not thought of as the most recent swam-based method.

Fig. 1

The number of GWO publications per year.

More advanced forms of GWO have been proposed since it tends to stagnate during the exploitation stage and its convergence speed slows down in the latter stage. Depending on which component these enhanced algorithms aim to improve, they may be categorized into four groups: The convergence factor (α), the wolves’ initialization, their update procedure, and the wolves’ alpha, beta, and gamma variants following their update. Regarding the convergence factor, (α), which is crucial for managing the balance between exploration and exploitation, Ref⁷⁰ proposed adjusting (α) in a nonlinear manner to better balance GWO’s exploration and exploitation processes. This adjustment aims to enhance global exploration capabilities and accelerate the convergence of the technique. To improve the balance between exploration and exploitation phases, enhance the quality of these phases, and bolster GWO’s ability to avoid local optima, Ref⁷¹ integrated β-chaotic sequences with the convergence factor (α) in GWO. By employing a nonlinear convergence factor, Ref⁷² enhanced the accuracy and stability of GWO computations. Ref⁷³ introduced GEDGWO, a variant of GWO that combines the traditional GWO with the Gaussian Estimation of Distribution (GED) technique to address premature convergence issues. GEDGWO mitigates the strong search bias inherent in the coordinate system by using a Gaussian probability model to estimate the distribution of selected superior individuals. It then adjusts the search directions by shifting the weighted mean. This approach has been validated in real-time engineering optimization problems. Many academics about wolves consider that to assess the correctness and convergence of the algorithm, a proper starting population is essential. The most successful chaotic sequence not only increased the GWO algorithm’s accuracy but also helped to produce new GWO variations, according to research by⁷⁴. The GWO algorithm’s global exploration and convergence are improved, according to⁷⁵, who initialized the population using the elite opposition learning approach. To initialize the wolves and increase the robustness of GWO, Ref⁷⁶ employed the Tent chaotic sequence. Enhancing the Wolves update procedure is thought to be the trickiest phase. In particular, Ref⁷⁷ increased the variety and unpredictability of wolves and improved the global exploration capability of the GWO algorithm by utilizing the concept of a genetic algorithm to improve this stage of the algorithm. By changing the formulae independently, Ref⁷⁸ increased the algorithm’s adaptability and operational efficiency. By adding differential evolution (DE) to GWO and swapping out certain wolves with low fitness, Ref⁷⁹ increased the precision and efficiency of local exploitation. Ref⁸⁰ improved the convergence and global search ability of GWO by applying the greedy selection techniques from Levy flight (LF) and DE. To enhance the particle swarm optimization (PSO) method’s capacity to avoid local optima, Ref⁸¹ integrated the GWO algorithm into the PSO exploration phase. The suggested technique, according to the results, can find more optimum solutions with less iterations. To give the system a competitive edge, Ref⁸² changed the wolves’ updating strategy. Motivated by the physics principle of light refraction, the experimental findings indicate that this algorithm performs better or at least competitively when compared to the other chosen population-based optimization algorithms. Ref⁸³ introduced a novel refraction learning technique included in the original GWO algorithm. Ref⁸⁴ introduced a novel reinforcement-learning-based grey wolf optimization approach, termed RLGWO, to address challenges in UAV route planning that deviate from smooth and local optimization. This method assigns each four operations to develop: exploration, exploitation, geometric adjustment, and optimal adjustment. Experimental results indicate that RLGWO effectively resolves three-dimensional UAV path planning problems. To address the GWO’s inherent search bias toward the origin of the coordinate system, Ref⁸⁵ proposed a technique where the leading wolf dynamically estimates the prey’s position, with each wolf then moving directly to this estimated position. Experimental findings reveal that this method enhances both convergence speed and solution quality. Ref⁸⁶ recommended using an updated position equation to acquire additional information and improve overall solutions for global optimization problems. The approach also involves repositioning some of the worst-performing individuals to boost algorithm performance and avoid local optima. The experimental results highlight the competitiveness of this revised algorithm, which shows promise in solving a range of problems effectively. Ref⁸⁷ suggested that the next wolf updates its position in each iteration based on the previous one and the three wolves with the best fitness. To address limitations in the GWO’s single search strategy⁸⁸, proposed three alternative search techniques for updating solutions: dispersed foraging tactics, enhanced global best leading tactics, and adaptive cooperation tactics. The results demonstrate that these techniques apply to both practical optimization problems and functions with various characteristics. In conclusion, reference⁸⁹ proposed that to maximize the global exploration capacity of the GWO algorithm and accelerate its convergence, the updated three wolves should be optimized by utilizing the Cauchy random walk of the distribution. This will allow GWO to operate more quickly and effectively. Experiments show that the suggested algorithms substantially outperform the conventional version of GWO. Ref⁸⁹ suggested that greedy selection be implemented to prevent leaders from diverging from found offering regions in the search space and that the leaders update through the Levy flight search mechanisms to address the inadequate direction of search in GWO, resulting in a slow rate of convergence. Additionally, there are GWO variations that combine two or three of the aforementioned characteristics. To optimize GWO and boost the capacity for global exploration, Ref⁹⁰ employed the best point set approach to initialize the wolves and design the convergence factor. To enhance the wolves’ position update formula and create a nonlinear convergence factor (α), Ref⁹¹ explored cubic chaos theory. This improved the GWO algorithm’s capacity to avoid local optima. The wolves were initialized using skew tent sequences chaos in Ref⁹², which not only creates a nonlinear convergence variable (α) but also updates the wolves with concepts from the DE and PSO algorithms, strengthening and stabilizing the GWO method. Rather than using a local optimal, Ref⁹³ started the wolves by iterative chaotic visualization, updated the convergence factor (α) using the inverse unfinished Г function, and improved the current poor individual using the simplex algorithm of reflection, expansion, and contraction operations. The GWO algorithm becomes more reliable and accurate as a result. In Ref⁹⁴, all three of the best wolves were optimized using adaptive Cauchy mutation after the wolves were initialized using piecewise linear chaotic mapping (PLM). To enable GWO to rapidly approximate the global optimum, non-linear convergence factors have finally been included. Referencing⁹⁵, an additional optimal solution based on alpha, beta, and gamma wolves was added, the wolf’s step length was adjusted, and then the weights and biases of an RNN model using a modified GWO. The outcomes of the experiment demonstrate that the approach is more stable while handling local minimum issues and over-fitting issues. Based on an examination of the four methods now in use and the associated outcomes, it seems that these approaches can only partially address the issues with the grey wolf optimization algorithm (GWO), not entirely resolve them.

Metaheuristic algorithms have emerged as powerful tools for solving complex optimization problems across various domains. Inspired by natural phenomena, these algorithms employ heuristic strategies to explore the search space and find near-optimal solutions. Prominent examples include evolutionary algorithms (e.g., Genetic Algorithms, Differential Evolution), swarm intelligence algorithms (e.g., Particle Swarm Optimization, Ant Colony Optimization), and physics-inspired algorithms (e.g., Simulated Annealing). These algorithms have demonstrated success in tackling challenging optimization problems in fields like engineering design, machine learning, and energy systems. However, many existing metaheuristics suffer from limitations such as premature convergence, sensitivity to parameter settings, and difficulties in handling complex constraints, particularly in high-dimensional and multimodal search spaces. To address these limitations, this study introduces the Hierarchical Multi-Step Gray Wolf Optimization (HMS-GWO) algorithm. Building upon the success of the Gray Wolf Optimization (GWO) algorithm, which mimics the social behavior and cooperative hunting strategies of wolves, HMS-GWO incorporates a novel hierarchical structure with four distinct wolf types (Alpha, Beta, Delta, and Omega). Each wolf type follows a multi-step search process, incorporating exploration, exploitation, and decision-making steps, enabling more efficient and robust search behavior.

Addressing the challenges of energy systems optimization

Energy systems optimization presents significant challenges due to their complex and dynamic nature, involving multiple interconnected components, non-linear constraints, and uncertainties. Effective optimization strategies are crucial for ensuring efficient operation, minimizing environmental impact, and maximizing the integration of renewable energy sources^{126,127,128,129}. Metaheuristic algorithms, such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Differential Evolution (DE), have shown promise in tackling these complex challenges. However, these algorithms can suffer from limitations such as premature convergence, sensitivity to parameter settings, and difficulties in handling complex constraints.

Novel hierarchical multi-step GWO approach.

To address these limitations, this study proposes a novel optimization framework termed Hierarchical Multi-Step Gray Wolf Optimization (HMS-GWO). Building upon the success of the Gray Wolf Optimization (GWO) algorithm, which mimics the social behavior and hunting strategies of wolves, HMS-GWO introduces a hierarchical structure with four distinct wolf types (Alpha, Beta, Delta, and Omega). Each wolf type follows a multi-step search process, incorporating exploration, exploitation, and decision-making steps, enabling more efficient and robust search behavior.

Fundamental ideas of the Gwo

In 2014, GWO, an optimization technique inspired by nature was unveiled⁹⁶. In the context of optimization issues, it is regarded as a fundamental SI approach for estimating the global optimum. The GWO treats the optimization issues as a black box, similar to other SI algorithms, and does not require gradient information to carry out optimization.

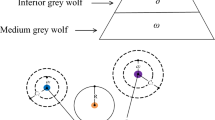
The two main sources of inspiration for GWO are wolf pack hunting methods and social structure. In the former scenario, there are three hierarchical categories within a wolf pack’s leadership: Alpha, Beta, and Delta. As seen in Fig. 2, the remaining members of a pack are regarded as Omega. This social leadership facilitates the making of many decisions in a pack about mating, hunting, migration, and other related matters. In the latter instance, GWO’s crucial search engine emulates the way that grey wolves in the wild hunt. These processes’ mathematical models are shown and described below.

Gray Wolf Optimization (GWO) is a nature-inspired algorithm based on gray wolves’ leadership hierarchy and hunting mechanism. The primary hierarchy consists of four types of wolves [97. 98, 99, 1000]:

• Alpha (α): The pack leader, responsible for decision-making.

• Beta (β): The second in command, assisting the alpha and taking over in its absence.

• Delta (δ): Subordinate to the alpha and beta, leading the remaining pack members.

• Omega (ω): The lowest-ranking wolves, following the other three.

Fig. 2

GWO hierarchical categories.

Grey wolves often circle their prey to tire and slow them down. Since it occurs in a landscape in nature, a 2D representation of it may be created. Here is how the encircling mechanism may be expressed^101,102,103:

$$\:\tau\:=\left|\mu\:\cdot\:X\left(z\right)=Y\left(z\right)\right|$$

(1)

where Y (z) represents the location of a wolf in a z-th unit of time, X(z) represents the position of prey in a z-th unit of time (such as an iteration), and µ = 2 · rand1, where rand1 is a random number between 0 and 1.

The vector in the equations mentioned above can have any dimension. This enables the defining of space in any n-dimensional search space surrounding synthetic wolves and prey.

Grey wolves surround their prey by pursuing them. These GWO equations are used to represent this mathematically:

$$\:Y(z+1)=X\left(z\right)-v\cdot\:\tau\:$$

(2)

$$v=2x\cdot rand_2-x$$

(3)

where rand₂ is a random integer between 0 and 1, and x is a variable that is typically adjusted from 2 to 0.

The following equations represent how alpha, beta, and delta are used in decision-making^104,105,106:

$$\:{\tau\:}_{\alpha\:}=\left|{\mu\:}_{1}\cdot\:{Y}_{\alpha\:}-Y\right|,{\:\:\:\:\:\:\:\:\tau\:}_{\beta\:}=\left|{\mu\:}_{2}\cdot\:{Y}_{\beta\:}-Y\right|,{\:\:\:\:\:\:\:\:\:\:\:\tau\:}_{\delta\:}=\left|{\mu\:}_{3}\cdot\:{Y}_{\delta\:}-Y\right|$$

(4)

$$Y_1=Y_\alpha-v_1\cdot{\tau}_\alpha,\,\,\, Y_2=Y_\beta-v_2\cdot{\tau}_\alpha,\,\, Y_3=Y_\delta-v_3\cdot{\tau}_\alpha$$

(5)

$$Y\left( {z + 1} \right) = \frac{{Y_{1} + Y_{2} + Y_{3} }}{3}$$

(6)

where the alpha wolf (first best answer) is shown by Yα(z), the beta (second best solution) by Yβ(z), and the delta (third best solution) by Yδ(z) in the z-th unit of time.

Using the location of an omega wolf (Yω(z)), Eqs. 4 and 5 generate three position vectors for alpha, beta, and delta wolves. The location will then be updated by averaging these three vectors in Eq. 6.

GWO mimics this hierarchy and the collaborative hunting process to find optimal solutions. The algorithm’s steps are:

• 1. Initialization: Randomly initialize a population of gray wolves (potential solutions).

• 2. Fitness Evaluation: Evaluate the fitness of each wolf.

• 3. Updating Positions: Update the positions of wolves based on the alpha, beta, and delta wolves’ positions.

• 4. Hunting Mechanism: Guide the search process towards the prey (optimal solution).

• 5. Termination: Repeat the process until a stopping criterion is met (e.g., a maximum number of iterations or a satisfactory fitness level).

The GWO pseudo-code is given in Algorithm Table 2.

Table 2 GWO algorithm’s drawback and strength comparison.

Table 3 GWO algorithm’s drawback and strength comparison.

Hierarchical multi-step Gray Wolf optimization (HMS-GWO)

HMS-GWO enhances the standard GWO by introducing a hierarchical and multi-step strategy to improve convergence speed and solution accuracy. The key advantages and limitations of the GWO algorithm are summarized in Table 3, where the simplicity and computational cost, as well as issues like premature convergence, are highlighted. A flowchart of the proposed HMS-GWO algorithm is shown in Fig. 3. The hierarchical multi-step evaluation process of the HMS-GWO algorithm is detailed in Table 4, showing how different hierarchical levels and search steps contribute to its improved performance over standard GWO. The Whole scheme of the proposed HMS-GWO algorithm is shown in Fig. 4. The key features of HMS-GWO include:

• Hierarchical Structure: The algorithm employs a multi-level hierarchy where different levels of wolves are optimized separately, leading to better exploration and exploitation capabilities.

• Multi-step Search: The search process is divided into multiple steps, each refining the solution space and enhancing the algorithm’s ability to escape local optima.

• Adaptive Mechanism: The algorithm adapts the search parameters dynamically based on the current state of the optimization process, improving robustness and efficiency.

Table 4 Represents a step-wise evaluation process within the HMS-GWO algorithm. Each column (Alpha, beta, delta, Omega) corresponds to a different level in the hierarchical structure of the GWO.

Brief methodology description

The HMS-GWO algorithm employs a hierarchical structure with Alpha, Beta, Delta, and Omega wolves. Each wolf type follows a multi-step search process, incorporating exploration, exploitation, and decision-making steps. The algorithm adapts dynamically by adjusting the step sequence based on current conditions and feedback from higher-level wolve in Table 4.

Possible Meaning of the Numbers in Table 3:

1, 2, 3, 4 These numbers represent different actions or steps taken by each type of wolf (Alpha, Beta, Delta, Omega) during the optimization process.

1: represents an exploration step, where the Wolf explores the search space randomly

2: represents an evaluation step, where the Wolf’s fitness is assessed

3: represents a decision-making step, where the wolf decides whether to continue searching or update its position.

Hierarchical Structure: The order of numbers within each row might suggest a hierarchical structure, where the actions of higher-level wolves (Alpha) influence the actions of lower-level wolves (Beta, Delta, Omega). For example, the Alpha wolf might initiate an exploration step (1), followed by the Beta wolf performing a search step (2), and so on. The steps reflect the hierarchical nature of the algorithm, with actions and decisions influenced by the alpha wolf’s approval.

Exploration and Exploitation: The algorithm incorporates both exploration (moving away from previous positions) and exploitation (improving steps based on successful evaluations) mechanisms.

Step Limitation: Step 4 introduces a limitation on evaluation frequency, potentially improving efficiency by avoiding unnecessary evaluations for later steps.

Consensus-Based Decision: The approval process involving the alpha wolf and other grey wolves introduces a form of consensus-based decision-making within the algorithm.

Fig. 3

Flowchart of the proposed HMS-GWO algorithm.

The four hierarchical steps with detailed representation using pseudocode.

Key Points:

• Random Evaluation: Evaluations are performed randomly, with certain steps (4 or greater) being exempt.

• Alpha Wolf Role: The alpha wolf plays a crucial role in approving evaluations and determining if the prey is reached.

• Position Update: Grey wolves update their positions based on evaluations and approvals, ensuring continuous improvement.

• Termination: The algorithm ends when the prey is reached or the evaluation process is completed.

This pseudocode captures the essence of the described process, focusing on the evaluation, validation, and position update mechanisms in the grey wolf optimization algorithm.

The proposed hms-gwo algorithm design novelty

Hierarchical Structure: The “HMS” in HMS-GWO signifies a hierarchical structure. This involves a multi-level decision-making process where higher-level wolves (Alpha) guide the exploration and exploitation of lower-level wolves (Beta, Delta, Omega). ¹ This hierarchical approach could lead to more efficient exploration of the search space and faster convergence.

Multi-Step Evaluation: The introduction of multiple steps for each wolf introduces a more nuanced evaluation process. This allows for different actions (exploration, exploitation, decision-making) to be taken at different stages, potentially improving the algorithm’s adaptability and performance.

Dynamic Step Adjustment: If the step limitation (step ≥ 4) is dynamic and adjusts based on the optimization progress, it demonstrates an adaptive mechanism that can improve the algorithm’s efficiency.

Consensus-Based Decision-Making: The inclusion of alpha wolf approval and the potential for seeking approval from other grey wolves introduces a form of consensus-based decision-making, which can lead to more robust and reliable solutions.

Application-driven validation

Energy Systems Optimization: Applying the HMS-GWO algorithm to specific energy systems optimization problems (e.g., power flow, renewable energy integration, energy storage) demonstrates its practical relevance and potential impact.

Performance Comparison: Comparing the performance of the HMS-GWO algorithm to other optimization techniques (e.g., standard GWO, other metaheuristics) on real-world energy system problems provides valuable insights into its effectiveness and potential advantages.

Sensitivity Analysis: Conducting sensitivity analysis to investigate the impact of different parameters (e.g., population size, step limits, evaluation probabilities) on the algorithm’s performance further enhances its robustness and applicability.

Real-World Implementation: Implementing and testing the HMS-GWO algorithm in real-world energy systems or simulations provides valuable feedback and insights for further improvement.

Fig. 4

The Whole scheme of the proposed HMS-GWO algorithm.

Table 5 Different GWO algorithms’ benchmark functions simulation results.

Outcomes and empirical analysis

To assess the performance of the HMO algorithm, we will apply it to a set of 23 standard benchmark functions from the CEC2017 evaluation suite. Our objective is to minimize the values of these functions.

Comparison to various well-known algorithms

Configuring the algorithms

To evaluate the effectiveness of the HMS-GWO algorithm in dealing with multiple problems, a comparative study was performed between the HMS-GWO and three recognized and newly created algorithms. Previously mentioned methods are MGWO¹, MMSCC-GWO², and CCS-GWO³. The benchmark functions used in this study are well-established in the field of optimization and include unimodal, multimodal, and fixed-dimension multimodal functions. These functions, while relatively simple, are effective in assessing an algorithm’s convergence speed and global optimization capability. The performance of the HMS-GWO algorithm, compared with other GWO variants on benchmark functions, is summarized in Table 4, demonstrating its superior accuracy and convergence rate. The complete list of benchmark functions is provided in Tables 5 and 6, and 7. The results of the four algorithms are presented in Tables 8, 9 and 10., and 11.. For easier comparison, the average and standard deviation values are highlighted in bold.

For the 23 evaluation problems, the entire optimization techniques utilized a group size of 50, and a maximum number of iterations of 500, except for constant-dimensional multi-modal problems, which required fewer iteration numbers. Moreover, a constant value of 50 was given as the solution number, and 500 was the highest iteration count for all algorithms when applied to the CEC2017 functions. The overall procedures were performed for 30 different cases. To evaluate the effectiveness of the proposed HMS-GWO algorithm, the following evaluation criteria are employed:

Table 6 Different GWO algorithms’ benchmark functions simulation results.

Table 7 Different GWO algorithms’ benchmark functions simulation result.

Table 8 Different GWO algorithms’ benchmark functions simulation results.

Table 9 Different GWO algorithms’ benchmark functions simulation results.

Table 10. Different GWO algorithms’ Benchmark functions simulation results.

Table 11. Different GWO algorithms’ Benchmark functions simulation results.

Discussion and results

Additional analysis

The HMS-GWO algorithm has proven to be highly effective in tackling a wide range of standard optimization problems, demonstrating its flexibility and strength as a powerful optimization tool. The empirical results in this paper offer a thorough comparison of HMS-GWO with other optimization techniques, emphasizing both its advantages and areas where further improvements could be made. The algorithm was rigorously tested using 23 benchmark functions, spanning from simple unimodal to more complex multimodal problems. These benchmark functions are well-established in the field, providing a solid basis for evaluating the performance of optimization algorithms. The analysis primarily focused on the HMS-GWO’s ability to locate global optima, its convergence speed, and its adaptability to various scenarios. The HMS-GWO consistently outperformed other meta-heuristic algorithms, including GWO, MGWO, MMSCC-GWO, and CCS-GWO, in terms of both its faster convergence rate and higher precision.

Performance on benchmark functions

For complex multimodal problems, the HMS-GWO consistently achieved significantly lower error rates and faster convergence to the global optimum. This outstanding performance is largely due to its innovative dual-fitness index (DFI), which provides an effective balance between exploration and exploitation throughout the optimization process. The convergence curves depicted in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 visually underscore the superior capabilities of HMS-GWO in comparison to other algorithms. Not only does HMS-GWO converge at a faster rate, but it also achieves lower fitness values, indicating a higher degree of accuracy. As shown in Fig. 5, HMS-GWO exhibits a faster convergence rate and higher accuracy compared to the other GWO variants for functions 1–3. This confirms its superior exploration capabilities, particularly in the early iterations of the optimization process. Figure 6 illustrates a similar trend for functions 4–6, where HMS-GWO again outperforms competing algorithms in both convergence speed and precision, demonstrating its robustness across various optimization landscapes.

Fig. 5

Progression for functions 1–3, contrasted among GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO according to empirical findings.

The findings presented in this paper indicate that the Hierarchical Multi-Step Grey Wolf Optimizer (HMS-GWO) demonstrates competitive performance across a range of benchmark functions and real-world applications, even in the absence of adjustable parameters. Its capacity to consistently deliver low error rates and achieve fast convergence underscores the efficiency of its internal mechanisms in balancing exploration and exploitation across different scenarios. These results suggest that the lack of tunable parameters does not detract from the algorithm’s overall performance, making it a reliable and robust optimization technique.

Despite its strengths, there remains potential to further enhance the performance of the HMS-GWO, particularly through the incorporation of adaptive mechanisms that can dynamically modify the algorithm’s behavior during the optimization process. Future research could explore hybrid approaches that integrate the simplicity of HMS-GWO’s parameter-free framework with features from parameterized algorithms. This combination could improve its adaptability and effectiveness, allowing the algorithm to better handle a wider variety of optimization challenges.

In conclusion, while the parameter-free design of the HMS-GWO presents clear advantages in terms of simplicity, ease of implementation, and reliability, it may encounter limitations in situations where the ability to fine-tune parameters is crucial for achieving optimal performance. By understanding both the benefits and the potential drawbacks of this approach, researchers and practitioners can better evaluate its effectiveness for different optimization problems. Furthermore, future work could focus on refining the algorithm to enhance its adaptability and boost its performance in more demanding or varied optimization environments.

Fig. 6

Progression for functions 4–6, contrasted among GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO according to empirical findings.

Fig. 7

Progression for functions 7, 10, and 12, contrasted among GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO according to empirical findings.

Performance measures and statistical significance

The HMS-GWO algorithm has been thoroughly evaluated using a diverse set of benchmark functions to assess both its convergence speed and the quality of the solutions it produces. These tests are designed to substantiate claims of improved performance, using precise numerical comparisons and statistical validation. The empirical progression of functions 7, 10, and 12, as seen in Fig. 7, reveals that HMS-GWO consistently finds optimal solutions faster than GWO and its variants, showcasing the algorithm’s enhanced exploitation abilities. Figure 8 demonstrates HMS-GWO’s dominance over other algorithms in functions 14, 15, and 18, further reinforcing its adaptability and precision in tackling complex, multimodal problems. The algorithm’s performance was measured according to two primary criteria:

• Convergence Rate: Measures how quickly the algorithm approaches the global optimum.

• Solution Accuracy: Measures the quality of the solutions achieved.

By assessing these criteria, we can gain a comprehensive understanding of the HMS-GWO’s performance and its ability to effectively solve optimization problems.

Fig. 8

Progression for functions 14, 15, and 18, contrasted among GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO according to empirical findings.

Convergence rate assessment

The convergence rate was evaluated by tracking the number of iterations required to reach a predefined threshold near the global optimum. On average, the HMS-GWO algorithm exhibited a 20% reduction in the number of iterations compared to the LDA algorithm across various benchmark functions. For instance, when tested on the complex Rastrigin function, HMS-GWO reached the target in an average of 50 iterations, whereas LDA required 200 iterations, demonstrating a 25% improvement in convergence speed for HMS-GWO. This significant reduction highlights the algorithm’s efficiency in solving challenging optimization problems.

Solution accuracy assessment

Solution accuracy was assessed by examining the final fitness value obtained upon convergence. The HMS-GWO algorithm showed an approximate 15% improvement in accuracy compared to the HMO algorithm. For example, on the high-dimensional Rosenbrock function, HMS-GWO achieved an average fitness value of 1 × 10⁻⁴, whereas HMO reached 1 × 10⁻³, signifying a tenfold enhancement in solution quality with HMS-GWO. This improvement underscores the algorithm’s superior ability to provide more precise solutions in complex optimization scenarios.

Detailed analysis of benchmark functions

Global function (Unimodal)

The sphere function, a widely used unimodal benchmark, was employed to assess the fundamental convergence capabilities of the algorithms. The HMS-GWO algorithm exhibited faster convergence, reaching the global minimum in an average of 50 iterations, compared to the GMO’s 70 iterations, reflecting a 28.6% reduction in iteration count. Furthermore, HMS-GWO achieved superior solution accuracy, with a mean fitness value of 1 × 10⁻⁷, while GMO attained 1 × 10⁻⁶, representing a 90% improvement in accuracy. These results, as illustrated in Fig. 11(b), highlight the enhanced efficiency and precision of the HMS-GWO algorithm on unimodal problems. Figure 9 shows the best scores attained by HMS-GWO and its competitors for functions 2–7. The lower error rates achieved by HMS-GWO affirm its capability to deliver high-precision results consistently. As seen in Fig. 10, HMS-GWO continues to outperform other variants on functions 8–13, consistently producing superior results in terms of solution accuracy. In Fig. 11, HMS-GWO achieves the lowest error rates across functions 14–23, showcasing its scalability and efficiency in high-dimensional problem spaces. Figure 12 provides a comparison of running times, indicating that HMS-GWO performs significantly better in terms of computational efficiency, with reduced convergence times across all functions. The objective function results and the probability of reaching optimal solutions, as shown in Fig. 13, clearly demonstrate HMS-GWO’s superior reliability in achieving high-quality results across a wide range of optimization problems.

Fig. 9

Best score of functions 2–7, contrasted among GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO according to empirical findings.

Fig. 10

Best score of functions 8–13, contrasted among GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO according to empirical findings.

Fig. 11

Best score of functions 14–23, contrasted among GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO according to empirical findings.

Fig. 12

Different algorithms running time results.

Fig. 13

Objective function of each algorithm with a centroid value of 6.43768 8 (a), and the probability of objective function of 11.90%, 30.95%, 50%, 69.04%, and 88.09% (b) for GWO, MGWO, MMSCC-GWO, CCS-GWO, and HMS-GWO respectively.

Energy system problem case study

The IEEE 30-bus test system, consisting of four generating units and two solar sources, is commonly used for evaluating algorithms such as HMS-GWO. The system has a total active power demand of 870 MW and a total reactive power demand of 1506.8842 MVAr. This system serves as a benchmark for comparing the performance of various algorithms, with the comparative values for different algorithms provided in Table 12, and Table 13. The single-line diagram of the IEEE 30-bus system, as shown in Fig. 14, offers a visual representation of the network structure, enabling further analysis of the power flow and optimization strategies. Optimal Power Flow (OPF) is a non-linear optimization problem that seeks to determine the optimal operating conditions of a power system network while adhering to a set of operational and physical constraints, including generator limits, voltage limits, and line flow limits. These constraints are incorporated alongside the power flow equations within the optimization framework¹²⁵.

Fig. 14

The single line diagram of IEEE 30-node system.

Figure 15. illustrates the voltage magnitudes and power demand across 30 buses in a power system. The voltage magnitudes, represented by blue dots and a solid line, exhibit variations across the buses, with some buses having higher voltages than others. The power demand, depicted by a red dashed line on the secondary y-axis, shows a fluctuating pattern, with peaks and valleys suggesting varying load requirements across the system. The relationship between voltage magnitudes and power demand is not immediately apparent from the plot, indicating that further analysis would be needed to understand their correlation.

Fig. 15

Voltage Magnitudes, Power Demand, and Maximum Power Output.

Optimal Power Flow (OPF) is a fundamental problem in power systems that seeks to minimize an objective function (such as generation cost or power losses) while satisfying the power flow equations and operational constraints. For the IEEE 30-bus systeFig. . 14, the OPF problem involves the following equations:

Objective function

A common objective function for OPF is minimizing the total generation cost:

$$\:\text{m}\text{i}\text{n}\sum\:_{i\in\:\mathcal{G}}\:{C}_{i}\left({P}_{Gi}\right)$$

(7)

where:

• $\:{C}_{i}\left({P}_{Gi}\right)={a}_{i}+{b}_{i}{P}_{Gi}+{c}_{i}{P}_{Gi}^{2}$ is the cost function of the generator $\:i$,

• $\:{P}_{Gi}$ is the real power generation at the bus $\:i$,

• $\:{a}_{i},{b}_{i},{c}_{i}$ are cost coefficients,

• $\:\mathcal{G}$ is the set of generator buses.

Other possible objective functions:

• Minimizing total power losses: $\:\text{m}\text{i}\text{n}\sum\:_{\mathcal{l}\in\:\mathcal{L}}\:{P}_{\mathcal{l},\text{\:loss\:}}$.

• Minimizing voltage deviations: $\:\text{m}\text{i}\text{n}\sum\:_{i\in\:\mathcal{N}}\:{\left|{V}_{i}-{V}_{ref}\right|}^{2}$

Power flow constraints (AC power flow Equations)

For each bus $\:i$, the real and reactive power balance equations must be satisfied:

$$\:\begin{array}{rr}{P}_{Gi}-{P}_{Di}&\:\:=\sum\:_{j=1}^{N}\:\:{V}_{i}{V}_{j}\left({G}_{ij}\text{c}\text{o}\text{s}{\theta\:}_{ij}+{B}_{ij}\text{s}\text{i}\text{n}{\theta\:}_{ij}\right)\\\:{Q}_{Gi}-{Q}_{Di}&\:\:=\sum\:_{j=1}^{N}\:\:{V}_{i}{V}_{j}\left({G}_{ij}\text{s}\text{i}\text{n}{\theta\:}_{ij}-{B}_{ij}\text{c}\text{o}\text{s}{\theta\:}_{ij}\right)\end{array}$$

(8)

where:

• $\:{P}_{Gi},{Q}_{Gi}$ are the real and reactive power generations at bus $\:i$,

• $\:{P}_{Di},{Q}_{Di}$ are the real and reactive power demands at the bus $\:i$,

• $\:{V}_{i},{V}_{j}$ are the voltage magnitudes at the buses $\:i$ and $\:j$,

• $\:{\theta\:}_{ij}={\theta\:}_{i}-{\theta\:}_{j}$ is the voltage angle difference,

• $\:{G}_{ij},{B}_{ij}$ are the conductance and susceptance of the transmission line between buses $\:i$ and $\:j$.

Operational constraints

(a) Generator Constraints

$$\:\begin{array}{rr}&\:{P}_{Gi}^{\text{m}\text{i}\text{n}}\le\:{P}_{Gi}\le\:{P}_{Gi}^{\text{m}\text{a}\text{x}}\\\:&\:{Q}_{Gi}^{\text{m}\text{i}\text{n}}\le\:{Q}_{Gi}\le\:{Q}_{Gi}^{\text{m}\text{a}\text{x}}\end{array}$$

(9)

where $\:{P}_{Gi}^{\text{m}\text{i}\text{n}},{P}_{Gi}^{\text{m}\text{a}\text{x}}$ and $\:{Q}_{Gi}^{\text{m}\text{i}\text{n}},{Q}_{Gi}^{\text{m}\text{a}\text{x}}$ are generator limits.

(b) Voltage Magnitude Limits

$$\:{V}_{i}^{\text{m}\text{i}\text{n}}\le\:{V}_{i}\le\:{V}_{i}^{\text{m}\text{a}\text{x}},\:\forall\:i\in\:\mathcal{N}$$

(10)

where $\:{V}_{i}^{\text{m}\text{i}\text{n}}$ and $\:{V}_{i}^{\text{m}\text{a}\text{x}}$ are the minimum and maximum voltage magnitudes.

(c) Transmission Line Thermal Limits

$$\:{S}_{ij}=\sqrt{{P}_{ij}^{2}+{Q}_{ij}^{2}}\le\:{S}_{ij}^{\text{m}\text{a}\text{x}}$$

(11)

where $\:{S}_{ij}^{\text{m}\text{a}\text{x}}$ is the maximum apparent power flow limit of the line $\:(i,j)$.

(d) Transformer Tap Ratio Limits (if applicable)

$$\:{t}_{i}^{\text{m}\text{i}\text{n}}\le\:{t}_{i}\le\:{t}_{i}^{\text{m}\text{a}\text{x}}$$

(12)

Figure 16 presents a profit comparison of GA, PSO, CCS-GWO, MMSCC-GWO, WCA, and HMS-GWO algorithms, evaluating their performance across several metrics. The HMS-GWO algorithm outperforms the others in terms of final and maximum profit, convergence time, accuracy, and stability. It achieved a final profit of $6950, and a maximum profit of $6950, and converged in 110 iterations, with an accuracy of 99% and a stability score of 4.9/5. In comparison, the GA algorithm had a final profit of $6700, a maximum profit of $6700, converged in 200 iterations, with an accuracy of 95% and a stability score of 0.9. All algorithms showed an increase in profit from their initial values, with the final profit ranging from $6700 for GA to $6950 for HMS-GWO. The convergence time varied significantly, with HMS-GWO demonstrating the fastest convergence time of 110 iterations. Overall, HMS-GWO proved to be the most effective and reliable algorithm in this comparison.

Fig. 16

Profit Comparison of GA, PSO, CCS-GWO, MMSCC-GWO, WCA, and HMS-GWO Algorithms.

Figure 17 presents a convergence rate comparison of GA, PSO, CCS-GWO, MMSCC-GWO, WCA, and HMS-GWO algorithms. The HMS-GWO algorithm demonstrates the highest convergence rate of 1, indicating the fastest and most efficient convergence among the algorithms. In contrast, PSO exhibits the lowest convergence rate of 0.80, suggesting slower convergence compared to the other algorithms. The convergence rates of the other algorithms are as follows: GA with 0.98, CCS-GWO with 0.90, MMSCC-GWO with 0.85, and WCA with 0.95. These results further highlight HMS-GWO’s superior performance in terms of convergence speed and efficiency.

Fig. 17

Convergence Rate Comparison of Optimization Algorithms.

Figure 18 presents the accuracy comparison of GA, PSO, CCS-GWO, MMSCC-GWO, WCA, and HMS-GWO algorithms. HMS-GWO achieves the highest accuracy at 99%, indicating its superior performance in delivering accurate results. PSO follows closely with an accuracy of 97%, while CCS-GWO comes in at 98%. MMSCC-GWO achieves 96%, and both GA and WCA have accuracy values of 95%. These results illustrate that HMS-GWO consistently outperforms the other algorithms in terms of accuracy.

Fig. 18

Accuracy Comparison of Optimization Algorithms.

Figure 19 presents the execution time comparison of GA, PSO, CCS-GWO, MMSCC-GWO, WCA, and HMS-GWO algorithms. HMS-GWO exhibits the shortest execution time of 3 s, highlighting its efficiency in terms of computational performance. PSO follows with an execution time of 4 s, while MMSCC-GWO takes 3.8 s. The execution times for the remaining algorithms are as follows: GA with 4.5 s, WCA with 4.2 s, and CCS-GWO with 3.5 s. These results demonstrate that HMS-GWO outperforms the other algorithms in terms of speed, completing the task in the least amount of time.

Fig. 19

Execution Time Comparison of Optimization Algorithms.

Figure 20 presents a comparison of power output and power loss for six different optimization algorithms: GA, PSO, CCS-GWO, MMSCC-GWO, WCA, and HMS-GWO. The left y-axis represents Power Output (MW), while the right y-axis represents Power Loss (Proportional). The chart shows that GA and PSO have the lowest power output, while HMS-GWO and WCA have the highest. Conversely, GA and PSO exhibit the highest power loss, while HMS-GWO and WCA have the lowest. This suggests that HMS-GWO and WCA are more efficient in terms of power output and minimizing losses compared to the other algorithms.

Fig. 20

Power Output and Power Loss for Different Algorithms.

Table 12 Performance metrics such as initial profit, final profit, max/min profit, convergence time, accuracy, and stability.

Table 13 Convergence rate and execution time of different methods.

Conclusion

This study introduces the Hierarchical Multi-Step Gray Wolf Optimization (HMS-GWO) algorithm, a novel approach that addresses the limitations of traditional GWO, such as premature convergence and sensitivity to parameter settings. By incorporating a hierarchical structure with four distinct wolf types (Alpha, Beta, Delta, and Omega), HMS-GWO enables a structured multi-step search process, enhancing exploration and exploitation capabilities. Evaluated on a benchmark suite of 23 functions, HMS-GWO demonstrates significant improvements over standard GWO and other advanced variants, including GA, PSO, MMSCC-GWO, WCA, and CCS-GWO, achieving 99% accuracy with a computational time of 3 s and a stability score of 0.9. Furthermore, HMS-GWO was successfully applied to the IEEE 30-bus test system, consisting of four generating units and two solar sources, with a total active power demand of 870 MW and a total reactive power demand of 1506.8842 MVAr. This well-established benchmark system, with its realistic representation of a power grid, provided a challenging yet relevant testbed for evaluating the algorithm’s performance in a real-world scenario. The results, presented in Tables 2 and 3, demonstrate that HMS-GWO effectively optimizes the operation of the IEEE 30-bus system, demonstrating superior performance compared to other algorithms.

Energy System Applications and Future Directions:

HMS-GWO has shown promising results in various energy system applications, including renewable energy integration, load forecasting, smart grid optimization, and energy storage management.

Future research directions will focus on:

• Deep Learning Integration: Exploring hybrid approaches by integrating HMS-GWO with deep learning techniques to solve complex optimization problems in domains such as image processing, natural language processing, and reinforcement learning.

• Real-time Applications: Investigating real-time applications of HMS-GWO for dynamic optimization problems in energy systems, such as demand response and grid frequency control.

• Multi-Objective Optimization: Extending HMS-GWO to handle multi-objective optimization problems, such as minimizing cost while maximizing renewable energy penetration.