A semi-supervised domain adaptive medical image segmentation method based on dual-level multi-scale alignment

Abstract

In the actual image segmentation tasks in the medical field, the phenomenon of limited labeled data accompanied by domain shifts often occurs and such domain shifts may exist in homologous or even heterologous data. In the study, a novel method was proposed to deal with this challenging phenomenon. Firstly, a model was trained with labeled data in source and target domains so as to adapt to unlabeled data. Then, the alignment at two main levels was realized. At the style level, based on multi-scale stylistic features, the alignment of unlabeled target images was maximized and unlabeled target image features were enhanced. At the inter-domain level, the similarity of the category centroids between target domain data and mixed image data was also maximized. Additionally, a fused supervised loss and alignment loss computation method was proposed. In validation experiments, two cross-domain medical image datasets were constructed: homologous and heterologous datasets. Experimental results showed that the proposed method had the more advantageous comprehensive performance than common semi-supervised and domain adaptation methods.

Introduction

Deep learning has been extensively applied in many medical diseases. In machine learning models, domain shifts refer to the difference in data distribution between the test dataset and training dataset¹. Domain shifts are common in the tasks of machine learning algorithms and can largely decrease the performance. In particular, significant distributional variations exist in medical imaging data used in multi-center studies and domain shifts are prevalent among different imaging centers/sites due to the differences in scanning protocols, scanners, and populations. However, a domain shift is generally ignored in machine learning algorithms and decrease the performance². In recent years, domain adaptation methods have been widely concerned in machine learning-based medical image analysis³.

Semi-supervised learning (SSL), unsupervised domain adaptation (UDA), and semi-supervised domain adaptation (SSDA) have been developed in order to deal with the problem caused by less labeled data and more unlabeled data. However, unlike SSL, UDA and SSDA are targeted at solving the domain shift problem of less labeled data and more unlabeled data (Fig. 1)⁴. UDA methods transfer knowledge from a label-rich domain to an unlabeled target domain^5,6,7,8. UDA relies on the inter-domain alignment to alleviate inter-domain differences, but it also causes the alignment deviation due to the lack of supervision signals in the target domain. SSL utilizes a small amount of labeled data and a large amount of unlabeled data to enhance the generalization ability of the model. It is significant to efficiently utilize unlabeled data for the purpose of improving the model performance. It is assumed that the data distribution is consistent. SSDA uses both fully labeled data in the source domain and a small amount of labeled data in the target domain. SSDA considers the distribution differences between domains and also uses limited labeled data to adapt to the features of the target domain. A small amount of annotated data in the target domain largely improved the results of convolutional neural network (CNN) algorithms^9,10. Therefore, SSDA, a variant of UDA, was proposed based on the introduction of some labeled samples in the target domain for model training.

Fig. 1

Schematic diagrams of SSL, UDA, and SSDA.

However, SSDA models trained with one label-rich data domain (source domain) often perform poorly in another different and label-scarce data domain (target domain). Even small distribution differences between a training dataset and a test dataset may lead to model instability^11,12. The poor generalization of SSDA models is caused by the domain shift between datasets¹³. Therefore, it is necessary to address this problem of domain shifts. In addition, the medical images of the same organ or lesion usually exhibit similar structural features and stylistic variations are mainly responsible for domain shifts. To address the domain shift problem in SSDA tasks, previous studies focused on the global feature alignment by minimizing cross-domain difference metrics^14,15 and image style transfer¹⁶. Data augmentation techniques play an important role in this framework^17,18. These techniques significantly improve the performance and robustness of models in different tasks. However, these methods also have two key limitations. Firstly, they do not fully consider the importance of multi-scale feature decoupling in semantic segmentation, thus resulting in the coupling of stylistic and semantic information (such as the mixing of shallow texture and deep anatomical structure). Secondly, they only adopt a single hybrid alignment strategy, such as intra-domain alignment (from labeled target domain data to unlabeled target domain data)¹⁹ and inter-domain alignment (from labeled source domain data to labeled target domain data)²⁰. However, this approach may not achieve the global feature alignment well.

In the study, a novel dual-level multi-scale alignment SSDA method was proposed in the study in order to better learn the cross-domain features of medical images and further improve the performance of cross-domain medical image segmentation models. In terms of training strategy, we mainly aligned the network output at two levels (i.e., style level and inter-domain level). Firstly, at the style level, feature extraction was implemented with the multi-scale feature extraction module (MSFE) and the features of unlabeled target images and enhanced unlabeled target images were maximally aligned. Through multi-scale feature decoupling, MSFE eliminated local (tissue texture) and global (imaging device characteristics) style shifts while preserving the invariance of organ structure. At the inter-domain level, mixed image data and target domain images with labeled data were computed over the network. The centers of mass of the two image segmentation categories were computed separately with the category feature extraction module (CFEM) module. Finally, through inter-domain contrastive alignment, the similarity of class centroids across different domains was maximized. In addition, in this research framework, weighted loss, multi-scale feature loss, supervised loss, and alignment loss were used to construct the overall constraint objective. The contributions of the paper are provided below:

• 1. A novel SSDA method for medical image segmentation was proposed to better capture cross-domain features and thus enhance the model performance in cross-domain image segmentation tasks with less labeled data.

• 2. A dual-level multi-scale alignment training strategy was proposed and MSFE was introduced to decouple multi-scale features so as to eliminate local and global style shifts. In addition, CFEM was introduced to calculate the centroid of the category and further achieve the inter-domain alignment.

• 3. On two cross-domain medical image datasets (homologous and heterogeneous datasets), our method showed the highly competitive comprehensive performance. Various ablation studies and visualization further verified the effectiveness and superiority of our method.

Related studies

Semi-supervised medical image segmentation

Manual labeling of medical images is challenging and expensive because professional knowledge is required for ensuring labeling accuracy and the labeling process is often time-consuming. Therefore, semi-supervised medical image segmentation methods are promising in solving segmentation tasks with limited labeled data. By exploiting the information contained in unlabeled data, these methods can largely reduce the dependency upon a large amount of high-quality labeled data, thereby decrease the overall cost and accelerate the analysis process of medical images. Su et al.²¹ introduced intraclass consistency to assess the reliability of pseudo-labels and further yielded reliable pseudo-labels with inter-comparison methods to guide the semi-supervised medical image segmentation. Based on the combination of the ideas of SSL and self-training, Wang et al. proposed the FEW-SHOT learning framework, but its performance mainly depended on the selection and evolution of high-quality pseudo-labels in cascade learning²². A self-trained teacher-student model with self-attentive U-Net and an automatic label grader was proposed²³. Han et al. proposed a semi-supervised segmentation network based on GAN (BUS-GAN) in order to solve the segmentation problem of large breast ultrasound (BUS) images²⁴. Chen et al. introduced an adaptive attentional inter-cascade generative adversarial network to solve the segmentation problem of unbalanced atrial targets²⁵. However, existing semi-supervised methods could not solve the domain shift because these methods were based on the assumption on the shared distribution between labeled and unlabeled data, which often led to the degradation of their performance.

Semi-supervised domain adaptive medical image segmentation

Basak et al.²⁶ proposed a two-stage SSDA training process for medical image segmentation, in which domain-content dis-entangled contrastive learning (CL) and pixel-level feature consistency constraints were used and the encoder was pre-trained in a self-learning paradigm. Li et al.²⁷ designed an inter-domain teacher model was to respectively learn from the features of the target domain data and cross-modal priori knowledge from the source domain. Roels et al.²⁸ introduced a semi-supervised DA method to segment electron microscope images and designed a Y-Net with one feature encoder and two decoders respectively for segmentation and image reconstruction of target and source domains. The network was firstly trained in an unsupervised way and then fine-tuned with labeled target samples. Madani et al.²⁹ proposed a DA framework based on semi-supervised generative adversarial networks (GANs) for the classification of chest X-ray images. Unlike traditional GANs, the model used unlabeled target data, labeled source data, and generated images as the inputs and its discriminator implemented a triple classification task (i.e., normal, diseased, or generated images). Unlabeled target data could be categorized into one of the three categories and also contribute to loss computation when they were categorized into generated images. Semi-supervised training with this model allowed the simultaneous input of unlabeled and labeled data.

Methods

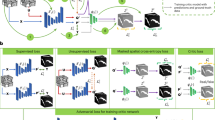
In this section, we firstly proposed the definition of the SSDA problem and then introduced the proposed image cut-mix augmentation strategy, CFEM, and double alignment strategy, respectively. Finally, the overall objective function was proposed. The proposed model and corresponding training process are displayed in Fig. 2.

Fig. 2

Flowchart of the method proposed in this study.

Problem definition

In the SSDA task, the datasets of both domains are included. The dataset of the source domain mainly contains labeled images and the $N$ source domains are defined as $\user1{\mathcal{D}}_{S} = \{ \user1{\mathcal{D}}_{S}^{1} ,\user1{\mathcal{D}}_{S}^{2} , \ldots ,\user1{\mathcal{D}}_{S}^{n} , \ldots ,\user1{\mathcal{D}}_{S}^{N} \}$, where $\user1{\mathcal{D}}_{S}^{n} = \{ (x_{i}^{nS} ,y_{i}^{nS} )\}_{i = 1}^{{\left| {\user1{\mathcal{D}}_{S}^{n} } \right|}} \subset \Re^{d} \times \user1{\mathcal{Y}}$ comes from the distribution $P_{S}^{n} (X,Y)$. In addition, two sets of data are sampled from the target domain distribution $P_{T} (X,Y)$. One set of labeled image data are defined as $\user1{\mathcal{D}}_{T} = \{ (x_{i}^{T} ,y_{i}^{T} )\}_{i = 1}^{{\left| {\user1{\mathcal{D}}_{T} } \right|}}$ and the other set of unlabeled image data are defined as $\user1{\mathcal{D}}_{U} = \{ (x_{i}^{U} ,y_{i}^{U} )\}_{i = 1}^{{\left| {\user1{\mathcal{D}}_{U} } \right|}}$ ($\left| {\user1{\mathcal{D}}_{U} } \right| \gg \left| {\user1{\mathcal{D}}_{T} } \right|$). $y_{i}^{nS}$ and $y_{i}^{T}$ respectively indicate the labels from the partial images from the source and target domains and contain K segmentation labels. The section aims to train a task-specific image segmentation model with $\user1{\mathcal{D}}_{S}$, $\user1{\mathcal{D}}_{T}$, and $\user1{\mathcal{D}}_{U}$ so as to accurately segment unlabeled target images from the target domain.

Image cut-mix augmentation strategy

Based on the previous reports^18,20, the image cut-mix augmentation strategy on source domain $\user1{\mathcal{D}}_{S}$ and labeled target domain $\user1{\mathcal{D}}_{T}$ was proposed to reduce the domain gap. As for a set of labeled left atrial images $\{ x_{i}^{S} ,y_{i}^{S} \}$ and $\{ x_{i}^{T} ,y_{i}^{T} \}$, the image cut-mix augmentation strategy is formulated as follows:

$$x_{i}^{M} = {\mathbf{M}} \odot x_{i}^{S} + (1 - {\mathbf{M}}) \odot x_{i}^{T}$$

(1)

$$y_{i}^{M} = {\mathbf{M}} \odot y_{i}^{S} + (1 - {\mathbf{M}}) \odot y_{i}^{T}$$

(2)

where ${\mathbf{M}}$ represents the binary mask matrix and $\odot$ represents the element-by-element multiplication. As shown in Fig. 3, the mixed image $x_{i}^{M}$ contains both $x_{i}^{S}$ and $x_{i}^{T}$. In other words, a rectangular region is cut from $x_{i}^{S}$ and pasted to the same position of $x_{i}^{S}$, and similarly the corresponding mixed label $y_{i}^{M}$ is obtained for each image. Region-level data mixing can generate intermediate samples between different domains and act as a bridge to connect different domains. This strategy can fill the gaps between domains, explore the underlying contextual semantics across domains from a local perspective, and improve the understanding and analysis.

Fig. 3

Schematic diagram of the image cut-mix augmentation strategy.

In this strategy, ${\mathbf{M}}$ used here is not unique. The position and size of ${\mathbf{M}}$ are defined as:

$$[i,j] = {\text{Mean}} \left( {f_{{{\text{BC}}}} (y_{i}^{S} ) + f_{{{\text{BC}}}} (y_{i}^{T} )} \right)$$

(3)

$$w,h = {\text{Random}} (0.5,1) \times {\text{Max}} \left( {f_{{{\text{E}}R\_w}} (y_{i}^{S} ),f_{{{\text{E}}R\_h}} (y_{i}^{S} )} \right)$$

(4)

where $i$ and $j$ indicate the center pixel coordinates of ${\mathbf{M}}$; $f_{{{\text{BC}}}} ( \cdot )$ is the function of the center of mass of the label; ${\text{Mean}} ( \cdot )$ is the mean function; $w$ and $h$ indicate the width and height of ${\mathbf{M}}$; ${\text{Random}} (0.5,1)$ is a function that generates a random floating-point number between 0.5 and 1; $f_{{{\text{E}}R\_w}} ( \cdot )$ and $f_{{{\text{E}}R\_h}} ( \cdot )$ indicate the width and height of the bounding box of the label; ${\text{Max}} ( \cdot , \cdot )$ is the maximum function and indicates the maximal value selected from the parameters.

Category feature extraction module

Some scholars indicated that the pixels in the same category were clustered in the feature space and that the center of mass of each category feature could indicate the distribution of the category feature^30,31. Therefore, in this section, the coarse output and depth features are input into CFEM so as to extract the category features. The depth feature ${\text{Decoder}} (x_{input} ) \in {\mathbb{R}}^{C \times H \times W}$ and the coarse output $Y^{\prime} \in {\mathbb{R}}^{K \times H \times W}$ are firstly extracted from the given input feature $x_{input}$ by the U-Net decoder (Fig. 4), where $C$ and $K$ respectively indicate the numbers of channels and categories ($K = 2$ in this section); $H$ and $W$ respectively denote the height and width. The category feature $F_{{\text{c}}} \in {\mathbb{R}}^{N \times C}$ is calculated as:

$$F_{{\text{c}}} = \frac{{\sum\nolimits_{i}^{H \times W} {Y^{\prime}_{i} } \times {\text{Decoder}} (x_{input} )}}{H \times W}$$

(5)

Fig. 4

Schematic diagram of CFEM.

Inter-domain contrastive alignment

The domain adaptation performance of a model depends mainly on whether the samples of the same category from different domains can be clustered in the latent space or not. However, the features from the target domain cannot be aligned with those from the source domain because of the domain shift between source and target distributions. By aligning the centers of mass of each category in the source and target domains, the differences among the clusters of the same category in different domains can be reduced. In this section, CFEM is used to compute category features with coarse output and deep features so as to align the clustering of domains.

The mean values of the $K$ category features of the source domain are computed separately to obtain the category center of mass ($K = 2$ in this study). The $k = [1, \ldots ,K]$-th category center of mass $C_{k}^{S}$ in the source domain is expressed as:

$$C_{k}^{S} = \frac{{\sum\nolimits_{b = 1}^{B} {Mean(F_{c}^{k} )} }}{B}$$

(6)

where $B$ indicates the batch size; $Mean( \le )$ is the mean computation function; $F_{c}^{k}$ indicates the features of the $k$-th category. In the model, an array $C^{S} = [C_{1}^{S} ,C_{2}^{S} , \ldots ,C_{K}^{S} ]$ is defined to store the centers of mass of each category in the source domain and further update them during the training process based on priori knowledge:

$$C_{k}^{S} = m(C_{k}^{S} )_{step} + (1 - m)(C_{k}^{S} )_{step - 1}$$

(7)

where $m$ is the momentum term and its values are chosen as described below; $(C_{k}^{S} )_{step}$ and $(C_{k}^{S} )_{step - 1}$ indicate the center of mass of the $k$-th class at the current and previous iterations, respectively.

The data in the unlabeled target domain has no corresponding labeled data, so it is necessary to define pseudo-labels for calculating the $K$ category centers of mass of the unlabeled target domain. Firstly, the weight parameters of the U-Net model are obtained through weight sharing. Then, the unlabeled images are input into the U-Net for computation. Finally, the U-Net output is used as the pseudo-labels of the data in the unlabeled target domain. Consistent with Eq. (6), the center of mass $C_{k}^{U}$ of the k = [1...K]-th category in the unlabeled target domain is calculated as:

$$C_{k}^{U} = \frac{{\sum\nolimits_{b = 1}^{B} {Mean(F_{c}^{k} )} }}{B}$$

(8)

The inter-domain contrastive alignment error is computed with the cross-entropy loss function:

$$L_{1} = - \mu \sum {\left[ {\left( {1 - C^{U} } \right)\log \left( {1 - C^{S} } \right)} \right] - } \left( {1 - \mu } \right)\sum {\left[ {C^{U} \log \left( {C^{S} } \right)} \right]}$$

(9)

where $\mu$ is the balanced hyperparameter for positive and negative samples. The ground truth data of the medical image segmentation task tends to be a small area mask, so it is set as $\mu = 0.3$ in the study, as verified by experimental results.

Style contrastive alignment

The details of style contrastive alignment are introduced below. The core idea is to perform multi-level feature decoupling with the original input image and its enhanced version. In other words, when they have consistent contour structures, the feature extractor focuses on the invariant features based on the difference between the two styles. MSFE is used as a feature extractor in the style contrastive alignment strategy. MSFE is defined as follows:

With an unlabeled input $x_{k}^{u} \in {\mathbf{D}}^{u}$, Model 1 yields a set of multiscale prediction features $\varphi_{s}^{1} \left( {s = 1,2, \ldots ,S} \right)$, where $\varphi_{s}^{1}$ indicates the predicted result at the scale s. Model 2 also yields a set of multiscale prediction features $\varphi_{s}^{2} \left( {s = 1,2, \ldots ,S} \right)$. The smaller s indicates the higher resolution and S is the total number of scales. The two models adopt the 2D-UNet structure, so the value of S is set as 5. For the convenience of presentation, the predicted results at the same scale in Model 1 and Model 2 are denoted as $\varphi_{s}^{t} \left( {t = 1,2;s = 1,2, \ldots ,S} \right)$, where t is the model number.

An enhanced version of the unlabeled target image is firstly generated: $x_{i}^{SA} = f_{SA} (x_{i}^{U} )$, where $f_{SA} ( \cdot )$ is the enhancement function. Inspired by the previous study³², the data augmentation function $f_{SA} ( \cdot )$ is defined as a data augmentation strategy composed of a hyperparameter $r$, where $r$ represents the order of the data augmentation strategy. It is worth noting that $f_{SA} ( \cdot )$ changes randomly as the model is trained. In addition, a set $A$ with $N$ data augmentation methods is defined. In each time that $f_{SA} ( \cdot )$ is called, there is a $1/N$ probability to select a data augmentation function in the set A and this selection is repeated $r$ times. In other words, $f_{SA} ( \cdot )$ provides $N^{r}$ data augmentation strategies. Our goal is to make the feature extractor focus on the invariant features under the difference between two styles when the image contour structures are completely consistent. Data augmentation of $f_{SA} ( \cdot )$ is only expected in terms of image style. Therefore, the data augmentation methods in set $A$ do not change the structure of images. In this study, $r = 2$ and $A$ are defined as:

$$A = \left\{ {\text{Identity,AutoContrast,Equalize,Solarize,Color,Contrast,Brightness,Sharpness}} \right\}$$

(10)

Then, $x_{i}^{U}$ and $x_{i}^{SA}$ are calculated with U-Net to obtain the multiscale features $\varphi_{s}^{U}$ and $\varphi_{s}^{SA} \left( {s = 1,2, \ldots ,S} \right)$ in the U-Net decoder. Finally, the style contrastive alignment error is computed with the following loss function:

$$L_{2} \left( {\varphi^{U} ,\varphi^{SA} } \right) = \sum\limits_{s = 1}^{S} {\left\| {\varphi_{s}^{U} - \varphi_{s}^{SA} } \right\|_{F} } = \sqrt {\sum\limits_{i = 1}^{r} {\sum\limits_{j = 1}^{c} {\left| {(\varphi_{s}^{U} )_{i,j} - (\varphi_{s}^{SA} )_{i,j} } \right|} } }$$

(11)

Overall optimization objective

In SSDA, when labeled target data are scarce, the target distribution is divided into aligned and non-aligned sub-distributions⁹. Aligning the non-aligned sub-distribution can improve the comprehensive performance, whereas interfering with the aligned sub-distribution may lead to a negative shift. Therefore, in this section, only the gradients of strongly augmented images propagate in order to avoid the interference with the aligned sub-distribution¹⁴. Furthermore, in the style contrastive alignment, the consistency prediction between the strongly augmented unlabeled image and the original unlabeled image forces the non-aligned sub-distribution to shift from low-density regions toward the aligned distribution. In this way, the better clustering effect of the unlabeled target distribution can be realized.

Style contrastive alignment ensures the consistency of features in unlabeled data under different data augmentation methods and further guides the model to converge towards the correct direction. However, it cannot guarantee data alignment between the source domain and the unlabeled target domain. Inter-domain contrastive alignment can decrease the difference between the unlabeled target domain and the source domain, but the samples of the unlabeled target domain near decision boundaries may be classified into a wrong class and lead to a negative shift. Therefore, the combination of style contrastive alignment and inter-domain contrastive alignment can better align unlabeled target samples with the source domain, thereby improving the performance.

Firstly, the inference result $f(x_{i}^{M} , \cdot )$ is obtained by U-Net operation with the mixed image $x_{i}^{M}$. Then, with $f(x_{i}^{M} , \cdot )$ and mixed label $y_{i}^{M}$, through weighted loss function computation $f(x_{i}^{M} , \cdot )$, $L_{s}$ is calculated as follows:

$$L_{s} = \alpha \cdot L_{BBCE} + \beta \cdot L_{Dice} + \gamma \cdot L_{MIoU}$$

(12)

where $\alpha$, $\beta$, and $\gamma$ respectively indicate the weights of the three loss functions and are set based on our previous report³³: $\alpha = 0.2$, $\beta = 0.4$ and $\gamma = 0.4$. $L_{Dice}$, $L_{BBCE}$, and $L_{MIoU}$ are respectively Dice loss function, balanced binary cross-entropy loss function, and MIoU loss function and expressed as follows:

$$L_{BBCE} = - \mu \sum {\left[ {\left( {1 - \overline{y}} \right)\log \left( {1 - y} \right)} \right] - } \left( {1 - \mu } \right)\sum {\left[ {\overline{y}\log \left( y \right)} \right]}$$

(13)

$$L_{Dice} = 1 - 2\left| {y \cap \overline{y}} \right|\left( {\left| y \right| + \left| {\overline{y}} \right|} \right)^{ - 1}$$

(14)

$$L_{MIoU} = 1 - K^{ - 1} \sum\limits_{k = 1}^{K} {\left| {y_{k} \cap \overline{y}_{k} } \right|} \left| {y_{k} \cup \overline{y}_{k} } \right|^{ - 1}$$

(15)

where $\mu$ denotes the equilibrium hyperparameter of negative and positive samples; $\overline{y}$ indicates the labeled image; $y$ indicates the predicted result; $K$ indicates the number of categories ($K = 2$ in this study).

The overall optimization objective function is composed of inter-domain contrastive alignment loss, weighted loss, and style contrastive alignment loss:

$$\mathop {\text{argmin}}\limits_{{\theta^{1} ,\theta^{2} }} L_{total} \left( {f\left( { \, \cdot \, ;\theta^{1} } \right),f\left( { \, \cdot \, ;\theta^{2} } \right)} \right) = \mathop {\text{argmin}}\limits_{{\theta^{1} ,\theta^{2} }} \left( {L_{s} + \lambda_{1} L_{1} + \lambda_{2} L_{2} } \right)L_{total}$$

(16)

where $\lambda_{1}$ and $\lambda_{2}$ are respectively the weighting coefficients of inter-domain contrastive alignment loss and style contrastive alignment loss and their values are chosen below.

Experiments

The experimental details, including data, experimental setup, and evaluation metrics, are introduced below. In order to validate the proposed model, the datasets from different domains were used to test the model and its segmentation performance was then compared with that of several advanced domain adaptation semantic segmentation methods. Finally, a series of ablation experiments were carried out to verify each module in the model.

Datasets

In this study, we constructed two cross-domain medical image datasets: homologous and heterologous datasets. The homologous cross-domain medical image dataset consisted of three publicly available datasets on COVID-19.

The first dataset contained 9 CT scans from the website³⁴. Its annotations consisted of the lung masks and COVID-19 lesion masks segmented by a radiologist.

The second dataset^35,36,37 contained 20 shared volumetric CT scans. The left and right lungs and the infection were labeled by two radiologists and then validated by an experienced radiologist.

The third dataset was provided by the Municipal Hospital in Moscow, Russia³⁸. A subset of this dataset related to COVID-19 had been annotated and the CT scans were obtained between March 1, 2020 and April 25, 2020.

The heterologous cross-domain medical image dataset consisted of one private dataset and three public datasets, namely, the 2018 Left Atrium Segmentation Challenge Dataset, the Lung Vein CT Dataset from the Second Hospital of Shanxi Medical University, the 2022 MICCAI Left Atrium Segmentation Challenge Dataset, and the Left Atrium Segmentation Dataset of King’s College London.

The 2018 Left Atrium Segmentation Challenge Dataset was from the University of Utah (The NIH/NIGMS Center for Integrative Biomedical Computing (CIBC) and several research institutes)³⁹. The challenge aimed to propose an intelligent fully automated left atrium (LA) segmentation algorithm for the accurate reconstruction and visualization of atrial structures. The dataset included 3D gadolinium-enhanced magnetic resonance imaging (LGE-MRI) of 154 atrial fibrillation patients and corresponding ground truth labels. The volume size of the data was 576 × 576 × 88. The pixel spacing was 0.625 × 0.625 × 0.625 mm.

The Lung Vein CT Dataset was from the Second Hospital of Shanxi Medical University. To protect patients’ privacy, all personal data had been de-identified. The dataset included CT scans of the lung veins from 150 patients with the scan slice thickness of 5 mm and 0.625 mm. The 5-mm non-contrastive CT scans of each patient were selected for the experiment and a radiologist from the Second Hospital of Shanxi Medical University annotated the left atrium in CT scans. The volume size of the data was 512 × 512 × (400–600). The pixel spacing was 0.933 × 0.933 × 0.625 mm.

The 2022 MICCAI Left Atrium Segmentation Challenge, known as LAScarQS (Left Atrial and Scar Quantification & Segmentation Challenge)^40,41,42, is a dataset on atrial fibrillation patients. The data were sourced from three centers, in which different scanning devices and resolutions were adopted. The dataset included both pre-ablation and post-ablation LGE MRI scans, The data contained LGE MRI data and corresponding ground truth labels of 130 patients. The volume size of the data was (576–640) × (576–640) × (44–88) and the pixel spacing was (0.625–1.0) × (0.625–1.0) × (1.0–2.5) mm.

The Left Atrium Segmentation Dataset of King’s College London was from the 2018 Medical Image Segmentation Decathlon (MSD) Competition⁴³. This dataset included 30 monomodal MR images. The volume size of the data was 320 × 320 × (90–130) and the pixel spacing was 1.25 × 1.25 × 1.37 mm.

Evaluation metrics

Various metrics, including Dice Similarity Coefficient (DSC), Jaccard Similarity Coefficient (JSC)⁴⁴, and 95% Hausdorff Distance (HD95)⁴⁵, were often used to evaluate the performance of image segmentation models in related medical studies.

DSC represents the overlap between the ground truth G and the predicted result S:

$${\text{DSC}} = \frac{{2\left| {S \cap G} \right|}}{\left| S \right| + \left| G \right|}$$

(17)

JA represents the set similarity between the ground truth G and the predicted result S:

$${\text{JA}} = \frac{{\left| {S \cap G} \right|}}{{\left| {S \cup G} \right|}}$$

(18)

HD₉₅ represents the quantified value of 95% of the maximum distance in the surface distance between the predicted results and the labels:

$${\text{HD}}_{95} = \max_{k95\% } \left[ {d\left( {S,G} \right),d\left( {G,S} \right)} \right]$$

(19)

Implementation details

The used deep learning framework was PyTorch 1.9.0 + cu111 in the experiments. The used CPU was an AMD Ryzen 9 9950X and the used GPU setup consisted of two NVIDIA GeForce RTX 3090 with 48 GB of VRAM. The system memory was 64 GB. The network was trained by using the Adam optimizer with a weighted combination loss function, a batch size of 4, and an initial image size of 256 × 256. Fifty training iterations were performed. To ensure reliable experimental results, comparative experiments were performed under the same experimental conditions.

Comparative experiments with existing methods

The proposed model was compared with common methods used in medical image segmentation, including SSL methods, domain adaptation methods, and SSDA methods. The U-Net was firstly trained with labeled target domain data and defined as a baseline model. From the perspective of domain adaptation, the proposed method was compared with UDA methods and multimodal learning methods (MML). Two UDA methods^46,47 were used for comparison. MML methods in this section included several methods, in which different strategies were adopted to share modal knowledge, including knowledge distillation proposed by DOU et al.⁴⁷, mutual learning (MKD) proposed by Li et al.⁴⁸, and appearance alignment model proposed by CAI et al.⁴⁹. The proposed method was compared with SSL method, FixMatch⁵⁰, which had been successfully applied in many semi-supervised image segmentation benchmark tests. The proposed method was further compared with UA-MT⁵¹, ConfKD⁵², and MUE-CoT⁵³, which used self-integrated models for image segmentation. Finally, the proposed method was compared with two SSDA methods: Dual-Teacher +  + ²⁷ and IDMNE⁵⁴.

To simulate the real-world data distribution, the following configurations were set for the two datasets. In the homologous dataset, the first subset of data was designated as the target domain, whereas the remaining subsets were considered as the source domain. In the heterologous dataset, the Lung Vein CT dataset from the Second Hospital of Shanxi Medical University was set as the target domain, whereas the remaining MRI data subset was set as the source domain. For UDA methods, the data in the target domain were unlabeled. For semi-supervised and SSDA methods, the target domain data contained partial labels (10% and 5%).

To ensure experimental fairness, all methods in this study were implemented with the same optimizer, learning rate decay, data preprocessing, and structural and hyperparameter settings as those used in this experiment. Additionally, in the above comparison, some models used U-Net and the feature scale was uniformly set to 2. The number of filters was set to be [32, 64, 128, 256, 512]. To eliminate randomness, the average value from three separate runs with different random seeds was computed and experimental results were re-checked in this section.

The unlabeled data $\user1{\mathcal{D}}_{U}$ and cross-domain data $\user1{\mathcal{D}}_{S}$ could be well utilized with the proposed method in this section on the homologous dataset. When the percentage of data with labels in $\user1{\mathcal{D}}_{T}$ was 10%, compared to the best methods in SSL, MML, UDA, and baseline models, the proposed method respectively improved the average DSC by 4.7%, 6.7%, 17.1%, and 22.1%, decreased the average HD95 by 1.324 mm, 3.846 mm, 3.549 mm, and 12.584 mm, and increased the average JA metrics by 7.3%, 10.1%, 23.9%, and 29.7%. When the percentage of data with labels in $\user1{\mathcal{D}}_{T}$ was 5%, compared to the best methods in SSL and MML, and baseline models, the proposed method respectively improved average DSC by 2.6% and 5.7%, decreased the average HD95 by 0.403 mm and 0.643 mm, and increased the average JA by 3.9% and 8.1%.

Some segmentation results are visualized in Fig. 5. The method proposed in this section yielded more accurate COVID-19 lesion segmentation maps in the homologous dataset than other methods.

Fig. 5

Visualization of segmentation results of different models on homologous dataset.

The unlabeled data and cross-domain data could be well utilized with the method proposed in this section on heterologous datasets. Under the condition of 10% labeled data, compared to the best methods in SSL, MML, UDA and baseline models, the proposed method respectively improved average DSC by 5.3%, 10.2%, 15.7%, and 25.1%, decreased average HD95 by 0.012 mm, 2.248 mm, 13.332 mm, and 10.814 mm, and increased average JA by 7.5%, 14%, 20.7% and 30.7%. Under the condition of 5% labeled data, compared to the best methods in SSL and MML, the proposed method respectively improved average DSC by 7.9% and 9.3%, decreased average HD95 by 0.037 mm and 0.321 mm, and increased average JA by 10.4% and 12.3%.

Some segmentation results are visualized in Fig. 6. The method proposed in this section provided more accurate left atrial segmentation maps for pulmonary vein CT in heterologous datasets than other methods.

Fig. 6

Visualization of the segmentation results of various models on the heterologous dataset.

Ablation experiments

In this study, inter-domain contrastive alignment and style contrastive alignment were two key modules. In order to verify their roles in this study, three sets of ablation experiments were designed in this section on the source domain dataset $\user1{\mathcal{D}}_{S}$ with a label proportion of 5%. In the first group of experiments, only the labeled target domain data $\user1{\mathcal{D}}_{T}$ was used to train U-Net. In the second group of experiments, the source domain data $\user1{\mathcal{D}}_{S}$ and the labeled target domain data $\user1{\mathcal{D}}_{T}$ were used in the training process and the inter-domain contrastive alignment was introduced. In the third group of experiments, the unlabeled target domain data $\user1{\mathcal{D}}_{U}$ and the labeled target domain data $\user1{\mathcal{D}}_{T}$ were used in the training process and the style contrastive alignment was introduced. Obviously, the segmentation performance obtained with both inter-domain contrastive alignment and style contrastive alignment was much better than that of other three ablation experiments (Table 3). The application of inter-domain contrastive alignment and style contrastive alignment improved average DSC by 3.6% ~ 9.9%, decreased average HD95 by 0.134 mm ~ 9.044 mm, and increased average JA by 4.9% ~ 13%.

Analysis of label proportion sensitivity

In order to explore the influence of target domain samples with label proportions on the sensitivity of segmentation results, a set of comparative experiments were designed in this section. In this experiment, target domain data $\user1{\mathcal{D}}_{T}$ with different label proportions of 5%, 7%, and 10% were selected for training. The experimental results are shown in Fig. 7. Obviously, the average DSC of the method proposed in this study increased with the increase of the proportion of labeled data, and the value distribution of DSC was also relatively stable.

Fig. 7

DSC distribution diagram with different label proportions.

Analysis of weighting factor selection

To explore the effect of momentum $m$ in inter-domain comparison alignment on segmentation results, a group of comparison experiments were designed under different combinations of common momentums in this section (Table 4). The segmentation performance under the weighting factor of $m = 0.9$ was significantly improved compared with that under other weighting factor settings. DSC and JA were respectively improved by 1.2% ~ 1.5% and 1.7% ~ 2.1% and HD95 was decreased by 1.816 mm ~ 5.887 mm. Therefore, the value of $m = 0.9$ was selected in subsequent experiments.

To investigate the effects of inter-domain style loss weights $\lambda_{1}$ and $\lambda_{2}$ on segmentation results, a group of comparison experiments were designed under different combinations of weighting coefficients in this section (Table 5). The segmentation performance under the weighting coefficients of $\lambda_{1} = \lambda_{2} = 0.5$ was significantly improved compared with that under other weighting factor settings. DSC and JA were improved by 1.8% ~ 3% and 2.4% ~ 4.2% and HD95 was decreased by 0.225 mm ~ 1.373 mm. Therefore, the setting of $\lambda_{1} = 0.5,\lambda_{2} = 0.5$ was chosen in subsequent experiments.

Analysis of complexity

The complexity of the proposed method was analyzed and the FLOPs and parameters of all semi-supervised methods and semi-supervised domain adaptation methods discussed above were provided below. In the experiments, the heterologous dataset with a label proportion of 5% was selected and the input image size was set as 1 × 256 × 256. Our method consisted of two models based on U-Net ⁵¹ without any additional network structure (Table 6). Furthermore, compared to the listed SSDA methods, the proposed method realized the best performance with acceptable parameters and computational complexity, which further validated the effectiveness of our method.

Discussion and conclusions

In this study, a novel dual-level multi-scale alignment SSDA method was proposed to better learn cross-domain features of medical images and further improve the performance of cross-domain image segmentation models. To validate the effectiveness of our method and simulate the real data distribution, two cross-domain medical image datasets (homologous and heterologous datasets) were constructed separately and the target data in each dataset contained partial labels (i.e., 10% and 5%). Our study aligned the network outputs respectively at style level and inter-domain level. Firstly, at the style level, feature extraction was performed with multiscale feature extraction module (MSFE) and the unlabeled target image features and the enhanced unlabeled target image features were maximally aligned. At the inter-domain level, mixed image data and target domain images with labeled data were computed with the network. The centers of mass of the two image segmentation categories were computed separately by CFEM. Finally, inter-domain contrastive alignment was performed to maximize the similarity of centroids of the same class across different domains. In the framework, weighted loss, multi-scale feature loss, supervised loss and alignment loss were used to construct the overall constraint objective.

The proposed model was compared with SSL methods, UDA methods, and SSDA methods commonly used in medical image segmentation. Our method realized the competitive results from both homogeneous and heterologous datasets compared to other methods such as baseline models (Tables 1 and 2). Moreover, several groups of ablation experiments were designed to validate the structure and parameters in the framework based on the consideration of the effects of inter-domain contrastive alignment, style contrastive alignment (Table 3), the analysis of the proportion of sample labels in the target domain (Fig. 7), momentum choices in the inter-domain contrastive alignment (Table 4), and the inter-domain style loss weight coefficients (Table 5). The ablation experiments verified the rationality and effectiveness of various parts of the proposed method. Subsequently, the model was analyzed based on the number of parameters and FLOPs. Our method realized the best performance with acceptable parameters and computational effort (Table 6).

Table 1 Performances of various methods on the homologous dataset with different proportions of labels.

Table 2 Performance comparison of different methods on the heterologous dataset with different proportions of labels.

Table 3 Ablation results for inter-domain/style contrastive alignment structures.

Table 4 Segmentation results obtained with different momentum combinations in inter-domain contrastive alignment.

Table 5 Segmentation results with different inter-domain style loss weight coefficients.

Table 6 Parameter performance and complexity of selected methods.

The manual annotation of medical images is a challenging and costly process and labeled data are scarce in real-world research. In real clinical scenarios, different imaging devices (e.g., different models of computed tomography devices or magnetic resonance imaging devices) may produce different image characteristics. For exmaple, the field strength magnitude in magnetic resonance imaging devices has a great influence on the imaging quality of MRI. Therefore, it is necessary to explore SSDA methods for medical image segmentation. Our approach was designed based on the consideration of the generalization ability of imaging modalities in a wide variety of 2D medical images. In the study, we only showed the SSDA task based on two kinds of representative imaging data. The core module of the framework is robust and can be applied in other common 2D imaging modalities. Implementing our framework in 3D images is complex due to higher computational cost and longer training time. However, the spatial information contained in 3D medical images are significant for more accurate segmentation and assisted diagnosis. Therefore, in future work, we will apply SSDA methods in 3D imaging.