Introduction

A lot of scientists are interested in both periodic and non-periodic photonic crystals (PCs), which are made of dielectric materials that change their refractive indices (RIs) over time1,2,3,4,5,6. The regular configuration of the RIs results in the photonic bandgap (PBG), which is the most notable characteristic of PCs7,8,9,10. A specific wavelength or frequency of propagating electromagnetic waves (EMWs) will not be allowed to pass through PCs and be reflected within the range of PBG11,12. 1D-PCs are constructed materials with different RIs, arranged in alternate multilayered patterns. 1D-PCs offer effective purposes in different fields of sensors, smart windows, etc. Porous silicon (PSi) has garnered increasing attention in several sectors and PC structures due to its high sensitivity (S) and large surface area13,14,15. PSi preparation technology is one of the quickest and easiest ways to create PC structures13,14. A quasi-configuration that has gained significant interest in detection fields is the Cantor sequence PCs (CS-PCs)16,17,18. Zaky et al.19 proposed a RI detector with outstanding performance using a CS-PC configuration of gyroidal graphene and PSi. The unique properties and advantage of CS-PC configuration is the ability to simultaneously establish a coupling between many types of resonance. This coupling strongly enhances the sensitivity of sensors19.

Highly efficient solid-state detectors for radiation are widely used in various fields, including scientific investigations, industrial inspection, military purposes, medical diagnostics, and therapy20,21,22,23,24,25,26,27. One of the most popular detectors for data collection is the photodetector28. Gamma radiation has been employed extensively in numerous medical dosimetry for stereotactic radiosurgery29, environmental monitoring30, industrial31, and others applications32,33. Nuclear power plants must continuously monitor environmental pollutants, both within and outside their boundaries, to control radiation pollution34.

Polymer nanocomposites (PNCs) can be prepared by forming ionic chain or networks within the geometry of polymers by dissolving salts within the matrix of polymers35. PNCs have emerged as a potentially useful class of energy storage and conversion application components. PNC’s distinct structures offer excellent ionic conductivity, great mechanical and thermal stability, and broad electrochemical stability. PNCs have attracted more attention as active materials in potential applications, including batteries, supercapacitors, fuel cells, and radiation detectors35,36,37,38,39. PNCs are low-cost, flexible, and can be simply formed into films. Bich et al.40 used indigo dye samples for radiation sensing with \(S =0.0002\)nm/Gy. Zaky et al.41 designed a CS-PC using PSi contains a polymer of Poly Vinyl Alcohol, carbol fuchsin, and crystal violet to detect gamma radiation. Besides, Kher et al.42 discussed the ability to use long-period gratings as a radiation detector with \(S = 0.00018\) nm/Gy. A radiation detector with \(S =0.0012\)nm/Gy was practically and theoretically built in 2018 by Stancalie et al.43 utilizing long-period gratings.

Using PCs in gamma detection is a cutting-edge approach to improve radiation detection systems’ sensitivity, selectivity, and functionality. Furthermore, PCs allow for the miniaturization of gamma detectors while maintaining high performance and open the door to portable or embedded radiation detection systems. In order to detect and measure radioactive items in public areas, shipping containers, and security checkpoints, high-sensitivity gamma detectors are essential. They can help protect national and international security by spotting the illegal movement of nuclear materials.

In this study, CS-PCs separated by a sensitive PSi layer doped with poly nanocomposite of ethylene oxide (PNCEO) is designed as a gamma indicator. The RIs of PNCEO before and after irradiation at different concentrations of potassium iodide (KI) are fitted from experimental data35. The effect of doping PNCEO with different concentrations of KI is investigated. Besides, number of CS-PCs cells and the porosity of PSi are investigated to achieve high performance. The proposed detector offers high sensitivity, excellent Q-factor, and strong performance in low-dose gamma detection, making it a promising candidate for precise and reliable radiation monitoring applications.

Theoretical model and basic equations

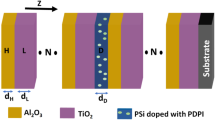
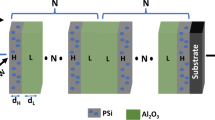
This section outlines the theoretical framework and key equations utilized to analyze the data and interpret the results. Figure 1 is the schematic representation of CS-PC defected with nanocomposite of poly(ethylene oxide) doped with Potassium Iodide as Cantor 1D-PC of \(\left[\text{A}\text{i}\text{r}\text{*}{\left(\text{H}\text{L}\text{H}\text{L}\text{L}\text{L}\text{H}\text{L}\text{H}\right)}^{N}\text{*}\text{D}\text{*}{\left(\text{H}\text{L}\text{H}\text{L}\text{L}\text{L}\text{H}\text{L}\text{H}\right)}^{N}\text{*}\text{S}\text{i}\:\text{S}\text{u}\text{b}\text{s}\text{t}\text{r}\text{a}\text{t}\text{e}\right]\). Layers H, L, and D are \(Ti{O}_{2}\), \({Al}_{2}{O}_{3}\), and PSi contains PNCEO, respectively. The thicknesses of high RI (\(H\)), low RI (\(L\)) and defect (\(D\)) layers are 200 nm, 150 nm, and 110 nm, respectively. The porosity of PSi layer is 10% (as initial condition and it will be optimized later). \(N=5\) denotes how many times the cantor sequence is repeated. θ of 0 degrees is the angle of incidence of EMWs from air to CS-PC. The RIs of substrate and air are 1.52 (SiO2) and 1, respectively. As will be discussed in the “Results and discussion” section, the above parameters are selected to adjust the PBG in the stable range of refractive indices. PNCEO is considered a sensitive medium for radiation. Doping of PNCEO in silicon is done to control the sensitivity and prevent the overlap of peaks, as we will discuss later.

Fig. 1
figure 1

Schematic structure of CS-PC defected with nanocomposite of poly(ethylene oxide) doped with Potassium Iodide.

Full size image

The RIs of \(Ti{O}_{2}\), and \({Al}_{2}{O}_{3}\) can be calculated as follows (\(\lambda\) in µm)44:

$${n}_{TiO2}^{2}=1.786377+\frac{ 1.730580 {\lambda }^{2}}{{\lambda }^{2}-{0.258114}^{2}}+\frac{ 1.142411{\lambda }^{2}}{{\lambda }^{2}-{0.258073}^{2}},$$
(1)
$${n}_{\text{A}\text{l}2\text{O}3}^{2}=-2.012168+\frac{ 4.352187{\lambda }^{2}}{{\lambda }^{2}-{0.045773}^{2}}+\frac{ 0.117166{\lambda }^{2}}{{\lambda }^{2}-{0.187027}^{2}}.$$
(2)

Bruggeman’s effective equations are utilized for calculating the PSi RI45:

$$\begin{aligned} &{\text{n}}_{\text{P}\text{S}\text{i}} =0.5\sqrt{{\uppsi}+\sqrt{{{\uppsi}}^{2}+8\:{\text{n}}_{\text{s}\text{i}}^{2}\:{\text{n}}_{\text{P}\text{N}\text{C}\text{E}\text{O}}^{2}}}, \\ & {\uppsi}=3\text{P}\:\left({\text{n}}_{\text{P}\text{N}\text{C}\text{E}\text{O}}^{2}-{\text{n}}_{\text{s}\text{i}}^{2}\right)+\left(2\:{\text{n}}_{\text{s}\text{i}}^{2}-{\text{n}}_{\text{P}\text{N}\text{C}\text{E}\text{O}}^{2}\right),\end{aligned}$$

where \({\text{n}}_{\text{S}\text{i}} =3.7\) and \(P\) is the ratio of PNCEO in PSi. The final form of PSi layers will not contain pores. It will be Si doped with polymer. The effect of gamma radiation on \(Si\), \(Ti{O}_{2}\), and \({Al}_{2}{O}_{3}\) can be neglected44,46,47. The refractive indices of PNCEO before and after exposure to gamma radiation at various KI concentrations can be determined within the range of 0.30 μm to 0.80 μm35:

For 0 Gy of Gamma radiation:

At 0% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-\:50.99\:{\lambda}^{3} + 109.7{\:\lambda}^{2} - 78.54\:\lambda + 20.21.$$
(4)

At 2% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-\:46.95\:{\lambda}^{3} + 105.8{\:\lambda}^{2}-78.89\:\lambda + 21.39.$$
(5)

At 6% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-\:60.4\:{\lambda}^{3} + 131.5{\:\lambda}^{2} - 95.17\:\lambda + 25.18.$$
(6)

At 10% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-\:73.35\:{\lambda }^{3} + 156.2{\:\lambda}^{2} - 110.6\:\lambda + 28.81.$$
(7)

At 15% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-\:72.09\:{\lambda }^{3} + 152.8{\:\lambda}^{2} - 107.7\:\lambda + 28.65.$$
(8)

For 100 Gy of Gamma radiation:

At 0% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=1267.32\:{\lambda}^{6}-\:4530.09\:{\lambda}^{5}+6714.24\:{\lambda}^{4} -\:5289.53{\lambda}^{3}+2341.49{\:\lambda}^{2}-\:554.456\:\lambda + 61.5716.$$
(9)

At 2% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-\:1488.09\:{\lambda}^{6}+ 4895.6\:{\lambda}^{5}- 6459.26\:{\lambda}^{4}+4310.89\:{\lambda}^{3}-1491.21{\lambda}^{2}+236.067\:\lambda-\:3.60999.$$
(10)

At 6% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=- 1182.16{\:\lambda }^{6}+ 3396.84{\lambda}^{5}- 3650.39{\lambda }^{4} + 1664.29{\:\lambda}^{3}- 151.357{\:\lambda }^{2}- 111.995 \lambda + 33.0753.$$
(11)

At 10% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=- 1893.5756\:{\lambda }^{6} + 5662.3128{\:\lambda }^{5}- 6482.5177{\:\lambda }^{4}+ 3388.8925{\:\lambda }^{3}- 652.19091{\:\lambda}^{2}-\:62.673597\:\lambda +35.444653.$$
(12)

At 15% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-12267.773\:{\lambda}^{6}+41466.212{\:\lambda}^{5}-56985.283{\:\lambda}^{4}+40557.169{\:\lambda}^{3}-15652.727{\:\lambda}^{2}+3069.8131\lambda-226.99954.$$
(13)

For 200 Gy of Gamma radiation:

At 0% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=41.43\:{\lambda}^{4}-101.9{\:\lambda}^{3}+93.13{\:\lambda}^{2}-37.84\lambda+14.15.$$
(14)

At 2% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=48.272\:{\lambda}^{4}-119.4{\:\lambda}^{3}+109.444{\:\lambda}^{2}-44.2615\:\lambda+15.1746.$$
(15)

At 6% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=949.75067\:{\lambda}^{6}-3433.6385{\:\lambda}^{5}+5125.2784{\:\lambda}^{4}-4043.0836{\:\lambda}^{3}+1778.3724{\:\lambda}^{2}-414.05+48.834.$$
(16)

At 10% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=5351.9877\:{\lambda}^{6}-18789.386{\:\lambda}^{5}+27120.403{\:\lambda}^{4}-20591.516{\:\lambda}^{3}+8671.926{\:\lambda}^{2}-1921.0129\:\lambda+183.98745.$$
(17)

At 15% KI:

$${n}_{\text{P}\text{N}\text{C}\text{E}\text{O}}=-48.248516\:{\lambda}^{6}-130.7218{\:\lambda}^{5}+698.57593{\:\lambda}^{4}-987.25331{\:\lambda}^{3}+642.74304{\:\lambda}^{2}- 202.43792\:\lambda+36.135108.$$
(18)

The above equations are fitted from experimental data35 using nonlinear least squares fitting. This method minimizes the difference between the experimental data and the predicted Sellmeier equations. KI was chosen for the initial investigation because PNCEO films are frequently prepared using KI salts as a dopant to enhance the conductivity of PNCEO films. The conductivity of PNCEO films is enhanced because the negative charges on the PEO chains are neutralized by the counterion function of the K+ ve ions. Besides, I− ve ions have the ability to help PEO chains create complex ions, which will further increase conductivity35.

The transfer matrix method (TMM) will be used to find the transmittance (T) of transverse electric (TE) EMWs moving through the CS-PC detector before and after gamma radiation3,48,49,50:

$$T\:\left(\%\right)=100\times \frac{{p}_{s}}{{p}_{0}}{\lfloor t \rfloor}^{2},$$
(19)

where,

$$t=\frac{2{p}_{0}}{\left({A}_{11}+{A}_{12}{p}_{s}\right){p}_{0}+\left({A}_{21}+{A}_{22}{p}_{s}\right)},$$
(20)
$$\left|\begin{array}{cc}{A}_{11}& {A}_{12}\\ {A}_{21}& {A}_{22}\end{array}\right|={\left({a}_{H}{a}_{L}{a}_{H}{a}_{L}{a}_{L}{a}_{L}{a}_{H}{a}_{L}{a}_{H}\right)}^{N}*{a}_{D}*{\left({a}_{H}{a}_{L}{a}_{H}{a}_{L}{a}_{L}{a}_{L}{a}_{H}{a}_{L}{a}_{H}\right)}^{N},$$
(21)
$${p}_{i}={n}_{i} cos\left({\theta }_{i}\right),\:i=\text{H},\:\text{L},\:\:\text{a}\text{n}\text{d}\:D,$$
(22)

where \({p}_{0}\) is for air and \({p}_{s}\) is for substrate. TMM has already been applied to design sensors19,51,52,53,54, filters55, and other simulations.

Wang et al.56 investigated the reflectance of a 1D reflector using 1DPC both theoretically and empirically (using TMM) with very good matches. Gutierrez et al.57 modeled and fabricated a chemical, optical, and thermal sensor. The experimental and numerical (using TMM) results coincided with each other.

Results and discussion

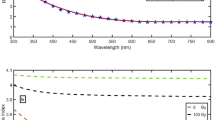
This section presents the results of the study, including the impact of gamma radiation on the refractive index and the performance of the proposed dosimeter. A detailed discussion of the findings and their implications is provided. Figure 2A–E shows the RIs of PNCEO at different doses from 0 Gy to 100 Gy, and 200 Gy by changing the concentration of KI in PNCEO from 0 to 2%, 6%, 10%, and 15%. By growing the gamma doses from 0 to 200 Gy, RI of PNCEO substantially increases. When gamma rays hit polymer composites, they break chains, which leads to changes such as cross-linking, releasing, absorption by carbon, formation of interband states, a smaller energy gap, and a higher RI58,59. The inverse relation between RI and energy gap theoretically agrees with Penn model60.

Fig. 2
figure 2figure 2

Fitted and measured35 RIs of PNCEO at different doses (0 Gy, 100 Gy, and 200 Gy) by changing the concentration of KI in PNCEO from (A) 0%, (B) 2%, (C) 6%, (D) 10%, and (E) 15%.

Full size image

The RIs of PSi doped with 10% of PNCEO at different doses from 0 Gy to 100 Gy, and 200 Gy with changing the concentration of KI in PNCEO from 0%, to 2%, 6%, 10%, and 15% are clear in Fig. 3A–E. As clear in Fig. 2, by increasing the gamma doses, the RI of PNCEO substantially increases, and the RIs of PSi doped with 10% of PNCEO increase, according to Eq. (3). For wavelengths lower than 550 nm, the RI of PSi strongly decreases versus wavelength. For \(550\:nm\le\lambda \le 800\:nm\), the RI of PSi seems more stable. As a result, the range of wavelengths of \(550\:nm\le \lambda \le 800\:nm\) is a good choice for the proposed detector. At 800 nm and gamma doses of 0 Gy, the RI of PSi increases from 3.480 to 3.522, 3.555, 3.602, and 3.667 with changing the concentration of KI in PNCEO from 0%, to 2%, 6%, 10%, and 15%. For gamma doses of 100 Gy, the RI of PSi increases from 3.922 to 3.933, 3.952, 3.959, and 3.967 with changing the concentration of KI in PNCEO from 0%, to 2%, 6%, 10%, and 15%. For gamma doses of 200 Gy, the RI of PSi increases from 4.043 to 4.052, 4.071, 4.076, and 4.146 with changing the concentration of KI in PNCEO from 0%, to 2%, 6%, 10%, and 15%.

Fig. 3
figure 3figure 3

RIs of PSi doped with PNCEO at different doses (0 Gy, 100 Gy, and 200 Gy) with changing the concentration of KI in PNCEO from (A) 0%, (B) 2%, (C) 6%, (D) 10%, and (E) 15%.

Full size image

It can be observed that the change in RI of PSi due to changing gamma doses from 0 Gy to 200 Gy is 0.563, 0.530, 0.516, 0.474, and 0.479 at concentrations of KI in PNCEO from 0%, to 2%, 6%, 10%, and 15%, respectively. This means that doping PNCEO with KI has a negative effect on the change in RI of PSi due to changing gamma doses from 0 Gy to 200 Gy. As the idea of the proposed detector builds on the RI change of defect layer (PSi doped with PNCEO), PSi layer will be doped with PNCEO at 0% concentration of KI.

Fig. 4
figure 4

The proposed CS-PC’s transmittance (A) with and without PSi doped with PNCEO defect (black line vs. red line) and when gamma dose is not present (B) with PSi doped with PNCEO defect at gamma doses of 0 Gy, 100 Gy, and 200 Gy.

Full size image

Through simulating a CS-PC without a defect cavity using the transfer matrix method (TMM) (Fig. 4A), a photonic bandgap (PBG) extends from 592.3 nm to 617.2 nm due to the refractive index difference between the layers. Separating two CS-PC with a \(PSi\) doped with PNCEO defect creates a distinct peak inside the PBG at 598.5 nm. By increasing the gamma doses from 0 Gy to 100 Gy, and 200 Gy, the RI of PSi doped with 10% of PNCEO substantially increases, and the distinct peak is shifted from 598.5 nm to 605.9 nm, and 607.8 nm, as clear in Fig. 4B. This dependence between the effective RI of the device and distinct peak position (\({\lambda }_{d}\)) is explained according to the standing wave relation:

$$m{\lambda }_{d}={n}_{eff}D,$$
(23)

where \(\:m\) and D are integer and geometric path difference. By increasing RI of doped PSi of defect, the effective RI increases, and the \(\:{\lambda\:}_{d}\) increases. Any sensor begins to function better when it has low bandwidth (FWHM), high S, high quality-factor (Q), high figure of merit (FoM), and low detection limit (LoD) according to the following formulas:

$$S=\frac{\varDelta {\lambda }_{d}}{\varDelta\gamma},$$
(24)
$$FoM=\frac{S}{FWHM},$$
(25)
$$Q=\frac{{\lambda }_{d}}{FWHM},$$
(26)
$$LoD=\frac{{\lambda}_{d}}{20\:S\:Q}.$$
(27)
Fig. 5
figure 5

Transmittance of the proposed CS-PC with PSi doped with PNCEO defect for (A) porosity of 10%, (B) porosity of 15%, (C) porosity of 20%, (D) porosity of 25%, and (E) porosity of 30% at 0 Gy, 100 Gy and 200 Gy gamma doses (\({d}_{H}=200\:nm\), \({d}_{L}=150\:nm\), \({d}_{D}=110\:nm\), and \(N=5\)).

Full size image

As clear in Figs. 5A–E and 6B, increasing the porosity of the defect layer of PSi doped with PNCEO from 10 to 15%, 20%, 25%, and 30% increases the shift between distinct peaks. This increase in shift (\(\varDelta\:{\lambda}_{d}\)) enhances the sensitivity and the function of the sensor. Besides, the transmittances of all distinct peaks are near to 100% due to the good confinement of incident EMW in the cavity of PSi layer, as clear in Fig. 6A. On the right axis of Fig. 6A, increasing the shift moves the distinct peak of 0 Gy close to the left edge of the PBG. As a result, the FWHM increases gradually with increasing the porosity of the defect layer of the PSi doped with PNCEO from 10 to 30%. As FoM and Q have inverse relations with FWHM, they decrease, as clear in Fig. 6B, C. Finally, LoD gradually increases with decreasing Q, according to Eq. (27). If the porosity exceeds 30%, the distinct peaks will no longer be within the photonic bandgap (PBG). So, the porosity of 30% will be selected as a suitable condition.

Fig. 6
figure 6

(A) Transmittance and FWHM at 0 Gy, (B) sensitivity and FoM, and (C) Q and LoD of the proposed CS-PC versus porosity of PSi defect doped with PNCEO (\({d}_{H}=200\:nm\), \({d}_{L}=150\:nm\), \({d}_{D}=110\:nm\), and \(N=5\)).

Full size image

As the is FWHM adversely affected by increasing porosity, N will be exploited to decrease FWHM and make the edges of PBG sharper. Figure 7A–E clear the positive effect of N on decreasing FWHM. It is noted that increasing N higher than 8 cells negatively affects the distinct peak of 100 Gy gamma dose due to backscattering and absorption. At \(N=9\) and 10, the transmittance of 100 Gy gamma dose is 58% and 2%, respectively. The transmittance seems to be unaffected for distinct peaks of 0 Gy and 200 Gy gamma doses. Increasing the cell’s units from 6 to 10 didn’t affect the transmittance of distinct peaks at 0 Gy gamma doses, as clear in Fig. 8A. On the right axis of Fig. 8A, increasing N from 6 cells to 10 cells decreases FWHM from 0.325 nm to 0.009 nm. As a result, FoM and Q increase, as clear in Fig. 8B, C. However, it was unaffected by the changing of N because the position of distinct peaks didn’t change. LoD gradually decreases with increasing Q, according to Eq. (27).

Fig. 7
figure 7

Transmittance of the proposed CS-PC with PSi doped with PNCEO defect for (A) \(N=6\), (B) \(N=7\), (C) \(N=8\), (D) \(N=9\), and (E) \(N=10\) at 0 Gy, 100 Gy and 200 Gy gamma doses (\({d}_{H}=200\:nm\), \({d}_{L}=150\:nm\), \({d}_{D}=110\:nm\), and \(P=30\%\)).

Full size image
Fig. 8
figure 8

(A) Transmittance and FWHM at 0 Gy, (B) sensitivity and FoM, and (C) Q and LoD of the proposed CS-PC versus N (\({d}_{H}=200\:nm\), \({d}_{L}=150\:nm\), \({d}_{D}=110\:nm\), and \(P=30\%\)).

Full size image

From the above investigations, N of 9 cells on both sides of the PSi defect layer is suitable. And yet, they will be verified to ensure that all intermediate values of radiation doses will have suitable transmittance. As we don’t have the RIs of PNCEO at intermediate gamma doses, the RIs of PNCEO at 0 Gy, 100 Gy, and 200 Gy will be determined, and intermediate RIs will be selected. The refractive indices of PSi doped with PNCEO are 3.04, 4.42, and 4.89 at the positions corresponding to 0 Gy, 100 Gy, and 200 Gy, respectively. By taking intermediate RIs, many peaks have very low transmittance, as clear in Fig. 9. So, these conditions are not satisfied for a suitable detector.

Fig. 9
figure 9

Transmittance of the proposed CS-PC by changing the RIs of PSi doped with PNCEO defect from 3.04 (0 Gy) to 3.02, 3.40, 3.60, 3.80, 4.00, 4.20, 4.42 (100 Gy), 4.60, and 4.89 (200 Gy) at \({d}_{H}=200\:nm\), \({d}_{L}=150\:nm\), \({d}_{D}=110\:nm\), \(N=9\), and \(P=30\%\).

Full size image

Besides, a wide PBG is observed at higher wavelengths extended from 724.8 nm to 767.3 nm. By controlling the thickness of the defect (at \({d}_{D}=150\:nm\)), all distinct peaks are adjusted inside the PBG in the correct order. By the same way, at \({\lambda}_{d}=727.91\:\text{n}\text{m}\) (the position of 0 Gy), \({\lambda}_{d}=749.70\:\text{n}\text{m}\) (the position of 100 Gy), and \({\lambda}_{d}=762.82\:\text{n}\text{m}\) (the position of 200 Gy), the RIs of PSi doped with PNCEO is 3.02, 4.41, and 4.88, respectively. By taking intermediate RIs, all peaks have good transmittance, as clear in Fig. 10. So, these conditions are satisfied for a suitable detector.

Fig. 10
figure 10

Transmittance of the proposed CS-PC by changing the RIs of PSi doped with PNCEO defect from 3.02 (0 Gy) to 3.02, 3.40, 3.60, 3.80, 4.00, 4.20, 4.41 (100 Gy), 4.60, and 4.88 (200 Gy) at \({d}_{H}=200\:nm\), \({d}_{L}=150\:nm\), \({d}_{D}=150\:nm\), \(N=8\), and \(P=30\%\).

Full size image

When transitioning from 0 Gy to 100 Gy of gamma radiation, the transmittance of the distinct peak decreases from 96.1 to 88.1%, while the peak shifts from 727.91 nm to 749.70 nm. Additionally, the full width at half maximum (FWHM) increases from \(1.2\times{10}^{-2}\) nm to \(4.4\times{10}^{-4}\) nm, sensitivity is 0.22 nm/Gy, figure of merit (FoM) is 490 \({\text{G}\text{y}}^{-1}\), quality factor (Q) improves, and the limit of detection (LoD) is \(1.02\times{10}^{-4}\) Gy. With increasing the gamma doses from 100 Gy to 200 Gy, the transmittance of the distinct peak increases from 88.1 to 98.5%, the position of the distinct peak is moved from 749.70 nm to 762.82 nm, the FWHM is enhanced from \(4.4\times {10}^{-4}\) nm to \(2.8 \times {10}^{-2}\) nm, the sensitivity is 0.13 nm/Gy, the FoM is 4.65 \({\text{G}\text{y}}^{-1}\), the Q enhanced from \(1.7 \times {10}^{6}\) to \(2.7 \times {10}^{4}\), and LoD is \(1.08 \times {10}^{-2}\) Gy. The decrease in sensitivity at doses exceeding 100 Gy, as shown in Fig. 10, may be attributed to the nonlinear response of the polymer refractive index to gamma radiation35. Table 1 clearly shows that the proposed gamma dose detector containing a defect of PSi doped with 30% of PNCEO has excellent performance in gamma detection, such as sensitivity and Q-factor.

Table 1 Comparison with other gamma doses detectors.
Full size table

The results of this study demonstrate that the optimal design for a highly sensitive gamma radiation detector consists of a defect layer of PSi doped with 30% PNCEO, without KI doping, and an optimum number of 8 photonic crystal cells. The findings indicate that KI doping negatively impacts detector performance, reducing both sensitivity and Q-factor. The proposed detector exhibits high sensitivity of 0.218 nm/Gy and a Q-factor of 1,686,804 for low gamma doses (0–100 Gy), making it highly suitable for low-dose detection applications. For higher gamma doses (100–200 Gy), the sensor maintains a moderate sensitivity of 0.131 nm/Gy with a Q-factor of 27,050, ensuring continued functionality but with reduced efficiency. These results suggest that the designed detector is particularly effective for low-dose gamma radiation detection, with the potential for further optimization in higher dose applications.

Conclusion

The study presented CS-PCs separated by a sensitive PSi layer doped with PNCEO as a gamma indicator. Doping PNCEO with KI has a negative effect on the sensor’s performance. On the other hand, the number of cells, porosity, and thickness of the defect PSi layer are tuned to maximize the indicator performance. This gamma indicator can discriminate between different gamma doses accurately and simultaneously. The proposed detector has a relatively high sensitivity of 0.218 nm/Gy for low doses (from 0 Gy to 100 Gy) and a moderated sensitivity of 0.131 nm/Gy for higher gamma doses (from 100 Gy to 200 Gy). A comparison with similar studies illustrates the exceptional feature of the suggested gamma indicator.