Multi-scale feature fusion and feature calibration with edge information enhancement for remote sensing object detection

Abstract

Vision Transformer-based detectors have achieved remarkable success in the field of object detection, but the application of these models to high-resolution remote sensing imagery faces challenges in computational costs and performance bottlenecks due to the increased computational complexity required to process high-resolution imagery, especially when capturing fine-grained edge features. Therefore, there is significant potential for performance optimization. To address these challenges, we propose an improved EMF-DETR based on RT-DERT-ResNet-18. EMF-DETR introduces a multi-scale edge-aware feature extraction network named MEFE-Net. The network improves object recognition and localization capabilities by extracting multi-scale features and enhancing edge information for targets at each scale, demonstrating exceptional performance in small object detection. To further enhance feature representation, the model introduces the CSFCN method, which adaptively adjusts contextual information and precisely calibrates spatial features, ensuring accurate alignment and optimization of features across different scales. In evaluations on the VisDrone2019 dataset, the proposed method achieved a 2.0% improvement in mAP compared to the baseline model, with increases of 1.5% and 2.6% in small (AP_S) and medium (AP_M) object detection respectively. Meanwhile, the number of parameters was reduced by 20.22%, demonstrating not only improved detection accuracy but also lower computational cost, highlighting its practical application potential in remote sensing image analysis.

Introduction

Object detection in remote sensing imagery has become a critical area of research in computer vision, with significant application potential across various fields, including environmental monitoring, disaster response, land management, and national defense¹. The rapid advancement of high-resolution remote sensing technology enables detailed representation of geospatial targets but also exacerbates the challenges associated with detecting small-scale objects. Unlike regular-sized targets, small-scale objects (such as vehicles and compact structures) in high-resolution images face three primary limitations: (1) limited spatial coverage (often spanning only a few tens of pixels), (2) ambiguous feature representations (with poorly defined edges), and (3) increased susceptibility to imaging noise². These characteristics fundamentally limit the effectiveness of conventional detection methods in complex operational scenarios. For instance, densely distributed geographical elements in high-resolution images introduce severe background interference, while variations in imaging across different platforms increase the uncertainty of target features. To address these challenges, it is essential to develop a robust framework for detecting small-scale objects in high-resolution images. This requires innovative algorithms that enhance feature representation and leverage multi-scale modeling, ultimately enabling precise target recognition and localization in challenging environments.

With the rapid development of deep learning and substantial advancements in hardware computational capabilities, the field of computer vision has made breakthrough progress, particularly in object detection algorithms. Early classical object detectors were primarily based on Convolutional Neural Networks (CNNs), such as the R-CNN series^3,4,5,6, SSD series^7,8, and YOLO series^{9,10,11,12,13,14,15,16,17}. Among these, the R-CNN series models (including Fast R-CNN, Faster R-CNN, and Mask R-CNN) have played a pivotal role in object detection tasks. Through a series of key technological innovations, the R-CNN series has gradually overcome the limitations of earlier models, and the theoretical contributions of the R-CNN series (such as the anchor mechanism and RoI operations) remain fundamental components in modern object detection algorithms. However, despite achieving high detection accuracy, R-CNN models suffer from slow training and inference speeds, poor real-time performance, and limited small object detection capabilities, which hinder their applicability in real-time scenarios. In contrast, the YOLO series models have gained widespread attention due to their computational efficiency and outstanding real-time detection capabilities. However, YOLO models exhibit higher miss rates and lower detection accuracy for small objects, primarily because their representations are compressed into smaller regions after downsampling in feature maps, resulting in sparse features and weakened detail preservation. This presents a significant challenge for small object detection. While CNNs are effective at extracting local features and achieving high precision in object detection and recognition tasks, their convolutional operations have inherent limitations. Specifically, CNNs often struggle to capture global information and cannot explicitly learn long-range dependencies. This limitation makes it challenging to extract meaningful global context from limited features when processing high-resolution images. Therefore, addressing these challenges and enhancing the performance of small object detection performance has become a key research focus in the field.

In recent years, Carion et al.¹⁸ introduced the Detection Transformer (DETR) model, representing a groundbreaking approach that successfully integrated Transformer¹⁹ and self-attention mechanisms into the object detection for the first time. This marks a significant advancement in the field. DETR simplifies the object detection pipeline by providing an end-to-end training framework while eliminating complex components such as Region Proposal Networks (RPN) and Non-Maximum Suppression (NMS) that were commonly used in traditional methods. DETR utilizes object queries and its attention mechanism to extract object-specific features from global information and generates a set of predictions through a feed-forward neural network (FFN). The Hungarian algorithm is then used to assign labels to these predictions. This end-to-end approach not only simplifies the detection process compared to traditional methods but also enhances the model’s adaptability to objects of varying scales, shapes, and quantities. However, despite these significant progress achievements, DETR still faces several challenges in practical applications. For instance, DETR struggles with high computational complexity, slow convergence during training, and optimization issues, particularly in high-resolution image detection tasks. Its performance remains particularly inadequate in scenarios involving small object detection and complex backgrounds. To address these limitations, researchers have proposed several improvements, such as Deformable DETR²⁰ and DN-DETR²¹, which have set the foundation for algorithms like RT-DETR²². These developments suggest that DETR-based methods are gradually maturing. However, DETR’s performance in detecting objects in high-resolution images and real-time applications continues to be limited by computational efficiency and convergence speed issues. Further improvements are still needed, especially for small object detection and complex background handling.

In high-resolution remote sensing images, objects typically appear small and densely packed, resulting in limited pixel information and sparse features. This makes it challenging to distinguish between objects and the background. During the multi-scale feature fusion process, the alignment of low-resolution semantic information with high-resolution detailed features becomes problematic. Additionally, the features of small-scale objects can be easily overwhelmed by larger ones, and background noise is amplified during fusion, further degrading small objects detection performance. To enhance the accuracy of small object detection in high-resolution images, developing more adaptive context modeling methods and optimizing multi-scale feature fusion strategies are imperative. Addressing these issues is fundamental for advancing the field.

To address the challenges of neglecting or losing small objects in complex backgrounds, insufficient multi-scale fusion, limited context modeling, and the ​speed-accuracy trade-off in small object detection, we propose EMF-DETR. This method aims to improve the performance of DETR-based models in small object detection tasks ​through enhanced edge information extraction and dynamic adjustment strategies. The framework comprises three key components: a Multi-Scale Edge Feature Enhancement Backbone (MEFE-Net), a Transformer-based encoder-decoder architecture, and a Context and Spatial Feature Calibration Network (CSFCN)²³. Experimental results demonstrate that our approach effectively overcomes small object detection challenges in high-resolution images, achieving enhanced robustness and ​superior accuracy.

Our main contributions are summarized as follows:

(1) We propose a novel backbone architecture, MEFE-Net, which employs the MSEI Block to divide feature maps into multiple scales via average pooling for enhanced multi-scale feature extraction. At each scale, WTConv²⁴ captures fine-grained image details and high-frequency information of the image, while the EEnhance module improves edge feature representation. This design effectively ​extracts fine details from high-resolution images and strengthens the model’s ​edge perception capability.

(2) To tackle the challenges posed by high-resolution and large-scale remote sensing images in object detection—such as variations in scale, the loss of local details, and inadequate fusion of features across different levels—we present the Context and Spatial Feature Calibration Network (CSFCN) module. The Context Feature Calibration (CFC) module employs a ​cascaded pyramid pooling structure to capture nested contextual information. It aggregates pixel-specific context through similarity-based contextual aggregation, enabling precise calibration. Simultaneously, the Spatial Feature Calibration (SFC) module partitions features along the channel dimension into multiple sub-feature groups. These sub-features are then propagated across respective channels via learnable sampling mechanisms, achieving adaptive spatial feature calibration. This innovative architecture significantly improves overall detection accuracy and robustness.

(3) We comprehensively evaluate the proposed method on the VisDrone2019 dataset²⁵ to evaluate its effectiveness and efficiency. Experimental results demonstrate that our approach not only matches but surpasses current state-of-the-art object detectors in both detection accuracy and computational efficiency, confirming its practical superiority.

Related methods

CNN-based object detection

The evolution of deep learning-based object detection algorithms can be summarized in several key stages. Initially, R-CNN generates region proposals using selective search, cropping each candidate region to input into a CNN for feature extraction. Classification and localization are carried out using a classifier and a linear regression model. While this approach showes promise, it comes with a high computational cost. Next, Fast R-CNN improves upon this method by introducing the Region of Interest (RoI) Pooling layer, which standardizes candidate regions of varying sizes into a fixed-size feature map. This innovation allows for the sharing of features across all candidate regions, thereby enhancing computational efficiency. Faster R-CNN further advances​​ the framework by introducing Region Proposal Networks (RPNs) to generate high-quality candidate boxes in real-time. This development enables end-to-end training and significantly increases detection speed.

Despite improvements in accuracy, many object detection methods still face challenges such as low computational efficiency, limited performance in detecting small and densely packed targets, and complex training and optimization processes. These issues hinder their application in real-time, resource-constrained, or complex scene settings. To address these challenges, single-stage object detectors gradually emerge, with notable models including the SSD series, YOLO series and its variants, the EfficientDet series²⁶, and RefineDet²⁷ models. The SSD (Single Shot Multibox Detector) performs detection across multiple scale feature maps, effectively balancing speed and accuracy, and excels in complex scenes. The YOLO (You Only Look Once) series redefines object detection as a regression task. The first YOLO model transformes object detection into a regression problem, and since then, it has undergone several iterations. YOLOv3 introduces multi-scale predictions and employes a deeper backbone network (Darknet-53), enhancing its feature extraction capabilities. YOLOv5 is known for its highly modular architecture, which allows for easier adjustment, expansion, and deployment, achieving impressive detection performance and speed across various domains. YOLOv7 adoptes dynamic label assignment strategies to improve the detection of multi-scale targets and to reduce the rates of small target misses. YOLOv8 adopts an anchor-free design to directly predict the center point and bounding box dimensions of objects. This simplification of the model structure improves detection accuracy. Finally, YOLOv10 introduces NMS-free (Non-Maximum Suppression) training, achieving competitive performance with low inference latency. The continuous evolution of the YOLO series, especially with the latest version, YOLOv12, has built a concise and efficient framework centered around attention mechanisms, significantly enhancing detection performance while maintaining high detection speed.

The YOLO series is popular in the industry due to its real-time performance, simple architecture, and advantages in multi-scale detection. However, CNN-based object detection models have inherent limitations in local feature extraction. These models struggle to balance global semantic understanding with the retention of fine-grained details. Additionally, they depend on manually designed mechanisms such as anchor boxes and non-maximum suppression, which can limit their performance based on predetermined parameter settings. While they achieve excellent results in object detection tasks, this non- end-to-end architecture hinders the models’ ability to optimize adaptively.

Transformer-based object detection

Vaswani et al.¹⁹ proposed a novel network architecture, the Transformer model, based on the self-attention mechanism, which is used to compute dependencies between input elements and capture global contextual information. This subsequently became a cornerstone in natural language processing and other related fields. Later, researchers attempted to apply the self-attention mechanism in visual detection tasks, leading to the development of the Transformer-based object detection model, which has led a deep learning revolution in the field of object detection and has driven the cutting-edge development of this area through a series of optimizations. By eliminating the need for region proposal-based methods traditionally used in detectors, Transformer-based object detection model introduces an end-to-end detection framework that greatly simplifies the pipeline of conventional approaches. Over time, several improved versions have been proposed to enhance the model’s efficiency and accuracy. Initially, Vision Transformer (ViT) is a model that applies the Transformer architecture to computer vision tasks. Its core idea is to divide an image into multiple patches and treat these patches as a sequence, which is then processed by the Transformer to achieve global modeling. ViT is the first to demonstrate the effectiveness of a pure Transformer architecture in image classification tasks, successfully breaking the dominance of traditional CNNs in visual tasks. DETR (Detection Transformer) (2020) is the first model to employ a Transformer for end-to-end object detection. Its innovative design removes the reliance on anchor boxes and utilizes a standard Transformer architecture to directly predict object categories and bounding boxes. However, DETR faces challenges in training speed, especially when trained on the COCO dataset, where its convergence is slow, and it also has limitations in small object detection. To address these issues, Deformable DETR (2021) introduces a novel deformable attention mechanism. By incorporating deformable convolutions, Deformable DETR is able to flexibly focus on important regions in the image, rather than performing calculations over the entire image, thus significantly improving training speed and performance, particularly for small object detection. DINO (2021) further refines DETR’s training strategy by introducing self-supervised learning techniques aimed at optimizing the model’s performance in the presence of noisy data. The self-supervised learning approach enhances the model’s object recognition capability, providing a substantial advantage in rare object detection tasks. DAB-DETR²⁸ reintroduces learnable anchor boxes into DETR to enable the model to adapt to objects of different sizes while also accelerating model convergence. Group-DETR²⁹ divides objects into different groups for processing and introduces additional supervision. This improvement in the training approach enhances the model’s detection performance and efficiency in complex scenarios. Cascade DETR³⁰ introduces a cascade decoder architecture, progressively refining detection accuracy. Unlike traditional single decoders, Cascade DETR utilizes multiple cascaded decoders to iteratively optimize detection results, improving detection precision, particularly for challenging-to-detect objects. In an effort to further improve the efficiency and accuracy of DETR, Efficient DETR³¹ proposes a computationally more efficient method by modifying the computational mechanism within the Transformer architecture. This modification enables the model to operate more efficiently on large-scale datasets, making it particularly suitable for real-time object detection applications. DETR++³² combines both self-attention and region-based attention mechanisms to further enhance the model’s precision and efficiency, which excels in handling multiple objects in complex scenes, especially when detecting small and overlapping objects. To address the high computational cost of DETR, RT-DETR²² introduces an efficient hybrid encoder design that decouples intra-scale feature interactions and cross-scale feature fusion, enabling more efficient handling of multi-scale features. Additionally, an IoU-aware query selection method is proposed to optimize the initialization of object queries, thereby improving both detection accuracy and efficiency. AO2-DETR³³ addresses the complex processing steps and feature misalignment issues in arbitrary-oriented object detection by introducing a directional proposal generation mechanism, a guided proposal refinement module, and a rotation-aware set matching loss. PR-Deformable DETR³⁴ addresses challenges such as small object detection, size variations, and dispersed object distribution by introducing an adaptive feature fusion pyramid network, a Res-Deformable Encoder, and a dynamic reference point module decoder. BiF-DETR³⁵ combines CNNs and pyramid-pooled transformer blocks, addressing challenges in multi-scale and small object detection, semantic differences in feature maps, and data imbalance with a Coordination Attention mechanism and Cascade Mixture Data Augmentation technique.

These models have progressively improved DETR’s performance, incorporating innovations ranging from efficiency optimizations to accuracy enhancements. They not only propel the development of object detection but also lay a solid foundation for addressing more complex application scenarios.

Methods

Overall architecture

This paper adopts RT-DETR-ResNet-18²² as the baseline framework. RT-DETR is an end-to-end object detector based on the DETR architecture, which removes the need for Non-Maximum Suppression (NMS). This design achieves significantly lower latency than traditional CNN-based object detectors like the YOLO series. RT-DETR employs ResNet³⁶ as its backbone, leveraging residual blocks to address vanishing gradients and network degradation in deep architectures. During feature extraction, the stacking of multiple convolutional layers enhances feature representation capability. However, since each convolution operation has a local receptive field, individual kernels can only process localized image regions. Although the receptive field expands with network depth, integrating long-range contextual information remains challenging. This limitation is particularly pronounced when detecting small objects against complex backgrounds.

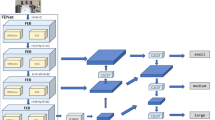
This paper introduces EMF-DETR, an enhanced end-to-end framework for small object detection that extends RT-DETR with innovative multi-scale edge information extraction and feature calibration. As illustrated in Fig. 1, EMF-DETR comprises three core components: (1) MEFE-Net - a multi-scale edge feature enhancement backbone, (2) a Transformer encoder-decoder for prediction generation, and (3) CSFCN (which effectively mines contextual and spatial information). First, MEFE-Net functions as the backbone for feature extraction. It incorporates a built-in Multi-Scale Edge Information (MSEI) module that integrates edge information from feature maps of different scales, resulting in multi-scale feature maps (S3-S5). Next, the AIFI module processes the lowest-resolution S5 feature map. It performs intra-scale feature interaction using attention mechanisms to fuse contextual information at each spatial location, ultimately producing a refined feature map, F5. The feature maps S3, S4, and F5 undergo further processing through the Cross-Scale Feature Fusion Module (CCFM), a CNN-based component that models cross-scale dependencies. This module facilitates interaction between features across scales, improving the representation of key features while minimizing redundant information and ensuring high-quality cross-scale feature representations. Subsequently, contextual features are refined using the CFC module, while spatial features are calibrated through the SFC module. An Uncertainty-Minimal Query Selection strategy is applied to the integrated features, prioritizing high-confidence queries for decoder input. This approach ​reduces detection ambiguity during the process. Finally, the decoder and detection head decode the optimized query features to generate bounding boxes and classification results for the objects.

The proposed EMF-DETR effectively handles small object detection, resolving feature integration issues for objects of different scales in complex backgrounds.

Fig. 1

Overall structure of the proposed model.

Multi-scale edge feature enhancement backbone

Module structure

In high-resolution remote sensing image object detection, models face several challenges. These include high false-negative rates for small objects, confusion between objects and their backgrounds, inaccurate boundary localization, limited multi-scale detection capabilities, and heightened sensitivity to noise and interference. In complex backgrounds, such as vegetation and roads, it becomes difficult for the model to differentiate between targets, like vehicles and buildings, and the background, especially when they share similar colors and textures. Target boundaries may appear blurred due to limitations in resolution or occlusions, making it difficult for the model to accurately determine the boundaries. This leads to reduced localization accuracy. For targets that occupy only a few dozen pixels, edge information becomes the most discriminative feature. To tackle these challenges, we propose MEFE-Net, a multi-scale edge feature enhancement backbone that extracts features at various scales and enhances edge information for each scale. This approach significantly improves the distinction between objects and the background, thereby enhancing target localization accuracy and increasing the robustness and precision of small object detection.

The backbone network, as illustrated in Fig. 2, consists of four stages (Stage 1 to Stage 4). Each stage features a combination of convolutional layers and MSEI Blocks, resulting in a five-layer feature pyramid. For an input image of size C×H×W, initial feature extraction is performed using convolutional layers (Conv). In the following stages, feature extraction continues with Conv modules, followed by MSEI Blocks for enhancement. As the network depth increases, the resolution gradually decreases, allowing the network to capture more abstract and higher-order features.

Fig. 2

The overall architecture of MEFE-Net. MEFE-Net adopts a hierarchical network, using convolutional layers to down-sample the input image and extracting features through multiple MSEI Blocks.

The MSEI Block is based on the CSP³⁷ architecture, as shown in Fig. 3. In this structure, the input feature map is partitioned into two branches, each ​processing features independently through dedicated pathways. The mathematical formulation is expressed in Eq. (1):

The input feature map $\:X\in\:{\mathbb{R}}^{C\times\:H\times\:W}$ undergoes a convolution to expand the number of channels and is then evenly split into two parts.

$$\:\begin{array}{c}X_{1},\:X_{2}\:=\:Split(X,\:sizes=(C,\:C\left)\right)\end{array}$$

(1)

where $\:X₁\in\:{\mathbb{R}}^{C\times\:H\times\:W},\:{X}_{2}\in\:{\mathbb{R}}^{C\times\:H\times\:W}$.

Fig. 3

The structure of the MSEI Block. The MSEI Block consists of a 1 × 1 convolutional layer, a CSEI module, and another 1 × 1 convolutional layer, designed for efficient feature extraction and integration.

Following this architecture, the extracted features undergo cross-layer fusion. This design minimizes computational redundancy while preserving feature integrity, promoting stable gradient propagation and thereby improving model training efficiency and feature representation capability.

WaveletTransformConvolution (WTConv)

In CNNs, expanding the receptive field enhances feature detection capability, particularly for complex scenes. However, conventional approaches for receptive field enlargement often result in prohibitive parameter growth, consequently increasing computational overhead and model complexity. As shown in Fig. 4, WTConv represents an innovative large-kernel convolution technique that employs wavelet transforms to mitigate the parameter expansion problem inherent in receptive field scaling. This method achieves equivalent receptive field coverage with substantially fewer parameters. Furthermore, through cascaded operations, WTConv demonstrates enhanced sensitivity to low-frequency signals while superior spatial information preservation.

Fig. 4

Architecture of the WTConv.

WTConv applies a 2D wavelet transforms to individual input channel, enabling the separation of low-frequency and high-frequency information. This 2D wavelet transform utilizes four distinct filters: LL, which captures low-frequency information; LH, which captures horizontal information; HL, which captures vertical information; and HH, which captures diagonal information. As shown in Eq. (2), these filters form an orthogonal basis.

$$\:\begin{array}{c}{f}_{LL}=\frac{1}{2}\left[\begin{array}{cc}1&\:1\\\:1&\:1\end{array}\right]{,f}_{LH}=\frac{1}{2}\left[\begin{array}{cc}1&\:-1\\\:1&\:-1\end{array}\right]{,f}_{HL}=\frac{1}{2}\left[\begin{array}{cc}1&\:1\\\:-1&\:-1\end{array}\right],{f}_{HH}=\frac{1}{2}\left[\begin{array}{cc}1&\:-1\\\:-1&\:1\end{array}\right]\end{array}$$

(2)

Applying these filters, as shown in Eq. (3).

$$\:\begin{array}{c}\left[{X}_{LL},{X}_{LH},{X}_{HL},{X}_{HH}\right]={Conv}_{5\times\:5}\left(\left[{f}_{LL},{f}_{LH},{f}_{HL},{f}_{HH}\right],X\right)\end{array}$$

(3)

Conv represents the convolution operation, $\:{f}_{LL}$ is the low-pass filter, and $\:{f}_{LH},{f}_{HL},{f}_{HH}$ are a set of high-pass filters. $\:{X}_{LL}$ is the low-frequency component of X, and $\:{X}_{LH},{X}_{HL},{X}_{HH}$ are the horizontal, vertical, and diagonal high-frequency components, respectively. These four filters form a set of orthogonal bases, and through the inverse wavelet transform (IWT), also known as transpose convolution, we can obtain Eq. (4).

$$\:\begin{array}{c}X={Conv}_{5\times\:5}-transposed\left(\left[{f}_{LL},{f}_{LH},{f}_{HL},{f}_{HH}\right],\left[{X}_{LL},{X}_{LH},{X}_{HL},{X}_{HH}\right]\right)\end{array}$$

(4)

Recursively decompose the low-frequency component $\:{X}_{LL}$ to obtain the cascaded wavelet decomposition. The decomposition at each level is shown in Eq. (5).

$$\:\begin{array}{c}{X}_{LL}^{\left(i\right)},\:{X}_{LH}^{\left(i\right)},\:{X}_{HL}^{\left(i\right)},\:{X}_{HH}^{\left(i\right)}={WT}_{5\times\:5}\left({X}_{LL}^{\left(i-1\right)}\right)\end{array}$$

(5)

where $\:{X}_{LL}^{\left(i\right)}=X$, and i represents the current level.

This approach decouples convolution operations from frequency components, ​allowing small convolution kernels to ​efficiently process larger regions. ​The hierarchical decomposition exponentially expands the receptive field ​while maintaining parameter efficiency. ​By isolating high and low-frequency information, small kernels ​specialize in respective frequency bands. ​Notably, enhanced low-frequency response ​improves shape-related feature extraction.

MSEI block

The MSEI Block is a CNN module designed to enhance multi-scale edge features representation in images, as shown in Fig. 3. By extracting features from four different scales, it aims to capture edge feature information across different scales, with a focus on details such as edges and gradients. This approach ultimately improves the model’s robustness and enhances the feature representation capability of the image data.

In the MSEI Block, feature extraction is performed using CSEI modules. The ​structure of the CSEI modules is shown in Fig. 5. First, a local convolutional layer is applied to extract local features, followed by an average pooling convolutional layer for adaptive pooling of the input, which reduces the spatial resolution of the image to different scales. For each scale, wavelet transform convolution (WT) is used to expand the ​receptive field. This approach effectively improves the network’s ability to fit data and resist interference while also reducing the number of parameters and the model complexity. The EEnhancer module strengthens edge information in the image by emphasizing key details. It extracts edge information by calculating the difference between the input feature map and its average pooling result, then applies the Sigmoid activation function to weight this edge information. The enhanced edge information is finally added to the original input, as shown in Fig. 5. Ultimately, the locally convoluted image and the feature maps enhanced at various scales are concatenated, integrating information from different scales and types. This fusion enhances the model’s understanding of both image details and the overall structure, resulting in richer feature representations.

Fig. 5

CSEI module architecture. The module applies four distinct pooling scales, performing edge information enhancement at each scale and integrating results through a series of convolutional operations. This approach leverages different receptive fields to capture multi-scale fine-grained details.

Key Module of CSEI Operation in MEFE-Net: Let the input be $\:x\in\:{\mathbb{R}}^{C\times\:H\times\:W}$, and $\:B=\{b1,b2,\dots\:,bn\}$ represent a set of n different pooling scales.

Local Feature Extraction: The input $\:x$ passes through a $\:3\times\:3$ convolutional layer to extract local features, as shown in Eq. (6):

$$\:\begin{array}{c}{x}_{local}={Conv}_{3\times\:3}\left(x\right)\end{array}$$

(6)

where $\:{x}_{local}\in\:{\mathbb{R}}^{C\times\:H\times\:W}$ represents the feature map after local convolution processing. Multi-scale Feature Extraction: For each scale $\:b\in\:B$, the following operations are performed:

a. Adaptive Average Pooling: The input $\:x$ undergoes adaptive average pooling, yielding a feature map of size $\:b\times\:b$ as described in Eq. (7):

$$\:\begin{array}{c}{x}_{b}=AdaptiveAvgPool2d\left(x,b\right)\end{array}$$

(7)

where $\:{x}_{b}\in\:{\mathbb{R}}^{C\times\:b\times\:b}$ is the pooled feature map.

b. Feature Extraction: The pooled feature map $\:{x}_{b}$ processed for multi-scale feature extraction as shown in Eqs. (8), (10):

WTConv2d Operation:

$$\:\begin{array}{c}{x}_{b}^{{\prime\:}}={WTConv2d}_{1\times\:1}\left({x}_{b}\right)\end{array}$$

(8)

where $\:{x}_{b}^{{\prime\:}}\in\:{\mathbb{R}}^{C\times\:b\times\:b}$is the feature map after the WTConv2d operation.

Channel Adjustment: A $\:1\times\:1$ convolution is applied to adjust the channel number to $\:\frac{C}{\left|B\right|}$, as shown in Eq. (9):

$$\:\begin{array}{c}{x}_{b}^{{\prime\:}{\prime\:}}={Conv}_{1\times\:1}\left({x}_{b}^{{\prime\:}},\frac{C}{\left|B\right|}\right)\end{array}$$

(9)

where $\:{x}_{b}^{{\prime\:}{\prime\:}}\in\:{\mathbb{R}}^{\frac{C}{\left|B\right|}\times\:b\times\:b}$ is the channel-adjusted feature map, and $\:\left|B\right|$ is the number of scales, C represents the number of input channels.

Apply depthwise separable convolution to the feature map $\:{x}_{b}^{{\prime\:}{\prime\:}}$ for further feature extraction:

$$\:\begin{array}{c}{x}_{b}^{{\prime\:}{\prime\:}{\prime\:}}={Conv}_{3\times\:3}\left({x}_{b}^{{\prime\:}{\prime\:}},3\right)\end{array}$$

(10)

where $\:{x}_{b}^{{\prime\:}{\prime\:}{\prime\:}}\in\:{\mathbb{R}}^{\frac{C}{\left|B\right|}\times\:b\times\:b}\:$is the feature map after depthwise separable convolution.

c. Edge Enhancement for Each Scale: For each scale feature map $\:{x}_{b}^{{\prime\:}{\prime\:}{\prime\:}}$, edge enhancement is performed through the EEnhancer module, as described in Eq. (11):

$$\:\begin{array}{c}{\widehat{x}}_{b}={x}_{b}^{{\prime\:}{\prime\:}{\prime\:}}+{Conv}_{3\times\:3}\left({x}_{b}^{{\prime\:}{\prime\:}{\prime\:}}-AvgPool\left({x}_{b}^{{\prime\:}{\prime\:}{\prime\:}}\right)\right)\end{array}$$

(11)

where $\:{\widehat{x}}_{b}\in\:{\mathbb{R}}^{C\times\:H\times\:W}$ represents the enhanced edge feature map, the symbol$\:+$ denotes the fusion of global information with local details, and the symbol $\:-$ denotes the residual computation of edges and details.

Feature Aggregation and Final Output: The enhanced feature maps from all scales are concatenated along the channel dimension and processed through the final convolutional layer, as shown in Eq. (12):

$$\:\begin{array}{c}\widehat{x}={Conv}_{1\times\:1}\left(concat\left({x}_{local},{\widehat{x}}_{1},{\widehat{x}}_{2},\dots\:,{\widehat{x}}_{n}\right)\right)\end{array}$$

(12)

where $\:\widehat{x}\in\:{\mathbb{R}}^{C\times\:H\times\:W}$ is the final multi-scale enhanced feature map, and the final convolution operation adjusts the concatenated feature map to the desired output dimensions.

The MSEI Block employs a CSP branch structure to minimize redundant computations, ​enabling effective capture of local details while incorporating global contextual information across scales. By integrating local information with global structural insights from various scales, this architecture significantly enhances the ability to process objects of different sizes and levels of detail. This design highlights the contours of objects while maintaining a lightweight performance, resulting in richer gradient flow information and improved resistance to complex background noise. Consequently, the MSEI Block demonstrates exceptional efficacy in detecting small objects and capturing fine-grained details.

Context and spatial feature calibration network

One of the main limitations of the DETR model lies in its limited local receptive field. While the Multi-Head Self-Attention (MHSA) mechanism in Transformers effectively captures global context, it struggles to handle multi-scale information. Furthermore, many existing methods frequently neglect critical challenges such as contextual misalignment and feature misalignment, wherein fine-grained features are often obscured by background noise, ​thereby degrading detection accuracy. To address these challenges, this paper introduces the Context and Spatial Feature Calibration Network, aiming to enhance multi-scale information fusion, feature alignment, and local context modeling in CNNs, especially when processing high-resolution remote sensing images in complex scenes.

Context feature calibration module

The CFC module ​enhances the model’s perceptual capacity through ​multi-scale feature aggregation, ​employing a local attention mechanism to ​precisely align fine-grained features, ensuring effective fusion and alignment of ​cross-scale features. The ​structural design of the CFC module is ​illustrated in Fig. 6.

Fig. 6

Implementation pipeline of the context feature calibration module. Where $\:N\:=\:H\:\times\:\:W$ and M denote the total number of pixels and contexts, the symbol $\:\times\:$ represents a matrix multiplication, the symbol $\:+$ represents an element-wise summation, the CRB is a local attention module designed to enhance feature representation by capturing both global and local contextual information.

The input feature map first undergoes four different sizes of adaptive average pooling operations to generate the Key and Value, extracting multi-scale contextual information. Next, the similarity between the Query and Key is calculated using matrix multiplication, producing a similarity map. The attention weights are then computed with the softmax function. Based on these attention weights, the Value is weighted and fused to obtain the contextual features. Finally, the local attention module, CRB, is applied to refine these contextual features. The adjusted contextual features are added to the original input features, enhancing detailed information and generating the final output.

The CFC module first reduces the channel dimension of the input image, as shown in Eq. (13):

$$\:\begin{array}{c}{x}_{reduced}={Conv}_{3\times\:3}\left(x\right)\end{array}$$

(13)

The operation $\:Conv\left(\cdot\:\right)$ is a $\:3\times\:3\:$convolution used to reduce the number of channels.

Queries, keys, and values are then computed through convolution operations, as defined in Eqs. (14), (15), and (16):

$$\:\begin{array}{c}query={query\_conv}_{1\times\:1}\left({x}_{reduced}\right)\in\:{\mathbb{R}}^{32\times\:H\times\:W}\end{array}$$

(14)

$$\:\begin{array}{c}key={key\_conv}_{1\times\:1}(key\_psp({x}_{reduced})\in\:{\mathbb{R}}^{32\times\:S}\end{array}$$

(15)

$$\:\begin{array}{c}value={value\_conv}_{1\times\:1}(value\_psp({x}_{reduced}\left)\right)\in\:{\mathbb{R}}^{\frac{C}{2}\times\:S}\end{array}$$

(16)

The $\:query\_conv$ is a convolutional layer used to generate the query feature map, the $\:key\_psp({x}_{reduced}$) represents the feature map obtained through multi-scale pooling applied to the reduced feature map, $\:key\_conv$ performs a convolution on the pooled feature map, producing an output of size $\:32\times\:S$, where $\:S$ is the spatial dimension of the pooled feature map. The $\:value\_psp\left({x}_{reduced}\right)$ is obtained by applying pooling to the reduced feature map, where the number of channels passing through $\:query\_conv$ and $\:key\_conv$ is adjusted to 32 and the number of channels passing through $\:value\_conv$ remains unchanged.

The similarity is computed and normalized using the softmax function, as shown in Eq. (17):

$$\:\begin{array}{c}sim\_map=softmax\left(query\cdot\:{key}^{T}\right)\end{array}$$

(17)

The context is obtained by performing a weighted summation of the value feature map using the similarity map, as shown in Eq. (18):

$$\:\begin{array}{c}context=value\cdot\:{sim\_map}^{T}\end{array}$$

(18)

As shown in Eq. (19), the contextual information is further processed through the local attention CRB.

$$\:\begin{array}{c}\widehat{x}=local\_\_attention\left(context\right)\end{array}$$

(19)

The details of the calculation of $\:local\_\_attention$ are shown in Eqs. (20), (21) and (22):

Input dimensionality reduction (using$\:1\times\:1$convolution):

$$\:X{\prime\:}={Conv}_{1\times\:1}(X,in\_channels={C}_{in},out\_channels={C}_{inter},kernel=1)$$

(20)

Restoring channels (using $\:3\times\:3$ convolution):

$$\:Y={Conv}_{3\times\:3}(X{\prime\:},in\_channels={C}_{inter},out\_channels={C}_{in},kernel=3)$$

(21)

Activation function (Tanh):

$$\:\begin{array}{c}Z=Tanh\left(Y\right)\end{array}$$

(22)

where: $\:X$ is the input feature map, $\:{C}_{in}$​ is the number of input channels, $\:{C}_{inter}$ is the intermediate channel size, $\:Z$ is the output feature map with local attention applied.

The final output is the summation of the original feature map and the enhanced feature map, as shown in Eq. (23).

$$\:\begin{array}{c}{x}_{out}=x+\widehat{x}\end{array}$$

(23)

Spatial feature calibration module

The SFC module ​facilitates effective cross-scale feature fusion, ​precisely aligning high-level semantic features with low-level detail-oriented features. By ​integrating complementary features across scales, this module ​augments the model’s ​multi-scale object recognition capacity in high-resolution imagery. The ​architectural design of the SFC module is ​depicted in Fig. 7.

Fig. 7

Detailed overview of the spatial feature calibration module. Where $\:{F}_{ħ}$ and $\:{F}_{\mathcal{l}}$ represent high-resolution features and low-resolution features, respectively. $\:{\varDelta\:}_{\mathcal{l}}$ represents offset maps, $\:{\varDelta\:}_{\mathcal{l}}\in\:{\mathbb{R}}^{(2\times\:G)\times\:H\times\:W}$, $\:G$ is the number of groups, the symbol $\:\times\:$ represents a matrix multiplication, the symbol $\:+$ represents an element-wise summation.

The module processes two feature types: Semantic Feature (SF) and Context Feature (CF). First, the SF undergoes convolution to enhance semantic information before upsampling to match CF resolution ensuring spatial alignment. Meanwhile, CF ​is refined through convolution to extract fine-grained details, such as edges and textures. Next, processed SF and CF are concatenated, after which spatial offsets are computed. These offsets comprise two components controlling horizontal and vertical deformation, indicating positional adjustments ​across scales. Spatial sampling ​applies computed offsets for multi-scale alignment. Finally, dynamic weighting ​employs 1 + tanh function to clamp weights within [0, 2], preventing gradient explosion. This weighting scheme balances SF and CF contributions, yielding a fused feature map ​with preserved multi-scale context.

In the SFC module, $\:{x}_{CF}$ and $\:{x}_{SF}$ are the contextual feature map and semantic feature map, respectively, and are processed using convolution, as shown in Eq. (24).

$$\:\begin{array}{c}{x}_{SF}={conv\_32}_{3\times\:3}\left({x}_{SF}\right),{x}_{CF}={conv\_8}_{3\times\:3}\left({x}_{CF}\right)\end{array}$$

(24)

The semantic feature map $\:{x}_{SF}$ is then upsampled to match the size of the contextual feature map, as shown in Eq. (25).

$$\:\begin{array}{c}{x}_{SF}=interpolate\left({x}_{SF},size\left({x}_{CF}\right)\right)\end{array}$$

(25)

The contextual feature map $\:{x}_{CF}$ and the semantic feature map $\:{x}_{SF}$ are concatenated and the offset is computed through convolution, as shown in Eq. (26).

$$\:\begin{array}{c}O=conv\_offset\left(concat\right({x}_{CF},{x}_{SF}\left)\right)\end{array}$$

(26)

$\:conv\_offset$ is a convolutional layer used to compute the offset, where $\:conv\_offset:{\mathbb{R}}^{2C\times\:H\times\:W}\to\:{\mathbb{R}}^{(2G+2)\times\:H\times\:W}$, $\:G$ is the number of groups, O is the offset generated by the offset prediction network.

The offset $\:O$ is decomposed into low-resolution offsets $\:{O}_{l}\:$and high-resolution offsets $\:{O}_{h}$, as shown in in Eq. (27).

$$\:\begin{array}{c}{O}_{l}=O[:,0:2G,:,:],{O}_{h}=O[:,2G:4G,:,:]\end{array}$$

(27)

Grid Generation: A standard grid $\:G\in\:{\mathbb{R}}^{N\times\:H\times\:W\times\:2}$ is generated, where $\:N$ is the batch size, as shown in Eq. (28).

$$\:\begin{array}{c}{G}_{i,j}=\left(\frac{2j}{{W}_{c}-1}-1,\frac{2i}{{H}_{c}-1}-1\right)\end{array}$$

(28)

Offset Grid Calculation: The low-resolution offset grid $\:{G}_{l}$ and high-resolution offset grid $\:{G}_{h}$​ are computed, as shown in in Eq. (29):

$$\:\begin{array}{c}{G}_{l}=G+\frac{{O}_{l}}{norm},{G}_{h}+\frac{{O}_{h}}{norm}\end{array}$$

(29)

Grid sampling is applied to the contextual and semantic feature maps, as shown in Eq. (30).

$$\:\begin{array}{c}{x}_{CF}=grid\_sample({x}_{CF},{G}_{l}),{x}_{SF}=grid\_sample({x}_{SF},{G}_{h})\end{array}$$

(30)

$\:grid\_sample$ is an operation used to sample a feature map according to a given grid.

The attention is computed using the tanh activation function and fused, as shown in Eqs. (31) and (32).

$$\:att=1+tanh\left(O\right[:,4G:\left]\right)$$

(31)

$$\:\begin{array}{c}{x}_{SF}=att\left[:,0:1\right]\cdot\:{x}_{SF}+att\left[:,1:2\right]\cdot\:{x}_{CF}\end{array}$$

(32)

The final output is the weighted semantic feature map, as shown in Eq. (33).

$$\:\begin{array}{c}{x}_{out}={x}_{SF}\end{array}$$

(33)

Experiments and discussion

Dataset

The VisDrone 2019 dataset is a large-scale, high-resolution collection of UAV-captured images and videos designed for multi-object detection, tracking, and classification tasks. It ​contains 288 video clips (totaling 261,908 frames) alongside ​10,209 static images. This dataset features over 2.6 million manually annotated object bounding boxes across all frames, covering various object categories, including pedestrians, cars, bicycles, and tricycles. The dataset captures diverse environmental contexts, encompassing both urban and rural scenes with varying object scales and occlusion levels. It includes objects in both sparse and densely clustered configurations, making it particularly suitable for evaluating and improving small object detection algorithms. The data collection process accounts for varying weather and lighting conditions, introducing realistic challenges encountered in real-world applications. We selected images for our object detection task from the VisDrone 2019 dataset, which is organized into 6,471 training images, 548 validation images, and 3,190 test images. The specific types and quantities are illustrated in Fig. 8. VisDrone 2019 is especially effective for detecting densely packed small objects and partially occluded targets, ​serving as a standard benchmark in UAV vision research and performance evaluation.

Fig. 8

Details of the VisDrone 2019 dataset.

Evaluation metrics

In this paper, we adopt the mean Average Precision (mAP) as the primary metric to evaluate the performance of the algorithm. This has been widely proven to be an effective evaluation method³⁸. We strictly follow the mainstream COCO evaluation metrics to assess the overall performance of the model. (1) The Average Precision (AP) value is computed by averaging mAP scores calculated at IoU thresholds ranging from 0.5 to 0.95 with a step size of 0.05. Specifically, AP@0.5 and AP@0.75 refer to the mAP values calculated at IoU thresholds of 0.5 and 0.75, respectively. (2) AP Across Scales assesses model performance by categorizing objects into small, medium, and large based on their area. Specifically, objects smaller than 32 × 32 pixels are classified as small, those larger than 96 × 96 pixels are classified as large, and objects with sizes in between fall into the medium category. By calculating the mAP for each of these object size categories, we can gain a deeper understanding of the model’s performance across different object sizes.

The mAP is defined as the average of the AP across all classes. It can be calculated using the following formula:

For each class, the AP is calculated by computing precision and recall at different thresholds, followed by averaging the results. The specific methods for calculating Precision(P) and Recall(R) are outlined in Eq. (34) and Eq. (35), respectively.

$$\:\begin{array}{c}P=\:\frac{TP}{TP+FP}\end{array}$$

(34)

$$\:\begin{array}{c}R=\:\frac{TP}{TP+FN}\end{array}$$

(35)

where TP denotes the true positive scenario, in which a sample is correctly predicted to be positive, FP represents the false positive case, where a sample is incorrectly predicted to be positive despite being negative, and FN signifies the false negative scenario, where a sample is erroneously predicted to be negative whereas it is actually positive.

AP and mAP are calculated as shown in Eqs. (36) and (37).

Formula for AP:

$$\:\begin{array}{c}AP={\int\:}_{0}^{1}P\left(r\right)dr\end{array}$$

(36)

where: P (r) is the precision at a given recall level.

Formula for mean Average Precision (mAP):

$$\:\begin{array}{c}mAP=\frac{1}{n}{\sum\:}_{i=1}^{n}A{P}_{i}\end{array}$$

(37)

where N is the number of classes. $\:A{P}_{i}$ is the Average Precision for class i.

The F1 curve is typically calculated by adjusting the threshold to obtain different values of precision and recall. A higher F1 score indicates that the model is better at balancing precision and recall. If the value of the curve is closer to 1, it means the model’s performance is better.

The formula for calculating the F1 score is as shown in Eq. (38).

$$\:\begin{array}{c}F1=\frac{2\times\:\text{P}\times\:\text{R}}{\text{P}+\text{R}\text{}}\end{array}$$

(38)

Implementation details

In this study, the model is implemented using the PyTorch framework and trained on an NVIDIA 4090 GPU with 24GB of memory. The batch size is set to 4, and the input image resolution is 640 × 640 pixels to ensure comprehensive coverage of spatial details and features. The training is conducted over 150 epochs. For the hyperparameter settings, all parameters—except for the number of workers, batch size, and total epochs—are adjusted based on the specific experimental setup and requirements. The remaining parameters are configured according to the officially recommended best practices of RT-DETR²² to maintain the rigor of the experiment. The detailed experimental environment for training and testing is listed in Table 1.

Table 1 Experimental environment.

Index curve analysis

To validate the effectiveness of our proposed method, we integrate five advanced modules into the baseline RTDETR architecture for ablation studies:

(1) Additive Token Mixer³⁹: A cross-channel interaction mechanism from Transformer-based models. We replace the decoder’s self-attention layer in RTDETR with this module, denoted as RTDETR-AdditiveTokenMixer. (2) KAGNConv2DLayer⁴⁰: KAGNConv2DLayer is a convolutional layer that replaces the traditional linear convolutional kernel with a nonlinear function, enabling nonlinear transformations. By efficiently capturing nonlinear relationships, it enhances the model’s generalization ability and efficiency. We introduce it into the RTDETR encoder and name it RTDETR-KAGNConv2DLayer. (3) Local feature extraction⁴¹: An efficient convolution operation from ELAN networks for local structure modeling. We integrate it into the encoder, denoted as RTDETR-Local feature extraction. (4) SPD-Conv⁴²: A space-to-depth convolution block proposed for preserving fine-grained information in low-resolution scenarios. (5) Omni-Kernel⁴³: A multi-scale receptive field module combining global, large, and local branches. We insert SPD-Conv and Omni-Kernel in RTDETR’s encoder, named RTDETR-SPDConv-OmniKernel.

Analysis of F1 value curve

As shown in Fig. 9, when the Confidence value is 0.373, the best F1 score of the RTDETR algorithm is 0.51. In Fig. 9b, the RTDETR-AdditiveTokenMixer algorithm has the best F1 score of 0.51 at a Confidence value of 0.376. In Fig. 9c, the RTDETR-KAGNConv2DLayer algorithm achieves the best F1 score of 0.51 at a Confidence value of 0.383. When the Confidence value is 0.386, the RTDETR-Local feature extraction algorithm in Fig. 9d achieves the best F1 score of 0.50. In Fig. 9e, the RTDETR-SPDConv-OmniKernel algorithm has the best F1 score of 0.51 at a Confidence value of 0.383. Lastly, when the Confidence value is 0.388, the best F1 score of 0.54 is achieved by Our method, as shown in Fig. 9f.

Fig. 9

Analysis of the F1 value curve.

Precision value curve analysis

As shown in Fig. 10, when the Confidence value is 0.967, the best Precision value of the RTDETR algorithm is 1. In Fig. 10b, the RTDETR-AdditiveTokenMixer algorithm achieves the best Precision value of 1 at a Confidence value of 0.971. When the Confidence value is 0.966, the best Precision value of the RTDETR-KAGNConv2DLayer algorithm is 1, as shown in Fig. 10c. In Fig. 10d, the RTDETR-Local feature extraction algorithm has the best Precision value of 1 at a Confidence value of 0.969. In Fig. 10e, the RTDETR-SPDConv-OmniKernel algorithm achieves the best Precision value of 1 at a Confidence value of 0.963. Lastly, in Fig. 10f, our method achieves the best Precision value of 1 at a Confidence value of 0.969.

Fig. 10

Analysis of precision value curve.

Precision-recall value curve analysis

The Precision-Recall (PR) curve is an important tool for evaluating the performance of object detection models. It shows the relationship between precision and recall at different confidence thresholds. The PR curve plots recall on the vertical axis and precision on the horizontal axis, representing the model’s performance at various confidence thresholds. The larger the area under the curve, the better the model’s performance. Figure 11 illustrates the PR curves for different RTDETR-based algorithms.

In Fig. 11a, the RTDETR algorithm achieves the best Precision-Recall value of 0.468 at mAP@0.5. In Fig. 11b, the RTDETR-AdditiveTokenMixer algorithm achieves the best Precision-Recall value of 0.464 at mAP@0.5. In Fig. 11c, the RTDETR-KAGNConv2DLayer algorithm achieves the best Precision-Recall value of 0.466 at mAP@0.5. In Fig. 11d, the RTDETR-Local feature extraction algorithm achieves the best Precision-Recall value of 0.454 at mAP@0.5. In Fig. 11e, the RTDETR-SPDConv-OmniKernel algorithm achieves the best Precision-Recall value of 0.464 at mAP@0.5. Finally, in Fig. 11f, our method achieves the best Precision-Recall value of 0.499 at mAP@0.5.

Fig. 11

Analysis of precision-recall value curve.

Ablation experiments

In this section, we present the results of an ablation study conducted on the VisDrone 2019 dataset, aimed at evaluating the effectiveness of each module proposed in our model. Table 2 shows the results of the ablation experiments.

Table 2 Detection results of the algorithm using different modules.

In this ablation study, we evaluate the performance of the baseline model and its combinations with the MEFE-Net and CSFCN modules, providing an in-depth analysis of their impact on model performance. The experimental results show that the baseline model achieves an AP₅₀ of 43.8%, with AP_M and AP_L at 36.4% and 43.2%, respectively,

The experimental results show that the mAP of the baseline model reached 26.0%, with AP₅₀, AP_M and AP_L of 43.8%, 36.4% and 43.2%, respectively, demonstrating superior performance in detecting medium and large objects. However, the baseline model exhibits limitations in small object detection, with an APs of only 18.1%. This performance gap indicates that while the baseline model effectively recognizes large objects, it struggles with small object detection, particularly in terms of precision.

After incorporating MEFE-Net, the model’s AP₅₀ and AP₇₅ increase to 45.1% and 27.3%, respectively, showing improvements of 1.3% and 1.1% over the baseline model. Furthermore, the model’s performance on small and medium object detection also improves, with AP_S and AP_M rising to 18.7% and 37.6%, respectively, reflecting improvements of 0.6% and 1.2%. Additionally, MEFE-Net significantly reduces the model’s parameter count, indicating that it achieves a balance between improved detection accuracy and computational efficiency. Although AP_L slightly decreases, MEFE-Net overall enhances the model’s multi-scale feature learning capability by reinforcing edge details and local information processing, thereby improving small object detection performance.

When CSFCN is added to the model, AP₅₀ and AP₇₅ reach 44.3% and 27.1%, respectively, with increases of 0.5% and 0.9% over the baseline. The model also shows notable improvements in small and medium object detection, with AP_S and AP_M increasing by 0.7% and 0.6%, respectively. This suggests that CSFCN improves the model’s robustness and detection capability through multi-scale contextual feature fusion. However, the inclusion of CSFCN introduces additional modules and parameters, leading to an increase in the model’s parameter count.

Finally, when both MEFE-Net and CSFCN are combined, the model reached 28.0% at mAP, a 2% improvement compared to 26.0% in the baseline model, and achieves an AP₅₀ of 46.6% and an AP₇₅ of 28.6%, representing significant performance improvements of 2.8% and 2.4%, respectively. For small, medium, and large object detection, the model achieves AP_S, AP_M, and AP_L of 19.6%, 39%, and 43.8%, with improvements of 1.5%, 2.6%, and 0.6%, respectively, compared to the baseline. This demonstrates that the combination of MEFE-Net and CSFCN significantly enhances the model’s comprehensive detection ability, especially in terms of small and medium object detection. MEFE-Net enhances edge details and local information processing, while CSFCN improves multi-scale feature fusion, enabling better perception of objects at different scales. The complementary effects of these modules substantially improve detection accuracy. Additionally, due to the efficient reduction in computational complexity by MEFE-Net, the final model’s parameter count is 15.86M, achieving a good balance between accuracy and computational cost.

Effectiveness analysis of the proposed MEFE-Net

We propose a multi-scale edge feature information-focused network that incorporates the ideas of CSPNet, effectively enhancing gradient flow, reducing computational cost, and alleviating the vanishing gradient problem. To evaluate the effectiveness of the proposed MEFE-Net, we integrate it with various models and conduct experiments on the VisDrone dataset. The results demonstrate that the proposed feature extraction network performs excellently across different network architectures, and the incorporation of MEFE-Net leads to significant improvements in multiple metrics. Table 3 shows the results on the VisDrone dataset. Specifically, after adding MEFE-Net, both YOLOv8 and YOLOv10 show improvements in AP50, AP75, and small object detection (AP_S), highlighting the effectiveness of MEFE-Net in enhancing small object recognition. For RTDETR, after integrating MEFE-Net, AP₅₀ and AP₇₅ increase by 1.3% and 1.1%, respectively, with further improvements in AP_S. Additionally, the integration of MEFE-Net optimizes feature fusion and computational efficiency, reducing model parameter count while boosting overall performance. Although MEFE-Net slightly decreases AP_L in YOLOv10 and RTDETR, it significantly enhances the target detection capability of the original models, particularly in fine-grained object recognition.

Table 3 The effectiveness analysis of MEFE-Net.

Comparison with state-of-the-art models

We conducted comprehensive comparative experiments on the VisDrone dataset, evaluating the proposed model against other state-of-the-art object detection models. The experimental results demonstrate that the proposed EMF-DETR outperforms in various object detection metrics, particularly in small object and multi-scale object detection. Table 4; Fig. 12 outline a comparison of various object detection models on the VisDrone dataset. Compared to the YOLO series models, such as YOLOv5l, YOLOv6m, YOLOv7x, YOLOv8m, YOLOv9m, YOLOv10m, and the latest YOLOv11l, the proposed model shows significant advantages in performance and exhibits the highest accuracy on mAP, particularly in small object detection precision (AP_S), achieving increases of 4.7%, 7.6%, 1.7%, 5.6%, 5.9%, 6%, and 4.2%, respectively. Additionally, the model has a relatively low parameter count of 15.86 M, showcasing high computational efficiency. In comparison with other DETR-based object detection models, the proposed model maintains excellent detection performance with fewer parameters. Compared to D-fine-m, the proposed model shows clear advantages in AP₅₀ and AP₇₅, with improvements of 3.7% and 2.7%, respectively, and particularly excels in small object detection (AP_S) with a 1.8% improvement. When compared to Deformable-DETR, the proposed model demonstrates a more comprehensive performance lead. Our proposed approach achieves an FPS of 58.4, demonstrating a strong performance with a good balance between efficiency and accuracy.

Table 4 Comparison with state-of-the-art models on the visdrone dataset.

Fig. 12

The detection AP of different models and parameters of the model.

The Fig. 13 visualizes the model’s object detection results in terms of predicted bounding box localization. We evaluate detection performance using True Positives (TP), False Positives (FP), and False Negatives (FN). Specifically, green boxes represent correctly detected objects, where both the position and class match the ground truth annotations. Blue boxes indicate correctly localized objects, but with a mismatch in class between the prediction and ground truth. Red boxes highlight missed detections, where the model fails to identify the object.

Fig. 13

Visualization of the detection results of our method.

Feature attention visualization

We evaluate the model’s performance through heatmap visualization analysis, which provides an intuitive representation of the model’s focus on different regions. The heatmap uses color gradients to indicate the attention distribution across the image, especially for small object detection in dense or complex backgrounds, allowing us to clearly identify the regions or objects that the model focuses on. As shown in the Fig. 14, darker areas represent regions with higher attention from the model. In the baseline model’s heatmap, the detected object regions are more dispersed, particularly in areas with small objects or rich details, where the concentrated regions in the heatmap are fewer, leading to imprecise object localization and boundary detection. Additionally, background noise can interfere with object recognition, particularly in complex and multi-scale scenes, where the boundaries of objects are less clear.

In our proposed model, the heatmap exhibits more concentrated object regions, especially for small objects and complex backgrounds. The dense regions in the heatmap correspond more accurately to the object locations, particularly in small object detection, such as small objects on road lanes, where the improvement is especially evident. This improvement is attributed to the introduction of the cross-attention mechanism and multi-scale feature fusion, which optimizes the accuracy of object localization. The offset learning and adaptive feature fusion precisely align the feature maps, reducing interference from the background. Finally, the enhancement of edge features improves the recognition of fine details, allowing clearer identification of object boundaries, particularly in complex scenes and multi-object detection tasks.

Fig. 14

We employ a visualization algorithm to generate heatmaps of the small object features in the network, where the red regions represent areas of high feature attention.

Conclusion

In this paper, we propose EMF-DETR, a novel model designed to address challenges such as sparse feature representation, insufficient localization features for small-scale targets, and inadequate multi-scale fusion in high-resolution remote sensing images. The core innovation lies in the MEFE-Net, which enhances the target feature recognition and edge information extraction capabilities. Leveraging WTConv’s ​large receptive field and lightweight architecture, we ​achieve computational efficiency ​without sacrificing accuracy. To address pixel context mismatch and spatial feature misalignment induced by repeated downsampling operations, we introduce the CSFCN. This module performs contextual and channel features calibration, resulting in significant performance enhancement. Extensive experiments on the VisDrone 2019 dataset demonstrate that our method outperforms competing models across various evaluation metrics. Compared with the baseline model, our approach ​achieves comprehensive improvements with a 20.22% reduction in parameters, effectively reducing computational overhead. This advancement establishes a robust framework ​while providing new perspectives for high-resolution object detection.

Despite achieving competitive accuracy and parameter efficiency, our model exhibits limitations in real-time processing due to computational complexity constraints. ​Future work will focus on optimizing high-resolution image processing speed ​while maintaining accuracy, towards enabling real-time monitoring applications.