Introduction

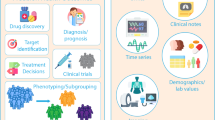
Clinical data obtained from diverse diagnostic modalities offer a comprehensive perspective on an individual’s physiological status (Fig. 1a). In the context of cardiovascular health, for example, combining insights from electrocardiograms (ECG) and cardiac magnetic resonance imaging (cMRI) provides a richer, more integrated view of cardiac function than either modality alone1,2,3. While ECG captures the heart’s electrical activity, cMRI delivers detailed images of heart anatomy and function, each offering unique and complementary information of cardiac health4,5.

Fig. 1: Overview of the proposed Decoupled Multimodal Representation Fusion (MODES) framework.
figure 1

a Clinicians use different diagnostic modalities to learn a holistic view of patient health in order to make clinical diagnosis. b Overview of MODES: The fine-tuned unimodal encoders learn the decoupled shared and modality specific representations. The representation component can then be used by unimodal generators to obtain reconstructed samples. c The fused representations decouple information that are unique to each modality and the shared information. The cMRI-specific representation encodes information such as the anatomy and size of the heart, while the ECG-specific modality encodes information about the electrical activity of the heart. The fused representation can be used by downstream models to predict a variety of diagnostic phenotypes or diagnoses, and offers interpretability to the predictive power of each modality. d The masking component learns the right size of the representations for each shared and modality-specific component. The final size reflects the amount of information embedded in each subspace, and can vary depending on the pair of modalities considered. e MODES learns to embed cross-modal information into the shared space using unimodal encoders. This can be used to infer phenotypes of the missing modality, or to estimate the range of possible samples for the missing modality. The three icons in Fig. 1a are from www.flaticon.com by various authors (Vectors Tank, Linector), used under the Flaticon Free License.

Full size image

As the field of precision medicine evolves, the development of multimodal representation learning is increasingly vital for integrating diverse information into a cohesive representation of patient health. Relying on a single modality may not suffice to capture the heterogeneity of complex diseases6,7,8,9. Previous research in multimodal representation learning has shown success in merging information from different modalities, enabling models to leverage complementary data for enhanced performance across various tasks10,11,12,13.

Nonetheless, a significant challenge persists in effectively fusing information from multiple modalities while recognizing the distinct contributions of each14. Current approaches typically fall into three categories: early, intermediate, and late fusion, which denote the stages at which different modalities are combined15,16. A common drawback of many existing frameworks is the entanglement of information encoded in latent representations, complicating the task of identifying the distinct insights each modality provides. For successful implementation of multimodal machine learning in precision medicine, it is crucial to ascertain the diagnostic value of each modality. This information can also be generalized to understand the added value of obtaining a diagnostic measure to predict a certain outcome. There is a growing body of work aimed at improving the interpretability of latent representations by decoupling shared and modality-specific components. However, many of these approaches are task-driven and rely on labeled data or additional learning components such as discriminators, which increase training complexity and limit applicability in fully self-supervised settings17,18,19.

Another limitation of current multimodal fusion frameworks is their reliance on extensive paired observations for training20. This is a significant limitation in healthcare, where simultaneous diagnostic data from multiple modalities for the same patient is often unavailable. Multimodal training also provides a mechanism to leverage modalities that are more abundant due to lower acquisition costs, enabling the model to enhance representation learning across modalities with scarce and high-cost data.

Here, we introduce MODES, a framework designed for learning a unified representation of multimodal data that decouples modality-specific information from shared information within the latent space (Fig. 1b). By ensuring that the unique contributions of each diagnostic tool are clearly understood, MODES facilitates the learning of diagnoses or phenotypes associated with each modality. Our proposed framework is based on latent optimization for representation learning21,22. It is designed to leverage unimodal pre-trained encoders (foundation models) and fine-tune them to encode the shared and modality-specific representations. More recently, foundation models have become very popular in different fields, including in healthcare. These self-supervised models, that are trained on large datasets, learn to extract rich and generalizable representations of the data23,24,25,26. By utilizing the knowledge embedded in these models, our approach enables efficient multimodal representation learning with fewer paired training samples. By reducing this dependency on paired observations, our framework makes multimodal learning more feasible and adaptable to real-world clinical datasets.

We also introduce a dynamic masking mechanism for learning the best size for different representation components by removing low-information dimensions from the representations during training. Setting the size of each representation typically requires prior knowledge of how much information each component encodes, which is often unavailable. Our masking mechanism allows the framework to start with a large latent space and progressively reduce its size to reflect the amount of information embedded in each component.

We show that the multimodal representations learned by our framework not only improve the prediction of clinical phenotypes but also provide insights into real-world decision-making. By decoupling shared and modality-specific information, the model identifies which components are most informative for different downstream diagnoses, helping determine which modalities should be prioritized for collection to improve predictive performance (Fig. 1c). We demonstrate the effectiveness of our masking strategy in learning the appropriate size of shared and modality-specific latent representations in different pairs of modalities, providing information about the amount of shared and modality-specific information that exists for any pair of modalities (Fig. 1d). Learning the shared information space involves capturing the joint properties of the data through paired training and utilizing cross-modal information, where one modality provides insights that enhance understanding in another. In a cardiovascular model, we demonstrate by leveraging the shared representation learned from a reference modality that we can infer the range of possible measurements for the other modality (Fig. 1e). Ultimately, our method has the potential to support a wide range of diagnostic and prognostic tasks, making it a powerful tool for advancing multimodal clinical diagnostics.

Results

Learning a latent space of shared and modality-specific representations from multimodal data

The proposed MODES framework utilizes latent optimization21 to create a unified representation of multimodal data that decouples shared information from modality-specific details in the latent space. Latent optimization allows us to explicitly structure the latent space into shared and modality-specific components, rather than relying on the model to discover this separation implicitly. This explicit control is critical for effective decoupling, ensuring that shared factors capture cross-modal information while modality-specific factors remain disentangled. This framework consists of four key components (Fig. 2a): (1) Unimodal encoders, (2) unimodal generators, (3) latent representations, and (4) masking components. All components undergo a three-step iterative training process designed to ensure that the information is appropriately encoded within each element. Using paired samples from the two modalities, unimodal encoders are trained to encode the shared (\({Z}_{s}\)) and modality-specific representations (\({Z}_{M1}\), \({Z}_{M2}\)), and the generators are trained to reconstruct samples based on these representations. To facilitate this, we build upon pre-trained unimodal encoders and augment them with two prediction heads, designed to capture both shared and modality-specific features. In this study, we employ previously introduced ECG and MRI encoders3, although the framework is compatible with alternative pretrained models. Leveraging such encoders allows us to transfer domain-specific knowledge acquired from large unimodal datasets, thereby reducing the reliance on extensive paired data for training the multimodal system.

Fig. 2: MODES architecture and training procedure.
figure 2

a Overview of the three iterative steps of training MODES. b The loss trends of the training steps of MODES.

Full size image

In order to determine the size of each latent representation, MODES employs a masking strategy that learns to mask the dimensions of the latent space with lower information density. We train the learnable binary masks for each subspace using the Gumbel-Softmax approximation27,28. We set the temperature parameters of this distribution using exponential annealing during training iterations to encourage early exploration of the parameter space, allowing the model to consider different masking configurations, and later guide the process toward a stable configuration with lower entropy, ensuring that only the most informative dimensions are retained. The specifics of the training procedure are as follows:

Step 1 - This step learns a modality-specific representation that, when combined with information from the paired modality, can generate the original sample. This forces the modality-specific representation to capture all the unique information about a modality that is not present in the other modality. We simultaneously train the generators to reconstruct the original sample using this complementary information. In this step, we also train the masks for the shared latent representations. The parameters of the mask explore and find the most informative dimensions of the shared space.

Step 2 - Leveraging the learned modality-specific representations from Step 1, we learn the shared representation that complements this information to generate an accurate sample for all modalities. The unimodal generator training also continues in this step. Using the learned representations of step 1, we also train the parameters of the modality-specific binary masks to remove dimensions with low information density from the modality-specific representations.

Step 3 - We finetune the unimodal encoders to map the data into the modality-specific and shared representations learned in Steps 1 and 2. Each modality’s encoder is equipped with two prediction heads: one that estimates the shared representation and another that estimates the modality-specific representation. This enables the encoder to decouple information while still capturing the rich, modality-specific nuances of each input.

More details on each training step and the objective function of each step are provided in Methods. In the following, we evaluate this framework on a cardiovascular model with ECG and cMRI modalities to learn a representation of an individual’s cardiovascular health using data from the UKBiobank29. We show that MODES learns unified representations that enhance performance across a range of downstream tasks and facilitates the identification of modality-specific and shared phenotypes. More details on the data, cohort and processing are provided in Methods.

Learning fused representations that incorporate multimodal information

We compare the predictive performance of our representation to: 1) unimodal representations, 2) representations from different fusion strategies, namely early and late fusion, and 3) fused representations with disentangled information. For early fusion, we follow Mei X, et al.30 to combine information from various modalities at the data level, and for late fusion, we use the method in Akselrod-Ballin, A. et al.31 to fuse information at the output level. We also compare against DRIM18, a multimodal representation learning framework that decouples shared and modality-specific representations through an adversarial objective. To ensure a fair comparison, all models have the same encoder architecture, and the difference in performance stems from the number of modalities included (unimodal vs. multimodal) and the representation fusion strategy. We train a kernel regressor on the representations of 4150 samples from a held-out set to predict the value of various phenotypes like the RR interval, Ejection Fraction, etc., and different diagnoses such as Atrial Fibrillation, valvular diseases, etc. Performance results of diagnostic phenotypes across 3 folds (with 0.6 train split) compared using R-squared are shown in Fig. 3a and using predictive AUROC in Fig. 3b. Our results highlight two main points. First, MODES representations perform better or are identical to the best-performing unimodal representation, indicating that the framework effectively combines information from various modalities. Second, our representations consistently perform better or as well as other multimodal representations with different fusion strategies. This shows that our approach captures and combines complementary information across modalities more effectively, providing a better holistic view of patient health.

Fig. 3: Benchmarking MODES over unimodal representations and other representation fusion strategies.
figure 3

a Kernel regression on the proposed fused representations outperforms kernel regression on unimodal representations and other fusion strategies for predicting general physiological phenotypes (n = 4143, mean values are reported with error bars indicating one standard deviation). b Kernel regression on the proposed fused representations outperforms kernel regression on unimodal representations and other fusion strategies on various diagnostic tasks (n = 4143, mean values are reported with error bars indicating one standard deviation). c Kernel regression on the proposed fused representations outperforms kernel regression on unimodal representations and representations learned with the DropFuse model3 on predicting cMRI-derived phenotypes from ECG only, and predicting ECG derived phenotypes from cMRIs only. d Generated samples of one modality using reference samples of another modality. The first row shows the most probable ECG measures for a given cMRI sample and the second row shows what the cMRI would most likely look like given a reference ECG sample.

Full size image

One of the key advantages of jointly learning the shared latent representation is the ability to encode shared properties of different modalities into the same space, using unimodal encoders. This allows MODES to infer shared information even when one modality is missing. To demonstrate this, we compare the predictive performance of unimodal representations with that of representation extracted by our framework from a single modality (Fig. 3c) for estimating phenotypes related to the missing modality. This shows that ECG representations can infer cMRI-related phenotypes, and vice versa. We show that our representations improve the predictability of phenotypes related to the other modality compared to the unimodal encoders. We also compare the performance to a state-of-the-art model for learning cross-modal representations (DropFuse3) that uses a contrastive objective to train unimodal encoders. We show that we achieve comparable or better performance than DropFuse in the cross-modal task. Contrastive models can achieve higher performance if given considerably more sample pairs, but this shows the advantage of MODES that achieves better performance in data-scarce settings, like multimodal settings where finding paired samples for individuals is challenging. We also show that our unimodal representations improve over regular unimodal representations in predicting different diagnoses. This highlights an important benefit of the MODES framework, showing that even when one modality is missing, we can achieve a better diagnostic performance using a single modality with our framework.

In addition, we demonstrate that by leveraging the shared representation, we can estimate what the missing modality would be like. With our framework, we capture all possible shared information in the shared representation, which allows us to investigate the missing information of the modality-specific representation. When one modality is missing, the shared representation provides some information about that modality, but the modality-specific information which is uniquely encoded by that modality would remain unknown. Using our generative models, we can generate the range of possible samples for the missing modality by leveraging the latent space learned from the training data (Fig. 3d). Specifically, we encode the available modality and in the shared latent space, identify the most similar training samples using cosine similarity. For each of these samples, we then combine its modality-specific component of the missing modality with the encoded shared representation of the available modality to generate a plausible reconstruction of the missing modality. The cosine similarity measures provide an indication of how likely each generated sample is, allowing us to estimate the range of possible variations for the missing modality. This method not only enhances our understanding of how each modality contributes to the overall representation, but also provides valuable clinical insight. For instance, in diagnostic scenarios where certain data is unavailable, this approach can offer a probabilistic view of what the missing data might look like, based on the available information, thereby supporting more informed decision-making.

Decoupling shared and modality-specific information in the latent space

Decoupling the shared and modality-specific information in the latent space allows us to understand what unique clinical information each modality captures and which modality is more predictive of a certain phenotype or diagnosis. For different downstream tasks, our framework can estimate how predictable each modality-specific or shared latent representation is. Phenotypes in Fig. 4a, b span a broad range of electromechanical features and cardiometabolic diseases. Among the quantitative measures (Fig. 4a), the PQ and QT intervals, QRS duration, and RR interval are electrical metrics that are typically measured from ECG in clinical practice. We observe the ECG-specific representation having the largest predictive power for these variables. Of these, the shared representation predictability for RR interval is higher, which can be explained because RR Interval reflects heart rate, which can also be derived from MRI if multiple beats are included in the imaging loop. In contrast, LVEDV, LVESV, RVEDV, RVESV, LVM, LVSV, and RVSV are mechanical measures, as they rely on direct visualization of cardiac volumes and myocardial mass at defined points in the cardiac cycle. These parameters are more routinely obtained from cardiac MRI in clinical practice. Overall, the relative strength of modality-specific signals in Fig. 4a aligns with the standard methods of measurement used clinically.

Fig. 4: MODES learns a disentangled latent space.
figure 4

a, b Kernel regression on different components of the representations (shared and modality-specific) shows which component is more predictive of a downstream prediction task, such as for (a) clinical phenotypes or (b) diagnostic labels. c Scatter plots of the 2-dimensional projection of the different components of the learned representation shows what features are more separable in each component. d Samples from extreme ends of the first 2 principle components of the modality-specific representations demonstrate what features these subspaces capture.

Full size image

With respect to Fig. 4b, atrial fibrillation (Afib), normal sinus rhythm, and sinus bradycardia are rhythm diagnoses, typically determined from ECG patterns in practice. Afib, however, is also associated with structural changes in the left atrium (e.g., atrial dilatation in advanced stages), where adjunctive MRI findings can support risk stratification and disease staging; this can explain the signal present in the shared component. Valvular diseases and mitral regurgitation are predominantly mechanical in nature, and their diagnosis is usually made through imaging modalities such as MRI, which can explain the higher predictability of the cMRI-specific representations. Taken together, the results in Fig. 4b reflect clinical practice patterns in selecting the most appropriate modality for diagnosing these conditions.

We can also see the separation of information in the latent space through scatter plots of the 2D projection of the different representation components (Fig. 4c). For a measure like ejection fraction that is best inferred clinically using cMRI images, we see clear distinction of higher and lower values in the modality-specific representations of cMRIs, indicating that this component of the representation is encoding information about this phenotype. Such distinction is not at all present in the ECG-specific, and not as well presented in the shared space. On the other hand, for a phenotype like biological sex, which is partially identifiable through both modalities, we see that the shared representation best separates the population. The modality-specific representations also have some separability. For cMRI, this could be due to the correlation that exists between sex and the size of the heart, which is captured by cMRI.

To better understand what information about the data is encoded in the modality-specific representations, we visualize samples from the extreme ends of the different principle components of the modality-specific representation space. The principal components determine the orthogonal axes with highest variability, and comparing the samples at the extreme of each axis will tell us what feature characteristic is being captured by each component. Figure 4d shows the most positive and negative samples in the direction of different principle components of the modality-specific representations of cMRI and ECG. Each row represents one of the principle components and the 3 samples on the right are from one extreme, and the ones from the left are from the other extreme. The data characteristic that changes the most along each direction is the characteristic captured by that principal component of the modality-specific space. For instance, the first principle component of the cMRI-specific representation captures information about the size of the heart, which aligns with our expectation that the anatomy and size of the heart is mainly captured by cMRI. These dimensions most likely encode various and more complex characteristics, but such analysis provides us with intuition about the type of characteristics the modality-specific representations capture.

In Supplementary Fig. 1, we show the results for a similar evaluation on a different modality pair of cardiac and brain MRI (bMRI). Without the ECG modality, the predictive performance of the multimodal representation drops significantly for the electrical metrics (Supplementary Fig. 1a). Unlike with the ECG-cMRI pair, the shared component contains very little information, and the prediction mainly relies on the cMRI modality. For mechanical measures like RVEDF, we observe the separation of information in the cMRI representation, but not in the shared or bMRI representation (Supplementary Fig. 1c), this is while such information is partially observable in the shared representation of the ECG-cMRI pair, which are both cardiac diagnosis tools.

Effective masking strategy for learning the representation size

Knowing the proper size of representations in self-supervised methods is a difficult task. A common practice is to encode information in large representation spaces in order to ensure minimal information loss. This can be challenging in multimodal settings as the number of modalities grows. Also, it can impose further hurdles for training downstream models on large representations in data-limited settings. The masking component of MODES eliminates dimensions in the representation that contain redundant information in order to learn the size of each subspace. As we incorporate additional modalities, this compactness ensures that the size of the representation space remains manageable and does not grow excessively. Figure 5a shows how MODES starts with a large representation space and learns the number of dimensions throughout the training process. Through exponential temperature decay, in early iterations, the masks explore the entire representation space and towards the end of training, the masks converge. We also examine the learned latent space for a different set of modality pairs (Fig. 5b), specifically ECG and brain MRI, as well as brain MRI and cardiac MRI. Comparing the size of the learned shared spaces of ECG-cMRI versus ECG-bMRI shows that the shared information of ECG is significantly lower with bMRI compared to cMRI. While this seems intuitive, this approach can generally be applied to infer the amount of shared information for any two modalities. Note that the shared space is larger for cMRI and bMRI, which can be explained by the similarity of modality types (image versus time series).

Fig. 5: The masking component of MODES learns the appropriate size of modality-specific and shared space.
figure 5

a The binary mask values of the modality-specific and shared representation throughout the training epochs. The color indicates the masking value, the x-axis represents the dimensions of the representation and the y-axis represents the training epoch. The 2 columns represent the masks through training for the cMRI/ECG modality pair with different initial representation sizes. b The binary mask values through the training epochs for bMRI-cMRI and bMRI-ECG modality pairs showing the masking mechanism converges to different sizes for different modality pairs, depending on the information content. c Predictive performance of MODES on various phenotypes and diagnoses, with and without the masking strategy. Blue bars show the performance with masking, and the orange bars without masking. The near identical performance suggests that removing low-information dimensions of the representations during training achieves more compact representations without loss of performance.

Full size image

We also compare the predictive performance of our representations with and without the masking component, for predicting different diagnostic phenotypes and diagnostic labels. Figure 5b shows that the predictive performance of masked representations is as good or even better than the unmasked higher-dimensional representations. This indicates that the dimensions removed by the masking component contain redundant information and removing them doesn’t degrade the quality of the representations. The fewer number of dimensions is particularly beneficial when using simpler models for downstream tasks, such as a kernel regressor in our case, as we show that we can achieve better performance with the more compact representations.

Discussion

In this study, we introduce MODES, a framework for multimodal representation learning. We evaluate the framework on a cardiovascular model using ECG and cardiac MRI modalities. We show that MODES effectively unifies information in different modalities to provide a better picture of an individual’s health state that downstream models can use to improve diagnostics. Our framework decouples shared and modality-specific information in the latent space to enhance the interpretability of the learned representations, allowing for a clearer understanding of each modality’s unique contribution to clinical diagnoses. This unique capability has the potential to inform the choice of a particular modality for diagnosis or prognostication of a specific condition.

Our framework is designed to leverage pre-trained foundation models to learn multimodal representations without needing an extensive dataset of paired samples. By utilizing the knowledge embedded in these models, our approach enables efficient multimodal representation learning with fewer training samples. By reducing the dependency on paired observations, our framework makes multimodal learning more feasible and adaptable to real-world clinical datasets. In addition to interpretability and usability, our framework is designed with scalability in mind. The masking strategy deployed as part of MODES allows it to infer the size of each representation without prior knowledge. This allows for efficient representation fusion and reflects the amount of information content shared vs. unique to each modality. The clinical applicability of our framework lies in its ability to unify and disentangle information from complex multimodal data, allowing for a more nuanced understanding of patient health.

Our results demonstrate improved predictive performance across a range of phenotypes compared to unimodal and simple fusion strategies, highlighting the effectiveness of our approach. Future work could explore extending this framework to more modalities and other domains, potentially broadening its applicability in diverse clinical settings. Also, this work provides a proof-of-concept for the framework’s ability to provide a probabilistic view of synthetic samples that can be generated conditioned on information from one modality. This opens exciting opportunities in clinical practice, allowing clinicians to explore and visualize plausible scenarios when data is missing or incomplete, ultimately supporting more informed decision-making and personalized treatment planning.

Methods

Our framework learns a latent space that separates modality-specific and shared information, enabling more effective and interpretable multimodal representations. To achieve this, we train modality-specific generators that generate the original data from these latent representations and unimodal encoders that map each modality to its respective modality-specific and shared representations. The main components of the framework are the parametric models for learning the disentangled space and the masking component that removes representation dimensions with redundant information. The following sections provide further details on the design and training of each component.

Dataset

The UK Biobank is a longitudinal prospective cohort of over 500,000 healthy adults aged 40–69 during enrollment, which took place from 2006 to 201029. A subset of these individuals participated in the imaging study32. At the time of our study, this includes magnetic resonance imaging for over 44,644 participants, 38,686 of whom also had a 10-second resting ECG acquired on the same day in the same assessment center. While different MRI views were obtained, we consider the 4-chamber long axis view with balanced steady-state free-precession movies, containing 50 frames throughout the cardiac cycle. The ECG data also spanned a single cardiac cycle, as we used 12 leads from the 1.2 second median waveforms (12 leads, 600 voltages) derived from the full 10 second ECG. All voltages were transformed to millivolts, and all MRI pixels were normalized to have mean 0 and standard deviation 1 for each individual. The MRIs were cropped to the smallest bounding box, which contained all cardiac tissues in all 50 frames as determined by the semantic segmentation33.

Framework notation and components

We consider two modalities, denoted as \({M}_{1}\) and \({M}_{2}\), and aim to learn a unified representation \(Z\) that integrates information from both. This representation \(Z\) is composed of three distinct components: a shared representation \({Z}_{s}\), which contains the information common to both modalities, and two modality-specific representations, \({Z}_{M1}\) and \({Z}_{M2}\) that capture information unique to each modality, M1 and M2, respectively. To learn these representations, we use unimodal Generators (\({G}_{M1},\,{G}_{M2}\)), which reconstruct the original input data based on the latent components. Each modality is also paired with an encoder (\({E}_{M1}\) and \({E}_{M2}\)), that estimates the modality-specific representations (\({{Z}^{* }}_{M1},{{Z}^{* }}_{M2}\)) and the shared representations (\({{Z}^{* }}_{S1},{{Z}^{* }}_{S2}\)), aligning them to the learned latent space. To approximate the shared representation, we average the shared representations estimated by each encoder and the final fused representation is the concatenation of all modality-specific and the shared representations.

Masking component

A key challenge in multimodal representation learning is managing the size of the latent space, which tends to grow with the number of modalities. As the dimensionality increases, it can impede the effectiveness of the representations for downstream tasks. Additionally, determining the size for each latent subspace is difficult. This is particularly challenging when trying to disentangle shared and modality-specific spaces, as we may not know in advance how much information is unique to a specific modality versus shared across all modalities.

To address this, we integrated a masking strategy within our framework that learns which dimensions of the latent space carry the most useful information, allowing us to mask those with lower information density. We define learnable binary masks for each subspace of the latent space, learned through the iterative training process described in the next section. For training binary parameters through gradient-descent we employ the Gumbel-Softmax distribution27,28. Gumbel-Softmax is a continuous distribution that approximates the discrete binary distribution of the masks with a temperature parameter that controls how closely the samples approximate the binary values. We apply an exponential temperature annealing technique to gradually decrease the temperature parameter at each training iteration. This encourages early exploration of the parameter space, allowing the model to consider different masking configurations, and later guiding the process toward a stable configuration with lower entropy, ensuring that only the most informative dimensions are retained. Figure 5a shows the learned binary masks in each iteration of training, and we can see that after more exploration in early iterations, the masks converge. To encourage convergence and discourage stochasticity, we use entropy regularization on the binary mask values during training. More details on the regularization and all the training objectives are presented in the next section.

Learning disentangled representations

Our framework leverages latent optimization for learning disentangled shared and modality-specific representations21,22. We define the shared representation \({Z}_{s}\) to embed information that is present in both modalities, and the modality specific representation of each modality (\({Z}_{M1}\), \({Z}_{M2}\), …) to capture information unique to that modality. We would like these representations to be disentangled, meaning each representation should encode unique information not present in other representations. Latent optimization allows us to explicitly structure the latent space into shared and modality-specific components, rather than relying on the model to discover this separation implicitly. This explicit control is critical for effective decoupling, ensuring that shared factors capture cross-modal information while modality-specific factors remain disentangled. To ensure disentanglement, we employ an iterative 3-step algorithm to train the encoders, generators, and latent representations, while simultaneously learning a mask that filters out dimensions with redundant information. The details of each step are as follows:

Step 1 - Modality-specific latent optimization and decoder training

In this step, the goal is to capture modality-specific information that, when combined with shared information, can fully reconstruct the original data. To achieve this, we feed into the generator of each modality, the modality-specific representation of that modality and the shared information captured from the other modality. We simultaneously train the modality-specific latent representations along with the generators. This process forces the modality-specific latent space to capture all the unique information about a modality that is not present in the other modality, while training the generator to reconstruct the original sample using this complementary information. In this step, we also train the masks for the shared latent representations. This allows the mask training to explore and find the most informative dimensions while these latent representations are frozen.

The objective function of Step 1 for modality \(n\) (presented in the Equation below) is composed of the reconstruction error ℒreconst, and regularization for the elements of the latent representation and mask parameters \({||}{Z}_{n}|{|}_{1}\) and \({||}{M}_{s}|{|}_{1}\). The regularization on the latent space constrains the parameter space to be contained, and the regularization of the mask values, controlled by the parameter \(\beta\), controls the amount of masking. Higher \(\beta\) values encourage more compact representations while lower values enforce fewer dimensions to be masked. The final regularization term \((-\mathop{\sum }\limits_{i\in {M}_{S}}{m}_{i}\log {m}_{i})\) is an entropy regularization for the mask values that encourages lower uncertainty on the mask probabilities.

$${{\mathscr{L}}}_{1}^{\left(n\right)}={{\mathscr{L}}}_{{reconst}}+\lambda \left|\left|{Z}_{n}\right|{|}_{1}+\beta \right|\left|{{\bf{M}}}_{{\boldsymbol{S}}}\right|{|}_{1}+\gamma \left(-\mathop{\sum }\limits_{i\in {M}_{S}}{m}_{i}\log {m}_{i}\right)$$
(1)

Step 2 - Shared latent optimization and decoder training

Once we learn modality-specific representations, we proceed to learning the shared latent space. Here, we freeze the modality-specific representations and focus on learning the shared representation \({Z}_{s}\) that, combined with the modality-specific representation, can generate an accurate sample. While optimizing the shared latent space, we continue to train the generator, ensuring that the model can utilize both the modality-specific and shared representations to accurately reconstruct the original samples. Similar to Step 1, we train the binary masks of the modality-specific representations, which are kept frozen during this step.

The objective function of Step 2 for modality \(n\) is presented in the Equation below. Similar to the previous step, it includes a reconstruction error and 3 regularization terms.

$${{\mathscr{L}}}_{2}^{\left(n\right)}={{\mathscr{L}}}_{{reconst}}+\lambda \left|\left|{Z}_{S}\right|{|}_{1}+\beta \right|\left|{{\bf{M}}}_{n}\right|{|}_{1}+\gamma \left(-\mathop{\sum }\limits_{i\in {M}_{n}}{m}_{i}\log {m}_{i}\right)$$
(2)

Step 3 - Encoder training

In this final step, we train or fine-tune (in case of using pre-trained models) the encoders of each modality to best estimate the modality-specific and shared representations that were optimized in Steps 1 and 2. Each modality’s encoder is equipped with two heads: one that estimates the shared representation and another that estimates the modality-specific representation. This dual-head structure enables the encoder to decouple information while still capturing the rich, modality-specific nuances of each input. The objective function that is optimized in this step is the mean squared error of the encoder estimated representations and the learned latent representations.