Bridging clinical knowledge and AI: an interpretable transformer framework for ECG diagnosis

Abstract

Cardiovascular disease remains a major global health burden, highlighting the need for automated electrocardiogram (ECG) interpretation systems that are accurate, efficient, and interpretable. We present MDOT (Momentum Distillation Oscillographic Transformer), where a lightweight student model learns diagnostic classification from a teacher model enriched with physician-derived knowledge. Clinically salient electrophysiological indicators such as heart rate, QRS duration, ST segment changes, and QTc interval are integrated as auxiliary features to embed clinical reasoning. A novel OSC module converts one-dimensional ECG signals into two-dimensional oscillographic representations, enabling a Transformer backbone to capture long-range dependencies and detailed waveform morphology. Attention mechanisms further generate heatmaps that highlight diagnostically relevant segments, enhancing interpretability. On strict inter-patient splits of the MIT-BIH (8 classes) and Chapman (12 classes) datasets, MDOT achieves state-of-the-art accuracies of 99.53% and 99.03%, respectively. By combining accuracy with physician-oriented interpretability, MDOT offers a robust solution for clinical decision support and edge deployment.

Introduction

Cardiovascular diseases (CVDs) represent the preeminent public health crisis of the 21st century, standing as the leading cause of mortality worldwide¹. The scale of this challenge is staggering; in 2022 alone, an estimated 19.8 million individuals succumbed to CVDs, accounting for nearly a third (32%) of all global deaths¹. The burden is particularly acute in developed nations like the United States, where heart disease is the primary cause of death across most demographic groups, claiming a life every 34 seconds and contributing to approximately 1 in every 3 deaths in 2023². This relentless mortality rate translates into a profound economic toll, with the cost of CVDs in the U.S. reaching an estimated $417.9 billion between 2020 and 2021, a figure that encompasses healthcare services, medications, and lost productivity². Projections indicate this financial strain is set to worsen dramatically, with costs forecasted to triple to an unsustainable $1.8 trillion by 2050³.

While CVDs are a global phenomenon, their impact is disproportionately borne by low- and middle-income countries (LMICs), where over three-quarters of all CVD-related deaths occur¹. This disparity underscores a critical issue of global health inequity; populations in these regions often have limited access to the effective and timely diagnostic and therapeutic services necessary for managing cardiac conditions¹. The consequence is a vicious cycle where catastrophic out-of-pocket health expenditures for CVD treatment drive families into poverty¹.

Compounding this crisis is an alarming trend: after decades of progress, the global decline in CVD mortality rates has begun to stall and, in some regions, is at risk of reversing⁴. Data from the United States, for instance, shows that while the age-adjusted death rate for coronary heart disease (CHD) declined between 2011 and 2021, the actual number of deaths has remained static or even increased slightly⁵. This stagnation suggests that existing public health strategies and clinical tools are reaching the limits of their efficacy against a backdrop of rising risk factors. The global prevalence of hypertension, diabetes, and obesity—key drivers of CVD—continues to climb, fueled by demographic shifts such as population aging and urbanization⁶. This confluence of factors creates an urgent and unmet need for a new generation of diagnostic technologies. The current trajectory is insufficient to meet critical global health targets, such as the World Health Organization’s goal of a 25% reduction in premature mortality from noncommunicable diseases¹. To alter this course, a paradigm shift is required, moving towards diagnostic solutions that are not only more accurate but also more scalable, efficient, and accessible, thereby addressing the profound challenge of health equity on a global scale.

For over a century, the 12-lead electrocardiogram (ECG) has served as the cornerstone of non-invasive cardiac diagnostics⁷. Figure 1 Its ubiquity in clinical practice—from routine screenings to emergency assessments of acute coronary syndromes—stems from its unparalleled ability to provide a cost-effective, real-time window into the heart’s electrical activity⁷. The ECG is indispensable for diagnosing a vast spectrum of cardiac pathologies, including arrhythmias, myocardial ischemia and infarction, conduction abnormalities, and chamber hypertrophy⁸. However, the enduring utility of the ECG is shadowed by profound and persistent challenges in its interpretation, creating a paradox where this foundational tool is simultaneously a critical bottleneck and a significant source of potential clinical error⁹.

Fig. 1

Schematic representation of an ECG Signal with its various intervals marked from Ansari et al.¹⁴.

The manual interpretation of ECGs is a complex cognitive task that demands years of specialized training and experience. It is inherently subjective, leading to considerable inter-observer variability even among expert cardiologists, which can compromise diagnostic consistency¹⁰. Furthermore, it is a time-intensive process; a comprehensive analysis of a 24-hour Holter monitor recording, for instance, can require 30 to 60 minutes of a specialist’s time, a significant constraint in high-volume healthcare settings. This reliance on scarce human expertise limits the scalability of high-quality ECG analysis, particularly in underserved regions. The integrity of the ECG signal itself is frequently compromised long before it reaches an interpreter. Procedural errors, such as the incorrect placement of limb or precordial leads, are common and can drastically alter the ECG waveform, creating patterns that mimic or mask serious pathologies like myocardial infarction or bundle branch blocks¹¹. Beyond acquisition errors, the signal is highly susceptible to contamination from noise, including muscle artifacts, baseline wander due to respiration, and power line interference, all of which can obscure subtle but clinically significant features¹¹.

Early attempts to overcome these limitations with first-generation computerized ECG interpretation (ECG-C) systems have proven inadequate. While widely deployed, these algorithmic systems have consistently demonstrated inferior performance compared to human experts¹². Their diagnostic accuracy is particularly poor for complex, non-sinus rhythms, where correctness can fall to as low as 54%¹². The clinical consequences of these algorithmic failures are severe; studies have shown that misinterpretations by ECG-C systems have led to inappropriate and potentially harmful changes in patient management in up to 10% of cases and have triggered unnecessary downstream diagnostic testing in 24% of patients¹². These challenges are not isolated issues but represent a cascade of potential failure points—from patient-side acquisition to signal processing and final interpretation. This systemic vulnerability indicates that a truly robust solution cannot merely be a more accurate classifier operating on idealized data. Instead, it must be an integrated system engineered to be resilient to the inherent imperfections of real-world clinical data, capable of decoding complex cardiac signals with a level of accuracy and efficiency that exceeds both human and conventional algorithmic capabilities.

The emergence of deep learning has catalyzed a paradigm shift in medical data analysis, offering a powerful new approach to surmount the long-standing challenges of ECG interpretation¹³. Unlike traditional machine learning methods, which depend on a laborious and often incomplete process of “handcrafting” features—manually defining and extracting specific signal characteristics like R-R intervals or QRS durations deep learning models can learn relevant diagnostic patterns directly from raw data¹⁰. This end-to-end learning capability allows them to automatically discover and hierarchically assemble complex, high-level features and subtle morphological variations that may be imperceptible to the human eye or too intricate to be explicitly programmed¹⁴.

This technological leap has spurred a wave of innovation in automated ECG analysis, with deep learning models consistently demonstrating superior performance in arrhythmia classification and the detection of other cardiac abnormalities when compared to both traditional algorithms and earlier computerized systems¹⁴. A diverse array of neural network architectures has been successfully adapted for this purpose. Convolutional Neural Networks (CNNs) have proven adept at identifying morphological patterns within individual heartbeats, while Recurrent Neural Networks (RNNs) excel at capturing the temporal dynamics across sequences of beats¹⁵. More recently, Transformer models, with their powerful self-attention mechanisms, have set new benchmarks by effectively modeling long-range dependencies across extended ECG recordings¹⁶.

As the field matures, the focus of cutting-edge research is evolving beyond the singular pursuit of classification accuracy on curated, noise-free benchmark datasets. The initial wave of research has firmly established the potential of deep learning; now, the scientific community is turning its attention to the more nuanced, practical challenges that must be overcome for these models to achieve widespread, trusted clinical adoption. These new frontiers include enhancing model interpretability to make the “black box” transparent to clinicians, improving computational efficiency to enable deployment on low-power wearable or edge devices for continuous monitoring, and increasing model robustness to ensure reliable performance in the face of the noisy, artifact-laden data characteristic of real-world clinical environments¹⁰. It is at the intersection of these critical next-generation challenges that the present work is situated, proposing a solution designed not just for superior accuracy, but for practical, interpretable, and robust clinical application.

To address these multifaceted challenges, we introduce the Momentum Distillation Oscillographic Transformer (MDOT), a novel framework engineered for superior diagnostic performance through the synergistic integration of specialized components for signal representation, feature extraction, classification, and optimization. Rather than a monolithic model, MDOT is a comprehensive system designed to be accurate, efficient, and clinically transparent.

Our approach begins at the input stage with the Oscillographic (OSC) module, which transforms the one-dimensional ECG time-series into a dense, image-like representation. This crucial step enriches the input signal, exposing subtle morphological and oscillatory patterns that are otherwise difficult to capture from raw waveforms. This enriched data representation creates an ideal substrate for MDOT’s analytical core: a hybrid architecture that pairs a Transformer-based deep feature extractor with an eXtreme Gradient Boosting (XGBoost) classifier. The Transformer’s self-attention mechanism excels at learning complex, long-range spatio-temporal dependencies from the OSC images, producing a rich, high-dimensional feature vector. By then delegating the final classification task to XGBoost—a model renowned for its performance and efficiency on structured data—our framework synergistically combines the unparalleled representational power of deep learning with the robust decision-making of gradient-boosted trees.

To maximize both accuracy and computational efficiency for clinical deployment, we embed this hybrid core within a momentum-based knowledge distillation paradigm. A compact “student” MDOT model is trained to emulate the outputs of a larger, pre-trained “teacher” model, effectively inheriting its generalized diagnostic knowledge. This knowledge transfer enables the final, deployable model to achieve state-of-the-art performance without the computational burden of its larger teacher. Crucially, this architecture is designed for clinical trust and utility. Interpretability is not an afterthought but an intrinsic property of the Transformer core. Its self-attention mechanism generates saliency maps that directly highlight the specific regions of the input ECG waveform most influential to the diagnostic conclusion. This provides clinicians with a transparent, verifiable window into the model’s reasoning, a critical step towards safe and effective integration into clinical decision-support workflows.

The analytical core of MDOT is a powerful hybrid architecture. It first utilizes a Transformer-based model as a deep feature extractor. The Transformer’s self-attention mechanism excels at capturing complex, long-range spatio-temporal dependencies within the oscillographic images, learning a rich, high-level feature representation of the cardiac cycle. These learned features are then passed not to a conventional softmax classifier, but to an Extreme Gradient Boosting (XGBoost) model. This fusion leverages the unparalleled feature representation power of deep learning with the exceptional classification performance, efficiency, and robustness of gradient boosted decision trees on structured feature sets. To optimize both performance and computational efficiency, MDOT incorporates a momentum-based knowledge distillation process. In this paradigm, a compact “student” MDOT model is trained to learn not only from the ground-truth diagnostic labels but also from the nuanced, generalized knowledge encoded in the outputs of a larger, more complex, pre-trained “teacher” model. This transfer of knowledge allows the final, deployable model to achieve superior accuracy and generalization capabilities without inheriting the computational overhead of its larger teacher. A foundational design principle of MDOT is clinical utility, which necessitates transparency. The framework achieves this through the intrinsic properties of its Transformer core. The self-attention mechanism naturally generates attention maps that highlight which specific regions of the input ECG waveform were most influential in the model’s diagnostic decision. This provides a direct, built-in window into the model’s reasoning process, enabling clinicians to verify the anatomical and physiological plausibility of its findings and fostering the trust required for integration into clinical decision support workflows.

The pursuit of automated ECG interpretation has evolved through several distinct paradigms, each defined by the sophistication of its feature extraction and classification methodologies. Early approaches were dominated by traditional machine learning pipelines that relied heavily on domain-specific, handcrafted features. In this paradigm, clinical experts and signal processing engineers would manually define a set of features presumed to be diagnostically relevant. These often included fiducial-based measurements such as R-R intervals for heart rate variability (HRV) analysis, QRS complex duration, P-wave and T-wave morphology, and various interval and segment lengths¹⁷. These extracted features would then serve as input to conventional classifiers like Support Vector Machines (SVMs), k-Nearest Neighbors (KNN), or shallow Artificial Neural Networks (ANNs)¹⁸. While foundational, this approach was fundamentally limited by the quality and completeness of the predefined features. It was often brittle, sensitive to noise, and incapable of capturing the full spectrum of complex, non-linear patterns present in the ECG signal, particularly for subtle or atypical disease manifestations.

The advent of deep learning marked a revolutionary shift from this feature-engineering-dependent paradigm to an end-to-end learning approach. Deep neural networks, particularly CNNs, obviated the need for manual feature extraction by learning relevant diagnostic features automatically and hierarchically from raw signal data¹⁰. This allows the model to discover novel, data-driven patterns that may not align with traditional clinical definitions but are nonetheless highly predictive¹⁶. This ability to learn directly from data has consistently enabled deep learning models to achieve superior performance across a wide range of ECG classification tasks, establishing them as the current state of the art and the foundation upon which modern research, including the MDOT framework, is built.

Within the deep learning paradigm, several distinct architectural families have been explored for ECG analysis, each offering a unique set of strengths and weaknesses. The evolution from one architecture to the next has been driven by the goal of more effectively modeling the complex spatio-temporal nature of the ECG signal.

Initially developed for image analysis, Convolutional Neural Networks (CNNs) were quickly adapted for 1D signal processing and proved highly effective for ECG analysis. The core strength of a CNN lies in its use of convolutional filters, which act as learnable pattern detectors that scan the input signal¹⁹. In the context of ECGs, these filters can learn to recognize specific morphological features, such as the characteristic shape of a premature ventricular contraction (PVC), the ST-segment elevation indicative of myocardial infarction, or the bifid P-wave associated with atrial enlargement¹⁷. By stacking multiple convolutional layers, the network can build a hierarchical representation, learning simple features like edges and slopes in early layers and combining them to detect complex waveform shapes in deeper layers²⁰.

This architectural aptitude for morphological analysis has led to numerous successful applications, with CNN-based models achieving high classification accuracies, often exceeding 98–99% on benchmark arrhythmia datasets like the MIT-BIH Arrhythmia Database²¹. However, the primary limitation of standard CNNs is their inherently local receptive field. Each neuron only processes information from a small, localized region of the input, making it difficult for the network to model long-range temporal dependencies between distant heartbeats, a crucial element for diagnosing rhythm disorders that are defined by their sequential context¹⁷.

To address the temporal limitations of CNNs, researchers turned to Recurrent Neural Networks (RNNs), an architectural class explicitly designed for sequential data processing²². Unlike feedforward networks, RNNs possess cyclic connections that create an internal hidden state, or “memory,” which allows them to retain information from previous time steps and use it to inform the processing of the current time step. This makes them naturally suited for analyzing the rhythmic, time-dependent nature of the ECG signal²³.

Advanced RNN variants, such as the Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU), were developed to overcome the “vanishing gradient” problem of simple RNNs, which limited their ability to learn long-term dependencies²⁴. These gated architectures use specialized mechanisms to control the flow of information, enabling them to selectively remember or forget information over extended sequences²². LSTMs have demonstrated strong performance in ECG classification, particularly for tasks requiring context from multiple preceding heartbeats²³. Hybrid models that combine a CNN feature extractor for individual beats with an LSTM to analyze the sequence of beat features have become a popular and effective strategy¹⁷. Despite their strengths, RNNs have two key drawbacks: their inherently sequential processing makes them computationally intensive and difficult to parallelize, and even LSTMs can struggle to effectively capture very long-range dependencies in lengthy ECG recordings due to their step-by-step memory mechanism²⁵.

The Transformer architecture, originally developed for natural language processing, has recently emerged as the new state-of-the-art for sequence modeling, offering a powerful solution to the limitations of both CNNs and RNNs¹⁶. The core innovation of the Transformer is the self-attention mechanism²⁵. Instead of processing a sequence step-by-step like an RNN, self-attention allows the model to dynamically weigh the importance of every other element in the sequence when encoding a single element¹⁶. This enables it to directly model relationships between distant data points, capturing global context and long-range dependencies with unparalleled efficacy.

Furthermore, because these attention calculations can be performed for all sequence elements simultaneously, Transformers are highly parallelizable, offering significant computational efficiency advantages over sequential RNNs¹⁶. Early applications of Transformers to ECG analysis have yielded exceptional results, with models like ECGformer demonstrating superior performance on standard benchmarks¹⁶. By leveraging a Transformer as its primary feature extractor, the MDOT framework positions itself at the cutting edge of this architectural evolution, capitalizing on the most advanced technology for capturing the full complexity of ECG signals.

The architecture of MDOT is not a monolithic invention but a principled synthesis of several advanced, state-of-the-art methodologies. Each component of the framework is informed by a distinct and evolving line of research, and its novel combination is what defines MDOT’s contribution.

A significant trend in modern time-series analysis is the conversion of 1D sequential data into 2D image-like representations. This approach is motivated by the desire to leverage the extraordinary power and sophistication of deep learning models developed for computer vision, such as advanced CNNs and Vision Transformers, which have been trained on massive image datasets and possess unparalleled feature extraction capabilities²⁶.

Several techniques for this signal-to-image transformation have been proposed. The simplest methods involve reshaping, where segments of the 1D signal are stacked as columns or rows to form a grayscale image matrix. More complex approaches aim to embed richer information into the image. Time-frequency representations, such as the Short-Time Fourier Transform (STFT) or the Continuous Wavelet Transform (CWT), generate 2D spectrograms or scalograms that visualize the signal’s frequency content as it evolves over time, a technique particularly useful for non-stationary signals. Another prominent method is the Gramian Angular Field (GAF), which encodes the time series into an image by first representing it in a polar coordinate system and then computing a Gramian matrix to capture temporal correlations as geometric relationships.

While these methods have proven effective in various domains, they may not be optimally suited for the unique characteristics of ECG signals, which are often sparse and defined by their distinct oscillatory morphology. This creates a research gap for a transformation technique specifically designed for cardiac signals. The Oscillographic (OSC) module within MDOT is proposed to fill this gap. It is a purpose-built method designed to convert the 1D ECG trace into a dense, feature-rich 2D representation that explicitly preserves and enhances the waveform’s oscillatory patterns, thereby creating an input format that is highly optimized for analysis by advanced vision models.

Knowledge Distillation (KD) is a powerful model compression and knowledge transfer technique, first formalized by Hinton et al., that enables the creation of smaller, more efficient models without a significant loss in performance. The central idea is a “teacher-student” training paradigm. A large, complex, and high-performing “teacher” model is first trained on a dataset. Then, a smaller, computationally cheaper “student” model is trained to mimic the teacher’s behavior.

The key mechanism for this knowledge transfer is the use of “soft targets”. Instead of training the student solely on the ground-truth “hard” labels (e.g., this ECG is “Normal”), it is also trained to match the full probability distribution produced by the teacher model’s final softmax layer. These “soft” probabilities—for instance, predicting a “Normal” ECG with 90% probability, but also assigning a 5% probability to “Atrial Fibrillation” and a 2% probability to “Left Bundle Branch Block”—contain rich, nuanced information about how the teacher model generalizes and perceives similarities between classes. The student’s training objective becomes a weighted combination of a standard loss function against the hard labels and a distillation loss (typically the Kullback-Leibler divergence) that measures the difference between the student’s and teacher’s soft probability distributions.

This technique is particularly valuable in medical imaging, where it can be used to compress large, cumbersome models into lightweight versions suitable for deployment on edge devices or in real-time clinical systems. It can also facilitate transfer learning, where knowledge from a teacher trained on a vast general dataset is distilled into a student being fine-tuned on a smaller, specialized medical dataset²⁷. The Momentum Distillation component of MDOT builds upon this established foundation, proposing a more dynamic and potentially more effective mechanism for this knowledge transfer process.

While deep neural networks are state-of-the-art feature extractors, their final classification layers are often relatively simple. An alternative and increasingly popular approach involves creating hybrid models that combine the feature learning power of deep networks with the classification prowess of more traditional, yet highly effective, machine learning algorithms. For structured or tabular data—such as the high-level feature vectors extracted by a deep network—tree-based ensemble methods like eXtreme Gradient Boosting (XGBoost) are often unparalleled in performance and efficiency²⁸.

XGBoost is an advanced and optimized implementation of the gradient boosting algorithm²⁸. It works by building an ensemble of “weak” decision tree learners in a sequential, additive manner. Each new tree is trained to correct the errors (residuals) of the preceding trees, effectively performing gradient descent in function space to minimize a loss function. The strength of XGBoost lies in its numerous systemic optimizations, including a highly parallelized tree-building process, cache-aware algorithms for efficient memory usage, and built-in L1 and L2 regularization to prevent overfitting, making it exceptionally fast, scalable, and robust²⁸.

The fusion of a deep feature extractor with an XGBoost classifier is a key innovation of the MDOT framework. This hybrid architecture is designed to leverage the best of both worlds: the Transformer’s ability to learn rich, hierarchical, and context-aware features from complex raw data, and XGBoost’s proven ability to make highly accurate and robust classifications based on those well-formed features.

For any artificial intelligence system to be successfully integrated into high-stakes decision-making environments like clinical medicine, accuracy alone is insufficient. The model must also be interpretable²⁹. Clinicians must be able to understand, or at least interrogate, the reasoning behind a model’s prediction to build trust, verify its conclusions against their own domain knowledge, and ultimately retain responsibility for patient care³⁰. This need has given rise to the field of explainable AI (XAI).

Broadly, XAI methods can be categorized into two groups. The first is post-hoc interpretability, where external techniques are applied to an already-trained “black-box” model to explain its behavior. Prominent examples include LIME (Local Interpretable Model-Agnostic Explanations), which explains an individual prediction by approximating the model’s behavior with a simpler, interpretable model in the local vicinity of that prediction, and SHAP (Shapley Additive exPlanations), which uses principles from cooperative game theory to assign an attribution value to each feature for its contribution to a prediction²⁷.

The second category is intrinsic interpretability, where the model’s architecture is inherently transparent. The attention mechanism at the core of the Transformer model is a prime example of this¹⁶. The attention weights computed by the model for each input element provide a direct and faithful map of which parts of the input sequence the model focused on most heavily when making its decision³¹. MDOT’s reliance on this built-in attention mechanism for explainability is a significant advantage. It provides a more direct and less abstracted view of the model’s internal logic compared to post-hoc methods, offering a clear and intuitive visualization for clinical review.

The landscape of automated ECG analysis has seen a clear progression from handcrafted feature engineering to end-to-end deep learning, with architectures evolving from CNNs and RNNs to the current state-of-the-art Transformer models. Concurrently, parallel research streams have advanced powerful supplementary techniques, including signal-to-image conversion, knowledge distillation for model optimization, and the development of hybrid classification systems. However, a review of the existing literature reveals that these powerful concepts have largely been explored in isolation. There is a clear research gap for a unified framework that thoughtfully integrates these disparate advancements to address the multifaceted challenges of clinical ECG analysis simultaneously.

Current models may achieve high accuracy but often lack robust interpretability, or they may be efficient but fail to capture the global context necessary for complex diagnoses. The MDOT framework is proposed to fill this critical gap. It is not an incremental improvement upon a single methodology but rather a novel synthesis of several cutting-edge concepts. MDOT combines the global context-awareness of Transformers, the feature-densifying power of a novel signal-to-image technique (OSC), the performance-boosting and efficiency gains of Momentum Distillation, the robust classification power of XGBoost, and the clinical necessity of intrinsic interpretability. By integrating these elements into a single, cohesive architecture, MDOT aims to advance the state of the art not just in terms of raw classification metrics, but in the creation of a diagnostic tool that is accurate, efficient, trustworthy, and ultimately, clinically useful.

Results

Datasets

Our study utilizes two publicly available electrocardiogram (ECG) benchmarks: the MIT-BIH Arrhythmia Database³² and the Chapman-Shaoxing dataset³³. A key challenge in ECG analysis is the inherent variability in signal length across recordings. To address this and create uniform model inputs, we employ our proposed Overlapped Segment Chunking (OSC) module, which resamples the raw signals into fixed-length tokens. Given typical ECG sampling rates (f) ranging from 250 to 1000 Hz, we set the module’s chunk size parameter to C = 2f for all datasets. This configuration ensures that each token encapsulates approximately two seconds of physiological data, sufficient to capture multiple cardiac cycles.

To ensure a robust and clinically relevant evaluation, we implemented a strict inter-patient data splitting protocol for both datasets, preventing any patient’s data from appearing in both the training and testing sets. For the MIT-BIH database, we adhered to the standard inter-patient division recommended by the Association for the Advancement of Medical Instrumentation (AAMI), a common practice for ensuring comparability across studies³⁴. For the Chapman-Shaoxing dataset, for which no standard split exists, we performed a patient-level random partition, assigning 70% of unique patients to the training set and holding out the remaining 30% for testing. This patient-disjoint methodology is critical for assessing the model’s ability to generalize to unseen individuals, a prerequisite for real-world clinical deployment.

MIT-BIH Arrhythmia Database comprises 48 half-hour ECG records collected by the BIH Arrhythmia Laboratory between 1975 and 1979. Each record includes two digitized ECG lead signals lasting for thirty minutes each at a rate of 360 samples per second. The dataset provides annotations for both heartbeat class and timing information, verified by an independent expert. Twenty-three recordings serve as typical clinical ECG examples, while the remaining twenty-five feature complex ventricular, junctional, and supraventricular arrhythmias.

Chapman Database collected and disseminated this novel database that contains 12-lead ECGs of 10,646 patients with a 500Hz sampling rate that features 11 common rhythms and 67 additional cardiovascular conditions, all labeled by professional experts. The dataset consists of 10-second, 12-dimensional ECGs and labels for rhythms and other conditions for each subject. The dataset can be used to design, compare, and fine-tune new and classical statistical and machine learning techniques in studies focused on arrhythmia and other cardiovascular conditions.

Methodology

We model our experiments on the LeViT work, while there are not appropriate baseline methods to measure our approach, we compare our proposed methods with other several ECG classification methods, e.g.^{35,36,37,38,39,40,41,42,43,44,45}. Through the OSC module we proposed, we preprocessed ECG data into image data, so the model does not need to be pretrained on other time series data.

We modified the knowledge distillation loss to fit our approach and task. As we notice that in a certain number of datasets and practical applications, ECG data has a large category deviation, so we replace the original cross-entropy loss in distillation loss with label-smooth focal loss, which can reduce the impact of the uneven number of categories. Distillation loss takes a teacher model prediction and uses it as additional supervision. The overall loss can be calculated as Eq. (1).

$${{\mathcal{L}}}_{d}({y}_{true},{y}_{pred},{y}_{teacher})=(1-\alpha )\cdot {{\mathcal{L}}}_{f}({y}_{true},{y}_{pred})+\alpha \cdot KLD({y}_{teacher},{y}_{pred})$$

(1)

where y_true is the ground truth label. y_pred is the predicted probability distribution from the student model. y_teacher is the predicted probability distribution from the teacher model. α is a hyper-parameter that balances the importance of the label smooth focal loss ${{\mathcal{L}}}_{f}$ and the knowledge transfer loss KLD.

Meanwhile, label-smooth focal loss ${{\mathcal{L}}}_{f}$ can be calculated as Eq (2)

$${{\mathcal{L}}}_{f}(p,y)=-\alpha \cdot {(1-p)}^{\gamma }\cdot \log (p)-(1-\alpha )\cdot LS(y,k)$$

(2)

where p is the predicted probability. y is the true label. α is the balancing parameter between focal loss and label smoothing, where 0 ≤ α ≤ 1. γ is the focal loss focusing parameter. LS( ⋅ , k) is the label smoothing term applied to the one-hot encoded true label k, can be calculated as Eq (3).

$$LS(y,k)=(1-\epsilon )\cdot {\delta }_{yk}+\frac{\epsilon }{C}$$

(3)

where ϵ is the label smoothing parameter, where 0≤ϵ≤1, δ_yk is the Kronecker delta, equal to 1 when y = k and 0 otherwise, C is the number of classes.

Implementation Details are shown in Fig. 2: All models were trained for 100 epochs, a duration found necessary for the convergence of transformer-based architectures. We used the AdamW optimizer⁴⁶ with parameters β₁ = 0.9, β₂ = 0.999, and a weight decay of 0.05. The learning rate was managed by a cosine annealing scheduler, with a 5-epoch linear warm-up phase from 1 × 10⁻⁶ to a peak of 1 × 10⁻³, after which it decayed to a minimum of 1 × 10⁻⁶. We employed a batch size of 64 and applied adaptive gradient clipping to stabilize training. For our knowledge distillation setup, we set the loss balancing hyperparameter α to 0.7 and the distillation temperature to T = 4.0. The label smoothing factor ϵ in Eq (3) was set to 0.1. To ensure reproducibility of our results, all experiments were conducted with a fixed random seed of 42.

Fig. 2: Several Indicators in Training Procedure, using default configuration on MIT-BIH dataset.

a Learning Rate: This plot displays the learning rate schedule used during training. It begins with a warm-up phase where the learning rate gradually increases, followed by a decay phase where it is slowly reduced. This strategy helps to ensure stable convergence. b Total Loss: The stacked area chart illustrates the composition of the total loss, which is a combination of Focal Loss and Knowledge Distillation (KD) Loss. Both loss components, and therefore the total loss, decrease steadily over the training epochs, indicating that the model is effectively learning to minimize its errors. c Training Accuracy: This plot shows a smooth and consistent increase in the model’s accuracy on the training data, eventually approaching saturation. This upward trend signifies that the model is successfully learning the patterns within the training dataset. d Testing Metrics: The final subplot presents a suite of evaluation metrics on the test set, including accuracy, precision, sensitivity, specificity, and the F1-score. All these metrics show a clear upward trend and converge to high values, demonstrating the model’s strong generalization capabilities and robust performance on unseen data.

We perform 100 training epochs in each round of experiments. This is more than the usual schedule for convolutional networks, but visual transformers require a longer training than convolutional neural networks. We use AdamW as optimizer and adjust the learning rate by cosine anneal scheduler with warm-up. Considering the number of samples in the dataset, we applied gradient clipping mechanism in adaptive.

We use Accuracy as the main metric to evaluate the performance of methods, which is indicated as the number of correctly classified samples divided by the total number of input samples, can be calculate as Eq. (4).

$$Acc=\frac{{\sum }_{t}T{P}_{t}}{{\sum }_{t}T{P}_{t}+{\sum }_{t}T{N}_{t}+{\sum }_{t}F{P}_{t}+{\sum }_{t}F{N}_{t}}$$

(4)

Alongside with Acc, we compute another four statistical metrics, namely, macro-averaged precision $Prec=\frac{1}{N}{\sum }_{t}\frac{T{P}_{t}}{T{P}_{t}+F{P}_{t}}$, sensitivity $Sen=\frac{1}{N}{\sum }_{t}\frac{T{P}_{t}}{T{P}_{t}+F{N}_{t}}$, specificity $Spe=\frac{1}{N}{\sum }_{t}\frac{T{N}_{t}}{T{N}_{t}+F{P}_{t}}$ and F1-score $F1=\frac{1}{N}{\sum }_{t}\frac{T{P}_{t}}{T{P}_{t}+\frac{F{P}_{t}+F{N}_{t}}{2}}$. Where t is the corresponding class and N is the number of classes. TP_t, FP_t, TN_t, and FN_t are true positives, false positives, true negatives, and false negatives, respectively. Precision is the proportion of true positive samples to the overall predicted positive observations. Sensitivity refers to the proportion of actual positive cases predicted as positive, while specificity refers to the proportion of actual negatives predicted as negative. The F1 score is the harmonic mean of precision and sensitivity, making it more meaningful compared to other metrics.

Results & comparison

This is evident from the comparative analysis shown in Table 1, where the MDOT method outperforms other models across various metrics, including Accuracy, Precision, Sensitivity, Specificity, and F1 score. The results from the MIT-BIH dataset demonstrate the superior performance of MDOT, with an accuracy of 99.53%, precision of 98.44%, sensitivity of 99.06%, specificity of 99.21%, and F1 score of 97.26%. When compared to other models, such as CNN-based and clustering approaches, MDOT shows a noticeable improvement, particularly in handling a larger number of classes (8 in this case). Similarly, in the Chapman ECG DB dataset with 12 classes, the MDOT method again outperforms the distilled models, achieving an accuracy of 99.68%, precision of 99.25%, sensitivity of 97.51%, specificity of 99.08%, and F1 score of 96.38%.

Table 1 Comparisons with other models

These results underscore the effectiveness of MDOT in providing accurate and reliable ECG classification. Its ability to integrate medical insights with algorithmic precision and feature enhancement through its unique components - the OSC module, Medical Momentum Distillation Structure, and Attention Model - is a key factor in its superior performance. This approach not only improves diagnostic accuracy but also offers enhanced interpretability, which is critical in medical applications.

Ablation study

To isolate the contributions of each component within our proposed MDOT framework, we conducted a series of systematic ablation experiments. Our baseline model is a standard LeViT classifier. We incrementally integrated three key modules: (A) the attention mechanism, (B) the OSC module for multi-dimensional image transformation, and (C) the complete momentum distillation structure.

The results, summarized in Table 2, demonstrate a consistent and significant performance improvement with the addition of each component. Within the distillation module (C), we further assessed the impact of the XGBoost classifier by comparing the full model against a variant that instead uses a standard softmax head, highlighting the efficacy of our chosen teacher architecture.

Table 2 Ablation study of MDOT components

Finally, to specifically quantify the value of incorporating physician knowledge into the learning process, we ablated the clinical indices from the teacher model during distillation. As shown in Table 3, training the student with a physician-informed teacher (i.e., one trained with access to clinical indices) yields superior final performance compared to a student trained by a teacher who learned from ECG data alone. This result underscores the critical role of physician-informed guidance in our framework.

Table 3 Impact of physician-informed distillation

Interpretability analysis

Experimental results demonstrate the efficacy of the introduced attention bias. The integration of local channel attention augments the Transformer architecture by capitalizing on the strengths of Convolutional Neural Networks (CNNs) in the refinement of localized features and the amplification of saliency. As shown in Fig. 9, the model strategically incorporates an attention bias module following each convolutional pooling stage. This module meticulously computes the weights for each channel within the pooled feature matrix.

When this computational process is applied to a singular heartbeat signal, the result is a set of triple weights. To elucidate this mechanism, we visualized the weights associated with three distinct heartbeat signal types. Notably, the contrast between the V- and N-type heartbeats, as depicted in Fig. 3, is pronounced.

Fig. 3: Visualizing the local attention Mechanism.

The attention map highlights the significance of the local attention mechanism, particularly in light of the substantial local heterogeneity observed between these classifications.

Additionally, the heatmap visualization warrants attention; it reveals numerous weights nearing zero (indicated by white on the heatmap). This finding underscores the model’s proficiency in distinguishing and identifying various arrhythmic events throughout the cardiac cycle.

To validate that the model’s attention mechanism provides a causal explanation for its predictions, we conducted a comprehensive faithfulness analysis (Fig. 4).

Fig. 4: Occlusion/perturbation faithfulness analysis of MDOT.

a MDOT attention overlaid on the oscillographic (OSC) ECG representation highlights physiologically meaningful segments (QRS/ST). b Patch-wise occlusion importance, computed as the drop in class confidence when a token grid cell is masked, co-localizes with attention. c Deletion and insertion curves show that masking the most-attended patches yields a steep, monotonic decline in confidence, whereas progressively restoring them from a blurred baseline increases confidence. d Lead-ablation analysis demonstrates that precordial leads (V2-V5) contribute most to performance, with lead-wise drops tracking the attention mass. e Temporal window perturbations identify peaks around QRS/ST intervals and rhythm windows. f Summary metrics across datasets indicate strong rank agreement between attention and occlusion-derived importance, low deletion AUC, and high insertion AUC, consistent with faithful, causal attributions.

Qualitatively, attention maps overlaid on oscillographic ECGs highlight physiologically meaningful segments, primarily the QRS complex and ST segment (Fig. 4a). This observation was quantitatively confirmed through patch-wise occlusion analysis, which demonstrated that importance scores—measured as the drop in class confidence when a patch is masked—strongly co-localize with high-attention regions (Fig. 4b). Deletion and insertion curve analyses further substantiated these findings; progressively masking the most-attended patches resulted in a steep, monotonic decline in model confidence, whereas sequentially restoring them from a blurred baseline produced a similarly monotonic increase (Fig. 4c).

This relationship between attention and model prediction held at coarser granularities. A lead-ablation analysis revealed that the precordial leads (V2-V5) contribute most significantly to the prediction, with the magnitude of the drop in confidence correlating directly with the lead-wise attention mass (Fig. 4d). Likewise, perturbations of discrete temporal windows confirmed that the model’s sensitivity peaks around clinically critical QRS/ST and rhythm intervals (Fig. 4e).

In summary, quantitative metrics revealed a strong rank agreement between attention and occlusion importance, a low Area Under the Curve (AUC) for the deletion metric, and a high AUC for the insertion metric. Collectively, these results provide robust evidence that the model’s attention mechanism generates faithful and causal attributions for its predictions (Fig. 4f).

We assessed faithfulness by targeted perturbations in OSC space. The OSC image is partitioned into non-overlapping token patches; patches are ranked by mean attention. For the deletion curve, the top-k patches are iteratively masked (mean-fill or Gaussian noise), and predicted-class confidence is recorded. For the insertion curve, patches are progressively restored into a blurred baseline. Curves are summarized by AUC (lower is better for deletion; higher is better for insertion) and by Δaccuracy at fixed masking levels (10%, 20%). Agreement between attention and occlusion-derived importance is quantified using Spearman’s ρ over patches and sliding temporal windows (150–250 ms). Clinical faithfulness is probed via lead ablation by removing one lead at a time and correlating Δaccuracy with lead-wise attention mass. Controls include random patch orders and intensity-matched perturbations; uncertainty is estimated by bootstrap resampling.

Deletion-insertion analyses corroborate the causal character of the highlighted evidence. In the exemplar record of Panel C, the deletion curve declines monotonically as the top-ranked patches are masked, yielding AUC_del = 0.29, while the insertion curve rises monotonically as these patches are restored, yielding AUC _ins = 0.82. Early perturbations have substantial predictive impact: masking only the top 10% patches reduces accuracy by −7.9 percentage points, and masking 20% reduces it by -14.8 points. Together, the asymmetric AUCs (low for deletion, high for insertion) and the steep early drops argue that the model’s attention concentrates on features whose perturbation materially alters the output-quantitative evidence for interpretability under standard faithfulness criteria.

Discussion

This study introduces the Momentum Distillation Oscillographic Transformer (MDOT), a novel and integrated method that significantly enhances the accuracy and interpretability of ECG classification. By synergistically combining a unique signal-to-image conversion technique (the OSC module), a powerful hybrid classification core (Attention Model and XGBoost), and an advanced training methodology (Momentum Distillation), MDOT addresses several key challenges in automated cardiac diagnostics.

Our work makes a principal contribution by demonstrating that treating ECG data as multi-dimensional images via the specialized OSC module allows for more effective feature extraction by state-of-the-art vision transformer architectures. This approach successfully overcomes the data sparsity issues inherent in 1D signal representations. The fusion of a deep attention model with an XGBoost classifier leverages the strengths of both paradigms: deep feature learning and robust, efficient classification. Furthermore, the integration of knowledge distillation not only boosts performance but also enables the development of a computationally efficient model suitable for clinical deployment.

Crucially, the inherent interpretability of the attention mechanism provides a transparent view into the model’s decision-making process, a vital feature for fostering clinical trust and adoption. Extensive testing on benchmark datasets confirms that MDOT achieves state-of-the-art performance, surpassing existing methods in accuracy and other key metrics.

Future work will focus on validating the MDOT framework on larger and more diverse clinical datasets, extending its capabilities to predict a wider range of cardiovascular conditions, and exploring its potential for real-time monitoring on wearable and edge devices. By bridging the gap between advanced machine learning and clinical expertise, MDOT paves the way for more reliable, efficient, and trustworthy AI-driven tools in cardiac care.

Methods

Calculation of diagnostic indicators

Based on the systematic clinical approach to ECG interpretation⁴⁷, the most efficient and safe method and the required observations are shown in Table 4.

Table 4 Clinical diagnostic indicators of electrocardiogram

To obtain these diagnostic indices, the following procedures are employed: First, to determine the heart rate, multiply the number of QRS wave clusters within a 6-second interval by 10. To measure the QRS amplitude, calculate if S − wave_v1orv2 + R − wave_v5 > 35, If true, it indicates high amplitude. Second, for ST-segment analysis, baseline calibration is essential. The PR interval’s end serves as the reference line, and the endpoint of the QRS complex (J point) is the test point. Following this, the ST segment displacement can be calculated using the formula:

$$S{T}_{disp}=EC{G}_{cal}\times ({A}_{meas}-{A}_{base})$$

(5)

where ST_disp represents the ST segment displacement, ECG_cal is the ECG’s calibration value for amplitude, A_meas is the amplitude measured at the test point, and A_base is the baseline amplitude. The displacement is positive if the measurement point is above the baseline (indicating ST elevation) and negative if below (indicating ST depression). Additionally, assess the similarity between the T-wave and QRS complex using the Pearson correlation coefficient. Lastly, evaluate the presence of T-wave quarter-band waves, particularly when the heart rate is around 60 beats/min. Parameters such as P-wave duration, P-wave amplitude, PR interval, QRS duration, Q-waves, Q-amplitude, and QTc duration can be directly obtained from the ECG time series data.

OSC module

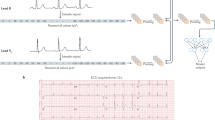
When treating ECG data as multidimensional image data, a notable challenge arises due to its inherent sparsity. This characteristic may not be conducive to subsequent image model processing. To address this issue, we introduce the Oscillation and Stacking Convolution (OSC) module.

For each lead L in the ECG dataset, represented as a tensor of size (B, 1, T), where B denotes the batch size, and T represents the number of sample points, we employ an unfolding operation. This operation is a memory-efficient method for creating sliding windows or patches from the data. Using a kernel size of (1, C), we extract overlapping segments of the time series. Padding is applied to fill the vacant positions at the end with zeros, forming the patch size of the model. Stacking these matrices yields the original feature map F_original of size (B, 1, N, C), where N = ⌈T/C⌉. This process transforms raw data of varying lengths into a set of equally long tokens through matrix manipulation. Given the periodic nature of ECG wave-forms, the processed matrix retains the relative positional relationships between sampling points, preserving the time series nature of the data.

In practical scenarios, ECG data comes in various formats, such as 3 leads, 5 leads, 12 leads, and rhythm strip data, which means L usually can be 1, 3, 5, 12. To accommodate diverse lead configurations, we stack matrices along the second dimension of the feature map. For missing lead data, we replace it by introducing a zero matrix of the corresponding size, resulting in a feature F_m of size (B, L, N, C).

For cases where the feature becomes too sparse, as in 3-lead or rhythm strip data, negatively impacting subsequent feature extraction, we utilize a series of convolutional layers with 1 × 1 kernel to interact across different channels for lead data fusion. Given the feature map F_m, we initially up-sample it to (B, 128, N, C) to unify expressions from different leads with -layer. This alignment in feature space facilitates more convenient downstream processing. We then transpose the feature to (B, C, 128, N) and perform convolution with -layer, preserving the input channels on the C channel.

Reverting the matrix dimensions back to their original order, we use another convolution to up-sample the feature to (B, 256, N, C). Finally, we reshape the feature map to size (B × N, 256, C), optimizing the learning of sample characteristics while expanding the number of samples for periodic time series. At the same time, the target of the dataset, which as a size of (B, 1) is also repeated to fit the expanded batch size (B × N, 1).

Algorithm 1

OSC (Oscillation and Stacking Convolution) Module

Require: ECG data $X\in {{\mathbb{R}}}^{B\times {L}_{in}\times T}$, Labels $Y\in {{\mathbb{R}}}^{B\times 1}$, Patch size C, Target leads L_out

Ensure: Processed feature map ${F}_{out}\in {{\mathbb{R}}}^{(B\times N)\times 256\times C}$, Repeated labels ${Y}_{out}\in {{\mathbb{R}}}^{(B\times N)\times 1}$

 1: Initialize an empty list F_leads

 2: for each lead l from 1 toL_in do

 3:  X_l ← X[: , l, : ] ▹ Select data for the current lead

 4:  F_patch ← Unfold(X_l, kernel_size = (1, C)) ▹ Create patches of size C

 5:  F_leads. append(F_patch)

 6: end for

 7: ${F}_{stacked}\leftarrow Stack({F}_{leads},\dim =1)$ ▹ Stack along the lead dimension

 8: if L_in < L_out then

 9:  N ← ⌈T/C⌉

10: P_zeros ← Zeros(B, L_out − L_in, N, C) ▹ Create zero padding

11: ${F}_{m}\leftarrow Concatenate({F}_{stacked},{P}_{zeros},\dim =1)$

12: else

13: F_m ← F_stacked

14: end if

15: F_conv1 ← Conv1X1(F_m, in_channels = L_out, out_channels = 128) ▹ Size: (B, 128, N, C)

16: F_transposed ← Transpose(F_conv1, dims = (0, 3, 1, 2)) ▹ Size: (B, C, 128, N)

17: F_conv2 ← Conv1x1(F_transposed, in_channels = 128, out_channels = 128) ▹ Size: (B, C, 128, N)

18: F_reverted ← Transpose(F_conv2, dims = (0, 2, 3, 1)) ▹ Size: (B, 128, N, C)

19: F_conv3 ← Conv1x1(F_reverted, in_channels = 128, out_channels = 256) ▹ Size: (B, 256, N, C)

20: F_out ← Reshape(F_conv3, (B × N, 256, C))

21: Y_out ← Repeat(Y, repeats = (N, 1)) ▹ Size: (B × N, 1)

22: return F_out, Y_out

The general procedure is shown in Fig. 5. After the processing of original ECG data, the feature map produced will be more suitable to the vision Transformer model.

Fig. 5: OSC module.

This module transforms the original ECG data into a dense matrix of a specified size, facilitating effective feature mapping.

Momentum model structure

ResNeSt⁴⁸, a sophisticated modular architecture, seamlessly integrates channel-wise attention with a multi-path network design. Its innovative Split-Attention block, depicted in Fig. 6a, divides feature maps into groups (cardinal groups) and further subgroups (radix splits). It then applies a channel-wise attention mechanism across these splits within each cardinal group, enabling focused attention across different feature map groups and allowing the network to learn more diverse and robust representations. This architecture surpasses other CNN models in terms of speed-accuracy trade-offs, demonstrating exceptional performance in transfer learning applications such as object detection and semantic segmentation, thereby highlighting its versatility.

Fig. 6: Modules in the Momentum Model.

a A key component of ResNeSt. It enhances feature extraction by dividing feature maps into cardinal groups and radix splits, then applying channel-wise attention to learn more diverse representations. b A high-performance gradient boosting algorithm that builds an ensemble of decision trees to make robust predictions based on the features extracted by ResNeSt.

XGBoost²⁸, an abbreviation for eXtreme Gradient Boosting, represents a cutting-edge development in gradient boosting algorithms. It is renowned for its exceptional performance in classification and regression tasks, offering high-speed computation and precise results. XGBoost works by sequentially building an ensemble of “weak” decision tree learners, where each new tree is trained to correct the errors (residuals) of the previous ones. Key features of XGBoost include its ability to handle missing data, implement L1 and L2 regularization to prevent overfitting, and accommodate a wide range of custom optimization objectives and evaluation criteria, making it highly scalable and robust. The main structure of XGBoost is illustrated in Fig. 6b.

In this paper, we explore the synergistic combination of ResNeSt’s superior image feature extraction capabilities with XGBoost’s robust feature evaluation prowess. This fusion aims to maximize the integration of clinical ECG metrics with modeling features, ultimately training an advanced teacher model.

Presenting training dataset X = {(x_j, y_j)∣1≤j≤M}, where M is the size of the training dataset. Initialize training dataloader. Set the parameters of the ResNeSt for learning features learn features, the process is shown in Fig. 7. Initialize parameters for the prediction step (XGBoost). Categorize labels ${\widehat{y}}_{i}$, where $\,{f}_{k}\in {\mathcal{F}}$, K is the number of trees, f_k is a tree, and ${\mathcal{F}}$ is the space of all possible trees. Use the regularization to improve the final result ${\mathcal{R}}(\phi )$, where ω(f_k) is the complexity of the tree f_k. Get the best objective reduction: ${w}_{j}^{* }$, ${{\mathcal{R}}}^{* }$. Calculate the best splitting scores: ${{\mathscr{L}}}_{split}$. The well-trained teacher agent ${\theta }_{t}^{{\prime} }$ is constructed. The specific algorithm and model are schematically shown in Algorithm 2.

Fig. 7: Momentum model.

It serves as the “teacher” model. It integrates a ResNeSt module for advanced image feature extraction from ECG data, combined with an XGBoost module for robust classification and evaluation.

Algorithm 2

ResNeSt-XGBoost Momentum Model

Require: X, epoch_total

Ensure: ${\theta }_{t}^{{\prime} }$

 1: Initialize training dataloader

 2: Set the parameters of the ResNeSt.

 3: Initialize parameters for the prediction step (XGBoost).

 4: for epoch = 0 to epoch_total do

 5:  ${\widehat{y}}_{i}=\phi ({x}_{i})={\sum }_{k=1}^{K}{f}_{k}({x}_{i})$                       ▹ Categorize labels

 6:  ${\mathcal{R}}(\phi )={\sum }_{i}^{n}l({y}_{i},{\widehat{y}}_{i})+{\sum }_{k=1}^{K}\omega ({f}_{k})$                        ▹ Regularization

 7:  ${w}_{j}^{* }=-\frac{{G}_{j}}{{H}_{j}+\lambda }$                ▹ Get the best objective reduction

 8:  ${{\mathcal{R}}}^{* }=-\frac{1}{2}{\sum }_{j=1}^{T}\frac{{G}_{j}^{2}}{{H}_{j}+\lambda }+\gamma T$

 9:  ${{\mathscr{L}}}_{split}=\frac{1}{2}[\frac{{G}_{L}^{2}}{{H}_{L}+\lambda }+\frac{{G}_{R}^{2}}{{H}_{R}+\lambda }-\frac{{({G}_{L}+{G}_{R})}^{2}}{{H}_{L}+{H}_{R}+\lambda }]-\gamma$                ▹ Calculate the best splitting scores

10: end for

Diagnostic distillation model

By employing knowledge distillation⁴⁹, we facilitate the transfer of features learned by the momentum model to the primary model. This approach enables us to discern the impact of clinical ECG metrics and image features on classification accuracy. Through this training process, we aim to develop a more precise classification model. Presenting the training dataset X = (x_j, y_j)∣1≤j≤M, teacher model θ_t, and student model θ_s, where M is the size of the training dataset. Initialize the training dataloader and set the parameters of the models. For each epoch, forward pass of training data through the teacher model to get soft labels ${\widehat{y}}_{i}^{t}$, then forward pass of training data through the student model ${\widehat{y}}_{i}^{s}$, calculate the distillation loss L_kd, where the loss function is a function measuring the difference between teacher and student outputs. Update the Student model parameters θ_s, where η is the learning rate. Finally, we got a well-trained Student agent ${\theta }_{s}^{{\prime} }.$

The specific details of the knowledge distillation process and the algorithms used are illustrated in Fig. 8 and Algorithm 3.

Fig. 8: knowledge distillation model.

Pre-trained “teacher” model (ResNeSt-XGBoost) generates soft labels from the input data. The “student” model (LeViT) is then trained to mimic the outputs of the teacher. This process transfers the teacher’s learned knowledge, allowing the student model to achieve higher accuracy and better generalization.

Algorithm 3

Diagnostic Distillation Model

Require: X, θ_t, θ_s, epoch_total

Ensure: ${\theta }_{s}^{{\prime} }$

 1: Initialize training dataloader, θ_t, θ_s.

 2: Set the parameters of the θ_t for feature extraction.

 3: Initialize parameters for θ_s.

 4: for epoch = 0 to epoch_total do

 5:  ${\widehat{y}}_{i}^{t}=\rm{TeacherModel}({x}_{i};{\theta }_{tea})$                      ▹ Forward θ_t

 6:  ${\widehat{y}}_{i}^{s}=\rm{StudentModel}({x}_{i};{\theta }_{stu})$                      ▹ Forward θ_s

 7:  ${{\mathcal{L}}}_{KD}(\widehat{y}{i}^{t},y{i}^{s},\tau )={\sum }_{i=1}^{I}{\tau }^{2}KL(\sigma (\frac{{\widehat{y}}_{i}^{t}}{\tau }),\sigma (\frac{{\widehat{y}}_{i}^{s}}{\tau }))$                    ▹ Calculate Loss

 8:  ${\theta }_{s}\leftarrow {\theta }_{s}-\eta {\nabla }_{{\theta }_{s}}{{\mathcal{L}}}_{kd}$                   ▹ Update parameters

 9: end for

Model

Our primary model leverages the LeViT architecture³¹, a hybrid design combining convolutional layers with transformer blocks to optimize the trade-off between speed and accuracy. The network employs a pyramid structure with pooling layers to create activation maps of decreasing resolution—a strategy borrowed from CNNs that facilitates highly efficient inference. LeViT also introduces an “attention bias” to effectively integrate positional information. This hybrid approach demonstrates superior performance over conventional CNNs and vision transformers under equivalent memory constraints.

To adapt this architecture for electrocardiography, we developed the specialized Oscillation and Stacking Convolution (OSC) module, which preprocesses ECG signals for the vision backbone. Furthermore, we integrated a knowledge distillation framework where our primary model (the student) learns from the pre-trained ResNeSt-XGBoost Momentum model (the teacher). This integration not only augments classification performance but also significantly enhances the model’s clinical interpretability. The complete architecture is depicted in Fig. 9.

Fig. 9: Model structure overview.

The figure details our proposed model architecture. Raw ECG data is initially transformed by the Oscillation and Stacking Convolution (OSC) module to create a feature map suitable for image-based models. The core of the system is a knowledge distillation framework where a powerful “teacher” model (ResNeSt-XGBoost) guides the training of a more efficient “student” model (LeViT). The teacher model generates “soft labels” by processing both ECG features and clinical diagnostic data. The student model then learns from both these soft labels and the original “hard” labels, effectively inheriting the teacher’s comprehensive knowledge to enhance its final diagnostic accuracy.

For the purposes of our ablation studies, we established a baseline model to empirically quantify the contributions of our proposed components. This baseline consists of the core LeViT backbone connected to a linear classifier head. It is trained directly on the raw, one-dimensional ECG time-series data, which is reshaped to meet the input dimensionality requirements of the transformer, bypassing both our OSC module and the knowledge distillation process.

Ethics approval and consent to participate

This study exclusively used publicly available and fully anonymized electrocardiogram datasets, namely the MIT-BIH Arrhythmia Database and the Chapman University ECG Database. All patient identifiers had been removed prior to public release. According to the policies of these repositories, the use of these datasets is exempt from institutional review board (IRB) approval and informed consent requirements. Therefore, ethics approval was waived, and no additional consent was required.