Introduction

Pulmonary hypertension (PH) is a progressive cardiopulmonary disorder characterized by elevated mean pulmonary artery pressure (mPAP), which increases the workload of the right ventricle and may ultimately progress to right heart failure and death. With the estimation of affecting 1% global population, the etiology of PH ranges from rare conditions such as genetic deficiency to common disorders like cardiac valvular disease1,2. Once mPAP exceeds 20 mmHg, patients tend to have a poor prognosis, irrespective of their underlying primary disease. Right heart catheterization (RHC) remains the gold standard for measuring mPAP, a critical parameter for diagnosing PH and subclassifying it based on hemodynamic profiles. However, the invasive nature of RHC limits it clinical application due to considerable risks, including infection, allergic reactions, and anesthesia-related complications.

Current guidelines recommend echocardiography for the early recognition and follow-up of PH3. Although mPAP can be estimated via tricuspid regurgitation velocity (TRV), the consistency between echocardiographic estimates and RHC measurements is less than 60%, primarily due to interoperator variability and suboptimal imaging quality4,5. In contrast, cardiac magnetic resonance (CMR) offers accurate and reproducible imaging, along with reliable right ventricle assessment. Furthermore, quantification of pulmonary artery blood flow using time-resolved, three-directional MR phase contrast (4D-flow) imaging has been shown to yield over 90% accuracy in detecting elevated mPAP in small-scale studies6. However, given the lack of precise prediction of mPAP, imaging modalities are typically used for semi-quantification of mPAP or combined with other parameters for risk stratification in PH7.

With the accumulation of clinical data and the advancement of artificial intelligence theory, learning-based approaches to PH diagnosis have emerged as a promising trend. Representative cases include the work by Kwon, J. et al.8, who integrated demographic features and electrocardiograms into a deep learning model for PH diagnosis, achieving an area under the curve (AUC) of 0.859. Zhao, W. et al.9 further developed a deep learning pipeline capable of processing multimodal data-including tabular, textual, and imaging inputs-with a significantly improved AUC of 0.965. Recent efforts have leveraged AI models to improve the accuracy of PH classification10. However, classification-based approaches inherently fall short in identifying borderline patients (with mPAP ∈ [18, 20] mmHg) and supporting clinical risk stratification11, as both tasks require a more nuanced understanding of the continuous variations in mPAP. Capturing such subtle dynamics demands accurate regression modeling-a task that remains highly challenging in real-world clinical settings.

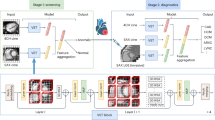
In this work, we tackle this challenge by proposing an effective assessment framework by integrating ensemble learning, symbolic regression, and sensitivity analysis (see Fig. 1). This framework quantitatively learns mPAP using a series of non-invasively measurable features, e.g., vital signs, CMR data, and demographic characteristics. Ensemble learning possesses powerful nonlinear learning capabilities and is employed in our study to construct accurate predictive models. It also serves as a surrogate model for high-dimensional feature selection, facilitating the preliminary identification of key features. Although symbolic regression entails a higher training cost compared to ensemble learning, it achieves a similarly reliable level of accuracy. More importantly, its white-box nature makes it a crucial component of interpretable artificial intelligence. Mutual information (MI) serves as model-independent feature selection methods, making them suitable for the preliminary screening of high-dimensional features to retain a small set of key features. Beyond this, we employ a compressed sensing-based symbolic regression algorithm to provide fully transparent symbolic models. By integrating this approach with sensitivity analysis methods, we extract the most critical patient physiological features for mPAP modeling, offering insights for PH clinical decision support and prognosis assessment.

Fig. 1: Overview of the study.
figure 1

a A comparison between the classical paradigm and our AI-based paradigm for obtaining mPAP revealed that our proposed AI model demonstrated a high predictive performance for actual mPAP using non-invasive multivariate parameters. b Composition illustration of the data used in this study. These datasets comprise clinical features, biochemical factors, and imaging data from CMR. 90% of the dataset is used for testing, and 10% is used for validation. c The proposed AI pipeline employs mutual information and medical prior knowledge for key feature selection, leverages a black-box model for high-accuracy mPAP prediction, develops an analytical expression for mPAP using a white-box model, and finally applies sensitivity analysis to assess feature importance. d The AI model was evaluated by using the proposed symbolic model to predict mPAP in PH patients and by performing receiver operating characteristic (ROC) analysis, where the green line represents the ROC curve and the green area indicates the 95% confidence interval.

Full size image

Results

Study population

A total of 376 patients who underwent RHC between January 2022 and July 2025 were retrospectively reviewed. Among them, 157 patients underwent CMR with 4D-flow; however, 37 patients were excluded due to missing or incomplete clinical data, resulting in a final cohort of 120 patients for analysis. The baseline clinical characteristics of the study population are summarized in Table 1.

Table 1 Baseline clinical characteristics of study population
Full size table

Non-pulmonary hypertension (non-PH) patients were significantly younger than PH patients (23 years vs. 38 years, p < 0.001), as most of the former were apparently healthy individuals undergoing routine physical examinations. The majority of PH patients were classified as group 1 (pulmonary arterial hypertension, n = 64, 83.1%). Moreover, there was one patient (1.3%) with PH due to chronic obstructive pulmonary disease (COPD, group 3), 11 patients (14.3%) with chronic thromboembolic pulmonary hypertension (CTEPH, group 4), and one patient (1.3%) with PH secondary to fibrosing mediastinitis (FM, group 5). Patients with PH due to left heart disease (group 2) were not included in this study due to predominantly incomplete data.

Black-box-based reliable prediction and feature selection for mPAP

eXtreme Gradient Boosting (XGBoost)12 is an ensemble learning model well-suited for tabular datasets and easy to implement. In our case, the XGBoost model is implemented using scikit-learn13 package. To ensure the model achieves optimal performance, we first use grid search to determine the approximate range of the potential optimal hyperparameters space, followed by fine-tuning with Optuna library14. The tuning of hyperparameters in machine learning models can be abstracted as a multivariate function optimization problem15. Due to the diversity of hyperparameter combinations, optimization algorithms typically converge to a local optimum rather than a global one, as no algorithm can guarantee that the iterative results will always reach the global optimum16. In general, the model error obtained after multiple trials does not exhibit significant variation, i.e., hyperparameter optimization algorithms can provide satisfactory results within the constraints of limited computational resources.

In the initial training, the XGBoost prediction results are shown in Fig. 2a. The training dataset incorporated basic demographic characteristics, laboratory biomarkers, and hemodynamic parameters. The data generated from echocardiography (LV, LA, RV, RA, PA, EF, and TRV) and CMR were both included in the initial training dataset. To ensure a reliable and objective assessment of model performance, XGBoost was evaluated using ten-fold cross-validation, thereby minimizing the potential uncertainty arising from dataset partitioning17. Under this setting, an R2 value of 0.992 and a MAPE as low as 4.49% collectively underscore the model’s remarkable predictive fidelity. Benefiting from the comprehensiveness of the available information, the aforementioned features were sufficient to enable highly reliable predictions. Given the inherent subjectivity associated with echocardiographic assessment, we retrained the model after excluding all echocardiography-derived variables from the input space. Intriguingly, this modification yielded a modest improvement in both R2 and MAPE (see Fig. 2b).

Fig. 2: Performance of XGBoost on mPAP via ten-fold cross-validation across four different input feature spaces.
figure 2

a The original complete dataset including echocardiography features; b Dataset without echocardiography features; c Dataset retaining the top 8 features selected by MI; d Dataset with RWMaxWSS and LWMaxWSS (from the MI feature set) removed and BMI and UA manually added. Here, \({\mathcal{P}}\) denotes the true values of mPAP, and \(\hat{{\mathcal{P}}}\) represents the model estimates. Scatter points correspond to the mean predicted values from ten-fold CV on the y-axis scale, and error bars represent the variability of the predictions.

Full size image

Although the exclusion of the aforementioned seven echocardiographic features reduced the input dimensionality, a total of 168 variables, including RMC-derived metrics, remained. This level of complexity is readily handled by black-box models such as XGBoost; however, from a clinical standpoint, the sheer volume of required data imposes a substantial and arguably impractical burden on routine diagnostic workflows. At this stage, the limitation shifts from model complexity to data availability, making the overall process time-consuming and less efficient. Moreover, as shown in Fig. 2a, b, an increase in the number of features does not necessarily lead to better model performance—typically, a considerable portion of the features are redundant18. Therefore, it is essential to extract key features to achieve dimensionality reduction.

As discussed in Section “Feature Reduction”, we employ MI19 to assess and achieve feature dimensionality reduction, the computation of MI is available in Section “Computing Mutual Information”.

In order to identify the minimal feature dimensionality that retains maximal model performance, we sequentially retained the top 20 features ranked by MI and evaluated the corresponding XGBoost performance, as shown in Fig. 3. Notably, an R2 exceeding 0.90 was already achieved with only 6 features. When the number of retained features reached 8, the R2 peaked at 0.97 (see Fig. 2c). Beyond this point, R2 exhibited fluctuations, suggesting the inclusion of additional features-despite their high MI scores-may introduce redundancy. Although comparable performance can be maintained at dimensionalities of 10, 16, and 20, incorporating more features risks redundancy and significantly increases the computational burden for downstream symbolic regression. Thus, retaining eight features represents a judicious balance between parsimony and predictive fidelity.

Fig. 3: The relationship between XGBoost model performance and feature dimensionality.
figure 3

Here, the x-axis denotes the number of features retained according to the maximal MI criterion, while the y-axis displays the ten-fold cross-validation R2 achieved by the XGBoost model at each corresponding dimensionality.

Full size image

The features with the highest MI are summarized in Table 2. Although, as shown in Fig. 2c, the model retains excellent predictive performance when built upon this feature subset, an underlying limitation emerges: the feature set is derived solely from CMR metrics and thus lacks a holistic representation of the patient. To address this, we manually replaced RWMaxWSS and LWMaxWSS with BMI and UA, respectively, yielding the revised set listed in Table 4. Interestingly, the incorporation of BMI and UA led to a marked improvement in model performance, accompanied by reduced variance across folds, as illustrated in Fig. 2d. The symbolic regression model introduced in Section “Symbolic Regression for Analytical Modeling of mPAP” is accordingly constructed upon this refined feature composition.

Table 2 Features ranked by mutual information
Full size table

Symbolic regression for analytical modeling of mPAP

To construct a fully interpretable symbolic model for mPAP, we employ the sure-independence screening & sparcifying operator (SISSO) method, which is implemented via SISSO.3.320. This method was originally proposed by Ouyang, R. et al.21 and has been widely applied in the field of materials science22,23. SISSO is essentially a data-driven algorithm that can be seamlessly transferred from materials science data to medical data. As a symbolic regression algorithm, SISSO can describe the mapping relationship between features and the target by constructing symbolic models (i.e., analytical expressions). In this work, the target is the mPAP.

In SISSO, one or more primary features are combined with operators to construct new variables, referred to as “descriptors,” which capture the nonlinear relationships between features, as discussed in Section “Single-Task SISSO (ST-SISSO)”. In contrast to traditional genetic programming symbolic regression24, SISSO systematically explores all conceivable descriptors that can be constructed, resulting in a much higher time complexity. This process is fundamentally an NP-hard problem21,25. In the experimental process, to maximize the accuracy of the model, we do not impose constraints on the unit of the variables. That is, operations such as “area + height” are considered permissible. Different hyperparameter settings of the model do have a significant impact on its performance and impose varying requirements on computational resources. Table 3 presents the hyperparameter settings for the SISSO model. Notably, the descriptor dimension desc_dim = 6 means that mPAP will be mapped through a linear combination of six descriptors. The feature complexity fcomplexity = 6 indicates that each descriptor can include at most six features. method_so = 'L0' signifies that the final model will use ℓ0 regularization to sparcify descriptors. Denoting the features listed in Table 4 as \({\mathcal{X}}=\{{x}_{1},{x}_{2},\ldots ,{x}_{8}\}\), and the predicted value of mPAP as \(\hat{{\mathcal{P}}}\), the symbolic model can thus be expressed as:

$$\begin{array}{lll}\hat{{\mathcal{P}}}=13.52+56.68\left(\frac{{x}_{1}+{x}_{6}}{{x}_{2}}+\left| \frac{{x}_{2}}{{x}_{3}}-\frac{{x}_{5}}{{x}_{4}}\right| \right)+1.07\times 1{0}^{4}\frac{{x}_{1}^{2}}{{x}_{3}^{3}\sin (\log ({x}_{7}))}\\\qquad\, -\,6.21\times 1{0}^{-4}\frac{\sin ({x}_{8}^{3})\cdot {x}_{8}\cdot \log ({x}_{4})}{{x}_{4}}-5.25\sin \left(\frac{{x}_{7}}{{x}_{5}}\right)\left[\cos ({x}_{1})+\cos ({x}_{4})\right]\\\qquad\, -\,4.73\left[\sin ({x}_{3}+{x}_{8})-\frac{{x}_{7}}{{x}_{8}}+\sin ({x}_{8})\right]-1.21\times 1{0}^{-3}\frac{{\cos }^{3}({x}_{1})}{\left\vert \frac{{x}_{4}}{{x}_{3}}-\,\text{scd}\,({x}_{2})\right\vert }.\end{array}$$
(1)
Table 3 List of key hyperparameters in SISSO
Full size table

The symbolic model constructed by SISSO has a MAPE of 17.01% and an R2 of 0.9239, see Fig. 4. The previously optimal empirical model was derived by Chemla, D. et al.26 as:

$${\rm{mPAP}}=0.61\times {\rm{RVSP}}+2,$$
(2)

where RVSP represents right ventricular systolic pressure, with an R2 of 0.7427. Eq. (1) presents a reliable quantitative estimation of mPAP using laboratory biomarkers, and hemodynamic parameters generated from CMR. If additional features are incorporated through the XGBoost model discussed in Section “Black-box-based reliable prediction and feature selection for mPAP”, the accuracy could potentially rival that of invasive diagnostic methods. Existing empirical formulas for mPAP primarily rely on features extracted from echocardiography, a process susceptible to subjective errors. In contrast, the SISSO-derived symbolic model does not incorporate echocardiographic information; instead, it integrates more objective and comprehensive indicators, such as CMR and demographic characteristics, thereby offering a more reliable approach to prediction.

Fig. 4: A parity plot is presented to compare the true values of mPAP (denoted as \({\mathcal{P}}\)) with those predicted by the SISSO model.
figure 4

The shaded region along the diagonal represents a ±5% error margin. Histograms on the top and right margins illustrate the distribution of mPAP across different PH subtypes. The horizontal and vertical gray dashed lines mark the clinical threshold of 20 mmHg for both the predicted and true values, respectively, providing a qualitative visual reference for assessing the incidence of PH. Distinct PH subtypes are denoted using different marker shapes: circles for non-PH, squares for PAH, diamonds for PH associated with lung diseases and/or hypoxia, upward triangles for PH due to pulmonary artery obstructions, pentagons for PH of unclear or multifactorial mechanisms. The performance of the SISSO model is quantitatively assessed using R2, MAPE, and the p value.

Full size image

Deepening medical interpretability via sensitivity analysis

As mentioned in Section “Symbolic regression for analytical modeling of mPAP”, symbolic models do enhance the transparency of the decision-making process; however, the quantitative identification of feature importance still requires sensitivity analysis. Therefore, we employ the Sobol indexes, SHAP index, and LIME index to achieve this purpose. In our study, the computation of Sobol indexes is implemented in UQLab28, while the calculations of SHAP and LIME indexes are performed using their respective Python libraries. Due to the black-box nature of XGBoost, Sobol indices cannot be directly applied.

Figure 5a compares the feature sensitivity of the CMR-based SISSO model under different measurement methods. To facilitate comparison with the Sobol index, we calculated the absolute mean values of the SHAP and LIME indexes for each feature across all 120 patients. The Sobol index is a global measurement method, whereas SHAP and LIME contain local information, allowing the identification of regions in patient characteristics that do not follow global trends. In contrast, the advantage of the Sobol index lies in its ability to quantify feature dependencies and interactions. Si reflects the correlation between the variance of mPAP and the variance of an initial feature, while \({S}_{i}^{{\rm{T}}}\) quantifies not only the correlation between the variance of mPAP and the initial feature itself but also includes the interaction effects between this feature and other features. If the Sobol index of a certain feature is 0, it indicates that mPAP is independent of that feature; if the value is 1, it means that mPAP can be fully described by that initial feature29,30.

Fig. 5: Sensitivity analysis of CMR-based SISSO & XGBoost models.
figure 5

a Sensitivity analysis results from SISSO. Each feature corresponds to four bars, from left to right: the Sobol main effect index Si, the total effect index \({S}_{i}^{{\rm{T}}}\), SHAP, and LIME. The left y-axis represents the scale of the Sobol indices, while the right y-axis corresponds to the mean absolute values of the SHAP and LIME indices. b Sensitivity analysis results from XGBoost. The blue bars indicate the mean absolute SHAP values for each feature, while the yellow bars represent the mean absolute LIME values. Here, {x1, x2, …, x8} correspond sequentially to the features listed in Table 4.

Full size image

In Fig. 6, we denote the input variables from Table 4 as x1 to x8, and use \({\mathcal{P}}\) to represent the prediction target, i.e., mPAP. Here, we focus on the symbolic model derived from SISSO, as only such continuous expressions allow us to construct detailed maps of how \({\mathcal{P}}\) varies with the inputs. In the off-diagonal subplots, \({\mathcal{X}}\) in the expected value of \({\mathcal{P}}\), \({E}_{{\mathcal{X}}}(\hat{{\mathcal{P}}}| \bar{{\mathcal{X}}})\), refers to a selected subset of input variables (e.g., {x1, x2}), while \(\bar{{\mathcal{X}}}\) denotes the dataset-averaged values of the remaining variables ({x3, …, x8}). The diagonal subplots represent the variation of \({\mathcal{P}}\) as a function of a single feature, while the remaining features are fixed at their average values. This visualization helps facilitate an intuitive comparison of the dominant influences each variable or variable pair has on the predicted value of \({\mathcal{P}}\).

Fig. 6: Partial dependence plots based on the SISSO model.
figure 6

For simplicity, features are denoted as {x1, x2, …, x8} and the prediction target mPAP as \({\mathcal{P}}\). The diagonal plots show the 1D mappings between each x-axis variable and \({\mathcal{P}}\), with vertical axes indicated by the red ticks on the right; the red curves represent univariate functions from the SISSO symbolic model, where all other variables are fixed to their dataset means. The off-diagonal plots depict the 2D distributions of the x- and y-axis variables, where background colors indicate \({E}_{{\mathcal{X}}}(\hat{{\mathcal{P}}}| \bar{{\mathcal{X}}})\), i.e., the expected value of mPAP when the remaining variables are set to their dataset-averaged values.

Full size image
Table 4 List of CMR-related features and corresponding information
Full size table

Interestingly, although RVWT (x1) ranks highest in MI and is repeatedly identified as the most critical feature across various sensitivity analyzes methods, its actual impact on mPAP (\({\mathcal{P}}\)) appears to be limited. In contrast, RWMaxWSS (x4) exhibits a markedly stronger dominant influence. Across the entire x4 column in Fig. 6, regardless of which other variable it interacts with, a consistent negative correlation is observed between x4 and \({E}_{{\mathcal{X}}}(\hat{{\mathcal{P}}}| \bar{{\mathcal{X}}})\). Specifically, the left region of each subplot-corresponding to lower x4 values-is consistently highlighted in red, indicating higher predicted mPAP and thus the presence of PH subtypes. Conversely, the right region shows a dominant green zone, associated with lower mPAP values and mostly populated by non-PH individuals. This negative correlation is even more clearly illustrated in the diagonal plot of x4 versus \({\mathcal{P}}\): in the absence of interaction effects from other variables, nearly all non-PH individuals are concentrated in the region where x4 > 0.45.

As shown in Fig. 5, only the SHAP analysis based on the SISSO model correctly identifies the dominant role of RWMaxWSS, whereas other methods tend to overestimate the importance of RVWT. The results from LIME are particularly unreasonable-its index values for four features from RWMaxWSS to LPNPV are all zero, despite these features being actively involved in the model’s decision-making process. Compared to global sensitivity methods such as Sobol, SHAP demonstrates a distinct advantage as a local sensitivity metric by identifying regions in the feature space that deviate from global trends29.

It is worth noting that, although the Sobol indices exhibit certain biases in our case, they remain advantageous in effectively capturing feature interdependencies. According to Fig. 5 and Section “Calculating the Sobol Indexes”, RVWT, RWMaxWSS, and PRAvgWSS primarily influence mPAP prediction through interactions with other variables. This helps explain why RVWT, although showing limited direct influence on mPAP in Fig. 6, is still identified as important by several sensitivity analysis methods. Furthermore, while SHAP based on the SISSO model yields the most reasonable interpretation overall, it still presents inconsistencies. For example, RWMaxWSS and PRAvgWSS exhibit a high linear correlation (R = 0.86), yet their SHAP values in Fig. 5 differ notably. In principle, correlated features should yield similar sensitivity values31. This correlation was correctly recognized only by the Sobol indices based on the SISSO model, which assigned similar sensitivity scores to the two features.

Model performance

Figure 7 demonstrates the diagnostic performance of the symbolic model. The area under the receiver operating characteristic curve (AUC) was 0.987 (95% confidence interval [CI]: 0.975, 0.997). The sensitivity and specificity of the model for overall diagnosis of PH were 0.935 and 0.953, respectively (see Fig. 7a). Since our model was developed based on a population with PAH as the primary research subject, we were concerned about its potential insufficient accuracy in other subgroups. Therefore, we validated the model in 13 non-PAH patients and found that there remained a good consistency between the model-predicted mPAP and the mPAP measured by RHC (R2 = 0.825, p = 8.6 × 10−6, Fig. 7b).

Fig. 7: Diagnostic performance of the symbolic model.
figure 7

a ROC curves for PH, with the light blue shaded area indicating the 95% confidence interval; b parity plot assessing the accuracy of mPAP predictions for Non-PAH patients, where diamonds denote group 3 PH, triangles represent cases with group 4 PH, and plus signs indicate conditions with group 5 PH.

Full size image

Clinical application

In the multivariate model, we identified RVWT, BMI, RVEDV/BSA, RWMaxWSS, RPAvgWSS, LPBV, LPNPV, and UA as key predictors of mPAP. In contrast, traditional indicators such as NT-proBNP and 6MWD exhibited weaker correlations (R6MWD = −0.314, p6MWD = 4.86 × 10−4; RNT-proBNP = 0.185, pNT-proBNP = 4.27 × 10−2. Further details are available in Supplementary Table 2.). Beyond mPAP, important hemodynamic parameters assessed via RHC include PVR and PAWP. To develop a non-invasive assessment approach for PH, we further constructed predictive models for PVR (Eq. 3) and PAWP (Eq. 4) using the aforementioned 8 parameters. The predicted PVR showed a strong correlation with the actual PVR (R2 = 0.9111, p = 7.5 × 10−64, see Fig. 8a). However, the consistency between predicted PAWP and PAWP measured by RHC was lower than that observed for mPAP and PVR (R2 = 0.7535, p = 1.1 × 10−37), see Fig. 8b.

$$\begin{array}{lll}{\hat{{\mathcal{P}}}}_{{\rm{PVR}}}=9.65\frac{\root{3}\of{\frac{{x}_{5}}{{x}_{7}}}}{\frac{{x}_{4}}{{x}_{1}}-\frac{{x}_{6}}{{x}_{3}}}-0.34\frac{\cos ({x}_{8})+{\rm{scd}}({x}_{5})}{\sin \left(\log ({x}_{5})\right)}+1.46\times 1{0}^{-3}\frac{\sqrt{{e}^{{x}_{1}}}}{\cos ({x}_{7})+\sin ({x}_{3})}\\\qquad\quad\,\,\,\,-\,0.22\frac{\cos ({x}_{3}{x}_{5})}{\sin ({x}_{1}-{x}_{3})}-7.74\times 1{0}^{-3}\frac{{x}_{1}/\sin ({x}_{1})}{{x}_{1}/{x}_{3}-\sin ({x}_{8})}\\\qquad\quad\,\,\,\,+\,1.15\times 1{0}^{-2}\sin ({x}_{7}^{6})\left[\frac{{x}_{1}}{{x}_{7}}({x}_{3}-{x}_{8})\right]+0.11,\end{array}$$
(3)
$$\begin{array}{lll}{\hat{{\mathcal{P}}}}_{{\rm{PAWP}}}=4.15\times 1{0}^{3}\frac{{x}_{1}{x}_{5}(2{x}_{6}+{x}_{1})}{{x}_{2}^{3}}-2.72\left| \cos ({x}_{3}{x}_{7})-\frac{\sin ({x}_{1})}{\log ({x}_{7})}\right| \\\qquad\qquad\,\,+\,5.01\times 1{0}^{-4}\frac{({x}_{6}-{x}_{7})}{\cos ({x}_{8})\sin ({x}_{5}+{x}_{7})}+4.06\frac{\cos ({x}_{7}/{x}_{4})}{{x}_{3}{x}_{4}\sin ({x}_{1})}-1.24\times 1{0}^{-1}\frac{\sin ({x}_{7}^{3})}{\cos ({e}^{{x}_{1}})}\\\qquad\qquad\,\,-\,1.15\left| \sin ({x}_{3}-{x}_{7})-\left| \cos ({x}_{2})-\sin ({x}_{1})\right| \right| +10.45.\end{array}$$
(4)
Fig. 8: Evaluation of symbolic prediction models for PVR and PAWP.
figure 8

a Parity plot for PVR prediction; b Parity plot for PAWP prediction.

Full size image

Discussion

In this study, we developed regression prediction models based on XGBoost and SISSO algorithms, incorporating patient demographic data, multi-parametric CMR measurements, and serological test results to enable non-invasive and accurate quantitative assessment of mPAP. Among the multivariate predictors analyzed, we identified RVWT, BMI, RVEDV/BSA, RWMaxWSS, RPAvgWSS, LPBV, LPNPV, and UA as key determinants of mPAP. Additionally, we incorporated sensitivity analysis32 as a complementary method to systematically quantify the impact of each feature on mPAP values. Importantly, we optimized the predictive performance through two key strategies: (1) refining CMR-derived parameters, and (2) integrating novel 4D-flow CMR hemodynamic metrics. This approach established, to our knowledge, the first CMR-based, hemodynamics-enhanced framework for non-invasive mPAP estimation.

PH refers to a broad category of diseases characterized by elevated mPAP, with the common feature across its subtypes being an mPAP exceeding 20 mmHg. Right ventricular function becomes impaired and gradually progresses to failure as mPAP increases, which leads to recurrent hospitalizations and eventual death in patients, regardless of their underlying diseases. It should be noted that mPAP acts as a compensatory mechanism to maintain pulmonary blood flow and left ventricular filling during rising PVR, whereas in advanced right ventricular failure mPAP may plateau or even decline as cardiac output falls33. Therefore, mPAP, along with other hemodynamic parameters such as RAP and CI, is primarily assessed and measured via RHC for prognostic assessment in PH patients34,35. Nevertheless, due to its invasive nature and high professional expertise requirement, current guidelines recommend that RHC be performed in specialized centers and restricted to the diagnosis and annual follow-up of PH patients3. CMR plays an important role in the non-invasive diagnosis and assessment of PH. Conventional 2D CMR imaging can provide routine measurements of right heart structure and function, and our previously study found that CMR-based right ventricular assessment distinguished potentially high-risk patients, allowing for timely intensification of treatment to improve their prognosis36. Although 4D-flow CMR enables quantitative hemodynamic measurements and flow visualization, and has shown correlation with RHC parameters, it has not previously provided accurate mPAP estimation37,38. Our study here not only found that the correlation between CMR and mPAP is stronger than that between echocardiography and mPAP, but also established a CMR-based model for accurate prediction of mPAP. Our results further demonstrated the reproducible and reliable imaging from CMR.

To realize such predictive capability, we explored advanced machine learning algorithms capable of integrating heterogeneous clinical and imaging data. In this context, we first adopted eXtreme Gradient Boosting (XGBoost)12 as an effective feature-selection and predictive tool, and then applied SISSO for interpretable symbolic regression to provide transparent predictive formulas. We further enhanced interpretability by incorporating sensitivity analysis32 to systematically quantify the influence of each feature on mPAP, thereby providing both accurate predictions and mechanistic insights. Through model analysis, integrating basic patient characteristics, laboratory data, and CMR variables achieved an internal accuracy of approximately 92% in predicting mPAP in this cohort. The final model incorporated WSS along with BMI, UA, RVWT, and RVEDV/BSA. As two key CMR markers of right heart function, RVWT and RVEDV/BSA reflect PH disease progression39,40. UA is well-established as being associated with PH prognosis and pathogenesis41,42. Although NT-proBNP has shown independent correlation with PH diagnosis and prognosis in previous studies43,44,45, its correlation here was weaker than that of UA, consistent with the clinical observation that PAP elevation does not always parallel NT-proBNP changes. This suggests that reliance on NT-proBNP alone may result in missed diagnoses and delayed intervention. Furthermore, PH patients with lower BMI have shown poorer treatment responses46, and our study observed a strong correlation between BMI and mPAP. A plausible explanation is that elevated mPAP leads to right heart failure, causing gastrointestinal congestion and impaired digestion, ultimately reducing BMI-a pattern particularly evident in advanced disease. To our knowledge, this is the first study to highlight BMI changes in PH patients as a potential indicator for timely assessment of disease progression.

A key focus in PH diagnosis and assessment is distinguishing between subtypes, which relies on accurate measurement of mPAP, PAWP, and PVR. Previous non-invasive models have largely focused on PH screening-specifically, binary classification of mPAP-with limited research on PAWP and PVR6,47. Building on our successfully developed model for accurate mPAP prediction, we used highly correlated factors to predict PAWP and PVR, achieving favorable performance-particularly for PVR, with an accuracy exceeding 90%. This may be attributed to our model’s inclusion of both 2D CMR imaging and 4D-flow parameters, which enhanced hemodynamic information and enabled non-invasive, accurate PVR prediction. However, PAWP prediction accuracy was only 75%, potentially due to the exclusion of group 2 PH patients, which limited the availability of characteristic data for model training. Nevertheless, as the largest subgroup of PH patients globally, group 2 PH warrants further research, and future studies should develop non-invasive models to assess their mPAP and other hemodynamic parameters. In a small-scale validation with non-PAH patients, our model achieved over 85% accuracy in mPAP prediction. While the small sample size precluded subtype-specific analysis, our results have largely achieved the goal of non-invasive mPAP measurement.

Admittedly, our study has certain limitations. First of all, we established the model based on a small PH cohort and we excluded group 2 patients due to the incomplete clinical data. The clinical utility of our non-invasive model was limited by the unequal contribution of the five PH subgroups in our study population. In clinical practice, however, most patients initially suspected of having PH are ultimately diagnosed with group 2 or group 3 PH, whereas only a minority belong to group 148. Therefore, to fully establish its reliability and clinical applicability, the model should be further validated in a larger and more representative cohort that includes all PH subgroups. External, prospective, and multicenter validation is also needed to confirm generalizability. Second, we incorporated several common 4D-flow CMR parameters into the AI model for the clinical management of PH in our preliminary study. While 4D-flow CMR offers richer hemodynamic information, it also demands higher acquisition and post-processing expertise and longer scan times; future work should therefore explore more clinically feasible acquisition and analysis pipelines and consider additional pulsatile hemodynamic metrics (e.g., reflected waves, characteristic impedance, pulsatile pressure gradients) that may add prognostic value. Third and last, from a methodological perspective, symbolic regression in SISSO is computationally expensive, which led us to adopt a simplified hyperparameter configuration. With greater computational resources, more accurate symbolic formulas could likely be achieved.

In conclusion, we developed a CMR-based, AI-driven multivariate model for predicting mPAP in PH patients. This model validates the feasibility of integrating CMR-derived parameters into an AI framework to support PH management. It may serve as a potential noninvasive alternative in settings where RHC is unavailable or not feasible. Future studies should focus on incorporating additional hemodynamic indices and simplifying workflow for broader clinical adoption. Despite limitations in sample size and subgroup distribution, the proposed methodology offers a transferable framework not limited to PH. The value of interpretable AI lies in uncovering latent patterns from data to inform and refine medical theory. This methodology can be applied to modeling other diseases, providing novel insights for medical research.

Methods

Study design

Patients receiving RHC and CMR at the Center of Structural Heart Disease, Zhongnan Hospital of Wuhan University, between January 2022 and July 2025 were reviewed. PH was diagnosed according to current guidelines as the mPAP > 20 mmHg meacured by RHC. Patients with incomplete date and congenital heart disease, valvular disease due to the different 4D-flow CMR profile were excluded. Demographic and clinical parameters were systematically extracted from electronic medical records, including age, sex, height, weight, body mass index (BMI), N-terminal pro-B-type natriuretic peptide (NT-proBNP), hemoglobin (HB), Aspartate Aminotransferase (AST), Alanine Aminotransferase (ALT), albumin (ALB), and creatinine (CREA) levels. WHO/NYHA functional class and 6-min walk distance (6MWD) were documented to assess physical activity limitations. Transthoracic echocardiography provided assessment of left ventricular function (left ventricular ejection fraction, LVEF), cardiac chamber sizes (LA, RA, LV, RV), TRV, and pulmonary artery width (PA). Hemodynamic measurements were obtained from RHC. The study protocol adhered to Declaration of Helsinki and received approval from the ethics committee of Zhongnan Hospital of Wuhan University (2023046K). Informed consent was waived because of the retrospective observational study.

Cardiac magnetic resonance imaging

Electrocardiographically (ECG)-gated CMR imaging was performed for all patients and healthy subjects using a 3T CMR scanner (uMR 790, United Imaging Healthcare, Shanghai, China). All acquisitions in this study were conducted with a 12-channel body phased-array coil in combination with a 12-channel spine coil.

A standard cine balanced steady-state free precession (SSFP) technique with retrospective gating and end-respiratory breath-holds was employed to generate short-axis images along the long axis at 6-mm intervals, as well as 4-chamber and 2-chamber views. The typical CMR protocol parameters for the cine real-time sequence were as follows: repetition time (TR) = 3.01 ms, echo time (TE) = 1.39 ms, flip angle = 60°, spatial resolution = 1.61 × 1.61 × 6.0 mm3, number of acquired cardiac phases = 25, and bandwidth = 1000 Hz/pixel for the 4-chamber series. For the short-axis series, the parameters were: TR = 2.98 ms, TE = 1.38 ms, flip angle = 39°, spatial resolution = 1.6 × 1.6 × 6.0 mm3, number of acquired cardiac phases = 25, and bandwidth = 1000 Hz/pixel.

4D-flow CMR data were acquired in the right ventricular outflow tract (RVOT) orientation during free breathing, covering the pulmonary trunk and bilateral main pulmonary arteries, with respiratory and ECG gating. Velocity encoding was set at 150 cm/s in all directions, and 20–25 cardiac frames were acquired per cardiac cycle with a spatial resolution of 2.5 × 2.5 × 2.5 mm3. The relevant sequence parameters were as follows: flip angle (FA) = 7°, TR = 20.2 ms, TE = 2.56 ms, field of view (FOV) = 400 × 280 mm, and bandwidth = 600 Hz/pixel.

Image analysis

Biventricular function quantification and quantitative flow analysis were performed through consensus between two observers (G.L. with 5 years of experience and R.S. with 4 years of experience in cardiac imaging diagnosis) using commercial post-processing software (cvi42, version 6.0.2; Circle Cardiovascular Imaging, Calgary, Canada). Endocardial and epicardial contours were automatically delineated with careful manual corrections. Trabeculae and papillary muscles were excluded from the myocardial mass. Volumetric function parameters assessed included end-diastolic dimension (DD), end-diastolic volume (EDV), end-systolic volume (ESV), stroke volume (SV), ejection fraction (EF), and left ventricular (LV) myocardial mass (LVM), all indexed to body surface area. Additionally, cardiac output (CO) was calculated by multiplying the heart rate by stroke volume.

All 4D-flow CMR data were preprocessed to correct for eddy currents using a planar fit to static tissue. Subsequently, a phase-contrast magnetic resonance angiogram (PC-MRA) was generated, allowing interactive placement of two-dimensional cutplanes perpendicular to the direction of flow in the main pulmonary artery (MPA), right pulmonary artery (RPA), and left pulmonary artery (LPA). The locations of the MPA, RPA, and LPA cutplanes were positioned approximately 1 cm downstream from the pulmonary valve or the LPA/RPA bifurcation. Peak systolic velocity (Vmax), peak flow (Qmax), stroke volume (SV), and wall shear stress (WSS) were computed in the MPA, RPA, and LPA.

Feature reduction

Feature reduction methods include model-independent Filter methods49, e.g., MI and Pearson correlation coefficient; model-dependent Wrapper and Embedded methods50, with the former exemplified by recursive feature elimination and the latter by feature importance ranking based on tree models; and manifold learning techniques51, such as principal component analysis (PCA). Model-dependent dimensionality reduction methods are largely influenced by the decision-making process of the surrogate model. Taking tree-based models as an example, these methods assign different weights to features based on their frequency of participation in decision-making. However, this approach has notable limitations52:

  • Features with lower usage frequency may still play a crucial role;

  • A single feature may dominate the importance that should ideally be distributed among multiple correlated features.

Given that we integrate symbolic regression for interpretable modeling, such model-dependent feature reduction approaches are impractical in this context. Manifold learning methods achieve dimensionality reduction by projecting the feature space from high to low dimensions. However, these methods exhibit intrinsic limitations:

  • The original physical interpretation of the features is obscured, thereby compromising the interpretability of the model53,54;

  • The amalgamation of multiple features hinders the effective separation of noise55, which can subsequently impair the model’s performance.

Above all, MI is an imperfect yet feasible dimensionality reduction method. In Section “Black-Box-Based Reliable Prediction and Feature Selection for mPAP”, we first used MI to extract key features and then incorporated medical prior knowledge to refine the feature set.

Computing mutual information

MI is a metric of the dependency between variables. Unlike correlation coefficients, MI is not limited to real-valued random variables; rather, it is a more general measure that quantifies the similarity between the joint distribution p(X, Y) and the product of the marginal distributions p(X)p(Y). Formally, MI is defined as:

$$I(X;Y)=\sum _{x\in X}\sum _{y\in Y}p(x,y)\log \frac{p(x,y)}{p(x)p(y)},$$
(5)

where X and Y represent the random variables, p(x, y) is the joint probability distribution of X and Y, and p(x) and p(y) are the marginal probability distributions of X and Y, respectively. Intuitively, it measures the extent to which knowing one variable reduces the uncertainty of the other. Similar to MI, the Pearson correlation coefficient (PCC)56 is also model-independent but represents a relatively weaker metric, as it is limited to detecting only linear relationships between random variables and allows highly correlated features to be reconstructed from one another, thereby offering limited benefits for predictive performance57.

Single-Task SISSO (ST-SISSO)

SISSO generates a symbolic model for n-dimensional variables Φ0 = (ϕ1, ϕ2, …, ϕn) and the target property \({\mathcal{P}}\). Here, Φ0 and \({\mathcal{P}}\) represent patient physiological features and corresponding RHC metrics (mPAP, TPR, PVR, CO, CI, RAP, PAWP). SISSO applies a set of mathematical operators to Φ0 to construct high-dimensional descriptors. The operator set is defined as:

$${\hat{H}}^{\left(\text{m}\right)}\equiv \left\{I,+,-,\times ,\div,\exp ,\log ,\,\text{abs}\,,\sqrt{}{,}^{-1}{,}^{-2}{,}^{-3}\right\}\left[{\phi }_{1},{\phi }_{2}\right],$$
(6)

where ϕ1 and ϕ2 are terms in variables (descriptors) set. The superscript (m) indicates that SISSO retains only descriptors with physical meaning. For instance, features involved in addition or subtraction must have the same dimensionality, and those subjected to logarithmic or square root operations must be non-negative. It should be noted that in our work, to minimize the fitting error, we prioritize numerical validity and disregard dimensional consistency. The high-dimensional descriptor space is recursively constructed from the low-dimensional space. The new descriptors generated in the i-th iteration can be expressed as:

$${\Phi }_{i}\equiv \bigcup _{k}{{\hat{h}}_{k}}^{\left(\text{m}\right)}\left[{\hat{\phi }}_{i},{\hat{\phi }}_{j}\right],\forall {{\hat{h}}_{k}}^{\left(\text{m}\right)}\in {\hat{H}}^{\left(\text{m}\right)}\text{and}\,\forall {\phi }_{i},{\phi }_{j}\in {\Phi }_{i-1},$$
(7)

where ϕ1 as well as ϕ2 are terms in Φi. After the construction of the n-D descriptor set Φn is completed, sure independence screening (SIS) computes the Pearson correlation coefficients between all descriptors and P, retaining the descriptors with the highest linear correlations as the first-order subspace S1D. In the subsequent i-th iteration, the algorithm computes the residuals between S(i−1)D and P, and selects the new subspace SiD with the highest correlation. The descriptor subspace is then expanded to SiD ∪ S(i−1)D, thus reducing the error. Among the vast descriptors constructed by SIS, the sparsifying operator (SO) performs regularization through ℓ058,59 or LASSO60 to find the optimal Ω-dimensional descriptors. Finally, based on the optimal descriptor, SISSO solves the following least-squares problem:

$$\mathop{{\rm{argmin}}}\limits_{{\bf{c}}}\parallel\!{\mathcal{P}}-{\bf{D}}\cdot {\bf{c}}{\parallel }_{2}^{2}+\lambda \parallel\!{\bf{c}}{\parallel }_{0},$$
(8)

where \({\bf{D}}\in {{\mathbb{R}}}^{N\times \Omega }\) denotes the SIS-selected subspace matrix, c is the sparse coefficient vector of the descriptors, and ∥c∥0 represents the ℓ0 norm of c, weighted by a regularization parameter λ.

It is worth noting that the medical domain often faces the challenge of small sample sizes. Common strategies to address this issue include transfer learning61, multi-task learning62, federated learning63, and generative AI64. In this work, due to the novelty of our dataset design, transfer learning and federated learning were not applicable; however, we present an application case of generative AI in Supplementary Note 1. In addition, SISSO is also capable of performing multi-task learning62,65, and we employed this approach to jointly model the three targets mPAP, PVR, and PAWP, as detailed in Supplementary Note 2.

Calculating the SHAP Index

In this study, the SHAP computation follows the method proposed by Lundberg, S et al.66 and is implemented using the SHAP package in Python. SHAP is a game-theoretic approach, where its prototype, the Shapley value, is originally designed to evaluate each player’s contribution to the overall outcome in a cooperative game. This concept can be transferred to machine learning by quantifying the contribution of each input feature to a single prediction made by any model, including black-box models. By computing the marginal contribution of each feature to the model output, SHAP helps interpret why a model makes a particular decision, thereby opening the so-called “black box” of machine learning.

In our case, taking the estimation of mPAP as an example, we assume that each patient’s mPAP can be characterized by a set of clinical features \({\mathcal{U}}\in {{\mathbb{R}}}^{N}\). For a specific mPAP prediction \(\hat{{\mathcal{P}}}({\mathcal{U}})\), the core idea of SHAP is to decompose the prediction into the sum of individual feature contributions:

$$\begin{array}{r}\hat{{\mathcal{P}}}({\mathcal{U}})={\phi }_{0}+\mathop{\sum }\limits_{j=1}^{N}{\phi }_{j},\end{array}$$
(9)

where ϕj represents the contribution of the j-th feature to \(\hat{{\mathcal{P}}}({\mathcal{U}})\) (i.e., its Shapley value), and ϕ0 is the baseline output. Let \({\mathcal{V}}\subseteq {\mathcal{U}}\) denote a subset of features excluding the j-th feature. Then, the Shapley value for the j-th feature is computed as:

$${\phi }_{j}=\mathop{\sum}\limits_{{\mathcal{V}}\subseteq {\mathcal{U}}\setminus \left\{j\right\}}\frac{\left\vert {\mathcal{V}}\right\vert !\left(N-\left\vert {\mathcal{V}}\right\vert -1\right)!}{N!}\left[v\left({\mathcal{V}}\cup \left\{j\right\}\right)-v\left({\mathcal{V}}\right)\right],\quad{j}=1,\ldots ,N.$$
(10)

In Eq. (10), \(| {\mathcal{V}}|\) denotes the dimensionality of the feature subset \({\mathcal{V}}\) that excludes the j-th feature67. The function \(v({\mathcal{V}})\) represents the expected model output given the subset \({\mathcal{V}}\):

$$v({\mathcal{V}})={\mathbb{E}}\left[\hat{{\mathcal{P}}}({\mathcal{X}})| {{\mathcal{X}}}_{{\mathcal{V}}}={{\mathcal{X}}}_{{\mathcal{V}}}^{* }\right],$$
(11)

where \(\hat{{\mathcal{P}}}({\mathcal{X}})\) denotes the model’s prediction given input features \({\mathcal{X}}\), and \({{\mathcal{X}}}_{{\mathcal{V}}}^{* }\) denotes the specific value of the subset \({\mathcal{V}}\) in the instance being explained. In practice, the computation of \(v({\mathcal{V}})\) is typically approximated via sampling or model-specific simplifications, such as Tree SHAP68 or Kernel SHAP69,70.

Calculating the LIME Index

LIME (Local Interpretable Model-agnostic Explanations) approximates black-box model predictions using locally weighted linear models, but it suffers from several limitations. A key issue is local fidelity71, as LIME assumes a linear model can approximate the decision boundary within a neighborhood. This assumption fails when the true boundary is highly non-linear, leading to misleading feature attributions. Formally, the fidelity loss is defined as

$${\mathcal{L}}(f,g,{\pi }_{x})=\sum _{z\in Z}{\pi }_{x}(z){\left[f(z)-g(z)\right]}^{2},$$
(12)

where f(z) is the black-box prediction and g(z) is the surrogate model. Additionally, stability72 is a concern, as different perturbation samples can yield inconsistent explanations, reducing reliability. The method also enforces sparsity73 by selecting only k features, which, while improving interpretability, risks omitting relevant factors. These limitations suggest that while LIME provides useful insights, its explanations should be interpreted cautiously, especially in cases involving complex decision boundaries.

Calculating the Sobol Indexes

Sobol proposed a global sensitivity analysis74, which aims to quantify the impact of input variables on the model’s output. This method is based on analysis of variance (ANOVA)75.

The main- and total- effect Sobol indexes are defined as:

$${S}_{i}=\frac{\,\text{Var}\,\left[{\text{E}}_{ \sim i}\left[Y| {X}_{i}\right]\right]}{\,\text{Var}\,\left[Y\right]},$$
(13)
$${S}_{i}^{\,\text{T}}=\frac{{\text{E}}_{ \sim i}\left[\,\text{Var}\,\left[Y| {{\bf{X}}}_{ \sim i}\right]\right]}{\,\text{Var}\,\left[Y\right]}.$$
(14)

For a given value of Xi, the value of Y could be obtained by averaging the model outputs over a sample of X~i, while keeping \({X}_{i}={x}_{i}^{* }\) constant, where X~i refers to all the variables except Xi. The assumption of Sobol indexes is that all features in the input X are independent of each other. When there is dependence between features (e.g., BMI can be calculated from height and weight, and when both BMI and weight are included in the input, there exists dependence between them), Sobol indexes can lead to spurious analysis29. This phenomenon also occurs in SHAP and LIME indexes. Kucherenko, S et al.30,76 refined this method by incorporating dependence into the calculation. The key to Kucherenko indexes is that before calculating Sobol indexes, the marginal distributions of individual features are determined by Copula sampling (typically Gaussian Copula), which effectively reduces the analysis error caused by feature dependence. Sobol indices in this work were calculated following the method provided by Kucherenko, S et al.

The main-effect index Si quantifies the proportion of output variance attributable to the variance of an individual input variable, while the total-effect index \({S}_{i}^{{\rm{T}}}\) accounts for the contribution of that input including its interactions with all other variables77,78. For example, in the bivariate function \(f({x}_{1},{x}_{2})={x}_{1}+\log ({x}_{2})+\sin ({x}_{1}-\cos ({x}_{2}))\), the terms x1 and \(\log ({x}_{2})\) are captured by Si, whereas the interaction term \(\sin ({x}_{1}-\cos ({x}_{2}))\) is reflected in \({S}_{i}^{{\rm{T}}}\). A case where \({S}_{i} < {S}_{i}^{{\rm{T}}}\) indicates that the feature exhibits significant interaction effects29,30.

Statistical Analyzes

Continuous variables were expressed as mean ± standard deviation (SD) for normally distributed data or median (interquartile range, IQR) for non-parametric distributions. Intergroup comparisons utilized Mann–Whitney U tests for non-normally distributed continuous variables and χ2 tests for categorical variables. Model discrimination was evaluated through receiver operating characteristic (ROC) curve analysis, reporting AUC with 95% confidence intervals.Statistical significance was set at p < 0.05. All analyzes were performed using SPSS Statistics (version 25.0; IBM Corp.).