Unraveling the role of gravity in shaping intruder dynamics within vibrated granular media

Abstract

Our experiments aboard the Chinese Space Station reveal a gravity-driven transition in intruder dynamics within vibrated granular media. While vibrations typically enable an intruder to ascend in a granular bed, low-gravity conditions induce it to descend under similar vibrations. Using a Hall-sensor array tracking method, we monitor the intruder’s movement throughout each vibration cycle and identified two competing mechanisms: inertia and gravity-dependent penetration. As gravity decreases, we observe a significant reduction in the scaled damping coefficient and hydrostatic pressure coefficient indicating that bed particles disperse more readily upon intruder impact, facilitating deeper penetration. Our findings highlight a critical transition from downward to upward motion of the intruder as vibration acceleration exceeds a threshold, which increases as gravity decreases. These insights into intruder dynamics in low-gravity environments have significant implications for asteroid exploration and lunar base construction, enhancing our understanding of the Brazil nut effect and the formation of planetesimal.

Introduction

The surface morphology of celestial bodies is often shaped by impact craters formed by meteorite collisions, such as the impact craters observed on the lunar surface. These impacts can also lead to the rearrangement of surface materials on asteroids, as evidenced by the observed seismic shaking of asteroid surfaces that results in the aggregation of large rocks^1,2,3. Granular segregation, is found playing a possible role in shaping the surface features of small celestial bodies, such as the formation of craters and the distribution of large boulders on the surface of asteroid. Reasonable explanations include ballistic sorting⁴ and Brazil-nut effect (BNE)^5,6,7,8,9. The low gravity intruder dynamics is crucial in providing insights into the mechanism of BNE on microgravity celestial bodies and the formation and evolution of planetesimals. With the increasing frequency of human deep space exploration activities, the detection of lunar regolith composition by small satellite impacts, and the landing and traversal of rovers, it is essential to further investigate and gain a deeper understanding of the penetration dynamics of intruder particles in low-gravity granular media.

A common challenge in this engineering context is the movement of an intruder within the regolith^10,11. In experimental studies, intruders are often simplified into basic geometric shapes, with spherical intruders^12,13,14,15 receiving the most attention. The penetration depth of the intruder in a range of impact velocities has been examined previously by various experiments and analytical models^12,13,16 for earth gravity and also extended to low-gravity environment.

The motion of an intruder within a shaken granular bed is, however, more complicated¹⁷. The intruder may move either upward or downward when the bed is disturbed. These phenomena are known as the Brazil nut effects (BNE) for large intruder moving upward and reverse Brazil nut effects (RBNE)^{18,19,20,21,22} for downward movement. The intruder’s behavior results from the interplay of various mechanisms, including convection^{23,24,25,26,27,28,29,30}, void-filling^31,32,33,34, arching³⁵, inertia^36,37,38, buoyancy^{37,39,40,41,42}, condensation^19,22, and thermal diffusion³³. Mechanisms such as void-filling and arching primarily promote BNE, while thermal diffusion and condensation contribute to RBNE. Nevertheless, convection and buoyancy can lead to either effect depending on specific conditions. (i) Mechanisms promoting BNE: Void-filling involves smaller particles randomly percolating into spaces beneath larger ones, while arching is a deterministic process where smaller particles block voids beneath larger ones. (ii) Mechanisms promoting RBNE: Thermal diffusion causes larger particles to accumulate in regions of lower granular temperature, and condensation-driven segregation occurs when the granular temperature lies between the critical fluidization thresholds of large and small particles. (iii) Mechanisms for either BNE and RBNE: In convection-driven segregation, BNE typically occurs when rising central streams carry large particles upward. Direction of motion of the large intruder can be reversed by inverting the sense of convection. For fully-fluidized and nonconvective granular systems, buoyancy effects can lead to BNE or RBNE according to the Archimedean law.

Vibration conditions, as well as the properties of granular materials, significantly influence the segregation. For instance, convection can occur in low-frequency, high-amplitude vibrations and low-density intruder; inertia-driven segregation is valid under weak excitation for heavy intruder. This complex interplay of mechanisms and parameters governs the fascinating dynamics of granular segregation, highlighting the rich physics involved in these seemingly simple systems. A good overview on segregation in vibrated granular systems can also be found in book by Anthony Rosato and Kit Windows-Yule¹⁷.

Previous experimental studies on the BNE primarily focused on observing the initial and final states of the intruder, lacking a detailed dynamical analysis of the intermediate processes. Experiments conducted during parabolic flights also faced limitations that parabolic flights cannot provide prolonged and stable gravity, and thus only few gravity levels were tested⁴³. Centrifuge aboard the Space Station can overcome this shortage and provide platform for systematic investigations in various reduced gravities. Furthermore, advancements in magnetic particle tracking technology to trace the intruder trajectory within a three-dimensional granular bed allow us to observe not only the initial and final states of the intruder but also the dynamic processes occurring during the interaction.

In this study, we experimentally investigate the influence of gravity on intruder dynamics in granular bed in low-gravity environments provided by the centrifuge aboard the Chinese Space Station (CSS). Our findings reveal that, unlike under Earth’s gravity, the downward movement of the intruder dominates in low-gravity environments with low vibration accelerations. We observe a transition from downward motion of the intruder to upward when the vibration acceleration exceeds a threshold, with this critical value increasing as gravity decreases. Analyzing the movement of the intruder within a single vibration cycle indicates that the transition from downward to upward results from the competition between downward impact and upward inertia mechanisms. In low-gravity conditions, when the vibration acceleration is below a certain threshold, downward impact dominates the motion of the intruder, causing it to penetrate deeper in each vibration cycle compared to the scenario under earth’s gravity. This hints that objects moving within the regolith layer on asteroid surfaces may go deeper than previously expected. This finding provides valuable insights into gravity effects of intruder dynamics in low-gravity conditions, with significant implications for future asteroid exploration missions and lunar base construction.

Results and discussions

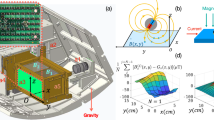
The experiment is conducted in a centrifuge aboard the CSS. The experimental setup is depicted in Fig. 1. The artificial gravity generated by the centrifuge is directed opposite to the z-axis. Six low-gravity scenarios were tested: g_env = 0.05 g, 0.07 g, 0.1 g, 0.125 g, 0.15 g and 0.167 g, where g is the Earth’s gravitational acceleration. The experimental chamber, driven by a linear motor along the z direction, is divided into two containers, as shown in Fig. 1. Each cubic container B₁(B₂) has a side length of 70 mm. The container’s four corners are rounded off with a 20 mm radius. This experiment is conducted in container B₁. The front and top of the containers are transparent for video observation of granular flow. The container is filled with glass beads to a height of 50 mm. The diameters of glass beads ranged from 0.6 to 0.8 mm (0.7 mm on average), with a density ρ_B = 2.5 g ⋅ cm⁻³. The intruder, a hollow copper sphere embedded with a permanent magnet, is tracked using Hall sensor arrays. Two Hall-sensor arrays are located in the xOy and yOz planes. Details of the tracking method can be found in a previous article⁴⁴. Two reference positions are set for the intruder, one is Z = 0.4 cm at the container’s bottom and the other Z = 5 cm at the granular surface.

Fig. 1: The experimental instrument on board the Chinese Space Station.

a1, a2 Are video cameras, (b) the Hall sensor array, and (c) the linear motor. d The container B₁ and (e) the container B₂.

To investigate the gravity effects on the intruder motion, we scale the vibration parameters by the environmental gravitational accelerations provided by the centrifuge, g_env, and the bed particle diameter d: the scaled angular vibration frequency ${\omega }^{{\prime} }=2\pi f/\sqrt{{g}_{{{\rm{env}}}}/d}$, where ω = 2 πf; the scaled vibration amplitude is defined as ${A}^{{\prime} }=A/d$. Thus, the dimensionless vibration acceleration Γ is scaled as Γ = Aω²/g_env, equal to ${A}^{{\prime} }{\omega }^{{\prime} 2}$. We scaled the velocity of the intruder v by $\sqrt{{g}_{{{\rm{env}}}}/d}$, i.e., ${v}^{{\prime} }=v/\sqrt{{g}_{{{\rm{env}}}}/d}$. Because of the linear motor’s maximum output power constraint, the maximum Γ decreases as g_env increases. For g_env = 1 g, Γ is limited to less than 1.54. With this motor power constraint, we conducted the CSS experimental investigation in gravity ranges from 0.05 g to 0.167 g. These low-gravity measurements are compared with 1 g results obtained in the laboratory.

Transition of intruder motion from downward to upward in reduced gravities

For each gravity condition, we first scan over a range of vibration parameters to assess the granular bed’s fluidization and the intruder’s motion. Using two video cameras, we observe bed particle movement from both top and side views. Fluidization of the granular bed requires Γ > 1. At low Γ, instead of upward motion, the large intruder is observed moving downwards (Fig. 2a), with heaping observed in the granular bed. The convection direction of the bed particles on the front window is moving upward, in the opposite direction of the intruder, as shown in Fig. 2c. A detailed description about the convection can be found in Methods section. The front window faces the thicker particle accumulation, with the flow field depicted in Fig. 2d. For Γ > 4.5, the intruder is seen moving upward (Fig. 2b). As Γ increases further, heaping disappears, and convection shifts to rising from the center and descending along the walls (Fig. 2e). Notably, the intruder moves counter to the granular bed’s convection in both cases (Fig. 2c, e), allowing us to discount convection’s influence on the intruder’s motion.

Fig. 2: The motion of the intruder and the convection of the bed particles during the preparation procedures.

a The procedure S₁ (an example: g_env = 0.125g, f = 5 Hz, Γ = 1.8) to place the intruder to the bottom, and (b) the procedure S₂ (an example: g_env = 0.125 g, f = 8 Hz, Γ = 4.53) to place the intruder to the top. The frame line in red, located at Z = 5 cm, represents the particle filling height, and the yellow sphere indicates the intruder. The blue dots are bed particles. c The diagram of the granular convection and intruder for S₁. d The flow field observed from the front window during procedure S₁. e The diagram of the granular convection and intruder for S₂.

After completing the scan of all parameter modes (f, Γ, g_env), we select two sets of excitation parameters as preparation procedures: one driving the intruder to the bottom (referred to as the procedure S₁) and the other to the top (as procedure S₂). For example, at g_env = 0.125 g, f = 5 Hz, and Γ = 1.8 are chosen for S₁, (Fig. 2a), and f = 8 Hz and Γ = 4.5 for S₂, (Fig. 2b). Each preparation procedure lasts 120 s.

For each of the six low-gravity conditions, we measure intruder trajectories using vibration frequencies from 3–10 Hz and amplitudes ranging from 0.5 to 6 mm. As vibration occurs along the z-axis, we primarily focus on the intruder’s displacement in the z-direction, with the initial position Z(t = 0) set either at the bottom (prepared by S₁) or the top (prepared by S₂) of the container. We repeat each parameter mode (f, Γ, g_env) twice, following procedures S₁ and S₂ respectively. We compare these low-gravity results with those obtained at g_env = 1 g, in laboratory conditions, with frequencies of 15, 20, and 25 Hz. To facilitate comparison across different gravity conditions, we employ the scaled frequency ${\omega }^{{\prime} }$. For instance, ${\omega }^{{\prime} }=1.0$ corresponds to a vibration frequency of 6 Hz at g_env = 0.1 g and 20 Hz at g_env = 1 g.

The magnetic particle tracking method offers a spatial resolution of up to 0.2 mm⁴⁴ at a sampling rate of 30 Hz, enabling observation of the intruder’s motion within a single vibration cycle. Figure 3 illustrates the Z-component of the intruder’s trajectory under gravity. The red curve depicts an upward trajectory Z(t) for f =  5 Hz and Γ = 4.70, while the blue curve shows a downward trajectory Z(t) for f = 3 Hz and Γ = 1.97. For f = 5 Hz and Γ = 4.70, the intruder rises stepwise at a frequency of 5 Hz. Conversely, for f = 3 Hz and Γ = 1.97, the intruder descends stepwise at a frequency of 3 Hz. The ascent (descent) curve of the intruder exhibits a ratchet-like behavior, where the duration of each upward (downward) step equals the vibration period 1/f (see the inset of Fig. 3). This high-precision tracking method is instrumental in studying dynamic processes on a microscopic timescale. From the curve, we can determine the intruder’s initial and final positions as well as the time taken to reach its final equilibrium position.

Fig. 3: Two examples of intruder’s heights shown as functions of time.

The red ascending curve is obtained at f = 5 Hz, Γ = 4.70, g_env = 0.07 g, while the blue descending curve is obtained at f = 3Hz, Γ = 1.97, g_env = 0.07 g. The zoom-in shows the clear ratchet-like motion, where the duration of each step equals to 1/f.

The equilibrium position of the intruder, $\langle Z\rangle =\int_{{T}_{1}}^{{T}_{2}}Z(t)dt/({T}_{2}-{T}_{1})$, is plotted in Fig. 4a–f as a function of Γ for each gravity condition, with typical averaging time from T₁ = 60 s to T₂ = 110 s. Error bars represent the standard deviations of the equilibrium positions, 〈(Z(t)−〈Z〉)²〉. Data points are color-coded and shaped differently for various frequencies. We use the scaled frequency ${\omega }^{{\prime} }$ instead of f to facilitate comparison of equivalent frequencies across different gravity conditions.

Fig. 4: The equilibrium position 〈Z〉 as functions of Γ under different gravities g_env.

a–f Data measured in gravities 0.05, 0.07, 0.1, 0.125, 0.15, 0.167 g respectively. Red circles are for f = 3 Hz, green squares for f = 4 Hz, blue diamonds for f = 5 Hz, yellow up triangles for f = 6 Hz, purple down triangles for f = 8 Hz and gray left triangles for f = 10 Hz. The error bars are the standard deviations obtained at the equilibrium positions 〈(Z(t)−〈Z〉)²〉. g Data measured in the laboratory at g_env = 1 g: Red circles for f = 15 Hz, green squares for f = 20 Hz, and blue diamonds for f = 25 Hz. h The critical vibration acceleration Γ_c plotted as a function of g_env.

It is found that the equilibrium position 〈Z〉 is independent of its initial positions as well as its preparation procedures S₁ or S₂. As shown in Fig. 4, it depends significantly on Γ. When Γ is less than a critical value Γ_c, the equilibrium position is at the bottom of the container (Z ≈ 0.4 cm), indicating that the large intruder moves to the bottom, which is considered as RBNE. For Γ > Γ_c, the equilibrium position of the intruder rises to a position near the surface of the granular bed, known as the BNE. Γ_c is observed strongly dependent on gravity. As shown in Fig. 4h, Γ_c decreases from 4.4 to 2.2 as g_env increases from 0.05 g to 0.167 g. For g_env≥ 0.167, the value of Γ_c further decreases. At g_env = 1g, no RBNE can be experimentally observed (see Fig. 4g).

Mechanisms

The RBNE observed previously was typically under conditions of strong vibration (Γ ≥ 4)^9,33, with suggestion of thermal diffusion mechanism. In our experiments, RBNE is observed at low Γ (Γ < Γ_c) under each reduced gravity(see Fig. 4a–f), where Γ_c is gravity-dependent. The condition of the RBNE discovered in our experiments is fundamentally different from previous observations, suggesting that there exists a gravity-dependent mechanism underlying this phenomenon.

From Fig. 3, it is evident that the intruder’s ascent (descent) path consists of multiple vibration cycles with a linear rising (sinking) trend. With this uniform rising (sinking) velocity, the total ascent (descent) distance of the intruder is equal to the rising (sinking) amount per vibration cycle times the number of cycles. Figure 5 provides an enlarged view of a typical descending vibration cycle, illustrating the intruder’s trajectory throughout one cycle. The blue curve represents the entire motion of the intruder relative to the container, from takeoff to the completion of penetration. This process can be divided into three distinct stages:

• 1. Flight stage: The intruder begins to ascend when the upward vibration acceleration is sufficient to counteract gravitational acceleration. During this stage, the intruder’s motion follows a parabolic trajectory. Under the influence of gravitational acceleration, the intruder descends from its peak height to the surface of the granular bed.

• 2. Impact stage: During this stage, the intruder begins to penetrate the bed particles with an initial impact velocity. The intruder experiences a hydrodynamic pressure and a viscous resistance during its penetration in the granular bed.

• 3. Stationary stage: The intruder’s velocity gradually decreases to zero due to the resistance from colliding with the bed particles. The intruder remains stationary within the granular bed until the onset of the next cycle.

Fig. 5: The three distinct stages of the descending intruder.

a The experimentally measured trajectory at f = 3 Hz, Γ = 1.97, and g_env = 0.07 g. b The schematic diagram of the intruder’s motion in one step period. The orange dashed curve is the vibration of the container ${z}_{T}=A\sin (\omega t)$. The green dot curve is the intruder’s motion, and the blue solid curve is the motion relative to the container frame of reference, which is comprised of three time segments: the flight stage (from t_to to t_imp), the impact stage, and the stationary stage. The red dot represents the time of impaction, t = t_imp.

With this picture in mind, we now further elucidate the underlying mechanisms of the RBNE phenomenon under low-gravity conditions. As illustrated in Fig. 5, the vibration of the container is described by $A\sin (\omega t)$. At t = t_to when the vibration acceleration value reaches the gravity g_env in the opposite direction, the intruder takes off from the container. The acceleration at take-off is expressed as follows:

$$\frac{{d}^{2}Z}{d{t}^{2}}=-A{\omega }^{2}\sin (\omega {t}_{{{\rm{to}}}})=-{g}_{{{\rm{env}}}},$$

(1)

and the take-off velocity of the intruder is

$${v}_{{{\rm{to}}}}=A\omega \sqrt{1-{\sin }^{2}(\omega t)}=\frac{{g}_{{{\rm{env}}}}}{\omega }\sqrt{{\Gamma }^{2}-1}.$$

(2)

Z is the intruder’s height relative to the container. Within the time period t_to < t < t_imp, Z can be expressed as:

$$Z={Z}_{0}+{v}_{{{\rm{to}}}}(t-{t}_{{{\rm{to}}}})-\frac{1}{2}{g}_{{{\rm{env}}}}{(t-{t}_{{{\rm{to}}}})}^{2}-\frac{{g}_{{{\rm{env}}}}}{{\omega }^{2}}(\Gamma \sin (\omega t)-1),$$

(3)

where Z₀ is the relative height of the intruder at t = t_to. At t = t_imp, the bed particles make contact with the container again. The impact time t_imp can be determined by setting Z(t) = Z₀, and the velocity of impact is calculated by ${v}_{{{\rm{imp}}}}=\frac{dZ(t)}{dt}{| }_{t = {t}_{{{\rm{imp}}}}}$. Considering a fully fluidized granular bed, the dynamical equation of the intruder during penetration is expressed as follows¹⁶:

$$\frac{{d}^{2}Z}{d{t}^{2}}=-\gamma \frac{dZ}{dt}-\kappa (Z-{Z}_{0})+{g}_{{{\rm{env}}}}(\Gamma \sin (\omega t)-1)$$

(4)

where the initial velocity of impact is v_imp. The first term represents the damping force, where $\gamma ={\gamma }^{{\prime} }/\sqrt{d/{g}_{{{\rm{env}}}}}$. The second term accounts for the hydrostatic pressure, where the factor κ is proportional to the instantaneous environmental acceleration:

$$\kappa ={\kappa }^{{\prime} }/d\cdot {g}_{{{\rm{env}}}}(1-\Gamma \sin (\omega t))$$

(5)

Once the intruder’s position reaches its penetration depth Z_p, it remains stationary until the next takeoff time, t_to +  2 π/ω.

With current sampling frequency, we are able to observe the cyclic downward motion of the intruder. For quantitative velocity measurements, we capture penetration depth across multiple cycles, which facilitates accurate calculation of the average descent velocity. By numerically solving Eq. (4), the dimensionless downward velocity can be calculated as ${v}_{1}^{{\prime} }(\Gamma )=\omega ({Z}_{p}-{Z}_{0})/(2\pi \sqrt{{g}_{{{\rm{env}}}}d})$. This expression depends on the parameters ${\gamma }^{{\prime} }$ and ${\kappa }^{{\prime} }$. For ${\gamma }^{{\prime} }$ and ${\kappa }^{{\prime} }$ ranging over wide intervals ($0 \, < \, {\gamma }^{{\prime} } < \, 20$ and $0 \, < \, {\kappa }^{{\prime} } < \, 25$), ${v}_{1}^{{\prime} }(\Gamma )$ exhibits an approximately linear relationship with Γ − 1, contributing to the downward penetration during each oscillation cycle. ${v}_{1}^{{\prime} }(\Gamma )$ can be expressed as follows:

$${v}_{1}^{{\prime} }(\Gamma )=a(\Gamma -1)$$

(6)

In the experiment, the Z(t) curve is measured for each experimental mode with different (f, Γ, g_env). From the curve, we can obtain the intruder’s initial and final positions, as well as the time duration required for the intruder to reach its final equilibrium position, and therefore the velocity can be measured. The experimentally measured ${v}_{1}^{{\prime} }(\Gamma )$ is plotted in Fig. 6 for different ${\omega }^{{\prime} }$ and gravity conditions. Three distinct regimes are observed:

• 1. No Movement Regime: For $\Gamma \, < \, 1,{v}^{{\prime} }=0$, indicating that there is no movement.

• 2. Descending Regime: For $1\, \lesssim \, \Gamma \, < \, {\Gamma }_{{{\rm{c}}}},{v}^{{\prime} } < \, 0$, signifying the intruder’s descent.

• 3. Ascending Regime: For $\Gamma \, > \, {\Gamma }_{{{\rm{c}}}},{v}^{{\prime} }$ becomes positive, indicating the intruder’s ascent.

Fig. 6: The decline velocity of the intruder in reduced gravities.

The intruder velocities in gravities (a) g_env = 0.05 g, (b) g_env = 0.07 g, (c) g_env = 0.1g, (d) g_env = 0.125 g, (e) g_env = 0.15 g and (f) g_env = 0.167 g. The dashed vertical line is at Γ = 1.0 and the solid vertical line is at Γ = Γ_c. For the meaning of the symbols, see the legend in each panel. The error bars represent the uncertainty from multiple experimental measurements. The gray hexagons are the fitted result of ${v}_{1}^{{\prime} }(\Gamma )$, where f = 4Hz. The blue curves are the fitted result of ${v}^{{\prime} }(\Gamma )={v}_{1}^{{\prime} }(\Gamma )+{v}_{2}^{{\prime} }(\Gamma )= a(\Gamma -1)+b({\Gamma }^{2}-1)$.

In the ascending regime, there must exist a competing mechanism allowing the intruder to move upwards. The intruder, due to its large kinetic energy, would follow a ballistic uprise after taking off, while the bed particles being dragged downwards by wall frictions. This induces an upward distance ΔZ during each cycle.

According to the experimental data shown in Fig. 6, as Γ increases, the relationship between ${v}^{{\prime} }$ and Γ looks like a quadratic function. This is in agreement with reference^36,38, where the ascending distance in each cycle are quadratic functions of the vibration amplitude at a fixed frequency. Furthermore, our experimental condition is similar to those references, for example, the density of the intruder is larger than that of the bed particles. Considering the inertia being the dominant mechanism as Γ > Γ_c, the kinetic energy dissipated by the friction on the intruder in each vibration cycle can be written as:

$$\frac{1}{2}m{v}_{\,{\mbox{to}}\,}^{2}=\beta {{\Delta }}Z$$

(7)

where m is the mass of the intruder, ΔZ is the upward penetration distance in each vibration cycle, and β is the friction force.

Taking Eq. (2) to Eq. (7), ΔZ can be written as:

$${{\Delta }}Z=\frac{m{g}_{\,{\mbox{env}}\,}^{2}}{2{\omega }^{2}\beta }({\Gamma }^{2}-1)$$

(8)

The upward velocity component of the intruder can then be expressed as:

$${v}_{2}^{{\prime} }(\Gamma )=\frac{\omega {{\Delta }}Z}{2\pi \sqrt{{g}_{{{\rm{env}}}}d}}=b({\Gamma }^{2}-1)$$

(9)

where $b=m{g}_{{{\rm{env}}}}/(4\pi {\omega }^{{\prime} }\beta )$. Summing Eqs. (6) and (9), we obtain the net velocity:

$${v}^{{\prime} }(\Gamma )={v}_{1}^{{\prime} }(\Gamma )+{v}_{2}^{{\prime} }(\Gamma )=a(\Gamma -1)+b({\Gamma }^{2}-1)$$

(10)

A critical value exists at Γ = Γ_c, where ${v}^{{\prime} }$ reaches zero, marking the transition point. We fit the data using Eq. (10), as illustrated in Fig. 6. The fitting parameters are a and b, where γ and κ are included in parameter a and vibration frequency is included in parameter b. The fitting parameters a and b are plotted in Fig. 7a, b as a function of g_env. The slope ∣a∣ decreases with increasing g_env, indicating that ${\gamma }^{{\prime} }$ and ${\kappa }^{{\prime} }$ increase with g_env. Parameter $b=m{g}_{{{\rm{env}}}}/(4\pi {\omega }^{{\prime} }\beta )$ remains nearly constant with respect to g_env, demonstrating that frictional force is proportional to gravity. This indicates the velocity of upward motion can be scaled by $\sqrt{{g}_{{{\rm{env}}}}}$. It is in agreement with previous works^7,43, all of which investigate the upward motion only.

Fig. 7: The fitting parameters as functions of g_env.

a The fitting parameter a in Eq. (10) vs. gravity. b The fitting parameter b in Eq. (10) vs. gravity. c The dimensionless damping coefficient ${\gamma }^{{\prime} }$ and hydrostatic pressure coefficient ${\kappa }^{{\prime} }$ as functions of gravity are obtained by numerically solving Eq. (4) for Z_p.

Parameter a, which includes γ and κ, is g_env dependent (see Fig. 7a), indicating that ${v}_{1}^{{\prime} }(\Gamma )$ can not be scaled by $\sqrt{{g}_{{{\rm{env}}}}}$. To clarify the dependence of damping coefficient γ and hydrostatic pressure coefficient κ on gravity, we fit the experimental results with the numerically solved function ${v}_{1}^{{\prime} }(\Gamma )$. Using γ and κ as fitting parameters, we plot ${v}_{1}^{{\prime} }(\Gamma )$ as a function of Γ in Fig. 5 to fit the experimentally measured velocities within weak vibrations. We select a fixed frequency f = 4 Hz for all fitting processes. As depicted in Fig. 7c, ${\kappa }^{{\prime} }$ and ${\gamma }^{{\prime} }$ increases with g_env.

Note that after scaled by $\sqrt{{g}_{{{\rm{env}}}}}$, the dimensionless damping coefficient ${\gamma }^{{\prime} }$ and hydrostatic pressure coefficient ${\kappa }^{{\prime} }$ still decrease significantly with decreasing gravity. It indicates that the intruder penetrates deeper when it impacts downward on the granular bed in low gravity. This is why the RBNE occurs. The reduction in gravity allows the deformation of the particles to decrease, and therefore the loss of energy becomes less during collisions, which means the bed particles can be moved away easier during the penetration of the intruder. From a macroscopic point of view, the particle bed becomes loose at low gravity⁴⁵, which allows the intruder to sink deeper, and enables the RBNE to occur in reduced gravity.

Conclusions

In conclusion, our study reveals a gravity-driven transition in intruder dynamics within vibrated granular media, highlighting the complex interplay between inertia and gravity in low-gravity environments. Our findings demonstrate that, contrary to expectations based on Earth’s gravity, intruder tend to descend in low-gravity conditions under specific vibration parameters. This downward motion transitions to upward movement when vibration acceleration exceeds a critical threshold Γ_c, which increases as gravity decreases.

The magnetic particle tracking method enables us to observe the intruder downward (upward) motion during each vibration cycle, which is divided into three stages: the flight stage, the impact stage and the stationary stage. We show that the net velocity of the intruder results from the competition between two mechanisms. The upward penetration component ωΔZ is contributed by the inertial mechanism, and the downward penetration component ω(Z_p − Z₀) is contributed by the impact mechanism. To quantitatively study the impact mechanism, we establish a dynamical equation for intruder during the impact stage, which is solved numerically to provide the penetration depth per cycle. By fitting this numerical function with the measured velocities, we demonstrate that both the dimensionless hydrostatic pressure coefficient ${\kappa }^{{\prime} }$ and the damping coefficient ${\gamma }^{{\prime} }$ decrease with decreasing gravity. The reduction in gravity allows the deformation of the particles to decrease, therefore they can be pushed away easier during the impaction. This allows the intruder to penetrate deeper, and suggests that the bulk density of the granular bed decreases with decreasing gravity.

Previous studies^7,9 used discrete element method (DEM) simulations to investigate granular segregation in low-gravity environments. They⁹ considered deformation of contacted particles to be constant across different gravity conditions to achieve consistent granular segregation behavior under low gravity. Their simulation approach is apparently insufficient to capture the feature of our findings. We plan to explore the simulation models in detail in upcoming research.

Our findings pave the way for further investigations into the mechanisms governing intruder dynamics in varying gravitational environments. Future research could explore the implications of these dynamics on the Brazil nut effect and the formation of planetesimal, ultimately enriching our understanding of planetary science and engineering in extraterrestrial settings.

Methods

Details of the experimental setup

The centrifuge, with a diameter of 900 mm, provides artificial gravity ranging from 0.01 g to 2 g (where g is the Earth gravitational acceleration). The centrifuge rotates clockwise, making the angular velocity $\vec{{{\Omega }}}$ opposite to the y axis (see Fig. 1). The rotation radius is 357 mm, which is the distance from the rotation center to the granular bed’s center of mass. Two video cameras with a resolution of 1920 × 1080 and a frame rate of 30 frames per second captured the bed particles’ motion from the top and side. During the experiment, the linear motor provided sinusoidal vibrations with frequencies ranging from 1–12 Hz and amplitudes up to 6 mm.

The bed particles were mixed with 1% black glass particles as tracers. An intruder particle with a diameter of 10 mm and a density of 8.05 g ⋅ cm⁻³ was pre-placed in the container. The intruder is embedded with a 5.7 mm-long and 1 mm-wide permanent magnet. The magnetic field generated by this magnet dipole is detected by two Hall sensor arrays located on the xOy and yOz planes. Each array consists of 105 sensors arranged in 7 columns with 15 sensors per column, spaced 1 cm apart. The intruder’s location (X, Y, Z) can be determined from its magnetic intensity measured by each sensor. The sensor resolution of the magnetic field is 0.1 5 μT in the horizontal directions and 0.25 μT in the vertical direction. The trajectory of the intruder can be reconstructed from the detected data, which is sampled at a rate of 30 Hz.

Artificial gravity levels can vary from natural gravity experienced on Earth or other planets. When evaluating the effects of artificial gravity, it is important to consider factors such as the Coriolis force and the gradient of centrifuge gravity. The Coriolis acceleration can be expressed as:

$$| {a}_{{{\rm{C}}}}| =2| {\vec{v}}\times \vec{{{\Omega }}}| =2| {v}^{{\prime} }\sqrt{{g}_{{{\rm{env}}}}d}\sqrt{\frac{{g}_{{{\rm{env}}}}}{r}}| =2{g}_{{{\rm{env}}}}{v}^{{\prime} }\sqrt{\frac{d}{r}}.$$

(11)

Here, ${v}^{{\prime} }$ represents the velocity of the particles. The influence of the Coriolis force on the particles’ motion can be estimated using the dimensionless parameter η = a_C/g_env. For the intruder moving downward, we select a typical value of ${v}^{{\prime} }\simeq 0.1$ (as indicated in Fig. 6a), yielding η = 0.8%, and the direction of the Coriolis force is on the positive direction of the x-axis, which does not affect the motion of the intruder in the z direction. Therefore, the effect of the Coriolis force is deemed negligible.

To quantify the influence of the gradient of the centrifuge gravity, we can compare the gravitational acceleration experienced by the intruder at different positions within the centrifuge. In Fig. 3, the local gravity at the center of mass, Z = 2.5 cm, is g_env = 0.07 g. When the height of the intruder increases from 0.4 cm–3.5 cm, the variation in gravitational force is within the range from g₋ = 0.97g_env to g₊ = 1.05 g_env. To examine the effect of gravitational gradients on experimental results, we analyze the height-time profile of the intruder when Γ < Γ_c. Under ideal gravity, the intruder’s downward penetration depth (Z_p − Z₀) within each cycle should be independent of its height Z₀, resulting in a constant descent velocity. Figure 8 shows height-time profiles for different vibration modes under a gravity setting of g_env = 0.1 g, including f = 4 Hz, Γ from 1.2 to 1.8 and f = 5 Hz, Γ from 1.36 to 2.34. These profiles indicate uniform descending rates, suggesting that the gradient of gravity on the experiment can be considered negligible.

Fig. 8: The positions Z of the intruder as functions of time in different vibration modes for g_env = 0.1 g.

a–c For f = 4 Hz, (d–f) for f = 5 Hz. Red circles are experimentally measured results, and blue lines are fitted results by using a linear function. r² is the determination coefficient.

Preparation procedures for the six gravities

For each gravity used in our experiments, preparation procedures requires different vibration parameters. Table 1 lists the vibration parameters for S₁ and S₂ across all gravity conditions.

Table 1 Vibration parameters for S₁ and S₂ in each gravity

The method for tracking the magnetic intruder

To illustrate the data processing steps, we use the Hall sensor array B₂ located on the xOy plane as an example. The raw data requires pre-processing at first. Each sensor located at position (x, y) collects raw magnetic field data consisting of four components:

$${B}_{i}^{(j)}(x,y)={C}_{i}^{(j)}+{G}_{i}(x,y)+{f}_{i}^{(j)}(x,y)+{\eta }_{i}^{(j)}.$$

(12)

The index i represents the components (x, y, z) of the magnetic field, and j represents the frame number. To ensure the reliability of the experimental results, we choose the z-component of the magnetic field to determine the position of the intruder. The first term on the right-hand side of Eq. (12) represents the geomagnetic field. Since all sensors shares the common z-axis, the z-component of the geomagnetic field can be expressed as a constant ${C}_{z}^{(j)}$. The second term represents the background magnetic field inside the experimental chamber, originating from different components near the sensor array, such as the linear motor. The third term ${f}_{z}^{(j)}(x,y)$ represents the dipole magnetic field excited by the magnetic intruder particle, depending on the position (X, Y, Z) and Euler angles (θ, ϕ). ${\eta }_{z}^{(j)}$ represents the noise generated by the analog-to-digital converter.

The background magnetic field G_z(x, y) can be collected in laboratory. After subtracting G_z(x, y) and reducing noise, the magnetic field data can be fitted with the dipole form, i.e., ${f}_{z}^{(j)}(x,y)+{C}_{z}^{(j)}$. After some algebra, this expression can be written as:

$${f}_{z}^{(j)}(x,y)+{C}_{z}^{(j)} = \, k(L\cos \theta \cos \phi -Z)/\left[{(L\cos \theta \cos \phi -Z)}^{2}\right. \\ + {\left.{(x-X-L\sin \phi )}^{2}+{(y-Y-L\sin \theta \cos \phi )}^{2}\right]}^{3/2} \\ + k(L\cos \theta \cos \phi +Z)/\left[ {(L\cos \theta \cos \phi +Z)}^{2}\right.\\ + \, {\left.{(L\sin \phi -X+x)}^{2}+{(L \sin \theta \cos \phi -Y+y)}^{2}\right]}^{3/2} + {C}_{z}^{(j)}$$

(13)

The Euler angles θ and ϕ are defined as follows:

$$\begin{array}{ll}&\left(\begin{array}{r}{x}_{\pm }-X\\ {y}_{\pm }-Y\\ {z}_{\pm }-Z\end{array}\right)=\\ &\left(\begin{array}{rcl}1&0&0\\ 0&\cos \theta &-\!\sin \theta \\ 0&\sin \theta &\cos \theta \end{array}\right)\left(\begin{array}{rcl}\cos \phi &0&-\!\sin \phi \\ 0&1&0\\ \sin \phi &0&\cos \phi \end{array}\right)\left(\begin{array}{r}0\\ 0\\ \pm \!L\end{array}\right)\end{array}$$

(14)

where (x_±, y_±, z_±) are coordinates of the magnet poles. The measured half-length of the permanent magnet is L = 2.85 mm, and the magnetic dipole strength k is 2.77 × 10⁴ μT ⋅ cm². We use MATLAB to fit the calibrated data ${B}_{z}^{(j)}(x,y)-{G}_{z}(x,y)$ with Eq. (12), with initial values of X = Y = Z = 0 and θ = 0, ϕ = 0. In reference⁴⁴, the reliability and robustness of the method is validated.

The convection of the granular bed

The convection of the granular bed is investigated. Here, as an example, we provide the investigation results for preparation procedures S₁ and S₂. The convection direction of the granular bed can be viewed from the video recorded by front (a1) and top (a2) cameras. An example is given in Fig. 9 for g_env = 0.125 g. Figure. 9a, b show snapshots of the top view, and Fig. 9c, d are front-view snapshots. For preparation procedure S₁, the tracer particles arise from the font window (see Fig. 9c), and flow to opposite x-direction on the granular surface (see Fig. 9a). In the preparation procedure S₂, the top view reveals that tracer particles move upward from the center toward the edges, as shown in Fig. 9b. The front-view recordings show these tracers descending along the sidewalls, as depicted in Fig. 9b. The particle convection diagrams illustrated in Fig. 2c, e are then drawn based on these original videos.

Fig. 9: Video snapshots of the container B₁.

a, b The top-view captured by camera (a2). c, d The front-view captured by camera (a1). Yellow arrows indicate the direction of particle flow on the surface (a, b) and the sidewalls (c,d) of the granular bed. In this case, g_env = 0.125 g. Preparation procedure S₁ is for (a, c), and preparation procedure S₂ is for (b, d).

In Eq. (4), the granular bed is considered fully fluidized. This can be evidenced by analyzing the velocity of tracer particles captured by cameras (a1) and (a2) within the chamber. As an example, the velocity field is obtained in Fig. 10, by tracking all tracer particles under preparation procedure S₁ (f = 5 Hz, Γ = 1.8) which is the lowest vibration acceleration at g_env = 0.125g. The velocity field is 0.14 mm ⋅ s⁻¹ at the bottom and 0.34 mm ⋅ s⁻¹ at the top of the container, with all values being non-zero.

Fig. 10: The velocity distribution of tracer particles measured on the front window during preparation procedure S₁ at g_env = 0.125 g.

The color represents the avraged velocity of tracer particles.