Introduction

Magnetic resonance imaging (MRI) plays a central role in clinical diagnosis and neuroscience. This modality is highly versatile and can be selectively programmed to generate a large number of image contrasts1, each sensitive to certain biophysical parameters of the tissue. In recent years, there has been extensive research into developing quantitative MRI (qMRI) methods that can provide reproducible measurements of magnetic tissue properties (such as: T1, T2, and \({{{{\rm{T}}}}}_{2}^{* }\)), while being agnostic to the scan site and the exact acquisition protocol used2. Classical qMRI quantifies each biophysical property separately3, using repeated acquisition and gradual variation of a single acquisition parameter under steady state conditions. This is followed by fitting the model to an analytical solution of magnetization vector dynamics4.

The exceedingly long acquisition times associated with the classical quantification pipeline have motivated the development of magnetic resonance fingerprinting (MRF)5, an alternative paradigm for the joint extraction of multiple tissue parameter maps from a single pseudorandom pulse sequence. Since MRF data are acquired under non-steady state conditions6, the corresponding magnetization vector can only be resolved numerically. This comes at the expense of the complexity of the inverse problem, namely finding tissue parameters that best reconstruct the signal according to the forward model of spin dynamics. Since model fitting under these conditions takes an impractically long time7, MRF is commonly solved by dictionary matching, where a large number of simulated signal trajectories are compared to experimentally measured data8. Unfortunately, the size of the dictionary scales exponentially with the number of parameters (the “curse of dimensionality”9), which rapidly escalates the compute and memory demands of both generation and subsequent use of the dictionary for pattern matching-based inference.

Recently, various deep learning (DL)-based methods have been developed for replacing the lengthy dictionary matching with neural-network (NN)-based inference10,11,12,13. While this approach greatly reduces the parameter quantification time, networks still need to be trained using a comprehensive dictionary of synthetic signals. Since dictionary generation may take days12, it constitutes an obvious bottleneck for routine use of MRF, and reduces the possibilities for addressing a wide variety of clinical scenarios. Even with a faster generation, the transfer of synthetic data-trained NN to experimental data raises concerns about biased estimates.

The complexity and time constraints associated with the MRF pipeline are drastically exacerbated for molecular imaging applications that involve a plurality of proton pools, such as chemical exchange saturation transfer (CEST) MRI14. While CEST has demonstrated great potential for dozens of biomedical applications15,16,17,18,19,20,21, some on the verge of entering clinical practice22, the inherently large number of tissue properties greatly complicate analysis23. This has prompted considerable efforts to transition from CEST-weighted imaging to fully quantitative mapping of proton exchange parameters24,25,26,27,28. Early CEST quantification used the fitting of the classical numerical model (based on the underlying Bloch-McConnell equations) after irradiation at various saturation pulse powers (B1)27. However, applying this approach in a pixelwise manner in-vivo is unrealistic because both the acquisition and reconstruction steps may require several hours. Later, faster approaches, such as quantification of the exchange by varying saturation power/time and Omega-plots25,29,30,31 still rely on steady-state (or close to steady state) conditions, and approximate analytical expressions of the signal as a function of the tissue parameters32,33. Unfortunately, a closed-form analytical solution does not exist for most practical clinical CEST protocols, which utilize a train of off-resonant radiofrequency (RF) pulses saturating multiple interacting proton pools. Similarly to the quantification of water T1 and T2, incorporating the concepts of MRF into CEST studies provided new quantification capabilities28,34,35,36,37 and subsequent biological insights, for example, in the detection of apoptosis after oncolytic virotherapy12. However, in order to further push the boundaries of CEST MRF research and expedite its progress, the long dictionary generation associated with each new application needs to be replaced by a rapid and flexible approach that adequately models multiple proton pools under saturation pulse trains.

Here, we describe a physics-based DL framework for rapid model fitting of the human brain tissue proton spin properties. While this approach is applicable for quantifying a variety of MRI parameters, we focus on a challenging CEST imaging scenario, involving multiple proton pools, a saturation pulse train, and non-steady-state MRF acquisition. The computational pipeline (Fig. 1) combines a spin physics simulator and a NN-based quantitative parameter reconstructor in a fully auto-differentiable manner38. Our system effectively solves and inverts the Bloch-McConnell ordinary differential equations (ODEs), which govern the multi-pool exchange, saturation, and relaxation dynamics of molecular MRI. Hence, we refer to this approach as “neural Bloch McConnell fitting” (NBMF). Importantly, the network can be be trained in a self-supervised manner, directly on the single-subject data of interest (inspired by related work on test-time-39, internal-40, and zero-shot-40,41,42 learning). This circumvents the need for prior curation of a large training dataset, which is often inaccessible, especially for molecular MRI.

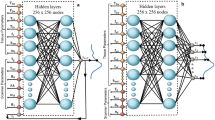
Fig. 1: Schematic representation of the core neural Bloch McConnell fitting (NBMF) pipeline.
figure 1

A quantitative parameter reconstructor parameterized as a multi-layer perceptron (MLP) and a differentiable Bloch-McConnell simulator are serially connected into a single computational graph. Single-subject Magnetic Resonance Fingerprinting (MRF) data serves both as the input and as the regression target for the reconstructor-simulator circuit. The network convergence (a) provides the fitted exchange parameter maps for the examined subject as well as a trained NN reconstructor; the latter can be used to extract parameter maps for new subjects within seconds (b). The simulator can be realized using the exact numerical Bloch McConnell ODE solver or using analytical approximations when available (e.g., for 2-pool semisolid Magnetization Transfer (MT) quantification33). While not shown in the diagram, auxiliary per-voxel data such as T1, T2, B0, and B1 maps can be added as input to the neural reconstructor and the simulator. Furthermore, the pipeline main block can be serially repeated so that estimated semisolid MT volume fraction (fss) and proton exchange rate (kssw) maps inferred at the first stage are joined to the raw data used in a second reconstructor aimed to quantify the amide proton exchange parameters (fs, ksw).

Full size image

Results and discussion

In-vitro CEST quantification

A phantom composed of six vials with different combinations of L-arginine concentration and pH was assembled and scanned in a 3T clinical scanner (Prisma, Siemens Healthineers, Germany) using a previously published non-steady-state rapid CEST protocol12,43. Good agreement was obtained between the NBMF-estimated and known L-arginine concentrations (Fig. 2a, c, e): Pearson’s r = 0.986, p = 3.0 × 10−4, root mean square error (RMSE) = 8.4 mM, mean absolute percentage error (MAPE) = 10.8%). The NBMF-reconstructed proton exchange rates were in good agreement with the corresponding values estimated by traditional MRF dictionary-matching (Fig. 2b, d, f): Pearson’s r = 0.999, p = 1.6 × 10−6, RMSE = 41.0 s−1, MAPE = 13.2%. The pH dependence of the NBMF reconstructed exchange rate (Fig. 2b) was a good fit for a base-catalyzed proton exchange model (R2 = 0.94, p = 1.4 × 10−3), as predicted by theory44. An additional in-depth comparison between traditional dictionary matching and NBMF is available in Supplementary Table 1, and Supplementary Figs. 1, 2.

Fig. 2: In-vitro study.
figure 2

L-arginine samples were imaged using a pulsed Chemical Exchange Saturation Transfer Magnetic Resonance Fingerprinting (CEST-MRF) protocol in a 3T clinical scanner. The neural Bloch McConnell fitting (NBMF)–based L-arginine concentrations (a) and proton exchange rates (b) were in good agreement with those obtained by dictionary-based pattern matching (c and d, respectively). The ground truth L-arginine concentrations and pH values are mentioned in the white text next to each vial. The pixelwise distributions are further compared in (e, f). Each point in the swarm plot reflects a single 1.8 mm × 1.8 mm × 5.4 mm voxel.

Full size image

Quantifying the semisolid-MT and CEST proton exchange parameters in the human brain

The NBMF pipeline used in-vitro was modified for semisolid-MT and amide proton exchange parameter mapping in the human brain. Two 3D and rapid acquisition pulse sequences were applied, as described previously12,43. The first sequence varied the saturation pulse frequency offset between 6 and 14 ppm (designed to encode semisolid-MT information), whereas the second sequence fixed it at 3.5 ppm (for amide proton parameter encoding). In both cases, a total of 31 raw information encoding images were generated, with the saturation pulse power randomly varied between 0 and 4 μT12,44. Water relaxation (T1 and T2) and field maps (B1 and B0) were acquired separately and used as an extra input to the neural reconstructor described in Fig. 1 in order to avoid water-pool- and inhomogeneity-associated biases, respectively12. A two-step NBMF (see “Methods” section) was used to fit the semisolid-MT and amide proton exchange parameters to the raw data.

Quantitative semisolid-MT and amide proton exchange parameter maps derived from a representative healthy volunteer are presented in Fig. 3 and Fig. 4, respectively. The resulting proton volume fractions and exchange rates were in agreement with the literature (although the large variability in previous reports is noted; see Fig. 3d, e and Fig. 4d, e). The mean values obtained for white/gray matter (WM/GM) were: fss = 13.09 ± 3.44(%), kssw = 34.7 ± 7.8(s−1), fs = 0.33 ± 0.08(%), ksw = 305.1 ± 34.0(s−1) for white matter and fss = 6.28 ± 1.88(%), kssw = 44.2 ± 7.5(s−1), fs = 0.21 ± 0.06(%), ksw = 235.9 ± 46.0(s−1) for gray matter.

Fig. 3: In-vivo study: semisolid magnetization transfer (MT) imaging.
figure 3

Results of neural Bloch-McConnell fitting (NBMF)-based quantification of the MT-related tissue parameters in the human brain scanned with a pulsed MT Magnetic Resonance Fingerprinting (MT-MRF) protocol are presented. Representative reconstructed parameter maps of the semisolid-MT proton volume fraction (a) and proton exchange rate (b), alongside a fidelity estimation (c) of the data-model agreement, computed as R2 = 1-NMSE (normalized mean square error). d, e Statistical analysis of the resulting proton exchange parameter values across the brain white matter and gray matter (WM/GM) regions of interest (box-plots, n=47,442/64,611 voxels, respectively), compared to literature (colored markers)12,43,45,90,91. In the boxplots, the central horizontal lines represent median values, box size represents the two central (2nd, 3rd) quartiles, the whiskers represent the 90 central percentiles, and outliers are omitted.

Full size image
Fig. 4: In-vivo study: amide proton transfer (APT) imaging.
figure 4

Results of neural Bloch-McConnell fitting (NBMF)-based quantification of the APT-related tissue parameters in a human brain scanned with a pulsed Chemical Exchange Saturation Transfer Magnetic Resonance Fingerprinting (CEST-MRF) protocol. Representative reconstructed parameter maps of the amide proton volume fraction (a) and proton exchange rate (b), alongside a fidelity estimation (c) of the data-model agreement, computed as R2 = 1-NMSE (normalized mean square error). d, e Statistical analysis of the resulting proton exchange parameter values across the brain white matter and gray matter (WM/GM) regions of interest (box-plots, n = 47442/64611 voxels, respectively), compared to literature (colored markers)12,45,91,92. In the boxplots, the central horizontal lines represent median values, box size represents the two central (2nd, 3rd) quartiles, the whiskers represent the 90 central percentiles, and outliers are omitted.

Full size image

The joint fit and training of the NBMF produced a neural reconstructor, optimized on a single subject. We then re-applied the trained reconstructors to additional subjects in a fast inference mode. A representative example comparing the parameter maps obtained from single-subject NBMF with those obtained by a rapid reconstructor reuse is shown in Fig. 5. The resulting agreement metrics (Fig. 5e) were as follows; NRMSE: 7 ± 1%, 12 ± 3%, 7 ± 1%, and 18 ± 1%; Intraclass correlation coefficient ICC(2,1): 0.87 ± 0.03, 0.82 ± 0.04, 0.86 ± 0.03, 0.86 ± 0.03; SSIM: 0.93 ± 0.02, 0.87 ± 0.07, 0.94 ± 0.01, 0.90 ± 0.03, for the fss, kssw, fs, and ksw, respectively. Additional analysis is provided in Supplementary Fig. 4.

Fig. 5: In-vivo study: rapid quantification by applying neural Bloch-McConnell fitting (NBMF) in “transfer mode”.
figure 5

A comparison between the results of single-subject NBMF (a, b) and real-time quantification of the same subject by inferring the neural reconstructor trained while fitting another subject (c, d). A perceptually and quantitatively similar outputs were obtained for both semisolid (a, c) and amide (b, d) exchange parameters mapping. e Similarity analysis using normalized root-mean-square (NRMSE), intraclass correlation coefficient (ICC(2,1), absolute agreement-assessing variant), and structural similarity index measure (SSIM) across all (n = 50) processed brain slices. In box plots, the central horizontal lines represent median values, box size represents the two central (2nd, 3rd) quartiles, whiskers represent 1.5× the interquartile range above and below the upper and lower quartiles, and circles represent outliers.

Full size image

Computational complexity, timing, and comparison with alternative approaches

The combined NBMF training and fitting procedure for all four semisolid-MT and amide proton volume fraction and exchange rate parameter maps from the whole brain of a single subject (169K–194K voxels) took 18.3 ± 8.3 min on a standard GPU-equipped (GeForce RTX 3060) desktop workstation, of which, the two-pool quantification of the semisolid MT pool parameters took 3.0 ± 0.4 min. Re-applying the trained reconstructors for whole-brain parameter mapping on a new subject took 1.0 ± 0.2 s. Overall, the complete quantification pipeline takes less than 30 min for NBMF, compared to at least several hours using previously reported implementations of traditional Bloch-Fitting45, or dictionary-based preparation and supervised neural network training.12,37 (Table 1).

Table 1 NBMF computational complexity compared to previously reported studies of semisolid-MT and CEST quantification
Full size table

Next, we performed unified benchmarking of dictionary generation, matching, and supervised learning, using the accelerated approach developed as part of this work (GPU-based JAX formulation of the Bloch McConnell numerical solution); see additional implementation details in Supplementary Note 2. Notably, this yielded comparable timing to self-supervision (Table 2), given that a non-cartesian sampling grid is used for dictionary generation. The benefit of nonetheless using the self-supervised approach compared to supervised training is highlighted in Supplementary Notes 1–3 in the context of consistency with the raw acquired data and per-subject discrepancy minimization. In general, by unlocking rapid direct fitting (via automatic differentiation) and coupling it with self-supervised learning, NBMF constitutes an alternative way to address the ill-posed in-vivo quantification challenge. It contributes to an improved consistency of the quantitative parameter estimates with the raw data given the model, compared to dictionary-based supervised learning (Supplementary Fig. 3). By combining the explicit objective of minimal data-model discrepancy with implicit neural regularization, NBMF created smoother maps with visible contrast, while keeping the data-model agreement close to that achieved by dictionary matching (Supplementary Fig. 5).

Table 2 Unified benchmarking of all methods using the accelerated approach developed as part of this work
Full size table

Automatic differentiation of the Bloch-McConnell (BM) equation solutions

Quantification of semisolid MT/CEST proton exchange parameters under non-steady-state conditions is a notable example of a biophysical estimation where the forward model is perceived as too complex for direct inverse solution via fitting (requiring several days for a single whole brain reconstruction45). While the solution can be approximated via MRF, the large simulated signal dictionaries12 associated with multi-pool imaging also demand significant computational resources46,47, limiting the development of new pulse sequences. A recently reported dictionary-free alternative48 proposed unsupervised learning for semisolid-MT parameter quantification. However, this method assumes continuous pulse irradiation, which is not available in many clinical scanners, and also relies on analytical solutions, which are not compatible with multi-pool pulsed CEST imaging.

The dictionary-free method presented in this work overcomes all such limitations. Our approach is based on a fundamental insight: by proper formulation, ODE models considered only numerically solvable can become step-wise analytical, and thereby compatible with automatic differentiation-based optimization. Specifically, the suggested formulation enables GPU-based matrix inversion and exponentiation, which translates into efficient gradient descent via back-propagation. Combining this concept with a recently reported high-performing automatic differentiator38 provides a new option for solving complex biophysical estimation tasks such as pulsed CEST quantification, demonstrated here. Compared to standard model fitting, this approach avoids (i) computationally expensive and inaccurate purely-numerical derivatives computed via multiple evaluations, and (ii) explicit analytical approximations, which can only be applied to a limited subset of cases and lack generalization (e.g., unsuitable for a multi-proton-pool pulsed-RF saturation). Unlike MRF dictionary-trained networks10,28, the suggested approach can provide parameter estimates that allow the model to best describe the raw data (Supplementary Fig. 3).

Supervised NN training using a synthetic signal dictionary requires the estimation of the application-specific parameter distribution, which is often unknown in advance. The self-supervised (NBMF) approach circumvents this challenge by training on the in-vivo data itself, offering improved parameter distribution matching. When it comes to re-using the trained network on new unseen subjects, one drawback of this approach lies in its reliance on previously represented proton exchange parameters. Dictionary-based approaches, on the other hand, have the flexibility for representing the expected abnormality values (if they are known) or simply using a very broad parameter distribution that covers both the healthy and diseased states. A future patient cohort investigation is needed to examine the clinical utility of transferring the self-supervised quantification approach, when trained on healthy volunteers, for quantification in unseen pathology (e.g., small lesions).

As shown in Table 1, the most time-consuming steps for supervised dictionary-based learning are the dictionary generation step followed by neural network training. However, if the imaging scenario is a priori known (e.g., brain cancer treatment monitoring) and the acquisition protocol parameters are fixed and optimized, these steps can be done once without affecting the rapid inference time for each new subject. Self-supervised data-based learning (NBMF), on the other hand, offers the flexibility of accommodating various imaging scenarios and is more easily adapted for new acquisition protocols and research directions. That being said, the biophysical modeling developed as part of this work (GPU-based JAX implementation of the Bloch McConnell numerical solution) can also accelerate both dictionary generation and supervised learning (Table 2), allowing the user to utilize and compare all different approaches.

The gradient of the forward model can be directly used for simple fitting of the unknown ODE coefficients corresponding to the physical parameters of interest (see voxelwise BMF in the “Methods” section, Supplementary Note 3, and Supplementary Fig. 6). However, when the core forward model automatic differentiator is also integrated into a self-supervised learning pipeline (NBMF, Fig. 1), a joint neural representation of the signal-to-parameter transformation can be trained and stored with little extra computational cost. This enables: (i) Faster convergence, which scales well with the number of voxels up to the full brain size, leveraging redundancy towards a spatially smoother solution (Supplementary Fig. 6). (ii) Later reuse for real-time inference on new subjects within a similar imaging scenario.

The human brain imaging results (Figs. 3–5, Supplementary Figs. 3–6, 8) reveal the potential for using an autodiff-compatible Bloch-McConnell solver for parameter quantification while training a simple multilayer perceptron (MLP) voxelwise. Combined with a 3D whole brain acquisition routine (which rapidly generates hundreds of thousands of voxels), the suggested system provides a rapid and efficient single-subject learning method. Notably, while this work presented a proof of concept for rapid inference by a network trained on a single subject, robustness and consistency of the transfer leaves a clear room for improvement (Fig. 5 and Supplementary Fig. 4). Future work could study different NN architectures with spatial awareness (via convolutional or attention layers), as well as larger datasets composed of multiple subjects and a combination of both dictionary-based synthetic data and real-world scans. Subsequent efforts could also improve the modeling accuracy by taking under consideration the contributions of additional proton pools (such as amine and guanidinium) to the 3.5 ppm signal.

The proposed approach could be further exploited for other tasks across the CEST-MRF pipeline, such as accelerated dictionary synthesis49,50(as demonstrated in Supplementary Note 2 and Table 2) and pulsed-wave irradiation compatible CEST protocol discovery and optimization46,47,51,52,53. Furthermore, NBMF is directly applicable to anatomical-MRF (proton density, T1, T2) dictionary-free parameter quantification and conversely, to classical non-MRF molecular MRI, such as pulsed multi-B1 Z-spectra fitting25,54 (see Supplementary Notes 4, 5). While auto-differentiation of the Bloch equations has previously been leveraged for several MRI-related applications47,52,55,56,57, to the best of our knowledge this is the first report of utilizing this concept for a generalized Bloch-McConnell-fitting task. Beyond molecular MRI and MRF, this approach can also be applied to any other diagnostic and biophysical domains that involve dictionary-matching58.

Learning to estimate ordinary differential equation (ODE) coefficients from observed data

The general strategy underlying NBMF can be applied to any inverse problem that involves fitting ODEs to observations of a dynamical system. In the biomedical realm alone, this includes cardiovascular59,60, pharmacokinetic61,62, and epidemiological63,64 modeling, among many other tasks. In parallel to the exponential growth and improvement in AI performance, the last decade has witnessed a surge of interest in harnessing DL for physics-based problem solving. These efforts have most often been directed into two routes: (i) seeking a solution to a partial differential equation (PDE) as an output of a physics-informed neural network (PINN) that operates on spatial and temporal coordinates65,66,67,68,69; widely applied for spatially-resolved dynamics in solid70- and fluid71 mechanics, heat transfer72, power systems73, weather/climate74, and diffusion MRI75. (ii) Modeling parts of the equation with a NN, yielding a neural ODE/PDE76, often employed as a semi-parametric approach for model discovery77,78,79. Interestingly, the relatively simple direct inverse solution approach described here (Fig. 1), whereby a NN is trained to infer the coefficients of an ODE model from a few samples of the dynamics, has not received similar attention. This could open opportunities for the current work to inform new approaches to ODE-driven inverse problems across a multitude of tasks.

Conclusions

The NBMF framework enables rapid, dictionary-free, pulsed-saturation and multiple proton-pool-compatible semisolid MT/CEST-MRF quantification. By combining a GPU-accelerated auto-differentiable numerical ODE solver and self-supervised DL, the NBMF pipeline is able to match alternative AI-reconstruction based inference, while removing the need for dictionary synthesis. NBMF is three orders of magnitude faster than traditional Bloch fitting, and provides a one-stop-shop for reconstructing quantitative molecular MRI data. The underlying approach has potential applications across a wide variety of ODE-driven inverse problem tasks.

Methods

CEST phantoms

A set of six 10 ml L-arginine (L-arg, chemical shift = 3 ppm, Sigma-Aldrich) phantoms was prepared at a concentration of 25, 50, 75, or 100 mM. The phantoms were titrated to different pH levels between 4.0 and 5.0 and placed in a 120 mm diameter cylindrical holder (MultiSample 120E, Gold Standard Phantoms, UK), filled with saline.

Human subjects

Four healthy volunteers (three females/one male, with average age 23.75 ± 0.83) were scanned at Tel Aviv University (TAU), using a 3T MRI equipped with a 64-channel coil (Prisma, Siemens Healthineers). The research protocol was approved by the TAU Institutional Ethics Board (study no. 2640007572-2) and the Chaim Sheba Medical Center Ethics Committee (0621-23-SMC). All subjects gave written, informed consent before the study.

MRI acquisition

All acquisition schedules were implemented using the Pulseq prototyping framework80 and the open-source Pulseq-CEST sequence standard81. The MRF acquisition protocols were implemented as described previously12,43, with an unsaturated M0 image added at the beginning of each sequence. A spin lock saturation train (13 × 100 ms, 50% duty-cycle) was used for each one of the 30 additional iterations of the sequence, which varied the saturation pulse power between 0 and 4 μT (average pulse amplitude). The saturation pulse frequency offset was fixed at 3 ppm for L-arginine phantom imaging44, 3.5 ppm for amide brain imaging12, or varied between 6 and 14 ppm for semisolid MT imaging43. The saturation block was followed by a 3D centric reordered EPI readout module82,83, providing a 1.8 mm isotropic resolution. The in-plane axial matrix size was 116 × 88, with 50 slices (169K–194K brain voxels) used per subject. The full sequences can be accurately reproduced using previously published Pulseq (.seq) files49. Each 3D MRF acquisition took 2:36 (min:s). The same readout module was used for acquiring additional B0, B1, T1, and T2 maps, via WASABI84, saturation recovery, and multi-echo sequences, respectively. The total scan time per subject was 9 min. The WASABI sequence used a preparation scheme realized by a rectangular pulse of 5 ms and nominal B1 = 3.7 μT. Twenty-four frequency offsets were equally spaced between −1.8 ppm and 1.8 ppm with a recovery time of 4.5 s. An M0 image was taken at -300 ppm with a recovery time of 12 s. The saturation recovery T1 mapping protocol used the following TR (s) values: 10, 6, 4, 3, 2, 1, 0.8, 0.5, 0.4, 0.3, 0.2, 0.1. The T2 mapping multi-echo sequence used the following echo times (s): 0, 0.01, 0.025, 0.03, 0.04 0.05, 0.1, 0.2, 0.3, 0.5, 1.0 with a TR = 10 s.

MRI data pre-processing

In vitro images with no L-arginine vials, partial vials, or severe image artifacts were removed. Regions of interest (ROIs) were defined using circular masks. In-vivo brain images were motion-corrected and registered using elastix85. WM/GM ROI segmentation of the T1 map was performed using statistical parameter mapping86. Quantitative reference CEST-MRF values (Fig. 2) were obtained using dot-product matching, as extensively described previously44,49.

NBMF architecture for semisolid-MT and CEST quantification

The self-supervised learning framework comprises two main components (Fig. 1, Top):

(A) Reconstructor \({{{\mathcal{R}}}}\) - a fully-connected multi-layer perceptron (MLP) NN, applied voxel-wise on the raw input data10,12,13,87. The NN is composed of three layers, with 256 neurons and ReLU activation in each hidden layer. The output layer consists of 5 neurons, encoding the estimates for the proton volume fraction and exchange rate of the compound of interest and their joint uncertainty expressed as noise covariance. It utilizes a sigmoid activation, with the output scaled to a predefined range of the parameter values, which effectively defines the prediction boundaries as follows: semisolid proton volume fraction fss ∈ [0, 30] (%), semisolid proton exchange rate kssw ∈ [0, 150] (s−1), amide proton volume fraction fs ∈ [0, 1.2] (%), amide proton exchange rate ksw ∈ [0, 400] (s−1), L-arginine concentration [L-arg] ∈ [10, 120] (mM) and Nα-amine (of L-arginine) proton exchange rate ksw ∈ [100, 1400] (s−1)44. Several auxiliary maps X, including water relaxation T1, T2, and B0/B1 inhomogeneities, are appended to the MRF raw data D to be used as inputs for the tissue parameter estimation: \(\tilde{{{{\bf{P}}}}}={{{\mathcal{R}}}}\left(({{{\bf{D}}}},{{{\bf{X}}}}),w\right)\) where w are the weights to be trained.

(B) Simulator \({{{\mathcal{F}}}}\)—a differentiable multi-pool spin physics solver. A numerical simulation of the piecewise-constant coefficient Bloch-McConnell (BM) differential equations was implemented in the open-source JAX38 computing framework, leveraging its strong auto-differentiation and GPU-acceleration capabilities for matrix operations. The simulator concatenated and chained the calculations of the BM closed-form solution across all pulses and delays of the protocol. This was carried out by inversion and exponentiation of the 9 × 9 BM-matrix A, which expresses all precession, saturation, relaxation and exchange terms of the multi-pool magnetization vector (M) dynamics, as previously defined33:

$$\dot{{{{\bf{M}}}}} = -{{{\bf{AM}}}}+{{{\bf{C}}}}\to {{{{\bf{M}}}}}_{eq.}={{{\bf{A}}}}\backslash {{{\bf{C}}}};{{{\bf{M}}}}(t+\Delta t) \\ = {e}^{-{{{\bf{A}}}}\Delta t}\left({{{\bf{M}}}}(t)-{{{{\bf{M}}}}}_{eq.}\right)+{{{{\bf{M}}}}}_{eq.}$$
(1)

This solver is compatible with the rectangular pulse-train shape employed in this study and others12,43,81, while arbitrary pulse shapes can be supported using a simple matched-RMS approximation, or to any order through a Magnus expansion88. For two-pool imaging cases (such as semisolid MT data acquired using saturation pulses with a frequency offset higher than 6 ppm), additional acceleration was obtained by implementing the interleaved saturation-relaxation (ISAR2) approximate analytical solution33 of the saturation stage. The RF pulses of spin-lock and readout flips were approximated as hard pulses generating precise flip angle rotations.

The model is designed to represent the whole sequence by simulating the Z-magnetization dynamics during the recovery, saturation, and readout stages, provided that spoilers are applied. For each of the two (semisolid MT/amide) sequences, the Nx31 non-steady-state MRF measurements from 169K-194K brain voxels were normalized using an unsaturated M0 reference image. Thus, the resulting acquired data \({{{\bf{D}}}}={\{{D}_{n}\}}_{n = 1}^{N}\in [0,1]\) is directly related to the magnetization vector governed by Eq. (1), at the end of the saturation pulse block. Therefore, given \(\tilde{{{{\bf{P}}}}}\), an estimate of the sought parameters, the simulator provides a re-synthesis of the data as: \(\tilde{{{{\bf{D}}}}}={{{\mathcal{F}}}}(\tilde{{{{\bf{P}}}}},{{{\bf{X}}}},{\omega }_{rf},{B}_{1})\), where ωrf and B1 are the saturation pulse frequency offsets and powers implemented in the MRF protocol, and X are any known tissue parameters.

The NBMF reconstruction of the semisolid-MT proton exchange parameters from the first (1) subject, was obtained by using the MT-MRF data \({{{{\bf{D}}}}}_{ss}^{(1)}\) alongside independently quantified auxiliary parameter maps \({{{{\bf{X}}}}}_{w,B}^{(1)}=\{{T}_{1w},{T}_{2w},{B}_{1},{B}_{0}\}\), for training the weights \({w}_{ss}^{(1)}\) of a neural reconstructor \({{{{\mathcal{R}}}}}_{MT}^{(1)}\), designed to quantify the associated proton exchange parameters (\({\tilde{{{{\bf{P}}}}}}_{ss}^{(1)}={f}_{ss},{k}_{ssw}\)). To that end, the NBMF optimizes the following self-supervised objective of consistency with the biophysical model \({{{\mathcal{F}}}}\):

$${w}_{ss}^{(1)} = {{{{\rm{argmin}}}}}_{w}\left\vert \left\vert \tilde{{{{\bf{D}}}}}-{{{{\bf{D}}}}}_{ss}^{(1)}\right\vert \right\vert \\ = {{{{\rm{argmin}}}}}_{w}\left\vert \left\vert {{{\mathcal{F}}}}\left({{{\mathcal{R}}}}\left(({{{{\bf{D}}}}}_{ss}^{(1)},{{{{\bf{X}}}}}_{w,B}^{(1)}),w\right),{{{{\bf{X}}}}}_{w,B}^{(1)}\right)-{{{{\bf{D}}}}}_{ss}^{(1)}\right\vert \right\vert$$
(2)

The L2 norm was used as the regression loss. A cosine-decay learning rate schedule and simple early-stopping upon convergence (loss trend reaching plateau) were applied. Augmentation by noise was applied, twice: (a) Adding a  ±0.1% Gaussian noise to the raw samples (b) Adding a Gaussian noise to the \(\tilde{f},\tilde{k}\) tissue parameters estimate, using covariance derived from extra outputs of the NN, inspired by a recent work89.

This process was repeated using the non-steady-state amide raw MRF data \({{{{\bf{D}}}}}_{s}^{(1)}\) for NBMF quantification of the amide proton exchange parameters (Ps = fs, ksw). For human brain experiments, we also appended the semisolid MT pool parameter estimates \({\widetilde{f}}_{ss}\) and \({\tilde{k}}_{ssw}\) (obtained from the semisolid MT NBMF procedure) to the auxiliary vector X. This vector served as input for the amide reconstructor \({{{{\mathcal{R}}}}}_{s}\) and the 3-pool biophysical model \({{{{\mathcal{F}}}}}_{s}\), so that: \({X}_{B,w,ss}=\{{X}_{B,w},{P}_{ss}\}=\{{T}_{1w},{T}_{2w},{B}_{1},{B}_{0},{\tilde{f}}_{ss},{\tilde{k}}_{ssw}\}\)12. For the two-pool L-arginine phantom experiments, the auxiliary parameters were assigned constant values based on previous reports (T1w = 2800 ms, T2w = 1200 ms)43.

Importantly, we obtain both the subject-specific proton exchange parameters \({\tilde{{{{\bf{P}}}}}}^{(1)}={{{{\mathcal{R}}}}}^{(1)}({{{{\bf{D}}}}}^{(1)},{{{{\bf{X}}}}}^{(1)})\) and the trained reconstructor \({{{\mathcal{R}}}}\) at the convergence of the NBMF. This enables ultra-fast quantification of the proton exchange parameters \({\tilde{{{{\bf{P}}}}}}^{(2)}={{{{\mathcal{R}}}}}^{(1)}({{{{\bf{D}}}}}^{(2)},{{{{\bf{X}}}}}^{(2)})\) from a new subject (2) (Fig. 1 bottom). Notably, this rapid inference is only applicable for new data drawn from the same distribution and cannot be applied to entirely new systems (such as muscle creatine quantification using brain-data trained NBMF).

As a natural ablation of the system by removing the neural component, the auto-diff simulator can be used for direct voxelwise parameter fitting: \({\tilde{{{{\bf{P}}}}}}^{(1)}=argmin| | {{{\mathcal{F}}}}\left({{{{\bf{P}}}}}^{(1)}\right)-{{{{\bf{D}}}}}^{(1)}| |\), referred to here as voxelwise Bloch-McConnell fitting (VBMF). This simpler process can be described in the context of Fig. 1 as stopping the gradients at the tissue parameters, which now assume the role of independent per-voxel variables. Apart from the obvious drawback of not yielding a neural reconstructor, VBMF’s performance is inferior to NBMF for brain imaging (Supplementary Fig. 6), which we ascribe to the implicit smoothing regularization by the neural network. However, it is a viable direct method for in vitro analysis that is equally able to converge to the minimum of the modeling-error landscape (Supplementary Figs. 1, 2).

Finally, additional acceleration was achieved by parallelization of the computational graph across consecutive readout pairs {Dn−1, Dn}, decoupling the single-iteration simulators \({{{{\mathcal{F}}}}}_{n}\). Assuming that the Dn−1 snapshot captures the preceding spin history evolution, the re-synthesis stage is now formulated as \(\tilde{{{{\bf{D}}}}}={\{{{{{\mathcal{F}}}}}_{n}(\widetilde{{{{\bf{P}}}}},{D}_{n-1})\}}_{n = 1}^{N}\) and embedded in Eq. (2) as such. See Supplementary Note 4 for further elaboration.

Statistical analysis

The SSIM and ICC(2,1) were calculated using the open-source SciPy and Pingouin scientific computing libraries for Python. In slice-statistic box plots (Fig. 5e), the central horizontal lines represent median values, box size represents the two central (2nd, 3rd) quartiles, whiskers represent 1.5× the interquartile range above and below the upper and lower quartiles, and circles represent outliers. In the voxel-statistic box plots (Figs. 3, 4) the central horizontal lines represent median values, box size represents the two central (2nd, 3rd) quartiles, the whiskers represent the 90 central percentiles and outliers are omitted. Numerical results in the text are presented as mean ±SD.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.