Designing cross-city symbiosis strategy in urban agglomeration by trading off decarbonization, health and economic benefits

Abstract

Leveraging the hyperconnectivity, geographical proximity, and comparative advantages of industrial structures among cities within urban agglomerations to promote cross-city symbiosis offers an effective and affordable approach in facilitating sustainable transition in cities to achieve the Sustainable Development Goals (SDGs). However, the effects of cross-city symbiosis featuring substantial plant diversity remain unknown. Focusing on the typical Beijing-Tianjin-Hebei urban agglomeration in China, our analysis reveals significant spatial mismatch between solid waste generation and co-consumption capacity across cities. The trade-offs among multiple SDGs across 160,875 symbiotic pathways under 322,772 constraints are fully considered to address pollution transfer issues stemming from cross-city symbiosis. Results show that in the optimized strategy, transboundary cooperation can further unlock 26.5% of waste co-consumption ability, contribute an additional 30.6% reduction in CO₂ emissions, avoid 24.7% disease cases from air pollution, and increase 35.5% of economic profits. The benefits vary significantly among cities, with industrial cities benefiting more than service-oriented ones. Even in the optimized strategy, pollution transfer among cities cannot be entirely avoided, highlighting the need for a top-down cross-city compensation mechanism. Subsequently, we propose a locally adapted (city-by-city and plant-by-plant) cross-city symbiosis plan. It provides scientific foundations for promoting refined and actionable symbiosis strategies for urban agglomerations worldwide.

Introduction

As the mainstream form of city development¹, urban agglomerations play an indispensable role in achieving the Sustainable Development Goals (SDGs), given that 65% of the 169 targets underlying the 17 SDGs require city engagement. Currently, half of the world’s production activities² and 25% of the population³ are concentrated in urban agglomerations that cover only 1.5% of the land area⁴. The compact spatial structure, highly concentrated population and industry, along with distinct and complementary industrial structures among the cities, make urban agglomerations the ideal carrier for cross-city symbiosis. Leveraging the hyperconnectivity, geographical proximity, and comparative advantages of industrial structures among cities within to promote cross-city symbiosis has emerged as a vital approach to systematically address the environmental challenges faced by cities and drive the achievement of the SDGs^5,6. Compared to the weakening marginal effectiveness of single-sector environmental management measures⁷ and the expensive carbon capture and storage technologies⁸, cross-city symbiosis enables traditionally independent cities, industries, and infrastructures to achieve competitive advantage through collaborative efforts. Thereby, it offers an effective and affordable approach in facilitating sustainable transition in cities^9,10.

Existing research has revealed the decarbonization, resource conservation, and other co-benefits of industrial symbiosis¹¹. Yet most previous studies have focused on waste material and energy exchange within individual cities¹² and industrial parks¹³, or have relied on a few hypothetical plants with specific wastes as examples¹⁴. Such approaches fail to capture the real-world complexity of cross-city industrial symbiosis, which involves numerous plants across different cities and sectors, varying widely in age, scale, technology, and waste generation or utilization capacity¹⁵. To advance cross-city symbiosis from concept to practice, a plant-by-plant strategy is needed. This strategy must define the specific matching relationships and quantify the flows of solid wastes (e.g., fly ash, blast-furnace slag, and steel slag), taking full account of the distinctive characteristics of each plant. Besides, when implementing cross-city symbiosis, the boundaries among cities are opened, allowing waste to flow freely among them. This raises concerns about pollution transfer, where waste flows across cities may improve the environmental performance of the waste-exporting city while exacerbating pollution in the waste-receiving city¹⁶. Trade-offs may also arise among different SDGs^17,18. For example, co-processing municipal solid waste in cement kilns may reduce carbon dioxide emissions but increase nitrogen oxide emissions^19,20. Traditional single-objective optimization methods are inadequate to address this challenge due to their narrow focus on economic or decarbonization goals. Classic multi-objective optimization methods (e.g., linear weighting²¹, equivalent index²², ε-constraint approaches²³) introduce strong subjectivity in dimension descending and may lead to suboptimal outcomes. They cannot facilitate the actionable design of a multi-objective optimized symbiosis strategy at the plant level to avoid pollution transfer among cities, industries, or SDGs.

Hence, this study aims to develop a plant-by-plant cross-city symbiosis strategy to effectively explore the decarbonization, economic, and health benefits, while avoiding the potential pollution transfer due to cross-city waste flows. We apply this strategy to the Beijing-Tianjin-Hebei (BTH) urban agglomeration in China, a region characterized by concentrated heavy industries and dense population²⁴, to offer practical and precise guidance. In 2023, the population density of the BTH urban agglomeration is eight times the world average, generating massive municipal wastes that urgently need to be disposed of²⁵. Its crude steel output equals the combined output of the world’s second and third largest producers²⁶, its cement production matches that of the world’s third largest producer²⁷, and its coal-fired power capacity far exceeds that of the world’s fourth largest producer²⁸. Notably, varying industrial structures across cities within this urban agglomeration create distinct comparative advantages that provide a foundation for cross-city symbiosis. For example, as the political center, Beijing generates substantial municipal solid waste but lacks adequate treatment capacity. In contrast, Hebei hosts a concentration of cement, steel, and coal-fired power plants with significant underutilized waste co-consumption potential. This complementarity is further reinforced by Beijing’s capacity to provide financial subsidies, ensuring the economic viability of inter-city waste exchanges. Following the six world-class urban agglomerations such as the Northeastern Seaboard of the United States, the Great Lakes Megalopolis in North America, and the Pacific Coast urban agglomeration in Japan, the BTH urban agglomeration has recently joined the ranks of world-class urban agglomerations²⁹. Thereby, studying the optimized cross-city symbiosis strategy in the BTH urban agglomeration is highly representative and can provide a replicable template for other urban agglomerations worldwide.

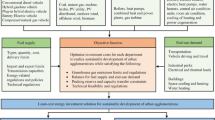
This study is structured around three key sections: (1) Compile a plant-level dataset comprising main plants and municipal facilities within a typical urban agglomeration to reveal the spatial characteristics of waste generation and co-consumption capacity, thus providing evidence for the necessity of cross-city symbiosis (the first part of the results). (2) Establish an optimized cross-city symbiosis strategy using a modified NSGA-III-fuzzy membership algorithm that fully considers the trade-offs among cities, industries, and multiple SDGs to address pollution transfer, and assess the resulting decarbonization, health, and economic effects (the second part of the results). (3) Identify vital cities, symbiotic measures, and plants with outstanding performances to propose a “city-by-city and plant-by-plant” cross-city symbiosis plan and advance precise management in urban agglomerations (the third part of the results). Based on the real operational and technical data from thousands of individual plants within urban agglomerations, the optimized plant-by-plant cross-city symbiosis strategy can not only reflect the real-world waste reutilization situation (ensuring the feasibility of the symbiosis strategy at the micro-level and avoiding pollution transfer), but also demonstrate the contribution of the symbiosis strategy to regional SDGs (ensuring the effectiveness of the symbiosis strategy at the macro level).

Results

Spatial mismatch between solid waste generation and co-consumption capacity

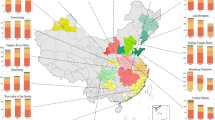
We observe a significant spatial mismatch between solid waste generation and co-consumption capacity across cities. Ideally, when industrial symbiosis is confined within each city without considering cross-city symbiosis, only up to 45.8% of solid waste in the BTH urban agglomeration can be co-consumed. Approximately half of the cities will reach or surpass their solid waste co-consumption capacities (Fig. 1a–e, Tables S1 and S2). The surplus co-consumption capacities of six cities (Baoding, Chengde, Qinhuangdao, Shijiazhuang, Xingtai, and Zhangjiakou), accounting for 24.1% of the total solid wastes, will remain unused (Fig. S1). Promoting a cross-city symbiosis strategy can effectively utilize these surplus co-consumption capacities.

Fig. 1: Spatial mismatch between solid waste generation and co-consumption capacity in the BTH urban agglomeration.

Waste generation amount in each iron and steel plant (a), thermal power plant (b), and municipal facility (c); waste co-consumption capacity in each cement plant (d); and the excess capacity of each city in dealing with solid waste across sectors (e). The excess capacity of each city in dealing with solid waste across sectors is measured by the gap between the intra-city co-consumption capacity and the total solid waste output. The asterisk indicates that the city has a surplus of local waste co-consumption capacity. The base map was adapted from the National Platform for Common Geospatial Information Services (https://www.tianditu.gov.cn/?4).

A city with matched total solid waste generation and co-consumption capacity may still face deficiencies or surpluses in co-consuming specific types of solid waste. Tangshan is such an example (Fig. 1e). Its blast-furnace slag output far exceeds the local co-consumption capacity (−23.7 Mt), while there is a surplus of local co-consumption capacity for steel slag (10.8 Mt). When cross-city symbiosis is considered, Tangshan can reutilize steel slag from Handan and transport excess blast-furnace slag to Shijiazhuang, Xingtai, and Zhangjiakou. This can lead to improved overall environmental and economic performances of the BTH urban agglomeration.

Due to different comparative advantages, cities with matched solid waste generation and co-consumption capacity also require cross-city symbiosis. Even in cases where all cities lack or have surplus co-consumption capacity for one type of waste, cross-city symbiosis can still be pursued based on comparative advantages. In fact, the co-consumption pressures of cities on various solid wastes differ significantly based on local industrial structures and economic statuses. Considering cities’ different comparative advantages in the urban agglomeration, the upstream and downstream plants matched by greater decarbonization, health, and economic effects may not necessarily be in the same city³⁰. Specifically, iron and steel plants and thermal power plants may prioritize co-disposal with neighboring cities in the same province due to similar siting options to cement plants. Municipal facilities concentrated in densely populated cities like Beijing and Tianjin are more inclined towards long-distance cross-city symbiosis with cities in Hebei Province that have sufficient clinker production capacities (Fig. 1e).

Consequently, going beyond geographical boundaries to promote cross-city symbiosis can significantly unlock waste disposal potential and other co-benefits inherent in the spatial mismatch between solid waste generation and co-consumption capacity. This requires: (1) considering the trade-offs among multiple SDGs to establish an optimized cross-city symbiosis strategy to avoid pollution transfer, and quantifying its effects on facilitating cities’ sustainable transition; and (2) assessing the heterogeneity in the performance of each specific plant and symbiotic measure in each city to form a locally adapted city-by-city and plant-by-plant action plan.

Decarbonization, health, and economic effects of the optimized cross-city symbiosis strategy

Compared with the non-symbiosis scenario, the optimized cross-city symbiosis strategy can co-consume 70.9 million tons of solid waste, thereby enhancing the co-consumption ability of the BTH urban agglomeration by approximately 43.9%. This optimized strategy enables the co-consumption of 87.6% of steel slag, 94.8% of bottom ash, 85.3% of FGD gypsum, 100% of sludge, as well as part of fly ash (31.2%), blast-furnace slag (28.4%), domestic waste (13.8%), and hazardous waste (55.7%) (Table S3). It indirectly provides substantial co-benefits, that is, reducing 26.1 Mt, 17.7 kt, 57.8 kt, and 28.1 kt of CO₂, SO₂, NOx, and PM emissions, increasing $258.3 million of economic profits, and avoiding 73,737 disease cases from air pollution annually (Fig. S2). This is equivalent to 69.9%, 92.3%, and 70.1% of the 14th Five-Year Plan targets for SO₂, NOx, and PM emission reductions in industrial sectors of the BTH urban agglomeration³¹.

In the optimized strategy, compared to intra-city symbiosis, transboundary cooperation can further unlock 26.5% of waste co-consumption ability, contribute an additional 30.6% reduction in CO₂ emissions, avoid 24.7% disease cases from air pollution, and increase 35.5% of economic profits. Cross-city symbiosis could realize substantial environmental and economic benefits through spatial redistribution, without disrupting normal plant operations or retiring additional production capacity (Fig. S2 and Table S3).

We further categorize the effects of cross-city symbiosis into two types: the industry-related effect⁹, which involves using waste from one industry as raw materials in another, and the infrastructure-related effect³², which involves reutilizing wastes from municipal infrastructures as alternative fuels or raw materials in industries (Fig. S3a).

Industry-related effect remains the dominant form of cross-city symbiosis, accounting for 90.1% of the overall co-processed solid waste (Fig. 2), along with 90.6% of decarbonization effects, 98.8% of health benefits, and 98.5% of economic profits (Fig. S3b–d). Infrastructure-related symbiosis enables the co-consumption of 7.0 Mt of municipal waste, representing 23.8% of the total municipal waste generated in the BTH urban agglomeration. This makes a significant contribution to the 11.6.1 sub-targets of SDGs on urban solid waste management by providing an effective and affordable approach in facilitating solid waste management of cities.

Fig. 2: Spatial redistribution of solid wastes in the optimized cross-city symbiosis strategy for the BTH urban agglomeration.

Industry-related effects in (a) and Infrastructure-related effects in (b). The abbreviations of the cities in the BTH urban agglomeration are Beijing (BJ), Tianjin (TJ), Baoding (BD), Cangzhou (CZ), Chengde (CD), Handan (HD), Hengshui (HS), Langfang (LF), Qinhuangdao (QHD), Shijiazhuang (SJZ), Tangshan (TS), Xingtai (XT), and Zhangjiakou (ZJK).

A structural distinction also exists in waste flow patterns: infrastructure-related symbiosis is dominated by inter-city exchanges, while industry-related symbiosis occurs mainly through short-distance intra-city pathways (Fig. 2). This difference reflects their distinct roles in waste management in urban agglomerations.

Specifically, 77.4% of industrial solid waste flows are intra-city, concentrated heavily in a few industrial hubs (Fig. 2a). Tangshan, Handan, and Tianjin together process 63.2% of the total industrial solid waste of the urban agglomeration. This spatially uneven distribution underscores the critical role of a limited number of cities in managing industrial waste across the BTH urban agglomeration.

In comparison, 62.3% of infrastructure-related waste flows cross-city boundaries (Fig. 2b). Examples include the transfer of sludge, municipal solid waste, and hazardous waste from Beijing and Tianjin to Tangshan. Although the scale of infrastructure-related symbiosis is considerably smaller than that of industry-related symbiosis, these inter-city flows utilize comparative advantages of cities within and help alleviate garbage siege challenges in urban agglomerations. Infrastructure-related activities are also more evenly distributed, with individual cities co-consuming between 1.2% and 10.1% of total municipal solid waste, highlighting their relevance to waste management in every city across the urban agglomeration.

Locally adapted city-by-city and plant-by-plant symbiosis plan

The benefits from cross-city symbiosis vary significantly among cities, highlighting the ineffectiveness of one-size-fits-all policies and the necessity of precise city-by-city and plant-by-plant management. In the optimized cross-city symbiosis strategy for the BTH urban agglomeration, the solid waste co-consumption, decarbonization, health, and economic gains in each of the 13 cities exhibit significant variations: ranging from 0.9 to 23.1 Mt of solid wastes co-consumed, 0.4 to 7.7 Mt of CO₂ emission reduction, 205 to 18,862 avoided disease cases from air pollution, and $4.5 to $58.5 million additional profits (Fig. 3a–d).

Fig. 3: Decarbonization, health, and economic effects of the optimized cross-city symbiosis strategy in each city of the BTH urban agglomeration.

Waste co-consumption (a), decarbonization (b), health (c), and economic (d) effects in each city; and effects of the 12 symbiotic measures M1–M12 in each city (e–p). e–p Illustrates the performance of the 12 symbiotic measures (M1–M12) across the 13 cities that are denoted by their abbreviations (e.g., BJ for Beijing, TJ for Tianjin). The measures are evaluated against three benefits: economic (green), decarbonization (orange), and health (gray). Each subplot (e–p) corresponds to a specific symbiotic measure (M1–M12). Within each subplot, each colored bar represents the performance of a specific symbiotic measure for a single city across all three benefits. The radial scale quantifies the percentage contribution of a symbiotic measure to a specific benefit for a given city. For instance, the green bar for Tianjin (TJ) in subplot (e) indicates that measure M1 contributes to 13% of the city’s total economic benefits from all 12 symbiotic measures. The base map was adapted from the National Platform for Common Geospatial Information Services (https://www.tianditu.gov.cn/?4).

Compared to service-oriented cities, industrial cities gain more significant benefits from cross-city symbiosis. The cities that gain the greatest environmental benefits are Tangshan, Handan, and Tianjin, where heavy industries are highly developed. Together, these three cities account for 61.5% of the total co-consumed solid wastes, 67.0% of avoided disease cases from air pollution, and 52.0% of CO₂ emission reduction realized through the optimized cross-city symbiosis strategy. The cities that gain the greatest economic profits are Tangshan, Tianjin, and Cangzhou, accounting for 51.2% of the total economic profits realized through the optimized cross-city symbiosis strategy. Prioritizing these cities as pilot cities for implementing cross-city symbiosis is imperative.

Even in the optimized cross-city symbiosis strategy, pollution transfer among cities cannot be entirely avoided. This calls for a top-down cross-city compensation mechanism. By balancing the synergetic and conflicting relationships among various SDGs, the Pareto-optimized cross-city strategy maximizes the avoidance of pollution transfer among cities and different goals. However, some cities and plants may still perform poorly on certain goals due to energy consumption during the cross-city transportation of solid wastes. For example, Tangshan gains a net reduction of 256.0 kt of CO₂, 198.0 t of SO₂, 121.5 t of NO_X, and 47.5 t of PM by co-consuming sludge from Beijing. However, it also incurs an additional economic cost of $11.3 million (Fig. S4). This is because the transport distance between Tangshan and Beijing surpasses the effective radius of sludge-clinker symbiosis concerning economic profitability. This indicates that cross-city symbiosis does not guarantee benefits for every city and every plant. Some will inevitably incur losses, and loss transfer cannot be entirely avoided. Therefore, in addition to pursuing bottom-up plant-by-plant symbiosis, there is a need for a top-down cross-city compensation mechanism. This mechanism requires cities and plants that gain more benefits to subsidize those that suffer losses, thereby helping to manage underperforming goals.

The effectiveness of key symbiotic measures varies significantly across cities. Each city should emphasize different symbiotic measures in its promotion efforts (Fig. 3e–p and Table S4). The performance of M2 (Produce ground granulated blast-furnace slag to be used as supplementary cementitious material) is extremely prominent in all cities (accounting for 39.4%~80.2% of decarbonization effects in each city, 9.4%~78.3% of health impacts, and 2.9%~277.5% of economic profits). M6 (Utilize bottom ash as supplementary cementitious material) alone accounts for more than half of the economic profits derived from cross-city symbiosis in Baoding (159.9%), Cangzhou (93.7%), Beijing (71.1%), and Tianjin (61.9%). It should hence be prioritized for promotion in these cities. M9 (Utilize fly ash as supplementary cementitious material) is more prominent in Beijing, Baoding, and Tangshan (19.2%~47.1%). M10 (Collaborative disposal of domestic waste in pre-calcining kiln) and M12 (Collaborative disposal of sewage sludge in pre-calcining kiln) underperform in terms of economic profits (−4.8%~−90.6% for M10, and −3.2%~−72.2% for M12), but exhibit good decarbonization and health benefits. M11 (Collaborative disposal of hazardous waste in pre-calcining kiln), on the other hand, produces significant economic profits of over 49.4% but offers little decarbonization and health benefits. These findings inform the development of a locally adapted cross-city symbiosis plan. Special attention should be paid to the needs and preferences of individual cities when adopting such measures in variance.

The top ten cement plants contribute more than one-third of the total benefits from cross-city symbiosis (Fig. 4). These key plants play pivotal roles in the cross-city symbiosis strategy. Ensuring the continuous and stable operation of these vital plants, particularly the top-ranked large cement plants, is essential for promoting cross-city symbiosis. Currently, the industrial sector often contends with “one-size-fits-all” industry clearing policies, seasonal production process control, and limitations on production output, which significantly affect the stability of the cross-city symbiosis system. Results of this study recommend that capacity adjustment and operation management policies in the iron and steel, cement, and thermal power industries in the BTH urban agglomeration should be appropriately relaxed for core plants with an orderly phased and scheduled scheme. This guarantees the operational efficiency and resilience of the cross-city symbiosis strategy.

Fig. 4: Role of each cement plant in the optimized cross-city symbiosis strategy.

The contribution of each cement plant to the total decarbonization effects (a), health impacts (b), and economic effects (c). The vertical axis represents the performance of each cement plant in terms of decarbonization effects, health impacts, and economic effects. The horizontal axis shows the cumulative number of cement plants ranked in descending order of their effects.

Discussion

When going beyond city boundaries to develop cross-city symbiosis in urban agglomerations, the environmental and economic benefits are significantly greater than the sum of the symbiotic benefits within individual cities. Our results show that promoting cross-city symbiosis can further unlock 26.5% waste co-consumption capacity, reduce 30.6% of CO₂ emissions, avoid 24.7% of disease cases from air pollution, and increase 35.5% of economic profits in the BTH urban agglomeration. Moreover, cross-city symbiosis can significantly reduce the resource demand of urban agglomerations, thereby lowering their dependence on external resource supplies to some extent and strengthening the network resilience of urban agglomerations. The optimized cross-city symbiosis strategy reutilizes 70.9 Mt of solid waste in the BTH urban agglomeration. About 60.5 Mt of resource demand can be reduced, including 41.7 Mt of cementitious materials, 7.2 Mt of raw coal, 7.3 Mt of bauxite, and 4.3 Mt of natural gypsum. It helps improve the resource security in urban agglomerations and mitigate the systemic risks arising from temporary resource shortage.

Proposing an optimized cross-city symbiosis strategy necessitates fully considering the synergistic and conflicting relationships among the SDGs across cities. The traditional single-objective, single-industry, and single-city management approach has been proven to cause severe pollution transfer issues across cities, industries, and SDGs^33,34. This study proposes a methodological framework to configure globally optimized Pareto solutions for cross-city symbiosis. Though pollution transfer among cities cannot be entirely avoided, the risk can be minimized. In the globally optimized cross-city symbiosis strategy, around 87% of transboundary waste flows can bring positive benefits to both waste-receiving cities and waste-exporting cities on decarbonization, health impacts, and economic profits. This provides an effective approach to address the series of environmental challenges faced by cities within urban agglomerations and drive the achievement of the SDGs on Goal 3 (good health and well-being), Goal 9 (industry, innovation and infrastructure), Goal 11 (sustainable cities and communities), Goal 12 (sustainable consumption and production), and Goal 13 (climate action).

Effective cross-city symbiosis requires not only designing a locally adapted city-by-city and plant-by-plant action plan, but also establishing a well-functioning top-down authority at the urban agglomeration level. Existing cross-city strategies primarily focus on government communication, information exchange, and common goal setting. A tailored cross-city symbiosis strategy specific to each city and plant should be implemented to support coordinated efforts among all plants in urban agglomerations. We clarify the varied benefits of decarbonization, health impacts, and economic profits derived from cross-city symbiosis across cities, symbiotic measures, and plants. The results can assist policymakers in identifying the priority of symbiotic measures and plants in each city, and identifying cities and plants that fall short on specific goals. Cross-city compensation mechanism is necessary to mitigate the unavoidable negative impacts of localized losses.

Given the trend of urban agglomeration expansion, the cross-city symbiosis strategy developed in the BTH urban agglomeration can serve as a replicable template for precise symbiosis management in other urban agglomerations worldwide. For example, the Pacific Coast urban agglomeration in Japan, which has similar industrial structures and environmental challenges to the BTH urban agglomeration, can directly replicate the cross-city symbiosis strategy provided in this study. In contrast, the Great Lakes Megalopolis in North America exhibits different industrial structures. Steel and automobile manufacturing are its two pillar industries. It also has significant cement production capacity and a highly concentrated population. By selectively adopting the cross-city symbiosis strategy of the BTH urban agglomeration, such as promoting cross-city symbiosis between municipal infrastructure and hard-to-abate steel and cement industries, the Great Lakes Megalopolis in North America can also achieve significant benefits.

Methods

The methodological framework of this study consists of three components: (1) constructing a plant-specific dataset to analyze the spatial characteristics of waste generation and co-consumption capacity in the BTH urban agglomeration; (2) evaluating the plant-by-plant decarbonization, health, and economic benefits in promoting cross-city symbiosis strategy through bottom-up modeling; and (3) an optimized cross-city symbiosis strategy is designed by considering trade-offs among multiple SDGs across 160,875 symbiotic pathways under 322,772 constraints, using a modified NSGA-III fuzzy algorithm (Fig. S5).

Constructing the plant-specific dataset

This study constructs a fine-scale dataset of main plants and municipal facilities in the BTH urban agglomeration, including 91 iron and steel plants, 116 thermal power plants, 195 cement plants, as well as 390 sewage treatment plants, 112 hazardous waste treatment plants, and 116 domestic waste treatment plants. This dataset covers the details on all the plants listed above, and the information comes from three categories of sources (Fig. S6).

Directly accessible data: Industrial structure and outputs of main solid wastes^35,36,37; production process and technology (Fig. S7), output, geographical location, and waste generation/co-consumption coefficient in the production process of each iron and steel/cement/thermal power plant (Table S6); treatment process, production capacity, and commissioning date of each sewage/hazardous waste/domestic waste treatment plant; CO₂, SO₂, NOx, and PM emission reduction coefficients, as well as energy conservation coefficients of the 12 proposed symbiotic measures³⁸ (Tables S7 and S9); coal equivalent coefficients of different energy types (Table S9) and pollutant emission coefficients in the combustion of different energy types (Table S10); and initial investment costs, operating costs, economic revenues of each symbiotic measure, transport costs, depreciation life, and discount rate, etc. (Table S8)^39,40,41.

Obtained from inventory analysis: Outputs of wastes in each upstream plant and the co-consumption ability of wastes in each downstream plant. Official data may not be available, and hence we calculate waste outputs of each iron and steel plant and thermal power plant based on the chain of “designed capacity of crude steel/power generation—run time—output coefficient of waste—end-of-pipe reduction rate” using the following formula^42,43:

$${{Output}}_{{waste},i,{type}}={{Designed\; capacity}}_{i,{run\; time}}\times {{Output\; coefficient}}_{{pro},{type}}\times \left(1-{\vartheta }_{{pro}}\right)$$

(1)

The notion ${{Output}}_{{waste},i,{type}}$ represents the generation amount of waste in plant i; ${{Designed\; capacity}}_{i,{run\; time}}$ is the production capacity of plant i in the run time; ${{Output\; coefficient}}_{{pro},{type}}$ is the waste output per ton of main product when adopting production process pro; and ${\vartheta }_{{pro}}$ is the end-of-pipe reduction rate of production process pro.

Based on the same principle, the co-consumption ability of different types of wastes in each cement plant is calculated as below:

$${{Co}-c{onsumption\; ability}}_{j,{type}}={{Designed\; capacity}}_{j,{run\; time}}\times Co-{consumption}{{coefficient}}_{{pro},{type}}$$

(2)

The notion ${{Co}-c{onsumption\; ability}}_{j,{type}}$ represents the upper limit of co-consumed waste in plant j; ${{Designed\; capacity}}_{j,{run\; time}}$ is the production capacity of plant j in the run time; and ${{Co}-{consumption\; coefficient}}_{{pro},{type}}$ is the waste co-consumption ability per ton of main product when adopting production process pro.

Geographical data obtained from API interfaces: The information on plant-specific geographical location is crucial for optimizing cross-city symbiosis. Latitude and longitude coordinates of the 1020 plants are obtained from AutoNavi⁴⁴ and visualized by ArcGIS. Given the complexity of road information, merely computing straight-line distances between two plants may be inaccurate. Therefore, we utilize the API interface of AutoNavi to measure off-site driving distances between upstream plants and downstream plants.

Evaluating the plant-by-plant decarbonization, health, and economic effects

The process-based method is employed to quantify the contribution of the optimized cross-city symbiosis strategy to decarbonization, health impacts, and economic profits^45,46.

Our analysis delves into the co-consumption processes of different types of wastes, examining their impacts on the production processes of the relevant downstream/upstream plants. Key impacts primarily come from raw material substitution, the displacement of fossil fuel usage, and additional energy consumption from waste transportation^47,48. Below, we present a detailed analysis of the impacts of each symbiotic measure compared to conventional production processes.

Energy conservation effects:

$${TEC}=\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{j}\mathop{\sum }\limits_{k}{x}_{i,j,k}\times \left(\mathop{\sum }\limits_{l}{(M}_{k-ref,l}-{M}_{k,l})\times {\zeta }_{l}+\mathop{\sum }\limits_{f}\left({(E}_{k-ref,f}-{E}_{k,f}\right)-{d}_{i,j}\times UEC\times {\zeta }_{gas}\right)$$

(3)

The notation x_i,j,k indicates the solid waste transferred from upstream plant i to downstream plant j that can be co-consumed by the k-type symbiotic measure; k-ref is the conventional production process relative to k-type symbiotic measure; and l and f represent the type of consumed raw material and energy, respectively. Energy directly saved by substituting fuel consumption with wastes is $({E}_{k-{ref},f}-{E}_{k,f})$. Energy indirectly saved by substituting raw material consumption with waste is $({M}_{k-{ref},l}-{M}_{k,l})\times {{\rm{\zeta }}}_{l}$, where ζ is the energy consumption coefficient in raw material production. The notation ${d}_{i,j}$ means the distance between the upstream plant i and the downstream plant j; UEC is the diesel oil consumption per unit freight transport; and ζgas is the coal equivalent coefficient of diesel oil.

Decarbonization effects:

$${TD}=\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{j}{x}_{i,j}\times \left(\mathop{\sum }\limits_{k=k-rc}\left(E{F}_{d}+E{F}_{c}+E{F}_{e}\right)+\mathop{\sum }\limits_{k=k-af}E{F}_{f}+\mathop{\sum }\limits_{k=k-arm}E{F}_{g}-{d}_{i,j}\times E{F}_{t}\right)$$

(4)

The notations ${{EF}}_{d}$, ${{EF}}_{c}$, and ${{EF}}_{e}$ represent the process emission factor, the combustion emission factor, and the electricity emission factor in clinker production, respectively; ${{EF}}_{f}$ represents the carbon emission factor of alternative fuels in cement production and ${{EF}}_{g}$ represents the carbon emission factor of alternative raw materials in cement production; ${{EF}}_{t}$ represents the carbon emission factor for unit-distance road freight transportation; k-rc represents the symbiotic measures that reduce the clinker-to-cement ratio; k-af represents the symbiotic measures that co-consume waste as alternative fuels in cement production; and k-arm represents the symbiotic measures that co-consume waste as alternative raw materials in clinker production.

Air pollutants mitigation effects:

$${{TAPM}}_{p}=\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{j}\mathop{\sum }\limits_{k}{x}_{i,j,k}\times \left(DE{P}_{k-ref,p}-DE{P}_{k,p}\right)+\left({E}_{k-ref,f}-{E}_{k,f}\right)\times {{EG}}_{p}+\left(\mathop{\sum }\limits_{f\ne elec}{(E}_{k-ref,f}-{E}_{k,f}\right)\times {{EP}}_{p}\times (1-{\theta }_{p})+\mathop{\sum }\limits_{f}\left({(M}_{k-{ref},l}-{M}_{k,l}\right)\times {\lambda }_{l,p}-{d}_{i,j}\times {UEC}\times {\zeta }_{{gas}}\times {{EI}}_{{gas},p}))$$

(5)

The notation p denotes the type of air pollution; $\left({{DEP}}_{k-{ref},p}-{{DEP}}_{k,p}\right)$ is the direct emission reduction from waste reutilization; ${{EG}}_{p}$ and ${{EP}}_{p}$ indicate the p-type emission coefficient in electricity generation and fossil fuel combustion, respectively; ${\theta }_{p}$ is the end-of-pipe reduction rate of p-type emission; ${\lambda }_{l,p}$ means the p-type emission coefficient of raw materials in production; and ${{EI}}_{{gas},p}$ is the p-type emission coefficient from diesel combustion.

Health impacts:

Combining the intake fractions (Table S11) and pollutants’ concentration-response coefficients (Table S12), we calculate the annual health benefits for residents resulting from air pollutants mitigation. This study primarily considers death, respiratory, cardiovascular, asthma, and bronchitis caused by PM, as well as the top four types of the above-mentioned diseases caused by SO₂ and NOx.

$${{THE}}_{h,p}=\frac{T{{APM}}_{p}\times {q}_{p}\times {M}_{h,p}\times {f}_{h,p}X{10}^{12}}{365\times B}$$

(6)

The notation ${{THE}}_{h,p}$ represents the avoided h-type disease cases due to the reduction of air pollutant p; ${{TAPM}}_{p}$ represents the emission reduction amount of air pollutant p; ${q}_{p}$ represents the intake fraction of air pollutant p, which is influenced by regional population density; ${M}_{{hp}}$ represents the concentration-response coefficient of h-type disease cases caused by air pollutant p; ${f}_{h,p}$ represents the morbidity and mortality rate of h-type disease cases by air pollutant p; and B is the breathing rate, with a standard value of 20 m³ ∙ d⁻¹.

Economic profits:

$${TEP}=\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{j}\mathop{\sum }\limits_{k}{x}_{i,j,k}\times \left({{{AEB}}_{k}-{ACC}}_{k}-\Delta O\& {M}_{k}-{d}_{i,j}\times {UTC}\right)$$

(7)

$${{ACC}}_{k}={I}_{k}\times \frac{r}{\left(1-{\left(1+r\right)}^{-n}\right)}$$

(8)

The notation TEP indicates the total economic profits of the cross-city symbiosis strategy; ${{AEB}}_{k}$, ${I}_{k}$, $\triangle \mathrm{O\& }{M}_{k}$, and ${{ACC}}_{k}$ denote the annual revenue, initialized investment cost, operating cost, and annual investment cost of the k-type symbiotic measure, respectively; UTC denotes the transport cost per kilometer to transfer one ton of waste; r is the discount rate; and n is the depreciation life.

Designing the optimized cross-city symbiosis strategy

Based on the plant-level spatial distribution data and the quantitative analytical approach outlined in the two above sub-sections, the NSGA-III-fuzzy membership algorithm is further adopted to identify the optimized cross-city symbiosis strategy. Specifically, this algorithm facilitates the transboundary matching of downstream plants with various upstream plants, strategically reallocating solid wastes to achieve optimized environmental and economic outcomes⁴⁹. Based on the plant-level spatial distribution characteristics, each downstream plant is matched with appropriate upstream plants, and the optimized amount of solid waste is redistributed to realize the best decarbonization, health, and economic performances.

Constraints setup

To ensure that the optimization results align with operational realities, this study establishes the following constraints.

Total production and consumption constraints

The total solid wastes co-consumed by a specific downstream plant must equal the total wastes supplied by all matched upstream plants.

$$\sum {x}_{i,j,k}=\sum {C}_{i,j,k}$$

(9)

$$\sum {x}_{i,j,k}=\sum {S}_{i,j}$$

(10)

The notation ${x}_{i,j,k}$ represents the solid waste transferred from upstream plant i to downstream plant j that can be co-consumed by the k-type symbiotic measure; ${C}_{i,j,k}$ denotes the co-production of solid waste by utilizing k-type symbiotic measure at downstream plant j; and ${S}_{i,j}$ denotes the solid waste supplied by upstream plant i to downstream plant j.

Transferred solid waste limitations

The transferred amount of wastes should not exceed the supply limitations in the upstream plant or the co-consumption upper limitations in the downstream plant.

$${0\le x}_{i,j,k}\le \min \left\{{C}_{i,j,k},{S}_{i,j}\right\}$$

(11)

$${C}_{i,j,k}\ge 0$$

(12)

$${S}_{i,j}\ge 0$$

(13)

Supply limitations in the upstream plant

The co-consumed amount of waste should not exceed the waste output of the upstream plant.

$${S}_{i,t}\le {Y}_{i,t}$$

(14)

The notations ${Y}_{i,t}$ and ${S}_{i,t}$ denote the maximum production and total supply of t-type solid waste in the upstream plant i.

Co-consumption limitations in the downstream plants

The co-consumed amount of wastes should not exceed the maximum co-consumption ability of the downstream plant.

$${C}_{j,k}\le {P}_{j}\times {\gamma }_{k}$$

(15)

The notation P_j denotes the total output of downstream plant j, and ${\gamma }_{k}$ denotes the maximum ratio of solid waste that can be mixed in the production process of downstream plant j by k-type symbiotic measure.

Accessibility constraints

The transportation distance of wastes must not exceed the maximum symbiotic radius⁵⁰.

$${\left({d}_{i,j}-{DIS}\right)\times x}_{i,j,k}\le 0$$

(16)

The notation ${d}_{i,j}$ denotes the distance between upstream plant i and downstream plant j, and DIS denotes the maximum radius of symbiosis achievable by k-type symbiotic measure. Excessive transport distances may make waste co-consumption economically unfeasible.

Modified NSGA-III with constraints

Modified NSGA-III with constraints. We introduce a modified version of NSGA-III, incorporating constraints, to solve the many-objective optimization problem of designing a cross-city symbiosis strategy. The optimization variables are the amounts of solid wastes transferred from upstream plants to downstream plants, and the optimization objectives are maximizing CO₂, SO₂, NOx, PM mitigation amount, and maximizing health and economic benefits. Convergence of the algorithm is assessed to ensure the robustness of both the model and the optimization procedure⁵¹ (Fig. S8). The key procedures are outlined below^52,53,54:

STEP 1 Population initialization:

The population size, denoted as N, is defined (Table S13). A total of 160,875 initial decision variables, denoted as V, are randomly generated within the feasible region. They represent genes in a chromosome.

STEP 2 Tournament selection:

(a) Calculate and sum the normalized violation value (transfer inequality constraints into the form of $g(x)\ge 0$, then the normalized violation value of each chromosome is calculated as ${CV}\left(x\right)={\sum }_{i=1}^{J}\left\langle {\text{g}}({\text{x}})\right\rangle$, where $\left\langle a\right\rangle$ = ${|a|}$ if a≤0 and $\left\langle a\right\rangle \,$= 0 otherwise);

(b) Two individuals, p1 and p2, are randomly selected as candidates from the population;

(c) If both p1 and p2 are feasible (CV = 0), then one of these two candidates is randomly selected as the parent individual; if p1 is feasible and p2 is not, then p1 is selected; and if both are infeasible, then the individual with the smaller CV is selected;

(d) Repeat steps (b) and (c) to generate another parent until the parent population size is N.

STEP 3 Offspring generation:

(a) Three types of parameters are defined, which are crossover probability (CP), mutation scale (MS), and probability of mutation (MP); Two parent individuals are selected from the parent population, where V × CP genes (decision variables) crossover each other to produce two offspring individuals;

(b) Repeat (a) until the offspring population size is N;

(c) Randomly select N × MS genes for mutation, where the number of mutation variables is V × MP. (Table S13)

STEP 4 Non-dominated sorting:

(a) Feasible solutions dominate infeasible solutions;

(b) If both solutions are feasible, the following domination principle is applied: if ∀ i, fi(x(1)) ≥ fi(x(2)) and ∃ i, fi(x(1)) > fi(x(2)), then x(1) dominates x(2), where i = 1,2,⋯,M and M denotes the number of objectives;

(c) If both x(1) and x(2) are infeasible, the one with the smaller constraint violation dominates the other solution.

STEP 5 Reference-points-based selection mechanism:

Reference points divide the hyperplane into multiple equal parts, ensuring a more uniform distribution of chromosomes and enhancing solution diversity. This study uses the Normal-Boundary Intersection method to generate H reference points uniformly distributed on the normalized (M-1)-dimensional hyperplane⁵⁵. $H={C}_{M+p-1}^{p}$, where M is the number of objectives and p is the number of divided parts.

Select the optimized solution with a fuzzy membership function

We employ a fuzzy membership function to identify the optimized cross-city symbiosis strategy from the Pareto-optimized solutions^56,57. The maximum and minimum values of the ${m}^{{th}}$ objective function are denoted by ${f}_{m,\max }$ and ${f}_{m,\min }$, respectively. The satisfaction level of the ${n}^{{th}}$ non-dominated solution is defined as ${\gamma }_{n,m}$, where M is the number of objectives, and Z is the number of Pareto solutions. The formula is as follows:

$${\gamma }_{n,m}=\left\{\begin{array}{l}1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{f}_{n,m}\le {f}_{m,\min }\\ \frac{{f}_{m,\max }-{f}_{n,m}}{{f}_{m,\max }-{f}_{m,\min }},\,\,\,\,\,\,\,{f}_{m,\min } < {f}_{n,m}\le {f}_{m,\max }\\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{f}_{n,m}\ge {f}_{m,\max }\end{array}\right.$$

(17)

Normalize the satisfaction value ${\gamma }_{n,m}$:

$${v}_{n}=\frac{{\sum }_{m=1}^{M}{\gamma }_{n,m}}{{\sum }_{n=1}^{Z}{\sum }_{m=1}^{M}{\gamma }_{n,m}}$$

(18)