Low power, non-intrusive 3D localization for underwater mobile robots

Abstract

Autonomous Underwater Vehicles (AUVs) face persistent challenges in localization compared to their counterparts on the ground due to limitations with methods like Global Positioning System (GPS). We propose a novel system for localization, Pisces, that leverages the Angle of Arrival (AoA) and Received Signal Strength Ratio (RSSR) of robot-mounted blue LED signals. This method provides a spectrally efficient training-free solution for estimating 3D underwater positions. The system remains effective despite high water turbidity with a relatively low impact on marine life compared to similar acoustic methods. Pisces is less complex, computationally efficient, and uses less power than camera-based solutions. Pisces enables robust relative localization, especially in swarms of robots with the potential for additional applications like docking. We demonstrate high localization accuracy with a Mean Absolute Error (MAE) of 0.031 m at 0.32 m separation and 0.16 m MAE at 1 m separation. Moreover, it achieved this with minimal power consumption, utilizing only 11 mA of transmitter LED current and performing 3D localization within 10 ms for distances up to 3 m.

Introduction

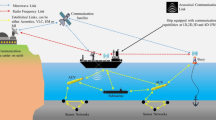
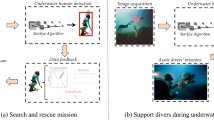
Autonomous underwater vehicles (AUVs) and robots have broad applicability in aquatic environments for various applications ranging from 3D mapping of the underwater environment¹, detection of seabed mines² to inspection and monitoring of ports³. Such applications benefit from having cost-effective and autonomous swarms of AUVs that can carry out such tasks and communicate the information back to the surface. Since the coverage area is large in such applications, swarms of such robots are required. To this end, good localization between these underwater robots is needed to build and maintain swarms. Such underwater mobile robots must both relatively localize other robots and have spatial awareness of their surroundings. In particular, they might need to locate the position of ships or fixed infrastructure, including harbors. This can be useful for docking applications⁴. Robots with such an ability can enable implicit coordination, swarming behaviors, and highly efficient control⁵. Collaborative AUV missions can indeed propel such applications. However, they require a method for fast intra-swarm localization⁶.

Underwater localization: the underwater environment is challenging compared to traditional on-ground localization. This is due to the higher absorption and scattering properties of water compared to the air⁷. This renders radio frequency-based localization systems practically unusable inside the water⁸. Acoustics are a viable alternative because of their low absorption rate, especially for underwater and long-distance communication (in kilometres range). However, they perform poorly in shallow waters due to acoustic reflections from the surface and bottom⁹. OFDM-based acoustic links can also contain large impulsive noise¹⁰. Additionally, acoustic links have been reported to affect marine life and can be pretty intrusive to such ecosystems, which is a critical consideration¹¹. Acoustics are relatively expensive when used in short-range mobile robots¹².

On the other hand, optical signals in the fluorescent light spectrum have a larger bandwidth for ranges up to 10 m than radio or acoustic signals. This, however, differs in different waters, with 450 nm being the least attenuated in the open ocean, which shifts to 540 nm for more turbid waters¹³. Visible light systems have been demonstrated to work in underwater communication. Still, they experience signal multi-path, especially near the sea bed or surface¹⁴ and are subject to the water’s visibility and turbidity¹⁵.

Challenges and Requirements: underwater mobile robots must operate in challenging environments that impose certain system limitations on their localization methodology. Such robots, especially untethered ones, have a strict power budget due to limited onboard batteries. Thus, conserving battery life is of great importance. Another consideration is that such systems are often compact and have resource constraints regarding space and computing. As many small-scale, agile, and mobile underwater robots are typically under 1 m in length, we need a system that can localize these robots well within a few meters. This should be possible despite different water turbidity and visibility conditions. Most importantly, the effects of the system on marine life should also be considered, as acoustic signals can potentially harm marine interactions. At the same time, optical and RF do not have any known adverse effects¹⁶.

The key requirements of such a localization system for AUVs are: ① the system should consume as little energy as possible; ② be compact and space efficient while enabling onboard robot-robot coordination; ③ must localize other robots when swimming together as a group inside water in three dimensions; ④ only rely on the constrained resources found in AUVs of small scales, thus limiting processing overhead, energy consumption, and additional weight; and, importantly ⑤, the system should work with different water turbidity or ambient light conditions without requiring extensive and time-consuming re-calibration. These requirements allow for a more widespread usage of Pisces.

Pisces System: we build a 3D localization system that uses two blue 455 nm LEDs that act as transmitters and a tri-photodiode (PD) array oriented in a specially designed tetrahedral structure acting as a receiver on each AUV. An advantage of using an optical system is reduced power consumption at smaller distances due to the availability of efficient and compact optical devices¹⁷. Pisces can be described by exemplifying two key components below.

LED-based implicit localization: we place two blue LEDs (blue wavelength shows least attenuation underwater¹³) vertically on the AUVs, such as a robotic fish in our case. By fixing the vertical separation of the LEDs (spatial gain or spatial diversity) we calculate the angle each LED makes at the receiver. Using this information, we can then estimate the robot’s 3D location. We find these angles using the Received Signal Strength Ratio (RSSR) parameter and our theoretical model, which eliminates the need for extensive calibration or training. This way, we tackle the challenging underwater environments with different characteristics, making the same system work in waters with different scatter and absorption rates and turbidity. The two vertical LEDs are placed on the tail of each AUV and act as transmitters.

Photodiode-based sensing: instead of relying on cameras to deduce the location of the LEDs like other works in the literature¹⁸, we use a three-photodiode array that is mounted in a specifically designed structure that places each diode at a fixed angle. This method consumes far less energy, and we can infer the location an order of magnitude faster while being less complex¹⁹. High-speed sensing also allows us to encode data effectively using the LEDs as optical transmitters communicate through this light channel along with localization if required. Even though it is possible, demonstrating joint communication and localization is beyond the scope of this work. Our system requires the two robots (one with LED transmitters and the other with PD receiver) to maintain a direct Line Of Sight (LOS) between them. This LOS is not expected to break often for underwater robotic swarms.

In this paper, we provide:

• ❶ Theoretical modeling of the optical channel between an LED and PD, including the effect of the receiver’s physics and the channel’s length, i.e., the distances between the transmitter and receiver, which supports quick localization (illustrated in section “Methods”).

• ❷ A novel localization system design that aims to provide a low power, low complexity localization method for underwater robots with a provision for combining communication and localization using a training and calibration free learning algorithm (discussed in section “Design of Pisces”);

• ❸ Experimental dataset building upon the first two contributions, we provide an extensive characterization of the localization system (described in section “Results”), along with a discussion of adapting it for different types of underwater conditions (given in section “Discussion”). We will make the datasets open source to aid in future research.

Pisces can localize objects within 10 ms at high confidence levels with a mean absolute error of 0.032 m at 0.32 m and 0.16 m error at a distance of 1 m separation using only 11 mA LED current. The system is implemented for the open-source bio-inspired fish robot OpenFish²⁰, augmenting it with localization to enable swarming behavior. However, without loss of generality Pisces finds applicability in a wide range of AUVs.

Background and Motivation

Although there are significant prior works on underwater communication and messaging using both acoustic^21,22 and optical modalities^23,24, we focus primarily on underwater localization.

Underwater 3D localization: great interest exists in tracking static sensors and mobile robots underwater^25,26,27. Acoustic pressure waves from floating buoys that act as anchors are used to estimate location using time of arrival²⁸, time difference of arrival²⁹, angle of arrival³⁰ or received signal strength³¹. These leverage acoustic pulse waves to perform ultra short baseline³² and long baseline positioning³³. Such methods require a bouy or a surface vessel to localize in 3D an underwater mobile robot. These methods can estimate both distances and angles. Still, they cannot be used ad-hoc and are often power-hungry and large-sized, which limits their deployability, especially for resource-constrained mobile robots³³.

Tracking underwater mobile targets: different anchor-based methods to create an underwater GPS have been explored for tracking small mobile targets inside water. Some methods use hydrophone beaconing devices on the water surface to communicate and locate underwater divers^34,35. In contrast, another uses the divers’ smart watches for relative localization by combining acoustic signals with pairwise equation solving³⁶. Another work that proposes using an underwater pinging device requires a high-precision GPS synchronized clock³⁷. Surface buoys have also been augmented with GPS to track inside water³⁸.

Position estimation based on time of arrival measurements is in²⁸ and using specialized directional beacons in³⁹. These are unsuitable for low-power, small-sized robots and often require a separate communication system. A recent approach involves using a transponder that sends an underwater acoustic signal and reads the signal reflected back by the batteryless sensor node using backscatter communication (similar to RFID). While promising, this system has been shown to only work for 1-dimensional positioning⁴⁰.

Visible light localization: researchers have found that sound-based acoustic positioning systems can have a detrimental and hazardous impact on marine and amphibious life^41,42. Acoustic localization is inadequate, especially in the purview of the safety of small robot swarms, which requires higher accuracy and update rates⁴³. Moreover, the high bandwidth communication that underwater visible light-based systems can offer makes them attractive alternatives⁴⁴. Some visible light-based localization methods are focused on underwater docking applications. They use active light markers placed on static infrastructure for close-range localization^45,46. These methods rely on a camera to locate the position of LEDs. They do not need to estimate the orientation of the mobile robots and have no requirement for their identification⁴⁷.

We know from the vast body of literature that complex 3D swarming behavior in nature stems from making visual observations of nearby neighbors without any explicit communication⁵. A well-established underwater visible light localization approach is, thus, to use cameras with LEDs or lasers acting as active markers^48,49. Such systems can track multiple simultaneous robots with high accuracy and speed at short distances⁴³. Moreover, such computer vision systems are power-hungry and offer extremely slow tracking refresh rates in the order of a few Hz.

Different indoor methods have used different physical parameters to extract localization information from LED light signals and multi-directional PDs^50,51,52. In particular, PD-based indoor visible light communication systems use RSS for 3D localization⁵³ and have not been explored for underwater localization. A qualitative comparison with other underwater visible light-based methods from literature is summarized in Table 1. Our system provides a method of implementing 3D localization utilizing an array of multi-directional photodiodes to localize underwater robots while agnostic to the water visibility conditions.

Table 1 Comparison of underwater visual mobile robot localization methods from the literature

Results

Design of pisces

Underwater mobile robotic fishes

The underwater mobile robot used in this work is based on the open-source soft robotic fish - OpenFish design²⁰. This bio-inspired robot is specially optimized for higher speed and efficiency. It features a DC motor that drives a soft tail segment accurately mimicking the Thunniform swimming mode of real fish, which is rapid swimming with a large, powerful crescent-shaped tail⁵⁴. Such robotic fishes are more advantageous than rotor-based AUVs as they do not create disturbing vibrations in the water, do not suck in objects or wildlife into the propeller, and provide more efficient propulsion in battery-powered mobile vehicles⁵⁵. OpenFish’s higher speed and small size make it an ideal system benefiting from the features of our localization method. The Pisces mounted on the OpenFish is depicted in Fig. 1.

Fig. 1: Application setting: Multiple robotic fishes using the Pisces localization system with transmitters on the tail and a receiver structure in the front.

Our system applied to the open source OpenFish soft robotic fish to augment it with localization capability. Pisces can be applied to any fin or rotor-based Autonomous Underwater Vehicle (AUV).

Each of the two LEDs communicates with the receiver on the nearby fish using a different ON-OFF frequency. The receiver uses this information to tell the two LEDs apart. Using the light intensity received by each photodiode in the array (method described in Section “Angle Estimation Using Multiple PDs”), the receiver can tell which direction each LED is in. Combining the directions of two LED beacons that correspond to the same AUV with a known length of the tail (or vertical separation of the LEDs), the receiver can calculate the position of the target AUV in 3D.

Transmitter design

Two mono-color LEDs are used for the transmitters, with a half-intensity beam width of 125 degrees⁵⁶. This is the angle at which the light emitted by the LED is 50% or higher than its maximum intensity. Its blue light has a wavelength of 455 nm, chosen for its high propagation through the water compared to other colors in clear water¹³. The transmitters are placed 190 mm vertically apart in the setup – the same distance as the length of the OpenFish tail. Placing the two LEDs apart makes it possible to triangulate the distance towards the tail if the direction towards both LEDs is known, as explained in the section “Distance & 3D Position Estimation”. Due to the mechanics of the OpenFish, the tail is always expected to be vertical and never skewed in any direction. The LEDs are placed on the OpenFish’s tail at the robot’s rear end. This ensures that the maximum light intensity is received by any follower robots located behind the transmitting leader robot. A forward current of 5.5 mA is chosen, which clips the signal at the receiver PDs only at distances of 10 mm or closer when no ambient light is present, which is not expected. The variation in the illuminance for the chosen LED with distance when measured in the air is shown in Fig. 2c. The LED was transmitted with a 50% ON-OFF keying cycle and measured using a Uni-T’s UT383 light meter. Different forward currents can be chosen to increase the Lumens at the transmitting robot.

Fig. 2: Localization system design for Pisces.

a Schematic for the blue LED transmitter circuit driven by a microcontroller unit (MCU)-generated Pulse Width Modulated(PWM) signal and a Bipolar Junction Transistor (BJT). b Schematic for the receiver configuration for a single photodiode. c Variation of Illuminance with the distance of one transmitter 455 nm ceramic water-clear LED. d The fabricated receiver structure with one glass filter removed and the waterproofed OPT101 photodiode.

Different frequencies up to 1.8 kHz can be used to perform ON-OFF Keying of the LED using the microcontroller’s PWM output. The ON-OFF keying (or flashing) frequencies chosen for the two transmitter LEDs in each robot must differ by at least 50 Hz for them to be distinguished at the receiver robot. This limit is imposed due to the photodiode circuit described in section “Design of Receiver for Localization”. The different frequencies help distinguish each LED uniquely and thus are used to deduce the locations of the individual LEDs faster. Each robot fish uses LEDs to communicate its uniquely assigned beacon through the ON-OFF Keying method. More details about this process can be found in Supplementary Fig. 1. The driving circuit for the LED is shown in Fig. 2a.

Design of receiver for localization

The receiver uses a novel tetrahedral-like 3-photodiode structure with each photodiode bent inside. This is depicted in Fig. 2d. This structure uses the difference in the PDs’ angles to deduce the LEDs’ individual locations, as explained in section, “Methods”. Using the Received Signal Strength Ratio (RSSR) between each PD pair creates robustness to the medium that the light travels through⁵³. The ideal ratio stays the same irrespective of the scatter and absorption rate of the medium, the only difference being in the noise level that is present when the signal is weaker. Varying the tilt between the PDs creates a trade-off between the FOV and the accuracy. A tilt of 35° from the normal vector of the receiver was chosen for each PD. This results in the angle difference of 60° between the projections of the normal to each PD on the transversal plane (i.e., orthogonal to the normal vector of the receiver) (the theory behind this design and its implications are described in detail in Section “Methods”). This choice gives us a FOV of around 60° at 0.15 m and 95° horizontally at  >1 m. The reasons for this design choice are explained in the section “Characterizing A Tri-Photodiode Receiver”. An optical blue glass filter is placed in front of the diode to attenuate all other wavelengths of light and prevent full PD saturation when the fish is closer to the surface or another light source.

The OPT101, a monolithic photodiode with an on-chip trans-impedance amplifier with linear light intensity to output voltage response, is used⁵⁷. A 10x amplification configuration is used as shown in Fig. 2b. The LED cannot fully saturate the PD in this configuration, but its bandwidth is capped at 1.8 kHz. This configuration does improve the captured signal’s SNR since the PD’s responsiveness increases linearly with the resistance and the noise with the square root of the resistance. The output from the three PDs is analog and needs to be sampled by a microcontroller’s Analog-to-Digital Converter (ADC). We use a Teensy 3.2 microcontroller to sample the output at 40 kHz. The Goertzel FFT algorithm is applied to scan for the specific frequencies tied to each LED using bins of 400 samples. This caps the maximum speed of localization at 40000/400 = 100 Hz⁵⁸. The Goertzel algorithm has been chosen due to its lower computing complexity than full FFT algorithms since we are interested in only a portion of all frequencies. The resulting power components of these frequencies are then fed to the localization algorithm. The working methodology is explained in the section “Distance & 3D Position Estimation”.

With the use of Algorithm 1, the relative 3D location of the other AUVs can be deduced as long as there is LOS between them. The farther the LEDs are, the lower the SNR; this will translate to a more significant error and the need for averaging. With the current configuration of 1.8 kHz bandwidth at the PD, Pisces can allow communication of additional data at this rate from each transmitter LED.

Controlled experiments

A controlled test rig was created to test the performance of Pisces. This setup (shown in Fig. 3a) will offer repeatable experiments in different water conditions for different distances and angles for comparison and statistically valid measurements. The setup allows for exact measurements at different yaw and vertical offsets in a controlled manner. The stepper above the receiver rotates the aluminium rod around its axis to create a specific yaw offset. The stepper above the fishtail trolleys it up or down, from which the desired vertical offset can be obtained. This is defined as the angle between the axis of the two fishes On the fishtail, two LEDs are connected, one at the top and one at the bottom, facing the receiver (Fig. 2d). The steppers are mounted on a wooden plank and can be moved to the needed positions to measure at different distances. More details about the experimental setup can be found in Supplementary Fig. 2. The receiver was submerged at a depth of 0.25 m below the water’s surface.

Fig. 3: Experimental setup and test conditions.

a controlled test rig used to vary vertical offset, yaw, and distance between the receiver (green) and the transmitter (blue) and (b) the 3 m wide indoor pool used for data collection and evaluation. The measured water turbidity of various sources is also contrasted with the test setup.

The PD signals from the top and bottom LEDs are captured at different yaws, vertical offsets, and horizontal distances between the rod of the receiver and the fishtail. The blue LEDs on the transmitter communicate their ID using the beacon frequencies they have been assigned. This is controlled by an Arduino Atmega 2560 with an independent battery supply. For the results shown in section “Effect of Multipath and Noise”, a sweep was done at the distances (in m) 0.32, 0.34, 0.39, 0.59, 0.64, 0.87, 1.0, 1.50, 2.20, and 3.0. Due to the nature of the setup, limited elevation angles can be recorded at larger distances. This is also expected in the fish swarm scenario, where the vertical separation between fishes will not be substantial. The underwater measurements were carried out in a circular pool of 3 m diameter. The submerged setup is shown in Fig. 3b to highlight the high water turbidity used during testing, comparable to real-life deployment scenarios.

Effect of multipath and noise

A sweep according to the procedure explained in the section “Controlled Experiments” was done for different distances in water. The received power for the distance of 0.32 m for the diode B is shown in Fig. 4a. Here, a vertical smear can be seen that is caused by signal multipath. To test the validity of Algorithm 1, the overhanging test rig is placed in different locations within the pool, which enables testing under different scenarios with the multipath effect. The plot showing the variation of the received power by taking a combination of photodiodes is shown in Fig. 4b and c for robot-robot distances of 0.32 and 0.64 m respectively. These plots are obtained by subtracting the different PD RSSR found using Eq. (5). The resultant values from each PD pair are then mapped on top of each other in the same plot for each distance. Measurements were repeated with and without overhead lighting. Measurements in the presence of ambient light showed that it did not factor into the localization results. Besides the effects of multipath highlighted in yellow in Fig. 4b, the apparent effect of reflective noise can also be seen as dots at the edges of the plots.

Fig. 4: Received light power plots in Pisces.

a Received power in dB at diode B when the bottom LED is at 0.32 m distance, and Received Signal Strength Ratio (RSSR) plot for each diode pair when placed (b) 0.32 m and (c) 0.64 m away from the receiver.

Localization performance

Before we detail the measurements and localization error calculations, we explain the Illumination Index (Γ).

Illumination Index (Γ). The illumination index indicates when the light from the LEDs located at the fishtail is received the strongest; thus, the receiver is fixed as close to the fishtail. This confidence level follows a logarithmic relationship to the received power, as seen in Eq. (12). The exponential decay of Γ becomes linear in water. Based on the measurements, we model the linear equation Γ = −0.000039d + 1, with Γ as the illumination index and d as the distance in meters. This equation has been fitted to intersect (0, 1) by adapting the ${P}_{\max \Gamma }$ value from Eq. (12). According to the curve-fit, the coefficient of determination (R²) is 0.9976.

The positioning error was calculated to determine the performance. This is the Euclidean distance offset between the actual position of the bottom LED (on the fishtail) and the position estimated by the localization algorithm. This positioning error is categorized using an ‘Illumination Index (denoted by Γ)’ metric (explained in Section 5.5) when all the received power values are evaluated using the localization algorithm. The result for one of the distances can be seen in Fig. 5a. Note that in these graphs, the maximum error scale has been capped at 0.30 m, but some errors did reach a value up to 2.5 m. These errors, however, were observed in the region where the Illumination Index is very low, as seen in Fig. 5b. Combining this, all measured inputs are considered to estimate the final position – either used or discarded based on the value of Γ corresponding to the confidence of the produced localization output. The Γ correlates very well with detecting robots when present within the FOV of the receiver. But even when the value of Γ is high, indicating a high confidence level, some error can still be seen in Fig. 5b. This is partly due to the multipath effect but can also be attributed to the inaccuracies of the diode layout structure and its gain profile. The MAE for angle and distance estimation across all distances shows that we can operate up to 3.0 m (Fig. 5c, d). Combining the Γ and the positioning error, CDF plots are made for three different distances (Fig. 6). Here, Γ can clearly distinguish performance, especially when it drops below 0.55. The measurements were also averaged for longer distances (like ≥1 m). This was beneficial as the received signals have a lower SNR at these distances. This is shown in Fig. 6d, where the measurements were taken ten times and averaged before using the localization algorithm. Using the Γ, the measurements can estimate the position of the fishtail with a Mean Absolute Error (MAE) of 0.031 m for the 0.32 m distance and 0.39 m for the 1 m distance. This goes down to 0.16 m for the average over ten measurements. The instantaneous positioning can be further improved by averaging over time at the cost of increased latency.

Fig. 5: Localization error plots.

a Positioning error and (b) Confidence of estimated positions for a transmitter-receiver distance of 0.32 m. The Mean Absolute Error (MAE) for (c) angle estimation and (d) distance estimation across various measured robot-robot distances.

Fig. 6: Positioning error plots across multiple experimental conditions.

Cumulative Distribution Function (CDF) plot of positioning error categorized by the illumination index (Γ) at (a) 0.32 m and (b) 0.64 m and at (c) 1 m (after averaging), (d) 1 m (without averaging).

Power consumption

The current consumption was measured for the transmitted (LED), receiver (PD), and Teensy MCU. Further, a Raspberry pi 4B-based camera system (similar to that in ref. ⁵) was also constructed to compare power consumption (summarized in Table 2). Pisces’ total power consumption is 237 mW per AUV, which is 10x lower than the state-of-the-art camera-based approach. The LEDs can be driven with much higher currents to increase the range and keep Pisces’s power consumption much lower than that of camera-based solutions. This shows another merit of using Pisces for AUVs.

Table 2 Power consumption of Pisces and comparison with a camera based approach

Discussion

We discuss the results, the applicability of Pisces and the vistas for possible improvements.

Environments. The OPT101 diode used in Pisces was measured outside water first to characterize its fabrication parameters and incorporate them into the theoretical model. The estimated positioning accuracy in turbid water was sufficiently high to be used in a feedback control loop with a Kalman filter to enable swarming behaviors. Pisces can be used in waters with different values of scattering and absorption rates by using only the signal strength and without any additional calibration or drop in accuracy. If the fish is used in even more turbid waters, the LED output intensity can be tuned to increase the received strength at the diodes. This will effectively increase the c constant in Eq. (13), creating a larger range where the receiver can follow the transmitting fish when pointed towards it. The blue glass optical filters ensure that the diodes are not saturated by ambient light.

Applicability. Pisces can be used in all robots that need inexpensive or high-speed short-range tracking within LOS for swarm behavior. The absence of audio frequencies makes it possible to observe marine life without affecting them with acoustic interference. By using these high-frequency light signals, communication can also be combined with localization. This way, the AUVs can also be used as high-speed communication links with a base station on shore. The most important feature is that no training or calibration is needed for different mediums immune to water turbidity and working in clear and dirty waters as well. If the expected medium is predominantly muddier, the blue LEDs can be swapped for green ones, which have less absorption for more shallow surfaces with highly turbid waters. The only aspects that will require change are the optical filter and the transmitting LEDs.

Enabling Communication. Currently, Pisces extracts the power spectrum density to know which LED beacon is received. This can directly work with On-Off-Keying (OOK), where the power component of that frequency would be affected in all PDs, keeping the RSSR the same. However, this means that every LED would need a different frequency with a frequency gap of 50 Hz as explained in the section “Design of Receiver for Localization”. A higher spectral efficiency can be achieved using OFDM. A guard interval could be added to counter inter-symbol interference (ISI) caused by the multipath effect.

Moreover, OPT101 can be configured to have higher bandwidth at the cost of increased noise. This would enable the LED frequencies to be driven up to 58 kHz to achieve double the data rate (since every AUV will have two transmitting LEDs). However, the sampling rate needs to be adjusted appropriately to prevent aliasing.

Improving Accuracy and FoV. To further improve accuracy, a flat, 2D gain profile for each diode can be added that accounts for minor variations in the diodes that arise from each diode’s manufacturing process and can affect their response to light rays hitting the die at varying angles. These rays have different scattering and refraction within the rectangular package. More details about the variation of the error bias can be found in Supplementary Fig. 3. A higher LED intensity would also increase the SNR. In that case, the feedback loop gain should be adjusted, or a higher voltage range should be given to the OPT101 to prevent full saturation at close distances. A higher-quality optical glass filter can reduce power loss for the blue wavelength if ambient light saturation is to be expected. Multiple receiver structures can be added on either side of the AUV, each behaving as an “eye” to increase the robot’s FoV.

Conclusion

We presented Pisces, our solution to underwater localization for swarms of small resource-constrained AUVs. Pisces can be mounted easily on robotic fish or other AUVs. We presented a thorough design of Pisces wherein two LEDs mounted with known separation are used to measure the relative intensity to find the robot’s underwater 3D position. We provided a detailed theoretical basis for Pieces, including a lightweight, low-computational complexity, and low-power localization algorithm that does not require calibration for different water turbidity. We evaluated extensively using a test rig to repeat the experiments and the conditions to get statistically stable measurements in waters with high turbidity at different distances. We get 0.032 m best case 3D localization error within 10 ms while consuming current around 11 mA. Compared to a camera-based solution, this is  ≈ 12x lower in power consumption and 10x faster. Using spatial diversity, Pisces works without training or extensive calibration for different application scenarios.

Methods

We explain the theoretical background of our work here and build the foundation that guides us in our design choices for the Pisces localization system. We model the optical channel between an LED light source and a Photo Diode (PD) receiver by simulating the physics of light propagation. This enables us to create a database of RSSR values between the different PDs for a given LED distance and orientation. This can be used to contrast and compare the experimentally measured received power. Such a database can thus be used to deduce the relative direction of the transmitting LED.

Modelling visible light links

Pisces requires two blue 455 nm LEDs that constitute the transmitter to be placed on every underwater robot’s rear. If using a robotic fish-styled AUV, this would be placing one on each end of the tail. Additionally, a three-photodiode receiver structure is placed in front of the body of the AUV. All coordinates are referenced to the centre point of the photodiode receiver structure, with each PD having its own optical filter. The possible blue LED locations and the three photodiode vectors are depicted in Fig. 7c for a 3.0 m horizontal distance. For a known distance, by calculating the orientation angle of the pair of LEDs, we can find the relative 3D position of the transmitter.

Fig. 7: Pisces photodiode array receiver design and modelling.

a The side and top views show vertical and yaw offsets of an underwater fish robot with respect to a distant observer. Clockwise yaw is considered as positive. b Pisces receiver structure with a 35^∘ angle between each Photo Diode’s (PD) normal vectors (green, blue, red) and the fish axis, i.e., normal to the receiver (yellow). c The coordinate system is modelled with LEDs at a horizontal distance of 3 m. d Received Signal Strength Ratio (RSSR) for a pair of photodiodes with varying angle differences between them in 2D space (Eq. (5)).

The model is derived using the PDs properties, their position, and the channel length, i.e., the distance between the transmitter and receiver. The received power of a blue LED on LOS at each PD is,

$${P}_{{{{\rm{r}}}},i,j}=C{G}_{{{{\rm{r}}}}}({\theta }_{i,j}){G}_{{{{\rm{t}}}}}({\lambda }_{i,j})\frac{{P}_{{{{\rm{t}}}},j}}{4\pi {({d}_{{{{\rm{i}}}},{{{\rm{j}}}}})}^{2}}.$$

(1)

Here, each PD is denoted with i( ∀ i ∈ {A, B, C}), and each LED with j( ∀ j ∈ {1, 2, . . . , N}) for an even number of N. Every fishtail will have two LEDs, as explained in the section “Transmitter Design”. For this, we denote f( ∀ f ∈ {1, 2, . . . , N/2}), where each f would have a f_t and f_b to indicate the top and bottom LED respectively. P_r,i,j stands for the received light power at the PD with index i coming from the LED with index j. C is a constant factor of attenuation of the glass filter, assumed to be the same for all PDs. G_r is the gain at the diode dependent on angle θ. θ_i,j is the angle of the light ray coming from the j^th LED at the i^th PD, compared to the normal vector of the PD i. G_t is the gain factor of the LED transmitter. G_t depends on λ_i,j which is the angle that the light ray coming from j^th LED at i^th PD has compared to the normal vector of that j^th LED. P_t,j is the transmitted power by LED j. The last variable, d_i,j, is the distance between PD i and LED j. It is important to note that these gains also depend on the wavelength of the transmitted light. However, we only consider blue 455 nm wavelength light, which attenuates least in water, and, thus, have not included that factor in these equations.

Characterizing A Tri-Photodiode receiver

For the PDs, the angle over which the light is coming from, with respect to the length or width of the die, has a different response due to diffraction and scattering in the package⁵⁷. In practice, this difference was negligible when measuring over both angles. The response was measured in air and modelled using a third-order polynomial fit. This step is done only once.

To calculate angle θ_i,j, the vector r_i,j between the LED j and PD i is calculated with,

$${{{{\bf{r}}}}}_{i,j}={{{{\bf{v}}}}}_{j}-{{{{\bf{v}}}}}_{i}.$$

(2)

where:

$$\begin{array}{rcl}{{{{\bf{r}}}}}_{i,j}&=&\quad\quad\left[\begin{array}{c}{{{{\bf{r}}}}}_{i,j,x}\\ {{{{\bf{r}}}}}_{i,j,y}\\ {{{{\bf{r}}}}}_{i,j,z}\end{array}\right]\,\,{{{\rm{is}}}}\, {{{\rm{the}}}}\, {{{\rm{vector}}}}\, {{{\rm{from}}}}\, {{{\rm{the}}}}\, {{{\rm{LED}}}}\,\,j\,\,{{{\rm{towards}}}}\, {{{\rm{PD}}}}\,\,i,\\ {{{{\bf{v}}}}}_{j}&=&\;\;\left[\begin{array}{c}{{{{\bf{v}}}}}_{j,x}\\ {{{{\bf{v}}}}}_{j,y}\\ {{{{\bf{v}}}}}_{j,z}\end{array}\right]\,\,{{{\rm{is}}}}\, {{{\rm{the}}}}\, {{{\rm{vector}}}}\, {{{\rm{from}}}}\, {{{\rm{origin}}}}\, {{{\rm{towards}}}}\, {{{\rm{LED}}}}\,\,j,\\ {{{{\bf{v}}}}}_{i}&=&\left[\begin{array}{c}{{{{\bf{v}}}}}_{i,x}\\ {{{{\bf{v}}}}}_{i,y}\\ {{{{\bf{v}}}}}_{i,z}\end{array}\right]\,\,{{{\rm{is}}}}\, {{{\rm{the}}}}\, {{{\rm{vector}}}}\, {{{\rm{from}}}}\, {{{\rm{origin}}}}\, {{{\rm{towards}}}}\, {{{\rm{PD}}}}\,\,i.\end{array}$$

The resulting vector is then used to calculate the angle between the light ray falling in PD i and the direction the PD faces,

$${\theta }_{i,j}=\arccos \left(\frac{{{{{\bf{d}}}}}_{i}\cdot {{{{\bf{r}}}}}_{i,j}}{\parallel {{{{\bf{r}}}}}_{i,j}\parallel }\right).$$

(3)

Here, d_i is the unit vector in the direction that the PD is facing. Finally, for the d_ij element of Eq. (1), ∥r_i,j∥ is used.

Angle estimation using multiple PDs

We take the ratio of the received powers between two PDs for the same LED. This is then converted to a logarithmic scale. We represent RSSR with RSSR_AB,j for the ratio between two PDs PD_A and PD_B for LED j. For all PD combinations, we can see,

$$RSS{R}_{i,k,j} =\log ({P}_{{{{\rm{r}}}},i,j})-\log ({P}_{{{{\rm{r}}}},k,j})\\ =\log \left(\frac{{G}_{{{{\rm{r}}}}}({\theta }_{i,j})}{{G}_{{{{\rm{r}}}}}({\theta }_{k,j})}\right)+\log \left(\frac{{G}_{{{{\rm{t}}}}}({\lambda }_{i,j})}{{G}_{{{{\rm{t}}}}}({\lambda }_{k,j})}\right)+\log \left(\frac{{d}_{i,j}^{2}}{{d}_{k,j}^{2}}\right),\\ \;\;\forall (i,k)\in \{(A,B),(A,C),(B,C)\}$$

(4)

The small separation between each PD allows us to approximate λ_i,j to be equal to λ_k,j signifying the equivalent light path from different LEDs to a photodiode (PD). Moreover, d_k,j can be approximated to be equal to d_i,j since the difference in distances between the PDs is negligible compared to the total distance to the LED. This reduces Eq. (4) as,

$$RSS{R}_{i,k,j}=\log ({P}_{{{{\rm{r}}}},i,j})-\log ({P}_{{{{\rm{r}}}},k,j})=\log \left(\frac{{G}_{{{{\rm{r}}}}}({\theta }_{i,j})}{{G}_{{{{\rm{r}}}}}({\theta }_{k,j})}\right).$$

(5)

The way the PDs are oriented in the receiver is critical. By changing the angle difference between the PDs with respect to each other, we can change the response derived from Eq. (5). This is demonstrated in Fig. 7d for a 2D space by changing the tilt of the PD. By adjusting this relative orientation of the PDs, we can affect the total Field Of View (FOV) that the receiver captures. The FOV seen in the Fig. 7d can be approximated as,

$$\,{\mbox{FOV}}\,=18{0}^{\circ }-\arccos \left({{{{\bf{d}}}}}_{i}\cdot {{{{\bf{d}}}}}_{k}\right),\,$$

(6)

where the $\arccos$ term is the angle difference of the direction vectors between a PD pair. For the three PDs, the usable part between the three PD pairs will be only the overlapping part between the FOV of each pair, resulting in a smaller FOV. Moreover, the FOV will be smaller when the PDs are separated from each other in cases where the light source is relatively close by.

This highlights an important trade-off between having a larger FOV or a higher gradient in the received power of the transmitter LED. A steeper change in incoming light power would give a greater RSSR value, making it more robust to noise. Especially for small angle differences in Fig. 7d, the gradient of the log of the division does not vary significantly at the centre of the graph.

The result of the RSSR in dB for the three PDs with a 35° tilt with respect to the receiver’s normal vector (as seen in Fig. 7c) can be found in Fig. 8a to Fig. 8c. The values −4, −2, and −6 dB are highlighted in the graphs (a), (b), and (c) respectively. This indicates what the input could be at the PDs. Note that all values only until −12 dB are shown for readability. The localization method considers received powers lower than  − 12 dB. The yaw and vertical offset shown on the axes of the graphs represent the transmitter angles as indicated in Fig. 7a. They are calculated as,

$${\theta }_{{{{\rm{y}}}},j}={\sin }^{-1}\left(\frac{{{{{\bf{v}}}}}_{j,x}}{\parallel {{{{\bf{v}}}}}_{j,x,y}\parallel }\right),$$

(7)

$${\theta }_{{{{\rm{p}}}},j}={\tan }^{-1}\left(\frac{{{{{\bf{v}}}}}_{j,z}}{\parallel {{{{\bf{v}}}}}_{j,x,y}\parallel }\right),$$

(8)

where θ_y,j and θ_p,j are yaw and vertical offset, respectively.

Fig. 8: Plots characterizing the relative recieved light power across photodiode pairs in Pisces.

Power received at a distance of 0.30 m with different yaw and vertical offsets at (a) Photo Diode (PD) A (-4dB highlighted in red), (b) PD B (−2 dB highlighted in red) and (c) PD C (-6dB highlighted in red). Also shown are the Received Signal Strength Ratio (RSSR) plots for each diode pair AB, AC, and BC with a horizontal LED-receiver distance of (d) 0.15 m, (e) 0.30 m, and (f) 1.50 m.

While the graphs in Fig. 8a–c show the variation of the received power in individual PDs, the result of their combination is shown in the plots of Fig. 8d–f. This is done by subtracting the different PD RSSR found using Eq. (5). The resultant values from each PD pair are then mapped on top of each other in the same plot. The red lines indicate a specific highlighted value of RSSR for each PD pair that is meant to represent a specific measured value found empirically.

We see from Fig. 8e that only one unique yaw and vertical offset combination exists when comparing the measured values from the three PD pairs (AB, AC, and BC). This is represented by the intersecting point of the three red lines. Note that although only using two diode pairs is already sufficient to arrive at a unique yaw, vertical coordinates, including a third one, add more robustness to finding the precise intersection.

Distance & 3D position estimation

Once the 2D orientation of both the top and bottom LEDs has been found (f_t and f_b), the horizontal distance to the LEDs can be estimated. This would correspond to the separation between the receiver and the transmitter in Fig. 7a. Using the knowledge of the LED placement, we can calculate this distance using,

$$\parallel {{{{\bf{v}}}}}_{f.{{{\rm{t}}}},z}-{{{{\bf{v}}}}}_{f.{{{\rm{b}}}},z}\parallel \, = (\tan ({\theta }_{{{{\rm{p}}}},f.{{{\rm{t}}}}})+\tan (-{\theta }_{{{{\rm{p}}}},f.{{{\rm{b}}}}}))\cdot \parallel {{{{\bf{v}}}}}_{j,x,y}\parallel ,$$

(9)

where ∥v_j,x,y∥ represents the horizontal distance between the receiver and LED, and ∥v_f.t,z − v_f.b,z∥ is the vertical distance between the two LEDs on a robot (tail).

$$\parallel {{{{\bf{v}}}}}_{j,x,y}\parallel \, =\frac{\parallel {{{{\bf{v}}}}}_{f.{{{\rm{t}}}},z}-{{{{\bf{v}}}}}_{f.{{{\rm{b}}}},z}\parallel }{\tan ({\theta }_{{{{\rm{p}}}},f.{{{\rm{t}}}}})+\tan (-{\theta }_{{{{\rm{p}}}},f.{{{\rm{b}}}}})}.$$

(10)

We see that from Fig. 8d, the RSSR plots depend highly on the distance between the LEDs and the receiver. This is due to the resultant vector as seen in Eq. (2). If the PDs were located in the same physical 3D space, it would result in r_i,j = v_j, and the ratio plot would only depend on the direction vector of the PDs. Since this is not the case, we need to know the horizontal separation between the LEDs and the receiver to generate the RSSR plots. However, the horizontal distance calculation needs the RSSR plots to find the angles relative to the top and bottom LEDs. This is solved using the algorithm described in Algorithm 1. Here, a subtraction pair, A-B, means that the logarithmic output from diode B is subtracted from diode A and distance stands for the horizontal distance between the receiver and the transmitter. In brief, the algorithm first uses an initial distance to generate the plot, and we label this db_distance; then, the resulting LED angles are used to estimate the distance, and a new distance estimate is found. This is then used to create a new plot with a db_distance closer to the estimated distance. This is iterated until the computed distance is close enough to db_distance. Scanning for the right distance is an operation that happens only when the receiver has no previously estimated distance, typically when scanning for the LEDs for the first time or when the LEDs are very close.

As an illustrative example, consider that LED to be 0.30 m away. Pisces starts by assuming the distance to be 1.50 m and generates the RSSR plot to estimate the angles, the estimated θ_p,f.b and θ_p,f.t will be further apart from each other than reality. Using these plots, the algorithm will try a distance closer than 0.30 m. However, we can see that the error reduces with each iteration, making the problem convex. To determine the absolute 3D position, the estimated values from the localization algorithm are used in the following equations,

$${{{{\bf{v}}}}}_{f.{{{\rm{b}}}},x} = \, \parallel {{{{\bf{v}}}}}_{f.{{{\rm{b}}}},x,y}\parallel \cdot \sin ({\theta }_{{{{\rm{p}}}},f.{{{\rm{b}}}}})\cdot \cos ({\theta }_{{{{\rm{y}}}},f.{{{\rm{b}}}}}),\\ {{{{\bf{v}}}}}_{f.{{{\rm{b}}}},y} = \, \parallel {{{{\bf{v}}}}}_{f.{{{\rm{b}}}},x,y}\parallel \cdot \sin ({\theta }_{{{{\rm{p}}}},f.{{{\rm{b}}}}})\cdot \sin ({\theta }_{{{{\rm{y}}}},f.{{{\rm{b}}}}}),\\ {{{{\bf{v}}}}}_{f.{{{\rm{b}}}},z} = \, \parallel {{{{\bf{v}}}}}_{f.{{{\rm{b}}}},x,y}\parallel \cdot \cos ({\theta }_{{{{\rm{p}}}},f.{{{\rm{b}}}}}),$$

(11)

where ∥v_f.b,x,y∥ represents the horizontal estimated distance from the fishtail. Furthermore, the bottom LED is used as the reference point for the location of the fish, which is why θ_p,f.b is used.

Algorithm 1

Localization Algorithm

Quantifying confidence level

As seen in Fig. 8, the overlapping area between the diode pairs depends on the LED’s horizontal distance from the receiver. Furthermore, the top and bottom LEDs of a fishtail need to be in the overlapping area, essentially defining the FOV. Even within this area, the values towards the edges are inferred with more error as they have a low SNR with the weakest received power signal for one of the PDs. This is why we introduce the term ‘Illumination Index’. In Fig. 9, the illumination index of all possible LED locations at a horizontal distance of 3 m is displayed. This is calculated using Eq. (12), where ${P}_{\max \Gamma }$ represents the highest power that is expected to be measured for $10\cdot \log ({P}_{{{{\rm{r}}}},i,j})$. Γ can then indicate how confident a measurement is, with a numerical value between 0 and 1. This value would, for example, also be weaker when the scattering rate is very high, or the LED is very far away. For a distance measurement, the minimum of the Illumination Index readings of the top and bottom LEDs is taken as the Γ for that distance estimation. Since the distance will weaken the RSSR in an exponentially decaying relationship, the Illumination Index will decrease linearly for the strongest signal received at a greater distance. This can be reduced to,

$${\min }_{i\in \{A,B,C\}}\left\{\frac{10\log \left({P}_{{{{\rm{r}}}},i,j}\right)}{10\log \left({P}_{\max \Gamma }\right)}\right\}$$

(12)

$$\Gamma =x\cdot d+c,$$

(13)

where ${P}_{\max \Gamma }$ can be adapted to make c equal to 1, and x is dependent on the medium.

Fig. 9: Pisces performance with varying Illumination Index.

Illumination index of light signals received when robot-robot distance is 0.30 m.