Memory-efficient full-volume inference for large-scale 3D dense prediction without performance degradation

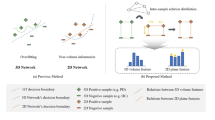
Abstract

Large-volume 3D dense prediction is essential in industrial applications like energy exploration and medical image segmentation. However, existing deep learning models struggle to process full-size volumetric inputs at inference due to memory constraints and inefficient operator execution. Conventional solutions—such as tiling or compression—often introduce artifacts, compromise spatial consistency, or require retraining. Here we present a retraining-free inference optimization framework that enables accurate, efficient, whole-volume prediction without performance degradation. Our approach integrates operator spatial tiling, operator fusion, normalization statistic aggregation, and on-demand feature recomputation to reduce memory usage and accelerate runtime. Validated across multiple seismic exploration models, our framework supports full size inference on volumes exceeding 1024³ voxels. On FaultSeg3D, for instance, it completes inference on a 1024³ volume in 7.5 seconds using just 27.6 GB of memory—compared to conventional inference, which can handle only 448³ inputs under the same budget, marking a 13 × increase in volume size without loss in performance. Unlike traditional patch-wise inference, our method preserves global structural coherence, making it particularly suited for tasks inherently incompatible with chunked processing, such as implicit geological structure estimation. This work offers a generalizable, engineering-friendly solution for deploying 3D models at scale across industrial domains.

Introduction

In a wide range of critical domains, including energy exploration^1,2,3,4,5,6 and medical image segementation^7,8,9,10,11, dense prediction tasks over 3D spatial domains are becoming increasingly prevalent and essential. These tasks sometimes require continuous estimation across the entire 3D volume, such as delineating subsurface structures^1,5,12, segmenting pathological regions, or recovering physical field distributions. To achieve spatially consistent and physically plausible results, models must not only capture local structural details but also encode cross-scale global context. Consequently, deep learning methods have been widely adopted for 3D dense prediction and have demonstrated remarkable success across disciplines.

Despite these advances, deploying such models in real-world scenarios faces a fundamental challenge: the volumetric size of data required for a single inference can be enormous. For instance, in seismic interpretation, a single 3D volume often exceeds dimensions of 1024³, amounting to billions of voxels. Current deep learning inference frameworks are generally unable to process such large-scale 3D data in a single forward pass without sacrificing resolution, global coherence, or model accuracy. This limitation not only hinders the practical adoption of high-resolution models but also constrains emerging expert-in-the-loop workflows^13,14,15, where timely and interactive inference is essential for real-time decision-making.

Unlike mainstream AI applications in computer vision^16,17,18 and natural language processing^19,20, particularly those driven by large-scale foundation models^21,22,23, where inference typically involves compact inputs (an image or a sentence) and large-scale models, 3D dense prediction tasks present an inverted computational pattern: relatively lightweight models are applied to large inputs. This “large input, small model” configuration imposes severe pressure on GPU memory, which is typically optimized for the opposite case. While latency requirements in 3D applications are often less stringent than in CV or NLP, timely responses remain important in practice. In seismic interpretation or medical analysis, users still expect predictions to be returned within an acceptable time window, especially in interactive settings where excessive delays may degrade usability and decision-making efficiency. Therefore, enabling memory-efficient and high-fidelity inference on ultra-large 3D volumes has become a critical bottleneck for real-world deployment.

Due to hardware constraints, particularly GPU memory limitations, most 3D models used in industry remain convolution-based, occasionally augmented with transformer or attention mechanism²⁴ at low-resolution stages to enhance representation. Although these models typically have modest parameter counts, they still struggle to process full-size volumes. For example, a minimalist 3D U-Net model¹ for fault segmentation in seismic data, with only 1.46M parameters and 16 channels in its first layer, requires up to 192 GB of memory for tensor concatenation in the final layer when processing a 1024³ volume using half-precision inference, which far exceeds the capacity of any commercially available GPU.

Existing approaches for alleviating memory bottlenecks during large-volume inference fall into three main categories: GPU-based tiling, CPU-based full-volume inference, and model compression techniques^25,26,27,28 such as distillation, pruning and quantization. However, each of these strategies presents substantial limitations. Tiling on GPUs, while memory-efficient, introduces visible boundary artifacts at tile edges, severely compromising the spatial continuity of predictions. This is particularly detrimental for tasks like relative geological time (RGT) estimation^12,29,30 or geological modeling^31,32,33 in energy exploration, where outputs represent global scalar fields—small local inconsistencies may propagate across the entire volume. CPU-based inference avoids such artifacts but is prohibitively slow and memory-intensive, making it impractical even for offline batch processing. As for model compression methods, which reduce memory usage by shrinking channel widths, removing redundant weights, or quantizing precision, they often require extensive retraining and are unlikely to mitigate the core memory overhead caused by high-resolution intermediate features, especially without marked loss in accuracy.

Through systematic analysis of widely-used 3D models, including UNet³⁴, DeepLab-v3³⁵, and HRNet³⁶, we find that the primary contributor to memory consumption during inference is not the model parameters themselves, but the massive volume of intermediate feature maps, especially those generated at high resolution near the network input and output. Moreover, we identify a non-obvious yet critical issue: as input volume size increases, inference time often rises disproportionately. This behavior stems from backend kernel implementations falling back to inefficient paths when processing large tensors. In some cases, inference may even fail altogether due to intrinsic operator limitations, despite sufficient memory being available.

Motivated by these challenges, we propose a general-purpose inference framework that enables memory-efficient, runtime-optimized, and performance-consistent processing of ultra-large 3D volumes (See Fig. 1). Without modifying model architectures or requiring retraining, our method restructures the execution of key inference-stage operators by introducing operator-level spatial tiling to avoid indexing overflows and kernel fallback, fusing operations acting on high-resolution feature maps to reduce memory footprint, aggregating normalization statistics to preserve numerical correctness, and applying on-demand recomputation to eliminate redundant caching. These optimizations are strategically applied near the input and output stages, where high-resolution representations dominate memory usage and computational cost. Taking mainstream tasks and architectures in energy exploration—particularly seismic interpretation—as representative examples, the framework supports inference on volumes exceeding 1024³ voxels. For instance, FaultSeg3D¹ achieves inference on 1024³ data using only 28 GB of memory and 7.5 s runtime on an NVIDIA H20 GPU, with no loss in model performance. On the same GPU, our method increases the maximum inferable volume size by 32 × compared to the original inference pipeline. Crucially, the approach provides a practical solution for tasks inherently incompatible with patch-wise inference, such as implicit geological structure modeling and relative geologic time estimation, where preserving global spatial continuity is essential.

Fig. 1: A scalable inference framework for seamless full-volume 3D prediction.

In industrial applications such as energy exploration, medical images segmentation, 3D dense prediction tasks require inference on large volumetric data (e.g., 1024³). However, naive full-volume inference quickly hits memory and runtime bottlenecks. Common remedies such as tiling often introduce visible seams at patch boundaries, which is unacceptable for tasks like seismic-RGT estimation that rely on spatially continuous outputs. We address these challenges through an inference-only strategy that combines operator-level tiling, fusion, and on-demand recomputation, without retraining or altering the model. As a representative case, FaultSeg3d¹ achieves seamless 1024³ inference in 7.5s using just 28 GB of GPU memory–a volume 13 × larger than the 448³ input limit under standard inference at the same memory budget–while preserving output fidelity.

Results

Architecture bottlenecks under large-volume inference

To reflect practical challenges in industrial-scale seismic exploration, we first examine the inference performance of mainstream 3D networks under large-volume input and categorize their architectures into three representative types (Fig. 2). The first and most widely adopted design traces its lineage to the UNet family, which preserves high-resolution shallow features into the decoding stage to enhance spatial detail modeling and enable multi-scale feature fusion. Variants of this architecture are prevalent in seismic tasks such as fault detection, karst or channel segmentation, RGT estimation, and implicit modeling. Another common variant employs a shallow stem for  × 4 downsampling before processing via a backbone and reinjecting shallow features during decoding, as seen in models like FaultSSL³⁷ and MDGAN².

Fig. 2: Representative architectural patterns of 3D networks for industry applications.

These networks can be broadly categorized into three types: a UNet-style designs that preserve high-resolution shallow features via skip connections to support multi-scale fusion, b progressive decoder architectures without skip connections, which generate high-resolution outputs through gradual upsampling, and c architectures that process decoder at low resolution and directly upsample predictions to the original size using interpolation, e.g., Deeplab-v3³⁵.

The second type shares similarities but omits the skip connection from the stem, instead generating high-resolution predictions through gradual upsampling and residual decoding, exemplified by GEM¹⁵. The third type, typified by the DeepLab-v3 family, extracts semantic features via a low-resolution backbone and then directly upsamples predictions to the original resolution, as in ChannelSeg3D for channel segmentation.

Although these networks perform well at training scale, we observe clear engineering bottlenecks when scaling to large input volumes (Figs. 3 and S1). Some models fail to complete forward inference even with sufficient memory, due to implementation-level limitations in backend operators. For example, FaultSeg3d performs nearest-neighbor interpolation from a low-resolution feature map; when input volume exceeds a threshold, 32-bit indexing overflows internally, resulting in runtime errors or crashes. Similar issues arise in padding operations, especially convolutions with reflective padding.

Fig. 3: Improving memory and efficiency across representative 3d models.

We evaluate the impact of our inference strategies on four representative 3D networks: a FaultSeg3D¹, a UNet-style model with skip connections; b FaultSSL³⁷, which combines an HRNet backbone with skip connections; c GEM¹⁵, which progressively upsamples predictions without shallow feature reuse; and d ChannelSeg3D³⁹, which generates low-resolution outputs followed by direct interpolation. In all cases, our optimizations–including operator-level spatial chunking, operator fusion, and on-demand recomputation–substantially reduce memory usage and restore near-linear runtime scaling, enabling inference on volumes exceeding 1024³ voxels. For example, ChannelSeg3D achieves a 52 × speedup at 1024³, and FaultSeg3D reduces memory to just 27.64 GB without sacrificing accuracy. These results hold across different model types and design paradigms, underscoring the generality and practical value of the approach. The numerical comparison can be seen in Table S1. Zoom in to view details.

A more subtle but equally critical issue is a sharp degradation in inference efficiency. For all models tested, inference time shows a nonlinear jump—often over an order of magnitude—once the input size crosses a threshold. Nsight Systems profiling reveals that this stems from backend kernel path switching: when tensor sizes exceed the 32-bit addressable range, cuDNN silently falls back to a less-efficient direct implementation using int64 indexing, disabling Tensor Core-accelerated paths like GEMM, FFT, or Winograd. These fallback kernels incur substantial memory and register overheads and lack optimized matrix multiply scheduling, leading to severe performance drops (Fig. S2). This bottleneck is widespread (see raw and strategy-1 curves) and represents a key limiting factor in scaling 3D inference.

Improving inference performance

To overcome the dual bottlenecks of memory and efficiency, we propose a suite of inference-stage optimization strategies that require no model retraining or architectural modifications, and evaluate them across the three representative network types (Figs. 3 and S1).

We first identify critical operators prone to 32-bit indexing overflow—such as nearest-neighbor upsampling and convolutions with reflective padding—and replace them with spatially chunked implementations (strategy 1, applied to FaultSeg3d and GEM). This allows the model to process larger volumes and fully utilize available memory until limited by out-of-memory (OOM) errors. However, these operators tend to invoke inefficient direct paths at large sizes, leading to dramatic increases in inference time and degraded performance.

To address this, we next replace all high-cost operators near the input and output stages (e.g., convolutions, interpolations) with chunked variants (strategy 2). In principle, the inference cost of convolution and interpolation scales linearly with the input volume when fast GPU kernels are used, because the per-voxel compute cost remains nearly constant. The nonlinearity observed under strategy 1 mainly arises because a subset of remaining operators still fall back to slow direct implementations at large spatial sizes. By chunking all such operators, strategy 2 ensures that every tile stays within the fast-kernel regime, thus restoring the expected near-linear relationship between inference time and input size. For instance, in ChannelSeg3d, inference speed improves by 22 × and 52 × at volumes of 768³ and 1024³ respectively, reducing runtime from 266 s to just 5.1 s. Similar accelerations are observed across models. However, since this strategy does not reduce feature map size, it offers no gain in maximum input size over the raw or strategy-1 versions.

To simultaneously reduce memory and runtime, we further propose operator fusion and unified chunking (strategy 3). In particular, by merging multiple layers near the output stage, we retain only the input and output of the fused block—eliminating intermediate high-resolution features—without sacrificing speed. This leads to substantially lower memory consumption and allows most models to process volumes up to or exceeding 1024³, all while maintaining stable runtime. In FaultSeg3d, this strategy yields the fastest inference time. Even for GEM, which includes InstanceNorm layers requiring repeated computation of statistics, the runtime is substantially improved over the original version.

Finally, in models of the first type (e.g., FaultSeg3d, FaultSSL), we introduce an on-demand recomputation strategy (strategy 4). Instead of storing shallow high-resolution features during inference, we dynamically recompute them via chunking when needed during decoding. This further reduces memory overhead and enables FaultSeg3d to handle input volumes equivalent to 14 GB of float32 data—32 × larger than the original model. Although this introduces minor time overhead, recomputation is limited to shallow layers (e.g., stem), and the overall speed remains superior while memory consumption is substantially reduced.

The applicability and impact of the four strategies depend on architectural details. Models without skip connections (Fig. 2b and c) cannot benefit from Strategy 4 and therefore rely only on Strategies 1–3. Moreover, models with lightweight decoders, such as ChannelSeg3D, store only small low-resolution feature maps and perform a single high-resolution interpolation step, leaving little room for memory savings from Strategies 3–4. This explains the limited memory reduction observed for ChannelSeg3D in Fig. 3. Finally, even when Strategy 4 is applicable, its recomputation overhead may make Strategy 3 or Strategy 2 faster for moderate input sizes, as illustrated in the final example of Fig. S1.

Beyond the four models shown in Fig. 3, we also test additional representative networks (Fig. S1). After applying our optimizations, all models exhibit markedly improved inference scalability, with near-universal support for 1024³-scale inputs and substantial speed gains, underscoring the generality and practical value of our approach.

Enabling accurate whole-volume inference

Most 3D dense prediction models face memory constraints during deployment. Even on high-end GPUs, original models struggle to process volumes beyond 1024³, resorting to overlapping chunked inference. While chunking enables scale, it often introduces artifacts—spatial discontinuities, edge effects, and loss of contextual coherence—especially problematic in tasks sensitive to global spatial consistency.

To assess the real-world impact of our approach, we evaluate two representative 3D tasks in seismic exploration: Relative Geologic Time (RGT) estimation and fault segmentation, representing regression- and segmentation-style dense prediction tasks respectively.

A widely-used and geologically meaningful task is RGT estimation, which reconstructs the relative deposition order from seismic data and serves as a backbone for full-sequence geological modeling. Implicit modeling tasks share similar structure: from limited geological annotations (e.g., faults or horizons), the model infers a spatially continuous scalar field encoding relative stratigraphic relationships and structural trends. Crucially, the outputs in these tasks are not absolute quantities but global relative metrics. As such, spatial continuity and structural smoothness must be preserved—any discontinuity or misalignment can compromise geological validity. As shown in Fig. 4a and b, chunked inference with GEM introduces visible seams and structural shifts that appear as artificial faults. In contrast, our optimized inference (Fig. 4c) enables full-volume prediction using the original model architecture, yielding geologically plausible and structurally coherent outputs.

Fig. 4: Our whole-volume inference strategy eliminates chunking artifacts.

a–c Results from an RGT estimation task using non-overlapping chunked inference, overlapping chunked inference, and our full-volume inference strategy, respectively. Chunked inference disrupts spatial continuity, introducing visible seams, layer shifts, and artificial faults (e.g., red arrow), even with overlap. In contrast, our method produces geologically smooth, coherent horizons and consistent stratigraphic surfaces. In fault segmentation tasks, chunked inference d may also introduce misaligned or fragmented fault traces in complex regions (red boxes and ellipses). Our strategy e allows the model to access complete spatial context, eliminating artificial boundaries introduced by chunking and improving structural continuity. Note that our method removes only artificial discontinuities introduced by chunking and does not modify genuine geological breaks, which remain governed by the model’s inherent predictive capacity.

In segmentation tasks such as fault detection, spatial context requirements are less stringent, and chunked inference with moderate overlap often yields acceptable results. Still, artifacts may persist in complex fault systems (Fig. 4d), with discontinuities or misaligned traces—especially for subtle faults requiring large-scale context for recognition. With our strategy, the model can ingest larger volumes in one pass, enhancing spatial continuity and topological completeness without sacrificing accuracy (Fig. 4e).

Our full-volume inference framework removes only the artificial discontinuities introduced by tiled computation. It does not alter genuine geological breaks present in the data, nor does it change the model’s inherent ability to represent such discontinuities. Whether real faults or stratigraphic terminations appear in the output remains determined solely by the data and by the predictive capacity of the trained model, consistent with prior observations on true subsurface discontinuities³⁸.

Discussion

With the growing application of 3D dense prediction models across domains such as energy exploration, medical image segementation, and climate simulation, the ability to handle large-scale volumetric inputs during inference has emerged as a key bottleneck for real-world deployment. Although current mainstream models perform well during training, they often rely on patch-wise inference at test time, rendering them incapable of processing entire full-size volumes end-to-end. This limitation not only introduces spatial discontinuities and edge artifacts but also hinders model deployment in resource-constrained environments. To address this long-overlooked yet critical challenge, we propose a general, non-invasive, and retraining-free optimization strategy that substantially improves the inference capability of 3D models on large volumes, without altering their architecture or performance.

We validate the effectiveness of this strategy across several representative models used in seismic interpretation, encompassing three mainstream architectural designs. Our results demonstrate that full-volume inference on inputs larger than 1024³ becomes feasible without modifying the model architecture, while inference time and memory usage are considerably reduced. More importantly, unlike conventional overlapping tiling methods, our approach avoids context fragmentation, which can lead to substantial performance degradation—especially in tasks that demand strong spatial coherence, such as relative geologic time (RGT) estimation and implicit modeling. Even for relatively robust segmentation tasks, our strategy enables models to perceive larger spatial contexts, thereby improving the continuity and accuracy of the predicted structures. Notably, the optimization focuses on the inference pipeline at the input and output stages, with emphasis on managing high-resolution feature maps, rather than altering the backbone network. Since the stem and decoder stages are typically lightweight and structurally simple, these adjustments are more tractable and preserve the model’s overall functionality and parameters, enabling broad applicability with minimal engineering cost.

Despite its general applicability to most convolution-based 3D models, the strategy has some limitations. For common operations such as convolution and interpolation, we provide reusable modules for spatial tiling that can be easily integrated into multiple architectures. However, strategies involving operator fusion or on-demand recomputation require model-specific customization, such as identifying and modifying composite operator paths or inserting dynamic recomputation branches, which entail higher engineering effort. Furthermore, the proposed optimizations are primarily suited for operators based on local computation. They are not directly applicable to transformer-based models with global attention, such as Swin-UNETR¹⁰, where memory consumption from self-attention at mid- to high-resolution stages often dominates. In these cases, the memory demand exceeds that of the largest convolutional feature maps, limiting the effectiveness of our tiling and fusion strategies. Finally, we note that the proposed strategies target the inference stage and are not directly applicable to training. Although the tiled and fused forward computations remain numerically equivalent to their native operators, autograd cannot automatically derive correct gradients for such composite tiled operators. Extending the strategies to training would require defining custom backward implementations (e.g., tiled convolution and normalization), which is theoretically feasible but involves substantial engineering effort and lies beyond the scope of this inference-focused work. Nonetheless, this limitation remains marginal in current 3D dense prediction tasks, where transformer layers are rarely used at high resolutions in practical deployments.

In summary, the proposed inference optimization strategies offer a practical and reproducible engineering solution to the long-standing scalability challenge in 3D dense prediction. Through operator-level restructuring and memory-efficient feature handling, our method removes key computational bottlenecks and enables full-volume inference for datasets as large as 1024³ voxels—without compromising model performance. While currently best suited for convolutional architectures, the core principles behind our method are readily extendable to a broad range of 3D applications, including medical image segementation, climate simulation, and computational fluid dynamics. Moreover, in scenarios demanding interactive, expert-in-the-loop interpretation, our strategy shows promising deployment potential. By addressing the key engineering barriers in inference, our work extends the applicability of 3D deep learning models to large-scale, real-world volumetric data.

Methods

We develop an inference optimization framework tailored for the high-resolution feature pathways in 3D dense prediction models, with a focus on three major directions: spatial operator-level tiling, operator fusion with normalization recomputation, and on-demand recomputation of shallow features. Our approach requires no changes to model architecture or parameters and instead replaces the inference execution paths of selected operators to enhance a model’s ability to process large volumetric inputs. As shown in Fig. 3, these strategies are evaluated across multiple representative seismic interpretation models, with their individual contributions labeled as Strategy 1–4.

We begin by addressing operators prone to index overflow when processing large input volumes, such as nearest-neighbor interpolation and reflective-padding convolution. To this end, we introduce spatial tiling within operators (Strategy 1). Unlike conventional data tiling, where the input volume is split into multiple independent sub-volumes for separate inference, our method applies tiling internally within the operator implementation, preserving the continuity of the input and output tensors. This ensures that upstream and downstream tensor flows remain unaffected and avoids the context discontinuity and boundary artifacts commonly associated with patch-based inference. In theory, spatially tiled execution yields numerically identical results to full-volume execution, as it decomposes a global operator into local computations with proper aggregation. This mechanism effectively circumvents runtime errors caused by int32 indexing limits, enabling stable inference on larger volumes.

Moreover, even for convolution operators that technically support large inputs, exceeding the int32 indexing threshold often triggers a fallback to inefficient direct computation paths, resulting in a sharp increase in inference latency. To mitigate this, we replace high-cost convolution operators—particularly those near the input or output stages—with tiled implementations (Strategy 2). This restores a linear relationship between inference time and input size, substantial accelerating model execution without increasing memory consumption (and sometimes reducing it). The key to tiled execution lies in carefully managing boundary regions: each tile includes a padded computation region that accounts for necessary boundary context, and the final output is cropped to retain only the valid central region, as illustrated in Figs. S3 and S4. In practice, each tile is expanded with a halo region whose width matches the operator’s receptive-field radius (for example, half the convolution kernel size). This guarantees that every voxel in the center of the tile receives exactly the same spatial context as it would in a full-volume convolution. After computation, the halo region is discarded and only the central valid region is kept. If the boundary region is not handled correctly—for instance, if the tile is processed without a sufficiently wide halo—neighboring tiles will see different spatial context. This leads to visible seams or small spatial shifts at tile boundaries, even when the underlying field is smooth. Proper halo padding and cropping therefore ensures that each tile is computed consistently and prevents such artifacts.

Formally, the equivalence between tiled and full-volume execution follows from the locality of convolution and other spatial operators. Let ${{{\mathcal{L}}}}$ denote any operator whose output at voxel p depends only on a finite receptive-field stencil ${{{\mathcal{R}}}}$:

$$({{{\mathcal{L}}}}X)(p)=f(\{\,X(p+r)\,| \,r\in {{{\mathcal{R}}}}\}).$$

(1)

For an output tile region Ω, we extend it with a halo of width

$$h={\max }_{r\in {{{\mathcal{R}}}}}{\parallel }r{\parallel }_{\infty },$$

(2)

and extract the padded tile $\widetilde{X}=X{| }_{\Omega \oplus h}$. Applying the operator to the padded tile yields

$$({{{\mathcal{L}}}}X)(p)=({{{\mathcal{L}}}}\widetilde{X})(p),\,p\in \Omega ,$$

(3)

because every voxel in Ω receives exactly the same spatial neighborhood as in full-volume execution. If the halo is insufficient, the neighborhoods seen by adjacent tiles differ, producing seams or small spatial shifts at tile boundaries. Correct halo padding and valid-region cropping therefore guarantee numerical equivalence between full-volume and tiled execution.

While the above two strategies enable inference on large inputs and improve execution speed, they do not drastically reduce memory usage. To further reduce memory consumption, we propose Strategy 3: fusing multiple consecutive operators and applying unified tiling. For example, decoder paths in UNet-like models often involve several convolutions and interpolations, where the high resolution intermediate feature maps consume marked memory. Operator fusion can be expressed compactly in functional form. Let ${{{{\mathcal{L}}}}}_{1},\ldots ,{{{{\mathcal{L}}}}}_{k}$ denote a sequence of local operators (e.g., convolutions, interpolations, normalizations) applied in the decoder. Their unfused execution creates k − 1 intermediate feature maps. By defining the fused operator

$${{{\mathcal{F}}}}={{{{\mathcal{L}}}}}_{k}\circ {{{{\mathcal{L}}}}}_{k-1}\circ \cdots \circ {{{{\mathcal{L}}}}}_{1},$$

(4)

the decoder path can be executed as a single composite mapping without materializing intermediate tensors. For tiled execution, the fused operator acts on a halo-extended region whose width matches the composite receptive field:

$${{{{\mathcal{F}}}}(X)| }_{\Omega }={{{\mathcal{F}}}}({X| }_{\Omega \oplus {h}_{composite}}),$$

(5)

which preserves numerical equivalence to the full-volume computation while eliminating the need to store high-resolution intermediate buffers. By fusing these operators into a single execution path and retaining only the input and output tensors, we substantially reduce intermediate buffer allocations.

In paths that include normalization layers (e.g., InstanceNorm, GroupNorm), we adopt a two-stage computation scheme to ensure numerical correctness: we first compute per-tile statistics (mean and variance), then aggregate them into global statistics used for normalization (Fig. S5). As demonstrated in Fig. 5a, even under half-precision inference, a single-channel 1024³ input, i.e., V = 2 would require 192 GB of memory just for the concat operator’s input/output in the decoder stage of UNet, not including the subsequent convolution layers. With operator fusion (Fig. 5b), the memory requirement drops to just 42 GB, with minimal memory overhead from intermediate tiled computations. When using BatchNorm or other normalization layers that do not require global statistics, this strategy incurs negligible additional cost compared to Strategy 2, and can even be faster. In the case of global-statistics-based layers like InstanceNorm, although repeated computations introduce some overhead, the overall latency remains substantially lower than in the original implementation.

Fig. 5: Illustrative example of memory optimization in the decoder of UNet-like architectures.

a A baseline design with skip connections and stacked convolutions incurs high memory usage due to large intermediate buffers (e.g., 192 GB for the “concat” operator, suppose that input size is 1024³, i.e., V = 2). b Fusing operators eliminates intermediate buffers, retaining only input/output tensors, and reduces memory to 42 GB. c Further applying on-demand recomputation of shallow features to avoid storing high-resolution skip connections, lowering memory to 12 GB.

Lastly, for models with skip connections (Fig. 2a), such as the UNet family, we introduce Strategy 4: on-demand recomputation of shallow features. Instead of caching high-resolution feature maps from early stem layers, we discard them during inference and recompute only the necessary portions during decoding. Since these shallow features are close to the input and computationally inexpensive, this strategy incurs minimal overhead while notably reducing memory usage. As shown in Fig. 5c, after recomputation and operator fusion, the total memory requirement drops to just 12 GB, offering substantial memory savings and further alleviating inference bottlenecks.

Together, these strategies systematically overcome the memory and performance bottlenecks faced by 3D dense prediction models during inference, without requiring any modifications to model architecture or retraining. Spatial tiling eliminates runtime failures and efficiency drops caused by index overflows or kernel fallback. Operator fusion with global normalization recomputation greatly reduces the memory footprint of high-resolution feature maps, and shallow feature recomputation removes redundant caching from early-stage branches. We have systematically validated these strategies across several benchmark seismic interpretation models, including FaultSeg3D¹, FaultSeg3DPlus⁵, FaultSSL³⁷, ChannelSeg3d³⁹, Wang25Channel⁴⁰, KarstSeg3d⁴¹, DeepISMNet³³, Bi21RGT3d¹² and GEM¹⁵, on tasks including fault detection, paleokarst and channel segmentation, implicit structural modeling, and RGT estimation. In addition, we demonstrate the applicability of our framework beyond geoscience by applying it to SegFormer3D¹¹, a transformer-based model for volumetric medical image segmentation. In all cases, the proposed methods yield substantial improvements in inference performance and scalability to high-resolution volumetric inputs (Figs. 3, S1).