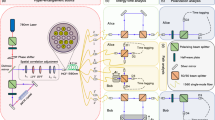
Abstract
Optical losses and environmental noise present significant challenges for the coherent propagation of entangled states of light over large distances in quantum communication protocols. To cope with optical losses, one possible strategy is to increase the emission rate as much as possible. Decoherence, related to thermal and pressure fluctuation and to the presence of parasitic processes, can be overcome by encoding information via hyper-entanglement, i.e. entanglement over multiple degrees of freedom (DoFs). In this work we experimentally demonstrate a silicon-integrated device implementing both strategies, demonstrating the emission of spectrally multiplexed and hyper-entangled photon pairs. The pair generation rate exceeds 109 pairs per second at the output of the device over an 8 THz-wide comb of multiplexed frequency modes. Hyperentanglement is proved by showing entanglement in the frequency-bin and time-energy DoFs, along with high purity of the states when tracing over the time-energy degree of freedom. Quantum state tomography shows both fidelity and purity to be greater than 95% in the frequency domain, while, in the time-domain encoding, Bell’s inequality is violated by more than 10 standard deviations.
Similar content being viewed by others
Introduction
The generation of entangled states of light in integrated photonics devices is of paramount importance for a number of quantum technologies1, including several protocols in quantum communication2,3,4, quantum simulation5 and computation6. In general, entanglement between two photons can be generated in different degrees of freedom. Polarization based entanglement7 constitutes the most widespread choice for free-space experiments and applications, while path entanglement8 is the most obvious choice for on-chip quantum information processing. In quantum communication protocols, the ability to increase the distance between receiving parties implies propagation in highly lossy channels, with a typical budget loss of about 40 dB for an 80 km fiber link9 or a low earth orbit satellite link10,11,12,13.
The most direct approach to overcome optical losses consists in building sources of quantum states of light with emission rates significantly higher than the typical sources, potentially exceeding 1 billion photon pairs per second (1 GPair/s) at the source. The pair generation rate R for most silicon-integrated parametric sources of entangled photon pairs has so far been limited to the millions of photon pairs per second (MPairs/s)14, while rates exceeding 1 Gpairs/s have been recently demonstrated using bulk parametric sources15,16,17 as well as with other platforms like AlGaAs-on-insulator18, which may offer higher efficiency but are still at an earlier stage of technological maturity. Integrated sources, in particular silicon integrated sources, with rates exceeding 1 Gpairs/s would be highly beneficial in many applications for their inherent scalability, ease of use and low operating powers. A key trade-off that constrains the operational rate of probabilistic sources is the inverse relationship between the quality of the emitted quantum state and the rate itself. This trade-off can be effectively quantified using a commonly employed figure of merit known as the Coincidences over Accidentals Ratio (CAR). In the continuous-wave regime, and when sources of noise like Raman or other luminescent processes can be disregarded, the CAR can be simply expressed as \(\,\text{CAR}\,=\frac{1}{R\tau }\), where τ is the convolution time between the photons’ dwelling time and the time resolution of the detectors19.
This result can be understood by noting that, as the generation rate increases, so does the probability that the detectors are simultaneously triggered by signal and idler photons originating from different, uncorrelated events, hence not time-energy entangled. Visibility in quantum experiments, and consequently the viability of a source of entangled photon pairs for its use in quantum communication protocols20, is limited by \({\mathcal{V}}\le \frac{\,\text{CAR}}{\text{CAR}\,+2}\). As a consequence, actual physical implementations would require CAR values larger than at least 20.
One possible strategy to overcome this trade-off is the use of frequency multiplexing. The generation of photon pairs over a comb of frequencies can be used to “flag" the correlated photons, distinguishing them from the other pairs in the stream. At the receiving ends, by demultiplexing the photons, it is possible to send each correlated frequency to different detectors thus ensuring high rates while maintaining high values of CAR and visibility.
Aside from losses, when propagating through long optical channels decoherence effects can reduce the yield and accuracy of quantum communication protocols21. Such decoherence can come from thermal and pressure fluctuation in the atmosphere or in optical fibers, and from parasitic processes such as photoluminescence and Raman scattering22. A way to overcome these processes is to encode quantum information redundantly via the use of hyperentanglement, i.e. entanglement over multiple degrees of freedom. The use of hyper-entanglement has already been experimentally shown to improve quantum communication protocols over noisy channels23,24,25,26.
In this work we report on a silicon integrated source of hyper-entangled photon pairs in the time-energy and frequency-bin DoFs. Our source based on a racetrack resonator geometry, is capable of generating via Spontaneous Four-Wave Mixing (SFWM) up to 8 GPairs/s and delivering more than 1 GPairs/s to a free-space optical channel while retaining high CAR values (≳ 100) for each pair of resonances. These rate values were obtained through multiplexing in the frequency domain and the off-chip value in particular is derived after separating the signal and idler channels thanks to a high bandwidth (> 4 THz) demultiplexer.
The photon pairs are hyper-entangled over the time-energy and frequency degrees of freedom, proved by measuring entanglement and high purity in the reduced spaces while tracing over the other DoF. Although time and energy are conjugate variables, here the temporal degree of freedom can be treated as independent from the spectral (energy) one because the time separation between the photons in a pair is much larger than the coherence time of each photon, yet shorter than the coherence time of the pump. This condition is essential in Franson-type and time-bin experiments. In this regime, the relevant measurement operators act on temporal modes (arrival times or interferometric superpositions thereof), while the spectral/energy DOF can be engineered or filtered independently; this operational separation underlies demonstrations of hyperentanglement in time/frequency DOFs27,28,29.
Results
Device design and linear characterization
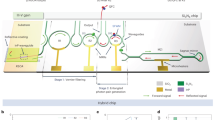
The source consists of a racetrack silicon resonator (Fig. 1a) made with ridge silicon waveguides. The waveguides have a cross section of 500 nm by 220 nm, are embedded in silica and present propagation losses ≃ 0.9 dB/cm at 1550 nm. The resonator adopts an all-pass configuration, so it features only one coupling point to the bus waveguide. In this case, the coupling point consists in a directional coupler. The resonator has a perimeter of 7 mm corresponding to a free spectral range (FSR) of 10 GHz, equal to 0.08 nm around 1550 nm (see measured spectra in Fig. 1b). The measured loaded quality factors are around 2.5 × 105.
a Scheme of the integrated device. The input and output channels waveguide are inverse tapered. The rainbow block represent the demultiplexer. b-i,ii Transmission spectra from the output signal and idler channels in the spectral region of one of the pairs employed in the frequency-bin entanglement experiment. The dashed and the solid line are a Lorentzian fit for the resonance pair labelled as \({\left\vert 1\right\rangle }_{s}{\left\vert 1\right\rangle }_{i}\) and \({\left\vert 0\right\rangle }_{s}{\left\vert 0\right\rangle }_{i}\), respectively. c Transmission spectrum of the DEMUX’s channels-only, i.e. input and output coupler contribution have been removed. The dotted vertical lines represent one example of employed resonances (blue for signal and red for idler) and the pump wavelength (green).
The ring resonator is followed by an integrated demultiplexer (DEMUX) to separate a large number of idler resonances from their signal counterparts and direct them to two different output channels. The DEMUX consists of two consecutive and identical interferometric filters per channel, each one made of three cascaded Mach-Zehnder interferometers (more details on the layout can be found in the Supplementary information). Each stage has two spectrally interlaced outputs for signal and idler. The filter is designed to have a passband of 35 nm (4.35 THz) comprehending approximately 435 resonances for the signal and idler output channels, a bandwidth sufficient to collect almost the totality of the generation band of the resonator as discussed below. These values were experimentally validated, as it can be appreciated from the device response reported in Fig. 1c. The linear characterizations were performed with the setup reported in the Methods section. More detail on the design and fabrication of the device are reported in the Supplementary material.
Generation rate
The total generation rate as a function of pumping power was assessed using two independent methods: a measure of the emitted optical power using a calibrated CCD camera coupled to a spectrometer and a recostruction of the emission rate from coincidence counts on selected pairs of resonances. See the Methods section for a complete description of the setups used.
The first measurement was taken at different input powers (from 40 μW to 25 mW inside the input waveguide). The measured spectra for every input power, normalized by the integration time to obtain the counts per second, are reported in Fig. 2a. The resolution of the CCD is not sufficient to discriminate different frequency modes, so every point on the graph corresponds, on average, to about four resonances. From these measured curves, it was possible to reconstruct the rate of single photons generated inside the ring and, from that, the generated pairs in the waveguide (on-chip), as well as after outcoupling.
a Spontaneous emission spectra acquired on a spectrometer varying the on-chip input power. Each CCD pixel comprises 4 resonances, on average. The central green band, centered at 1546 nm outlines the pump region where the output is suppressed by off-chip filtering. The four green dashed vertical lines, symmetrically positioned in respect to the pump and numbered accordingly, mark the locations of the four pairs of frequency qubits used for the quantum measurements, same of Fig. 3. In the lower panel, we report for convenience the data in c, in linear scale. b Total emission rate in the waveguide at the output of the device, inferred from singles detection rate from the CCD measurements (filled squares) and reconstructed from the coincidences (empty diamonds). The errors on the input powers and the rate are calculated propagating the uncertainties on the insertion losses of the input and the output section of the setup, respectively.
A conversion factor (≃ 3 × 10−17 W per count per second), obtained from a calibration of the CCD, was used to convert the measured counts to optical power in the fiber at the spectrograph input. With this strategy, the CCD could serve as a power meter with sub-fW sensitivity. Subsequently, the setup and coupling losses (including the frequency-dependent losses of the DEMUX and the coupling losses, reported in Table 1) were added to get the power inside the bus waveguide (after the ring). At this point, the expression for the energy of one photon (E = hν where h is the Planck constant) was exploited to pass from power to single-photon rate. Before proceeding, it is necessary to take into account also the contribution of the coupler between the ring and the bus waveguide, by considering the probability of extraction of a single photon from the resonator which can be written as:
where σ is the square root of the measured transmission of the directional coupler of the resonator (more details on this can be found in the supplementary material) and a is equal to e−αL/2, where α is the waveguide propagation loss (expressed in m−1) and L is the length of the resonator in meters. This expression is employed to reconstruct the rate of single photons inside the ring.
To go from the total rate of single photons to the rate of photon pairs generated via SFWM, we made the reasonable assumption that the total rate R can be considered as the sum of two contributions: one that grows quadratically with the pump power and that is only due to photon generated via SFWM, one that is linearly dependent on the pump and that is due to parasitic phenomena (mainly Raman in the fibers30 of the input setup). Therefore, the rate of single counts as a function of the pump power can be fitted, for every CCD pixel, by the quadratic function
where Pin is the pump power in the waveguide, while the fit coefficients a(λ), b(λ) describe the spectral dependence of the SFWM and photoluminescence, respectively. The wavelength dependence of the quadratic coefficient a quantifies the generation bandwidth process and the spectral brilliance of the SFWM. The value of the derived coefficients, as well as theirs dependence on λ is reported in the Supplementary material.
Notice that the fit of the experimental data with Eq. (2) was performed for Pin < 1 mW, a pumping regime where other nonlinear effects such as two-photon absorption (TPA) and free-carrier absorption (FCA)31 can be neglected. Additional data supporting this approach can be found in the Supplementary material. After subtracting the linear contribution from every spectrum, only the quadratic rate remained.
It is now necessary to consider once again the contribution of the coupler, but this time the escape probability to be considered is the one of a pair of photons, calculated as the product of the escape probability of signal and idler. Then, it is possible to recover the generation rate in the resonator from the pair rate in waveguide as Rwg = pexit,pairRring. To obtain the total rate of pairs in the waveguide after the source as reported in Fig. 2, the computed rate values were summed over frequency for every input power. The maximum estimated rate is 9.7 Gpair/s in the waveguide after the source and before the DEMUX, which corresponds to 3.2 Gpair/s after the DEMUX and 1.2 Gpair/s off chip considering the losses of around 1 dB per channel (Table 1) associated to free-space coupling. This loss value was estimated by measuring the light directly from the output facet of the integrated waveguide, after removing the output-coupled fibers and collimating the emission.
Comparable results were found reconstructing the total rate from the coincidence measurements. Similarly to what was done for the previous measurement, a large range of input powers (between 0.38 mW and 22.4 mW) was employed to assess the scaling of the generation rate. For each of the four different spectral regions, the coincidence counts were rescaled using the quadratic coefficient a obtained from the CCD measurement in order to derive the rate of the whole spectrum from the one of a single frequency pair. Finally, the results for the four regions were averaged. The full dataset used for the coincidence scaling analysis is provided in the Supplementary information, as well as more details on the total rate computation procedure. Fig. 2 (b) presents the results of both measurements, which exhibit good agreement, with discrepancies within the experimental error.
For each input power and measure frequency couple, starting from the coincidence histogram, the CAR was computed as the ratio between the sum of the counts over the bins that are found within the full width at half maximum of the histogram peak and the average of the counts that contribute to the noise outside the peak, multiplied by the same number of bins that was used to sum the coincidences. As reported in Fig. 3, all the CAR values remain above the required value of 20 for most of the employed input powers, while being around 20 for the highest employed powers where the emission saturates because of the onset of parasitic nonlinear processes.
We report the CAR obtained with a direct measurement of the coicindence rate, for four selected pairs of resonances. For most lower powers, the CAR exceeds the safe threshold of 20. However, at the highest powers, where the emission saturates due to nonlinear parasitic processes, the CAR drops to this threshold.
Energy-time entanglement
To measure two-photon correlation, an in-fiber Mach-Zehnder interferometer was used in a Franson interference configuration27,32,33, i.e., with an imbalance (ΔL = 2 m in our case) that is longer than the coherence time of each photon in the pair (≃ 4 cm) but shorter than the coherence length of the wavepacket that describes the photon pair, which is equal to the coherence length of the pump laser (≃ 10 km in our case). This ensures that first-order interference is not observed at the interferometer’s output, while two-photon interference with a global and non-local phase dependence for the measured coincidence rate is retained. See the Methods section for a more detailed description of the setup and the stabilization mechanism used for the interferometer.
For each energy-matched pair of resonances, the output state of the device, in the frequency domain, is a tensor product of two-mode squeezers. In the low squeezing regime, when the multi-photon contribution can be neglected, the state can be approximated by a coherent superposition of single photon pairs emitted simultaneously. Photon pairs that satisfy the energy-matching condition are strongly correlated on the arrival-time basis, and can be exploited to prepare entangled states in the time-bin variable32.
At the output of the Franson interferometer, we measure the coincidences between signal and idler photons coming from one of the output ports. When collecting the histogram of the time delays we observe the characteristic three peaks of Fig. 4b that are labelled according to the path in the interferometer the photons have undergone, i.e. a coincidence for the state \(\left\vert LS\right\rangle\) arises from the signal photons that took the long path (L) and the idler photon the short one (S). If the states \(\left\vert LL\right\rangle\) and \(\left\vert SS\right\rangle\) are indistinguishable, the amplitude of the central peak shows strong two-photon interference and the coincidences vary according to
where ϕs and ϕi are the phases of the signal and idler photons respectively and ϕp is the phase of the pump. Since the photons are generated via SFWM, they satisfy the phase relation ϕs + ϕi = 2ϕp. The visibility \({\mathscr{V}}\) of this fringe violates the associated Clauser-Horne-Shimony-Holt (CHSH) inequality if \({\mathscr{V}} > 1/\sqrt{2}\)27. In Fig. 4a is shown the Franson interference fringe for the resonance pair λs, λi = 1536nm, 1558nm, for a pump power that corresponds to the on-chip 1 Gpairs/s emission rate. The fitted visibility is equal to 93.81 ± 0.57% violating Bell’s inequality by more than 40 standard deviations. Moreover, we remark that the CHSH inequality is violated consistently for all the measured resonance pairs (see a, b and c green dashed lines in Fig. 2) and across all the input powers even well above the 1 Gpairs/s emission rate as summarized in Fig. 5. The measured points are compared with the theoretical limit imposed by the measured CAR. If the visibility of the central fringe in the Franson experiment is limited solely by the background of accidental coincidences Cacc, then the maximum amplitude of the interference fringe is \({A}_{\max }=\frac{{C}_{{\rm{corr}}}}{2}+{C}_{{\rm{acc}}}\), while the minimum corresponds to the accidental background alone, \({A}_{\min }={C}_{{\rm{acc}}}\). Here, Ccorr denotes the total number of correlated coincidences that manifest interference. This leads to a visibility limit given by:
where \(\,\text{CAR}=\frac{{C}_{{\rm{corr}}}}{{C}_{{\rm{acc}}}}\) is the coincidence-to-accidental ratio.
a Franson interference fringes obtained at 1 Gpairs/s emission rate (Pin = 12mW) for the resonance pair λs, λi = 1536 nm, 1558 nm. The experimental coincidence rates (blue markers and left axis) are fitted with a sinusoidal function with a visibility \({\mathscr{V}}=93.81\pm 0.57 \%\). The experimental coincidence rates are obtained by the FHWM integral of the central peak of the coincidence histogram shown in b. The red and green squares represent the singles count rate (right axis) that does not vary during the measurement, attesting the absence of first order interference. The poissonian error is not represented because the error bar is smaller than the marker size. b Snapshot of the coincidence histogram at four notable phase settings of the interferometer.
We performed a Franson experiment for each correlated resonance pair, labelled as \({\left\vert 0\right\rangle }_{s}{\left\vert 0\right\rangle }_{i}\) and \({\left\vert 1\right\rangle }_{s}{\left\vert 1\right\rangle }_{i}\), from which the frequency bin qubits are constructed (Fig. 2a). The points are obtained from the central peak of the coincidence histogram (see Fig. 4b). The solid green line represents the upper limit of the visibility achievable given the measured CAR as described by Eq. (4). The green dashed line marks the power for which the device generates 1 Gpair/s on-chip, while the red dashed line marks the power that correspond to a net rate of 1 Gpair/s after fiber coupling.
The measured visibility points are compared with the theoretical limit imposed by the measured CAR (\({{\mathscr{V}}}_{{\rm{meas}}}\le {{\mathscr{V}}}_{\max }\)), showing that the measured values are consistent with this limit within the error bars.
Frequency-bin entanglement and hyper-entanglement
The maximally entangled canonical Bell state \(\left\vert {\Phi }^{+}\right\rangle =\frac{\left\vert 00\right\rangle +\left\vert 11\right\rangle }{\sqrt{2}}\) can be prepared starting from the output state by filtering two corresponding pairs of resonances for emission band and tracing on the temporal degree of freedom. In the context of frequency bins the resonances that are spectrally closer to the pump are labelled as \(\left\vert 0\right\rangle\) while those that are spectrally farther are labelled as \(\left\vert 1\right\rangle\) (refer to Fig. 1b). The Hilbert space for the final state is the tensor product of the signal and the idler Hilbert spaces.
To demonstrate the effective generation of the target frequency-bin state, we performed the quantum state tomography in the frequency-bin subspace34. The quantum state tomography procedure is described in the Methods section, together with the setup, depicted in Fig. 9.
The tomography was performed on three two-qubit states, each corresponding to one of the three detunings from the pump used in the energy-time entanglement experiment—labeled as a, b, and c in Fig. 2—since the resonances at detuning d fell outside the range accessible to the waveshaper. From the reconstructed density matrix it is possible to calculate the state purity \({\mathcal{P}}=\,\text{tr}\,({\rho }^{2})\) and the fidelity with the state \({\rho }_{0}=\left\vert {\Phi }^{+}\right\rangle \left\langle {\Phi }^{+}\right\vert\), defined as \({\mathcal{F}}={\left(\text{tr}\sqrt{\sqrt{\rho }{\rho }_{0}\sqrt{\rho }}\right)}^{2}\). We report in Fig. 6a the reconstructed density matrix for the qubit built with the resonance pairs in the region λs, λi ≃ 1540 nm, 1550 nm, at a pumping power of 12 mW corresponding to R = 1 GHz on-chip. In Fig. 6b the dependence of the purity and fidelity for the reconstructed state to the input power is reported. The measured fidelity is 98.5% at the lowest measured pump power, 96.3% at the on-chip 1 Gpairs/s rate, and over 90% (94%, averaging on the three states measured) at the off-chip 1 Gpairs/s rate, where the off-chip value refers to the rate measured accounting for the coupling losses. Although the purity is near unity at the lowest measured input power, it decreases to 94.6% at the on-chip 1 Gpairs/s rate, and to 90.4% at the off-chip 1 Gpairs/s rate, on average.
a Reconstructed density matrix for the input power corresponding to the 1 Gpair/s emission rate for qubit a. b Dependence of the Purity and Fidelity of the reconstructed density matrix on the pump power for the three measured qubits. The green dashed line marks the power for which the device generates 1 Gpair/s on-chip, while the red dashed line marks the power that corresponds to a net rate of 1 Gpair/s after fiber coupling.
As pointed out in ref. 35, demonstrating entanglement in multiple individual subspaces is not, in general, sufficient to verify hyperentanglement, since the global state could be a statistical mixture of states entangled in different DOFs. However, in our case, the measured high purity in the frequency-bin subspace (higher than 95%, on average) ensures separability between the two DOFs and rules out such classical mixtures (a detailed proof of this statement is reported in the Purity and Separability section of the Supplementary Information). Therefore, the simultaneous observation of entanglement in both subspaces and purity in one of them is sufficient to confirm the presence of hyperentanglement.
Discussion
We demonstrated a silicon integrated source of energy-time and frequency hyper-entangled photon pairs with a net delivered rate of pairs exceeding 1 Gpairs/s. The hyperentanglement of the generated pairs has been verified by showing entanglement in both the time-energy and frequency-bin DoFs and high purity in one of the two subspaces. This result is reported for three spectral regions, distinguished by their detuning from the pump resonance. We proved that the source can deliver more than 1 Gpairs/s to an outside optical channel, even when combined with on-chip wide-band demultiplexers to route signal and idler combs to different outputs. The generated qubits retain 94.6% of fidelity with respect to a maximally entangled Bell state, and 96.3% of purity, on average, when the on-chip generation rate exceeds the 1 Gpairs/s rate. This work sets a new standard for high throughput sources of quantum states of light and we expect these results to be particularly useful for quantum communication over long distance channels, in particular via the use of high loss satellite links. The fact that the source is integrated on a chip greatly reduces its operational costs in terms of weight and energy usage. Even when accounting for the external laser pump and filters, the whole source would weight less than 1 kg and use less that 1 W, especially if implemented in a self-pumping configuration36,37,38,39, making this source feasible for flight with nanosatellites40 or leading to the possibility of having multiple sources working in parallel. Another possible domain of application for easy-to-deploy high rate source of entangled photon pairs is security in data centers, where high bandwidth is of extreme importance41.
Methods
Device characterization setup
The device was characterized with the setup depicted in Fig. 7. A continuous-wave (CW) tunable laser (Santec TSL-710) was tuned at the pump resonance frequency and then amplified with an Erbium doped fiber amplifier (Keopsys). The pump frequency mode of the resonator is chosen in correspondence with the crossing between the integrated DEMUX channels (λp ≃ 1546.9 nm). An isolator and a variable optical attenuator were added after the amplifier to control the input power. A fiber optical filter was used to suppress the pump amplified spontaneous emission. The input optical fiber was spliced to an ultra-high numerical aperture fiber (UHNA-7) that matches the numerical aperture of the integrated inverse taper coupler. The chip-fiber optical contact, as well as the mechanical stability of the coupling, are ensured by using index matching gel.
A tunable laser (Santec TSL-710) tuned to the pump resonance is amplified by an Erbium-doped fiber amplifier (Keopsys, EDFA). An isolator and a variable optical attenuator (VOA) regulate the input power, while a fiber optical filter suppresses amplified spontaneous emission (ASE). The signal is then coupled to the chip using UHNA-7 fiber spliced to match the integrated inverse taper coupler, with index matching gel ensuring stable optical contact.
Generation rate setup
The measurement of the generation rate of photon pairs emitted from a parametric process in silicon micro-ring resonators usually relies on coincidence measurements, whose purpose is to reveal the strong time correlation of the generated photon pairs33,42.
Due to the relatively narrow free spectral range (FSR), which results in a large number of frequency modes, we adopted two independent approaches to assess the generation rate of the source. First, we used a spectrograph coupled to a liquid nytrogen-cooled InGaAs CCD camera (SpectraPro 2500i from Princeton Instruments) to estimate how the generation efficiency changes as a function of the frequency shift from the pump and allowing us a first measure of the total rate. Secondly, we performed coincidence measurements on four selected pair of resonances (the employed wavelengths are reported in Figs. 2a and 3), to confirm that the generation efficiency as well as the measured rate were matching with the first measurement.
Before the photonic chip, four cascaded DWDM filters (Opneti) centered at the standard ITU (International Telecommunication Union) channel 38 (≃ 1546.92 nm) and of 100 GHz of bandwidth were employed as band-pass filters to attenuate the unwanted amplified spontaneous emission (ASE) of the laser. A series of eight notch filters, nominally complementary to those employed as ASE filters, was used as notch filter to attenuate the residual pump. The nitrogen-cooled spectrograph was used to monitor the spectrum of photon pairs generated by SFWM in the integrated resonator. In both configurations, the cascaded filters ensured a total rejection rate well above 100 dB.
A similar setup was used for the coincidence measurements, where we arbitrary select four pairs of resonances in the broad emission band of our source (see Fig. 2). Single photon detectors (SPD) with time tagging electronics were used instead of the CCD, while fiber Bragg gratings (from O/E Land, with bandwidth ≃ 12 GHz) were added in each output channel to select only one pair of resonances at a time.
Energy-time entanglement demonstration, setup
The experimental setup is schematically depicted in Fig. 8. To pump the process the amplified pump laser polarization is optimized with a polarization controller (PC) to match the designed TE mode. To avoid pollution of the spontaneous generated signal the amplified spontaneous emission (ASE) was suppressed with a narrowband bandpass filter (Opneti WDM centered at ITU channel 38, similarly as described in the previous section) before coupling to the chip with UHNA-7 fibers (3.5 dB/facet). Light was coupled out of the chip with two UHNA-7 fibers for the signal and the idler on-chip DEMUX channels, respectively. Then, for each channel the pump was rejected using a series of four notch filters, complementary to those employed as ASE filter in the input stage. A pair of energy-correlated resonances was then selected, one per channel, using a combination of a fibered Bragg filter and a circulator that serves as a narrowband filter and is indicated by the BPF (bandpass filter) block in Fig. 8.
The interferometer was stabilized using an auxiliary laser frequency-offset locked to the pump laser. A PID controller (Vescent d2-125) regulated a fiber phase shifter in the long arm of the interferometer. The auxiliary laser was injected counter-propagating to the photon pairs, and its transmission, held constant near the midpoint of the interference fringe, served as the error signal for the feedback loop. This operating point maximizes sensitivity to phase drifts due to the high fringe slope. The frequency offset is tunable, enabling control of the interferometer’s phase imbalance relative to the pump laser. The absolute accuracy in phase control of the interferometer is ≃ 0. 8°, mainly because of the limited 10 kHz bandwidth of the phase shifter.
The energy correlated pair was injected in the Franson interferometer and then collected from one of the output port where the pair was again split using a commercial DWDM (FS) and routed towards superconducting nanowires single-photon detectors (SNSPDs) with 37 ps time jitter and 85% quantum efficiency (PhotonSpot). A quTAG timetagger (1 ps digital resolution) logs all the arrival events and allows the coincidence histograms to be retrieved.
Frequency-bin entanglement demonstration, setup
The input stage of the setup, as well as the cascaded notch filter used to reject the pump at the output of the sample, were identical to those described in the Energy-time entanglement section. At the output, after pump rejection, for each of the demultiplexed signal and idler channels, two adjacent resonances were selected by means of a programmable waveshaper (Finisar). These pairs were spectrally symmetric in respect to the pump such that they were energy-correlated. Each channel was then routed through two electro-optic phase modulators and, last, to tunable fiber Bragg gratings with a 10 GHz stopband that allowed to filter out only one of the two resonances (Fig. 9).
The generated pairs are multiplexed on chip. An arbitrary projector is implemented by a waveshaper that is used as a bandpass filter to select two adjecent resonances per channel that are energy-correlated between the channels. An electro-optic phase modulator (EOM) realizes a superposition of frequency bins and finally tunable Bragg gratings (TBG) realize the projector on the computational base.
The modulation frequency corresponded to one FSR and the modulation amplitude was chosen in order to equalize amplitude of the carrier and the first order sidebands. Higher-order sidebands can be neglected, as they are subsequently suppressed by the fiber Bragg gratings. The combination of a phase modulator and a fiber Bragg grating implements, by setting independently the phase of each modulator as in \(\left[0,\pi /2,\pi ,3\pi /2\right]\) and tuning the Bragg filters, the projector on an arbitrary vector spanned by the canonical, and mutually unbiased, basis vectors \(\left\{\left\vert 0\right\rangle ,\left\vert 1\right\rangle \right\},\left\{\left\vert L\right\rangle ,\left\vert R\right\rangle \right\},\left\{\left\vert +\right\rangle ,\left\vert -\right\rangle \right\}\)43,44,45.
Then, switching off the modulators, the 4 projections on the computational basis are measured, for a total of 20 projections. For each setting of the modulators, the delay histogram was integrated for a time interval variable between 15 s when at low pump power (well below the 1 Gpairs/s emission rate) to 1 s of integration at a high emission rate. The integration time was selected to ensure that the estimated Poissonian error on each histogram bin remained below 5%. After the projection stage, photons reflected from Bragg filters are directed through fiber circulators to our SNSPDs. The combination of a Bragg grating and a circulator serves the purpose of a narrow-bandwidth bandpass filter (BPF) and it is indicated by the TBG block in Fig. 9. Raw time correlations are recorded with a time-tagger module (quTAG) and later processed with a custom library. The density matrix is then reconstructed with a standard maximum-likehood technique45 given as input the retrieved event histograms and the corresponding modulators settings.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Caspani, L. et al. Integrated sources of photon quantum states based on nonlinear optics. Light.: Sci. Appl. 6, e17100–e17100 (2017).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145 (2002).
Diamanti, E., Lo, H.-K., Qi, B. & Yuan, Z. Practical challenges in quantum key distribution. npj Quantum Inf. 2, 1–12 (2016).
Curty, M., Lewenstein, M. & Lütkenhaus, N. Entanglement as a precondition for secure quantum key distribution. Phys. Rev. Lett. 92, 217903 (2004).
Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. Nat. Phys. 8, 285–291 (2012).
Slussarenko, S. & Pryde, G. J. Photonic quantum information processing: A concise review. Appl. Phys. Rev. 6 (2019).
Kwiat, P. G., Waks, E., White, A. G., Appelbaum, I. & Eberhard, P. H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 60, R773 (1999).
Silverstone, J. W. et al. Qubit entanglement between ring-resonator photon-pair sources on a silicon chip. Nat. Commun. 6, 7948 (2015).
Calculating Fiber Optic Loss Budgets — thefoa.org. https://www.thefoa.org/tech/lossbudg.htm. [Accessed 21-07-2024].
Liang, J., Chaudhry, A. U., Erdogan, E. & Yanikomeroglu, H. Link budget analysis for free-space optical satellite networks. In 2022 IEEE 23rd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM) (IEEE, 2022). https://doi.org/10.1109/WoWMoM54355.2022.00073.
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Sidhu, J. S., Brougham, T., McArthur, D., Pousa, R. G. & Oi, D. K. Finite key effects in satellite quantum key distribution. npj Quantum Inf. 8, 18 (2022).
Ecker, S. et al. Strategies for achieving high key rates in satellite-based qkd. npj Quantum Inf. 7, 5 (2021).
Caspani, L. et al. Integrated sources of photon quantum states based on nonlinear optics. Light.: Sci. amp; Appl. 6, e17100–e17100 (2017).
Neumann, S. P., Selimovic, M., Bohmann, M. & Ursin, R. Experimental entanglement generation for quantum key distribution beyond 1 gbit/s. Quantum 6, 822 (2022).
Cabrejo-Ponce, M., Spiess, C., Muniz, A. L. M., Ancsin, P. & Steinlechner, F. Ghz-pulsed source of entangled photons for reconfigurable quantum networks. Quantum Sci. Technol. 7, 045022 (2022).
Mueller, A. et al. High-rate multiplexed entanglement source based on time-bin qubits for advanced quantum networks. Opt. Quantum 2, 64–71 (2024).
Steiner, T. J. et al. Ultrabright entangled-photon-pair generation from an AlGaAs-on-insulator microring resonator. PRX Quantum 2, https://doi.org/10.1103/PRXQuantum.2.010337 (2021).
Takesue, H. & Shimizu, K. Effects of multiple pairs on visibility measurements of entangled photons generated by spontaneous parametric processes. Opt. Commun. 283, 276–287 (2010).
Silverstone, J. W. et al. On-chip quantum interference between silicon photon-pair sources. Nat. Photonics 8, 104–108 (2014).
Heiss, D. Fundamentals of quantum information: quantum computation, communication, decoherence and all that, vol. 587 (Springer, 2008).
Zhang, Q., Xu, F., Chen, Y.-A., Peng, C.-Z. & Pan, J.-W. Large scale quantum key distribution: challenges and solutions [invited]. Opt. Express 26, 24260 (2018).
Kim, J.-H. et al. Noise-resistant quantum communications using hyperentanglement. Optica 8, 1524–1531 (2021).
Smith, J. F. Using hyperentanglement to enhance resolution, signal-to-noise ratio, and measurement time. Optical Eng. 56, 031210–031210 (2017).
Graffitti, F. et al. Hyperentanglement in structured quantum light. Phys. Rev. Res. 2, 043350 (2020).
Prabhu, A. V., Suri, B. & Chandrashekar, C. Hyperentanglement-enhanced quantum illumination. Phys. Rev. A 103, 052608 (2021).
Franson, J. D. Bell inequality for position and time. Phys. Rev. Lett. 62, 2205–2208 (1989).
Xavier, G. B., Larsson, J.-Å, Villoresi, P., Vallone, G. & Cabello, A. Energy-time and time-bin entanglement: past, present and future. npj Quantum Inf. 11, 129 (2025).
Congia, S. et al. Generation of hyperentangled photon pairs in the time and frequency domain on a silicon photonic chip. Opt. Lett. 50, 5117–5120 (2025).
Agrawal, G. P.Nonlinear Fiber Optics (Academic Press, 2019), 6th edn.
Lin, Q., Zhang, J., Fauchet, P. M. & Agrawal, G. P. Ultrabroadband parametric generation and wavelength conversion in silicon waveguides. Opt. Express 14, 4786 (2006).
Brendel, J., Gisin, N., Tittel, W. & Zbinden, H. Pulsed energy-time entangled twin-photon source for quantum communication. Phys. Rev. Lett. 82, 2594–2597 (1999).
Grassani, D. et al. Micrometer-scale integrated silicon source of time-energy entangled photons. Optica 2, 88–94 (2015).
Kues, M. et al. On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 546, 622–626 (2017).
Vallone, G., Ceccarelli, R., De Martini, F. & Mataloni, P. Hyperentanglement witness. Phys. Rev. A 78, 062305 (2008).
Reimer, C. et al. Integrated frequency comb source of heralded single photons. Opt. Express 22, 6535 (2014).
Reimer, C. et al. Cross-polarized photon-pair generation and bi-chromatically pumped optical parametric oscillation on a chip. Nat. Commun. 6, https://doi.org/10.1038/ncomms9236 (2015).
Garrisi, F. et al. Electrically driven source of time-energy entangled photons based on a self-pumped silicon microring resonator. Opt. Lett. 45, 2768 (2020).
Mahmudlu, H. et al. Fully on-chip photonic turnkey quantum source for entangled qubit/qudit state generation. Nat. Photonics 17, 518–524 (2023).
Oi, D. K. L. et al. Nanosatellites for quantum science and technology. Contemp. Phys. 58, 25–52 (2016).
Jain, N., Hoff, U., Gambetta, M., Rodenberg, J. & Gehring, T. Quantum key distribution for data center security – a feasibility study https://arxiv.org/abs/2307.13098 (2023).
Azzini, S. et al. Ultra-low power generation of twin photons in a compact silicon ring resonator. Opt. Express 20, 23100–23107 (2012).
Clementi, M. et al. Programmable frequency-bin quantum states in a nano-engineered silicon device. Nat. Commun. 14, 176 (2023).
Lu, H.-H., Liscidini, M., Gaeta, A. L., Weiner, A. M. & Lukens, J. M. Frequency-bin photonic quantum information. Optica 10, 1655–1671 (2023).
Borghi, M. et al. Reconfigurable silicon photonic chip for the generation of frequency-bin-entangled qudits. Phys. Rev. Appl. 19, 064026 (2023).
Acknowledgements
D.B. acknowledges the support of the Italian MUR and the European Union—Next Generation EU through the PRIN project number F53D23000550006—SIGNED. M. Borghi, E.B, M. Bacchi and M.L. acknowledge the PNRR MUR project PE0000023-NQSTI. A.B. S.O. and M.G. acknowledges European Union funding from the HyperSpace project (project ID 101070168).
Author information
Authors and Affiliations
Contributions
L.G. and A.B equally contributed to the manuscript writing. L.G. realized the design of the device, performed the measurements related to the generation rate characterization and contributed to the realization of the setup to measure the quantum state tomography. A.B and M.Ba. jointly contributed to the realization of the setup and performed all the measurements for the measurement of the quantum state tomography and processed the data. S.C. contributed to the linear characterizations at the wafer scale, assisted with manuscript revisions, and handled the submission. N.T. and M. Bo. provided the codebase for the analysis of the timestamps. M.L. and M. Bo. provided theoretical support. S.C., J.F.-T., Q.W., and S.O. supervised the design and the fabrication of the sample. M.G. and D.B. supervised the experimental activities. All authors reviewed and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gianini, L., Barone, A., Bacchi, M. et al. A silicon integrated source of hyper-entangled photon pairs with rate exceeding 1 billion pairs per second. npj Nanophoton. 3, 1 (2026). https://doi.org/10.1038/s44310-025-00093-2
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s44310-025-00093-2