Interpretable Kolmogorov-Arnold networks for enzyme commission number prediction

Abstract

Accurate prediction of enzyme commission (EC) numbers remains a significant challenge in bioinformatics, limiting our understanding of enzyme functions and their roles in biological processes. This paper presents the integration and evaluation of Kolmogorov-Arnold networks (KANs), a new deep learning paradigm, in state-of-the-art models for EC prediction. KAN modules are incorporated into existing models to assess their impact on predictive performance. Additionally, we introduce a novel interpretation method designed for KANs to identify relevant input features, addressing a key limitation of these networks. Our evaluation demonstrates that KAN integration substantially improves predictive accuracy, with up to a 15.7% increase in micro-averaged F₁ score and a 34.2% increase in macro-averaged F₁ score. Moreover, our interpretation method enhances the trustworthiness of predictions and facilitates the discovery of motif sites within enzyme sequences. This approach provides insight into enzyme functionality and highlights potential new targets for research. The code is available at: https://github.com/datax-lab/kan_ecnumber.

Introduction

Identification of protein chemical properties is essential for various biomedical applications, including protein-protein interaction prediction¹, diagnosing neurodegenerative diseases², and pharmaceutical development³. The protein chemical properties are categorized by Enzyme Commission (EC) numbers. This EC number system is critical for characterizing unknown enzymes which catalyze various commercial processes, such as pharmaceutical biosynthesis, food production, and bioremediation⁴. EC numbers categorize biological roles of enzymes in catalyzing major chemical reactions to biological processes across all organisms⁵. This classification system is organized into hierarchical levels: a class, a subclass, a sub-subclass, and a serial number (e.g., EC 1.2.3.4)^6,7,8.

Deep learning has significantly enhanced the automation of EC number predictions, enabling biologists to collaborate with advanced models to reduce the need for extensive and potentially unnecessary biological experiments. State-of-the-art deep learning models such as CLEAN⁹, DeepECtransformer¹⁰, DeepEC¹¹, ECPICK¹², ifDEEPre³⁰, HDMLF¹³, and HECNet¹⁴, have been developed to be increasingly effective when predicting enzymatic functions. This allows researchers to quickly annotate new sequences with high confidence, facilitating the functional characterization of enzymes.

Model interpretability is a crucial aspect of deep learning as it facilitates its understanding and assesses its robustness and trustworthiness. Interpretation of deep learning models for EC number predictions could provide insights into uncovering patterns in enzyme sequences, which could deepen the understanding of the enzymatic activities and guide future research efforts. DeepECtransformer showed a preliminary approach to identify active site and binding residues in EC number prediction¹⁰. ECPICK introduced an interpretation method that enhances the trustworthiness of its predictions and uncovers potential new motif sites in enzyme sequences¹².

Recently, Kolmogorov-Arnold Networks (KANs) have been highlighted as a promising alternative to multilayer perceptrons (MLPs)¹⁵. In KANs, weight parameters are replaced by learnable functions, parameterized as splines, based on the eponymous theorem¹⁶. KANs combine the strengths of splines and MLPs’ compositional layer structures by optimizing both feature learning and univariate function approximation. The resulting architecture shows better performance than MLPs for simple tasks, such as predicting multi-variable functions or solving partial differential equations¹⁵. KANs have demonstrated their effectiveness and interpretability for low-dimensional problems and non-stochastic datasets. However, to fully leverage their potential for high-dimensional challenges, including protein sequence analysis, further exploration is needed. While KANs offer excellent interpretability for simpler tasks, developing advanced methods for interpreting these models in complex, high-dimensional contexts will be crucial for their successful application in real-world biological analyses.

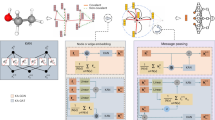
In this study, our hypotheses are (Fig. 1): (1) KANs could significantly enhance performance when integrated in state-of-the-art models for EC number prediction and (2) KANs could increase model interpretability and further enhance biological understanding of the parts of enzyme sequences that are relevant to a predicted EC number. To test these hypotheses, we explore the applicability of KANs as an alternative to MLPs for high-dimensional protein sequence analysis and propose a novel interpretation approach for KANs. We also explore the KAN architecture pruning strategy. The contributions of this study include (1) the first introduction of KANs to the real-world application of protein sequence analysis, (2) significant improvement of the predictive performance with KANs for EC number predictions, (3) the introduction of the pruning strategy to high-dimensional data, and (4) the development of a novel interpretation strategy for KANs.

Fig. 1: Overview of the study.

A KANs are integrated in state-of-the-art EC number prediction models by replacing the MLPs. B The resulting models are interpretable as they can identify motif sites in enzyme amino-acid sequences, as in^18,36. C State-of-the-art models with KAN yield enhanced performances compared to original ones.

Results

Overview of the study

We conducted experiments to evaluate whether KANs improve predictive performance and interpretability for the prediction of enzyme commission numbers. We considered three categories of state-of-the-art models: (1) convolutional neural network-based architectures, (2) attention-based architectures without pretraining, and (3) large language model-based architectures with pretraining. We selected (1) DeepEC¹¹, (2) DeepECtransformer¹⁰, and (3) CLEAN⁹ as representative models for these categories. These models provide a broad coverage of state-of-the-art approaches and establish a comprehensive basis for evaluating the effect of KAN integration across different paradigms. In addition to predictive performance, we developed an interpretation strategy specifically designed for KANs. Our interpretation scheme quantifies the contribution of amino acids in the input sequence to the model’s predictions, thereby inferring biologically relevant sites. The performance of the KAN integrated models, the effectiveness of the interpretation strategy, and the applicability of pruning are evaluated in the following sections. The details of the state-of-the-art models, their KAN-integrated models, and the interpretation strategy are provided in Methods.

Dataset

For this study, we used protein sequences from Swiss-Prot¹⁷ and the Protein Data Bank (PDB)¹⁸ released before September 2022. We retained sequences up to 1000 amino acids, removed redundancy by eliminating exact duplicates, and required complete four-level EC annotations; entries with incomplete EC numbers (e.g., “1.14.15.-”) were excluded.

Only identical sequences were removed to preserve sequence diversity, as minor variations may correspond to distinct enzyme functions. This decision was counterbalanced by evaluating the models on a dedicated low-similarity test set to avoid performance overestimation.

The dataset contains more than 200,000 protein sequences, approximately two-thirds from Swiss-Prot and one-third from PDB. We reported results at all four levels of the EC hierarchy. Fourth-level analyses are restricted to classes with at least 10 sequences. We also evaluated on a homology-reduced test subset in which each test sequence shares less than 50% sequence identity and less than 80% alignment coverage with any training sequence. Proteins annotated with multiple EC numbers were treated as multi-label, and performance is reported at each EC level using micro- and macro-averaged F₁.

The integration of KANs enhances predictive performance

We compared the predictive performance of three representative state-of-the-art architectures, DeepEC, DeepECtransformer, and CLEAN, with their KAN integrated counterparts. We split the dataset into training (80%), validation (10%), and test (10%) sets using stratified random sampling to preserve class ratios. Specifically, the sample sizes were approximately 160,000 for the training set, 20,000 for the validation set, and 20,000 for the test set. We optimized the models with the training dataset, while the hyper-parameters were fine-tuned with the Optuna framework¹⁹ using the validation dataset. Hyperparameter tuning was applied to both the MLP and KAN variants under a common search protocol. For each baseline architecture, we constrained model depth to not exceed the number of layers reported in the corresponding original manuscript. For width, the search space for the number of nodes per layer was {32,64,128,256,512}. The learning-rate range was [10⁻⁵, 10⁻²], and the dropout rate range was [0, 1]. For KAN variants, we also tuned KAN-specific hyperparameters: the spline order was selected from {1,2,3,4,5}, and the grid size from {3,5,10,20}.

All models were trained until convergence using identical early-stopping criteria based on the validation loss. Training was automatically terminated when no improvement in validation loss was observed for five consecutive epochs.

We assessed the performance of the models on the test dataset. We repeated the experiment ten times for reproducibility. We computed the micro- and macro-averaged F₁ score to evaluate the models. For each model, we selected the threshold for the final discriminative function that maximizes the macro-averaged F₁ score on the validation set. Then, we computed the evaluation metrics on the test set using these thresholds.

EC number prediction is a multi-label classification problem characterized by substantial class imbalance, making conventional metrics such as accuracy or AUC less informative. F₁-based metrics, including both macro- and micro-averaged variants, provide a balanced and reliable assessment by jointly considering false positives and false negatives across enzyme classes. This choice follows standard practice in enzyme function prediction studies, where F₁-scores are consistently used for fair and comparable evaluation^9,10,11. Each training run used a single NVIDIA A100 GPU (80GB RAM).

Across all models, KAN increased F₁ scores at every EC level (Table 1). DeepECtransformer showed relative gains in micro-averaged F₁ scores of 15.4% (level 1), 15.7% (level 2), 14.6% (level 3), and 10.2% (level 4) over the MLP variant. KAN-integrated DeepEC also improved the predictive performance consistently, with increases of 2.2%, 3%, 1.1%, and 1.7% across levels 1-4. CLEAN showed measurable gains (0.3 -1.1% across levels 1-4). Macro-averaged F₁ was also enhanced by KAN: DeepECtransformer improved by 13.3%, 19.2%, 34.2%, and 24.2% at levels 1-4, while DeepEC improved by 1.9%, 11.3%, 9.9%, and 25.1%. CLEAN again exhibited modest increases. Collectively, these results indicate that KAN yields consistent micro-level gains and substantial macro-level gains across architectures. All improvements were significant by the Wilcoxon signed-rank test (p < . 05).

Table 1 Micro- and macro-averaged F1 scores for all models across EC levels 1-4 on the test set

Furthermore, we evaluated the models by considering only low-similarity test set, where proteins shared at most 50% sequence identity and at most 80% coverage with the training data (Table 2). This setup reduces potential information leakage and provides a more rigorous measure of generalization. In this setting, KAN integration consistently improved predictive performance across all EC levels. For the micro-averaged F₁ score, DeepECtransformer achieved substantial gains, with improvements of 29.4% at level 1, 31.9% at level 2, 32.1% at level 3, and 32.4% at level 4. DeepEC also benefited considerably, with increases of 19.3%, 23.4%, 26.2%, and 29.2% across the four levels, while CLEAN showed consistent improvements of up to 2.3%. The macro-averaged F₁ score exhibited significant improvements. DeepECtransformer improved by 29.3% at level 1, 61.5% at level 2, 69.4% at level 3, and 94.2% at level 4, while DeepEC improved by 21.5%, 40.1%, 43.2%, and 52.5% across the same levels. CLEAN again showed stable but modest gains ranging from 1.7% to 5.6%. All improvements were significant by the Wilcoxon signed-rank test (p < 0.05). These results highlight that the benefits of KAN integration are amplified under reduced sequence similarity, especially at deeper EC levels where functional prediction is more challenging.

Table 2 Micro- and macro-averaged F1 scores for all models across EC levels 1-4 on the test subset restricted to sequences with less than 50% sequence identity and less than 80% coverage relative to the training set

KANs identify existing motif sites using the proposed interpretation strategy

We verified the proposed KAN interpretation strategy by comparing the identified amino acids with well-characterized motif sites in enzyme sequences. We computed a contribution score for each amino acid to represent its impact in the model’s predictions from a given protein sequence. We focused on the KAN-integrated DeepEC model.

The proposed interpretation strategy computed the intermediate scores of the activation maps, which are the input of the KAN module. To map the intermediate scores (s = {s_q; 1 ≤ q ≤ 384}) to the contribution scores of the protein sequence (γ = {γ_q; 1 ≤ q ≤ 1000}), we identified the segments of the sequence that produced the 384-dimensional input vector to the KAN module (v = {v_j; 1 ≤ j ≤ 384}). Each input value v_j is the maximum value of the corresponding activation map f_j, and ι_j is its index, such as:

$${\bf{v}}=\{\max ({{\bf{f}}}_{{\bf{j}}});1\le j\le 384\},$$

(1)

$${\boldsymbol{\iota }}=\{{\rm{argmax}}({{\bf{f}}}_{{\bf{j}}});1\le j\le 384\}.$$

(2)

We grouped the intermediate scores from the activation maps of size z (i.e., kernel size: 4, 8, or 16) and index i in a set ${{\mathcal{J}}}_{i,z}$. Mathematically, ${{\mathcal{J}}}_{i,z}$ is:

$${{\mathcal{J}}}_{i,z}=\left\{{s}_{j}\in {\bf{s}}{| \iota }_{j}=i\wedge {{\bf{f}}}_{{\bf{j}}}\in {{\mathbb{R}}}^{1000-z+1}\right\},$$

(3)

where ∧ is the logical AND operator. Thus, the intermediate scores (${\lambda }_{q}^{(z)}$) of the q^th amino acid from the activation maps of size z is:

$${\lambda }_{q}^{(z)}=\mathop{\sum }\limits_{i=\max (1,q-z)}^{\min (q,1000-z+1)}\sum _{j\in {{\mathcal{J}}}_{i,z}}j,$$

(4)

where the range from $\max (1,q-z)$ to $\min (q,1000-z+1)$ represents all the possible indices of an activation map of size z, which is computed from the q^th amino acid. To compute the contribution score (γ_q) of the q^th amino acid in the input protein sequence, we summed the intermediate scores of activation maps of size 4, 8, and 16 computed from the q^th amino acid, such as:

$${\gamma }_{q}={\lambda }_{q}^{(4)}+{\lambda }_{q}^{(8)}+{\lambda }_{q}^{(16)}.$$

(5)

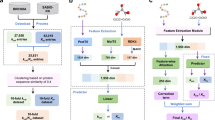
For the validation of the proposed interpretation strategy, we considered enzyme sequences from Cytochrome P450 (CYP) (CYP106A2 family [EC 1.14.15] and CYP7B1 family [EC 1.14.14]), whose biological functions are well-reported in various organisms, from bacteria to mammals²⁰. CYPs belong to a super-family of enzymes that have been extensively studied and widely utilized in the pharmaceutical industry and in clinical and disease-related medicine²¹. CYPs are monooxygenases that catalyze the incorporation of a single oxygen atom into substrates. For example, CYP106A2 and CYP7B1 enzymes perform similar biological functions in different organisms (e.g., bacteria and humans). The bacterial CYP106A2 group plays a crucial role in attaching a hydroxyl group to steroid structures. Whereas, the human CYP7B1 group is involved in the metabolism of endogenous oxysterols and steroid hormones, including neurosteroids, in eukaryotic cells. Despite these functional differences, both CYP106A2 and CYP7B1 share the same first and second digits in their EC numbers, indicating that they belong to the same general category of oxidoreductases (EC 1) that act on paired donors and involve the incorporation or reduction of molecular oxygen (EC 1.14).

We performed the model interpretation on 13 sequences from the bacterial CYP106A2 enzyme family. Specifically, we considered 5XNT²² and 4YT3²³ from the Protein Data Bank (PDB), along with 11 protein sequences from Swiss-Prot that share over 90% sequence similarity with 5XNT and 4YT3. We computed the contribution scores of amino acids for each protein sequence using the KAN interpretation method and ECPICK, which is the current state-of-the-art interpretation strategy to identify motif sites in enzyme sequences¹². Both KAN and ECPICK correctly predicted all of the protein sequences as belonging to the 1.14.15 class.

The 13 protein sequences were aligned by a multiple sequence alignment (MSA) tool (e.g., Clustal Omega²⁴) for graphical comparison. Conserved amino acids were identified by ESPript3²⁵, colored in red. Fig. 2A illustrates the corresponding contribution scores of KAN and ECPICK along with motif sites (e.g., oxygen-binding, EXXR, and heme-binding domains) in black boxes and substrate recognition sites (SRS 1-6) in green boxes, which are key regions relevant to the enzyme function. High contribution scores are indicated in dark red, with lower scores gradually transitioning to white along the gradient scale.

Fig. 2: The model identifies significant amino acids contributing to the prediction, demonstrating trustworthiness in its predictions and discovering motif sites.

High contribution scores are indicated in dark red, with lower scores gradually transitioning to white along the gradient scale. A A partial sequence, spanning positions 182 to 418, from the CYP106A2 family is displayed. This segment was selected for detailed analysis due to its significant role in CYP106A2. Motif sites are outlined in black boxes and substrate recognition sites (SRS 1-6) in green boxes. KAN interpretation highlights the oxygen-binding site and the hem-binding motif, which are primary active sites within the CYP106A2 group. On the other hand, ECPICK only recognizes the oxygen-binding motif site. B Visualizes the four motif sites in the protein sequences of the CYP7B1 family with contribution scores computed by the proposed KAN interpretation, which emphasizes the central role of these regions in predicting the enzymatic function (EC 1.14.14).

The proposed KAN interpretation method successfully identified both the oxygen binding motif site and hem-binding motif sites of the bacterial CYP106A2 family. The identification of the binding motif sites aligns with established biological knowledge, which determines the primary and secondary levels of the given EC number (e.g., 1.14). However, ECPICK did not recognize the hem-binding motif site, which is crucial for determining the CYP’s enzyme function. The EXXR motif site was not identified by either model, as EXXR may not be sufficiently discriminative for the given EC number (e.g., 1.14). Note that ECPICK and KAN-integrated DeepEC share the exact same CNN backbone. Therefore, the observed gains in motif localization reflect the contribution of KAN layers and the proposed interpretation rather than differences in architectures.

We quantitatively validated the proposed interpretation method by comparing the contribution scores with known motif sites, i.e., oxygen-binding, EXXR, and heme-binding motifs. For this evaluation, we computed the recall-at-k scores, where k corresponds to the top 1%, 2%, 5%, and 10% of amino acids ranked by contribution scores (Table 3).

Table 3 Quantitative evaluation of motif detection using recall-at-k

These ranges correspond to the expected density of functionally important residues: enzymes typically contain approximately 3–4 catalytic residues (≈3.5 per enzyme²⁶), while 10–13% of residues are estimated to contribute indirectly to function²⁷. Consequently, lower k values emphasize catalytic precision, whereas higher values capture motif-level interpretability.

We focused on recall because known motif sites enumerate only annotated positives (i.e., motif residues) and do not provide a validated negative set. Treating unannotated residues as negatives would conflate unknown sites with true negatives, whereas recall at k measures how well the highest-scoring positions recover curated positives without assuming negatives. Recall-at-k scores were computed separately for each protein sequence as the fraction of annotated motif residues captured within the top k% of positions ranked by contribution score, and the reported values are the arithmetic means across sequences. Our proposed KAN interpretation consistently achieved higher recall rates than ECPICK. For instance, at the 5% threshold, the KAN interpretation reached a recall of 0.73 compared to 0.26 for ECPICK. At the 10% threshold, the KAN method achieved 0.78 recall, while ECPICK achieved only 0.27. These quantitative results confirm that the proposed KAN interpretation strategy highlights biologically relevant motifs and achieves higher overlap with annotated motif sites compared to ECPICK.

We also analyzed the proposed strategy within the CYP7B1 group across the three organisms: mice, rats, and humans. KAN-integrated DeepEC accurately predicted the enzyme functions of the protein sequences (i.e., 1.14.14). Moreover, the contribution scores effectively highlighted the essential motif sites of this CYP enzyme family (Fig. 2B). Specifically, the hem-binding site was highly scored across the three species. The I-helix, which contains the oxygen-binding site, and the C-helix regions were identified by the proposed interpretation, whereas the steroidogenic conserved domain was assigned low contribution scores.

High contribution scores were observed in the essential motif sites on both the CYP106A2 and CYP7B1 families. The identified sequential patterns aligned well with conserved domains or existing motif sites. This analysis was achieved without the time-consuming computational processes typically required for sequence similarity and secondary structure comparison. The proposed interpretation strategy provides trustworthiness in prediction by identifying existing motif sites related to the enzyme function and could potentially discover unknown motif sites within enzyme sequences.

Pruning for architecture optimization

We conducted an additional experiment to evaluate the pruning strategy for KANs. We tested pruning to remove irrelevant connections of the KAN-integrated DeepEC model. We initiated this experiment by training a four-layer KAN of dimensions 512, 1024, 512, and 229 in KAN-integrated DeepEC optimized to predict the third level of the EC hierarchy. After training the model, we applied pruning as defined in (12) with varying thresholds (θ).

Figure 3 illustrates the macro-averaged F₁ scores of the pruned models in relation to the number of parameters controlled by varying thresholds, with the rightmost point corresponding to the unpruned baseline model.

Fig. 3: Pruning of a KAN-integrated DeepEC.

A KAN model is pruned with varying thresholds. The number of parameters thus decreases incrementally as the thresholds increase. The rightmost point corresponds to the unpruned baseline model, serving as a reference for comparison. We observed that the best performance is yielded by a pruned model. The unpruned model contains 36.68% more parameters than the best-performing model.

The best model achieved a macro-averaged F₁ score of 82% and contains 12,020,528 parameters, whereas the unpruned model yielded a macro-averaged F₁ score of 81.46% with 16,429,184 parameters. The unpruned model comprises 36.68% more parameters than the pruned model. Hence, the removal of the connections increases the efficiency and robustness of the model as well as its predictive performance. Pruning reduces the size of the network without retraining the model. However, the improvement in predictive performance and efficiency highly depends on the architecture of the unpruned model.

Discussion

In this study, we have investigated the potential of KAN for EC number prediction using protein sequences. We evaluated the integration of KAN modules in three state-of-the-art deep learning models for EC number prediction and observed consistent and statistically significant improvements across all EC levels. This demonstrates that KAN can enhance existing enzyme function predictors without altering their core architectures. We also proposed a novel interpretation method specifically designed for KAN that enables residue-level attribution of enzymatic function and successfully identifies biologically meaningful motif sites. The proposed method quantitatively outperforms existing approaches such as ECPICK in recovering known catalytic residues, providing both trustworthiness and biological insight. Furthermore, all interpretability evaluations were performed consistently across multiple homologous sequences and compared quantitatively against ECPICK using recall-at-k metrics, confirming the robustness and reproducibility of the proposed method. In future works, we plan to extend the interpretability analysis to a broader range of enzyme families as high-quality motif annotations become increasingly available. Finally, we have evaluated the pruning strategy for protein sequences. We have observed that pruning is applicable to this task and optimizes the KANs’ architecture without having to retrain the model. Overall, our results highlight KAN as a promising and interpretable modeling framework for advancing enzyme function prediction and supporting the discovery of new potential motif sites.

The consistent outperformance of KANs across architectures may be partly explained by properties highlighted in the original KAN paper, which make them particularly suitable for biological sequence modeling. Unlike standard MLPs that rely on fixed activation functions, KANs learn adaptive spline functions that can locally adjust curvature and smoothness during training. This flexibility allows fine control over nonlinear behavior, enabling the model to capture gradual biochemical variations while remaining sensitive to sharp functional changes near catalytic or binding residues. The structured and smooth function space of KANs was also shown to promote improved generalization. In our setting, these properties likely complement encoder modules such as CNNs or attention layers by refining the encoded sequence features into more accurate and biologically meaningful representations of enzyme function.

However, KANs introduce additional computational complexity due to their function-learning paradigm. We quantified this aspect by measuring the training and inference times of KAN-integrated architectures relative to their MLP counterparts under identical hardware and dataset conditions. The computational overhead varied across models and increased with the dimensionality of the KAN layers. The KAN-integrated DeepEC trained ~1.6 × slower and inferred ~1.1 × slower than the MLP version, the KAN-integrated CLEAN trained ~ 2 × slower and inferred ~1.2 × slower, and the KAN-integrated DeepECTransformer trained ~2.6 × slower and inferred ~2.5 × slower. We observe that models with higher-dimensional KAN layers exhibited proportionally larger differences in training and inference times compared to their MLP counterparts. These differences likely reflect the early-stage nature of current KAN implementations rather than intrinsic model inefficiency. The existing libraries are still undergoing active optimization, and recent updates have already demonstrated substantial improvements in computational speed and memory usage.

In this study, we evaluated the proposed interpretation strategy using a limited set of enzyme families for which high-quality and experimentally validated motif annotations are available. Such residue-level annotations are not systematically available across most enzyme classes, and consistent functional labeling remains scarce in public databases. For this reason, our assessment focused on well-characterized sequences to ensure reliable comparison between the identified residues and established motif sites. While this provides a controlled and biologically meaningful benchmark, a more comprehensive and robust evaluation will require broader, systematically curated motif annotations. Future work should extend the interpretability analysis to additional enzyme families as such high-quality data become more widely accessible.

This study opens several paths for future research into KANs. Their ability to capture complex relationships within protein sequences could be further explored by integrating them with other protein sequence analysis methods. Moreover, the interpretability of KANs could be enhanced by coupling the proposed method with other explainability techniques, allowing for a better understanding of how specific motifs contribute to the prediction of enzyme functions. Overall, this study demonstrates the promising future of KANs and emphasizes the importance of model interpretability regarding protein sequence analysis. Future work in this area could significantly advance the development of robust and efficient models for handling complex biological tasks, which will contribute to the advancement of biological understanding.

Methods

This section provides details about the fundamentals of the current deep learning models for EC number prediction, the KAN architecture, and its architecture-tuning approach called pruning. Then, we introduce our novel interpretation strategy, which identifies relevant input features to the predictions. Finally, we explain how KANs can be integrated into state-of-the-art models.

Current deep learning models for EC number prediction

Deep learning models for EC number prediction can be broadly categorized into two main types: CNN-based models and attention-based models. The attention-based models can be further divided by training paradigm: (1) conventional models trained directly for EC classification and (2) large language models pretrained on large-scale protein sequence datasets and subsequently fine-tuned for enzyme classification. CNN-based models, such as DeepEC¹¹, ECPICK¹², and ECNet²⁸, leverage convolutional layers to extract hierarchical features from enzyme sequences or structures, effectively capturing local patterns and spatial information. Conventional attention-based models, such as DeepECtransformer¹⁰ and BEC-Pred²⁹, utilize the self-attention mechanism to improve the models’ ability to capture long-range dependencies and context.

Recent studies have further advanced EC number prediction using large-scale protein language models and transformer-based architectures. Methods such as CLEAN⁹, BEC-Pred²⁹, ifDEEPre³⁰, and GraphEC³¹ leverage embeddings from foundation models to improve EC number prediction. Comparative analyses of protein language models like ESM-2 and ProtT5 have also demonstrated strong generalization for enzyme annotation³². In addition, hierarchical frameworks such as GloEC³³ highlight the importance of modeling the EC hierarchy explicitly. These advances underscore the rapid progress of pretrained transformer-based approaches in enzyme function prediction.

Each category offers unique strengths and applications, reflecting the diverse approaches in state-of-the-art EC number prediction.

DeepEC is a representative example of CNN-based models. At its core, DeepEC employs convolutional layers to capture patterns within protein sequences, which are crucial for identifying enzymatic functions¹¹. Its architecture includes multiple convolutional layers that extract hierarchical features, followed by pooling layers to reduce dimensionality and emphasize the most relevant information. This is then complemented by MLP layers, which integrate the extracted features and perform the final classification to predict the EC numbers. This approach enables DeepEC to leverage the strengths of convolutional neural networks in handling complex and high-dimensional enzyme sequences.

DeepECtransformer is a state-of-the-art attention-based architecture for enzyme function prediction¹⁰. It follows the Transformer paradigm³⁴, employing stacked self-attention layers directly optimized for EC number prediction. This design captures long-range dependencies and contextual patterns along the sequence. It is well-suited to enzyme classification, where residues critical for function are not necessarily adjacent in the primary sequence but interact across distant regions.

CLEAN stands out as a prominent example of LLMs as it builds upon the ESM-1b model³⁵ as its foundation, which is an LLM specifically designed for protein sequences. To make its predictions, CLEAN integrates MLP layers on top of ESM-1b. This combination allows CLEAN to leverage ESM-1b’s deep contextual embeddings while utilizing the MLP layers to output a representation of the input sequence. CLEAN employs contrastive learning techniques, which train the model to encode protein sequences such that enzymes with similar activities are represented closely in the embedding space, while those with different activities are positioned farther apart.

Architecture of Kolmogorov-Arnold Networks

KANs, like MLPs, are fully connected feed-forward networks that leverage dense connectivity to capture complex and non-linear relationships for inferring desired outcomes. MLPs learn weight parameters and use fixed activation functions, whereas KANs do not learn weights; rather, they replace fixed activation functions with learnable activation functions (Fig. 4). According to the Kolmogorov-Arnold representation theorem, any complex high-dimensional function can be represented by a polynomial number of univariate functions¹⁶. Thus, KAN, which is a neural network with compositions of univariate functions, can effectively model complex and high-dimensional functions. In KANs, each layer of a neural network represents a component of the compositions, which collectively model relevant relationships within the data.

Fig. 4: Representation of a two-layer KAN of dimensions 2 and 1, with an input of dimension 2.

(x_0,1, x_0,2). ϕ_l,j,i is the activation function between the ith node of the lth layer, and the jth node of the l + 1th layer. For any layer, each node is connected to all the nodes of the next layer.

A KAN (${\mathcal{K}}:{\bf{x}}\to \hat{{\bf{y}}}$) is formulated as:

$${\mathcal{K}}({\bf{x}})=({\Phi }_{L-1}\circ {\Phi }_{L-2}\circ \cdots \circ {\Phi }_{0})({\bf{x}}),$$

(6)

where L is the number of layers, Φ_l is a function matrix, and ∘ is the composition operator, such as (Φ₁ ∘ Φ₂)(x) = Φ₁(Φ₂(x)). The output $\hat{{\bf{y}}}$ is obtained by computing the composition of L functions (Φ_l) from the input x. The function matrix, Φ_l, is a set of activation functions ϕ_l,j,i, connecting the i^th neuron in the l^th layer to the j^th neuron in the l + 1^th layer, such as:

$${\Phi }_{l}(\cdot )=\left(\begin{array}{cccc}{\phi }_{l,1,1}(\cdot )&{\phi }_{l,1,2}(\cdot )&\cdots \,&{\phi }_{l,1,{n}_{l}}(\cdot )\\ {\phi }_{l,2,1}(\cdot )&{\phi }_{l,2,2}(\cdot )&\cdots \,&{\phi }_{l,2,{n}_{l}}(\cdot )\\ \vdots &\vdots &&\vdots \\ {\phi }_{l,{n}_{l+1},1}(\cdot )&{\phi }_{l,{n}_{l+1},2}(\cdot )&\cdots \,&{\phi }_{l,{n}_{l+1},{n}_{l}}(\cdot )\end{array}\right),$$

(7)

where the layer sizes are [n₀, n₁, . . . , n_L−1].

For the activation function, ϕ_l,j,i, the input value (x_l,i) is called pre-activation, and the output of the activation function (${\tilde{x}}_{l,j,i}$) is called post-activation, such as:

$${\tilde{x}}_{l,j,i}={\phi }_{l,j,i}({x}_{l,i}).$$

(8)

Then, the pre-activation value for the j^th neuron in the next layer is x_l+1,j, which is the sum of post-activations from the previous layer (${\tilde{x}}_{l,j,i}$), such as:

$${x}_{l+1,j}=\mathop{\sum }\limits_{i=1}^{{n}_{l}}{\tilde{x}}_{l,j,i}=\mathop{\sum }\limits_{i=1}^{{n}_{l}}{\phi }_{l,j,i}({x}_{l,i}).$$

(9)

A post-activation (ϕ_l,j,i(x_l,i)) is computed as:

$${\phi }_{l,j,i}({x}_{l,i})={w}_{b}b({x}_{l,i})+{w}_{s}\,\text{spline}\,({x}_{l,i}),$$

(10)

where w_b and w_s are trainable parameters that control the overall magnitude of the activation function, and the function b is the SiLU function (i.e., $b({x}_{l,i})={x}_{l,i}/(1+{e}^{-{x}_{l,i}})$) which allows the networks to bypass one or more layers, similarly to residual connections in MLPs. The spline function is defined as:

$$\,{\text{spline}}\,({x}_{l,i})=\mathop{\sum }\limits_{g=1}^{G}{c}_{g}{B}_{g}({x}_{l,i}),$$

(11)

where B_gs are piecewise polynomial functions called B-splines, and c_gs are trainable parameters. The resulting linear combination is a spline of order k, which is defined on a specific interval of G grid-points.

The complexity of a KAN with L layers of width N is O((G + k)N²L), which would be O(N²L) for the same dimension MLP. However, KAN has been proven to require much smaller networks¹⁵.

KAN Pruning Method

In this section, we present an architecture-tuning strategy for KANs named pruning¹⁵. Pruning is a sparsification technique to enhance the efficiency of KANs by systematically reducing the number of network parameters. The pruning strategy is explored with detailed explanations, highlighting its contribution to improving the performance and efficiency of KANs.

Pruning reduces the number of parameters of the network by suppressing irrelevant connections (Fig. 5A). The goal of pruning is to make the network sparser, which reduces computational costs and memory usage. Neurons are considered irrelevant if the maximum value between their incoming and outgoing scores is not higher than a threshold (θ). Mathematically, the i^th neuron of the l^th layer is pruned if:

$$\max\, (\mathop{\max}\limits_{k}\,(| {\phi }_{l-1,i,k}{| }_{1}),\mathop{\max}\limits_{j}\,(| {\phi }_{l+1,j,i}{| }_{1})) < \theta .$$

(12)

Pruning does not require the model to be retrained, which makes it a cost-effective sparsification technique that manages the trade-off between efficiency and predictive performance.

Fig. 5: A KAN before and after pruning.

Pruning removes the irrelevant connections of the network, allowing the model to contain fewer parameters and to perform faster predictions without retraining it.

KAN Interpretability

We propose a new systematic interpretation strategy that identifies a feature set which is relevant to the prediction and address a critical gap, as such interpretation methods do not exist for KANs. This strategy identifies relevant amino acids in the protein sequence that contribute to a given prediction, thereby offering insights into biological processes of enzyme functions.

In a KAN with L layers of dimensions [n₀, n₁, . . . , n_L−1], a posterior probability (${\hat{y}}_{c}$) is computed by applying the sigmoid function on the last activation value (s_c) for the class c, such as:

$$\,{\text{Sigmoid}}\,({s}_{c})={\hat{y}}_{c}.$$

(13)

The relative contribution to the prediction of each neuron in the L − 1^th layer is represented by a vector, s_L−1 = {s_L−1,j; 1 ≤ j ≤ n_L−1}, as:

$${s}_{L-1,j}=\frac{\max\,({\phi }_{L-1,c,j}({x}_{L-1,j}),0)}{{s}_{c}},$$

(14)

where ϕ_L−1,j,i is the activation function between the i^th node of the L − 1^th layer and the j^th node of the L^th layer.

For any layer l between 1 and L − 2, x_l,i is the pre-activation value of ϕ_l,j,i as defined in Eq. (9). We define s_l = {s_l,j; 1 ≤ j ≤ n_l} as the contribution scores for each neuron of the l^th layer, which is computed as:

$${s}_{l-1,j}=\mathop{\sum }\limits_{i=1}^{{n}_{l}}\left|\frac{{\phi }_{l-1,i,j}({x}_{l-1,j})}{\mathop{\sum }\nolimits_{k = 1}^{{n}_{l-1}}{\phi }_{l-1,i,k}({x}_{l-1,k})}\right|\times {s}_{l,i}.$$

(15)

This operation (Eq. (15)) is repeated on each layer, starting with the L − 2^th layer to the first layer, thus obtaining the contribution scores s₁ of the input x.

Integration of KAN in state-of-the-art models

In this study, we integrated KAN layers into state-of-the-art models in three categories: CNN-based models, attention-based models, and LLMs for protein sequences. We performed a thorough assessment of their impact and effectiveness, covering the most advanced and high-performing architectures available.

The KAN layers were implemented using established open source references, which we adapted and fine-tuned to ensure stable training and compatibility with the different model frameworks.

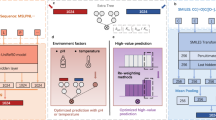
For the CNN-based model, we integrated KAN layers in the DeepEC architecture (Fig. 6A). We replaced the three MLP layers with two KAN layers of 512 and 1938 nodes, respectively, with a grid size of three and a spline order of three, obtained through fine-tuning the hyper-parameters of KAN-integrated DeepEC. The KAN layers were implemented using established open source references, which we adapted and fine-tuned to ensure stable training and compatibility with the different model frameworks.

Fig. 6: Integration of KAN into state-of-the-art models improves their predictive performances.

In DeepEC (A) KAN layers replace MLP layers after the three parallel CNNs. In the DeepECtransformer (B), both the neural networks following the multi-headed attention module and the output layer are replaced by KAN layers. In CLEAN (C), KAN layers replace the MLP layers after the ESM-1b transformer.

For the attention-based model, KAN layers were integrated into DeepECtransformer by replacing the MLP layers after the multi-headed attention modules and the classification layers (Fig. 6B)³⁴. After the hyper-parameter tuning, we replaced the two MLP layers following the multi-attention head module by two KAN layers comprising 512 and 128 nodes, with a grid size of three and a spline order of three. The KAN classification layers have a fixed size that corresponds to the number of EC numbers in our dataset (i.e., 1938).

For the LLM model, we enhanced the CLEAN architecture by replacing its three MLP layers with two KAN layers, while maintaining dropout and layer normalization as proposed in the original model. Following the hyper-parameter optimization, the KAN-integrated CLEAN model was configured with two KAN layers of 512 and 256 nodes, a grid size of ten, a spline order of three, and a dropout rate of 0.1. (Fig. 6C).