Introduction

Machine learning (ML) and artificial intelligence (AI) methods have been rapidly adopted in healthcare for a broad range of data-driven applications, such as predictive modeling1, personalized treatment recommendations2, and resource allocation in health systems3. However, ensuring health equity remains a critical challenge, particularly when algorithmic findings directly impact clinical decision-making and patient care within health systems4. Concerns have grown regarding the underperformance of ML and AI systems for historically underserved populations, including women and individuals from lower socioeconomic backgrounds5. For instance, studies have shown that Black patients are more frequently underdiagnosed with chronic obstructive pulmonary disease (COPD) compared to Hispanic White patients, emphasizing the need to address these disparities5,6. Similarly, in postpartum depression, ML models trained on gender-imbalanced data favored White women, even when Black women were predicted to be at higher risk, illustrating racial disparities in healthcare outcomes7. Medical imaging datasets, such as X-rays, also produce biased classifiers due to gender-imbalanced data, leading to consistently poorer performance for underrepresented genders8.

Algorithmic disparity9, often referred to as “biased” or “unfair” decision-making, arises when predictive models perform unequally across subgroups10,11 defined by sensitive attributes such as gender, race/ethnicity, and socioeconomic status12. These inequities span various healthcare domains, including COVID-194,9,10, stroke13, emergency medicine14,15,16, cardiovascular disease17, cancer18, and organ transplants19. Despite growing efforts to develop fair models12, most studies rely on single, centralized datasets. However, healthcare data are often distributed across multiple institutions, such as electronic health records (EHRs) from different hospitals or mobile health data from users’ devices20,21. Aggregating these diverse data sources could accelerate research and improve care quality22, but privacy regulations pose significant barriers23.

Federated learning (FL), or federated ML (FML), offers a promising solution by enabling participants to collaboratively train models without sharing sensitive data21, making it an increasingly popular approach in medical research24,25. However, while FL adoption is increasing, most studies focus primarily on overall predictive performance, often overlooking its potential to address algorithmic disparities25. Evidence suggests that standard FL algorithms struggle to reduce algorithmic biases26,27, leading to models that retain their unfairness when transitioning from single-site analyses to FL settings. Local biases may persist or even be amplified due to the lack of centralization, as each institution contributes heterogeneous data that reflect varying socio-demographic characteristics and clinical practices, introducing diverse biases.

Although some studies have investigated these disparities within FL contexts, they predominantly rely on conventional ML datasets rather than real-world clinical data27,28,29, raising concerns about the generalizability of their findings to actual healthcare systems. To address these gaps, we propose Fair Federated Machine Learning (FairFML), a unified solution to promote fairness in FL among distributed healthcare systems. As a proof of concept, we used real-world out-of-hospital cardiac arrest (OHCA) data from the United States, focusing on gender disparities—a critical concern for equity in OHCA care15,30,31. These disparities are often attributed to complex factors, including differences in layperson bystander cardiopulmonary resuscitation (CPR)15. This case study aims to demonstrate FairFML’s effectiveness in mitigating such disparities, while maintaining prediction performance comparable to both local and centralized analyses.

Results

Model performance and fairness evaluation

Figure 1 illustrates the partitioning of 7425 individual episodes into four or six sites following the cohort formation process, with a 7:3 split for training and testing data. Supplementary Table 1 in the Supplementary Materials summarizes the baseline characteristics of the overall cohort and each site under different experimental conditions. In cases I and III, where clients were partitioned by race/ethnicity, significant distribution differences were observed, with the proportion of White individuals ranging from 88.9% to 48.2%. In cases II and IV, where clients were partitioned by age, the mean age varied considerably, ranging from approximately 60 to approximately 70 years. Outcome prevalence varied from 7.5% to 12.6%, and other variables also exhibited heterogeneous distributions, reflecting the real-world demographic differences across regions.

Fig. 1: Cohort formation flow diagram.
figure 1

A total of 7425 episodes were partitioned heterogeneously across clients by race/ethnicity.

Full size image

Details of the experimental setup, including the tuning of \({\rm{\lambda }}\) and \({\rm{\gamma }}\) and other general hyperparameters for FL, are provided in Supplementary Fig. 2 and Supplementary Table 2 in the Supplementary Materials. This tuning process is crucial for managing the inherent trade-off between model fairness and predictive performance, as increasing λ prioritizes fairness, typically leading to a controlled decrease in overall accuracy.

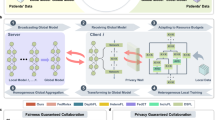
We assessed the performance of the federated model developed using FairFML by comparing it to the centralized model, local models trained independently at each site, and general FL models (FedAvg and Per-FedAvg). Specifically, FairFML integrates with these FL frameworks by replacing their standard model loss function with a \({\rm{\lambda }}\)-weighted fairness loss during training, forming FairFML (FedAvg) and FairFML (Per-FedAvg). This process is visually depicted in Fig. 2 and detailed algorithmically in Supplementary Fig. 1 in the Supplementary Materials. Figure 3 illustrates the performance of each model across the testing datasets for all sites in the Case IV experimental scenario. Results for the other three cases are provided in Supplementary Figs. 3–5 of the Supplementary Materials, detailing the performance comparison and fairness metrics for Case I (race/ethnicity, 4 sites), Case II (age, 4 sites), and Case III (race/ethnicity, 6 sites), respectively. These figures all show that fairness metrics generally improved across all clients, aligning with the overall trend across sites, with only a minor trade-off in predictive performance.

Fig. 2: Workflow of FairFML.
figure 2

(1) Client-side training; (2) Federated parameter exchange; (3) Fairness loss incorporation.

Full size image
Fig. 3: Results of case IV in our experiment.
figure 3

Performance comparison of the proposed FairFML method against baseline models using gender as the sensitive attribute. Area Under the Curve (AUC) measures predictive performance, while demographic parity difference (DPD), equalized odds difference (EOD), demographic parity ratio (DPR), and equalized odds ratio (EOR) assess fairness. Error bars represent the 95% confidence interval (CI) for each metric.

Full size image

Key findings from Fig. 3 and Supplementary Figs. 3–5 include: (1) FairFML consistently outperformed other baseline models in fairness, demonstrating substantial improvements across metrics such as decreases in DPD and EOD (moving closer to 0) and increases in DPR and EOR (moving closer to 1). It maintained predictive performance nearly identical to other baseline models, with a maximum AUC decrease of less than 0.02 relative to the centralized model. (2) FairFML sometimes narrowed the confidence interval compared to baseline models, suggesting more stable model performance in terms of the corresponding fairness metrics. (3) Although FedAvg and Per-FedAvg occasionally outperformed central and local models on specific fairness metrics for certain clients, their improvements were less substantial. In contrast, FairFML-based model consistently demonstrated significant and superior performance across all fairness metrics.

Discussion

FairFML offers a unified, model- and framework-agnostic solution25,32 for enhancing fairness in FL collaborations. Its adaptability to various FL frameworks and ML models—ranging from traditional statistical regressions and support vector machines to deep neural networks—makes it highly versatile for clinical and biomedical prediction tasks25. By reducing algorithmic disparities, as shown in our case study on gender disparities in cardiac arrest outcomes, FairFML mitigates bias for underserved populations when integrated with standard FL frameworks. This provides significant value to health systems by improving fairness in predictive models, which directly impacts clinical decision-making. At the system level, FairFML helps reduce care delivery disparities, enhances resource allocation, and optimizes healthcare services, particularly in distributed systems where data is private and cannot be shared.

Given that clients in cross-institutional FL collaborations often expect direct benefits for their research or clinical practice22,25, it is essential to evaluate models against both client-level (local) and central models. Our results show that FairFML consistently outperforms traditional FL and local models in terms of fairness between the two genders, as seen in Fig. 3 and Supplementary Table 3. While the maximum AUC decrease compared to centralized or standard FL models was <0.02, this modest reduction is a clinically acceptable trade-off, outweighed by the substantial gains in equitable care achieved through bias mitigation. Establishing the real-world impact necessitates future prospective analyses and close collaborations with clinicians to directly evaluate patient-level outcomes where fairness is explicitly prioritized in model predictions.

Beyond its strong performance characteristics, FairFML’s design ensures broad compatibility with a variety of FL algorithms, including FedAvg, FedProx, and Per-FedAvg, without requiring modifications to their underlying mechanics. While Per-FedAvg is known to improve client-level personalization through meta-learning33, our experiments show that FairFML (Per-FedAvg) often achieves superior fairness outcomes compared to FairFML (FedAvg), highlighting its alignment with established personalization benefits. These properties make FairFML highly scalable, adaptable, and practical for real-world biomedical FL scenarios where fairness, interpretability, and implementation feasibility are critical.

FairFML’s convex formulation enables efficient optimization using standard stochastic gradient descent and supports seamless integration into a wide range of predictive models, including logistic regression, ridge regression, support vector machines, and neural networks. Importantly, FairFML does not increase the underlying optimization complexity of the base model. For convex models, the overall objective remains convex; for non-convex models, the fairness penalty introduces no additional non-convexity, allowing training to proceed as usual. In such cases, practitioners may adopt more robust FL frameworks—such as FedProx—to better handle convergence in non-convex settings.

Another benefit of FairFML’s design is its preservation of model interpretability: while the convex fairness loss modifies model parameters to enhance fairness, it does so without fundamentally altering the model’s core architecture. Consequently, commonly used explainable AI tools, such as LIME34 and Shapley-Value-based ones35,36, remain fully applicable, as their methodologies primarily depend on analyzing the model’s input-output behavior rather than being sensitive to exact internal parameter values.

Building on its ability to enhance fairness for specific attributes, an important next step towards comprehensive health equity involves addressing multi-group fairness. Indeed, although gender disparities in cardiac arrest are a key focus, they are not the only relevant partition for group fairness in this context37. Studies show that individuals from Black, Hispanic, or lower socioeconomic status backgrounds experience pronounced disparities throughout the resuscitation pathway38. Our findings, presented in Supplementary Table 4 of the Supplementary Materials, highlight significant variations in gender disparities when further partitioned by race/ethnicity and age (≥65 vs. <65), demonstrating the relevance of intersectional multi-group fairness (i.e., multiple intersecting sensitive variables39) to further mitigate unfairness. Despite more than a decade of discussion on multi-group fairness40,41, it has received limited attention in FL settings. This is particularly challenging when group partitions are imbalanced or entirely absent from some clients; in such scenarios, the fairness penalty may become unstable or undefined due to the lack of valid group comparisons.

While these aspects present considerable challenges, FairFML’s model-agnostic and convex formulation provides a foundational framework that could be extended to address multi-group fairness in future work, allowing its penalty term to be integrated and trained using standard stochastic gradient descent strategies in FL. In addition, incorporating robust strategies such as oversampling (e.g., ROSE42), conditional data synthesis43,44, or generative models like GANs45 could help deal with imbalanced data. These adaptations would enable FairFML to operate more effectively in imbalanced or incomplete real-world clinical datasets.

Beyond the algorithmic fairness considerations discussed thus far, the concept of fairness in FL also encompasses broader aspects. This often involves client resource allocation and ensuring performance uniformity across clients46,47, commonly referred to as “system fairness”48. This is particularly relevant in scenarios involving client selection to optimize convergence speed and reduce computational costs49, as seen in cross-device FL21. However, cross-institutional FL21—which is more prevalent in healthcare settings and often involves fewer clients (typically fewer than five)25 —the focus shifts to algorithmic fairness. While various strategies have been proposed to enhance fairness in clinical models, including privacy-preserving collaborations, McCradden et al.50 caution that relying solely on technical solutions may inadvertently harm vulnerable groups. Thus, FairFML should be viewed as a starting point, followed by further analysis of downstream patient impacts, rather than assuming that fairness can be achieved solely through ML/AI metrics50.

Translating FairFML into real-world clinical practice also requires overcoming significant logistical and operational challenges. These include securing multi-site IRB approvals and data-sharing agreements, coordinating domain experts to harmonize heterogeneous variable definitions, and establishing secure infrastructure with sustained engineering support. Potential solutions include developing modular, GUI-based tools that minimize coding burdens and standardized governance frameworks—such as the FAIR-EC51 collaboration—to ethically and efficiently streamline privacy-preserving multi-site analyses.

Our clinical case study uses simulated partitioned clients for FL experiments as a proof of concept, in preparation for real-world applications. Although we simulated cross-site data heterogeneity, real-world collaborations may introduce additional complexities, particularly regarding model heterogeneity25,32. Further research is required to validate FairFML’s robustness and applicability in real-world cross-institutional collaborations.

While this study focused on group fairness, our proposed method can be extended to improve individual fairness52 by incorporating an individual fairness penalty within the convex framework53. A hybrid penalty combining both group and individual fairness metrics could offer a more comprehensive approach to mitigating unfairness in clinical research. In addition, the fairness penalty could be extended to handle multi-group fairness metrics, such as gender, ethnicity, and socioeconomic status, simultaneously by using the intersection of subgroups, given the convex property of the proposed fairness penalty, which could be easily trained using simple stochastic gradient descent strategies in FL training.

Moreover, to handle temporal distribution shifts in longitudinal or real-time settings, transfer learning54 techniques can be integrated into FairFML to update the model as new batches of data arrive, preserving previously learned fairness constraints while adapting to evolving patient populations. Future work will aim to explore these extensions and validate FairFML in real-world settings to ensure its robustness and applicability across diverse clinical environments.

FairFML effectively mitigates bias and enhances fairness in model co-training across multiple healthcare data owners while preserving privacy. In our proof-of-concept case study using real-world emergency medicine data, FairFML reduced fairness disparities and improved outcomes for underserved populations without compromising predictive performance. These findings highlight the clinical value of FairFML in fostering equitable decision-making within health systems, ensuring that AI models benefit all patient groups fairly. By embedding fairness into FL frameworks, FairFML supports healthcare systems in optimizing resource allocation and improving care delivery, particularly in settings where data is distributed and privacy concerns are critical.

Methods

Notation and problem setup

In this study, we adopt the notation introduced by Berk et al.53. Let \(y\in {\mathscr{Y}}=\left[-\mathrm{1,1}\right]\) represent the binary outcome and \(x\in \chi ={R}^{d}\) denote the feature vectors. Each instance is categorized into one of two groups based on a sensitive variable, denoted as \({\chi }_{{\mathcal{d}}+1}\). The joint distribution of \({\mathscr{X}}\) and \({\mathscr{Y}}\) is represented by \({\mathscr{P}}\). We consider a training set \(S=\{{\left({x}_{i},{y}_{i}\right)\}}_{i=1}^{n}\), consisting of \(n\) independent and identically distributed (i.i.d.) samples drawn from \({\mathscr{P}}\). This training set is divided into two groups, \({S}_{1}\) and \({S}_{2}\), based on the sensitive variable, with \({n}_{1}\) and \({n}_{2}\) representing the respective sizes of these groups, such that \({n}_{1}+{n}_{2}=n\).

The \({\rm{\lambda }}\)-weighted fairness loss for a given model is defined as \({\mathscr{L}}\left(w,S\right)+{\rm{\lambda }}f\left(w,S\right)\), where \({\mathscr{L}}\) represents the standard model loss function, \(w\) represents model parameters, and \(\lambda\) is a regularization parameter for the fairness penalty. Consistent with Berk et al.53, we focus on a group fairness penalty, defined as

$$f\left({\boldsymbol{w}},S\right)=\frac{1}{{n}_{1}{n}_{2}}\mathop{\sum}\limits_{\begin{array}{c} {\left({{\boldsymbol{x}}}_{{\boldsymbol{i}}},{{\boldsymbol{y}}}_{{\boldsymbol{i}}}\right)\in {S}_{1}}\\{\left({{\boldsymbol{x}}}_{{\boldsymbol{j}}},{{\boldsymbol{y}}}_{{\boldsymbol{j}}}\right)\in {S}_{2}}\end{array}}d\left({y}_{i},{y}_{j}\right)\left({\boldsymbol{w}}\,\cdot\, {{\boldsymbol{x}}}_{{\boldsymbol{i}}}-{\boldsymbol{w}}\,\cdot\, {{\boldsymbol{x}}}_{{\boldsymbol{j}}}\right)$$
(1)

Here\(,{d}({y}_{i},{y}_{j}){\mathbb{=}}{\mathbb{1}}[{y}_{i}={y}_{j}]\) serves as the cross-group fairness weight.

4.2 Group fairness metrics

Demographic parity (DP), also known as statistical parity, and equalized odds (EO) are two widely used algorithmic fairness definitions for binary classifications:

  • A model satisfies DP over a distribution \({\mathscr{P}}\) if its prediction \(\hat{Y}\) is statistically independent of the sensitive feature:

    $$P\left[\hat{Y}=1|{\chi }_{{\mathcal{d}}+1}=a\right]=P\left[\hat{Y}=1\right],\,\forall a$$
    (2)

  • A model satisfies EO over a distribution \({\mathscr{P}}\) if its prediction \(\hat{Y}\) is conditionally independent of the sensitive feature given the true outcome label:

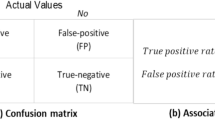
    $$P\left[\hat{Y}=1|{\chi }_{{\mathcal{d}}+1}=a,Y=y\right]=P\left[\hat{Y}=1,=|Y=y\right],\forall a,y$$
    (3)

    In this study, we focused on a total of four fairness metrics: demographic parity difference (DPD), demographic parity ratio (DPR), equalized odds difference (EOD), and equalized odds ratio (EOR), which are calculated using the definitions of DP and EO as follows:

  • \({\text{DPD}}=\mathop{\max }\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=a\right]-\mathop{\min }\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=a\right]\) measures the maximum difference in predicted outcomes across groups. A DPD closer to 0 indicates more equal predictions across groups.

  • \({\text{DPR}}=\frac{\mathop{\min}\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=\,a\right]}{\mathop{\max }\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=\,a\right]}\) measures the ratio of the minimum to maximum predicted outcomes across groups. A DPR closer to 1 indicates more balanced prediction rates.

  • \({\text{EOD}}=\mathop{\max }\nolimits_{y\in \{-{1,1}\}}\left(\mathop{\max }\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=a,Y=y\right]-\mathop{\min }\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=a,Y=y\right]\right)\) measures the difference in prediction errors (false positives/negatives) across groups. An EOD closer to 0 indicates more equal predictions across groups.

\({\text{EOR}}=\mathop{\min }\nolimits_{y\in \{-{1,1}\}}\frac{\mathop{\min }\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=\,a,Y\,=\,y\right]}{\mathop{\max }\nolimits_{a}E\left[{\hat{Y}}|{\chi }_{{\mathcal{d}}+1}=\,a,Y\,=\,y\right]}\) measures the ratio of error rates between groups. An EOR closer to 1 indicates more balanced prediction rates.

FairFML

We integrated the \({\rm{\lambda }}\)-weighted fairness loss described in “Natation problem setup” into the FL model training, and the workflow of our proposed FairFML is illustrated in Fig. 2. As shown, incorporating FairFML into any FL framework enhances the fairness of existing FL solutions by replacing the standard model loss function \({\mathscr{L}}\) with the \(\lambda\) -weighted fairness loss function during FL model training. The fairness regularizer \(f\) is convex53, meaning that it has a single global minimum and no local minima. This property is crucial for optimization because it guarantees that the combined objective function \({\mathscr{L}}\left(w,S\right)+{\rm{\lambda }}f\left(w,S\right)\) can be efficiently minimized without the risk of converging to suboptimal solutions. Convexity ensures that as we adjust \({\rm{\lambda }}\), the trade-off between fairness and model accuracy is stable and predictable, which is essential for effective optimization in typical FL frameworks, such as FedAvg55. To prevent overfitting, we incorporate \({{\rm{l}}}_{2}\) regularization, resulting in the final loss function: \({\mathscr{L}}\left(w,S\right)+{\rm{\lambda }}f\left(w,S\right)+{\rm{\gamma }}{{||w||}}_{2}^{2}\).

The trade-off between model accuracy and fairness, regulated by \({\rm{\lambda }}\), varies significantly across datasets53,56 where higher \({\rm{\lambda }}\) values impose greater fairness penalties. As \({\rm{\lambda }}\) increases from 0 to \(\infty\), model accuracy tends to decrease. Therefore, users need to select an appropriate \({\rm{\lambda }}\) value for each dataset to balance improved fairness with an acceptable reduction in model accuracy. To address this challenge, we propose a data-driven approach for efficiently selecting \({\rm{\lambda }}\) while minimizing computational costs. As outlined in the pseudocode (Supplementary Fig. 1, Supplementary Materials), \({{\rm{\lambda }}}_{k}\) is initially chosen independently for each client \(k\) by plotting prediction metrics (e.g., accuracy or mean square error (MSE)) against \({{\rm{\lambda }}}_{k}\). A practical method involves incrementing \({\lambda }_{k}\) in fixed steps until the prediction metrics degrade beyond a set threshold compared to the unregularized model (e.g., when accuracy falls below 0.995*\({\text{Acc}}_{0}\), where \({\text{Acc}}_{0}\) is the accuracy of the model without the fairness penalty). The maximum \({\lambda }_{k}\) across all clients is then used to define the range for FL training, from which a user-defined set of equally spaced \({\rm{\lambda }}\) values is selected.

For each \(\lambda\) value, we use a two-step strategy to determine the optimal \({\rm{\gamma }}\). First, we explore broad, equally spaced \({\rm{\gamma }}\) values starting from zero. The user selects the best \(\gamma\) based on changes in predictive performance and fairness metrics. We then narrow the search range around that value and repeat the process to finalize \(\gamma\) for the given \({\rm{\lambda }}\). Detailed pseudocode for selecting \(\gamma\) is provided in Supplementary Fig. 1.

Dataset and experiments

Our study population comprised OHCA patients treated by emergency medical services (EMS) providers, as recorded in the Resuscitation Outcomes Consortium (ROC) Cardiac Epidemiologic Registry (Epistry) (Version 3, covering the period from April 1, 2011, to June 30, 2015). The ROC, a North American database established in 2004, aims to advance clinical research on cardiopulmonary arrest57. Ethical approval was obtained from the National University of Singapore Institutional Review Board (IRB), which granted an exemption for this study (IRB Reference Number: NUS-IRB-2023-451).

For cohort formation and predictor selection, we followed established methodologies in out-of-hospital cardiac arrest (OHCA) research57,58. We included patients aged 18 and older who were transported by EMS, achieved return of spontaneous circulation (ROSC) at any point prehospital, and had complete data on gender, race, etiology, initial rhythm, witness status, response time, adrenaline use, and neurological status. The primary outcome was neurological status at discharge, measured by the Modified Rankin Scale (MRS), where scores of 0, 1, or 2 were classified as a good outcome. Variables used for outcome prediction included age (in years), etiology of arrest (cardiac/non-cardiac), witness presence (yes/no), initial rhythm (shockable/non-shockable), bystander cardiopulmonary resuscitation (CPR) (yes/no), response time (in minutes), and adrenaline use (yes/no).

We conducted four sets of experiments to simulate real-world cross-site data by partitioning the full study cohort heterogeneously: (I) by race/ethnicity into four sites, (II) by age into four sites, (III) by race/ethnicity into six sites, and (IV) by age into six sites. Specifically, the probability of an observation being assigned to each site depends on the variable used for partitioning (age or race/ethnicity). As a result, the marginal distributions of predictors and outcomes become heterogeneous across sites. Continuous variables were standardized using the mean and standard deviation from the full cohort, and logistic regression was employed for outcome prediction. We focused on two representative FL frameworks, FedAvg and Per-FedAvg33. FedAvg is the foundational FL framework, being the first proposed in the FL domain32,54, while Per-FedAvg is a widely adopted solution for personalized FL. The latter is particularly relevant in healthcare data analysis, as it allows researchers to determine whether FL can offer localized benefits that enhance the performance of existing models for individual institutions25. Its effectiveness for personalized improvements on local datasets has also been demonstrated with healthcare data59.

For each scenario, we conducted three types of analyses: (1) a central model trained on the full cohort and local models trained independently at each site, (2) federated logistic regression using FedAvg and Per-FedAvg, and (3) fairness-enhanced federated logistic regression using the proposed FairFML method with the two FL frameworks–FairFML (FedAvg) and FairFML (Per-FedAvg). We evaluated model performance using the area under the receiver operating characteristic curve (AUROC) and four fairness metrics, as described in “Group fairness metrics,” with gender as the sensitive variable, using the ‘Fairlearn’ package60.