Matrix stiffness drives drop like nuclear deformation and lamin A/C tension-dependent YAP nuclear localization

Abstract

Extracellular matrix (ECM) stiffness influences cancer cell fate by altering gene expression. Previous studies suggest that stiffness-induced nuclear deformation may regulate gene expression through YAP nuclear localization. We investigated the role of the nuclear lamina in this process. We show that the nuclear lamina exhibits mechanical threshold behavior: once unwrinkled, the nuclear lamina is inextensible. A computational model predicts that the unwrinkled lamina is under tension, which is confirmed using a lamin tension sensor. Laminar unwrinkling is caused by nuclear flattening during cell spreading on stiff ECM. Knockdown of lamin A/C eliminates nuclear surface tension and decreases nuclear YAP localization. These findings show that nuclear deformation in cells conforms to the nuclear drop model and reveal a role for lamin A/C tension in controlling YAP localization in cancer cells.

Introduction

Mechanical stiffening in many solid tumors is due in part to increased assembly of crosslinked collagen networks^{1,2,3,4,5,6,7}. Cancer cells adapt to this change in mechanical stiffness through increased proliferation and migration^8,9,10. Cancer cell cultures grown on model substrates of controlled stiffness have revealed complex mechanisms of cell adaptation to matrix stiffness involving a host of sub-cellular processes. In addition to the canonical differences between soft and stiff matrices in adhesion assembly and cytoskeletal organization, nuclear morphology is different on soft vs. stiff matrices^{11,12,13,14,15}. Because nuclear deformations can induce secondary effects in certain contexts, such as alterations in chromatin conformation^16,17,18,19, nucleoplasmic shuttling of transcription factors^20,21, and signaling^22,23, it is important to understand how mechanical cues from the extracellular matrix (ECM) modulate nuclear morphology.

The mechanical behavior of structural elements in the nucleus is crucial to understanding nuclear deformation in cells on soft and stiff microenvironments. The nuclear lamina, a ~15 nm thick structure under the nuclear envelope, is a major structural determinant of nuclear shape^{24,25,26,27,28,29}. The nuclear lamina is typically smooth in spread cultured cells that tend to be flat, but wrinkling of the nuclear lamina has been reported in several studies, including in stem cells^13,15,30, fibroblasts^31,32 and nurse cells in developing eggs in fruit flies³³. Varied explanations have been proposed for the source of the laminar wrinkles, including that the laminar wrinkles form due to a reduction in the volume of the originally smooth nucleus caused by cell rounding³¹ or by osmotic deswelling³³, or due to microtubule-based force generation on the surface of the nucleus³³.

In contrast, the recently proposed “nuclear drop” model is based on the premise that the surface area of the nuclear lamina in mammalian cells is intrinsically more than the area of a sphere of the same volume^34,35. As a result of this geometric feature, a rounded nucleus (i.e., a nucleus whose shape approaches a sphere) will necessarily contain wrinkles in its lamina. When such a nucleus deviates from its rounded shape at constant volume, geometry requires that the wrinkles be unfolded. Thus, the drop model predicts that the shape of the nucleus, whether round or flat, will modulate the wrinkling of the nuclear lamina. Given that nuclear shape is established by forces generated by dynamic changes in cell shape, nuclear laminar wrinkling is predicted by the drop model to be ultimately controlled by cell shape.

As cell shape is profoundly affected by ECM stiffness, the drop model offers a simple explanation for the appearance of nuclear laminar wrinkles on soft ECM^13,15,30. Cells are typically unable to spread on soft 2D ECMs and as a result, contain rounded nuclei¹¹. Nuclei will therefore be wrinkled on soft ECM. Likewise, stiff 2D ECM feature spread cells and flat nuclei. Therefore, the lamina is predicted to be smooth. Alternatively, differences in volume or cytoskeletal forces on the nucleus, as pointed out above, may also explain the differences in laminar morphology reported in cells cultured on soft and stiff ECM.

Cells cultured on hard substrates like glass or plastic contain nuclei with a smooth contour, with the lamina taking on a smooth, curved shape. Zidovska and coworkers³⁶ reported that the nuclear lamina in HeLa cells has a somewhat irregular contour 1 h after metaphase. The lamina tends to have a smooth contour more than 13 h after metaphase. They suggested that the smooth curved appearance of the lamina later in the cell cycle was either due to a gradual deposition of lamins into the lamina that stiffens it, or a decrease in cytoskeletal forces during the cell cycle progression that reduces fluctuations in the nuclear surface. In contrast, in the drop model, smooth laminar contours are predicted to be caused by a flattening of the nucleus driven by cell spreading. Furthermore, the surface tension of the curved, taut lamina, produced by its resistance to extensional strain, is predicted to be balanced by the difference between the pressure in the interior vs. the exterior of the nucleus³⁵, similar to the stress balance at the surface of a water drop. The pressure is posited to develop through osmotic pressure in the nucleus^37,38 that resists volume compression³⁹, and entropic pressure from chromatin⁴⁰. Because the lamina is molecularly coupled with the nuclear envelope, the tension in the lamina may in turn contribute to the regulation of nuclear transport²⁰, trigger signaling through a stretch in the nuclear envelope^22,23, or cause nuclear envelope rupture^41,42.

Models of elastic nuclear deformation during cell spreading or migration^43,44,45,46 do not account for the wrinkling of the nuclear lamina. As a result, the lamina in such models must undergo an in-plane extensional strain when the nuclear shape deviates from an assumed spherical original shape. In contrast, the nuclear drop model predicts that dynamic changes in cell shape associated with spreading or migration drive wrinkling and unwrinkling of the nucleus by altering its shape. The model also suggests threshold-like behavior for laminar mechanics: when the lamina is wrinkled in a rounded nucleus, it does not support in-plane tension. When smooth, the taut lamina, with its high extensional modulus, balances in-plane tension and prevents further flattening of the nucleus.

Here we tested the predictions of the nuclear drop model. We show that laminar wrinkles are present in five different cancer cell lines cultured on soft 2D hydrogels, and a taut lamina in cells cultured on stiff 2D hydrogels. The lamina assembles in a wrinkled state after mitosis. The unwrinkled lamina is inextensible to cellular forces. A computational model of drop-like nuclear deformation predicts the experimentally measured taut nuclear shapes in axisymmetric micropatterned cells, and a lamin tension sensor shows that the unwrinkled lamina supports tension. Finally, knockdown of lamin A/C eliminates laminar tension, and the sensitivity of nuclear YAP localization to the unfolding of laminar wrinkles caused by cell spreading. Thus, matrix stiffness drives cell shape-dependent drop-like nuclear deformation, and tension in the taut lamin A/C-containing lamina on stiff ECM promotes YAP localization to the nucleus.

Results

Laminar wrinkling is sensitive to matrix stiffness in diverse cancer cell types

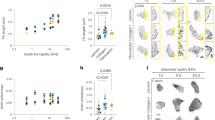
We cultured human oral squamous carcinoma cell lines HN and BHY, human breast adenocarcinoma cell line MDA-MB-231, human pancreatic adenocarcinoma cell line PANC-1, and fibrosarcoma cell line HT-1080 on 1 kPa (soft), 22 kPa (intermediate stiffness), or 308 kPa (stiff) collagen-conjugated polyacrylamide hydrogels. We chose the polyacrylamide gel system because it is a well-established model system in which cells have been shown to specifically sense stiffness^11,47,48,49. For all cancer cell lines, confocal fluorescence microscopy of immunostained lamin B1 revealed an irregular, wrinkled lamina on soft hydrogels but a smooth, curved lamina on stiff gels (Fig. 1a). Based on the Laplace law, the curved lamina indicates the development of surface tension in the taut lamina on stiff gels that is balanced by a difference between the pressure in the nuclear interior and exterior, and the wrinkled lamina indicates an absence of tension. We confirmed this by Förster resonance energy transfer (FRET) based lamin A/C tension sensor measurements⁵⁰ (Fig. 1b, c). Fluorescence lifetimes were higher in smooth nuclei compared to wrinkled nuclei, suggesting that tension in the smooth, taut lamina is high compared to tension in the wrinkled lamina. Our results align with measurements of laminar tension in cells on hard substrates by Ihalainen and coworkers using the same cell line⁵⁰, the phenomenon of nuclear envelope blebbing and rupture, which is indicative of a nuclear pressure^27,51, and the smooth curvature of the nuclear surface flanking nuclear invaginations during deformation against slender obstacles⁵². Laminar wrinkling in cancer cells on soft gels vs. taut nuclei on stiff gels is consistent with similar observations in mesenchymal stem cells by Mauck and coworkers¹³ and Discher and coworkers^15,30.

Fig. 1: Nuclear wrinkling is modulated by stiffness of the extracellular matrix (ECM).

a Confocal images of stained DNA (blue) and lamin B1 (LMNB1, green) in human cancer cells cultured on soft, intermediate (int.) stiff, or stiff hydrogels. The scale bar is 5 μm. b Fluorescence lifetime imaging microscopy (FLIM) images of MDCK cells expressing lamin A/C strain sensor (Lamin-SS) and truncated control sensor (Lamin-TM)⁵⁰; cytochalasin D treatment (cyto D) induces wrinkles. The scale bar is 10 μm. c Plot compares donor fluorescence lifetimes between control (smooth) and cytochalasin D-treated nuclei (wrinkled). n = 12, 17, 13, 19 for the four groups shown on the x-axis. Error bars, SEM. p-values from the two-sided Mann–Whitney U-test. Quantification of d nuclear EFC ratio, e volume, f surface area, and g height is shown for BHY, HN, and MDA-MB-231 cells cultured on soft, intermediate stiff, or stiff hydrogels corresponding to (a). n = 50, 45, 44, 43, 50, 61 for the six groups shown on the x-axis, based on three replicates. Error bars, SEM. p-values from two-sided Mann–Whitney U-test. h The mean EFC ratio correlated with mean nuclear height is shown for BHY (red), HN (green), and MDA-MB-231 (blue) cells cultured on soft, intermediate stiff, or stiff hydrogels. n = 50, 45, 44, 43, 50, 61 for BHY soft, BHY int. stiff, HN soft, HN int. stiff, MDA-MB-231 soft, MDA-MB-231 stiff. Error bars, SEM.

To quantify the laminar wrinkling, we performed a Fourier analysis of the lamin-stained nuclear periphery in cancer cells cultured on hydrogels^53,54. For each nucleus, we calculated the Elliptical Fourier Coefficient (EFC) ratio as a quantitative measure of the irregularity of the lamina for each of three different confocal z-planes and calculated a mean EFC ratio per nucleus (Fig. S1a). The nuclear EFC ratio was significantly lower in various cancer cell types cultured on soft gels vs. stiff gels (Fig. 1d), indicating that the periphery of the nucleus was smoother in the cells on stiff gels vs. soft gels. This suggests that the lamina supports an in-plane surface tension on stiff gels but not soft gels.

Nuclear flattening promotes a taut, inextensible lamina

The unfolding of laminar wrinkles on stiff gels may be due to an increase in nuclear volume during culture after seeding on stiff gels (with a constant lamina surface area)⁵⁵. Using confocal fluorescence microscopy of lamin-stained cancer nuclei, we collected images at different z-planes (spacing between the z-planes was 130 nm, lower than the Nyquist criterion; see “Methods” section) and quantified the volume from the confocal z-stacked images. Nuclear volume and surface area were not statistically different between soft and stiff gels for three cancer cell lines (Fig. 1e, f), and there was no significant correlation between EFC ratio and nuclear volume (Fig. S2). Therefore, the smoothness of the nuclear periphery observed on the stiff gel vs. the soft gel was not due to a greater nuclear volume for the same laminar surface area.

Alternatively, the unfolding of wrinkles as a rounded nucleus deviates from its shape could explain the taut lamina on stiff hydrogels. Indeed, we observed that the shape of the nucleus in the vertical plane was flattened considerably on the stiff hydrogel vs. the soft hydrogel (Fig. 1g). The EFC ratio inversely correlated with nuclear height, which is a measure of nuclear flattening (Fig. 1h), indicating that flattening unfolds the nuclear wrinkles. These results can be explained as follows. Round cells contain rounded nuclei that roughly approximate spheres. A sphere, when deviated from its shape at constant volume, must increase its surface area because a sphere is a shape with minimum surface area to its volume. If the spherical shape contains folds or wrinkles in it, to begin with, i.e., an “excess area” (defined as the surface area in excess of the area of a sphere of the same volume), then this would result in an unfolding of the surface as the shape deviates from a sphere.

Once all laminar wrinkles are fully unfolded, the nucleus is expected to reach a constant steady state shape owing to the relative inextensibility of the lamina. To test the hypothesis that the lamina does not undergo a measurable in-plane extensional strain in flattened nuclei, we photobleached the mid-planes of the GFP-lamin A labeled lamina to create measurable arcs (Fig. 2a). Bleached spots did not recover over a time of 2 h, which allowed us to track the length of the arcs to quantify strain in the lamina. When we rapidly rounded cells by treating them with trypsin, we observed irregular peripheries in the previously taut lamina, suggesting a loss of tension. However, the arc lengths in between the bleached spots remained unchanged for both cancer cells and fibroblasts (Fig. 2b). Thus, relaxing the tension in the lamina did not relax the in-plane extensional strain in the lamina, suggesting that the taut lamina was not strained measurably in flattened nuclei.

Fig. 2: Dynamic changes in laminar wrinkling are driven by cell rounding or spreading.

a Confocal images of photobleached GFP-LMNA (gray) expressing fibrosarcoma cells and fibroblasts before and after adding trypsin. Arcs separated by a T-shape photobleaching pattern are labeled with white numbers. The scale bar is 5 μm. b Quantification of arc length is shown for GFP-LMNA expressing fibrosarcoma cells (top) and fibroblasts (bottom) at 0 s and 40 s after adding trypsin. n = 20 and 20 for fibrosarcoma cells and fibroblasts, respectively. The arc examples in (a) are labeled in red. c Confocal images of GFP-LMNA (green) expressing fibrosarcoma cells and fibroblasts spread on glass substrates or suspended with trypsin. The scale bar is 10 μm. Corresponding quantification of d nuclear volume, e surface area, and f EFC ratio is shown for spread and suspended GFP-LMNA expressing fibrosarcoma cells and fibroblasts. n = 33, 33, 31, 31 for the four groups shown on the x-axis, based on three replicates. Error bars, SEM. p-values from the two-sided Mann–Whitney U-test. g Time-lapse confocal images of a GFP-LMNA (green) expressing fibrosarcoma cell and fibroblast spreading after seeding. F-actin (magenta) was stained with SPY650-FastAct. The scale bar is 10 μm. h Corresponding quantification of mean nuclear EFC ratio (green) and cell spreading area (magenta), both normalized to the corresponding value in the first time-frame, is shown for spreading fibrosarcoma cells (top) and fibroblasts (bottom). n = 12 and 9 for fibrosarcoma cells and fibroblasts, respectively, based on three replicates. Error bars, SEM.

Dynamic changes in laminar wrinkling at constant nuclear volume are driven by cell rounding or spreading

To determine whether rounding the nucleus induces laminar wrinkling, we trypsinized fibrosarcoma cells or fibroblasts, fixed them with paraformaldehyde, and quantified their nuclear volume and nuclear surface area from confocal z-stack imaging (Fig. 2c). For both cell types, there were no differences in volume or surface area of the lamin A/C stained nuclei for flattened vs. suspended cells (Fig. 2d, e), but suspended cells had greater laminar wrinkling, as shown by a lower EFC ratio compared to spread cells (Figs. 2f, and S1b). This further supports the concept that alterations to nuclear shape geometrically induce laminar wrinkling.

In a separate experiment, we examined the dynamics of the lamina during cell spreading. We tracked GFP-lamin A-labelled nuclei and cell spreading using FastAct-labeled F-actin (Fig. 2g, Supplementary Movie 1 and 2). As cells spread, the wrinkled lamina gradually unfolded and became taut, as indicated by the EFC ratio (Fig. 2h). The nuclear shape reached a steady state that coincided with the complete unfolding of the irregular lamina (see Supplementary Movie 1 and 2), indicating that the smooth lamina is too stiff to stretch on cellular force scales. Our results from Figs. 1 and 2 showed that (a) the lamina has excess area, (b) the lamina is unstrained once fully unfolded in spread cancer cells, (c) the volume is the same in wrinkled nuclei on soft gels and taut nuclei on stiff gels, and (d) the unfolding of wrinkles correlates with nuclear flattening. These results are consistent with the nuclear drop model.

The nuclear drop model quantitatively predicts the limiting nuclear shapes in micropatterned cells

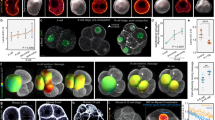
As cancer cells spread more on stiff gels vs. soft gels, we asked if laminar unfolding can be controlled by micropatterning cell shape. Cancer cells were micropatterned on 30-micron and 50-micron circular fibronectin islands, and the cell body and nucleus were visualized by F-actin staining and GFP-lamin A, respectively. Two types of cancer cells cultured on 30-micron circular islands had wrinkled lamina vs. cells cultured on 50-micron islands, which was evident in the x–y and y–z planes (Fig. 3a). Consistent with the nuclear morphometric comparisons between soft and stiff gels, the EFC ratio was lower, and nuclei were taller on smaller islands vs. larger islands (Fig. 3b, c), whereas nuclear volume and surface area were similar between 30-micron and 50-micron islands (Fig. 3d, e). These results are consistent with the nuclear drop model, in which nuclear deformation occurs at constant nuclear volume and surface area of the lamina.

Fig. 3: Limiting nuclear shapes are quantitatively predicted by the nuclear drop model.

a Confocal images of F-actin (magenta) stained in HT-1080 and HN cells expressing GFP-LMNA (green) cultured on a 30 or 50 μm diameter fibronectin micropattern. The scale bar is 10 μm. Corresponding quantification of b nuclear height, c EFC ratio, d volume, and e surface area is shown for HT-1080 and HN cells cultured on 30 or 50 μm diameter fibronectin micropattern. n = 42, 40, 40, 43 for the four groups shown on the x-axis, based on three replicates. Error bars, SEM. p-values from the two-sided Mann–Whitney U-test. f Geometric model for cell and nuclear shapes based on the excess area of the lamina. For sufficiently spread cells, minimizing the surface area of the cortex under the constraints of a constant cell volume, nuclear volume, and nuclear surface area yields unique, geometrically determined cell (blue) and nuclear (red) shapes with surfaces of constant mean curvature. g Model predictions for cell and nuclear shapes are compared to experimental cell x-z profiles. The percent excess area, defined as the area in excess of that of a sphere of the same nuclear volume, is shown. For these calculations, nuclear volume, cell volume, and lamina area were treated as fitted parameters. h When the excess area is large enough, or the cell is insufficiently spread, cells are predicted to form a spherical cap with no unique geometric solution to the nuclear shape, which may have any number of irregular nuclear folds, wrinkles, or undulations.

We determined whether the nuclear drop model could explain the limiting nuclear shapes we observed in micropatterned, axisymmetric shapes on circular islands. In the model, the flattened nucleus is assumed to be pressurized, and the lamina is taut and tensed due to compression from the cortex. The model assumes geometric constraints of fixed cell volume, nuclear volume, and nuclear surface area and predicts mathematically the shapes of flattened cells and nuclei with a fully taut lamina by minimizing the surface area of the tensed cell cortex. The spread cell and flattened nuclear surfaces consist of three surfaces of constant mean curvature: (1) the curvature of the cell cortex (H_cell), (2) the curvature of the nuclear interface with the cytoplasm (H_nuc), and (3) the curvature of the joint cap where the nuclear surface is in contact with the cell cortex (H_cap) (Fig. 3f). For axisymmetric cells, the cell and nuclear shapes can be expressed as elliptical integrals (see “Methods” section), yielding a spherical cap for the joint nucleus-cortex surface, an unduloid surface for the cortex, and a nodoid surface for the nuclear interface with the cytoplasm (Fig. 3f). We found good agreement between the predictions of the nuclear drop model and our experimental results (Fig. 3g), supporting the conclusion that the lamina is predictably smoothed and under tension when the cell is spread sufficiently to confine the flattened nucleus under the cell cortex. If not, the nuclear shape is not predictable and takes on irregular shapes characterized by folds, undulations, and wrinkles in the lamina (Fig. 3h). Moreover, experiments that controlled axisymmetric spreading radii (Fig. 3) validated a key prediction of the model that a critical radius of spreading is required to establish a unique nuclear shape with a smooth lamina and surfaces of constant mean curvature. For cells that spread less, the excess lamina surface area allows irregular shapes with wrinkled lamina without violating the constraints of constant nuclear surface area and nuclear volume.

Laminar wrinkling is sensitive to stiffness in three-dimensional cell culture

In rounded cells with excess area, the lamina exhibited folds and wrinkles on soft substrates (Fig. 1a), in suspension (Fig. 2c), or when their ability to spread was otherwise limited (Fig. 3a). To determine the extent of folding or wrinkling in the nucleus in three-dimensional (3D) cell culture, we cultured MDA-MB-231 cancer cells in 3D gelatin methacryloyl (GelMA) hydrogels in which stiffness is controlled by the concentration of nanoparticles serving as crosslink epicenters⁵⁶ (Fig. 4a, Supplementary Movie 3 and 4). In soft gels (1–3 kPa), cells were elongated with a taut lamina, but in stiff hydrogels (10–15 kPa), they were unable to elongate and rounded with a wrinkled lamina. The nuclear EFC ratio was significantly lower in the soft gels than in the stiff gels and was positively correlated with the cellular aspect ratio (Fig. 4b).

Fig. 4: Laminar wrinkling is sensitive to stiffness in three-dimensional (3D) culture and develops post mitosis.

a Confocal images of MDA-MB-231 cells expressing GFP-LMNA (green) stained with F-actin (magenta) in GelMA 3D culture. The scale bar is 10 μm. b Corresponding quantification of mean nuclear EFC ratio correlated to mean cell aspect ratio is shown for MDA-MB-231 cells expressing GFP-LMNA in GelMA 3D culture. n = 23 and 22 based on three replicates of soft (1–3 kPa) and stiff (10–15 kPa) gels, respectively. Error bars, SEM. c Confocal images of stained lamin A/C (green) and F-actin (magenta) in 344SQ lung cancer cells cultured on glass and acini in 3D Matrigel culture. The scale bar is 10 μm. d Corresponding quantification of nuclear EFC ratio is shown for 344SQ lung cancer cells cultured on glass and acini in a 3D Matrigel culture. n = 40 and 48 for 2D glass and 3D acini, respectively, based on three replicates. Error bars, SEM. p-values from the two-sided Mann–Whitney U-test. e Representative confocal images of lamin B1 (gray) stained in tumor microarray from n = 50 and 11 images of human invasive ductal carcinoma and larynx squamous cell carcinoma, respectively. The scale bar is 20 μm. f Time-lapse confocal images of a GFP-LMNA (gray) expressing fibrosarcoma cell and a fibroblast during cell mitosis. The scale bar is 10 μm. g Corresponding quantification of mean nuclear EFC ratio is shown for mother (red) and daughter cells (blue and green), normalized to the value in the first time-frame during cell mitosis. n = 4 and 15 for fibrosarcoma cells and fibroblasts, respectively, based on three replicates. Error bars, SEM.

To determine whether similar wrinkling of nuclei occurs in 3D acini assembled by cancer cells, we cultured non-small cell lung cancer (NSCLC) cells in Matrigel and imaged acini with distinct lumens (Fig. 4c). The cross-sectional views showed that cells in the acini were more rounded than cells cultured on 2D glass coverslips. Notably, laminar wrinkles developed in the nuclei of cells within 3D matrices, whereas these wrinkles were absent in cells cultured in 2D, indicating that nuclei in 3D acini are wrinkled because cells are not flattened in a way that confines the nucleus, unlike nuclei with a taut lamina in 2D culture. These differences were confirmed at a population level by comparing the EFC ratios (Fig. 4d). Consistent with the nuclear drop model, in 3D breast cancer single cells and acini formed by NSCLC cells, the rounder cells with a round nucleus showed laminar wrinkling. A similar laminar irregularity was also observed in a lamin B1-stained tumor microarray from human invasive ductal carcinoma and larynx squamous cell carcinoma (Fig. 4e), suggesting that the nuclear drop model might also be valid in vivo and may explain nuclear dysmorphia in cancer tissue.

Laminar wrinkling develops post mitosis

As the lamina assembles post mitosis, we imaged fibrosarcoma cells and fibroblasts expressing GFP-lamin A during mitosis to investigate laminar behavior. We observed that the wrinkled lamina assembled immediately after mitosis and gradually became smoother as the daughter cells spread and the nucleus flattened (Fig. 4f and Supplementary Movie 5 and 6). We confirmed this change by measuring a decrease in the nuclear EFC ratio in daughter cells vs. the mother cell immediately after mitosis, which increased slowly as cells spread (Fig. 4g). These findings suggest that the lamina assembles in a wrinkled state around chromosomes post mitosis.

Laminar irregularities correlate inversely with YAP nuclear localization

The mechanosensory Yes-associated protein (YAP)⁵⁷, downstream of the Hippo pathway, is cytoplasmic in rounded cells but translocates to the nucleus in spread cells^58,59,60. As nuclear YAP localization may be correlated with nuclear smoothing in stem cells¹⁴, we immunostained YAP in cancer cells grown on soft and stiff hydrogels. YAP was cytoplasmic in three types of cancer cells cultured on soft gels but became nucleoplasmic on stiff gels (Fig. 5a, b). Further, we determined that the YAP nucleoplasmic to cytoplasmic (N/C) ratio correlated positively with the EFC ratio (Fig. 5c), suggesting a correlation between the unfolding of wrinkles in the nucleus and YAP nuclear localization. We found a similar trend for cancer cells cultured on micropatterned substrates; the YAP N/C ratio was lower on smaller circular islands in which nuclei were wrinkled and correlated positively with the EFC ratio (Fig. 5d─f). As a smooth lamina supports tension, these results suggest a potential role for laminar tension in the regulation of YAP localization to the nucleus. Consistent with the concept that nuclear unwrinkling can drive YAP localization into the nucleus, we found that hypo-osmotic shock reduced nuclear laminar wrinkling in GFP-lamin A/C expressing wrinkled nuclei cultured on 30-micron circular islands through an increase in volume, and induced an increase in the YAP nuclear to cytoplasmic ratio (Fig. S3).

Fig. 5: Laminar wrinkling correlates inversely with YAP nuclear localization.

a Confocal images of stained lamin B1 (LMNB1, green) and YAP (red) in BHY, HN, and MDA-MB-231 cells cultured on soft and stiff hydrogels. The scale bar is 10 μm. b Quantification of nuclear to cytoplasmic YAP intensity ratio, correlated to nuclear EFC ratio (c) normalized to the corresponding value on soft hydrogels, is shown for BHY (red), HN (green), and MDA-MB-231 (blue) cells cultured on soft and stiff hydrogels. n = 50, 45, 44, 43, 50, 61 for the six groups shown on the x-axis, based on three replicates. Error bars, SEM. p-values from the two-sided Mann–Whitney U-test. d Confocal images of stained YAP (red) and F-actin (magenta) in GFP-LMNA (green) expressing HT-1080 and HN cells cultured on 30 and 50 μm diameter fibronectin micropattern. The scale bar is 10 μm. e Quantification of nuclear to cytoplasmic YAP intensity ratio, correlated to nuclear EFC ratio (f) normalized to the corresponding value on 30 μm pattern, is shown for HT-1080 (red) and HN (green) cells cultured on 30 and 50 μm diameter fibronectin micropattern. n = 42, 40, 40, 43 for the four groups shown on the x-axis, based on three replicates. Error bars, SEM. p-values from the two-sided Mann–Whitney U-test.

Lamin A/C is required for laminar surface tension and the sensitivity of YAP to laminar unfolding and cell spreading

Given that lamin A/C is implicated in the regulation of YAP localization to the nucleus⁶¹, we determined the relationship between lamin A/C, nuclear smoothing, and YAP nuclear localization. We depleted lamin A/C levels using siRNA transfection in HT-1080 and HN cells (Figs. 6a, b, and S4), cultured the cells on an array of fibronectin-coated polydimethylsiloxane (PDMS) micropost barriers as described previously⁵², and visualized the nuclear surface by immunostaining. Lamin A/C-depleted nuclei (immunostained for lamin B1) did not maintain their gross shapes on the microposts, whereas the control nuclei in cells transfected with scrambled siRNA (immunostained for lamin B1) took on drop-like shapes with free surfaces of constant curvatures when indented by the microposts (Fig. 6c and outlines). These results suggest that lamin A/C provides surface tension to the nuclear drop in these cancer cell lines which balances intranuclear pressure.

Fig. 6: Lamin A/C is required for laminar surface tension and the sensitivity of YAP to laminar unfolding and cell spreading.

a Efficacy of siRNA-mediated knockdown of lamin A/C expression is shown for HT-1080 and HN cells. Expression of lamin A/C in siRNA-treated cells relative to control cells treated with scrambled siRNA (siSCRM) after normalization of all Ct values to GAPDH expression using the 2^-∆∆Ct method. Data represents the mean from three biological replicates. Error bars, SD. b Immunoblotting of lamin A/C is shown for HT-1080 and HN cells transfected with siSCRM and siLMNA. c Confocal images of stained lamin B1 (green) in HT-1080 and HN cells transfected with siSCRM or siLMNA deforming around 5-μm-tall rhodamine-fibronectin-coated PDMS microposts (red). Nuclear outlines relative to the position of microposts are shown at the bottom. The scale bar is 5 μm. d Nuclear to cytoplasmic YAP intensity ratio, correlated to cell spreading area or nuclear EFC ratio, is shown for HT-1080 and HN cells cultured on soft and stiff hydrogels. n = 77, 83, 77, 73 for HT-1080 siSCRM, HT-1080 siLMNA, HN siSCRM, HN siLMNA, respectively. Slopes and R-squared values of linear fitting and p-values for slope comparisons using a one-tailed F-test are shown on the graphs.

We determined the correlation of the YAP N/C ratio with cell spreading and the nuclear EFC ratio. As expected, YAP N/C ratios correlated positively with the area of cell spreading in both cell types transfected with scrambled siRNA^{57,60,62,63,64}. siRNA depletion of lamin A/C reduced the sensitivity of YAP N/C ratios to both cell spreading and EFC ratio in HN cells (p < 0.0001 and p < 0.01, respectively; Figs. 6d, and S5). Thus, YAP did not localize to a nucleus with a smooth lamina (labeled for lamin B1) upon the depletion of lamin A/C, and lamin A/C depletion reduced surface tension in the nucleus. We note that the noise in YAP levels for a given spreading area may be due to variations in cell shape that are not fully captured by a simple index like cell spreading area. In HT-1080 cells, lamin A/C knockdown increased nuclear wrinkling, but the cells with smoother nuclear contours (EFC ratio > 6) still exhibited lower YAP ratios compared to control cells, and the sensitivity of YAP localization to cell spreading was abolished (p < 0.0001 for both). These results are consistent with a model in which surface tension in the lamina, supported by lamin A/C networks, regulates YAP translocation to the nucleus.

Discussion

Cancer cell nuclei deform in diverse contexts, such as during constrained cell migration^27,65, during the spreading of cells on the extracellular matrix (ECM)^46,66, and in response to mechanical cues from the ECM, such as ECM stiffness¹¹. Mechanical models of the nucleus generally assume its rounded shape to be a perfect sphere but here we found that the nuclear lamina assembles immediately after mitosis in a wrinkled state. This is aligned with the drop model in which the area of the lamina intrinsically exceeds the area of a sphere of the same volume. In a rounded nucleus, the excess area would create folds or wrinkles in the lamina. Wrinkles were indeed observed on a soft ECM for all the cell types studied while the lamina was smooth in cells cultured on a stiff ECM. The cells spread well on a stiff ECM, resulting in flattened nuclei; however, the volumes of the nuclei were comparable on a soft or stiff ECM, suggesting that the unfolding of the lamina results from a deviation of the nucleus from a rounded shape. Wrinkling can be caused by a decrease in nuclear volume with a constant area like a deflated soccer ball has folds on its surface, but this was not the case for cells on a soft ECM (Fig. 1). While wrinkling can be induced by cytoskeletal forces in other contexts³³, disruption of F-actin or microtubules had no effect on laminar wrinkling on soft ECM (Fig. S6).

Tracking of photobleached GFP-lamin spots in the nucleus of trypsinized cells (Fig. 2a, b) revealed that there is no in-plane extensional strain in the lamina in flattened nuclei. We cannot rule out that the lamina may be temporarily strained during the initial spreading, followed by a relaxation of the stored strain by an unknown mechanism. However, given our prior observations that there is no elastic energy stored in the nuclear shape in cells⁶⁷, the absence of strain in the lamina is not surprising. Also, movies of cell spreading (Supplementary Movie 1 and 2) showed that the nucleus reached a steady state shape when the lamina lost its wrinkles, indicating that once it is fully taut, the lamina acts as an inextensible surface on cellular force scales. Micropatterned cells on 30-micron islands contained rounded highly wrinkled nuclei, while well-spread cells on 50-micron islands contained smooth flattened nuclei. Collectively, these results show that cell shape regulates nuclear laminar wrinkling by modulating the overall or gross nuclear shape.

We and others have previously shown that cells can spread even when myosin activity is inhibited; nuclei in these cells are flattened^66,68,69. Consistent with these prior findings, we found that treatment of cells with Y-27632 to inhibit Rho kinase activity did not cause nuclear wrinkling but also did not impact overall cell spreading, while treatment with blebbistatin caused cell rounding and concomitant nuclear wrinkling (Fig. S7). As also reported previously with fibroblasts^32,66, these treatments also caused a decrease in nuclear volume (Fig. S7), but nuclei were flatter in Y-27632 treated cells compared to control, again underscoring the fact that nuclei will reach a steady state shape with a smooth lamina so long as cells are able to spread. Additionally, disruption of the linker of the nucleoskeleton and cytoskeleton (LINC) complex by inducible expression of KASH1 did not induce nuclear wrinkling and also did not affect cell spreading (Fig. S8). These results are consistent with our previously proposed concept^34,66,70 that rounded nuclei with laminar wrinkles are compliant, which allows cells to compress and flatten them even in the absence of actomyosin activity. This principle was demonstrated in mechanical measurements as well recently⁷¹. Once the lamina is smooth, however, even the presence of actomyosin contraction is not sufficient to compress the nucleus any further. Thus, the limiting nuclear shape, where the lamina is fully unfolded, is likely insensitive to the magnitude of cytoskeletal forces that compress it. Instead, the limiting shape is likely to depend on the amount of excess surface area in the nuclear lamina³⁴.

The predictions of our geometric model offer a mechanistic explanation for the key observations reported here. For a given spreading area of the micropatterned circular cells, the model correctly predicts a unique nuclear shape with a tensed lamina, assuming the cell is spread sufficiently to confine the pressurized nucleus under the cell cortex. However, when the nucleus is not sufficiently confined by the spread cells, only the cell shape is predictable. The nucleus, with no geometric constraints, may have any number of irregular shapes with a constant nuclear volume and constant (but excess) nuclear surface area restricted by the cell volume. Such nuclei would change shape with very little mechanical resistance. Even when they become flattened and the lamina becomes smooth, the nuclei can change shape in the x–y plane so long as surface area and volume are constant. As such, much smaller forces for deformation than evident in AFM measurements are required to deform the nucleus on the slow time scales of migration⁵².

Our results appear to connect cell shape-driven control of nuclear wrinkling to signaling and regulation of cell function. There is a positive correlation between YAP localization to the nucleus and unwrinkling (as quantified by an increase in the EFC ratio). The correlation was absent in lamin B1-containing nuclei in lamin A/C-depleted well-spread cells. YAP was absent in nuclei even when they had a taut lamina in these cells. Together with the observation of irregular nuclear shapes when indented by microposts in lamin A/C depleted cells, these results suggest that the tension in the lamina has a role in the regulation of YAP transport. Tension in the lamina might regulate YAP transport similarly to the mechanism by which F-actin nucleators are localized in the nucleus⁷² in the presence of lamin A/C but are localized to the cytoplasm after lamin A/C knockdown⁶¹. Lamin A/C knockdown has been shown to reduce the levels of a number of F-actin binding proteins¹⁵. This indirect modulation of F-actin structures in the cytoplasm may potentially promote YAP phosphorylation through MST1 kinases, preventing YAP association with importin 7 and subsequent nuclear import⁷³. Lamin-based regulation is probably only an additional or secondary mechanism of YAP regulation, as the dependence of YAP on laminar unwrinkling does not display threshold behavior (Fig. 6d).

The unfolding of wrinkles of the lamina may also affect other aspects of nuclear structure such as chromatin organization^74,75. However, we found no correlation between heterochromatin spatial patterns, quantified as the radial distribution of H3K9me3 and H3K27me3, with the unfolding of wrinkles in the nucleus in three cancer cell lines (Fig. S9). Further research is needed to fully identify the functional impacts of drop-like deformation of the nucleus.

The threshold-like mechanical behavior of the nuclear lamina, where tension is supported in the lamina only upon laminar smoothing, is reminiscent of the threshold behavior of the wrinkled nuclear membrane observed in experiments involving compression of cells in microdevices^22,23. In these experiments, the nuclear envelope became unwrinkled as the nucleus was compressed, resulting ultimately in a membrane strain that opened membrane channels with eventual signaling that increased actomyosin contractility. The extent to which this mechanism is operational in spread cells where the nucleus becomes flattened is unclear. Given that spreading occurs over slow time scales, there is likely sufficient time to allow lipid exchange between the nuclear envelope and the endoplasmic reticulum such that the nuclear membrane may not undergo a significant stretch during flattening.

Nuclei do not typically rupture spontaneously in spread wild-type cells, but the absence of lamin B1 can trigger rupture^51,76. One explanation for the lack of rupture in normal spread cells could be that nuclear flattening regulates actomyosin contractility at a ‘setpoint’ to prevent nuclear envelope rupture. Rho-mediated control of actomyosin contractility is regulated by the assembly of focal adhesions in the process of cell spreading. Thus, as opposed to a set-point-like regulatory mechanism, it may be that the total compressive force generated by the actomyosin cortex on the flattened nucleus is not high enough to rupture the nucleus with an intact lamina. Only in confinement by devices or during migration in confining spaces will the compressive force be high enough to cause ruptures.

Our finding that nuclear volume is constant across soft and stiff ECM contrasts with the findings of Guo et al. in other cell types⁵⁵. Such disagreement in volume measurements is present generally in the literature; volume has been variously reported to change, stay constant, or increase in various contexts^{32,46,66,77,78}. The reasons for these general disagreements are unclear and may be due to differences in stained targets. Volume here was measured from immunostained images of nuclear lamins instead of the more common DNA staining. Lamin staining directly delineates the nuclear surface, unlike DNA which can be shrunk relative to the nuclear surface depending upon the amount of DNA condensation. Also, nuclear volume is coupled with cell volume^{32,55,79,80,81,82} that, in turn, may be regulated by cell shape; as such, cell volume may not change depending on the context and cell type. Other possible reasons for the disagreements include differences in cell types, or errors in measurement (for accurate volumetric imaging, capturing confocal planes at a z-spacing that is below the Nyquist criterion and with a tight confocal pinhole is important). It is also possible that acrylamide fixation introduces variations in volume measurements, although we confirmed in our data that nuclear volumes were not different between soft and stiff ECM both in confocal imaging data taken from fixed cell populations and from live imaging of GFP-lamin A/C expressing cells (Fig. S10). Refractive index mismatch can additionally introduce artifactual increases in nuclear heights with errors ranging from 30% to 60%⁸³. It is important to note, however, that the nuclear drop model does not require volume to be constant, as the main principle of threshold-like behavior of the lamina, and dynamic nuclear shape control by cell shape, will remain valid.

Methods

Synthesis and functionalization of polyacrylamide hydrogels

Polyacrylamide hydrogels were prepared as described in ref. ⁸⁴. Acrylamide and bis-acrylamide (Bio-Rad Laboratories) were mixed in concentrations of 5%/0.1%, 8%/0.2%, and 15%/1.2% to prepare gels with Young’s modulus (E) of 1, 22, and 308 kPa, respectively, as described in ref. ¹¹. The precursor solution was degassed, mixed with 0.5% v/v ammonium persulphate (ThermoFisher Scientific) and 0.1% v/v tetramethylethylenediamine (ThermoFisher Scientific) to initiate polymerization, and 100 μl of the mixture was layered between a hydrophobic glass surface and a hydrophilic 18-mm diameter glass coverslip at room temperature for 20 min. The gels were functionalized using sulfosuccinimidyl 6-(40-azido-20-nitophenylamino) hexanoate (G-Biosciences) and coated with rat tail collagen type I (0.2 mg/ml; Corning) before cell seeding.

Cell culture

All cancer cell lines were maintained in a humidified incubator at 37 °C and 5% CO₂. Human breast adenocarcinoma cells MDA-MB-231 (ATCC, HTB-26), human head and neck cancer cells BHY and HN (Deutsche Sammlung von Mikroorganismen und Zellkulturen GmbH), and MDCK cells (obtained from Jennifer Lippincott-Schwartz lab) were cultured in Dulbecco’s Modified Eagle’s Medium with 4.5 g/l glucose (Corning), supplemented with 10% v/v donor bovine serum (Gibco) and 1% v/v penicillin/streptomycin (Corning). Human fibrosarcoma cells HT-1080 (ATCC, CCL-121), human pancreatic carcinoma cells PANC-1 (ATCC, CRL-1469), mouse fibroblasts NIH-3T3 (ATCC, CRL-1258), and retroviral packaging cells Phoenix-Ampho (ATCC, CRL-3213) were maintained in Dulbecco’s Modified Eagle’s Medium with 4.5 g/l glucose (Corning), supplemented with 10% v/v fetal bovine serum (FBS; Gibco) and 1% v/v penicillin/streptomycin (Corning). Mouse lung cancer cells 344SQ (a generous gift from Jonathan Kurie lab) were cultured in Roswell Park Memorial Institute medium (ThermoFisher Scientific), supplemented with 10% v/v FBS (Gibco) and 1% v/v penicillin/streptomycin (Corning). For 3D acinar cultures, Nunc Lab Tek II 8-well chamber slides (ThermoFisher Scientific) were coated with 40 μl of growth-factor-reduced (GFR) Matrigel (Corning) and allowed to gel for at least 1 h at 37 °C. Trypsinized 344SQ cells from tissue culture plates were suspended in growth medium supplemented with 2% v/v Matrigel to achieve a final concentration of 10 cells/ml, and 400 μl was added to each well of the chamber slide where the cells were allowed to form acini for 7–12 days before fixation. The growth medium was changed every 3–5 days.

Plasmid and stable cell line generation

MDCK cells with inducible mCherry-dominant-negative (DN) KASH1 were generated as previously described⁸⁵. MDCK cells expressing lamin A/C strain sensor (Lamin-SS) or lamin A/C truncated control sensor (Lamin-TM) were generated as previously described⁵⁰. pBABE-puro-GFP-wt-lamin A plasmid was a gift from Tom Misteli⁸⁶ (Addgene; plasmid #17662). GFP-fusion lamin A was stably expressed in cancer cell lines by retroviral transduction. Phoenix-Ampho cells were transfected with the pBabe plasmid DNA using lipofectamine 3000 (ThermoFisher Scientific) according to the manufacturer’s protocol. Transfected Phoenix-Ampho cells were incubated at 37 °C for 8 h, refed with fresh culture medium, and maintained at 32 °C for 48 h. The culture medium containing packaged retrovirus was filtered through a 0.45-μm filter (ThermoFisher). Filtered medium supplemented with polybrene (2.5 μg/ml; Sigma–Aldrich) was added to the target cancer cells. The target cells were incubated at 37 °C for 48 h and refed with a culture medium containing puromycin (Sigma–Aldrich) for selection of viral integration. After 2–3 days of antibiotic selection, the expression of GFP-lamin A in cancer cells was verified using immunofluorescence and immunoblot analysis.

Immunofluorescence staining and microscopy

Cultured cells were fixed in 4% paraformaldehyde (PFA, Alfa Aesar) for 20 min at room temperature, permeabilized with 0.1% Triton X-100 (ThermoFisher Scientific) in phosphate-buffered saline (PBS), and blocked with 1 mg/ml bovine serum albumin (ThermoFisher Scientific) for 1 h at room temperature. Cells were incubated with primary antibodies rabbit anti-lamin B1 (Abcam, ab229025; dilution 1:1000), mouse anti-YAP (Santa Cruz Biotechnology, sc-101199; dilution 1:100), mouse anti-lamin A/C (Invitrogen, MA5-35284; dilution 1:250), mouse anti-α-Tubulin (Cell Signaling, #3873; dilution 1:100), rabbit anti-H3K9me3 (Abcam, ab8898; dilution 1:100), or mouse anti-H3K27me3 (Abcam, ab6002; dilution 1:100) overnight at 4 °C. The cells were then washed with PBS and incubated with secondary antibodies Alexa Fluor 488 goat anti-rabbit (Invitrogen, A11034; dilution 1:250), Alexa Fluor 594 goat anti-rabbit (Invitrogen, A11012; dilution 1:200), Alexa Fluor 594 goat anti-mouse (Invitrogen, A11032; dilution 1:200), Alexa Fluor 647 goat anti-rabbit (Invitrogen, A21244; dilution 1:200), or Alexa Fluor 647 goat anti-mouse (Invitrogen, A21235; dilution 1:200) for 2 h at room temperature. DNA was stained with Hoechst 33342 (Sigma–Aldrich), and F-actin was stained using phalloidin conjugated to Alexa Fluor 405 or 488 (Invitrogen; dilution 1:400). The cells cultured on polyacrylamide hydrogels were mounted on 35-mm glass dishes (World Precision Instruments) before imaging. For staining tissue microarrays, 5-μm-thick formalin-fixed paraffin-embedded (FFPE) tissue samples were deparaffinized with xylene, rinsed in ethanol, and rehydrated with ethanol to deionized water gradient. Heat-induced antigen retrieval was performed in an instant pot with a 1× universal antigen retrieval solution (Abcam). After blocking with 3% w/v bovine serum albumin, 1% v/v goat serum, and 0.1% Triton X-100 in PBS, samples were incubated with primary antibodies rabbit anti-lamin B1 (Abcam, ab229025; dilution 1:2000) and guinea pig anti-pan-cytokeratin (LS-Bio, LS-B16812; dilution 1:50) overnight at 4 °C, followed by incubation with secondary antibodies Alexa Fluor 488 goat anti-rabbit (Invitrogen, A11034; dilution 1:500) and Alexa Fluor 594 goat anti-guinea pig (Invitrogen, A11076; dilution 1:500) for 1 h at room temperature and then mounted. Imaging was performed on an Olympus FV3000 confocal microscope using a 60×/1.3 NA silicone oil-immersion objective (Olympus Scientific Solutions Americas Corp.) or on a Zeiss LSM900 confocal microscope using a C Plan-Apochromat 63×/1.4 NA oil-immersion objective (Carl Zeiss Jena GmbH). A pinhole size of 1 Airy disk and a z-step size of 130 nm were used for 3D confocal imaging to ensure overlapping z-stacks and sampling at less than half the focus depth to satisfy the Nyquist criterion⁸⁷:

$$\frac{{\rm{FWHM}}}{2}=\frac{1}{2}\cdot \frac{0.88\cdot {\lambda }_{{\rm{ex}}}}{n-\sqrt{{n}^{2}-{{\rm{NA}}}^{2}}}=\frac{1}{2}\cdot \frac{0.88\cdot 488{\rm{nm}}}{1.5-\sqrt{{1.5}^{2}-{1.4}^{2}}}\approx 223{\rm{nm}}\, > \, 130{\rm{nm}}$$

(1)

where ${\rm{FWHM}}$ is the full width at half maximum, ${{\rm{\lambda }}}_{{\rm{ex}}}$ is the excitation wavelength, ${\rm{n}}$ is the refractive index of the immersion medium, and ${\rm{NA}}$ is the lens numerical aperture. For live imaging of cell spreading and mitosis, NIH-3T3 and HT-1080 cells stably expressing GFP-lamin A cultured in tissue culture plates were incubated with SPY650-FastAct (Cytoskeleton; dilution 1:1000) for 2 h to label F-actin. Then, the cells were passaged onto 8-well glass chamber slides (ThermoFisher Scientific) and maintained in a stage-top heated and humidified chamber (Tokia Hit USA Inc.). Live time-lapse cell imaging was performed with a time step of 5–6 min and a z-step size of 1 μm to provide sufficient temporal resolution and minimize phototoxicity and photobleaching of fluorescent probes.

Photobleaching and trypsinization experiments

NIH-3T3 and HT-1080 cells stably expressing GFP-lamin A were seeded in a complete medium onto 8-well glass chamber slides (ThermoFisher Scientific) coated with 20 μg/ml of fibronectin (Corning) for 12 h for cell attachment and were then placed in a stage-top heated and humidified chamber (Tokia Hit USA Inc.). Using the 488 nm line of a 400-mW Kr/Ar laser, cells within a region of interest were photobleached with a “T” pattern at the basal, middle, and apical nuclear planes to create three fluorescent lamina arcs. The well was washed with PBS to remove traces of serum, and 0.25% trypsin (Corning) was added to the well. Confocal mid-plane images of cell nuclei were captured before the PBS wash and approximately 40 s after the addition of 0.25% trypsin.

To prepare fixed samples of spread cells, NIH-3T3 and HT-1080 cells stably expressing GFP-lamin A were seeded in a complete medium on 35-mm glass dishes (World Precision Instruments) coated with 20 μg/ml of fibronectin (Corning) for 12 h for the cell to adhere. Cells were fixed with 4% paraformaldehyde (Alfa Aesar) at room temperature for 15 min and washed with PBS prior to imaging. For preparation of suspended cells, NIH-3T3 and HT-1080 cells stably expressing GFP-lamin A were trypsinized and centrifuged at 1000 RPM for 5 min. The cell pellet was gently washed with PBS, fixed with 4% paraformaldehyde (Alfa Aesar) at room temperature for 15 min, then washed and carefully resuspended in PBS and transferred to a 35-mm glass dish for imaging.

Micropattern fabrication and contact printing

PDMS stamp micropatterns were designed in AutoCAD 2018 and fabricated in PDMS using a two-step photolithography master mold fabrication process. This was followed by a soft lithography process of replica molding for the final PDMS device from the master mold. First, the AutoCAD design was patterned on a chrome-coated glass mask using a Heidelberg DWL66+ Laser Pattern Generator. Second, to create the master mold, a layer of photosensitive epoxy (Kayaku, SU-8) was patterned on a three-inch diameter silicon substrate (3″ N/Ph (1-0-0) 10–20 ohm-cm, 381 ± 25 μm PRIME SILICON WAFER, SSP, 2 SEMI FLATS) by spin coating SU-8 2015 (Microchem) at 2200 rpm for 30 s and soft baking at 95 °C for 5 min to obtain a thickness of 20 μm. It was then exposed to UV light using photolithography (EVG 610 Double-Slide Mask Aligner) at an exposure energy equal to 160 mJ/cm² through a photomask, followed by a post-exposure bake at 95 °C for another 5 min. Next, the wafer was developed with an SU-8 developer (Microchem). The master mold was then coated with (tridecafluoro1,1,2,2-tetrahydro octyl) trichlorosilane (United Chemical Technologies Inc., T2492) (≈50 nm thick using Chemical Vapor Deposition) for 30 min to facilitate PDMS release from the master mold after replication. The PDMS devices were replicated from the master mold by pouring PDMS prepolymer (Krayden, Sylgard 184 Clear Kit; 5:1 mixture) on the mold, mixed vigorously for 5 min, degassed for 30 min under vacuum to remove air bubbles, and cured at 85 °C for 45–60 min. To make the PDMS micropatterns hydrophilic for easy cell and culture medium loading, the PDMS layers were treated with oxygen plasma (Harrick Plasma) for 90 s.

Rhodamine-conjugated fibronectin circle patterns 30, 40, and 50 µm in diameter were printed on 35-mm tissue culture dishes (ibidi, µ-Dish) using a microcontact printing technique⁸⁸. Briefly, Sylgard 184 Silicone Elastomer base (Dow Corning) was mixed with Sylgard 184 Silicone Elastomer Curing Agent at a 10:1 ratio, then poured on the silicon wafer, degassed in a vacuum chamber, and cured in the oven at 65 °C for 2 h. After curing, the PDMS was removed and cut into approximately 1 cm × 1 cm stamps that were placed in a petri dish with the feature side up. The surface of the PDMS stamps was treated with a low-frequency plasma cleaner unit (PlasmaEtch, Inc., PE-25) for 2 min before 100 µl of rhodamine-conjugated fibronectin (Cytoskeleton) at 0.1 mg/ml was applied to the surface for 1 h to allow adsorption of rhodamine fibronectin onto the surface of the stamps. The 35-mm ibidi µ-Dishes were plasma treated for 2 min, and the stamps were placed feature down on the center of the dishes. The stamps remained in contact with the dishes for 30 min and then the stamps were gently removed. To prevent protein adsorption and cell adhesion on the non-micropatterned regions of the dishes, 200 µg/ml PLL-g-PEG [poly(L-lysine)-g-poly (ethylene glycol)] solution (Surface Solutions AG) was applied overnight at 4 °C.

Model for axisymmetric cell and nuclear shapes

Fully spread cells commonly have characteristics that consist of surfaces of constant mean curvature⁸⁹ for the joint nuclear/cell surface spherical cap (with mean curvature, ${{\rm{H}}}_{{\rm{cap}}}$), the cell surface exterior between the cytoplasm and cell (with mean curvature, ${{\rm{H}}}_{{\rm{cell}}}$), and the nuclear surface at the interface of the nucleus and cytoplasm (with mean curvature, ${{\rm{H}}}_{{\rm{nuc}}}$) (see Fig. 3f). Generally, an axisymmetric surface of constant mean curvature is characterized by radius ${\rm{R}}({\rm{\phi }})$ vs. vertical position ${\rm{z}}\left({\rm{\phi }}\right)$, parameterized by variable ${\rm{\phi }}$, with constant mean curvature H. The equations for ${\rm{R}}({\rm{\phi }})$ and ${\rm{z}}\left({\rm{\phi }}\right)$ are

$$R(\phi )=\sqrt{{\alpha }^{2}{\cos }^{2}\phi+{\beta }^{2}{\sin }^{2}\phi }$$

(2)

$$z\left(\phi \right)=\alpha E\left(\phi,k\right)+\beta F\left(\phi,k\right)$$

(3)

where ${\rm{F}}\left({\rm{\phi }},{\rm{k}}\right)$ and ${\rm{E}}\left({\rm{\phi }},{\rm{k}}\right)$ are incomplete elliptical integrals of the first and second kinds, respectively, and

$$\alpha=\frac{1+\sqrt{1-4{CH}}}{2{\rm{H}}}$$

(4)

$$\beta=\frac{1-\sqrt{1-4{CH}}}{2H}$$

(5)

In addition to ${\rm{H}}$, ${\rm{C}}$ is a 2nd parameter that establishes the specific shape of the cell cortical surface (${{\rm{C}}}_{{\rm{cell}}}$) or nucleus ${{\rm{C}}}_{{\rm{nuc}}}$). (See Dickinson and Lele³⁴ for a detailed mathematical derivation). For a spherical cap, C = 0. Let ${{\rm{R}}}_{1},{{\rm{z}}}_{1}$) be the junction point between the joint spherical cap (with mean curvature, ${{\rm{H}}}_{{\rm{cap}}}$), the cortical cell surface (with mean curvature, ${{\rm{H}}}_{{\rm{cell}}}$), and the free nuclear surface (with mean curvature, ${{\rm{H}}}_{{\rm{nuc}}}$). Matching the three surface tangents ${\rm{dR}}/{\rm{dz}}$ at ${{\rm{R}}}_{1}$ requires

$${C}_{{\rm{cell}}}=\left({H}_{{\rm{cap}}}-{H}_{{\rm{cell}}}\right){{R}_{1}}^{2}$$

(6)

$${C}_{{\rm{nuc}}}=\left({H}_{{\rm{cap}}}-{H}_{{\rm{nuc}}}\right){{R}_{1}}^{2}$$

(7)

Further, the radius ${{\rm{R}}}_{{\rm{n}}0}$ where the nucleus surface impinges tangentially on the substratum is given by

$${R}_{{\rm{n}}0}={R}_{1}\sqrt{1-\frac{{H}_{{\rm{cap}}}}{{H}_{{\rm{nuc}}}}}$$

(8)

For a given cell spread radius, specific cell and nuclear shapes can be calculated by solving for the values of ${{\rm{H}}}_{{\rm{cap}}}$, ${{\rm{H}}}_{{\rm{cell}}}$, and ${{\rm{H}}}_{{\rm{nuc}}}$ that satisfy specified values of cell volume, nuclear volume, and nuclear surface area. For a nuclear surface area greater than that of a sphere of the same nuclear volume, the resulting nuclear shapes are flattened against the surface (see Fig. 3g). In addition, assuming the Law of Laplace applies, the ratio of the surface tensions of the nuclear to cell surfaces is given by

$$\frac{{\tau }_{{\rm{nuc}}}}{{\tau }_{{\rm{cell}}}}=\frac{\left({H}_{{\rm{cap}}}-{H}_{{\rm{cell}}}\right)}{{({H}_{{\rm{nuc}}}-{H}_{{\rm{cap}}})}}$$

(9)

The solution yields unique cell and nuclear shapes for spreading radii up to a maximum radius where the cell edge becomes perpendicular to the substratum. Below a certain spreading radius, a unique solution with a non-zero spherical cap region requires ${{\rm{H}}}_{{\rm{cell}}}$ > ${{\rm{H}}}_{{\rm{cap}}}$ which would imply a negative tension on the lamina surface (by Eq. 9). However, since the nucleus is not attached to the cortex, this shape is not physically realized; rather the same constraints on cell volume, nuclear volume, and nuclear surface area, can be satisfied with the nucleus separated from the cell cortical surface, yielding a spherical cap-shaped cell cortical surface, and an undetermined, but possibly irregular nuclear shape without surface tension.

Synthesis and fabrication of gelatin-based hydrogels

Gelatin methacrylol (GelMA) hydrogels reinforced with polyethylene glycol (PEG)-dopamine-coated iron oxide nanoparticles (8 nm) were synthesized according to previously defined methods⁵⁶. Precursor solutions consisted of GelMA (5% w/v), DI water, and 0 or 0.5 µg/ml of nanoparticles to achieve elastic moduli of 1–3 or 10–15 kPa, respectively. Hydrogel precursors were mixed with MDA-MB-231 cells (4 × 10⁵ cells/ml) at 37 °C, then cast in droplets on glass coverslips and crosslinked under ultraviolet (UV) light (OmniCure Series 2000) at an intensity of 30 mW/cm² for 60 s. Crosslinked gels were submerged in media for 5 days prior to cell fixation and immunofluorescent imaging.

Micropost fabrication

Sylgard 184 Silicone Elastomer base (Dow Corning) was mixed with Sylgard 184 Silicone Elastomer Curing Agent at a 10:1 ratio, degassed, poured onto the micropost mold, and cured at 65 °C overnight. Micropost stamps were peeled off and used to make upright microposts on 35-mm glass dishes (World Precision Instruments). The dishes were coated with 0.1 mg/ml rhodamine-conjugated fibronectin (Cytoskeleton) for 1 h at room temperature, washed three times with PBS, and then cells were passaged on the microposts, incubated overnight at 37 °C and processed for immunofluorescence staining and microscopy.

Transfection of siRNAs

Cells were cultured in 12-well plates in an antibiotic-free medium at 80% confluency at the time of transfection. The transfection solution consisted of 0.5% lipofectamine RNAiMAX transfection reagent (Invitrogen) and 0.5% siRNA (Dharmacon, siGENOME Non-Targeting siRNA Pool #2, D-001206-14-05, target sequences: UAAGGCUAUGAAGAGAUAC, AUGUAUUGGCCUGUAUUAG, AUGAACGUGAAUUGCUCAA, UGGUUUACAUGUCGACUAA; LMNA siGENOME SMARTpool siRNA, D-004978-01, target sequence: GAAGGAGGGUGACCUGAUA; LMNB1 siGENOME SMARTpool siRNA, D-005270-01, target sequence: GAAGGAAUCUGAUCUUAAU) in the reduced serum Opti-MEM medium (Gibco). The culture medium was replaced with transfection solutions, and cells were incubated in 5% CO₂ for 3 days. On day 3, cells were collected for polymerase chain reaction (PCR) assay to verify siRNA knockdown and were passaged on microposts or polyacrylamide hydrogels.

Reverse transcriptase-quantitative PCR

To determine the efficiency of siRNA knockdown, cells were harvested and lysed using the RNeasy Plus Kit (Qiagen), and RNA was purified and quantified. The cDNA was prepared by mixing RNA, reverse transcriptase, oligo primers, and nucleotide triphosphates (dNTPs) (iScript™ Advanced cDNA Synthesis Kit, Bio-Rad Laboratories) in PCR-grade nuclease-free water (Invitrogen). The reaction mixture was incubated in the Bio-Rad thermocycler at the appropriate temperature and duration for reverse transcription. Forward and reverse primer sets (GAPD: VHPS-3541, forward (5′–3′): GAGTCAACGGATTTGGTCGT, reverse (5′–3′): TTGATTTTGGAGGGATCTCG, RealTimePrimers; LMNA: Ref# 460260112 & 13, forward sequence: ATGAGGACCAGGTGGAGCAGTA, reverse sequence: ACCAGGTTGCTGTTCCTC-TCAG; LMNB1: Ref# 460260114 & 15, forward sequence: GAGAGCAACATGATGCCCAAGTG, reverse sequence: GTTCTTCCCTGGCACTGTTGAC, IDT) were used to target the cDNA of the genes of interest. The PCR reaction combined cDNA, primers, DNA polymerase, dNTPs, and iQ™ SYBR® Green Supermix reaction buffer (Bio-Rad Laboratories). PCR amplification was performed using appropriate cycling conditions recommended by Bio-Rad. The standard curves and Ct values were used to quantify gene expression levels for the genes of interest normalized to the expression level of GAPD in the treatment group relative to the normalized gene expression levels in the siSCRM group.

Immunoblotting

Cells were washed with ice-cold PBS and lysed on ice with RIPA Buffer (ThermoFisher Scientific) supplemented with 1× Halt Protease and Phosphatase Inhibitor Cocktail (ThermoFisher Scientific). After centrifugation at 15,000 × g for 10 min at 4 °C, the supernatant was collected, and the protein concentration was determined using Pierce BCA Protein Assay Kit (ThermoFisher Scientific) and BioTek Cytation 5 (Agilent). The supernatant was mixed with 4× Laemmli Sample Buffer (Bio-Rad Laboratories) supplemented with 10% β-mercaptoethanol (Bio-Rad Laboratories) and boiled for 5 min. The samples were separated on a 4–15% polyacrylamide gel (Bio-Rad Laboratories) along with Chameleon Duo Pre-stained Protein Ladder (LI-COR Biosciences) and then transferred onto a nitrocellulose membrane (Bio-Rad Laboratories). The membrane was blocked with Intercept Blocking Buffer (LI-COR Biosciences) for 1 h at room temperature and incubated with primary antibodies mouse anti-lamin A/C (Santa Cruz Biotechnology, sc-376248; dilution 1:500) and rabbit anti-GAPDH (Novus Biologicals, NB100-56875; dilution 1:2000) overnight at 4 °C. After multiple membrane washes with TBST (20 mM Tris pH 7.6, 137 mM NaCl, 0.1% Tween 20), the membrane was incubated with secondary antibodies IRDye 680LT goat anti-mouse (926-68020; LI-COR Biosciences; dilution 1:5000) and IRDye 800CW goat anti-rabbit (926-32211; LI-COR Biosciences; dilution 1:5000) for 1 h at room temperature. The membrane was imaged using the Odyssey M imaging system (LI-COR Biosciences). The intensity of the fluorescent bands was quantified using Image Studio 4.0 software (LI-COR Biosciences).

Image analysis

Raw confocal images were loaded into Matlab, and a customized Matlab code was built for nuclear morphometric and phenotypic analysis. Maximum-projection images of the lamin channel were generated and segmented using an Otsu segmentation algorithm to create nuclear masks for the identification of nuclei. Nuclei that touched the image border or had a projected area smaller than the empirically determined lower bounds were removed to exclude small debris or imaging artifacts. The resulting nuclear masks were applied to lamin z-stack images to crop nuclei individually. To quantify nuclear height, mean lamin intensity was calculated for each z-plane, and the onset and offset points from the background intensity were determined as the bottom and top confocal planes. Nuclear height was calculated as the distance between these two confocal planes. Nuclear surface area and volume were quantified using Matlab Image Processing Toolbox.

Nuclear irregularity was quantified using an elliptical Fourier analysis, as we reported previously⁵³, which approximates nuclear shapes through the decomposition of the shape into a series of harmonic ellipses⁹⁰. We noticed that the bulk masks generated by Otsu segmentation were unable to capture accurate details of folds and wrinkles on nuclear contours. Therefore, we improved the segmentation by tracing the intensity maximum on each normal line along the bulk nuclear periphery to delineate the precise nuclear contour at sub-pixel resolution. The precise nuclear contour was fitted using a series of elliptic harmonics, defined by the Fourier series coefficients calculated from the x and y coordinates of the nuclear outline. A total of 15 harmonic ellipses were used for all the morphometric analyses, which were found to accurately approximate even the most complex, irregular nuclei^53,91. The single elliptic harmonic at each frequency can be geometrically visualized as a pair of orthogonal semiaxes. The first-frequency Fourier coefficients describe a rough ellipsoidal shape, and the Fourier coefficients at higher frequencies approximate more convoluted outlines. To quantify the shape irregularity, the elliptic Fourier coefficient (EFC) ratio is defined as the ratio of the length sum of the major and minor semiaxes at the first frequency to the semiaxes length sum for the subsequent 14 harmonics at the higher frequencies. A regular nuclear contour, where the first-frequency elliptic harmonic captures most of the contour with small axes lengths at higher frequencies, has a larger EFC ratio. In contrast, an irregular nuclear contour requires larger axes lengths at higher frequencies, resulting in a lower EFC ratio. In this study, we accommodated the variation of nuclear irregularity across different confocal planes by extracting nuclear contours from the z-plane at 75%, 50%, and 25% of nuclear height to calculate the EFC ratio at the top, middle, and bottom, respectively, and averaging the EFC ratios of three planes for each nucleus.

Maximum-projection images of the phalloidin channel were generated and segmented using an Otsu segmentation algorithm to create cell masks. Cell spreading area and aspect ratio were quantified using Matlab Image Processing Toolbox. To quantify the nuclear to cytoplasmic ratio of YAP, the nuclear masks and cell masks were applied onto maximum-projection images of the YAP channel, and the nuclear to cytoplasmic YAP ratio was calculated as: [(Nuclear intensity)−(Background intensity)] ÷ [(Cytoplasmic intensity)−(Background intensity)].

For chromatin marker analysis, a customized Matlab code was built based on the previous study⁷⁵. Briefly, maximum-projection images of the DNA channel were generated and segmented using an Otsu segmentation algorithm to create nuclear masks for determining the nuclear border and the nuclear center for each nucleus. For each pixel inside the nuclear mask, the distance to the nuclear center and the intensities for both H3K9me3 and H3K27me3 markers were measured. Nuclear center distances were normalized to the maximum distance of each corresponding center trajectory. Chromatin marker intensities were normalized to the total intensity per nucleus. Normalized nuclear center distances were binned in 0.01 steps and marker intensities of all pixels in the same bin were averaged for each nucleus.

Fluorescence lifetime imaging microscopy (FLIM)-FRET imaging and analysis

MDCK cells expressing Lamin-SS or Lamin-TM sensor⁵⁰ were cultured on the fibronectin-coated glass-bottom dishes and allowed to spread overnight. Cells were treated with 10 µg/ml of cytochalasin D (Sigma–Aldrich) for 1 h to induce nuclear wrinkling, followed by fixation with 4% PFA for 15 min. After washing, the samples were stored in PBS without mounting. FLIM imaging was performed on a Leica SP8 confocal microscope using an HC Plan-Apochromat 40×/1.1 NA motCORR CS2 water-immersion objective (Leica Microsystems). A pulsed laser at 440 nm was used to excite the sensors, and fluorescence lifetimes in the 455 to 495 nm range were collected using a HyD X detector to capture photon arrival times specific to the donor. n-Exponential reconvolution fitting model in Leica LAS X software was used to fit the pixel-by-pixel photon arrival times with biexponential decay components to obtain mean lifetimes for individual nuclei.

Cytoskeleton, contractility, and LINC complex disruption experiment

For cytoskeleton disruption experiments, HN cells expressing GFP-LMNA were cultured on soft hydrogels and treated with 4 µM cytochalasin D (Sigma–Aldrich) or 2 µM nocodazole (STEMCELL Technologies) for 1 h. Z-stack live imaging with a 130-nm step size was performed both before and after treatment to assess changes in nuclear wrinkling. F-actin and microtubule disruption were verified through immunofluorescence staining in cells cultured on glass-bottom dishes and fixed after the same treatment. For contractility disruption experiments, HN cells expressing GFP-LMNA were cultured on stiff hydrogels and allowed to spread overnight. Cells were then treated with 50 µM Y-27632 (Sigma–Aldrich), a Rho-associated kinase (ROCK) inhibitor, or 50 µM blebbistatin (Sigma–Aldrich), a direct inhibitor of myosin II activity, for 3 h. Z-stack live imaging with a 130-nm step size was performed both before and after treatment to assess changes in nuclear volume and height. Cells were then fixed and stained for YAP and F-actin and imaged with the same imaging parameters to compare the nuclear to cytoplasmic YAP ratio. For LINC complex disruption experiments, MDCK cells mCherry-DN KASH1 were cultured on 35-mm glass dishes and treated with 1 µg/ml doxycycline (Sigma–Aldrich) for 24 h to induce mCherry-DN KASH1 expression. Cells were then fixed with 4% PFA and stained for lamin B1 and F-actin to compare the nuclear wrinkling and cell spreading.

Statistical analysis

All quantitative data were measured from at least three biological replicates and presented as mean ± standard error of the mean (SEM). GraphPad Prism 10.0 was used for statistical analysis and graphic representations of data. Differences between values were considered statistically significant when p < 0.05 and non-significant (NS) for p > 0.05. The details of experimental conditions and statistical tests are provided in the figure legends.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.