Introduction

Interactions of low-temperature plasmas (LTP) with material surfaces are central to the fabrication of microelectronics1,2, as approximately 30 percent of the semiconductor manufacturing chain relies on plasma processing. A holistic understanding of the interactions of plasma with materials, termed plasma-surface interactions (PSI), is essential for maintaining greater uniformity in microelectronic features, implementing atomic-scale control and reducing defects, as well as for exploring new chemistries, materials, and fabrication techniques3,4. Despite huge strides in plasma modeling and surface science simulations, model-based investigations of atomic-scale plasma processes remain largely limited due to the lack of mechanistic models of complex PSI5.

The main challenges in modeling PSI stem from the vast array of possible atomistic processes at play. These include secondary electron emission6, spontaneous etching7,8, surface reactions9, surface adsorption and modification10, surface charging11, radical recombination10, diffusion12, and knock-on collisions13, to name a few. Moreover, PSI strongly depend on the plasma sheath, material surface condition, and bulk material properties, each of which is characterized by physics at different length and time scales5. Hence, PSI involve multiscale processes, spanning length scales from Å to cm and time scales from picoseconds to seconds. A comprehensive description of PSI must take into account the quantum interactions at the plasma-material interface, mesoscopic physics in the plasma sheath, and the macroscopic variations in the bulk plasma.

Multiscale modeling of PSI has received renewed interest as plasma processing of complex interfaces is becoming increasingly important in a wide range of emerging LTP applications4. Common multiscale modeling strategies for PSI include combining molecular dynamics (MD) and Monte-Carlo (MC) simulations5,12,14,15,16, coupling kinetic MC (KMC) simulations of surface with fluid descriptions of the bulk plasma17,18, rate equation approaches for describing specific interactions where kinetic rate constants are obtained from MD simulations19, and semiclassical models for charge transfer using separate Boltzmann equations for electrons and holes on either side of the interface along with quantum mechanical matching conditions at the interface20. However, these multiscale modeling strategies are generally tailored to describe one or a subset of plasma-induced surface processes5, often ignoring the interplay between a complex array of interactions and thus limiting the ability to “transfer” the model to similar systems in a systematic and efficient manner. Additionally, these approaches rarely provide equation-oriented model representations that can readily capture the effects of process-level operating conditions and parameters, and can often be prohibitively expensive.

Interactions at the plasma-solid interface can also be affected by the subsurface, for example, when modified through ion bombardment15. Typical strategies to account for the subsurface include assuming a well-mixed zone (called the mixing layer) and using Arrhenius-type global reaction models to describe surface reactions21,22,23,24. Such classical reaction rate models are empirical in nature and typically rely on experimentally determined reaction rate laws, where a key challenge stems from accounting for the complex series of reactions that can occur at the plasma-solid interface. On the other hand, KMC models describe the well-mixed subsurface layer of fixed depth through which chemical species can travel and reactions can progress5,15,16. KMC models evolve probabilistic events through stochastic sampling. As such, they do not provide analytical kinetic equations and can be computationally expensive.

In recent years, machine learning-assisted approaches have been widely used for data-driven modeling of plasma physics, chemistry, and PSI (e.g.,25,26,27,28,29,30,31,32). While there has been fairly significant progress on physics-informed, learning-assisted modeling of the bulk plasma behavior33,34,35, much of the machine learning work related to PSI modeling has focused on creating black-box, surrogate models for plasma-induced surface effects36,37,38. Although such black-box models can exhibit good predictive capabilities over the range of processing conditions covered in their training data, they do not generally provide interpretable representations of the multiscale processes governing PSI. Integration of physics into data-driven models can reduce overfitting, impart interpretability, extend extrapolative capabilities beyond the range of training data, and promote generalization to new systems39,40,41. As such, fusing physics-based and data-driven modeling can be particularly useful for problems involving complex multiphysics.

Physics knowledge can be included into data-driven models either through the loss function, as in physics-informed neural networks42, or through composite equations composed of physics-based expressions, such as conservation laws, and function approximators. The latter approach is termed as universal differential equations (UDEs)43, where parts of a differential equation are represented by neural networks or other function approximators as a substitute for unknown physics, such that the entire equation is differentiable44. UDEs have emerged as a powerful tool in scientific computing for dynamic modeling of partially known systems45, as well as discovery of governing equations of dynamical systems46. Example applications include modeling of nucleation kinetics47, neural systems in neuroscience45, and pandemic outbreaks48. The universality of UDEs, their ability to retain physics through the model structure, and the differentiable nature of the resulting equations can make them highly suited for inference of multiscale and multiphysics problems.

Master equations are widely used to model molecular processes49,50, such as adsorption from gas to an adsorbent surface51, mRNA interactions with a promoter52, and particle hopping in space during diffusion53. This work presents a neural master equation (NME) framework for multiscale modeling of PSI. The proposed NME framework builds a kinetic model through master equations, where unknown transition probabilities, which are mesoscopic averages of quantum-mechanical interactions, are represented with neural networks to form a set of UDEs. As such, the NME framework bridges the microscopic and mesoscopic scales, as it provides mesoscopic rate equations where the transition rates are obtained from atomistic simulations. Additionally, the proposed framework is able to admit spatial variations of quantities of interest that cannot be readily cast into a master equation form, such as those arising from transport.

The NME framework is demonstrated for multiscale modeling of Si atomic layer etch (ALE) with Cl2 and Ar ion, as well as Si reactive ion etch (RIE) with F and Ar ion, two LTP processes that are widely used in semiconductor manufacturing54,55,56. We demonstrate that the learned NME models provide an interpretable mesoscopic description of the evolution of surface processes by predicting experimentally relevant observables as a function of process parameters. The NME-based surface kinetic models exhibit extrapolative capabilities outside their training range in comparison to a fully data-driven model learned using neural ordinary differential equations57. Our results suggest that the NME framework can be used as a viable physics-based surrogate for computationally expensive MD simulations to investigate PSI. The remainder of the paper is organized as follows. The section “General overview of the NME framework” presents a general overview of the NME framework. In the sections “NME-Based Surface Kinetic Model of ALE” and “NME-based surface kinetic model of RIE”, the NME framework is demonstrated on ALE and RIE, respectively. The section “Discussion” presents a discussion on the results and the broader use of the NME framework, followed by the details of the NME framework in the section “Methods”.

Results

General overview of the NME framework

In atomic-scale plasma processes such as RIE and ALE, there are multiple chemical elements that exist in different states, taking part in surface reactions and sputtering. For a molecular process with M species, with each species denoted by subscript m that undergoes \({\mathcal{V}}\) possible state transitions, the occupation probability of a species m is defined as the probability of occupying a state ν and is given by

$${P}_{m}^{\nu }=\frac{{N}_{m}^{\nu }}{{N}_{m}},\quad \forall \,\nu =1,\ldots ,{\mathcal{V}},$$
(1)

with \({P}_{m}^{\nu }\) denoting the occupation probability of species m in state ν, Nm denoting the total number of species m in all the \({\mathcal{V}}\) states, and \({N}_{m}^{\nu }\) denoting the number of species m in state ν. The dynamics of the state-to-state transitions can be represented by master equations58

$$\frac{{{d}}{{\boldsymbol{P}}}_{m}}{{{d}}t}={{\boldsymbol{W}}}_{m}{{\boldsymbol{P}}}_{m},\quad \forall \,m=1,\ldots ,M,$$
(2)

where \({{\boldsymbol{W}}}_{m}\in {{\mathbb{R}}}^{{\mathcal{V}}\times {\mathcal{V}}}\) denotes the transition rates between the states of species m and \({{\boldsymbol{P}}}_{m}={[{P}_{m}^{1},\ldots ,{P}_{m}^{{\mathcal{V}}}]}^{\top }\in {{\mathbb{R}}}^{{\mathcal{V}}\times 1}\) is the vector of the occupation probabilities for species m in all of its \({\mathcal{V}}\) possible states.

Depending on the type of molecular interactions (e.g., quantum interactions for chemical reactions, or classical interactions for diffusion59), determining the transition probabilities in Eq. (2) can be particularly challenging. Here, we use neural networks as universal approximators60,61 to learn the transition probabilities in Eq. (2) as a function of local inputs (e.g., incident ion energy and dose) to an atomic-scale process. As such, the master equation takes the form of a composite differential equation with neural network components, as given by

$$\frac{{{d}}{{\hat{\boldsymbol{P}}}}_{m}}{{{d}}t}={{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }}){{\hat{\boldsymbol{P}}}}_{m},\quad \forall \,m=1,\ldots ,M,$$
(3)

where \({{\hat{\boldsymbol{P}}}}_{m}={[{\hat{P}}_{m}^{1},\ldots ,{\hat{P}}_{m}^{{\mathcal{V}}}]}{^\top }\) is the vector of predicted occupation probabilities of species m and \({{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }}):{{\mathbb{R}}}^{{n}_{x}}\times {{\mathbb{R}}}^{{n}_{\uptheta }}\mapsto {{\mathbb{R}}}^{{\mathcal{V}}\times {\mathcal{V}}}\) is a neural model of the transition matrix, with x being the inputs to the system and Θ being the vector of learnable parameters.

In addition to state transitions, ion bombardment can result in incorporation of surface species into the bulk solid62 and ion-enhanced diffusion in the bulk solid63,64,65,66,67,68,69. The ion-enhanced diffusion can result in the redistribution of material in the mixed layer and, thus, must be accounted for during state transitions, as during plasma etch, the moving etch front exposes underlying mixed layer material to the surface, effectively causing a state transition. The amount of material that is exposed depends on the local mixed layer concentration, which is affected by ion-enhanced diffusion. This non-linear state transition appears as an additive term to Eq. (3) as given by

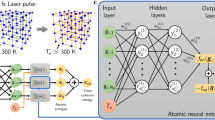
$$\begin{array}{ll}\frac{{{d}}{{\hat{\boldsymbol{P}}}}_{m}}{{{d}}t}={{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }}){{\hat{\boldsymbol{P}}}}_{m}+{\boldsymbol{g}}(\cdot ),\\ \,\,\forall \,m=1,\ldots ,M,\end{array}$$
(4)

where g( ⋅ ) is any linear or non-linear contribution to the probability current due to transport or moving boundaries. Figure 1 provides an overview of the NME framework. Ensemble atomistic simulations at different input conditions of ion energy and fluence are used to generate time-series trajectory data of “ground truth” occupation probabilities \({\{{{\boldsymbol{P}}}_{m}\}}_{m = 1}^{M}\) to train the learnable parameters of \({{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }})\) in Eq. (4).

Fig. 1: Overview of the neural master equation (NME) framework.
figure 1

At the microscopic scale, all-atom simulations are performed to generate time-series trajectory data of occupation probabilities \({\{{{\boldsymbol{P}}}_{m}\}}_{m = 1}^{M}\) for different values of system inputs x. The data are used to determine the learnable parameters of the neural model of mesoscopic transition rates \({{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\uptheta }})\) in the NMEs in Eq. (4) by minimizing the mean-squared-error loss function (Eq. (13)). The term g(⋅) is an addition to the master equation to account for possible probability currents due to additional physics, such as transport.

Full size image

NME-based surface kinetic model of ALE

The NME framework was used to obtain a mesoscopic kinetic model of surface processes for the case of Si ALE with Cl2 and Ar+. ALE is a layer-by-layer removal of material that progresses cyclically70. During the first half cycle, a reactive gas is adsorbed on the surface of the material to be etched, whereas during the next half-cycle the modified surface is bombarded by ions to sputter material off the surface. The two steps occur sequentially and, hence, are temporally decoupled from each other.

In the ALE process at hand, Cl adsorption equilibrates quickly compared to the cycle time of adsorption, with Cl atoms fully covering all available active sites according to the Langmuir isotherm71. Hence, the dynamics of the adsorption process were ignored and, instead, an equilibrium coverage of Cl atoms was assumed at the start of every bombardment cycle. Three distinct states in which Cl can be present were considered, i.e., ν ∈ {I, II, III}. Figure 2 depicts these states and the transitions among them. In state I, Cl atoms are mixed with bulk Si forming a mixed layer. This state is characterized by diffusion processes occurring in the mixed layer, with Cl only being able to interact with itself and Si. In state II, Cl atoms are present on the exposed surface of the Si-Cl block and are capable of interacting with both Ar+ and Si. It was assumed that Ar+ does not interact with Cl or Si in the mixed layer, and that the mixed layer composition can vary with depth, as opposed to the homogeneous mixed layer assumption in ref. 16. In state III, Cl atoms are present in bulk gas as SixCly. Due to high-energy Ar+ bombardment, Cl atoms can transition from the surface (II) to the bulk gas phase (III). Additionally, Cl atoms can be pushed down from the surface into the subsurface mixed layer (I), where they mix with Si. Other transitions, such as recombination from the bulk gas phase to the surface, are also possible, but were ignored here for simplicity. The transition from state II to III can be broken down into a series of first-order transitions for different Cl species in the bulk (SixCly); however, all such transitions were lumped together.

Fig. 2: Schematic representation of the three overarching states of Cl atoms in Si ALE with Cl2 and Ar+.
figure 2

Blue circles represent Si atoms, while yellow circles represent Cl atoms. Cl atoms can be either mixed with Si in the subsurface mixed layer (state I), on the exposed surface (state II), or in the bulk gas as atomic or compound Cl (state III).

Full size image

Following Eq. (4), the set of NMEs for the three Cl states can be easily derived (See Supplementary Section 1.2). A value of 1 × 10−19 m2/s was taken for the diffusion coefficient66. Since the length and time scales change with time, the problem becomes stiff and, thus, an adaptive solver was used to solve the coupled, non-linear set of NMEs for the occupation probabilities.

Model validation and predictions

MD simulations were performed to generate high-resolution time series data for the occupation probability of Cl in the three states (I, II, and III) at different conditions of incident Ar+ energy and dose, exactly following the parameters used in ref. 62. These time series data were used to train the surface kinetic model for Si ALE with Cl2/Ar+. Only one ALE cycle was simulated, starting with a pristine Si block, covered with an equilibrium concentration of Cl atoms. In the MD simulations, sputtered species were taken out of the simulation box, and only species on the surface and in bulk Si were kept. One sample was taken per impact of Ar+; thus, the total length of a time series at a particular condition is the number of ion impacts at that condition.

From ensemble MD simulations with three realizations per condition, time series data of the occupation probabilities were calculated at different conditions of Ar+ energy and dose. Ion energies from 30 to 70 eV with intervals of 1 eV and ion dose between 100 and 1000 impacts at intervals of 50 impacts were considered, totaling 779 distinct time series to train the surface kinetic model. The range of ion flux for the above impacts was 3.14 × 1013–3.14 × 1014 ion/cm2-s, as is of the order seen in experiments71. The ion dose and ion energy were the only inputs x to the neural network \({{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }})\) in Eq. (4). To keep parity with experimental results, the ion fluence in the MD simulations was selected to be the same as that in experiments62.

To classify Cl into the proposed states, the coordination number of all Cl atoms in the system was calculated: those having coordination number greater than two were classified as occupying state I, while all others were classified into state II, with the reasoning that Cl atoms inside the densely packed mixed layer would feel the effect of multiple neighboring species. This classification was based on heuristic arguments; however, more formal distinctions can be made, e.g., based on bond orders of individual Cl atoms from the modified reactive empirical bond-order potential used in ref. 72. The training details of NMEs in Eq. (4) for the ALE system are provided in Supplementary Section 2.1.

The transition rates in Eq. (4) were learned using the aforementioned time series data, as shown in Fig. 1. The resulting surface kinetic model was tested on combinations of ion dose and energy not present in the training dataset. Details of the neural network models, training procedure, and loss curves can be found in Supplementary Section 2.1. Figure 3 shows the comparison between the predicted occupation probability dynamics and those obtained from MD simulations; the statistical evaluation of the model performance is given in Table 1. The predicted occupation probability dynamics of all three states are in good quantitative agreement with test data for a variety of different ion dose and energy conditions. As bombardment starts with an equilibrium Cl coverage on a pristine Si block, the probability of finding Cl at the surface is unity. This probability decreases with time as Cl atoms transition to states I and III due to Ar+ bombardment. However, exponential decay in the surface occupation probability is arrested by the non-linear transition of Cl atoms to the surface through the moving etch front, which exposes the underlying Cl atoms of the mixed layer.

Fig. 3: Performance of the surface kinetic model for ALE on test data.
figure 3

The solid blue line, black dash-dot line, and red dashed line represent the occupation probabilities predicted by the surface kinetic model in the mixed layer (I), surface (II), and bulk gas (III), respectively, while the open circles denote the corresponding occupation probabilities from MD simulations. a 119 Ar+ impacts at 49 eV energy. b 261 Ar+ impacts at 51 eV energy. c 311 Ar+ impacts at 61 eV energy. d 593 Ar+ impacts at 43 eV energy. These combinations of ion dose and energy were not included in the training data, but the ion energy is within the training range of 30-70 eV.

Full size image
Table 1 The root mean squared error (RMSE) between the surface kinetic model predictions and MD simulations for all four cases of Fig. 3
Full size table

The surface kinetic model retains the physical structure of the system by using the master equations to describe the state transitions and the ion-enhanced diffusion for transport in the mixed layer. Consequently, it also uses relatively fewer trajectories (779) compared to learning a fully data-driven model38, and ensures that mass conservation, Eq. (11), is always satisfied. The retention of the physical form of the dynamical equations using NMEs promotes model performance for a wide range of operating conditions of ion energy and dose, while providing physically consistent results.

Figure 4 shows the profile of Cl atomic fraction in the mixed layer at 1000 Ar+ ion impacts. The profile arises due to competition between the rate of removal of material from the surface and rate of diffusion into the mixed layer. The penetration depth decreases with increasing ion energy. This is because at higher incident ion energies, Cl atoms are more rapidly sputtered off the surface due to higher etch rate, which results in subsurface Cl being exposed more rapidly. No clear trend between the total Cl concentration and the ion energy is observed due to the highly nonlinear nature of the process. At 40 eV, the ion energy is not sufficient to push too many Cl atoms into the mixed layer. The ability of Ar+ to push Cl atoms into the mixed layer increases with increasing energy, as seen for 60 eV and 80 eV, where there are more Cl atoms in the mixed layer compared to 40 eV. For 100 eV, the etch front depletes fastest, and Cl atoms rapidly and nonlinearly transition from the mixed layer to the surface. This leads to fewer Cl atoms in the mixed layer and a smaller penetration depth. The total Cl and its penetration depend upon the competition between the etch and diffusive transport away from the etch front. The atomic fraction depth of 22 Å for 100 eV is in agreement with MD simulations from ref. 62, even though the surface kinetic model was not trained on atomic fraction data. To obtain the relevant concentrations from the occupation probabilities, it is sufficient to multiply the probabilities with the total number of Cl atoms in the system. The time evolution of number of Cl atoms is shown in Fig. 5. Since the bombardment step of ALE is considered to be a closed system with respect to Cl, the dynamics closely follow the time evolution of occupation probabilities.

Fig. 4: Predicted profile of the Cl atomic fraction in the mixed layer. Profiles are drawn at the end of 1000 Ar+ impacts as predicted by the surface kinetic model.
figure 4

The solid golden line is at 40 eV, the red dashed line at 60 eV, the black dash-dot line at 80 eV, and the blue dotted line at 100 eV.

Full size image
Fig. 5: Time-evolution of the number of Cl atoms as predicted by the surface kinetic model for ALE for the three states under 1000 Ar+ impacts at 30 eV.
figure 5

The solid blue line represents the mixed layer (I), the black dash-dot line represents the surface (II), and the red dashed line represents the bulk gas (III).

Full size image

Figure 6 shows the evolution of Cl uptake and Si etched over ALE cycles, and compares them with MD simulations from ref. 62. The representative first-order dynamics of Cl is shown only for the first half cycle. Cl adsorption process equilibrates very fast; hence, an equilibrium coverage of Cl was assumed at the start of every bombardment half cycle62,71. The cases of 80 eV and 100 eV represent an extrapolation from the training data, since the training range was 30–70 eV. The surface kinetic model predicts incremental increases in the final Cl uptake from cycle to cycle (Fig. 6a), as increasingly more Cl atoms are incorporated into the mixed layer. More efficient removal of Cl is seen at higher ion energies in both the surface kinetic model predictions and the MD simulations. The surface kinetic model correctly predicts that the Cl retained in the substrate post-bombardment increases across cycles. While the prediction from the surface kinetic model is of the same order as MD simulations, the predictions are off by 0.15–1 monolayer (ML). The primary cause for this mismatch can be the classification of Cl atoms into states. The classification was made on the basis of coordination number, which is a discrete classifying feature and, thus, is limited. The surface kinetic model overestimates the amount of Cl left on the surface post bombardment, compared to MD simulations, which predict almost no Cl at the surface post bombardment. This reduces the amount of Cl that can be absorbed in the subsequent adsorption half cycle. It should be noted that the amount of Cl left on the surface is a matter of classification. A more accurate representation of the physical system may be made through using bond orders and bond energies of the pair potential used in MD simulations72. However, the cut-off value for the bond energies and orders is a parameter that will require tuning from system to system. Other potential causes for the mismatch could be the inability of the surface kinetic model to accurately account for the increase in active sites due to ion bombardment73 and the deficiency of the MD simulations in capturing diffusion, both of which can affect the concentration of Cl at the surface and subsurface. These effects can further cause a change in the total Cl uptake across cycles.

Fig. 6: Predictions of the surface kinetic model for ALE cycles at 1000 Ar+ impacts, compared with MD simulations from ref. 62.
figure 6

An equilibrium Cl coverage was assumed at the start of each bombardment cycle since Cl adsorption equilibrates very fast71. The blue, golden, red, and black lines represent Ar+ energies of 40 eV, 60 eV, 80 eV, and 100 eV, respectively. a Cl uptake in monolayers (ML); the adsorption half cycle is shown only for the first cycle (dashed line in teal). The dashed lines correspond to MD simulations, while the solid lines are the surface kinetic model predictions. b Distance of Si etched (Å). The open circles correspond to MD simulations, while the solid lines are predictions from the surface kinetic model.

Full size image

For the total Si etched (Fig. 6b), the model predicts an approximately constant etch per cycle. A very good agreement is found with the results of ref. 62, demonstrating the predictive capability of the NME-based surface kinetic model. The model can capture the physical idiosyncrasies of the system and maintain quantitative agreement, all while drastically reducing the problem to one of solving a set of ODEs.

A discrepancy is seen in the curvature gradient of the etch rate in Fig. 6b. However, when scalar values of the transition probabilities are judiciously chosen for particular conditions and the surface kinetic model is solved numerically with constant values of the transition probabilities, the correct curvature and a good fit is obtained, underlying the validity of the master equations. As neural networks are used to approximate the transition probabilities, the proposed approach is prone to getting stuck in local minima, and may not represent all of the physics correctly. Possible remedies for this are to include all the species and their respective states in the master equations and impose physically meaningful constraints on the loss function. Additionally, the surface kinetic model does not show a cyclic steady state for Cl uptake, as seen in long-time MD simulations. Potential reasons for this could be using a constant diffusion coefficient, or the absence of depth-dependent diffusion67.

The performance of the proposed NME framework is compared to that of a NODE model of the form of Eq. (14). To ensure that the results are physical, the loss function is constrained (See Supplementary Section 3) to obey Eq. (11) and provide probabilities in the interval [0,1]; this approach is termed as fully constrained NODE (FC-NODE). Figure 7 shows the performance of FC-NODE against test data. FC-NODE performs poorly on test data and both constraints, although not violated during training, are violated on test data. Unlike NME (Eq. (4)), FC-NODE (Eq. (14)) does not retain the physics-based structure of state transitions or transport. Furthermore, while Eq. (11) is built into the structure of NMEs, it only appears as a soft constraint in the loss function during training of the FC-NODE.

Fig. 7: Performance of the FC-NODE model on test data. The lines denote predictions from the model, while the open circles denote the test data from MD simulations.
figure 7

The solid blue line, the black dash-dot line, and the red dashed line represent the mixed layer (I), the surface (II), and the bulk gas (III) occupation probability dynamics, respectively. a 119 Ar+ impacts at 49 eV energy. b 261 Ar+ impacts at 51 eV energy.

Full size image

NME-based surface kinetic model of RIE

Surface kinetic modeling of RIE of Si with F and Ar+ is also studied using the NME framework shown in Fig. 1. RIE is a continuous process, where a plasma chamber is filled with reactive and neutral gases. Accelerated ions sputter the surface, and reactive neutrals and radicals chemically react with the exposed surface74. As in the Si ALE system above, three states were considered to represent the RIE system at hand: F atoms can exist in the mixed layer (state I), at the exposed surface of Si (state II), and as volatiles in the gas phase (state III). The NME model structure was kept the same as that for ALE, with two distinct differences: (i) RIE is an open system with respect to F atoms, and (ii) there is an additional adsorption process for F on the surface of Si. Hence, the master equations were modified to account for these differences; derivations are provided in Supplementary Section 1.3.

Similar to the Si ALE system, the characteristic length and time scales of ion-enhanced diffusion within bulk Si are D/v(t) and D/v(t)2, respectively. The atomic fraction is used, instead of the probability density function, to obtain a simpler representation of diffusion within bulk Si; however, the atomic fraction and probability density function share a linear relationship given by Eq. (9), where the total number of atoms Nm is now a function of time. There are two fluxes to the exposed surface: the flux of incident Ar+, JAr, and the flux of incident F atoms, JF. The net rate of addition of F into the system is described by an additional ODE that can be solved independently from the set of NMEs. In an actual RIE system, gases are continuously pumped out from the etch chamber. Here, it is assumed that any gases taken out are also in state III, an assumption that can be dropped by adding a removal term to the surface kinetic model. Another difference from the Si ALE system is the rate of adsorption of F to the exposed surface.

Model validation and predictions

MD simulations with appropriate interatomic potentials are extensively used to study surface dynamics in RIE processes13,75,76,77,78. Following ref. 79, we used MD simulationsto generate time series data of F occupation probabilities to train the NME-based surface kinetic model for RIE of Si.

The architecture of the neural networks representing the transition rates in Si RIE was kept the same as that for Si ALE, as similar kinetics are expected in both systems. The transition rates are functions of the incident ion energy and the combined dose of F and Ar in the system. The flux ratio of F to Ar was kept constant at 5. Ion energy was varied from 20 eV to 80 eV at intervals of 2 eV, while the combined dose values were in the range of 500 to 1000 impacts with an interval of 25 impacts, resulting in 651 distinct combinations. Figure 8 shows the performance of the NME-based surface kinetic model on unseen test data, where neither the dose nor the ion energy is present in the training dataset. Furthermore, a condition of 1100 total impacts at 90 eV Ar+ energy, outside of the domain of training data, is also considered. As can be seen, the NME-based surface kinetic model exhibits very good agreement with test data and can also generalize beyond the training dataset, as evident from Fig. 8a. The mixed layer concentration is negligible since the extremely strong Si-F bond80 significantly weakens the Si-Si bond and prevents F from being pushed into the mixed layer.

Fig. 8: Performance of the surface kinetic model for RIE on test data.
figure 8

The lines denote predictions from the model, while the open circles denote test data from MD simulations. The solid blue line, the black dashed–dot line, and the red dashed line represent the mixed layer (I), the surface (II), and the bulk gas (III) occupation probability dynamics, respectively. a 1100 total impacts at 90 eV Ar+ energy. b 560 total impacts 51 eV Ar+ energy. c 864 total impacts 79 eV Ar+ energy, and d 952 total impacts 29 eV Ar+ energy.

Full size image

Figure 9a shows the F occupation dynamics at different states with the learned model for a dose of 1100 total impacts and ion energy of 90 eV. The number of F atoms in the bulk gas phase quasi-linearly increases due to the flux of F atoms into the system, while that on the surface, plateaus and reaches a steady state due to competing sputtering and adsorption processes. Since the surface kinetic model also solves for the instantaneous velocity of the etch front, the instantaneous etch rate can be calculated. Figure 9b shows the dynamics of the instantaneous etch rate, and the area under the curve gives the total amount etched. The etch yield, which is the ratio of Si sputtered per incident Ar+, was not calculated here, but it can be modeled by including the master equation for Si.

Fig. 9: Predictions of the surface kinetic model for RIE.
figure 9

a Time-evolution of the number of F atoms at 1100 total impacts and 90 eV Ar+ energy. The solid blue line, black dash-dot line, and red dashed line represent the number of F atoms in the mixed layer (I), surface (II), and bulk gas (III), respectively. b Time-evolution of Si etch rate (Å/s) at 1100 total impacts and 90 eV Ar+ energy.

Full size image

Discussion

In this paper, an NME framework is introduced for multiscale modeling of plasma-surface interactions in atomic-scale plasma processes. The framework can be adopted for any system where chemical master equations can be used to describe the underpinning molecular processes, for example, in spin dynamics, lasers81, electroporation and electropore-transport82, and electron exchange from electrolyte phase to electrode surface83, amongst others. Here, the NME framework is used to derive surface kinetic models for ALE and RIE of Si with Cl2/Ar+ and F/Ar+, respectively, as these systems are industrially relevant. The NME-based surface kinetic model is informed by the physics of state transitions of the system81,82,83. The NME structure is adaptable, whereby additional physics can be accounted for.

The examples demonstrated for plasma processing have numerous reaction steps. Ideally, each reaction step should be modeled as a master equation in order to satisfy microscopic reversibility. The proposed NME framework can be readily used for master equations with microscopic reversibility, as the model structure makes no assumptions and proper NME training can result in a detailed balance being satisfied. However, for practical purposes, accounting for all the reaction steps and intermediate states can become intractable. While full knowledge of intermediate states and transitions and their incorporation into the master equation preserve the detailed balance, one can lump intermediate states ino an overall effective state. Omitting the states results in a set of reduced-order “quasi” master equations that yield a surface kinetic model useful for longer time scale investigation of the system of interest.

Retention of the physics of state transitions in the NME framework ensures that relevant constraints are inherently built into the structure of the model. Hence, predictions from the NME-based surface kinetic model do not show non-physical results, such as negative probabilities or sum of probabilities be greater than one at any time instant for any condition, as opposed to the black-box NODE models. Additionally, NME models whose transition rates are only parametrized by neural networks are expected to use lesser data compared to NODEs that use neural networks to represent the entire state transition dynamics47. With the same amount of data, NME vastly outperforms FC-NODE, although FC-NODE may provide improved predictions when trained with substantially more data. However, FC-NODE does not guarantee mass conservation, unlike the NME model, as seen in Fig. 7.

Due to their physics-based structure, NME-based surface kinetic models are also capable of extrapolation to regimes beyond their training data. Another advantage of NME-based surface kinetic models is that they enable exploration of longer time scales than is possible by MD simulations. For example, the MD simulations in Fig. 6 done on one core of Intel Xeon Gold 6330 took on the order of 8-10 hours, while the surface kinetic model simulations done on one core of Apple M2 took approximately 5 minutes, representing a 99% decrease in computation time. The significant computational speed up provided by NME-based surface kinetic models makes comparisons between model predictions of system observables, like concentrations in different phases, and experimental observations, such as optical emission spectroscopy signals84, possible. NME-based models can be deployed simultaneously with experiments or during fabrication, and be used to make online decisions. Furthermore, these models allow for exploration of large surfaces at longer length scales with ion energy distribution functions obtained from plasma simulations. This can be used in surface profile evolution with much smaller computational time, as opposed to traditional voxel-based methods with KMC85. A possible application is the study of roughness and critical dimension uniformity over a wafer surface, or in a smaller feature.

A possible extension of the proposed surface kinetic models for the plasma etch processes is to learn the ion-enhanced diffusion coefficient, in lieu of using guess values (Eq. (8)). Atomic fraction data from MD simulations can be used to learn the effect of ion dose and energy on the diffusion coefficient and, thus, obtain more accurate values of the ion-enhanced diffusion coefficient. This would enable better predictions of penetration depth and concentration profiles in the mixed layer. The microscopic resolution of state transitions provided by the NME framework can be used in the discovery of new materials and chemistries in atomic-scale plasma processing. The resultant scale-bridging surface kinetic models can also be used for surface evolution studies and recipe design for the next-generation semiconductor device fabrication.

Methods

Master equation for molecular processes

In molecular processes, the occupation probability for each species can be defined by an objective probability as given in Eq. (1), with the index m used for any species. The total possible states are fixed for a particular system with defined chemistry. The state-to-state transitions can be modeled as first-order processes that occur with some transition rate, also known as transition probability. While the assumption of first-order transitions may not always be true, higher or fractional order transitions can be converted to pseudo first-order transitions. In essence, the state-to-state transitions describe the dynamics of a molecular process, wherein the occupation number of different states can be averaged to obtain approximate dynamical rate equations.

For a molecular process consisting of M species that undergoes \({\mathcal{V}}\) possible state transitions among all its species Eq. (2) constitutes a set of linear ordinary differential equations (ODEs), describing the rate of change of occupation probabilities \({\{{{\boldsymbol{P}}}_{m}\}}_{m = 1}^{M}\). The rate of change in the occupation probability \({P}_{m}^{\nu }\) due to transitions into and away from any state ν is given by

$$\begin{array}{ll}\frac{{{d}}{P}_{m}^{\nu }}{{{d}}t}=\mathop{\sum }\limits_{{{\nu }^{{\prime} }\ne \nu}\atop{{\nu }^{{\prime} }=1}}^{{\mathcal{V}}}\quad\left\{-{\omega }_{m}^{\nu {\nu }^{{\prime} }}{P}_{m}^{\nu }+{\omega }_{m}^{{\nu }^{{\prime} }\nu }{P}_{m}^{{\nu }^{{\prime} }}\right\},\\ \qquad\qquad\qquad\forall \,\nu =1,\ldots ,{\mathcal{V}},\quad \forall \,m=1,\ldots ,M.\end{array}$$
(5)

The first term in Eq. (5) represents all possible transitions from state ν with an associated transition rate of \({\omega }_{m}^{\nu {\nu }^{{\prime} }}\), while the second term represents all possible transitions to the state ν from other states with an associated transition rate of \({\omega }_{m}^{{\nu }^{{\prime} }\nu }\). Hence, the probability of transition from state ν to state \({\nu }^{{\prime} }\) in a small time Δt is \({\omega }_{m}^{\nu {\nu }^{{\prime} }}\Delta t\). These transition rates form the elements of the transition matrix Wm in Eq. (5).

Neural representation of transition probabilities

In PSI, the transition probabilities are mesoscopic averages of the many-body quantum interactions between different species. Density functional theory and ab-initio MD simulations have been widely used to study these quantum mechanical interactions for a variety of systems86,87,88,89. While information of the energy barriers and other physical parameters would vastly improve the predictive power of mesoscopic reaction rate models90, obtaining exact transition probabilities from many-body quantum interactions is often not possible.

Machine learning-based approaches have been developed to learn approximate representations for transition rates91,92,93 for chemical reaction networks approximated as Markov processes on continuous state space. However, these use simulation trajectories to model transition kernels, which take in the current state and output the state at the next time interval91, which make the kernel time-dependent, without an explicit dependence on local system conditions. To mitigate that, we use neural networks to learn the transition probabilities in Eq. (5) as a function of system inputs (such as incident ion energy and ion dose), as opposed to the occupation probability at any time t. Thus, the neural networks represent discrete values of the transition rates, and not distributions, as has been done in the previous works91,92,93. The resulting master equation with neural network components is given by

$$\begin{array}{ll}\frac{{{d}}{\hat{P}}_{m}^{\nu }}{{{d}}t}=\mathop{\sum }\limits_{{{{\nu }^{{\prime} }\ne \nu}\atop {{\nu }^{{\prime} }=1}}}^{{\mathcal{V}}}&\left\{-{\tilde{\omega }}_{m}^{\nu {\nu }^{{\prime} }}({\boldsymbol{x}};{\boldsymbol{\theta }}){\hat{P}}_{m}^{\nu }+{\tilde{\omega }}_{m}^{{\nu }^{{\prime} }\nu }({\boldsymbol{x}};{\boldsymbol{\theta }}){\hat{P}}_{m}^{{\nu }^{{\prime} }}\right\},\\ &\forall \,\nu =1,\ldots ,{\mathcal{V}},\quad \forall \,m=1,\ldots ,M,\end{array}$$
(6)

where \({\hat{P}}_{m}^{\nu }\) is an approximation of the occupation probability \({P}_{m}^{\nu }\), \({\tilde{\omega }}_{m}^{\nu {\nu }^{{\prime} }}({\boldsymbol{x}};{\boldsymbol{\theta }})\) and \({\tilde{\omega }}_{m}^{{\nu }^{{\prime} }\nu }({\boldsymbol{x}};{\boldsymbol{\theta }})\) denote (deep) neural networks that are a function of nx system inputs, \({\boldsymbol{x}}\in {{\mathbb{R}}}^{{n}_{x}},\) and are parameterized by learnable parameters θ. We refer to the composite differential equation in Eq. (6) as a neural master equation (NME). The key advantage of NME is the flexibility that it offers in approximating the unknown transitions \(\tilde{\omega }\) from atomistic simulation data while preserving the physics-based structure of (5).

Following Eq. (2), the set of NMEs for a molecular process with M species can be cast as

$$\frac{{{d}}{{\hat{\boldsymbol{P}}}}_{m}}{{{d}}t}={{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }}){{\hat{\boldsymbol{P}}}}_{m},\quad \forall \,m=1,\ldots ,M,$$
(7)

where \({\hat{{\boldsymbol{P}}}}_{m}={[{\hat{P}}_{m}^{1},\ldots ,{\hat{P}}_{m}^{{\mathcal{V}}}]}^{\top }\) is the vector of predicted occupation probabilities of species m and \({{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }}):{{\mathbb{R}}}^{{n}_{x}}\times {{\mathbb{R}}}^{{n}_{\Theta }}\mapsto {{\mathbb{R}}}^{{\mathcal{V}}\times {\mathcal{V}}}\) is a neural model of transition rates, whose elements consist of neural networks \({\tilde{\omega}}({\boldsymbol{x}};{\mathbf{\uptheta }})\) in Eq. (6). The parameters θ constitute the concatenated vector of learnable parameters Θ. Equation (7) is, in fact, a set of continuous-time UDEs43 that synergizes the interpretable structure of the master equation with data-driven descriptions of hard-to-model transition rates. Equation 7 can be readily solved using state-of-the-art ODE solvers to obtain time-series predictions of occupation probabilities for different values of system inputs x.

Ion-enhanced transport in bulk solid

The set of NMEs in Eq. 7 describes PSI consisting of reactions and sputtering events. However, ion bombardment has two other consequences: incorporation of surface species into the bulk solid62 and ion-enhanced diffusion in the bulk solid63,64,65,66,67,68,69. Ion-enhanced diffusion is of great importance in small features, where characteristic diffusive length scales can become comparable to the feature size94. Incorporation of surface species can be considered as a state transition from the surface to the bulk solid, thus lending itself to a master equation representation. However, diffusion-driven species transport due to ion bombardment gives rise to spatial variations in the probability density of the corresponding occupation probability95 within a subsurface, amorphous mixed layer62,96,97,98. It is important to account for the mixed layer in the description of PSI, particularly in plasma etch wherein the removal of material from the surface exposes the mixed layer. Additionally, the removal or addition of material, in plasma etch or deposition, respectively, results in a moving surface, which constitutes a convective transport phenomenon. This drift-diffusion transport in the mixed layer results in a non-linear state transition.

While diffusive processes can be described by master equations99, the number of states to be accounted for can become prohibitively large. Instead, one can observe the process at timescales longer than the timescale of microscopic fluctuations to obtain a continuum diffusion equation within the bulk solid. These timescales are not short enough to resolve all the states and transitions associated with sputtering and reaction events on the surface. However, a master equation representation can be formulated for longer time state transitions on the surface by ignoring intermediate short-lived states. A consequence of this is that microscopic reversibility is no longer applicable to the state transitions. This simplifying assumption of using only long timescale states and transitions allows significant reduction in the number of states to be considered in the proposed NME framework, and makes it viable for modeling PSI that involve ion-enhanced diffusion in the bulk solid. Diffusion at the atomic scale can be understood by considering the motion of atoms that enter the mixed layer with some momentum. These atoms undergo a series of random collisions with other atoms in the mixed layer. The position and momentum after collision depend only on the last collision, and the atoms do not retain memory of previous collisions, a hallmark of a Markov process. Hence, we describe the drift-diffusion transport in the mixed layer by

$$\frac{\partial {{\hat{\boldsymbol{p}}}}_{m}}{\partial t}={{\boldsymbol{D}}}_{m}{\nabla }^{2}{{\hat{\boldsymbol{p}}}}_{m}-{\boldsymbol{v}}(t)\cdot {\boldsymbol{\nabla }}{{\hat{\boldsymbol{p}}}}_{m},$$
(8)

where \({\hat{{\boldsymbol{p}}}}_{m}={[{\hat{p}}_{m}^{1},...,{\hat{p}}_{m}^{{\mathcal{V}}}]}^{\top }\) is the probability density of the corresponding occupation probability, \({\hat{{\boldsymbol{P}}}}_{m}\). Eq. (8) is in fact a Fokker-Planck equation, where the drift term is due to a moving boundary, instead of an externally applied field, and the diffusive term is assumed to be a constant. Dm is a diagonal matrix of the ion-enhanced diffusion coefficient of species m in the corresponding state ν, and v(t) is the velocity of the translating plasma-solid interface. The occupation probability in each state is

$${\hat{P}}_{m}^{\nu }(t)={\int}_{{V}^{\nu }}{\hat{p}}_{m}^{\nu }(x,t){{d}}{V}^{\nu },$$

where Vν is the hypervolume of state ν. The probability density is related to the atomic fraction by

$${\hat{{\boldsymbol{p}}}}_{m}=\frac{{\boldsymbol{n}}\circ {{\boldsymbol{c}}}_{m}}{{N}_{m}},$$
(9)

where ∘ is the Hadamard product, n is the vector of atomic densities of all states, assumed constant66, Nm is the total number of species m in all the \({\mathcal{V}}\) states, and cm is the vector of atomic fraction of species m in all states. Accordingly, the set of NMEs in Eq. (7) can be modified as

$$\begin{array}{ll}\frac{{{d}}{\hat{P}}_{m}^{\nu }}{{{d}}t}=\mathop{\sum }\limits_{{{{\nu }^{{\prime} }\ne \nu}}\atop{\nu }^{{\prime} }=1}^{{\mathcal{V}}}&\left\{-{\omega }_{m}^{\nu {\nu }^{{\prime} }}{\hat{P}}_{m}^{\nu }+{\omega }_{m}^{{\nu }^{{\prime} }\nu }{\hat{P}}_{m}^{{\nu }^{{\prime} }}\right\}+{\delta }_{\nu {\nu }_{s}}A{\hat{p}}_{m}^{{\nu }_{s}}v(t),\\ &\forall \,\nu =1,\ldots ,{\mathcal{V}},\quad \forall \,m=1,\ldots ,M,\end{array}$$
(10)

where νs refers to the exposed surface state, \({\delta }_{\nu {\nu }_{s}}\) is the Kronecker delta function, and A is the area of the exposed surface. The final term in Eq. (10) represents a probability current for state ν, rendering the equations nonlinear. Notice that Eq. (10) must follow mass conservation, which is equivalent to the summability relation of probabilities, i.e.,

$$\sum _{\nu }\frac{{{d}}{\hat{P}}_{m}^{\nu }}{{{d}}t}=0.$$
(11)

To close the system of equations, boundary conditions are needed for Eq. (8). Probability current continuity must be imposed at the boundary between different states across which transitions can occur, while the current continuity equations must be consistent with mass conservation in Eq. (11). Conversely, substitution of Eq. (10) in Eq. (11) yields another boundary condition that ensures mass conservation.

Other transport phenomena that cause probability currents out of a state can be included in a similar manner, and will only contribute additional probability current terms in Eq. (10). Accordingly, the set of NMEs in Eq. 7 takes the form of Eq. (4)

$$\begin{array}{l}\frac{{{d}}{{\hat{\boldsymbol{P}}}}_{m}}{{{d}}t}={{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }}){{\hat{\boldsymbol{P}}}}_{m}+{\boldsymbol{g}}(\cdot ),\\ \,\,\,\forall \,m=1,\ldots ,M,\end{array}$$
(12)

where g(⋅) is any linear or non-linear contribution to the probability current due to transport or moving boundaries, as described in Eq. (10).

Learning framework

The proposed NME framework is shown in Fig. 1. The training data for learning the neural model of transition matrix \({{\widetilde{\boldsymbol{W}}}}_{m}\) in Eq. 12 are obtained from atomistic simulations for different values of system inputs x (e.g., incident ion energy and ion dose in atomic-scale plasma processes). An ensemble of atomistic simulation data collected at different input values is used to generate time-series trajectory data of “ground truth” occupation probabilities \({\{{{\boldsymbol{P}}}_{m}\}}_{m = 1}^{M}\). Accordingly, the learnable parameters Θ of the transition matrix \({{\widetilde{\boldsymbol{W}}}}_{m}({\boldsymbol{x}};{\mathbf{\Theta }}),\) are determined by minimizing the mean-squared-error (MSE) loss

$${\mathcal{L}}({\mathbf{\Theta }})=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\mathop{\sum }\limits_{m=1}^{M}{\left({{\boldsymbol{P}}}_{m}({{\boldsymbol{x}}}_{i})-{{\hat{\boldsymbol{P}}}}_{m}({{\boldsymbol{x}}}_{i};{\mathbf{\Theta }})\right)}^{2}.$$
(13)

Here i denotes the trajectory index of time-series occupation probabilities for different values of inputs xi, with N being the total number of trajectories. The occupation probabilities \({\{{{\hat{\boldsymbol{P}}}}_{m}({{\boldsymbol{x}}}_{i};{\mathbf{\Theta }})\}}_{m = 1}^{M}\) are predicted by numerical integration of the NMEs in Eq. 12 using standard ODE solvers (see Supplementary Section 2.1). Note that the differentiable nature of the NMEs allows for the use of backpropagation through the ODE solver when minimizing the loss function in Eq. (13).

Here, we briefly contrast the proposed NMEs with neural ordinary differential equations (NODEs)57, which can be used to take a fully black-box approach to describing the time-evolution of occupation probabilities

$$\frac{{{d}}{{\hat{\boldsymbol{P}}}}_{m}}{{{d}}t}={\boldsymbol{f}}({{\hat{\boldsymbol{P}}}}_{m},{\boldsymbol{x}};{\boldsymbol{\gamma}}),\quad \forall \,m=1,\ldots ,M,$$
(14)

where the function f is treated as a black box, approximated using (deep) neural networks with learnable parameters γ. The NODEs formulation in Eq. (14) does not include any physics in the structure of f and, thus, does not provide an interpretable representation of the mesoscopic behavior of the molecular process. Yet, from a computational standpoint, a significant advantage of NODEs over NMEs is that NODEs can make use of the adjoint sensitivity method57 to efficiently backpropagate through f. The savings in computational cost are, however, offset by the poor predictive capabilities of NODEs and its non-physical predictions outside the training range, as demonstrated in the section “NME-Based Surface Kinetic Model of ALE”.