Computational modeling of cancer cell metabolism along the catabolic-anabolic axes

Abstract

Abnormal metabolism is a hallmark of cancer, this was initially recognized nearly a century ago through the observation of aerobic glycolysis in cancer cells. Mitochondrial respiration can also drive tumor progression and metastasis. However, it remains largely unclear the mechanisms by which cancer cells mix and match different metabolic modalities (oxidative/reductive) and leverage various metabolic ingredients (glucose, fatty acids, glutamine) to meet their bioenergetic and biosynthetic needs. Here, we formulate a phenotypic model for cancer metabolism by coupling master gene regulators (AMPK, HIF-1, MYC) with key metabolic substrates (glucose, fatty acids, and glutamine). The model predicts that cancer cells can acquire four metabolic phenotypes: a catabolic phenotype characterized by vigorous oxidative processes—O, an anabolic phenotype characterized by pronounced reductive activities—W, and two complementary hybrid metabolic states—one exhibiting both high catabolic and high anabolic activity—W/O, and the other relying mainly on glutamine oxidation—Q. Using this framework, we quantified gene and metabolic pathway activity by developing scoring metrics based on gene expression. We validated the model-predicted gene-metabolic pathway association and the characterization of the four metabolic phenotypes by analyzing RNA-seq data of tumor samples from TCGA. Strikingly, carcinoma samples exhibiting hybrid metabolic phenotypes are often associated with the worst survival outcomes relative to other metabolic phenotypes. Our mathematical model and scoring metrics serve as a platform to quantify cancer metabolism and study how cancer cells adapt their metabolism upon perturbations, which ultimately could facilitate an effective treatment targeting cancer metabolic plasticity.

Introduction

Whatever traits a cancer cell might exhibit, corresponding metabolic activities are required to support required biomass production and bioenergetic needs. Understanding cancer metabolism thus provides critical insights into various hallmarks of cancer¹, such as metastasis and immune suppression. Aerobic glycolysis, termed the Warburg effect, has been often observed in cancer. The potential benefits of aerobic glycolysis include rapid ATP synthesis, microenvironment acidification, chromatin remodeling, and increased resources available for biosynthesis². Initially, it was believed that this mode was necessary due to dysfunctional mitochondria. However, the last two decades have witnessed increasing evidence that mitochondrial oxidative phosphorylation (OXPHOS) plays an important role in tumorigenesis, metastasis, and drug-resistance³. For example, murine breast cancer 4T1 cells, when entering the blood circulation, exhibit higher OXPHOS relative to the primary tumor⁴. Also, Braf^V600E-driven tumors exhibit increased resistance to BRAF inhibitors, accomplished in part by elevated OXPHOS and mitochondrial biogenesis⁵. In short, cancer cells have been shown to actively use both glycolysis and oxidation in a manner that is dependent on their environment.

In addition to glucose, fatty acids have emerged as another important metabolic ingredient for tumorigenesis and cancer progression⁶. Fatty acids support rapid tumor cell proliferation by sustaining membrane biosynthesis; furthermore, they can serve as an important energy source during periods of metabolic stress, such as hypoxia and lipid depletion. Indeed, fatty acid oxidation (FAO) has been shown to be essential for triple-negative breast cancer (TNBC) progression, the most aggressive subtype of breast cancer, regulated by oncoproteins such as SRC and Myc^7,8. Inhibiting FAO has been proposed to be a therapy for TNBC^8,9.

Another critical component of cancer metabolism is the increased consumption of glutamine¹⁰. Glutamine fuels tumor cells by driving the tricarboxylic acid (TCA) cycle via oxidation, synthesizing fatty acids via reductive carboxylation, and giving rise to glutathione (GSH) to maintain the redox balance. One master regulator of glutamine metabolism is Myc, which can upregulate glutamine transporters to support glutamine consumption, upregulate glutaminase at both transcriptional and translational levels to promote glutamine oxidation and drive de novo proline synthesis to support biosynthetic processes¹¹. Recent work suggests that limiting cancer progression by reducing glutamine availability can improve therapeutic outcomes; however, more work is required to more completely understand cancer resistance to glutamine metabolism inhibitor therapy, as well as to account for cancer heterogeneity and metabolic adaptation^12,13.

Altogether, cancer cells exhibit metabolic plasticity, which enables them to combine various metabolic ingredients and different metabolic modes to meet their biomass and energetic needs. To rationalize cancer metabolic plasticity, we initially created a model with purely genetic regulation, focusing on the interplay of two master gene regulators of OXPHOS and glycolysis - AMPK and HIF-1¹⁴. We demonstrated that while cells in general can acquire two stable metabolic phenotypes - OXPHOS (the ‘O’ state) and glycolysis (when oxygen is limited, referred to as the ‘W’ state)- cancer cells can acquire an additional hybrid metabolic phenotype characterized by high AMPK/high HIF-1 activities, referred to as the ‘W/O’ state. We subsequently provided a more direct analysis of the ‘W/O’ state by coupling genetic regulation with three main catabolic pathways: glycolysis, glucose oxidation, and FAO¹⁵. We observed that the ‘W/O’ state exhibits high TCA/FAO/glycolysis activity. We further identified that TNBC cells, e.g., MB-MDA-231 and SUM159, exhibit the hybrid ‘W/O’ phenotype at the population level. Therefore, dual inhibition of both OXPHOS and glycolysis in TNBC achieved the best treatment outcome (most pronounced decrease in cell proliferation and colony formation) relative to inhibiting only OXPHOS or inhibiting only glycolysis¹⁵. This model further suggested the existence of a metabolic low/low state, characterized by low AMPK/low HIF-1 and low TCA/FAO/glycolysis. We showed that drug-tolerant melanoma cells acquired such a metabolic low/low state¹⁶, which represents a state of metabolic dormancy where cancer cells reduce their metabolic activities to survive under stress conditions, such as drug treatment. In summary, our previous studies reveal cancer metabolic plasticity by identifying distinct phenotypes (W, O, W/O, low/low) and we have linked these phenotypes to specific gene regulators and their associated catabolic pathway activities.

In these previous efforts, we focused on the catabolic behavior of cancer cells by considering ATP-producing processes. It is clear, however, that to obtain a comprehensive understanding of cancer metabolism, we need to incorporate anabolic processes and study their interplay with the catabolic processes. In addition, as the experimental evidence of glutamine metabolism in cancer accumulates, we believe it is important to expand our approach to include various glutamine pathways. Therefore, we present here a novel metabolic network model (Fig. 1) that explicitly considers both the catabolic and anabolic modes and includes glutamine metabolism¹⁵. With this comprehensive metabolism model, we provide a more granular characterization of different cancer metabolic phenotypes by quantifying both catabolic and anabolic activity. Our model recapitulates the critical role of Myc in glutamine metabolism and reveals the role of glutamine metabolism in the four metabolic states. Finally, we demonstrate the functional consequence of the different metabolic states in patient survival prognosis across cancer types.

Fig. 1: A comprehensive network featuring genetic regulation and glucose, fatty acid, and glutamine metabolism in cancer.

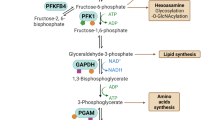
The ovals represent genes. The red ovals highlight the two master regulators of metabolism—AMPK and HIF-1. The green ovals represent oncogenes and the downstream target genes of AMPK and HIF-1. The orange ovals represent enzyme genes. The yellow rectangles represent metabolites. The black arrows represent excitatory regulatory links, and the black bar-headed arrows represent inhibitory regulatory links. The purple solid lines represent the chemical reactions involved in the metabolic pathways. The purple dotted lines represent the transportation of metabolites.

Results

The regulatory network of cancer metabolism

We first performed an extensive literature search^10,17,18, from which we constructed a comprehensive metabolic network featuring the uptake, transportation, and utilization of three main metabolic ingredients: glucose, fatty acids, and glutamine (Fig. 1). This metabolic network contains five types of regulatory interactions. First, metabolic pathways compete for common metabolic resources. Intracellular glucose can be used in catabolic processes in the form of glycolysis or glucose oxidation for ATP production, or alternatively in anabolic processes for biomass synthesis (creating lipids, triglycerides, etc.). Intracellular fatty acids can be used in the form of FAO for ATP production, and/or anabolic processes for synthesizing the plasma membrane¹⁹. Intracellular glutamine can be used in the form of glutamine oxidation for ATP production, reductive carboxylation for fatty acids synthesis, or GSH synthesis for redox balance²⁰. Second, the relative activities of these metabolic pathways are directly modulated by gene regulators (depicted as red or green ovals in Figs. 1–2). For example, HIF-1 modulates glycolysis by transcriptionally regulating the expression of glycolytic enzymes²¹. AMPK, as a key energy sensor, promotes FAO by inhibiting the lipogenic enzyme acetyl-CoA carboxylase (ACC)²². The oncoprotein Myc promotes glutamine oxidation by inducing glutaminase (GLS) which converts glutamine to glutamate to fuel the TCA cycle¹⁹. Third, metabolic intermediates (depicted as rectangles in Figs. 1–2) can in turn affect the activities of the gene regulators. One prominent example is the reactive oxygen species (ROS). ROS, including both mitochondrial ROS (mtROS) and NADPH oxidase-derived ROS (noxROS), can stabilize HIF-1 and activate AMPK²³. Fourth, the gene regulators interact with each other. For example, AMPK and HIF-1 mutually inhibit each other. This mutual inhibition between AMPK and HIF-1 have been shown in multiple studies. AMPK can inhibit HIF-1α by inhibiting the mTOR complex²⁴, via the phosphorylation of FOXO²⁵ and promotes the phosphorylation and subsequent degradation of HIF-1α^26,27. Conversely, HIF-1 directly inhibits the transcription of AMPK²⁸. In addition, Myc post-transcriptionally enhances HIF-1¹⁸. AMPK antagonizes the function of Myc through phosphorylating the transcription factor FOXO²⁹. Fifth, the gene regulators mediate the uptake of the metabolic ingredients by directly regulating the corresponding transporters. For example, HIF-1, AMPK, and Myc can increase the uptake of glucose via upregulation of the glucose transporter GLUT³⁰. Myc also promotes the uptake of glutamine via upregulating the glutamine transporter SLC1A5³¹.

Fig. 2: A minimal network model of cancer metabolism.

AMPK, HIF-1, and Myc serve as the master regulators of cancer metabolism and regulate both catabolic processes (glycolysis, glucose oxidation, glutamine oxidation, and fatty acid oxidation) and anabolic processes. The intracellular glucose can be used for glycolysis, glucose oxidation, and anabolic processes. The intracellular fatty acids can be used for oxidation and anabolic processes. The intracellular glutamine can be metabolized via glutamine oxidation, synthesis of glutathione (GSH), or reductive carboxylation. The metabolites generated in the metabolic pathways, mtROS, noxROS acetyl-CoA, and ATP, can in turn regulate AMPK and HIF-1. The black arrows/bar-headed arrows represent excitatory/inhibitory regulatory links. The purple dotted lines represent metabolic pathways. The magenta arrows represent the distribution of glucose, fatty acid, and glutamine into different metabolic pathways. The magenta dashed lines represent fatty acid biosynthesis from glucose or glutamine.

A phenotypic model of cancer metabolism

To develop a tractable mathematical model to simulate the dynamics of cancer metabolism, we coarse-grained the comprehensive metabolic network (Fig. 1) into a minimal network model that captures the essential features (Fig. 2). The minimal network model includes three main gene regulators (AMPK, HIF-1, and MYC), which modulate the uptake and utilization of the three key metabolic ingredients (glucose, fatty acids, and glutamine). The minimal network model considers the dynamics of four metabolites: ROS (both mtROS and noxROS) which mediate the interplay between AMPK and HIF-1, ATP which regulates AMPK activity, acetyl-CoA which controls the inputs to the TCA cycle, and GSH which modulates the cellular ROS level. The following metabolic pathways are analyzed: glycolysis, glucose oxidation, glutamine oxidation, FAO, GSH synthesis, and anabolic processes. For anabolic processes, we mainly considered the processes where glucose, fatty acids, and glutamine were not used for ATP production, but instead, for metabolic intermediate production. For example, glutamine can be used for glutathione synthesis, essential for maintaining redox balance and supporting protein synthesis. Fatty acid synthesis (lipogenesis) is driven by both glucose and glutamine, with glucose providing acetyl-CoA through glycolysis and glutamine contributing through TCA cycle intermediates. These mechanisms represent the ATP-consuming biomass-generating processes using glucose, fatty acid, and glutamine supporting the biosynthetic needs of cancer cells. As we will show in the following section, the minimal network model is able to capture important experimental observations about cancer metabolic plasticity.

Cancer cells can mix and match catabolic and anabolic processes and can acquire four different metabolic phenotypes

We first identify all the possible metabolic phenotypes enabled by the regulatory network (Fig. 2). As overexpression of Myc has often been associated with tumor formation, we investigated how different levels of Myc affect the dynamics of the regulatory network, especially in the acquisition of different stable states³². We discovered that when the Myc level is relatively low, cells mainly acquire two metabolic states—the Warburg state (‘W’, high HIF-1/low pAMPK) and an OXPHOS state (‘O’, high pAMPK/low HIF-1), representing the typical metabolism of cancer cells (Fig. 3A). As the level of Myc increases, the bistability converts to tristability, and a third metabolic state—“W/O”—characterized by intermediate pAMPK/HIF-1 activity emerges (Supplementary Fig. 1). For both Fig. 3A and Supplementary Fig. 1, we maintained the same parameter values provided in the Supplementary Table 1, except for the Myc level. We found that the critical transition from bi-stability to tri-stability occurs around Myc = 300 nM. As Myc levels increase, it alters the regulatory dynamics between AMPK and HIF-1, leading to changes in the nullcline shapes. We also found, that under certain conditions this network model can acquire tetra-stability (Fig. 3B). In addition to the W, O, and W/O states, the metabolic network enables cancer cells to acquire an additional stable state - the ‘Q’ state, which relies mainly on glutamine oxidation (as shown in the next section). This demonstrates the ability of the model to capture complex metabolic behavior, reflecting the metabolic plasticity of cancer cells, and allowing them to adapt to various environmental conditions. The ‘Q’ state exhibits both low pAMPK and low HIF-1 activity, and low glycolysis and glucose/fatty acid oxidation (Fig. 3B, C). This state is analogous to our previously identified “low/low phenotype” using a simplified regulatory network without glutamine metabolism¹⁶. We then reveal the metabolic pathway activities of the four states—W, O, W/O, and Q (Fig. 3C). The “W” state is distinguished by heightened glycolysis activity (G₂), and it exhibits increased anabolic activities, which are attributed to the reductive metabolism of glucose (G_re), fatty acids (F_re), and glutamine (Q_re). The “O” state is characterized by high catabolic activities including oxidation of glucose (G₁), fatty acids (F), and glutamine (Q₁), and notably high GSH synthesis (QSH) to balance the ROS production. The hybrid “W/O” state is characterized by intermediate levels of both catabolic and anabolic activities. Finally, the “Q” state is highly reliant on glutamine oxidation. We will show that the dependence of glutamine oxidation is a robust feature of the “Q” state in the next section.

Fig. 3: Model predicted association between gene states and metabolic pathway activities.

A Nullclines and steady states in the space of pAMPK and HIF-1 in normal cells. The red line represents the nullcline where the rate of change of HIF-1 is zero, and the blue line represents the nullcline where the rate of change of pAMPK is zero. Solid dots represent stable steady states while hollow dots represent unstable steady states. Each stable state is associated with a metabolic phenotype. Cancer cells can acquire an OXPHOS phenotype, referred to as the state ‘O’, characterized by high pAMPK/low HIF-1 activity. This phenotype represents a scenario where cells optimize energy production through oxidative phosphorylation, which can occur under specific physiological or mild stress conditions during cancer progression; the other state is the glycolytic phenotype that is when oxygen is limited, referred to as the state “W”. B The nullclines and steady states in the phase space of pAMPK and HIF-1 in cancer cells. Cancer cells can acquire two additional hybrid metabolic states—the ‘W/O’ state, characterized by intermediate HIF-1 and pAMPK activity, and the ‘Q’ state, characterized by low pAMPK/HIF-1 but high glutamine oxidation. C Net ATP production rates of different metabolic pathways for the “O”, “W/O”, “W”, and “Q” states. Positive rates represent catabolic processes where ATP is produced, while negative rates represent anabolic processes where ATP is consumed. Compared to the “W” state, the “O” state exhibits higher activities of glucose oxidation (G₁), fatty acid oxidation (F), glutamine oxidation (Q₁), and GSH synthesis (GSH), but lower activities of glycolysis (G₂), reductive glutamine carboxylation (Q_re), reductive glucose metabolism (G_re), and reductive fatty acid metabolism (F_re). The hybrid “W/O” state exhibits intermediate metabolic activities, while the “Q” state relies on high glutamine oxidation activity.

To identify the robustness of the stable states, we used a parameter randomization procedure. The overall strategy consists of randomizing the model parameters for each simulation and collecting all stable state solutions from all simulations for statistical analysis to identify robust solution patterns. For each Myc level (0, 300 nM, 1200 nM, and 3000 nM), we generated 500 random parameter sets, resulting in a total of 2000 test, of these, only 1812 provided stable solutions (Supplementary Fig. 16), which were further analyzed. For each set of parameters, we randomly sampled from a uniform distribution of (75% p₀, 125% p₀), where p₀ is the baseline value, and calculated the stable state solutions. Then we performed a clustering analysis of the results from all sets of parameters encompassing all Myc levels, to identify the patterns of the solutions (Fig. 4A). We depicted the Myc level, metabolic state (which were defined as the overall activity of glucose oxidation/FAO/glycolysis to be compared with the previous study¹⁵), glucose uptake and ATP production, ATP consumption, and the net values of ATP related to each cluster of solutions.

Fig. 4: Clustering analysis of stable state solutions.

A The primary heatmap displays four clusters of data derived from different Myc values (0, 300 nM, 1200 nM, 3000 nM). Each row in this heatmap represents a stable-state solution, and each column represents one variable in the model. The proportions of each Myc group are shown in the first one-column heatmap, with a summary annotation at the top presenting the proportion of each Myc level within each cluster in a boxplot format (from left to right: “Q”, “W”, “O”, and “W/O”). The second one-column heatmap, labeled ‘Metabolic State’, corresponds to rows indicating whether steady states are active or inactive based on their glucose oxidation, glycolysis, and fatty acid oxidation values having Z-scores greater or less than 0, respectively. The third one-column heatmap shows the glucose uptake rates and the average for each cluster on the top, units expressed in µM/s. The subsequent one-column heatmaps, labeled ‘ATP Prod’, ‘ATP Cons’, and ‘ATP Overall’, illustrate the total ATP production, consumption, and net ATP for each row, taking into account both anabolic and catabolic processes. B A plot of pAMPK vs HIF-1 illustrates the relationship between pAMPK and HIF-1 levels across all generated steady states. C A scatter plot showing the results of a principal component analysis (PCA). Each point in the plot represents a steady state, plotted according to its scores on the first two principal components (PC1 and PC2) of the output element values in the minimal regulatory network. Different clusters are indicated by different colors, providing a visual representation of the grouping of steady states in the reduced-dimensional space of the PCA. Both plots (B, C) show the state annotations for the ‘L/L’ cluster, indicating the position of the Low Metabolic State. These are considered low due to their glucose oxidation, glycolysis, and Fatty acid Oxidation values having Z-scores less than 0, respectively. Bar plots showcasing the loading variables PC1(D) and PC2 (E) derived from the PCA. The variables are ranked based on their loading values, signifying their contribution to each principal component. Variable abbreviations: glutathione synthase (GSH), HIF-1 (h), glycolysis (G₂), noxROS (R_nox), glucose uptake (G₀), reductive fatty acids (F_re), reductive glucose (G_re), glutamine uptake (Q₀), fatty acids uptake (F₀), pAMPK (A), rate of acetyl-CoA for mitochondrial respiration (C₀), FAO (F), reductive glutamine (Q_re), glucose oxidation (G₁), mitochondrial ROS (R_mt), glutamine oxidation (Q₁).

By analyzing the stable state solutions from parameter randomization for each Myc value (0, 300 nM, 1200 nM, 3000 nM representing an increasing level of Myc), four distinct groups of solutions were identified, corresponding to the four metabolic states - “W”, “O”, “W/O” and “Q” (Fig. 4A, left panel). The ‘O’ state and the ‘W’ state exhibit opposite patterns of metabolic activities, as the ‘O’ state exhibits higher overall ATP production (as a result of higher ATP production and lower ATP consumption) relative to the ‘W’ state. Notably, the “W/O” state, which was previously defined as high AMPK/HIF-1/TCA/FAO/glycolysis, now has an improved characterization - high AMPK/HIF-1/catabolic/anabolic activities and exhibits the highest glucose uptake rates among the four metabolic phenotypes. The ‘Q’ state, which was previously defined as ‘low/low’ state with low AMPK/HIF-1/TCA/FAO/glycolysis, now has further characterization of high glutamine oxidation activity (Q₁) and high reductive glucose activity (G_re). We confirmed that almost all the stable state solutions with negative Z-scores for glucose oxidation, glycolysis, and FAO (as shown in the Metabolic State one-column heatmap of Fig. 4A), previously categorized as the ‘low/low’ state in our earlier study¹⁶, were found to be in the “Q” state, characterized by additional features that allow for clearer separation in the present study. This indicates that cells in the previously defined ‘low/low’ (L/L) state do not completely shut down all metabolic activities. While these cells show low activity in both oxidative phosphorylation (OXPHOS) and glycolysis, they are not metabolically inert. Glutamine serves as a crucial substrate for the tricarboxylic acid (TCA) cycle, supporting energy production and biosynthetic processes. This reliance on glutamine allows L/L cells to maintain essential metabolic functions and survive under drug treatment. Our new model highlights that targeting glutamine metabolism could be a potential strategy to eliminate these drug-tolerant cells and improve therapeutic outcomes, which might have important implications for the use of metabolism-based therapies. We also showed that an increased level of Myc led to an increased proportion of the ‘W/O’ state and a decreased proportion of the ‘Q’ state through the parameter randomization analysis, indicating an important role of Myc in the acquisition of these hybrid states. This is illustrated in Fig. 4A, where the top annotation of the first one-column heatmap shows the distribution of metabolic states at different Myc levels (0 nM, 300 nM, 1200 nM, and 3000 nM). In addition, we summarized the ATP fluxes for each stable state (Supplementary Fig. 2) highlighting consistent metabolic outputs across all clusters after parameter randomization and the unique metabolic signature for each one.

Next, we tested our hypothesis that the activities of the two master regulators, pAMPK and HIF-1, can distinguish between the four metabolic states. By mapping all solutions onto the pAMPK/HIF-1 axes, we clearly distinguished among the four states, with the ‘Q’ state exhibiting a notably low pAMPK/low HIF-1 signature (Fig. 4B). We further visualized the differences between these four metabolic states using principal component analysis (PCA). By projecting all solutions onto the first two principal components (PC1 and PC2) (Fig. 4C), we found that PC1, characterized by high loadings of glucose oxidation (G₁) and fatty acid oxidation (F), primarily separates catabolic from anabolic variables, distinguishing between the (‘W’, ‘O’), and (‘W/O’, ‘Q’) states (Fig. 4D). PC2, on the other hand, characterized by the high loading of glutamine oxidation (Q₁), resolves between the ‘W/O’ and the ‘Q’ states (Fig. 4E). This metabolic shift enables cancer cells to adapt and meet their energy requirements, sustaining their functions³³. Studies by Wang et al.³⁴ and Li et al.³⁵ emphasize the critical role of glutamine in cancer cell survival and proliferation, especially under nutrient-limited conditions.

Our parameter randomization analysis shows that even upon relatively large perturbation to the model parameters, the characterization of the four metabolic phenotypes is robust. These results recapitulate many classical experimental observations, such as the ‘O’ state relying on OXPHOS and exhibiting a high net value of ATP, with the ‘W’ state, with lower efficiency in ATP production, exhibiting increased glucose influx.

Model-predicted associations between gene activity and metabolic pathway activity are confirmed in patient samples

To enable the testing of the model-predicted association between gene activity and metabolic pathway activity in each of the four metabolic states (“W”, “O”, “W/O”, and “Q”), we created scoring metrics for both gene regulators and metabolic pathways. To quantify metabolism, we applied our previously developed AMPK and HIF-1 signatures¹⁴, glycolysis and FAO signatures¹⁵, together with newly developed scoring metrics for G_re, Q₁, GSH, Q_re, R_nox, R_mt, F_re, and MYC. The full list of genes for these metrics can be found in Supplementary Table 2. For F_re and MYC, we followed the PCA-based method¹⁴ to obtain the most relevant genes that contribute to the pathway activity. The scoring metric for metabolic pathways was determined by the mean expression of the Z-score of pertinent genes within each pathway. Then, we analyzed the RNA-seq data of patient samples of multiple cancer types from The Cancer Genome Atlas Program (TCGA).

We first applied clustering analysis, taking into consideration all the genes of interest from the different anabolic and catabolic pathways (Supplementary Table 2) in our model, to classify the patient samples into “W”, “W/O”, “O”, and “Q” states. Then we quantify the gene or metabolic pathway activity of the samples in each state. For example, based on the metabolic gene expression, the hepatocellular carcinoma (LIHC) patient samples can be classified into four groups, corresponding to the “W”, “W/O”, “Q”, and “O” states (Fig. 5A). These four metabolic groups were also distinguishable according to their HIF-1 and pAMPK values: high HIF-1 and low pAMPK, intermediate HIF-1 and intermediate pAMPK, low HIF-1, and high pAMPK, and finally, low HIF-1 and low pAMPK (Fig. 5B). We include 15 one-column heat maps that illustrate the state of each evaluated metabolic parameter—for MYC, HIF-1, AMPK, glycolysis, glucose oxidation, FAO, glutamine oxidation, glycolysis, glucose reduction, GSH, glutamine reduction, FA reduction, ROS mitochondrial, ROS NADPH, overall catabolic, and overall anabolic activities, respectively, we also included some of the phenotypic data of cancer: TNM stage, metastasis stage, lymph node stage, and tumor stage. Next, we evaluated the predictions of our model related to the unique characterizations of the four metabolic states. The model posits that the metabolic states “W” and “Q” demonstrate diminished glycolysis and fatty acid oxidation activities in comparison to the ‘O’ and ‘W/O’ states. This proposition aligns well with the analysis derived from the RNA-seq data of LIHC samples (Fig. 5B). Furthermore, our model indicates that, in contrast to the ‘O’ and ‘W/O’ states, both the “W” and “Q” states display reduced catabolic activity. This is evidenced by the differences in ATP production (Fig. 4A). In the context of LIHC, this difference is also discernible by the catabolic score, primarily characterized by decreased glucose oxidation and FAO. The ‘W’ state exhibits a higher anabolic activity relative to the ‘Q’ state. It is important to note that this anabolic state is characterized by glycolysis, HIF-1, and reductive activities (F_re, GSH, Q_re) (Fig. 4A). This observation has been corroborated by the analysis of LIHC patient samples (Fig. 5). Thus, our model does a good job of accounting for LIHC data.

Fig. 5: The association between gene activity and metabolic pathway activity.

A Heatmap of RNA-seq data from liver hepatocellular carcinoma (LIHC). Each row represents a patient sample, and each column represents the expression of selected genes, which are divided according to their metabolic or anabolic activities. Four distinct clusters can be identified in the heatmap, corresponding to the four states identified in the metabolism model. The adjacent one-column heatmaps represent the scores for Myc, HIF-1, AMPK, glucose oxidation, FAO, glutamine oxidation, glycolysis, glucose reduction, GSH, glutamine reduction, FA reduction, ROS mitochondrial, ROS NADPH, overall catabolic, and overall anabolic activities, respectively. We also included some of the phenotypic data of cancer: TNM stage, metastasis stage, lymph node stage, and tumor stage. B Box plots summarizing and showing the differences in the scores according to each identified cluster in the LIHC data. For the box plots, a t-test was used to test the significance of each pair of clusters. Significance levels are indicated as follows: *, P < 0.05; **, P < 0.01; ***, P < 0.001; ****, P < 0.0001.

To further analyze and corroborate the differences in the clusters we performed pathway enrichment analysis and filtered the results of the analysis to obtain only those related to metabolism (Supplementary Fig. 15). Across all clusters, the Ribosome pathway is highly enriched, indicating a common increase in protein synthesis. The consistent enrichment of Carbon Metabolism and Glycolysis/Gluconeogenesis pathways reflects the importance of these pathways in supporting the metabolic flexibility and plasticity of cancer cells. The enrichment of Fatty Acid Degradation and Fatty Acid Metabolism pathways in “W/O”, “Q”, and “O” clusters highlights the role of fatty acids in these metabolic states and aligns with the FAO score (Fig. 5B). Lastly, the enrichment of Glutathione Metabolism in “Q” supports redox balance and oxidative stress management, which are crucial for cancer cell survival and proliferation.

Moving to the lung adenocarcinoma (LUAD) dataset, the LUAD samples also exhibit four distinct metabolic states - “W”, “O”, “W/O”, and “Q” based on the metabolic gene expression (Fig. 6A) and can also be discriminated against based on their pAMPK and HIF-1 activity (Fig. 6B). The LUAD samples in the “W” and “Q” states exhibit the expected low catabolic activity. This low activity is anticipated based on the metabolic characteristics defined in our model. These metabolic profiles are supported by our model’s predictions and validated by RNA-seq data analysis from LUAD samples, which show reduced catabolic activity in these states compared to others. In contrast, samples in the “O” state align with our model-predicted characterization of high catabolic activity, while samples in the “W/O” state exhibit both high anabolic and high catabolic activity. The results for many other cancer types can be found in the SI (Supplementary Figs. 3–9). In general, samples in the “W/O” state exhibit both high anabolic and high catabolic activity. samples in the “Q” state exhibit high glutamine oxidation, except for the melanoma case (Supplementary Fig. 4). For breast invasive carcinoma, tumors can be subclassified into different subtypes, namely luminal A, luminal B, HER2+, and basal-like. We show that the breast invasive carcinoma samples exhibit consistent characterization for the four metabolic states (Supplementary Fig. 8B). We further analyzed the relationship between the metabolic states and the cancer subtypes. Interestingly, we found that basal-like and HER2+ make up most of the “W” state, which shows the highest MYC and high glucose consumption activity in comparison with samples in other metabolic states. Finally, we conducted a correlation analysis between the different metabolic scores (Supplementary Fig. 10). In the LIHC dataset, the analysis reveals that MYC activity is strongly associated with hypoxic scores and negatively correlated with AMPK and FAO activities. This highlights MYC’s role in promoting anabolic processes while reducing catabolic activities. The LUAD dataset follows a similar trend (Supplementary Fig. 10B). Conversely, in the leukemia dataset (Supplementary Fig. 10E), the MYC score shows a strong positive correlation with the Glut Oxidation score and moderate positive correlations with the FAO and G₁ scores. This indicates that MYC is closely linked with glutamine oxidation and fatty acid oxidation in leukemia cells. These comparisons highlight the dynamic nature of metabolic and genetic interactions in a tissue-specific way. All told, we confirmed the basic findings of our model-predicted metabolic characterization by analyzing the RNA-seq data of patient samples from TCGA.

Fig. 6: The association between gene activity and metabolic pathway activity.

A Heatmap of RNA-seq data from lung adenocarcinoma (LUAD). Each row represents a patient sample, and each column represents the expression of selected genes, which are divided according to their metabolic or anabolic activities. Four distinct clusters can be identified in the heatmap, corresponding to the four states identified in the metabolism model. The adjacent one-column heatmaps represent the scores Myc, HIF-1, AMPK, glucose oxidation, FAO, glutamine oxidation, glycolysis, glucose reduction, GSH, glutamine reduction, FA reduction, ROS mitochondrial, ROS NADPH, overall catabolic, and overall anabolic activities, respectively. We also included some of the phenotypic data of cancer: TNM stage, metastasis stage, lymph node stage, and tumor stage. B Box plots summarizing and showing the differences in the scores according to each identified cluster in the LUAD data. For the box plots, a t-test was used to test the significance of each pair of clusters. Significance levels are indicated as follows: *, P < 0.05; **, P < 0.01; ***, P < 0.001; ****, P < 0.0001.

Quantification of glutamine metabolic activities

One novelty of the current metabolism model is the incorporation of glutamine metabolism and its master regulator—MYC. We next focus on studying the consumption of glutamine when cancer cells acquire different metabolic phenotypes. To relate to our previous characterization of the metabolic states¹⁵, we performed a clustering analysis of the stable state solutions based solely on the pAMPK and HIF-1 levels, and then determined the distribution of glutamine uptake (Q₀) in each cluster (Fig. 7A). Our model suggests that in all four metabolic states, increased MYC level led to increased uptake of glutamine (Fig. 7B). To validate this model prediction, we assessed the predicted glutamine pathway activities of the “W”, “W/O”, “Q”, and “O” states. We applied a previously defined glutamine metabolism gene signature (GMGS, focusing on glutamine uptake)³⁶ and our defined Q₀ signature (Supplementary Table 2) to the breast cancer samples and 45 corresponding adjacent normal tissue samples for comparison. Notably, while the GMGS and the Q₀ score share four genes, the Q₀ signature includes additional genes that are involved in the transport of glutamine and derivatives (e.g., glutamate) into the mitochondria (e.g., SLC25A22, SLC25A13, SLC25A12). We showed that relative to normal cells, cancer cells exhibit a much higher glutamine uptake rate (Q₀) (Fig. 7C bottom, p < 0.0001). We found no significant difference between the GMGS signatures of tumor and normal samples (Fig. 7C top). We then segregated the 45 tumor samples based on the pAMPK/HIF-1 signatures into four groups. By both GMGS and our Q₀ signature, we show that the samples in the “W” state exhibited significantly higher GMGS relative to the samples in the “O” and “W/O” states. The result suggests that the “W” state has a more efficient uptake of glutamine (Fig. 6D). Interestingly, we showed that samples in the “Q” state also exhibit enhancements of glutamine uptake relative to the ‘O’ state (Fig. 7D, bottom). In a similar way we also demonstrated that genes related to glucose and fatty acids uptake are also upregulated in breast cancer (Supplementary Fig. 11).

Fig. 7: Model-predicted glutamine uptake and expression values for genes encoding glutamine-utilizing enzymes.

A Clustering analysis of stable state solutions illustrating the relationship between the Glutamine uptake (Q₀) levels and the states of pAMPK (A) and HIF-1 (h), the first one-column heat map indicates the Myc level (0, 300 nM, 1200 nM, 3000 nM) found in each state, the second one-column heat map shows the glutamine uptake activity for each identified state and the overall summarized at the top. B Glutamine uptake identified in each cluster partitioned by Myc value. C Both the previously published glutamine metabolism gene signature (GMGS)³⁶ and our glutamine uptake signature (Q₀) were applied to a normal versus breast cancer dataset consisting of 45 normal tissue samples and 45 breast cancer samples⁵³. D Tumor samples were categorized into “W” (n = 13), “O” (n = 12), “W/O” (n = 6), and “Q” (n = 14) signatures to show the difference between the GMGS (top) and Q₀ (bottom). E Set of scatter plots comparing Q₀ Score (E1), GMGS (E2), Oxidative Glut Score (E3), and Reductive Glut Score (E4), with the MYC Score. The regression line, confidence interval, and Pearson correlation coefficient are included. T-test was used to test the significance *, P < 0.05; **, P < 0.01; ***, P < 0.001; ****, P < 0.0001.

As our model predicts a critical role of Myc in glutamine uptake rate in all metabolic phenotypes, we next evaluate how MYC activity is correlated with glutamine metabolic pathway activity. We found that there is a significantly positive correlation between the MYC score and the Q₀ score (r = 0.78, p < 0.001) (Fig. 7E-1), indicating that MYC significantly upregulates the glutamine uptake rate, aligning with our model expectation (Fig. 7B). Consistent results have been shown by the significant correlation between MYC and the GMGS signature (Fig. 7E2) (r = 0.56, p < 0.0001). Furthermore, we observed a strong correlation between the MYC score and the glutamine oxidation score (Fig. 7E3) and reductive glutamine metabolism score (Fig. 7E4), suggesting an important role of Myc in different aspects of glutamine metabolism.

To quantify the activity of various glutamine-related metabolic pathways in the four metabolic states, we developed gene signatures for different metabolic pathways using involved genes. These genes can be categorized into three types—(1) enzyme genes involved in glutamine oxidation in mitochondria (e.g., GLS, GLS2, GOT2, GLUD1 and GPT2) (2); enzyme genes used in anabolic processes of glutamine (e.g., ASNS for asparagine synthesis, GFPT1 for hexosamine synthesis, PPAT for purine synthesis), and (3); transporter genes that import glutamine (e.g., SLC38 A1/2 and SLC1A5). Then we analyzed the RNA-seq data of liver hepatocellular carcinoma (LIHC) and lung adenocarcinoma (LUAD) patient samples from The Cancer Genome Atlas Program (TCGA) to test the model-predicted characterization of glutamine metabolism in each of the four metabolic states (Supplementary Figs. 12–13). After applying clustering analysis and classifying the patient samples into “W”, “W/O”, “O”, and “Q” states, we quantified the expression of the glutamine metabolism genes among these four metabolic states. We found that for both LIHC and LUAD samples, the samples in the state “O” and “W/O” states exhibit pronounced expression in most of the glutamine oxidation genes (GLS2, GOT2, and GPT2). The samples in the “W” or ‘W/O” state exhibit a pronounced GLS expression, while the samples in the “O” state exhibit a pronounced GLS2 expression. The inverse association between GLS and GLS2 expression has been reported before, and GLS is often over-expressed in cancer, while GLS2 is regarded as a tumor suppressor³⁷. The tumor samples in groups “W” and “Q” exhibit higher gene expression involved in amino acid/nucleotide synthesis (ASNS, GFPT1, and PPAT). The tumor samples in group “W” exhibit higher glutamine update (SLC38A1, SLC1A5) relative to samples in the “O”, “Q”, and “W/O” states, which is consistent with our findings by applying our Q₀ or the GMGS signature (Fig. 7D). In summary, the “W” state exhibits high glutamine uptake and high anabolic processes involving glutamine, the “W/O” and the ‘O’ state exhibits high glutamine oxidation, whereas “Q” has genes high in glutamine oxidation and biosynthesis.

The metabolic state of patient samples is significantly correlated with survival outcomes

Finally, we proceeded to examine the relationship between the metabolic state of patient samples with the overall survival. For the LIHC patient samples (Fig. 8A), the ‘Q’ state was associated with the poorest survival outcome. Further inspection of the heatmap revealed that this particular cluster was characterized by elevated MYC activity, high glutamine oxidation activity, and high reductive glucose activity (Fig. 5A, B). By correlating this cluster with phenotypic data in the heatmap (Fig. 5A), it was evident that clusters ‘W’ and ‘Q’ had a higher proportion of patients in advanced stages (greater than stage II) than the rest of the clusters. This suggests that clusters associated with the poorest survival outcomes also have a higher proportion of patients in advanced stages. This correlation highlights the critical role of advanced TNM stages in predicting poor survival outcomes.

Fig. 8: Survival curves stratified by metabolic states.

Survival curves for liver hepatocellular carcinoma (A), melanoma (B), colorectal adenocarcinoma (C), leukemia (D), lung adenocarcinoma (E), and kidney carcinoma (F) datasets. Each dataset was separated into the four metabolic states—‘O’, ‘W’, ‘W/O’, and ‘Q’. Each row in the figure indicates the metabolic state associated with the worst outcome for each cancer dataset. The survival curves were estimated using the Kaplan-Meier method and compared using the log-rank test. Pairwise comparisons of survival distributions stratified by metabolic state are displayed above the survival curve for each pair of metabolic states. Significance levels are indicated as follows: *, P < 0.05; **, P < 0.01; ***, P < 0.001.

The melanoma patient samples also exhibited the poorest survival outcome when associated with the “Q” state (Fig. 8B). Our previous study showed that the drug-tolerant melanoma cells exhibit low glucose/fatty acid metabolic activity, thus being characterized as the ‘low/low’ phenotype¹⁶. Altogether, these drug-tolerant melanoma cells, which are associated with the ‘Q’ state, probably rely on glutamine for survival. Regarding the TNM stage in melanoma, cluster Q has a higher percentage of patients in advanced stages. Specifically, this cluster represents almost 50% of patients with a more advanced primary tumor stage, with 40% of patients in the T4b stage. This indicates a significant correlation between the ‘Q’ state and advanced melanoma stages.

We further observed that colorectal adenocarcinoma and leukemia exhibited the most unfavorable prognosis when in a hybrid ‘W/O’ (Fig. 8C, D). This finding underscores the efficacy of our model in identifying metabolic states, especially the ‘W/O’ or ‘Q’ states that correlate with poor survival and are associated with advanced TNM scores. For the LUAD dataset (Fig. 8E), the “O” state was associated with the best survival result, and both the LUAD dataset and the kidney cancer showed the worst outcome with the ‘W’ cluster having the highest MYC score value (Fig. 6 and Supplementary Fig. 6). Intriguingly, our analysis of the prostate cancer samples (Supplementary Fig. 14A) revealed a distinct pattern. The most favorable prognosis was associated with the “Q” cluster. This particular cluster stands out from the rest of the cancer datasets due to a notable reduction in the MYC score (Supplementary Fig. 7). This reduction appears to confer a survival advantage to the “Q” state, thereby underscoring the significant impact of MYC on survival outcomes. The rest of the cancers analyzed in this study, lung squamous cell carcinoma and breast invasive carcinoma, did not show any significant differences after being categorized by the four distinct phenotypes and analyzing the survival curves for each state (Supplementary Figs. 14B, C). In short, there is some evidence that everything else being equal, hybrid states seem to be the most aggressive. But, as we have seen for prostate cancer, other factors (such as Myc levels) are also critical and can overcome the purely metabolic effects.

Discussion

Cancer cells demonstrate remarkable metabolic versatility by utilizing a variety of nutrients such as glucose, fatty acids, and glutamine for both catabolic and anabolic processes. These metabolic pathways not only generate ATP but also produce intermediates essential for biosynthesis, supporting rapid cell proliferation. This versatility of cancer metabolism enables cancer cells to thrive in diverse microenvironments and contributes to their resistance against therapeutic interventions³⁸. To shed light on cancer metabolic versatility, we have developed a comprehensive mathematical model that, for the first time, integrates three indispensable metabolic ingredients (glucose, fatty acids, and glutamine) and captures the complex interplay of nutrient uptake and utilization and the dynamic shifts between energy production and biomolecule synthesis.

Through modeling, we demonstrated that cancer cells can achieve four main metabolic states, ‘W’, ‘O’, ‘W/O’, and ‘Q’, characterized by both gene activity (AMPK/HIF/MYC) and metabolic pathway activity. We show that the ‘O’ state, that was characterized by high AMPK and high OXPHOS, is high in overall catabolic activity, while the ‘W’ state, that was characterized by high HIF-1 and high glycolysis, is high in overall anabolic activity. We provide finer resolution for the hybrid ‘W/O’ state and the low/low state. We show that the hybrid ‘W/O’ state exhibits both high catabolic (glucose oxidation and fatty acid oxidation, not glutamine oxidation) and high anabolic activities (reductive fatty acid and reductive glutamine, but not glucose). We show that the previously defined ‘low/low’ state, while exhibiting low overall catabolic/anabolic activity relative to the rest states, exhibits pronounced glutamine oxidation activity (therefore we refer to this state as ‘Q’ in this manuscript) and reductive glucose metabolism. Our model recapitulates the critical role of Myc in glutamine metabolism. The model suggests higher levels of Myc upregulate glutamine uptake in all four metabolic states and promote both glutamine oxidation and reductive glutamine metabolism.

These predicted metabolic characterizations have been confirmed by analyzing RNA-seq data in patient samples from TCGA. Moreover, the model delineated the association between gene activity and metabolic pathway activity, which has also been verified by analyzing the patient sample data. Furthermore, we evaluated the functional consequences of different metabolic states of patient samples. We observed that patient samples characterized as metabolic hybrids exhibit the worst overall survival outcomes relative to samples with other metabolic states in hepatocellular cancer, colorectal adenocarcinoma, melanoma, and leukemia. One limitation of the current study is that Myc was treated as an input to the network. In the future, integrating the detailed feedback from other gene regulators and metabolic intermediates to MYC would improve our understanding of the effect of Myc. In summary, our integrated modeling-data analysis approach provides a holistic understanding of cancer metabolism and an extendable framework for including additional biological factors.

A promising direction would be to enhance the current metabolism model by coupling it with other biological processes that consume ATP and/or biomass in cancer cells. This could be done by determining the parameters in the current model as functions of additional processes, such as cell migration and division. This would be an improvement on the current modular modeling of the cancer process. For instance, the epithelial-mesenchymal transition (EMT) influences how cells acquire migratory and invasive properties. By incorporating EMT into our metabolism model, we can simulate how EMT affects nutrient utilization, and vice versa, how changes in metabolism affect EMT³⁹. This would help identify critical points of intervention where targeting metabolic adaptations and EMT dynamics concurrently may yield synergistic therapeutic benefits. Another important unresolved question is how cell metabolism regulates tumor dormancy, which places patients at risk of metastatic relapse for the remainder of their lives. It has been observed that whether tumor cells are proliferative or quiescent can result from a ‘tug of war’ between oxidative stress and antioxidative response. Coupling the metabolism model with the molecular networks regulating tumor dormancy processes should yield significant insights⁴⁰. One speculation is there may be a connection between the “Q” state which exhibits low activities of many metabolic processes (aside from glutamine oxidation), and tumor dormancy. Another promising direction is to extend the metabolism model from the intracellular level to intercellular cells by considering the competition for resources between cancer cells and immune cells⁴¹. Altogether, our metabolism model serves as a valuable tool for identifying potential metabolic vulnerabilities and designing targeted interventions to effectively disrupt metabolism relevant processes in cancer cells.

Methods

The model focuses on three master regulators of metabolism: HIF-1 and Myc (transcription factors), and AMPK (a protein kinase). In the model, the HIF-1 and pAMPK (the active form of AMPK) are variables, while the Myc is an input. The outputs of the model are the levels of regulatory proteins (HIF-1, pAMPK, etc.), the level of metabolites (ATP, GSH, etc.) and the metabolic pathway rates (glucose oxidation rate, glycolysis, etc.) at stable steady states. As the effect of pAMPK on HIF-1 and metabolic enzymes/transporters is mainly mediated through its three downstream transcription factors—CREB, FOXO, and PGC-1α, the activity of AMPK can be regarded as a ‘proxy’ of these transcription factors. (A similar idea has been used to develop a pAMPK signature, i.e., evaluating AMPK activity by quantifying the expression of the downstream genes of CREB, FOXO, and PGC-1α). To model the effects of transcriptional regulation, we used the shifted Hill function developed in Lu et al. (2013)⁴². The regulation of pAMPK is a mix of the production/degradation of its precursor AMPK and the activation/deactivation kinetics occurring via phosphorylation. As we are mainly concerned with steady-state behavior, there should be a simple linear relationship between AMPK and pAMPK levels, and therefore, transcriptional control of AMPK will be equivalent to transcriptional control of pAMPK. This relationship will depend on other variables in the model; for simplicity, we have opted to treat these dependencies via a Hill function assumption. Our previous two studies on modeling metabolism - Yu et al. (2017)¹⁴ and Jia et al. (2019)¹⁵ can be referred to for more details.

The steady state solutions of the model can be categorized into anabolic and catabolic. Anabolic parameters include glutathione synthase (GSH), involved in the synthesis of glutathione, HIF-1 (h), glycolysis (G₂), which, although traditionally catabolic, is considered anabolic in cancer cells because it provides intermediates for biosynthetic pathways^43,44,45; noxROS (R_nox), reactive oxygen species derived from NADPH oxidase, involved in anabolic signaling; reductive fatty acids (F_re), representing the reductive biosynthesis of fatty acids; and reductive glucose (G_re), representing the reductive biosynthesis of glucose-derived metabolites. Catabolic parameters include FAO (F), fatty acid oxidation, a process that breaks down fatty acids to produce ATP; glucose oxidation (G₁), representing the oxidative breakdown of glucose in the TCA cycle; mtROS (R_mt), reactive oxygen species derived from mitochondrial respiration, indicative of catabolic activity; reductive glutamine (Q_re), a metabolic process that converts α-ketoglutarate to citrate; glutamine oxidation (Q₁), representing the oxidative breakdown of glutamine in the TCA cycle; and pAMPK (A), a key energy sensor that regulates both anabolic and catabolic processes, here is considered a catabolic parameter in the model based on its predominant role in energy stress conditions. Both reductive Q_re and Q₁ are classified as catabolic parameters in this model because they involve the breakdown of glutamine into smaller metabolic intermediates, supporting rapid proliferation and survival. In both pathways, glutamine is deaminated to glutamate and further converted to α-ketoglutarate (α-KG), a key TCA cycle intermediate. This nutrient breakdown process is inherently catabolic, as it extracts carbon and nitrogen from glutamine for cellular metabolism. While Q₁ supports energy production through the oxidative TCA cycle, Q_re channels α-KG into reductive carboxylation to produce citrate, which fuels biosynthesis such as lipogenesis. Despite Qre’s anabolic outcomes, its reliance on upstream glutamine catabolism aligns both pathways under the ‘catabolic’ classification, reflecting their shared role in breaking down glutamine to sustain cellular demands^45,46. Lastly, we also included uptake parameters: glutamine uptake (Q₀), representing the rate at which glutamine is taken up by the cell; glucose uptake (G₀), representing the rate at which glucose is taken up by the cell; fatty acids uptake (F₀), representing the rate at which fatty acids are taken up by the cell; and the rate of acetyl-CoA being fed for mitochondrial respiration (C₀), indicating the rate at which acetyl-CoA is used in the TCA cycle for ATP production.

To simulate the temporal dynamics of the regulatory proteins pAMPK and HIF-1, as well as the temporal dynamics of metabolites mtROS and noxROS, we devise the following equations (eqs. 1–5).

$$\begin{array}{l}{\dot{R}}_{{mt}}={g}_{{R}_{{mt}}}\,\cdot\, \left({\gamma }_{{G}_{1}}{G}_{1}+{\gamma }_{F}F+{\gamma }_{{Q}_{1}}{Q}_{1}\right)-{k}_{{R}_{{mt}}}{\,\cdot\, R}_{{mt}}\,\cdot\, \left({H}^{s+}\left(A,{A}_{{R}_{{mt}}}^{0},{\lambda }_{A,{R}_{{mt}}},{n}_{A,{R}_{{mt}}}\right)\right.\\\qquad\;\;\;\,+\left.{\gamma }_{{GSH}}{Q}_{{GSH}}\right)\end{array}$$

(1)

(eq. 1) represents the temporal dynamics of mitochondrial reactive oxygen species (mtROS) (${R}_{{mt}}$). ${g}_{{R}_{{mt}}}$ is the basal production rate of mtROS, $({\gamma }_{{G}_{1}}{G}_{1}+{\gamma }_{F}F+{\gamma }_{{Q}_{1}}{Q}_{1})$ represents the increase of mtROS production due to glucose oxidation (${G}_{1}$), FAO ($F$) and glutamine oxidation (${Q}_{1}$). Notably, the two parameters ${\gamma }_{G1}$ and ${\gamma }_{F}$ have fixed ratio 2/9 because the ratio of the amount of acetyl-CoA entering TCA generated by glucose oxidation and FAO is 2/9. ${k}_{{R}_{{mt}}}$ represents the basal degradation rate of mtROS and the shifted Hill function (1) ${H}^{s+}(A,{A}_{{R}_{{mt}}}^{0},{\lambda }_{A,{R}_{{mt}}},{n}_{A,{R}_{{mt}}})$ represents the deoxidation effect of AMPK. ${\gamma }_{{GSH}}{G}_{{GSH}}$ represents the antioxidation effect of glutathione (GSH) due to the GSH synthesis pathway (${Q}_{{GSH}})$.

$$\begin{array}{l}{\dot{R}}_{{nox}}={g}_{{R}_{{nox}}}{\,\cdot\, C}_{{R}_{{nox}}}^{{comp}}\left({g}_{0},H,{{g}_{H,{R}_{{nox}}},H}_{{R}_{{nox}}}^{0},{n}_{{H,R}_{{nox}}},A{,{g}_{A,{R}_{{nox}}},A}_{{R}_{{nox}}}^{0},{n}_{{A,R}_{{nox}}}\right)\\\qquad\;\;\;\,-{k}_{{R}_{{nox}}}{\,\cdot\, R}_{{nox}}\,\cdot\, {Q}_{{GSH}}\end{array}$$

(2)

(eq. 2) represents the temporal dynamics of NADPH Oxidase-derived Reactive Oxygen Species (noxROS) (${R}_{{nox}}$). ${g}_{{R}_{{nox}}}$ is the basal production rate of noxROS, ${C}_{{R}_{{nox}}}^{{comp}}({g}_{0},H,{H}_{H{R}_{{nox}}}^{0},{n}_{{H}_{{nox}}},{g}_{1},A,{A}_{0},{g}_{2},{n}_{{A}_{{nox}}})$ represents the competitive regulation of noxROS production by AMPK ($A$) and HIF-1 ($H$) and ${k}_{{R}_{{nox}}}$ represents the basal degradation rate of noxROS. ${\gamma }_{{GSH}}{G}_{{GSH}}$ represents the antioxidant effect of GSH due to the GSH synthesis pathway (${G}_{{GSH}})$. In Eq. 2, the model assumes that AMPK and HIF-1 competitively regulate noxROS through both direct and indirect pathways. HIF-1 increases noxROS by targeting NOX and reduces mtROS by lowering OXPHOS and increasing glycolysis. Conversely, AMPK boosts mtROS through OXPHOS and enhances mtROS scavenging via the AMPK-FOXO pathway, while also inhibiting noxROS production in the cytosol by regulating NOX. Both mtROS and noxROS stabilize HIF-1α and activate AMPK, creating a feedback loop and influencing cancer cell metabolism²⁵. Supporting evidence includes the role of AMPK and HIF-1 as key regulators of OXPHOS and glycolysis, respectively, with ROS mediating their interplay¹⁴. Additionally, RAS, MYC, and c-SRC modulate the balance of glycolysis and OXPHOS¹⁵. AMPK activation leads to HIF-1α degradation, inhibiting its activity²⁶. AMPK down-regulates HIF-1 by inhibiting mTOR, while HIF-1 inhibits AMPK transcription^24,28)

$${R}_{T}={R}_{{mt}}+{R}_{{nox}}$$

(3)

(eq. 3) represents the total level of ROS (${R}_{T}$), which is the sum of mtROS (${R}_{{mt}}$) and noxROS (${R}_{{nox}}$).

$$\begin{array}{l}\dot{A}={g}_{A}\,\cdot\, {H}^{s+}\left({R}_{T},{{R}_{T,A}^{0},\lambda }_{{R}_{T},A},{n}_{{R}_{T},A}\right){\,\cdot\, H}^{s-}\left(H,{H}_{A}^{0},{\lambda }_{H,A},{n}_{H,A}\right)\\\qquad\cdot\, {H}^{s-}\left({X}_{{ATP}},{{X}_{{ATP},A}^{0},\lambda }_{{X}_{{ATP}},A},{n}_{{X}_{{ATP}},A}\right)-{k}_{A}A\end{array}$$

(4)

(eq. 4) represents the temporal dynamics of phosphorylated AMPK (pAMPK) ($A$). ${g}_{A}$ is the basal production rate of pAMPK, ${H}^{s+}({R}_{T},{{R}_{T,A}^{0},\lambda }_{{R}_{T},A},{n}_{{R}_{T},A})$ represents the excitatory regulation on pAMPK production by ROS (${R}_{T}$),${H}^{s-}(H,{H}_{H,A}^{0},{\lambda }_{H,A},{n}_{H,A})$ represents the inhibitory regulation on pAMPK by HIF-1 ($H$), ${H}^{s-}({X}_{{ATP}},{{X}_{{ATP},A}^{0},\lambda }_{{X}_{{ATP}},A},{n}_{{X}_{{ATP}},A})$ represents the inhibitory regulation on pAMPK by ATP (${X}_{{ATP}}$) and ${k}_{A}$ represents the basal degradation rate of AMPK.

$$\begin{array}{l}\dot{H}={g}_{H}{\,\cdot\, H}^{s-}\left(A,{A}_{H}^{0},{\lambda }_{A,H},{n}_{A,H}\right)-{k}_{H}\,\cdot\, {H\,\cdot\, H}^{s-}\left({G}_{2},{G}_{2,H}^{0},{\lambda }_{{G}_{2},H},{n}_{{G}_{2},H}\right)\\\qquad\cdot\, {H}^{s-}\left({R}_{T},{{R}_{T,H}^{0},\lambda }_{{R}_{T},H},{n}_{{R}_{T},H}\right){\,\cdot\, H}^{s-}\left(M,{{M}_{M,H}^{0},\lambda }_{M,H},{n}_{M,H}\right)\end{array}$$

(5)

(eq. 5) represents the temporal dynamics of HIF-1 ($H$). ${g}_{H}$ is the basal production rate of HIF-1, ${H}^{s-}\left(A,{A}_{H}^{0},{\lambda }_{A,H},{n}_{A,H}\right)$ represents the inhibitory regulation on HIF-1 production by pAMPK, ${k}_{H}$ represents the basal degradation rate of HIF-1, the shifted Hill functions ${H}^{s-}({G}_{2},{G}_{2,H}^{0},{\lambda }_{{G}_{2},H},{n}_{{G}_{2},H})$, ${H}^{s-}({R}_{T},{{R}_{T,H}^{0},\lambda }_{{R}_{T},H},{n}_{{R}_{T},H})$ and ${H}^{s-}(M,{{M}_{M,H}^{0},\lambda }_{M,H},{n}_{M,H})$ represent the stabilization of HIF-1 by the glycolytic activity (${G}_{2}$), ROS (${R}_{T})$ and Myc ($M$).

Since the chemical reactions in the metabolism processes are much faster than the genetic regulations, we assume the metabolites and the pathways are in the equilibrium state at a certain level of pAMPK and HIF-1. To capture the dynamics of metabolic flux, we derive the following equations (eqs. 6–16).

$$\begin{array}{l}{G}_{0}={g}_{H,{G}_{0}}{\,\cdot\, H}^{s+}\left(H,{H}_{{G}_{0}}^{0},{\lambda }_{H,{G}_{0}},{n}_{H,{G}_{0}}\right)+{g}_{A,{G}_{0}}\,\cdot\, {H}^{s+}\\\qquad\left(A,{A}_{{G}_{0}}^{0},{\lambda }_{A,{G}_{0}},{n}_{A,{G}_{0}}\right)+{{g}_{M,{G}_{0}}\,\cdot\, H}^{s+}\left(M,{M}_{{G}_{0}}^{0},{\lambda }_{M,{G}_{0}},{n}_{M,{G}_{0}}\right)\end{array}$$

(6)

(eq. 6) represents the glucose uptake rate $({G}_{0})$. Since HIF-1, pAMPK, and Myc can enhance the glucose uptake, one assumption is the maximum glucose uptake rate (${G}_{0}$) is determined by the HIF-1, pAMPK, and Myc levels. ${g}_{H,{G}_{0}}{H}^{s+}(H,{H}_{{G}_{0}}^{0},{\lambda }_{H,{G}_{0}},{n}_{H,{G}_{0}})$ represents the regulation of glucose uptake by HIF-1, ${g}_{A,{G}_{0}}{H}^{s+}(A,{A}_{{G}_{0}}^{0},{\lambda }_{A,{G}_{0}},{n}_{A,{G}_{0}})$ represents the regulation of glucose uptake by pAMPK and ${{g}_{M,{G}_{0}}H}^{s+}\left(M,{M}_{{G}_{0}}^{0},{\lambda }_{M,{G}_{0}},{n}_{M,{G}_{0}}\right)$ represents the regulation of glucose uptake by Myc.

$${Q}_{0}={g}_{M,{G}_{G\mathrm{ln},0}}{\,\cdot\, H}^{s+}\left(M,{M}_{{Q}_{0}}^{0},{\lambda }_{M,{Q}_{0}},{n}_{M,{Q}_{0}}\right)$$

(7)

(eq. 7) represents the glutamine uptake rate (${G}_{G\mathrm{ln},0}$). As Myc can enhance glutamine update, one assumption is the maximum glutamine uptake rate (${G}_{G\mathrm{ln},0}$) is determined by the Myc levels.

$${F}_{0}={g}_{{F}_{0}}{\,*\, H}^{s+}\left(A,{A}_{{F}_{0}}^{0},{\lambda }_{A,{F}_{0}},{n}_{A,{F}_{0}}\right)$$

(8)

(eq. 8) represents the fatty acid uptake rate $({F}_{0})$.

$${C}_{0}={g}_{A,{C}_{0}}{\,\cdot\, H}^{s+}\left(A,{A}_{{C}_{0}}^{0},{\lambda }_{A,{C}_{0}},{n}_{A,{C}_{0}}\right)$$

(9)

(eq. 9) represents the maximum utilization rate of acetyl-CoA for mitochondrial respiration $({C}_{0})$. Since the rate of acetyl-CoA entering the TCA cycle is limited by the mitochondrial activity that is determined by the pAMPK, one assumption here is the maximum utilization rate of Acetyl-CoA (${C}_{0}$) is determined by the pAMPK levels. The shifted Hill function ${g}_{A,{C}_{0}}{H}^{s+}(A,{A}_{{C}_{0}}^{0},{\lambda }_{A,{C}_{0}},{n}_{A,{C}_{0}})$ represents the regulation of pAMPK on the utilization of Acetyl-CoA for mitochondrial TCA cycle.

The glucose uptake rate (${G}_{0}$) and the utilization rate of Acetyl-CoA (${C}_{0}$) for TCA cycle restrict the activities of three metabolic pathway—glucose oxidation (${G}_{1}$), glycolysis (${G}_{2}$), and FAO ($F$).

$$G={G}_{1}+{G}_{2}+{G}_{{re}}$$

(10)

(eq. 10) represents the glucose consumption rate $(G)$, which is equal to the sum of the glucose oxidation rate (${G}_{1}$), and glycolysis rate (${G}_{2}$), and the reductive glucose metabolic rate (${G}_{{re}}$) (mainly representing fatty acid synthesis rate from glucose), since glucose is shared by these pathways.

$$Q={Q}_{1}+{Q}_{{GSH}}+{Q}_{{re}}$$

(11)

(eq. 11) represents the total glutamine consumption rate ($Q$), which is the sum of glutamine oxidation rate (${Q}_{1}$) and glutathione (GSH) synthesis rate (${Q}_{{GSH}}$) and the reductive glutamine metabolic rate (${Q}_{{re}}$) (mainly representing fatty acid synthesis rate from glutamine), since intracellular glutamine is shared by these three pathways.

$$F={F}_{1}+{F}_{r}-{\gamma }_{G,F}* {G}_{r}-{\gamma }_{G,Q}* {Q}_{{re}}$$

(12)

(eq. 12) represents the total fatty acid consumption rate ($F$), which is the sum of the FAO rate $({F}_{1})$, and the reductive fatty acid metabolism (${F}_{r}$) minus the contributions of reductive glucose metabolic rate (${G}_{{re}}$) (considered the efficiency of glucose-derived carbon incorporation into fatty acids) and the reductive glutamine metabolic rate (${Q}_{{re}}$) (considering the efficiency of glutamine-derived carbon incorporation into fatty acids.)

$$C=2* {G}_{1}+9* F$$

(13)

(eq. 13) represents the production rate of Acetyl-CoA for mitochondrial respiration $(C)$. The generated Acetyl-CoA that can enter the TCA cycle for ATP production is determined by glucose oxidation rate (${G}_{1}$) and FAO rate ($F$). 2 molecules of acetyl-CoA are produced by one glucose oxidation process, and 9 molecules of acetyl-CoA are produced in 1 FAO process, in which we assume the average carbon atoms contained in each fatty acid is 18 (Supplementary Table 1).

$${G}_{1}={g}_{{G}_{1}}{H}^{s-}\left(G,{G}_{0},{\lambda }_{G,{G}_{1}},{n}_{G,{G}_{1}}\right){H}^{s-}\left(C,{C}_{0},{\lambda }_{C,{G}_{1}},{n}_{C,{G}_{1}}\right)$$

(14)

$${G}_{2}={g}_{{G}_{2}}{H}^{s-}\left(G,{G}_{0},{\lambda }_{G,{G}_{2}},{n}_{G,{G}_{2}}\right){H}^{s+}\left(H,{H}_{{G}_{2}}^{0},{\lambda }_{H,{G}_{2}},{n}_{H,{G}_{2}}\right)$$

(15)

$$\begin{array}{l}{G}_{{re}}={g}_{{G}_{r}}\,\cdot\, {H}^{s-}\left(G,{G}_{0},{\lambda }_{G,{G}_{{re}}},{n}_{G,{G}_{{re}}}\right){\,\cdot\, H}^{s-}\left(A,{A}_{{G}_{{re}}}^{0},{\lambda }_{A,{G}_{{re}}},{n}_{A,{G}_{{re}}}\right)\\\qquad\,\;{\,\cdot\, H}^{s+}\left(M,{M}_{{G}_{{re}}}^{0},{\lambda }_{M,{G}_{{re}}},{n}_{M,{G}_{{re}}}\right)\end{array}$$

(16)

$$\begin{array}{l}{F}_{1}={g}_{{F}_{1}}{\,*\, H}^{s-}\left(F,{F}_{0},{\lambda }_{F,{F}_{1}},{n}_{F,{F}_{1}}\right)* {H}^{s-}\left(C,{C}_{0},{\lambda }_{C,F},{n}_{C,F}\right)\\\qquad{\,*\, H}^{s+}\left(A,{A}_{F}^{0},{\lambda }_{A,F},{n}_{A,F}\right){\,*\, H}^{s-}\left(H,{H}_{F}^{0},{\lambda }_{H,F},{n}_{H,F}\right)\end{array}$$

(17)

$${F}_{r}={g}_{{F}_{r}}{\,*\, H}^{s-}\left(F,{F}_{0},{\lambda }_{F,{F}_{r}},{n}_{F,{F}_{r}}\right)* {H}^{s-}\left(H,{H}_{{F}_{2}}^{0},{\lambda }_{H,{F}_{2}},{n}_{H,F2}\right)$$

(18)

(eqs. 12–18) represent the glucose oxidation rate $({G}_{1})$, the glycolysis rate (${G}_{2}$), the reductive glucose metabolic rate (${G}_{{re}}$), the FAO rate $({F}_{1})$, and the reductive fatty acid metabolism (${F}_{r}$) respectively.

The negative shifted Hill functions ${H}^{s-}(G,{G}_{0},{\lambda }_{G,{G}_{1}},{n}_{G,{G}_{1}})$, ${H}^{s-}(G,{G}_{0},{\lambda }_{G,{G}_{2}},{n}_{G,{G}_{2}})$ and ${H}^{s-}(G,{G}_{0},{\lambda }_{G,{G}_{{re}}},{n}_{G,{G}_{{re}}})$ represent the competition of glucose oxidation (${G}_{1}$), glycolysis (${G}_{2}$), and reductive glucose metabolism (${G}_{{re}}$) on glucose utilization. The threshold ${G}_{0}$, that is the glucose uptake rate, in these three shifted Hill functions adds a restriction on ${G}_{1}$, ${G}_{2}$ and ${G}_{{re}}$ since if $G \,>\, {G}_{0}$, that means the glucose utilization rate is larger than the glucose uptake rate, these negative shifted Hill functions will decrease ${G}_{1}$, ${G}_{2}$, and ${G}_{{re}}$ thus decrease $G$.

The negative shifted Hill functions ${H}^{s-}(C,{C}_{0},{\lambda }_{C,{G}_{1}},{n}_{C,{G}_{1}})$ and ${H}^{s-}\left(C,{C}_{0},{\lambda }_{C,F},{n}_{C,F}\right)$ representing the competition of glucose oxidation (${G}_{1}$) and FAO $(F)$ on acetyl-CoA production. The threshold ${C}_{0}$, that is the limiting utilization rate of acetyl-CoA for mitochondrial respiration, in these two shifted Hill functions adds restriction on both ${G}_{1}$ and $F$ since if $C \,>\, {C}_{0}$, that means the produced acetyl-CoA is beyond the limiting utilization rate of acetyl-CoA for mitochondrial respiration, these negative shifted Hill functions will decrease both ${G}_{1}$ and $F$ thus decreasing $C$.

${H}^{s+}(H,{H}_{{G}_{2}}^{0},{\lambda }_{H,{G}_{2}},{n}_{H,{G}_{2}})$ in (eq. 11) represents the regulation of glycolytic activity by HIF-1. ${H}^{s+}\left(A,{A}_{F}^{0},{\lambda }_{A,F},{n}_{A,F}\right)$ in (eq. 12) represents the regulation of FAO by AMPK. ${H}^{s-}(A,{A}_{{G}_{{re}}}^{0},{\lambda }_{A,{G}_{{re}}},{n}_{A,{G}_{{re}}})$ represents the inhibition of fatty acid synthesis by AMPK.

$$\begin{array}{l}{Q}_{1}={g}_{{Q}_{1}}{\,\cdot\, H}{^{s-}}{\left(Q,{Q}_{0},{\lambda }_{Q,{Q}_{1}},{n}_{Q,{Q}_{1}}\right)\,\cdot\, H}{^{s+}}\left(M,{M}_{{Q}_{1}}^{0},{\lambda }_{M,{Q}_{1}},{n}_{M,{Q}_{1}}\right)\\\qquad\,{\,\cdot\, H}{^{s-}}\left(H,{H}_{{Q}_{1}}^{0},{\lambda }_{H,{Q}_{1}},{n}_{H,{Q}_{1}}\right)\end{array}$$

(19)

$$\begin{array}{ll}{Q}_{{GSH}}={g}_{{Q}_{{GSH}}}\,\cdot\, {H}^{s-}\left(Q,{Q}_{0},{\lambda }_{Q,{Q}_{{GSH}}},{n}_{Q,{Q}_{{GSH}}}\right)\,\cdot\, {H}^{s-}\left(A,{A}_{{Q}_{{GSH}}}^{0},{\lambda }_{A,{Q}_{{GSH}}},{n}_{A,{Q}_{{GSH}}}\right)\\\,\cdot\, {H}^{s-}\left(M,{M}_{{Q}_{{GSH}}}^{0},{\lambda }_{M,{Q}_{{GSH}}},{n}_{M,{Q}_{{GSH}}}\right)\end{array}$$

(20)

$$\dot{{G}_{{GSH}}}={Q}_{{GSH}}-{k}_{{GSH}}* {G}_{{GSH}}$$

(21)

$$\begin{array}{ll}{Q}_{{re}}={g}_{{Q}_{r}}\,\cdot\, {H}^{s-}\left(Q,{Q}_{0},{\lambda }_{Q,{Q}_{{re}}},{n}_{Q,{Q}_{{re}}}\right){\,\cdot\, H}^{s+}\left(M,{M}_{{Q}_{{re}}}^{0},{\lambda }_{M,{Q}_{{re}}},{n}_{M,{Q}_{{re}}}\right)\\\qquad\,{\,\cdot\, H}^{s+}\left(H,{H}_{{Q}_{{re}}}^{0},{\lambda }_{H,{Q}_{{re}}},{n}_{H,{Q}_{{re}}}\right){\,\cdot\, H}^{s-}\left(A,{A}_{{Q}_{{re}}}^{0},{\lambda }_{A,{Q}_{{re}}},{n}_{A,{Q}_{{re}}}\right)\end{array}$$

(22)

(eqs. 19–22) represents the glutamine oxidation rate (${Q}_{1}$), the glutathione synthesis rate (${Q}_{{GSH}}$), the glutathione dynamics (${G}_{{GSH}}$), and the reductive glutamine metabolic rate (${Q}_{{re}}$) respectively.

The negative shifted Hill functions ${H}^{s-}(Q,{Q}_{0},{\lambda }_{Q,{Q}_{1}},{n}_{Q,{Q}_{1}})$, ${H}^{s-}(,{Q}_{0},{\lambda }_{Q,{Q}_{{GSH}}},{n}_{Q,{Q}_{{GSH}}})$ and ${H}^{s-}(Q,{Q}_{0},{\lambda }_{Q,{Q}_{{re}}},{n}_{Q,{Q}_{{re}}})$ represent the competition of glutamine oxidation (${Q}_{1}$), glutathione synthesis pathway $({Q}_{{GSH}})$ and reductive glutamine metabolism (${Q}_{{re}}$) on glutamine utilization. The threshold ${Q}_{0}$, that is the glutamine uptake rate, in these three shifted Hill functions adds restriction on ${Q}_{1}$, ${Q}_{{GSH}}$ and ${Q}_{{re}}$, since if $Q \,>\, {Q}_{0}$, that means the glutamine utilization rate is larger than the glutamine uptake rate, these negative shifted Hill functions will decrease ${Q}_{1}$, ${Q}_{{GSH}}$ and ${Q}_{{re}}$ thus decreasing $Q$.

${H}^{s+}(M,{M}_{{Q}_{1}}^{0},{\lambda }_{M,{Q}_{1}},{n}_{M,{Q}_{1}})$ represents the up-regulation of glutamine oxidation by Myc. ${H}^{s-}(H,{H}_{{Q}_{1}}^{0},{\lambda }_{H,{Q}_{1}},{n}_{H,{Q}_{1}})$ represents the down-regulation of glutamine oxidation by HIF-1. ${H}^{s-}(M,{M}_{{Q}_{{GSH}}}^{0},{\lambda }_{M,{Q}_{{GSH}}},{n}_{M,{Q}_{{GSH}}})$ represents the inhibition of glutathione synthesis by Myc. ${H}^{s+}(M,{M}_{{Q}_{{re}}}^{0},{\lambda }_{M,{Q}_{{re}}},{n}_{M,{Q}_{{re}}})$ represent the up-regulation of reductive glutamine metabolism by Myc. ${\,\cdot\, H}^{s+}(H,{H}_{{Q}_{{re}}}^{0},{\lambda }_{H,{Q}_{{re}}},{n}_{H,{Q}_{{re}}})$ represents the up-regulation of reductive glutamine metabolism by HIF-1. ${H}^{s-}(A,{A}_{{Q}_{{re}}}^{0},{\lambda }_{A,{Q}_{{re}}},{n}_{A,{Q}_{{re}}})$ represents the down-regulation of reductive glutamine metabolism by AMPK.

$${G}_{1,{ATP}}=29* {G}_{1}$$

(23)

$${G}_{2,{ATP}}=2* {G}_{2}$$

(24)

$${Q}_{1,{ATP}}=24* {Q}_{1}$$

(25)

$${F}_{1,{ATP}}=106* F$$

(26)

(eqs. 23–26) represent the production rates of ATP glucose oxidation (${G}_{1,{ATP}}$) and glycolysis (${G}_{2,{ATP}}$), glutamine oxidation (${Q}_{1,{ATP}}$), and FAO (${F}_{1,{ATP}}$), respectively. The constants for ATP production for Eqs. 23–26 are well-established in the biochemical literature. Complete oxidation of glucose through glycolysis, the TCA cycle, and oxidative phosphorylation typically yields approximately 29-32 ATP molecules. In contrast, glycolysis alone produces a net gain of 2 ATP molecules per glucose molecule^47,48. The ATP yield from glutamine oxidation is based on its entry into the TCA cycle, where it contributes to ATP production. This process yields an estimated 24 ATP molecules per glutamine molecule, reflecting the metabolic pathways involved^49,50. For fatty acid oxidation, the constant ATP production is derived from the oxidation of a typical fatty acid, such as palmitate. This process yields approximately 106 ATP molecules⁵¹

$${F}_{2,{ATP}}=7* {F}_{2}$$

(27)

$${G}_{{re},{ATP}}=(15-2)* {G}_{{re}}$$

(28)

$${Q}_{{re},{ATP}}=15* {Q}_{{re}}$$

(29)

$${Q}_{{GSH},{ATP}}=2* {Q}_{{GSH}}$$

(30)

(eqs. 27-30) represent the ATP consumption rates of reductive fatty acid (${F}_{2,{ATP}}$), reductive glucose (${G}_{{re},{ATP}}$), and reductive glutamine (${Q}_{{re},{ATP}}$) metabolism and GSH synthesis ${Q}_{{GSH},{ATP}})$, respectively. The constants for ATP consumption (Eqs. 27–30) in reductive fatty acid, glucose, and glutamine metabolism, as well as GSH synthesis, are based on the energy requirements for these biosynthetic processes. For instance, the synthesis of palmitate from acetyl-CoA requires 7 ATP molecules. Additionally, each molecule of glutathione synthesized requires 2 ATP molecules, one for each step in the process^51,52

$$\begin{array}{ll}{X}_{{ATP}}={G}_{1,{ATP}}+{G}_{2,{ATP}}+{Q}_{1,{ATP}}+{F}_{1,{ATP}}-{F}_{2,{ATP}}\\\qquad\quad-{G}_{{re},{ATP}}-{Q}_{r,{ATP}}-{Q}_{{GSH},{ATP}}\end{array}$$

(31)

(eq. 26) represents the net total production rate of ATP (${X}_{{ATP}}$).

The definition of the shifted Hill function and the function ${C}_{{R}_{{nox}}}^{{comp}}$ representing the competitive regulation of noxROS by AMPK and HIF-1 are as follows.

The shifted Hill function (1) ${H}^{s}\left(X,{X}_{0},\lambda ,n\right)$ is defined to be

${H}^{s}\left(X,{X}_{0},\lambda ,n\right)=\frac{1+\lambda {\left(\frac{X}{{X}_{0}}\right)}^{n}}{1+{\left(\frac{X}{{X}_{0}}\right)}^{n}}$, where $X$ represents the level of the regulator, ${X}_{0}$ represents the threshold, $\lambda$ represents the fold-change, and $n$ represents the Hill coefficient.

${H}^{s+}\left(X,{X}_{0},\lambda ,n\right)=\frac{1+{\lambda }^{+}{\left(\frac{X}{{X}_{0}}\right)}^{n}}{1+{\left(\frac{X}{{X}_{0}}\right)}^{n}}$, where ${\lambda }^{+} \,>\, 1$, representing the excitatory regulation.

${H}^{s-}\left(X,{X}_{0},\lambda ,n\right)=\frac{1+{\lambda }^{-}{\left(\frac{X}{{X}_{0}}\right)}^{n}}{1+{\left(\frac{X}{{X}_{0}}\right)}^{n}}$, where ${\lambda }^{-} \,<\, 1$, representing the inhibitory regulation.

The competitive regulations of noxROS by AMPK and HIF-1 (${C}^{{comp}}$) (2) are defined as follows:

$$\begin{array}{l}{C}_{{R}_{{nox}}}^{{comp}}\left({g}_{0},H,{{g}_{H,{R}_{{nox}}},H}_{{R}_{{nox}}}^{0},{n}_{{H,R}_{{nox}}},A{,{g}_{A,{R}_{{nox}}},A}_{{R}_{{nox}}}^{0},{n}_{{A,R}_{{nox}}}\right)\\=\frac{{g}_{0}+{g}_{H,{R}_{{nox}}}{\left(\frac{H}{{H}_{{R}_{{nox}}}^{0}}\right)}^{{n}_{{H,R}_{{nox}}}}+{g}_{A,{R}_{{nox}}}{\left(\frac{A}{{A}_{{R}_{{nox}}}^{0}}\right)}^{{n}_{{A,R}_{{nox}}}}}{1+{\left(\frac{H}{{H}_{{R}_{{nox}}}^{0}}\right)}^{{n}_{{H,R}_{{nox}}}}+{\left(\frac{A}{{A}_{{R}_{{nox}}}^{0}}\right)}^{{n}_{{A,R}_{{nox}}}}}\end{array},$$

where ${g}_{0}=1$ representing the basal noxROS production, ${g}_{H,{R}_{{nox}}}{\left(\frac{H}{{H}_{{R}_{{nox}}}^{0}}\right)}^{{n}_{{H,R}_{{nox}}}}$ represents the regulation of noxROS production by HIF-1, and ${g}_{A,{R}_{{nox}}}{\left(\frac{A}{{A}_{{R}_{{nox}}}^{0}}\right)}^{{n}_{{A,R}_{{nox}}}}$ represents the regulation of noxROS production by AMPK.

We used MATLAB (R2023b) to compute and plot the nullclines. First, we uploaded the baseline model parameters presented in Supplementary Table 1. For each combination of AMPK and HIF-1 levels, we calculated the ATP production and reactive oxygen species (ROS) levels. The results were stored and used to plot nullclines using the contour functions. These nullclines were then analyzed to find fixed points, which were categorized into stable and unstable states and visualized. This comprehensive approach helps in understanding the dynamic interactions between key regulatory proteins and metabolic processes in cancer cells.

Data analysis

PanCancer Atlas data, including the clinical data were downloaded from The cBio Cancer Genomics Portal (cBioPortal, https://www.cbioportal.org/), which includes RSEM-normalized expression data. The analyzed cancers were hepatocellular carcinoma (LIHC), breast invasive carcinoma (BRCA), kidney renal clear cell carcinoma (KIRC), lung adenocarcinoma (LUAD), lung squamous cell carcinoma (LUSC), colorectal adenocarcinoma (COAD), skin cutaneous melanoma (SKCM), acute myeloid leukemia (LAML), and prostate adenocarcinoma (PRAD). We also analyzed microarray data from 45 breast cancer samples and their paired adjacent benign tissue samples⁵³. The gene expression levels for each tumor type were first normalized to ensure comparability across different samples. This study does not include information on normal tissue samples from the PanCancer Atlas. Normalization was performed using the Z-score method, where the expression level of each gene was transformed to have a mean of zero and a standard deviation of one.

To develop the scoring metric, we used the previously evaluated HIF-1, AMPK, glucose oxidation, glycolysis, and FAO scores developed by Yu et al., and Jia et al.^14,15. For the generation of the rest of the signatures, we used the information obtained from PubChem (https://pubchem.ncbi.nlm.nih.gov), PANTHER Pathway, and Reactome pathway. These databases were used to identify pathways related to each process. For example, the keywords to obtain relevant genes to each molecule of interest in the anabolic sense were: “biosynthesis”, “biosynthetic”, “synthesis”, “de novo”, “anabolism”, “formation”, “-genesis”, “reduction”. The scoring metrics were determined by calculating the mean expression of the Z-score of pertinent genes within each pathway. In our analysis, the fatty acid reduction process was further delimited using the approach followed by Jia et al.¹⁵ where we performed PCA on the gene expression data from which the first principal components (PC1s) were used to quantify the activity, this ensures that only the genes that have more variability in the signature account in the data set. The anabolic and catabolic activity scores are the agglomeration of all the gene sets associated with anabolic and catabolic processes, respectively (Supplementary Table 2). The normalized expression levels were then averaged to calculate the overall anabolic and catabolic activity scores. K-means clustering analysis was applied to classify patient samples into the four metabolic states: Warburg (W), OXPHOS (O), hybrid (W/O), and glutamine-dominant (Q). Clustering was based on gene expression in anabolic and catabolic pathways. For the metabolic state labeling, for each cluster, we calculated the centroid by computing the mean values of AMPK and HIF-1 scores, These centroids were then categorized into a four-quadrant plot, each one representing a distinct metabolic state: high AMPK—low HIF-1: Assigned to the “O” (OXPHOS) state; high AMPK—high HIF-1: Assigned to the “W/O” (Warburg/Oxidative) state; low AMPK—low HIF-1: Assigned to the “Q” (Glutamine) state; low AMPK—high HIF-1: Assigned to the “W” (Warburg) state.

Data analysis and visualization were performed using several R packages. Heat maps and clustering analyses were conducted using the ‘ComplexHeatmap’ package⁵⁴. The ‘ggplot2’ package was utilized for data visualization, and the ‘ggpubr’ package was employed for statistical analysis, including the t-test. For the Kaplan-Meier plots, patient data were categorized based on the results of the clustering analysis. The overall survival analysis was conducted using the log-rank test. The ‘survival’ package⁵⁵ was used for survival analysis, and the ‘survminer’ package⁵⁶ was used to create the Kaplan-Meier plots. We conducted KEGG pathway enrichment analysis for each cluster in the LIHC data set using the clusterProfiler, edgeR, and org.Hs.eg.db packages in R. We extracted the top genes by average expression, filtering based on average log CPM greater than 5 and mapping to Entrez IDs. KEGG enrichment analysis, specifically Over-Representation Analysis (ORA), was performed for each cluster, and the results were filtered using keywords such as “glucose”, “glutamine”, “fatty acid”, “glycolysis”, “ROS”, “AMPK”, “HIF-1”, “ATP”, “GSH”, “Myc”, “Metabolism”, “Cellular Processes”, and “Genetic Information Processing”. The filtered results were converted to data frames, combined, and visualized using a bar plot to illustrate pathway enrichment by cluster.