Introduction

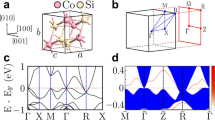
In recent years, topological semimetals have emerged as an attractive class of materials to explore exotic quantum properties, for both fundamental research and applications in electronics and photonics1,2,3. Among these materials, cobalt monosilicide (CoSi) has received significant research attention due to its unique transport features4,5. In its crystalline form, CoSi exhibits nearly ideal topological surface properties, hosting multifold chiral fermions within its Brillouin zone6,7. These chiral fermions contribute to among the longest Fermi arcs currently observed within chiral and Weyl fermion semimetals8. Furthermore, CoSi boasts a substantial topologically non-trivial energy window, allowing the existence of topological chiral fermions without the need for fine-tuning of the Fermi level4.

In semiconductor technologies, non-trivial topology resulting in surface states resilient to scattering could enable interconnects with improved scaling properties compared to traditional metals2,9,10. CoSi is attractive from this perspective due to its compatibility with standard Si CMOS technology. Co in particular is already being used in the first levels of back-end metallization to reduce the line resistivity11,12. Recent theoretical work on CoSi demonstrated that the unique band topologies of semimetals produce robust surface states that can dominate conduction, potentially leading to reduced resistivity with decreasing feature size, contrasting with conventional metals13. On the other hand, it is unclear whether the topological properties of CoSi extend to less-ideal or low-dimensional systems like thin films and nanowires14. Recent measurements found that an increased surface-to-bulk ratio results in a decreased resistivity in the topological semimetal NbAs3 while simulation showed improved conductivity in CoSi13, thanks to the contribution of Fermi-arc mediated transport. However, conclusive observation of surface transport in low-dimensional systems has been elusive so far15. Moreover, the properties of the amorphous state have remained unexplored. Although the possibility of non-trivial topology in an amorphous system is debated16,17,18,19,20,21, since disordered materials lack long-range order, amorphous materials do have unique electronic characteristics compared to their crystalline counterparts22,23 and may be technologically relevant24,25. Deposition of amorphous phase materials is less constrained by substrate crystallinity, which benefits Si CMOS integration14,26. Understanding the behavior of amorphous CoSi thin films is, in this context, of importance from theoretical and applications points of view27,28.

In this work, we report on the transport properties of amorphous CoSi thin-films, deposited by molecular beam epitaxy14. Specifically, we study the electronic and magnetotransport properties of CoSi at thicknesses ranging from 82.5 nm down to 2.0 nm, with the purpose of establishing the resistivity scaling behavior of this material at dimensions relevant for future interconnect technologies. Characterization and compositional analysis are performed in order to verify stoichiometry in scaled films. Charge transport is studied by means of longitudinal resistivity, Hall resistance and magnetoresistance measurements, and compared between amorphous and textured (multi-crystalline) samples. A reduction in resistivity and a significant enhancement of the magnetoresistance (MR) are observed in the amorphous state of scaled CoSi films.

Results

Material growth and characterization

We first characterize the structural properties of the grown CoSi thin films. In our work, unless otherwise stated, the films where all grown with an MBE process on a 1 mm thick MgO substrate and uncapped. This structure allows us to capture transport properties without influence of additional interfaces29, as, for technological applications, the surrounding material may vary widely. For these reasons, in this work we focus mainly on uncapped CoSi films. However, for comparison, textured samples of various thickness were grown and characterized as well.

Previous studies on CoSi thin films already noted difficulties in maintaining a pure cobalt mono-silicide phase, with a tendency to form spurious phases like Co2Si or CoSi230. Additionally, in our previous study14, we reported that the growth temperature significantly impacts the microstructure of CoSi films. Specifically, temperatures exceeding 100–175 °C induce a transition from an amorphous to a polycrystalline state, therefore, unless stated otherwise, all amorphous films were grown at room temperature. Thickness and chemical composition were calibrated using Rutherford backscattering spectroscopy (RBS) and X-ray photoelectron spectroscopy (XPS). Unless otherwise stated, we refer to the thicknesses measured by RBS and confirmed by scanning transmission electron microscopy (STEM) cross-section, though some deviation due to e.g. surface oxidation or chip-scale variability cannot be excluded. Figure 1a shows the diffraction pattern of a STEM image of a 4.8-nm thick sample. The absence of clearly resolved diffraction peaks confirms the amorphous state of the thin films17. The amorphous state of the films has been further validated by means of grazing-incident X-ray diffraction analysis (GIXRD) and STEM analysis. STEM results are shown in Fig. 1b and 1d. Specifically, Fig. 1b reports the STEM micrographs of the cross-section of the 4.8-nm film, while in Fig. 1d, the 2.0-nm one is shown. In both cases, it is possible to distinguish between the crystalline MgO substrate and the amorphous layer of CoSi, as well as a lack of crystalline phases in the CoSi. The roughness of the samples is evaluated by means of atomic force microscopy (AFM) and, in the ultra-thin film of 2.0 nm, is in the order of 1 Å (Fig. 1c).

Fig. 1
figure 1

Characterization of CoSi amorphous films. (a) FFT transform of the CoSi layer from STEM image of the 4.8-nm thick sample (shown in b). The circular dispersion reveals the amorphous nature of the film. (b) and (d) Cross-sectional STEM images of the 4.8-nm and 2.0-nm films, respectively, showing no signs of residual polycrystalline phase. (c) AFM measurement of the 2.0-nm sample showing a mean surface roughness of 0.11 nm.

Full size image

Transport characterization

We proceed to characterize the transport properties of the grown CoSi thin films to determine their scalability properties. In particular, we measured the resistivity as a function of the temperature for different film thicknesses. In Fig. 2a, we report the resistivity of the six samples used for this study in a temperature ranging from 2 up to 300 K. The measured resistivity is reduced from around 380 µΩcm in the thickest films of 82.5 nm, to around 320 µΩcm in the 3.2-nm film, while increasing again to 410 µΩcm for the 2-nm film. Theoretically, relatively flat resistivity scaling (both, as a function of scaling thickness and temperature) is consistent with the lack of long-range order in amorphous films, though experimental results in literature often do exhibit stronger scaling trends. For instance, amorphous indium tin oxide (ITO) showed increasing resistivity already at 9 nm, caused by simultaneous reduction of mobility and carrier concentration31. Another example is GeSbTe (GST), which showed sharp resistivity increase down to 10 nm thickness in the amorphous phase, while the crystalline phases showed relatively flat scaling trends32. Similar examples exist for amorphous C:Fe25 and CoFeB33. The temperature dependence of the different samples shows similar trends with a nearly flat resistivity down to 4.8-nm, in which is present a slight upturn in the resistivity for temperatures below 10 K. The reasons behind this behavior are likely electron–electron interaction and/or the Kondo effect, as discussed in previous works14,34,35.

Fig. 2
figure 2

Electrical transport and resistivity scaling of the different films. (a) Resistivity scaling as a function of the temperature. A clear decreasing trend is noticeable at all temperatures down to a thickness of 3.2 nm. The 2.0-nm thick film exhibits a considerably higher resistivity value. An upturn in the resistivity is observable in the ultra-scaled samples at cryogenic temperatures. (b) Hall resistivity for the 3.2-nm film. An anomalous component to the signal starts to be noticeable around 20 K. (c) Charge carrier density and mobility extracted from Hall measurements (as shown in b) as a function of the thickness, taken at T = 300 K. For extreme scaled thicknesses the mobility decreases and the carrier density increases.

Full size image

Figure 2b shows the Hall resistivity of the 4.8-nm thick sample, for different temperatures. A linear trend is observed down to 10 K, where at low magnetic field an anomalous component is present through a change of slope for low fields. As the interpretation of Hall data for semimetals and amorphous materials can be complex, we turn to a standard analysis of the Hall data. From the Hall resistivity, by fitting the high-field linear part of the curve, we extract the Hall coefficient and calculate the charge carrier density. The obtained results are shown in Fig. 2c as a function of the film thickness (the Hall measurements for the other films are reported in the Supplementary Materials). The carrier concentration is in the order of 1022 to 1023 cm−3, which is consistent with the values expected in metals. The negative slope of the Hall resistivity confirms that the majority carriers are electrons. The mobility is low, around 0.25 cm2/Vs in the thickest films, as expected in amorphous systems, but shows an increasing trend as the thickness is reduced down to 4.8 nm, reaching 0.55 cm2/Vs. From 4.8 nm down to 2 nm, a sharp reduction of the mobility is observed, countered by an increase in charge carrier density of almost an order of magnitude.

Next, we investigate the possible contributions of magnetic elemental Co spurious phases. Figure 3a shows EDX analysis of the 2-nm CoSi film along with a bar plot of estimated compositions along different parts of the cross-section. Despite the limits in resolution, EDX analysis evidences a slight Co enrichment within the CoSi film along with an O and Si enrichment at the film surface. This is indicative of the formation of a thin SiOx native oxide layer that draws Si from the CoSi film, leaving it with an excess of Co. Thicker films were similarly studied but did not show major signs of Co enrichment, as the ratio between CoSi film and native oxide thicknesses is much larger. However, the presence of an oxide layer, and consequently a Co-rich channel, might influence the analysis of the resistivity scaling by introducing a normalization error. To examine the resistivity scaling in scaled films without Co enrichment, we prepared a 2-nm CoSi film capped in situ with a Si sacrificial layer of about 2 nm. In this case, as shown in Fig. 3b, the CoSi film stoichiometry is uniformly preserved. The different compositions also translate to a different transport behavior, as revealed by the Hall measurements of the uncapped and capped 2-nm films reported in Fig. 3c and 3d, respectively. The Hall resistivity of the Co-rich sample shows a strong anomalous behavior, consistent with literature data of pure Co36. In the capped stoichiometric film, for comparison, the Hall signal is linear at all temperatures, in good accordance with the data measured in thicker films (see Supplementary Materials), where the oxide layer is present but has a negligible impact on the overall film behavior. From these Hall measurements, a mobility of 0.17 cm2/Vs and carrier concentration of 6.5 × 1022 cm−3 at room temperature is calculated for the capped 2-nm sample, compared to 0.07 cm2/Vs and 2.5 × 1023 cm−3 for the uncapped 2-nm sample.

Fig. 3
figure 3

EDX cuts and Hall resistivity for the uncapped and capped 2-nm samples. (a) EDX cut of the 2.0-nm film. A Co excess is observed in the film due to the formation of native oxide on top which depletes oxygen from the CoSi layer. (b) EDX cut of the 2.0-nm film (capped). The Si-cap prevents the oxidation and keeps the right stoichiometry in the deposited film. (c) Hall resistivity of the 2.0-nm uncapped sample. The Co-excess is responsible for the observed anomalous contribution to the Hall signal. (d) Hall resistivity of the 2.0-nm capped sample. The Hall signal is linear and consistent with the ones of thicker films, where the impact of the oxide on the composition is negligible (see Supplementary Materials).

Full size image

We may conclude from these studies that the increased resistivity to 410 µΩcm, as well as the sharp increase of carrier concentration, is, in part, due to this spurious Co phase in the 2-nm-film from formation of a native SiOx surface layer. Thicker CoSi films, as well as Si-capped samples, do not exhibit this behavior and indeed exhibit linear Hall signal. Another explanation may be the influence of the surface properties, with and without the Si cap, as surface scattering increases for scaled film dimensions.

Scaling behavior and anomalous magnetotransport

The resistivity versus thickness for the amorphous and textured samples are shown in Fig. 4a. Due to the surface oxide layers, we show this data with 0.5 nm error bars, so that the upper thickness range corresponds to the nominal thickness as measured by RBS. The reason is that we expect the native oxide to strictly reduce the effective CoSi thickness. For comparison, resistivity of a series of polycrystalline (textured) CoSi thin-film samples with a thickness in the range of 3 to 50 nm, are also shown. We observe a weakly decreasing trend in resistivity for decreasing thickness down to ~ 4 nm, in marked contrast to the textured films where the resistivity increases with decreasing thickness, in particular below 10 nm. The amorphous films are further shown in semi-logarithmic scale in Fig. 4b, including the Si-capped 2-nm sample.

Fig. 4
figure 4

Scaling trends for resistivity and magnetoresistance as a function of film thickness. (a) Resistivity scaling model for the amorphous CoSi and comparison with textured films. The error bars indicate a ± 0.5 nm uncertainty in thickness due to oxidation, where the upper thickness estimate correlates with the measured values using RBS (black dots represent the center values and not the RBS-normalized ones). (b) Resistivity scaling including the Si-capped sample. The value of the resistivity does not vary significantly from the value measured in the uncapped sample (RBS thickness values are used for the normalization). (c) Magnetoresistance as a function of the thickness, measured at T = 2 K and B = 9 T. The data point of the capped sample reveals a clear increasing trend for the MR in ultra-scaled films. Green dots report the scaling trend of textured films, which is in contrast with the observed increase in MR in amorphous films.

Full size image

Generally, there are two causes to an observed reduction of resistivity in thin films upon scaling the film thickness. (1) A change of physical properties, such as phase and composition, as the film thickness is reduced could lead to reduced resistivity. In the case of the studied CoSi films, two arguments speak against this explanation. Firstly, the comprehensive investigation by means of STEM, EDX, RBS, XPS and GIXRD analysis methods do not reveal any drift in physical properties except for the 2-nm film, as discussed above. Therefore, we exclude such a drift to within our measurement uncertainty. Secondly, the observed composition drift in the 2-nm film due to Co-enrichment evidently results in an increased measured resistivity, rather than reduced. Therefore, if a similar Co-enrichment is present also in the thicker films, though at levels below what our measurement tools can detect, we expect this to lead to an increase, rather than reduction, of measured CoSi resistivity. In addition, charge carrier concentration estimation from Hall measurements showed a reduction of the carrier concentration down to 3.2 nm thickness, which is not consistent with metallic enrichment. (2) In a different scenario, charge transport may be affected by the presence of non-bulk contributions, such as surface states or interfacial layers. In this case, the resistivity is expected to be progressively dominated by such contributions upon scaling down the film thickness. This is the transport model that has been employed in theoretical studies of CoSi interconnects based on topologically protected surface states13.

Although the understanding of topological surface states in amorphous materials is only emerging, literature suggests that even randomly assembled amorphous matter has patches of broken symmetry and corresponding surface states21. Therefore, when the size of localized surface states compares to hopping (or scattering) distances, they can contribute to conductance. However, the existence of surface states on two opposing surfaces, respectively, requires a certain minimum thickness of the conductor on the order of a few nanometers. Below this thickness, the two surfaces begin to communicate, meaning that overall measured resistivity forms a valley with a minimum. Such a decaying surface transport model is empirically fitted to the amorphous CoSi data in Fig. 4 to show that this kind of transport model is theoretically consistent with our measurement (more details can be found in the Supplementary Materials).

Finally, we examine the transverse magnetoresistance (MR) of the amorphous CoSi films, at 2 K and 9 T, as shown in Fig. 4c. For thicker samples (> 4 nm), MR approximately follows the observed mobility scaling trend in Fig. 2c, given the known relationship between mobility and MR37,38. Reducing the film thickness further, however, the MR keeps increasing while the mobility is reduced. The dashed trace in Fig. 4c highlights the empirical trend among stochiometric CoSi samples, where the capped 2-nm CoSi film substitutes for the off-stochiometric uncapped 2-nm. Following this apparent trend, a continuous increase (up to 7%) in MR is observed for reduced film thickness, even as the Hall mobility drops from 0.45 to 0.17 cm2/Vs. This MR behavior is only observed in the amorphous phase of the grown CoSi films, since the textured films show a decrease in MR as the thickness is reduced from 10 to 3 nm (see Fig. 4c). These unconventional magnetotransport properties are consistent with various possible interpretations, such as a drift in the balance between charge carrier types39, or more exotic effects related to non-trivial topology17. Qualitatively, both the MR and resistivity scaling properties may be explained by a picture where transport in scaled films is increasingly dominated by a surface transport layer which exhibits higher carrier mobility and stronger response to magnetic fields than the bulk of the film40.

Conclusions

In summary, this work reports a systematic study of the thickness dependence of the resistivity and the magnetotransport properties of textured and amorphous stochiometric CoSi thin films down to 2 nm thickness. We observe two unusual transport properties. Firstly, we observe a reduction of resistivity in amorphous CoSi films as the thickness is scaled down to 3.2 nm, correlated with an increased Hall mobility of ~ 100% and reduced carrier concentration. This is in contrast to textured films, which show a large resistivity increase. Secondly, by further decreasing the thickness from 3.2 to 2 nm we observe a rather sharp increase of magnetoresistance from 2.2 to 7%, while mobility is simultaneously reduced by more than 50%. We have here attempted to exclude trivial explanations for these observations, such as stochiometric and phase drifts, though this cannot be done with certainty. The results are signs of transport phenomena in amorphous phases of topological semimetal crystals, including surface layer transport, that are not yet understood, and merit further investigation. From an applications perspective are amorphous metallic films with strongly suppressed resistivity scaling below 10 nm thickness, as demonstrated for CoSi in this work, highly interesting as scaled CMOS interconnects. While the demonstrated resistivity values are too large to compete with Cu interconnects, future work should therefore aim to realize thin films with similar scaling trends and reduced resistivity of < 50 µΩ cm at dimensions below 10 nm.

Methods

Thin film growth and characterization

Prior to insertion in vacuum, (001)-oriented, epi-polished MgO substrates (size 10 mm × 10 mm × 1 mm) were ultrasonically cleaned for 5 min in isopropyl alcohol. After that, the MgO substrates were outgassed at about 450 °C for 30 min under ultra-high-vacuum conditions. The base pressure of the MBE system was around 10−10 mbar, which increased to 10−9 mbar during film growth. Co and Si elements were deposited from electron-beam sources at a deposition rate of ≈ 0.1 Å/s. The Co and Si fluxes were calibrated prior to MBE deposition via a quartz crystal microbalance and maintained constant during MBE deposition using quadrupole mass spectrometers coupled to the electron-beam sources. CoSi thin films were deposited following a layer-by-layer growth process by opening/closing the metal shutters in front of the electron-beam sources. The MBE growth temperature was monitored via a type K thermocouple after calibration with a pyrometer. After MBE growth, the structural characterization of the CoSi thin films were done via atomic force microscopy, grazing incident X-ray diffraction, synchrotron pole figures, and scanning transmission electron microscopy. The preparation of cross sectional lamellas for transmission electron microscopy (TEM) was done by means of focused ion beam (FIB) milling. In order to mitigate the damage induced by FIB preparation, a protective Al2O3 layer (about 40 nm) grown by atomic layer deposition was added onto the CoSi films. For chemical characterization, Rutherford backscattering spectroscopy, energy dispersive X-ray analysis, X-ray photoelectron spectroscopy and grazing-incident X-ray diffraction were employed. Additional details can be found in the Supporting Information of our related publication14.

Electrical transport measurements

The original CoSi thin films grown on a MgO substrate were sliced into Hall bars with a size of about 10 mm × 1.5 mm × 1 mm using a diamond cut tool. Metallic contacts for 4-point probe resistance and Hall effect measurements were prepared via wire bonding. The current leads were covered with silver paste in order to provide better uniformity of the current flow. The input current was set to 0.05 mA. The resistivity, MR and Hall resistance were characterized via a physical properties measurement system (PPMS) in the range of 2–300 K and applied magnetic fields up to ± 9 T. The PPMS system was externally connected to two lock-in amplifiers for the electrical measurements (Zurich Instruments MFLI 500 kHz/5 MHz). The measurements were taken applying a constant current at ~ 113 Hz. The analysis of the Hall effect data was carried out after removal of the symmetric Hall contribution, to account for possible misalignment of the voltage probes. For the analysis of the linear Hall effect observed in the capped sample, we employed a Savitzky-Golay filter to effectively mitigate measurement noise. Carrier density and mobility were extracted by fitting the Hall data in the high-field limit (no anomalous contribution) with a single-carrier band model.