A new multi-objective-stochastic framework for reconfiguration and wind energy resource allocation in distribution network incorporating improved dandelion optimizer and uncertainty

Abstract

Improving the reliability and power quality of unbalanced distribution networks is crucial for ensuring consistent and reliable electricity supply. In this research, multi-objective optimization of unbalanced distribution networks reconfiguration integrated with wind turbine allocation (MORWTA) is implemented considering uncertainties of networks load, and also wind power incorporating a stochastic framework. The multi-objective function is defined by the minimization of power loss, voltage sag (VS), total harmonic distortion (THD), voltage unbalance (VU), energy not-supplied (ENS), system average interruption frequency index (SAIFI), system average interruption duration index (SAIDI), and momentary average interruption frequency (MAIFI). A new improved dandelion optimizer (IDO) with adaptive inertia weight is recommended to counteract premature convergence to identify decision variables, including the optimal network configuration through opened switches and the best location and size of wind turbines in the networks. The stochastic problem is modeled using the 2m + 1 point estimate method (PEM) combined with K-means clustering, taking into account the mentioned uncertainties. The proposed stochastic methodology is implemented on three modified 33-bus, and unbalanced 25-, and 37-bus distribution networks. The results demonstrated that the MORWTA enhanced all study objectives in comparison to the base networks. The results also demonstrated that the IDO had superior capability to solve the deterministic- and stochastic-MORWTA in comparison to the conventional DO, grey wolf optimizer (GWO), particle swarm optimization (PSO), and arithmetic optimization algorithm (AOA) in terms of achieving greater objective value. Moreover, the results demonstrated that when the stochastic-MORWTA model is considered, the power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI are increased by 18.35%, 9.07%, 10.43%, 12.46%, 11.90%, 9.28%, 12.16% and 14.36%, respectively for 25-bus network, and also these objectives are increased by 12.21%, 10.64%, 12.37%, 9.82%, 14.30%, 12.65%, 12.63% and 13.89%, respectively for 37-bus network compared to the deterministic-MORWTA model, which is related to the defined uncertainty patterns.

Introduction

Motivation and background

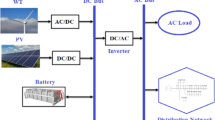
The issue that constantly occupies the focus of network administrators is the growing need to enhance network efficiency due to the proliferation of industrial nodes and distribution networks^1,2. Electric energy distribution companies incur substantial expenses as a result of consequences such as rising system losses and unwelcome voltage reductions resulting from the growth of electric demands^3,4. Reconfiguration of the distribution network and optimal resource allocation for distributed generation (DG) are approaches and tools that can be used to partially achieve the aforementioned objectives while spending the least amount of money^5,6. Wind energy sources are one of the renewable sources of DG⁷. Compared to other renewable energy sources, wind utilization has significantly increased. As a source of electric power production, wind energy sources have been integrated into power systems so that they are implemented in the optimal location and with the largest possible size in the installation network^8,9 to maximize their benefits. Obtaining the optimal network configuration while confronting the difficulty of network reconfiguration is necessary to modify the path of load flow and improve network efficiency¹⁰. Moreover, the optimal and concurrent use of both techniques in distribution networks can successfully increase the network's efficiency. This necessitates the use of a potent optimization technique with high search and estimation capabilities, as well as optimally describing the decision variables of each approach and establishing a comprehensive objective function while taking into consideration a variety of important objectives^11,12. In addition, both the production of wind turbines and the demand requirements of the network are uncertain¹³. Due to the complexity of load flow computations caused by these distribution network uncertainties, it is necessary to use appropriate probabilistic instruments to calculate load flow and determine the optimal decision variables in light of the objective function established for network configuration and wind resource installation^14,15.

Literature and research gaps

Numerous studies have addressed the problems of DG resource allocation and distribution network reconfiguration. Traditional methods, particularly heuristic methods, have demonstrated significant computational efficacy when addressing power optimization problems, despite their limited ability to reach global solutions. In recent years, meta-heuristic techniques have become increasingly popular for optimizing power systems. On the other hand, meta-heuristic algorithms can discover comprehensive solutions. Extremely complex real-world problems, which are typically addressed with numerical optimization techniques, can be addressed with meta-heuristic optimization techniques. In¹⁶, a genetic algorithm (GA) and PSO are used to optimize the network reconfiguration of a distribution network to enhance reliability and reduce losses. In¹⁷, discrete teaching–learning-based optimization (DTLBO) is employed to reconfigure the network to minimize the losses and enhance the voltage condition. To reduce losses and improve the network's voltage profile,¹⁸ constructs a multi-objective reconfiguration strategy for the distribution network. A method for reconfiguring a distribution network using a hybrid honey bee colony (HHBC) to reduce losses and unbalance is presented in¹⁹. In²⁰, the reconfiguration problem is addressed using a discrete-learning optimization technique to minimize losses and voltage condition enhancement. An improved GA is used in²¹, to reconfigure the distribution network while minimizing losses. For network reconfiguration, a branch exchange heuristic and a method are employed in²², where they are combined with other methods such as evolutionary meta-heuristics and cluster evaluation. In²³, a stochastic model based on Monte Carlo simulation (MCS) is applied to reconfigure the distribution network to reduce power losses and voltage sags as well as to improve reliability while taking into account load uncertainty. This is done by using an unscented transformation with an iterative mountaineering team-based optimization (IMTBO). A chaotic golden flower algorithm (CGFA) for the reconfiguration problem is presented in²⁴. In²⁵, a method for reconfiguring a distribution network is performed while also taking DG allocation into account using binary PSO (BPSO). Utilizing the MCS, the uncertainties of load fluctuation before network reconfiguration are also taken into account to reduce line loss costs and unsupplied energy. In²⁶, the usage of a gray wolf optimization (GWO) is evaluated to minimize the system's power loss and generate a better voltage profile while meeting the operating limits specified by various operational situations. According to²⁷, following an extreme event, the network is reconfigured using graph theory, and the least-cost option is found by using a minimum spreading tree and a radial topology that connects all grid users. In²⁸, two forms of optimal reconfiguration are applied to reduce losses, improving the voltage profile by integrating the simulated annealing technique and modified PSO, and attempting to find an optimal solution while taking time-dependent alterations into account. The use of sectionalized switches, DG, and optimal reconfiguration of networks in tandem with improved PSO (IPSO) reduces switch costs; increases switch reliability, minimize losses, and improve voltage profiles, according to²⁹. By using the multi-objective enhanced black widow optimization (MOIBWO), the integration of DG installation and network reconfiguration is described in³⁰ to decrease losses, voltage variation, and emission of carbon. In³¹, an improved golden jackal optimization (IGJO) is applied for optimal planning of WTs and electric vehicle parking lots in a distribution network to achieve the lowest possible annual costs of losses, wind energy, battery degradation cost, and network voltage changes. An improved equilibrium optimization algorithm (IEOA) is used in³² to implement the sitting and sizing of wind turbines (WT) in electrical grid to reduce losses, and voltage condition and reliability improvement. The ideal positions are established by minimizing the placement index using the distribution load flow, whereas the optimum amount of WT is investigated using a beluga whale optimization algorithm (BWOA) in the optimization framework in³³. In³⁴, the utilization of PV and WT systems is investigated, with the identification of the best size and position of these resources to reduce losses and enhance voltage profile. A modified analytical energy approach is described in³⁵ employing PSO and GA to locate energy resources in distribution networks while decreasing losses and yearly energy loss. In³⁶, a multi-objective artificial electric field algorithm (MOAEFA) is used to determine the best solutions utilizing a fuzzy decision-making technique for the WT placement in the network to reduce losses and voltage variations. In³⁷, a—chaotic sequence spotted hyena optimizer (SHO) is used to propose a deterministic and probabilistic allocation of WTs in the networks to minimize losses and enhance voltage characteristics and stability. A moth-flame optimization (MFO) technique is used in³⁸ to perform an optimal multi-criteria reconfiguration of distribution networks with wind sources to minimize losses and enhancing the reliability. In³⁹, distribution network WT allocation is assessed while attempting to minimize flicker output. In⁴⁰, the network reconfiguration is studied to improve the power quality indices such as VS, VU and THD improvement. In⁴¹, the allocation of various energy resources is studied to determine the best functioning of a grid-connected microgrid while taking into account the energy resource uncertainties and applying the MCS. According to⁴², the best way to operate virtual power plants in a reconfigurable network is to use MINLP to solve a potential contingency problem in the system's lines. An artificial ecosystem-based optimization with power and energy loss minimization is provided in⁴³ and improved utilizing opposition-based learning. The reconfiguration of a network that incorporates energy resources for minimizing the losses and enhance the voltage profile is studied in⁴⁴. A northern goshawk optimization (NGO)-based allocation of WTs in distribution networks is described in⁴⁵ to determine the WT's optimal size and position in order to minimize casualties.

The items that follow are a list of research voids in the literature:

• Several researchers utilized reconfiguration to take advantage of the network and improve its performance, according to a literature review. In some instances, they have utilized the optimal distribution of DG resources, particularly wind energy resources, to achieve this objective. In recent years, numerous studies have been published under the title "the method of simultaneous use of reconfiguration and resource allocation in distribution networks." However, simultaneous reconfiguration with wind energy sources to improve network performance has received less attention. In contrast, previous research for the hybrid-simultaneous reconfiguration-WT allocation approach did not adequately investigate the existence of uncertainty in the wind turbine power and network demand.

• The remaining references, except Refs.^23,26,32,41, did not examine how uncertainty affected the solution of the reconfiguration problem or the best site and size of WTs in the network. The majority of the uncertainty is associated with the use of the conventional Monte Carlo simulation (MCS). Due to the high scenario definition, this method takes a long time, has a high computing cost, and uses a wide number of samples from the probabilistic input space. When reducing the scenarios in the Monte Carlo approach, the clustering-based algorithm may result in inaccuracies when determining the output variables mean and standard deviation. While the number of clusters increases together with the elimination of these mistakes, increasing the computation time^46,47.

• The choice variables of the optimization problem have also been determined using meta-heuristic techniques, which work better than analytical and heuristic methods in terms of finding the global solution. However, it has been found that because of the complexity of the simultaneous hybrid reconfiguration and wind turbine allocation problem, it is preferable to enhance the efficiency of these algorithms by employing unique techniques to avoid premature convergence, which is presented in quantitative studies in the literature.

Contributions

The paper's contributions are summarized according to the identified research gaps in the literature:

• This study implements a coordinated solving process for multi-objective framework of distribution network reconfiguration and wind turbine allocation (MORWTA) in an unbalanced distribution network for minimizing the losses and increase quality of the power and reliability. Energy not-supplied (ENS), system average interruption frequency index (SAIFI), system average interruption duration index (SAIDI), and momentary average interruption frequency index (MAIFI) are defined as reliability indices, and voltage sag (VS), voltage unbalance (VU), and THD are power quality indices in the comprehensive multi-objective function with eight important objectives in the operation of the network.

• The stochastic multi-objective solving process considering uncertainty is implemented on three modified 33-bus, and unbalanced 25-, and 37-bus distribution networks. With the use of PEM, this method accurately calculates the mean value and standard deviation while dependably assessing its statistical qualities, and it has lower processing costs than the Monte Carlo method^48,49.

• The problem is optimized and the best choice variables are discovered using an improved dandelion optimizer (IDO). In order to achieve better goals, the IDO's superiority over the traditional DO, GWO, PSO, and arithmetic optimization algorithm (AOA) is also evaluated. The traditional DO algorithm⁵⁰is used in this research because of its straightforward computational structure and simplicity for comprehension, but also because its performance in the simultaneous-hybrid multi-objective problem has been enhanced in order to prevent getting stuck in Local the best through an adaptive inertia weight⁵¹. This is because, based on the no-free launch (NFL) theory, a meta-heuristic algorithm cannot be successful in solving optimization problems.

Structure of the paper

The rest of the study is organized as follows. The comprehensive objective function specified in this research is included in "Problem formulation"' section statement of the problem, together with any relevant restrictions. The stochastic model to model the uncertainties is offered in "Stochastic model" section. "Proposed meta-heuristic optimizer" section describes the suggested optimizer, how to improve it, and how to use it for the problem solving. In "Results and discussion" section, the simulation outcomes of the suggested approach using deterministic and stochastic methods are shown and contrasted. "model validation with previous studies" section presents a comparison with prior research, and "Conclusion" section concludes with a summary of the research's primary conclusions.

Problem Formulation

Multi-objective function

The multi-objective function of the coordinated solving process based on the MORWTA considering eight important objectives is defined as minimizing the objectives of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI using the weighted coefficient technique as follows:

$$\begin{aligned} {\mathcal{F}} & = \varpi _{1} \times \frac{{P_{{Loss}} }}{{P_{{Loss,max}} }} + \varpi _{2} \times \frac{{V_{{sag}} }}{{V_{{sag,max}} }} + \varpi _{3} \times \frac{{THD}}{{THD_{{max}} }} + \varpi _{4} \times \frac{{V_{{UN}} }}{{V_{{UNmax}} }} \\ & \quad + \varpi _{5} \times \frac{{ENS}}{{ENS_{{\max }} }} + \varpi _{6} \times \frac{{SAIFI}}{{SAIFI_{{\max }} }} + \varpi _{7} \times \frac{{SAIDI}}{{SAIDI_{{\max }} }} + \varpi _{8} \times \frac{{MAIFI}}{{MAIFI_{{\max }} }} \\ \end{aligned}$$

(1)

where ${P}_{Loss,max}$ is maximum value of network losses, ${V}_{sag,max}$ demonstrates the maximum of voltage sags, ${THD}_{max}$ is the highest value of THD, ${ENS}_{max}$,${SAIFI}_{max}$, ${SAIDI}_{max}$, and ${MAIFI}_{max}$ are maximum value of $ENS$, $SAIFI$, $SAIDI$, $MAIFI$ indices. The values mentioned above are derived from the network's load flow in condition of base network before reconfiguration and WT allocation. Furthermore, it is essential that the absolute values of all weight coefficients (${\varpi }_{1}, {\varpi }_{2}, {\varpi }_{3}, {\varpi }_{4}, {\varpi }_{5}, {\varpi }_{6}, {\varpi }_{7}and {\varpi }_{8}$) collectively sum up to 1. In this study, the problem is simulated for a set of different weight coefficients. The authors have come to the conclusion that for a more accurate compromise and a better solution, the coefficients should be equally distributed among all objectives. Therefore, considering that the absolute value of the set of all coefficients should be equal to 1, the value of the weight coefficient of each target is considered equal to 0.125.

Power losses

Minimizing network line losses is a prevalent objective in network operation. The aim of decreasing active power losses is outlined as follows^10,39:

$$P_{{Loss}} = Re\left( {\mathop \sum \limits_{{m = 1}}^{l} \left( {\mathop \sum \limits_{{j = a}}^{c} \left( {{\mathcal{E}}_{j} \left( p \right) - {\mathcal{E}}_{j} \left( k \right)CUR^{*} \left( m \right)} \right)} \right)} \right)$$

(2)

where let l represent the overall count of lines. Let ${\mathcal{E}}_{j} \left( p \right)$ denotes voltage at bus p, and phase j, and ${\mathcal{E}}_{j} \left( k \right)$ is voltage at bus k, and phase j, ddditionally, let $CUR^{*} \left( m \right)$ represent the complex conjugate of the current flowing through the mth line between bus p and bus k. The user provides phases a, b, and c.

${\mathcal{E}}_{j} \left( p \right) \;denote\; the \;voltage \;at \;bus \;p \;and \;phase\; j,\; and \;{\mathcal{E}}_{j} \left( k \right) \;represent\; the \;voltage \;at\; bus \;k \;and\; phase\; j.$ Additionally, let ${CUR}^{*}(m)$ represent the complex conjugate of the current flowing through the mth line between bus p and bus k. The user provides phases a, b, and c.

Voltage sag

Voltage sag (VS) is determined by quantifying the remaining voltage present in a bus system during a VS event. This research aims to enhance the VS of the entire network by raising the mean VS across all buses^10,39,40,55.

$${V}_{ SAG}=\frac{1}{m }{\sum }_{j=1}^{m}\frac{1}{n } {\sum }_{i=1}^{n}{\mathcal{E}}_{ i}^{ j}$$

(3)

The objective is to determine the voltage at bus i during fault scenarios at bus j (${\mathcal{E}}_{ i}^{ j})$. where, i is the number of buses and the variable j shows the potential faults number. Additionally, V_SAG denotes the average voltage of the bus under VS conditions. The analysis of VS is conducted through the execution of network fault analysis. The fault current resulting from the occurrence of a defect in bus p can be mathematically represented as stated in reference⁴⁰.

$${CUR}_{p\left(Fault\right)}^{a,b,c}=\frac{{Adm}_{F}^{a,b,c}{\mathcal{E}}_{p(0)}^{a,b,c}}{(UnM+{Imp}_{pp}^{a,b,c}{Y}_{F}^{a,b,c})}$$

(4)

The definition of voltage drop in buses is as follows:

$${V}_{Bus(F)}^{a,b,c}={Imp}_{pp}^{a,b,c}{CUR}_{Bus(F)}^{a,b,c}$$

(5)

The variable CUR_p(Fault) represents the p component of the bus injection current vector, ${Imp}_{BUS}^{a,b,c}, {Adm}_{F}^{a,b,c}, and {Adm}_{F}^{a,b,c}$ are the impedance matrix of the three phases of the network, the admittance matrix considering the fault, the bus voltage wattage in all three phases of the grid, respectively. $UnM$ is the unit matrix in the formulation.

The VS refers to the remaining voltage present in the bus system during a VS sag event. This study exclusively focuses on voltage dip occurrences just under fault circumstances. The computation of the residual voltage at the bus is determined using the following equation⁴⁰:

$${\mathcal{E}}_{sag}^{a,b,c}={\mathcal{E}}_{Bus(0)}^{a,b,c}-{\mathcal{E}}_{Bus(F)}^{a,b,c}$$

(6)

Total harmonic distortion

The calculation of total harmonic distortion (THD) minimization involves determining the overall level of harmonic distortion present in the bus voltage, as described in reference^10,40.

$$\text{\%}{V}_{THD,i}=\frac{{\mathcal{E}}_{d,i}}{{\mathcal{E}}_{rms,i}}\times 100, i=\text{1,2},3,...,n$$

(7)

$${V}_{rms,i}=\sqrt{{\mathcal{E}}_{1,i}^{2}+{\mathcal{E}}_{d,i}^{2}}$$

(8)

$${\mathcal{E}}_{d,i}=\sqrt{\sum_{h=2}^{m}{\mathcal{E}}_{h,i}^{2}}$$

(9)

where ${VOL}_{d,i}$ is the distortion component of the bus voltage. In order to mitigate voltage harmonic distortion, efforts are made to limit the maximum THD value over all bus voltages.

Voltage unbalance

The presence of an unbalanced network can be attributed to load imbalances. The calculation of the network imbalance value in this study involves the measurement of voltage asymmetry at the specified buses^10,40.

$$V_{{{ }UNB}} = \frac{1}{{n{ }}}\mathop \sum \limits_{i = 1}^{n} \left( {\mathop \sum \limits_{j = a}^{c} \left( {100\frac{{\left| {{\mathcal{E}}{ }_{{ - { },{ }i}}^{ } } \right|}}{{\left| {{\mathcal{E}}_{{ + { },i}}^{ } } \right|}}} \right){ }} \right)$$

(10)

where $\mathcal{E}$_{+, i} represents the positive-sequence voltage of bus i, and $\mathcal{E}$_-,i is the negative-sequence voltage at the bus i.

Energy not-supplied

The interruption of grid lines can result in a partial disruption of network load, leading to a phenomenon known as energy not supplied (ENS) for network consumers. The dependability index of ENS is derived by taking into account the outage rate of the grid lines, the average duration of each outage, and the quantity of lost load, as outlined in references^23,38:

$$ENS = \sum\limits_{i}^{{N_{{br}} }} {\left( {{\mathcal{L}}_{i} \times \vartheta _{i} \times \mho _{i} } \right)}$$

(11)

The rate of annual outage of the transmission line (${\mathcal{L}}_{i})$ pertains to the mean duration of each outage experienced on a certain line (${\vartheta }_{i})$. The variable ${N}_{br}$ represents the overall number of lines, while ${\mho }_{i}$ denotes the demand at bus i.

SAIFI

The SAIFI^9,14,16 represents the annual average frequency of power supply interruptions experienced by a client. The calculation is determined using the following mathematical expression.

$$SAIFI=\frac{\sum_{i\in \rho }{\tau }_{i}}{\beta }$$

(12)

Let denote the count of customers impacted by each incidence as ${\tau }_{i}$, the overall count of customers as $\beta$, and the set of all outage occurrences in the distribution network as $\rho$.

SAIDI

The SAIDI^9,14 quantifies the mean duration of energy supply disconnection experienced by customers for a year. The calculation is determined using the subsequent expression:

$$SAIDI=\frac{\sum_{i\in \rho }{({r}_{i}\tau }_{i})}{\beta }$$

(13)

where ${r}_{i}$ represents the restoration time for each incident i.

MAIFI

In the assessment of system reliability, the MAIFI^9,14 takes into account the occurrence of temporary interruptions. The metric is denoted as interruptions per client per year. The MAIFI is a metric that quantifies the total number of short-term disruptions experienced by consumers, divided by the overall count of customers.

$$MAIFI=\frac{\sum_{i\in \rho }{{\tau }_{pout,i}\tau }_{sh,i}}{\beta }$$

(14)

where ${\tau }_{pout,i}$ denotes the quantity of short-term power outages, while ${\tau }_{sh,i}$ indicates the number of users affected by each individual short-term power outage within the given statistical timeframe.

Constraints

The optimizing the e multi-objective function has to be performed while considering the limitations outlined below. The limitations or restrictions of the problem are outlined in the following manner^10,38,39,40:

Power balance

$${P}_{Post}+{\sum }_{i=1}^{{N}_{WT}}{P}_{WT}(i)={\sum }_{i=1}^{{N}_{br}}{P}_{loss}(i)+{\sum }_{q=1}^{{N}_{bus}}Pd(q)$$

(15)

$${Q}_{Post}+{\sum }_{i=1}^{{N}_{WT}}{Q}_{WT}(i)={\sum }_{i=1}^{{N}_{br}}{Q}_{loss}(i)+{\sum }_{q=1}^{{N}_{bus}}Qd(q)$$

(16)

where ${P}_{Post}$, ${P}_{WT}$, ${P}_{loss}$ and $Pd$ indicate the active power supplied by the post, the active power provided to the network via the wind turbine, active losses of the line, and active power demand of the network demand, respectively. The variables ${Q}_{Post}$, ${Q}_{WT}$, ${Q}_{loss}$ and $Qd$ denote the reactive power obtained from the post, the reactive power delivered into the grid by the wind turbine, the reactive power losses in the transmission line, and the reactive power requirement, respectively. The variable ${N}_{WT}$ denotes the number of hybrid systems, which, in the context of this study, is equal to 1.

Bus voltage

It is imperative that the voltage levels of the buses are maintained within a predetermined threshold.

$${\mathcal{E}}^{ min}\le {\mathcal{E}}_{pi}\le {\mathcal{E}}^{ max}$$

(17)

Lines current

It is imperative that the current flowing to the network does not beyond the maximum permissible current of the grid lines.

$${CUR}_{pl}\le {CUR}_{ pl}^{ max}$$

(18)

Voltage unbalance

The electrical potential difference the set value for bus imbalance should not be exceeded.

$$\frac{\left|{\mathcal{E}}_{+ , i}^{ }\right|}{\left|{\mathcal{E}}_{- ,i}^{ }\right|}\le {V}_{ unb}^{ max} , i=\text{1,2},3,\dots ,n$$

(19)

Voltage sag

The extent of VS in the network should not exceed the allowable threshold as defined by the distribution network standards.

$${V}_{ sag ,av}^{ }\ge {V}_{ sag}^{ min}$$

(20)

Radiality

To guarantee the radial topology of the distribution network, no loops should be formed, and also every bus of the system should be connected to a substation point which is described fully in Ref.²¹.

WT power

$${P}_{WT}^{Min}\le {P}_{WT}\le {P}_{WT}^{Max}$$

(21)

where ${P}_{WG}^{Min}$ and ${P}_{WG}^{Max}$ represents the lower and upper limit for wind turbine power generation.

For each of the constraints (15) to (21), a penalty, i.e. a very large number, is embedded in the objective function. During the simulation, if any of the constraints violates the allowed value or the logic governing it, a penalty is added to the objective function and the solution becomes impractical, and infeasible. In this way, unacceptable solutions are removed.

Power flow analysis

Forward–backward power flow is employed for research on distribution networks. Every line is represented using series impedance. A forward–backward sweeping method (FBSM) that iterates performs the power flow in order to obtain convergence and determine line and bus voltages^10,12,40. The FBSM consists of two fundamental phases that are simple to comprehend and apply across all radial networks. These two stages function as a ring. In the FBSM, the bus voltage is set to 1 p.u, and the current for line, and also voltage of each buses are simply determined. The voltage is adjusted through the feeder's final position. As previously indicated, the voltage has been set to 1 p.u to acquire the bus flow. This current generates a fresh voltage at the end of the feeder. The processes for power flow are outlined below: The voltage three-phase across all phases is regarded equivalent to the slack bus voltage. Each phase’s load is adjusted by a positive sequence and a 120-degree phase variance. In this stage, the forward–backward power flow is completed. Begin at the ending bus and work your way to the sending bus, updating the upstream current of lines to ensure that the upstream current of line corresponds to the all downstream lines current the fact that start at the ending bus of upstream branch, and this stage gets repeated until the current of branch is identified. Next, the forward load flow is carried out. The calculation moves from the sending bus to the ending bus of the network to determine the voltage at the ending bus of each line, denoted as ${V}_{down}^{a,b,c}={V}_{up}^{a,b,c}-{Z}_{up,down}^{a,b,c}{I}_{up,down}^{a,b,c}$. Here, ${V}_{down}^{a, b, c}$ represents the voltage of each phase at the load side (referred to as the lower bus), ${V}_{up}^{a, b, c}$ refers to the phase voltage of the sending bus in the line between the up and down buses, ${Z}_{up, down}^{a, b, c}$ denotes the branch impedance, and ${I}_{up, down}^{a, b, c}$ signifies the current in the line between the up and down buses.

The forward load flow process continues until the voltages of all buses are determined. The forward–backward load flow steps are repeated until the system reaches convergence. This method calculates the voltages at all buses at the main frequency. The harmonic flow problem is addressed using direct harmonic analysis. Harmonic-generating loads are represented by their Norton equivalents, while the lines and linear loads are modeled by their respective admittances at harmonic frequencies.

To maintain the radial structure of the network, the branch exchange method is applied. In this method, when a line is closed, another line must be opened to prevent the formation of loops and ensure the network remains radial. The advantage of this approach is that it automatically ensures the network's radiality without the need for additional computations or algorithms to detect the network's configuration.

Stochastic model

Various schemes can be implemented within the PEM approach⁴⁸, each characterized by a different number of deterministic methodologies to solve. Specifically, the schemes discussed in this paper require 2m + 1 deterministic runs, where m represents the number of random input variables. Additionally, 2m or 4m + 1 runs can be used. The more deterministic methodologies run, the more accurate the estimation of the statistical moments of the output random variables. However, an increase in the number of runs necessitates more information about the input random variables. For instance, in the 4m + 1 scheme, it is necessary to know up to the eighth standard central moment of the input random variables, resulting in a higher computational burden. Nevertheless, the PEM approach offers a significant reduction in computational efforts compared to the MCS method. Therefore, this paper uses the 2m + 1 PEM method to model uncertainties with fewer scenario definitions, striking a balance between the accuracy of estimating statistical moments of the output random variables and computational cost⁴⁹.

The stochastic solving process for multi-objective optimization of network reconfiguration and WT sitting and sizing in a distribution network is conducted considering uncertainties in WT generation and network load demand. This study utilizes a 2m + 1 PEM in conjunction with the IDO method to address the challenges of distribution network layout and wind turbine allocation within an uncertain environment. The primary objective is to determine the $output\; random \;variable\; \left( {ORV} \right)$ uncertainty level by utilizing the $input\; random\; variable \;\left( {IRV} \right)$ central moments at k specific locations for each variable. These points are commonly referred to as concentrations and are assessed using various mathematical functions to establish a relationship between IRVs and ORVs. This approach offers the benefit of precisely calculating the mean and std through the use of the PEM while also reliably assessing statistical features. The 2m + 1 approach often employs three concentration sites for each random variable, with one of these sites positioned at its mean^48,49.

Adhering to the principles of the PEM methodology, the ORV as Y is evaluated 3 times for each IRV, while the mean value is used for the remaining input random variables. ${Y}_{i,m}$ denotes the array of ORVs linked to the mth point of concentration related to the ith IRV, its computation involves the following procedure

$${Y}_{i,m}=F({\mu }_{1},\dots ,{p}_{i,m},\dots ,{\mu }_{n})$$

(22)

where ${\mu }_{1},\dots {\mu }_{n}$ correspond to the means of the IRVs, excluding the ith input variable. The concentration point corresponding to the mth instance of the ith IRV is denoted by the pair (${p}_{i,m}, {w}_{i,m}$), with ${p}_{i,m}$ indicating the location and ${w}_{i,m}$ representing the concentration point weight.

The calculation of position ${p}_{i,m}$ can be expressed in relation to the mean and std of the ith IRV, denoted as ${\mu }_{i}$ and ${\sigma }_{i}$, in the following manner^48,49:

$${p}_{i,m}={\mu }_{i}+{\xi }_{i,m}{\sigma }_{i}$$

(23)

where ${\xi }_{i,m}$ represents the location of the mth quantity of the ith IRV.

The determination of the position (${\xi }_{i,m}$) and weights (${w}_{i,m}$) for the corresponding IRV is presented by^48,49

$${\xi }_{i,m}=0.5{\lambda }_{i,3}+{(-1)}^{3-m}\times \sqrt{{\lambda }_{i,4}-0.75{\lambda }_{i,3}^{2}} m=\text{1,2}, { \xi }_{i,3}=0;$$

(24)

$${\lambda }_{i,3}=E\left[{\left({p}_{i-}{\mu }_{i}\right)}^{3}\right]{{\sigma }_{i}}^{-3}$$

(25)

$${\omega }_{i,m}={\left(-1\right)}^{3-m}{\xi }_{i,m}{\left({\xi }_{i,1}-{\xi }_{i,2}\right)}^{-1}, m=\text{1,2},$$

(26)

$${\omega }_{i,3}={n}^{-1}-{\left[{\lambda }_{i,4}-{\lambda }_{i,3}^{2}\right]}^{-1}$$

(27)

In this instance, $\lambda_{i,j} \;corresponds \;to\; the \;jth\; central \;moment \;of\; standard\; related\; to \;the\; ith\; IRV$. Subsequently, a deterministic power flow computation is executed using the mean of point related to the concentration as {${\mu }_{1},\dots ,{\mu }_{n}$}, resulting in the determination of ${Y}_{\mu }$. Consequently, the qth moment of ORVs, denoted as ${\mu }_{y}^{q}$ can be acquired using the following equation^48,49:

$${\mu }_{y}^{q}=\sum_{i=1}^{n}\sum_{m=1}^{3}{\omega }_{i,m}{Y}_{i,m}^{q}+{\omega }_{\mu }{Y}_{\mu }^{q}$$

(28)

where ${\omega }_{\mu }=1-\sum_{i=1}^{n}\sum_{m=1}^{3}{\omega }_{i,m}$ denotes the weighted coefficients for average point of concentration.

The uncertain input data set, consisting of network load and WT power, is grouped using the K-means clustering approach. A set of k starting agents is selected at random to serve as input sample points. Every individual data point is allocated to the cluster that corresponds to the nearest centroid. Subsequently, the means of each cluster are computed based on the individuals inside each cluster, and the agent associated with each cluster is subsequently updated. The latter two steps must be iteratively performed until the alterations in the clusters are below a specified threshold. Once the agents {${a}_{1},\dots ,{a}_{k}$} have been identified, the approach based on clustering in the MCS is applied to each cluster agent, resulting in the acquisition of the output random variable Y′. Hence, the utilization of cluster agents is limited to serving as a condensed representation of the complete data points in the input space for MCS computations.

The outcomes derived from the clustering technique are subsequently integrated with the average and std acquired from the PEM:

$$Y_{j} = \mu_{y} + \frac{{Y_{j}^{\prime } - \mu_{y}^{\prime } }}{{\sigma_{y}^{\prime } }}\sigma_{y} { }\;\,\;\;{ }j = 1, \ldots ,k$$

(29)

By utilizing the final findings Y, along with the average and std of the ORV, it becomes possible to compute the statistical characteristics of the ORV including distribution functions, probabilistically. The standard location in 2m + 1 schemes is independent of the IRVs total number. In this framework, it is evident that setting ${\lambda }_{i,3}$=0 restricts the variable to be centered on its mean, randomly. Consequently, all potential estimations of 2m + 1 schemes exhibit three deterministic points, accompanied by the distinctive mean value of the corresponding IRV. Flowchart of the 2m + 1 PEM method is depicted in Fig. 1.

Fig. 1

Flowchart of 2m + 1 PEM method.

Proposed meta-heuristic optimizer

This section provides a description of the framework of the suggested hybrid optimization approach for problem resolution, followed by an explanation of its implementation in problem solving.

Overview of DO

Dandelions undergo population evolution through a three-stage process wherein they transfer their seeds to subsequent generations. The primary source of inspiration for the concept of Dandelion optimizer (DO) is derived from the aforementioned three stages⁵⁰.

Initialization

The DO follows the principles of iterative optimization and population evolution through population initialization. Within The recommended DO takes each dandelion seed into account a potential candidate solution, and the entire population is represented by⁵⁰

$$Population = \left[ \begin{gathered} x_{1}^{1} \,\,\,\,\,\, \cdots \,\,\,\,\,\,\,\,\,\,\,x_{1}^{Dim} \hfill \\ \,\,\, \vdots \,\,\,\,\,\,\,\,\, \ddots \,\,\,\,\,\,\,\,\, \vdots \,\,\,\,\,\,\,\, \hfill \\ x_{pop}^{1} \,\,\,\,\,\, \cdots \,\,\,\,\,x_{pop}^{Dim} \,\, \hfill \\ \end{gathered} \right]$$

(30)

where "pop" represents the population size, and "Dim" signifies the variable dimension. Each potential solution is randomly generated within the constraints of the upper limit (UB) and lower limit (LB) specific to the problem at hand. The expression for the ith individual, denoted as Xi, is formulated as follows⁵⁰:

$${X}_{i}=rand\times \left(UB-LB\right)+LB$$

(31)

where i is an integer ranging from 1 to pop, and rand represents a randomly generated number within the interval of 0 to 1. The LB and UB are defined as follows:

$$\begin{aligned} LB & = \left[ {lb_{1} , \ldots ,lb_{Dim} } \right] \\ UB & = \left[ {ub_{1} , \ldots ,ub_{Dim} } \right] \\ \end{aligned}$$

(32)

During the initialization process, the DO selects the individual corresponding thighest fitness quantity in of the primary elite candidate. This candidate is perceived as the maximum favorable dandelion position grows to thrive. Using the lower limit as an illustration, the representation of the primary elite candidate, denoted as Xelite, is⁵⁰:

$$\left\{ {\begin{array}{*{20}l} {f_{best} = \min \left( {f\left( {X_{i} } \right)} \right)} \hfill \\ {X_{elite} = X\left( {find \left( {f_{best} = = f\left( {X_{i} } \right)} \right)} \right)} \hfill \\ \end{array} } \right.$$

(33)

where find() indicates two indices with same quantities.

Stage of rising

During the initial phase of development, dandelion seeds must attain a specific altitude in order to disperse from their parental plant. Dandelion seeds ascend to varying altitudes due to factors such as wind velocity and atmospheric moisture content. In this location, the weather can be categorized into two distinct cases⁵⁰.

Case 1: On a clear day, the wind velocities can be represented by a lognormal distribution lnY ∼ N($\mu$,${\sigma }^{2})$⁵⁰. Within this distribution, values are more densely spread randomly during the Y-axis, leading to an increased likelihood of dandelion grows being carried to distant areas. As a result, in this situation, the DO approach places a greater emphasis on exploration. In the search domain, the wind disperses dandelion seeds in a random manner, causing them to land in various locations. The elevation to which a dandelion seed rises is influenced by the wind's velocity. Stronger winds propel dandelions higher, causing their seeds to scatter over greater distances. Due to the variable nature of wind speed, the vortex formations above dandelion seeds undergo continuous adjustments, inducing a spiral ascent. This phenomenon can be mathematically expressed as follows⁴⁸:

$$X_{t + 1} = {\text{X}}_{{\text{t}}} + \upalpha {\text{* v}}_{{\text{x}}} {\text{*v}}_{{\text{y }}} {*}\ln Y{*}\left( {{\text{X}}_{{\text{s}}} - {\text{X}}_{{\text{t}}} } \right)$$

(34)

where ${\text{X}}_{\text{t}}$ is position of the dandelion kernel during iteration t, whereas ${\text{X}}_{\text{s}}$ is position randomly chosen from the search space throughout iteration t. Equation (35) furnishes the formula for generating this randomly selected position.

$${\text{X}}_{{\text{s}}} = rand \left( {1, Dim} \right)*\left( {UB - LB} \right) + LB$$

(35)

ln Y represents a lognormal distribution with parameters $\mu$=0 and ${\sigma }^{2}$=1, and its mathematical formulation is as follows⁵⁰:

$$\ln Y = \left\{ {\begin{array}{*{20}c} {\frac{1}{{y\sqrt {2\pi } }}\exp \left[ { - \frac{1}{{2\sigma^{2} }}\left( {lny} \right)^{2} } \right]} & {y \ge 0} \\ 0 & { y < 0} \\ \end{array} } \right.$$

(36)

where, y stands for an independent variable conforming to the normal distribution N (0,1). The parameter $\alpha$ is adaptively utilized to modify the search step length, and its mathematical representation is⁵⁰:

$$\upalpha = rand(){*}\left( {\frac{1}{{T^{2} }}t^{2} - \frac{2}{T}t + 1} \right)$$

(37)

where variable α represents a random perturbation ranging from 0 to 1. The aforementioned oscillations prompt the algorithm to prioritize global search during the initial phase and transition to local search during the subsequent phase. The variables v_x and v_y are used to clear the lift component coefficients associated with the separated eddy action on a dandelion. The magnitude of the force applied on the variable dimension is calculated by⁵⁰

$$r=\frac{1}{{e}^{\theta }}$$

(38)

$${v}_{x}=r*cos\theta$$

(39)

$${v}_{y}=r*sin\theta$$

(40)

Let $\theta$ is a random variable that follows a uniform distribution in the interval [− $\pi$,$\pi$].

Case 2: During inclement weather conditions, such as a wet day, the ability of dandelion seeds to effectively disperse through the wind is hindered due to the presence of air resistance, humidity, and various other influencing factors. In this particular scenario, the utilization of dandelion seeds occurs within the immediate vicinity, and the associated mathematical representation is⁵⁰

$${X}_{t+1}={X}_{t}*k$$

(41)

where the parameter k is employed to control the extent of the local search domain for a dandelion, and Eq. (42) is utilized to compute the domain⁵⁰.

$$q=\frac{1}{{T}^{2}-2T+1}{t}^{2}-\frac{2}{{T}^{2}-2T+1}t+1+\frac{1}{{T}^{2}-2T+1}$$

(42)

$$k = 1 - rand()*q$$

(43)

The variable k demonstrates a pattern of "downwards convex" oscillation, which facilitates the algorithm's ability to exploit local conditions by employing a large stride during the initial phase and a smaller stride during the subsequent phase. At the end of each cycle, the parameter k demonstrates a gradual approach towards the value of 1.

The formulation of dandelion grows during the rising step can be presented as:

$$X_{t + 1} = \left\{ {\begin{array}{*{20}l} {X_{t} + \upalpha * {\text{v}}_{{\text{x}}} *{\text{v}}_{{\text{y }}} *\ln Y*\left( {{\text{X}}_{{\text{s}}} - {\text{X}}_{{\text{t}}} } \right)} \hfill & {rand\;n < 1.5} \hfill \\ {X_{t} *k} \hfill & { else} \hfill \\ \end{array} } \right.$$

(44)

where randn () represents a number following the standard normal distribution, random.

Figure 2, illustrates the flight patterns of dandelion seeds in varying meteorological circumstances. The figure provides an approximation of the regeneration locations for dandelion seeds. In clear weather conditions, dandelion seeds undergo updates that prioritize the exploration process by incorporating randomly picked location information. The eddy located above the seed exerts an influence on the vector in motion by performing a multiplication operation on its x and y components, thereby adjusting the trajectory of the spiral movement pattern of the dandelion. In the second scenario, the dispersal of dandelion seeds occurs in many directions within the immediate vicinity of the community. The utilization of standard distribution of arbitrary numbers is employed to dynamically regulate the processes of utilization and discovery. To improve the method's focus on search globally, a cut-off point of 1.5 is established. In the initial step of iterative optimization, the chosen setting facilitates the extensive traversal of dandelion seeds throughout the whole search space, with the aim of obtaining accurate directional guidance for subsequent stages.

Fig. 2

The schematic diagram depicting the dandelion seeds rising stage⁵⁰.

Descending stage

During this stage, the proposed DO continues to prioritize exploration. Following their ascent to a specific height, dandelion seeds experience a gradual descent. The algorithm employs Brownian motion to simulate the movement trajectory of these seeds. This approach enables individuals to discover a broader range of search spaces during iterative updates, given that Brownian motion adheres to a standard distribution with each alteration. In order to assess the dandelion descent stability, the mean location data obtained during the rising phase is employed. This strategy contributes to steering the entire population toward favorable areas for further development. The corresponding mathematical representation is as follows⁵⁰:

$$X_{t + 1} = X_{t} - \upalpha * \upbeta_{{\text{t}}} {*}\left( {{\text{X}}_{{{\text{mean}}\_{\text{t}}}} - \upalpha *\upbeta_{{\text{t}}} {\text{*X}}_{{\text{t}}} } \right)$$

(45)

where ${\beta }_{t}$ represents Brownian movement and is a number drawn from the standard distribution, randomly. X_mean-t represents the average position of the population at the ith iteration, and the formulation is given by⁵⁰:

$${\text{X}}_{\text{mean}\_\text{t}}=\frac{1}{pop}\sum_{i=1}^{pop}{X}_{i}$$

(46)

The repeated updating of individuals relies on the average positional data of the population. This information plays a key role in determining the evolution direction of individuals.

Landing stage

During this phase, the DO shifts its focus towards exploitation. Building on the insights from the preceding stages, the dandelion seed undergoes a random selection process to determine its landing site. As iterations unfold, the algorithm aims to gradually converge towards the optimum solution, globally. Consequently, the identified optimum solution represents the estimated position where dandelion spores are likely to be found to thrive. To facilitate precise convergence to the global optimum, search agents utilize the valuable information from the current elite to exploit their local neighborhoods. As the population evolves, the ultimate revelation of the optimum solution globally becomes achievable. This behavior is mathematically captured by⁵⁰

$${\text{X}}_{\text{mean}\_\text{t}}={\text{X}}_{\text{elite}}+levy\left(\lambda \right)*\alpha *({\text{X}}_{\text{elite}}-{\text{X}}_{\text{t}}*\delta )$$

(47)

In this equation, X_elite denotes the optimum location of the dandelion seed in the ith iteration. The function Levy(λ) encapsulates the Levy flight and can be determined by⁵⁰

$$levy\left(\lambda \right)=s\times \frac{\omega \times \sigma }{{\left|t\right|}^{\frac{1}{\beta }}}$$

(48)

where β is a randomly generated number within the range [0, 2] (β = 1.5 in this study). The constant value of s is set to 0.01. Moreover, w and t represent random numbers chosen from the interval [0, 1]. The mathematical formulation for α is provided by⁵⁰

$$\sigma =\left(\frac{\Gamma (1+\beta )\times \text{sin}(\frac{\pi \beta }{2})}{\Gamma (\frac{1+\beta }{2})\times \beta \times {2}^{(\frac{\beta -1}{2})}}\right)$$

(49)

where β remains constant at 1.5. Furthermore, δ is determined as a linearly increasing function within the range [0, 2], and its computation is defined as follows:

$$\delta =\frac{2t}{T}$$

(50)

In order to effectively approach the solution globally, the utilization of a linear rising function is employed on individuals as a means to prevent excessive utilization. The Levy flight coefficient is employed at this stage to simulate the magnitude of individual movement steps.

Execution of the DO

This subsection presents a thorough explanation of the precise sequence of steps involved in the execution of the DO algorithm. In the case of DO, vectors clusters produced randomly within searching for space to begin optimization. Subsequently, dandelion grows undergo three distinct stages optimization by iteration cycles: rising, descending, and landing. It is important to highlight the protocols for generating new populations prior to the subsequent iteration. To elucidate this approach, consider the scenario where each dandelion grows is ranked in increasing order based on their fitness values. The individual corresponding to minimum fitness assumes the role of the elite individual for the subsequent production of the individuals. Consequently, the population is sorted, serving as the foundational population for the ensuing iteration. This arranging technique proves advantageous for preserving valuable information and prevents the algorithm from inadvertently discarding accurate optimization directions due to the iterative progression. The algorithm concludes its optimization process by reaching the predefined maximum iteration count.

Flowchart of the DO is depicted in Fig. 3.

Fig. 3

Flowchart of the DO.

The pseudo-code of the DO is presented in Algorithm 1.

Overview of improved DO (IDO)

The adaptive inertia weight (${\varnothing }$)⁵¹, adapted automatically based on the present physiological condition of the agent, is added to the local search and exploitation phase to prevent the algorithm from getting trapped in the local optimum. In this study, ${\varnothing }$ is used in the exploitation phase to increase diversity and avoid entering the local optimal. The position of the clouded leopard in the second phase, i.e., the exploitation phase, is updated using ${\varnothing }$ as follows:

$${\text{X}}_{{{\text{mean}}\_{\text{t}}}} = {\varnothing } {\text{*X}}_{{{\text{elite}}}} + levy\left( \lambda \right){*}\alpha {*}\left( {{\text{X}}_{{{\text{elite}}}} - {\text{X}}_{{\text{t}}} {*}\delta } \right)$$

(51)

The converging modification is governed by the operative ([0, 1]), which is automatically adjustable based on the present operator location. While the efficiency of a factor exceeds the mean quantity of the entire population, the weight operator ${\varnothing }$ of is assigned to its utmost quantity so that the population can quickly converges on the optimal location. Alternatively, as the current agent's fitness is below average, ${\varnothing }$ is designated a lesser quantity. The less the weight quantity, the weaker the impact of revising the dandelions' status, deteriorating the performance will be. The approach ${\varnothing }$ enhances the algorithm's localized search capabilities and prevents abrupt convergence. The accompanying equation explains depending on the improved Versoria mapping function.

$${\varnothing }_{m} \left( t \right) = \left\{ {\begin{array}{*{20}c} {1 - \frac{1}{{\left( {\varphi .\left( {a_{i} \left( t \right) - \frac{1}{2}} \right)^{2} + 2} \right)}} if a_{i} \left( t \right) \le 0.5} \\ {\frac{1}{{\left( {\varphi .\left( {a_{i} \left( t \right) - \frac{1}{2}} \right)^{2} + 2} \right)}} otherwise} \\ \end{array} } \right.$$

(52)

where a_i(t),a_i(t) ∈ [0,1] indicates the dandelion's classification among all other dandelions within the lowest fitness and the mean fitness, as specified below:

$${\text{f}}_{ave}\left(t\right)=\sum_{m=1}^{{N}_{p}}\frac{{f}_{i}(t)}{{N}_{p}}$$

(53)

$${\text{f}}_{min}\left(t\right)=min\left\{{\text{f}}_{1}\left(t\right), {\text{f}}_{2}\left(t\right), \dots , {\text{f}}_{{N}_{p}}\left(t\right)\right\}$$

(54)

$${a}_{i}\left(\text{t}\right)=\frac{{\text{f}}_{i}\left(t\right)-{\text{f}}_{min}\left(t\right)}{{\text{f}}_{ave}\left(t\right)-{\text{f}}_{min}\left(t\right)}$$

(55)

where fi(t) is the fitness of the ith dandelion at iteration t, f_ave(t) and f_min(t) represent the mean and smallest fitness values of all N_p size populations, respectively.

The IDO steps to solve the problem

The steps of the IDO implementation for addressing the deterministic MORWTA problem solving. Then, to solve the stochastic problem, the steps described in "Stochastic model" section have been solved considering the deterministic model. Flowchart of the IDO implementation to solve the deterministic approach is depicted in Fig. 4.

Fig. 4

Flowchart of the IDO implementation to solve the deterministic approach.

Step 1: Apply network data, which includes load demand data, network lines data, tie-lines, and WT maximum capacity.

Step 2: Identify the upper bound and lower boundary of each tie-line, and additionally the lower and upper size, power factor, and installation location of the WT (decision variable set) for each Dandelion of the algorithm's population. To solve simultaneous reconfiguration and WT allocation, the first component of the decision variable vector is the number of open distribution network branches, while the second, third, and fourth components are the WT installation location (bus), WT size, and power factor (p.f) of the WT, respectively.

Consequently, the solution vector (X) for the simultaneous-hybrid MORWTA problem corresponds to follows:

$$X=\left[\overline{{DV}_{WT}} \overline{{DV}_{TLs}}\right]$$

(56)

$${DV}_{WT}=\left[{IL}_{WT} {S}_{WT} { p.f}_{WT}\right]$$

(57)

$${DV}_{TLs}=\left[ {TL}_{1} {TL}_{2} {TL}_{3} { TL}_{4} { TL}_{5}\right]$$

(58)

where $\overline{{DV}_{WT}}$ and $\overline{{DV}_{TLs}}$ are decision vectors of WT and network tie-lines, respectively. ${IL}_{WT}$, ${S}_{WT}$ and ${p.f}_{WT}$ are site, capacity and power factor of the WT, and ${TL}_{1}$, ${TL}_{2}$, ${TL}_{3}$, ${TL}_{4}$, and ${TL}_{5}$ are the five network tie-lines.

Step 3: On the basis of the initial population of the Dandelion, the backward-forward power flow meeting the network radiality is utilized for calculating the objective function (Eq. (1)) of each Dandelion satisfying the constraints of Eqs. (15)–(21). The Dandelion with the best fitness is saved to the best member of the algorithm according to the fitness values.

Step 4: Update the population based on the DO in the fourth step. The solution vector has been chosen at random for each member of the updated population, and the fitness function (Eq. (1)) is computed for each set of variables by satisfying the operational and radial constraint (Eqs. (15)–(21)). The finest population member is the Dandelion with the highest value among the updated Dandelions. If its fitness function is lesser, the current best member of the population is substituted with the best acquired in step 3.

Step 5: Utilizing adaptive inertia weight, update the algorithm's population.

Step 6: The solution vector is selected randomly for each updated population according to the adaptive inertia weight (Eqs. (51)–(55)), and the fitness function (Eq. (1)) is calculated for each variable set satisfying the operational and radial constraints (Eqs. (15)–(21)). The best population member is the Dandelion with the highest value among the updated Dandelions. If its fitness function is lesser, the current best member of the population is replaced with the best gained in step 4.

Step 7: Convergence criteria. By executing the utmost number of iterations, repetition and achieving the best objective function value convergence criteria of the IDO are examined. If yes, go to step 4; otherwise, go to step 8.

Step 8: Terminate the algorithm and save the results.

Results and discussion

The results of many-objective reconfiguration and wind turbine allocation (MORWTA) for three modified 33-bus, unbalanced 25-bus, and 37-bus distribution networks under two different scenarios as Scenario#1) deterministic-MORWTA (without uncertainty), and Scenario#2) stochastic-MORWTA (with uncertainty) are presented. In this research, the line outage rate is considered to be 0.046 per km/yr⁵⁴. It is also incorporated that all other components are 100% availability. In the event of a branch outage, the time within the outage and repair is considered to be 8 h, and interruption duration for downstream customers is 8 h⁵⁴. Moreover, the MORWTA based on the IDO is compared with conventional DO, GWO, PSO, and AOA to demonstrate its superiority. Each algorithm's general and regulatory parameters are regarded as being identical to their respective reference papers. The number of population, the maximum number of iterations, and the independent runs number have been set to 50, 100, and 30 (according to the trial and error and user experience) for a fair comparison of the effectiveness of various optimization methods. In this study, besides the rearrangement of the distribution network, the allocation of a 1 MW turbine is also considered. In the stochastic framework, considering the uncertainty, the network loading probability distribution function (PDF) as well as the wind turbine power is considered as Fig. 5, based on which the output random variables are considered for the 2m + 1 PEM method.

Fig. 5

PDF of (a) distribution network loading, and (b) wind power considering 1000 scenarios.

The control parameters of each algorithm are considered as in their reference article for fair competition according to Table 1.

Table 1 The control parameters of different algorithms.

The simulation results are presented in two below scenarios:

Scenario#1: Deterministic-MORWTA without uncertainty.

Scenario#2: Stochastic-MORWTA with uncertainty.

Table 1 The control parameters of different algorithms.

Results of deterministic, and stochastic-MORWTA for modified 33-bus network

The schematic of the 33-bus network is depicted in Fig. 6. There are 33 buses, and 37 lines with five tie-lines within buses 8–21, 9–15, 12–22, 18–33, and 25–29. The 33-bus network has 3715 kW of active load and 2300 kW of the reactive load. In this simulation, the base voltage and the base apparent power are considered to be 12.66 kV and 100 MVA, respectively. The load data of this network is modified and an unbalanced network is extracted. The load and lines data of this modified network are derived from Ref.⁵⁵.

Fig. 6

Schematic of the 33-bus distribution network.

Deterministic results for modified 33-bus network (Scenario#1)

In the base network, the objective values for power loss, VS, total harmonic distortion, VU, ENS, SAIFI, SAIDI, and MAIFI are calculated 207.44 kW, 0.96 p.u, 0.1835%, 4.92%, 6.44 MWh, 1.36 failure/customer/yr, 1.21 h/customer/yr and 4.64 mom/customer/yr, respectively.

In this section, the simulation outcomes of the first deterministic-MORWTA scenario utilizing the IDO are presented and compared to the conventional DO, GWO, PSO, and AOA methods. Figure 7, depicts the convergence process derived from various optimization techniques. The IDO algorithm with the lowest convergence tolerance has obtained the greatest solution value with the least objective function value in comparison to other algorithms. Also, Fig. 7 demonstrated that improving the conventional DO has increased the system's effectiveness in locating the optimal solution with a quicker convergence rate.

Fig. 7

Convergence process to solve scenario#1 for modified 33-bus distribution network.

Table 2, presents the numerical results of the first scenario based on deterministic-MORWTA derived from various algorithms. IDO is preferable to other algorithms in solving the deterministic-MORWTA problem because the outcomes of the objective function and the eight problem objectives achieved through IDO are smaller than those derived by other algorithms. The IDO has put in 894 kW of WT generation with a p.f of 0.86 on bus 7 and determined the network configuration of 33-bus by considering tie lines as lines 10, 20, 28, 30, 35. As a consequence, the value of each of lines 10, 20, 28, 30 and 35. The values of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI are obtained 112.79 kW, 0.42 p.u, 0.1725%, 2.07%, 5.13 MWh, 1.16 failure/customer/yr, 1.03 h/customer/yr, and 2.38 mom/customer/yr, respectively. In addition, the results of the statistical analysis presented in Table 3 demonstrate that the IDO-solved deterministic-MORWTA scenario has yielded more effective results than those of other algorithms by attaining superior indicators of statistical effectiveness.

Table 2 Numerical results of scenario#1 optimization for modified 33-bus distribution network.

Table 3 Statistical analysis of different algorithms performance to solve Scenario#1 for modified 33-bus network.

Stochastic results for modified 33-bus network (Scenario#2)

This section depicts the power demand of all loads as a normal covariable with a mean of the nominal value and a standard deviation of 20% of the mean³⁰. In order to simulate the uncertainty of wind power, a Weibull PDF is applied to the speed change curve's parameters. In the stochastic approach, the sample points are grouped into a clusters prior substantial number to applying the K-mean clustering to find the optimal agent for each cluster. Then, based on the gathered agents, transmission computations are performed. Then, according to the achieved agents, calculations of power transmission are performed. Using the IDO, the simulation results of the next scenario based on stochastic-MORWTA are presented, with WT generation and load uncertainties, and the performance of this optimization technique is compared to the characteristics of conventional DO, GWO, PSO, and AOA with the application of stochastic simulation based on 2m + 1 PEM and established clustering. In the network's fundamental state (without reconfiguration and WT allocation), the values of each objective, including losses, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI, are calculated to be 218.43 kW, 1.02 p.u, 0.2001%, 5.40%, 6.63 MWh, 1.42 failure/customer/year, 1.26 h/customer/yr, and 5.03 mom/customer/yr, respectively. Figure 8 illustrates the convergence process of various stochastic-MORWTA problem-solving strategies. According to the convergence curves, the proposed IDO method has achieved a lower objective function value than other algorithms. In addition, it has a faster convergence rate and a lower tolerance for convergence than other problem-solving algorithms. As a result of solving the stochastic-MORWTA problem, the WT size has increased.

Fig. 8

Convergence process to solve scenario#2 for modified 33-bus distribution network.

Table 4 illustrates the numerical results of the second stochastic-MORWTA scenario via the IDO and the conventional DO, GWO, PSO, and AOA. Assessing the results demonstrated that, in comparison to other algorithms, the value of each objective is decreased more than their base values. The IDO has installed 926 kW of WT generation with a p.f of 0.88 on bus 7 and determined the configuration of the 33-bus network by considering the opened lines as lines 7, 11, 28, 34, and 36. As a result, the values of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI are determined to be 137.94 kW, 0.47 p.u, 0.1964%, 2.39%, 5.68 MWh, 1.30 failure/customer/yr, 1.15 h/customer/yr, and 2.75 mom/customer/yr, respectively. Furthermore, the statistical analysis depicted in Table 5 validates the superiority of the IDO in resolving the stochastic-MORWTA problem by achieving lower values for the Best, Mean, Worst, and std criteria (See Fig. 9). Also, the results of Table 5, showed the IDO has obtained lower convergence iteration (CI) similar to PSO, and convergence time (CT) to obtain the best solution.

Table 4 Numerical results of scenario#2 optimization for modified 33-bus distribution network.

Table 5 Statistical analysis of different algorithms performance to solve Scenario#2 for modified 33-bus network.

Fig. 9

Statistical analysis comparison of different algorithms to solve Scenario#2 for modified 33-bus network.

The overall objective function according to Eq. (1) has eight objectives, which are solved as a multi-objective structure based on the method of weight coefficients. If we solve the problem for each objective as a single objective and a total multi-objective problem, then we will face nine objective functions. Although the general objective of this study is to solve the multi-objective function (Eq. (1)). In Table 6, the results of the nonparametric test analysis of different algorithms for the 33-bus network are presented as Friedman's test rank, which shows the superiority of the proposed optimization method.

Table 6 Friedman’s test rank summary of statistical analysis results for different algorithms for modified 33-bus network.

Scenarios comparison for modified 33-bus network

In this part, the effectiveness of the MORWTA problem according to the IDO is contrasted with two deterministic and stochastic methods, illustrated in Table 7. Due to the WT generation and load uncertainties, the network configuration has been updated in addition to the change in installed WT generation in bus 7. The results demonstrated considering the WT generation and load uncertainties in the MORWTA problem in the form of stochastic-MORWTA, the value of each of the goals of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI is increased 22.30%, 11.90%, 13.86%, 15.46%, 10.72%, 10.17%, 11.65% and 15.55%, respectively in contrast to the deterministic scenario without uncertainty (Deterministic-MORWTA).

Table 7 Results comparison of Scenarios# 1, and 2 for modified 33-bus distribution network.

Figure 10, depicts a visual comparison of each objective, including power loss, VS, THD, voltage imbalance, ENS, SAIFI, SAIDI, and MAIFI, for both deterministic- and stochastic-MORWTA scenarios. Based on Fig. 10, in the deterministic and stochastic scenarios, the power loss is 112.79 kW and 137.94 kW, the voltage sag is 0.42 p.u and 0.49 p.u, the THD is 1.725% and 1.647%, and the VU is 2.07% and 2.39%, respectively. ENS has increased from 5.13 MWh in the deterministic scenario to 5.68 MWh in the stochastic scenario. Moreover, the SAIFI, SAIDI, and MAIFI indices have increased from 1.18 failures per customer per year, 1.03 h per customer per year, and 2.38 under the deterministic scenario to 1.30 failures per customer per year, 1.15 h per customer per year, and 2.75 under the stochastic scenario. Consequently, under the conditions of contemplating the uncertainty of the network demand as well as the wind turbine's electricity production, the value of each objective has been raised, which is related to the uncertainty patterns that have been defined. As a result, the uncertainties considered based on the power changes of the load and the power fluctuations of the wind turbine have an effect on the system optimal configuration, and with the change of the size and generation factor of the WT, it led to significant changes in each of the investigated objectives. Consequently is crucial to account for uncertainties in the operation of distribution networks based on the reconfiguration and optimal sitting and sizing of WT so that network operators can know the exact values of the loss measures, power quality, and reliability and make the right decision. Otherwise, if the uncertainties of demand and power of renewable resources are not factored into the operation strategy, it is not practicable to achieve reliable network utilization and superior power quality.

Fig. 10

Results comparison (a) Power loss, (b) VS and THD, (c) VU and ENS, (d) SAIFI, SAIDI, MAIFI for modified 33-bus network.

The variations in VS, VU, and THD of the buses are depicted in Figs. 11, 12 and 13. Clearly, the value of each of these goals has increased in the stochastic model considering uncertainty compared to the deterministic model. As depicted in Fig. 11, the value of VS in the stochastic-MORWTA model has increased in the majority of buses compared to the deterministic-MORWTA model (0.42–0.49 p.u). According to Fig. 12, the stochastic-MORWTA model has a higher value of voltage unbalance in all network circuits than the deterministic-MORWTA model (from 2.07 to 2.39%). In addition, Fig. 13 demonstrates that the value of THD in all network buses for the stochastic-MORWTA model has increased relative to the deterministic-MORWTA model (from 17.25 to 19.64%).

Fig. 11

Voltage sag changes comparison using the IDO for modified 33-bus distribution network.

Fig. 12

VU changes comparison using the IDO for modified 33-bus distribution network.

Fig. 13

THD changes comparison using the IDO for modified 33-bus distribution network.

Deterministic, and stochastic results for unbalanced 25-bus network (Scenarios#1, and 2)

Figure 14 illustrates the schematic of the 25-bus network, consisting of 25 buses and 27 lines, with three tie-lines connecting buses 5–22, 8–15, and 12–25 (lines 25, 26, and 27). The network has an active load of 3239 kW and a reactive load of 2393 kW. In this simulation, the base voltage and base apparent power are set at 4.16 kV and 30 MVA, respectively. The data for loads and lines in this network are sourced from references^56,57, while reliability data are taken from reference⁵⁵. The following section presents the deterministic and stochastic results for the unbalanced 25-bus network.

Fig. 14

Schematic of the unbalanced 25-bus distribution network.

Deterministic results for unbalanced 25-bus network (Scenario#1)

In the base unbalanced 25-bus network, lines 25, 26, and 27 are open. The outcomes for Scenario #1 of the 25-bus network are as follows: power loss is 150.12 kW (adapted from Ref.^40,58), voltage stability (VS) is 0.8059 p.u., total harmonic distortion (THD) is 0.4835%, voltage unbalance (VU) is 0.4300%, energy not supplied (ENS) is 3.82 MWh, system average interruption frequency index (SAIFI) is 1.09 failures/customer/year, system average interruption duration index (SAIDI) is 0.88 h/customer/year, and momentary average interruption frequency index (MAIFI) is 3.27 moments/customer/year. In Scenario #1 (deterministic approach), solved using the IDO, switches 15, 17, and 22 are opened, and a wind turbine with a capacity of 611 kW and a power factor of 0.89 is installed at bus 7. As a result, the values for each objective are power loss of 75.42 kW, VS of 0.5546 p.u., THD of 0.3450%, VU of 0.2791%, ENS of 2.94 MWh, SAIFI of 0.97 failures/customer/year, SAIDI of 0.74 h/customer/year, and MAIFI of 2.02 moments/customer/year, demonstrating improvements in various objectives via the IDO.

Stochastic results for unbalanced 25-bus network (Scenario#2)

Figure 15 shows the convergence process for solving Scenario #2 of the unbalanced 25-bus distribution network using the proposed IDO, conventional DO, PSO, GWO, and AOA algorithms. The convergence curves indicate that the proposed IDO attained a lower objective function value (best solution) than the other algorithms and did so with a faster convergence rate.

Fig. 15

Convergence process to solve scenario#2 for unbalanced 25-bus distribution network.

The numerical outcomes of Scenario #2 using the IDO, along with the conventional DO, GWO, PSO, and AOA algorithms are presented in Table 8. The evaluation of the results shows that, compared to other algorithms, each objective's value has decreased more than their base values. The IDO installed 673 kW of wind turbine generation with a power factor of 0.88 on bus 7 and determined the configuration of the 33-bus network by opening lines 13, 17, and 22. Consequently, the values for power loss, VS, VS, voltage unbalance (VU), ENS, SAIFI, SAIDI, and MAIFI are determined to be 89.26 kW, 0.6049 p.u., 0.3810%, 0.2801%, 3.29 MWh, 1.06 failures/customer/year, 0.83 h/customer/year, and 2.31 mom/customer/year, respectively. Additionally, the statistical analysis shown in Table 9 confirms the IDO's superiority in solving the stochastic-MORWTA problem by achieving lower values for the Best, Mean, Worst, and standard deviation criteria, as depicted in Fig. 16. The results in Table 9 also indicate that the IDO achieved lower CI and CT to find the best solution.

Table 8 Numerical results of scenario#2 optimization for 25-bus distribution network.

Table 9 Statistical analysis of different algorithms performance to solve Scenario#2 for 25-bus network.

Fig. 16

Statistical analysis comparison of different algorithms to solve Scenario#2 for 25-bus network.

In Table 10, the nonparametric test analysis results for different algorithms to solve the different objectives in the unbalanced 25-bus network are given as Friedman's test rank, which clears the better performance of the proposed IDO method.

Table 10 Friedman’s test rank summary of statistical analysis results for different algorithms for 25-bus network.

Scenarios comparison for unbalanced 25-bus network

This section compares the effectiveness of the MORWTA problem using the IDO with two deterministic and stochastic methods, as shown in Table 11. Due to the uncertainties in wind turbine (WT) generation and load, the network configuration and the installed WT generation at bus 7 have been adjusted. The results indicate that when accounting for these uncertainties in the MORWTA problem, represented as stochastic-MORWTA, the objectives of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI increased by 18.35%, 9.07%, 10.43%, 12.46%, 11.90%, 9.28%, 12.16%, and 14.36%, respectively, compared to the deterministic scenario without uncertainty, as illustrated in Fig. 17.

Table 11 Results comparison of the deterministic- and stochastic- stochastic-MORWTA for unbalanced 25-bus network.

Fig. 17

% of increasing value of each objective in stochastic approach compared with the deterministic approach for unbalanced 25-bus network.

Figure 18 provides a visual comparison of each objective such as power loss, VS, THD, voltage imbalance, ENS, SAIFI, SAIDI, and MAIFI for both deterministic and stochastic MORWTA scenarios in the unbalanced 25-bus network. The comparison shows that under the conditions of considering the uncertainties in network demand and wind turbine electricity generation, the value of each objective has increased. This increase is attributed to the defined uncertainty patterns. Additionally, the percentage increase in each objective's value under the stochastic approach, compared to the deterministic approach, is presented based on the results in Table 11 for the unbalanced 25-bus network. This comparison highlights the impact of uncertainty on the network's performance, demonstrating the importance of accounting for stochastic variables in network optimization.

Fig. 18

Results comparison (a) Power loss, (b) VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI for unbalanced 25-bus network.

Deterministic, and stochastic results for unbalanced 37-bus network (Scenarios#1, and 2)

The layout of the 37-bus network is shown in Fig. 19. This network is unbalanced and consists of 37 buses along with three tie-lines connecting buses 735–741, 701–722, and 727–732 (specifically lines 36, 37, and 38). The network has a total active load of 2472 kW and a reactive load of 1207 kVAr. For this simulation, the reference voltage and apparent power are set at 4.8 kV and 30 MVA, respectively. Data on the loads and lines for this network are sourced from Ref.⁵⁹, while the reliability information is obtained from Ref.⁵⁵.

Fig. 19

Schematic of the unbalanced 37-bus distribution network.

Deterministic results for unbalanced 37-bus network (Scenario#1)

In the initial 37-bus network configuration, the objective values for power loss, VS, THD, VU, ENS, and reliability indices such as SAIFI, SAIDI, and MAIFI are calculated at 81.56 kW (based on Ref.⁵⁹), 0.6352 p.u, 0.2075%, 0.13%, 2.186 MWh, 0.73 failures/customer/year, 0.61 h/customer/year, and 1.39 moments/customer/year, respectively. In Scenario #1, which employs a deterministic approach, the IDO is used, leading to the disconnection of three lines between buses 704–720, 708–732, and 734–737. Additionally, a wind turbine with a capacity of 548 kW and a power factor of 0.85 is installed at bus 722. As a result, the updated values for power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI are 34.56 kW, 0.4142 p.u, 0.1310%, 0.09%, 1.478 MWh, 0.63 failures/customer/year, 0.49 h/customer/year, and 1.20 moments/customer/year, respectively.

Stochastic results for unbalanced 37-bus network (Scenario#2)

The convergence process for solving Scenario #2 of the unbalanced 37-bus distribution network using the proposed IDO method, along with conventional DO, PSO, GWO, and AOA algorithms is presented in Fig. 20. The convergence curves indicate that the proposed IDO method not only reaches a lower objective function value (best solution) compared to the other algorithms but also does so at a faster rate.

Fig. 20

Convergence process to solve scenario#2 for unbalanced 37-bus distribution network.

The numerical results for Scenario #2 of the 37-bus network are as follows: power loss is obtained 83.17 kW, voltage stability (VS) is 0.6755 p.u, THD is 0.2183%, VU is 0.139%, ENS is 2.257 MWh, SAIFI is 0.76 failures/customer/year, SAIDI is 0.64 h/customer/year, and MAIFI is 1.48 moments/customer/year.

For Scenario #2, which employs a stochastic approach, the IDO method is applied, and according to Table 12, three lines between buses 704–720, 708–732, and 710–734 are disconnected, and a wind turbine with a 579 kW capacity and a power factor of 0.83 is installed at bus 706. With these changes, the updated values are: power loss is 38.78 kW, VS is 0.4583 p.u, THD is 0.1472%, VU is 0.101%, ENS is 1.689 MWh, SAIFI is 0.71 failures/customer/year, SAIDI is 0.55 h/customer/year, and MAIFI is 1.36 moments/customer/year. Additionally, statistical analysis in Table 13 demonstrates the effectiveness of the IDO method in addressing the stochastic-MORWTA problem. The IDO method achieves lower values for Best, Mean, Worst, and standard deviation criteria compared to other algorithms, as shown in Fig. 21. Table 13 also indicates that the IDO method requires fewer CI and less CT to reach the optimal solution.

Table 12 Numerical results of scenario#2 optimization for unbalanced 37-bus distribution network.

Table 13 Statistical analysis of different algorithms performance to solve Scenario#2 for unbalanced 37-bus network.

Fig. 21

Statistical analysis comparison of different algorithms to solve Scenario#2 for 37-bus network.

In Table 14, the Friedman's test rank results as a nonparametric test analysis are presented for different algorithms for unbalanced 37-bus network and the obtained results are proved the superior capability of the IDO to solve different objectives compared with the other algorithms.

Table 14 Friedman’s test rank summary of statistical analysis results for different algorithms for unbalanced 37-bus network.

Scenarios comparison for unbalanced 37-bus network

In this section, the performance of the IDO in addressing the MORWTA problem is compared with two other approaches, deterministic and stochastic, as shown in Table 15. The network configuration has been adjusted to account for uncertainties in WT generation and load, including changes in the WT generation at bus 7. The results reveal that incorporating WT generation and load uncertainties into the MORWTA problem, referred to as stochastic-MORWTA, leads to increases in the objectives of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI by 12.21%, 10.64%, 12.37%, 9.82%, 14.30%, 12.65%, 12.63%, and 13.89%, respectively, compared to the deterministic scenario without uncertainties, as depicted in Fig. 22.

Table 15 Results comparison of the deterministic- and stochastic- stochastic-MORWTA for unbalanced 37-bus network.

Fig. 22

% of increasing value of each objectives in stochastic approach compared with the deterministic approach for unbalanced 37-bus network.

A visual comparison of each objective—such as power loss, VS, THD, voltage imbalance, ENS, SAIFI, SAIDI, and MAIFI—for both deterministic and stochastic-MORWTA scenarios in the unbalanced 37-bus network is depicted in Fig. 23. The results show that when accounting for uncertainties in network demand and wind turbine electricity production, the values for each objective increase according to the defined uncertainty patterns. Without incorporating these uncertainties into the operational strategy, achieving reliable network performance and high power quality is impractical. Additionally, the percentage increase of the stochastic approach compared to the deterministic method for the unbalanced 37-bus network is detailed in Table 15.

Fig. 23

Results comparison (a) Power loss, (b) VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI for unbalanced 37-bus network.

Model validation with previous studies

Comparison for the modified 33-bus network

The numerical results of the deterministic-MORWTA method are compared with those from previous studies^15,40,60,61. Study⁶⁰ introduces the reconfiguration of unbalanced distribution networks using a fuzzy multi-criteria approach and the new improved coronavirus herd immunity optimizer algorithm (ICHIOA). The focus is on reducing losses, VU, VS, and energy that is not provided for customers. Voltage imbalances and VS are considered power quality metrics, and ENS represents energy not delivered. In⁶¹, the network reconfiguration is optimized for minimizing losses, VS, VU, and ENS on an unbalanced 33-bus network using an artificial electric field algorithm-pattern search (AEFAPS). Additionally, studies^15,40 implement the 33-bus network reconfiguration to minimize power losses and improve power quality indices. In Table 16, the performance of IDO is compared with ICHIOA and AEFAPS. The results show that IDO achieves lower losses, VS, VU, and ENS, demonstrating the superior performance of the proposed method.

Table 16 Comparison with previous studies for the modified 33-bus network.

Comparison for the unbalanced 25-bus network

A comparison of the deterministic and stochastic numerical results obtained in this study is presented in Table 7 for the unbalanced 25-bus distribution network with those from Refs.^40,56,62. In⁵⁶, the reconfiguration of the unbalanced 25-bus network focuses on minimizing power losses, while in⁶², both DG allocation and network reconfiguration are carried out simultaneously. According to Table 17, the proposed method in our study achieves lower power losses in both deterministic and stochastic approaches compared to Refs.^56,62.

Table 17 Comparison with previous studies for the unbalanced 25-bus network.

Comparison for the unbalanced 37-bus network

The numerical results of the deterministic and stochastic MORWTA methods are compared in Table 18 with the results of Ref.¹⁹, which utilized a hybrid honey bee colony algorithm (HHBCA) to allocate capacitors in the unbalanced 37-bus distribution network. The objective in Ref.¹⁹ was to minimize power system losses and unbalances while maintaining voltage levels and THD at the buses. As shown in Table 18, the proposed methodology in this study achieves lower values of power loss, THD, and voltage unbalance.

Table 18 Comparison with previous studies for the unbalanced 37-bus network.

Conclusion

In this study, a solving approach based on the MORWTA is proposed for minimizing the losses, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI in three modified 33-bus, and unbalanced 25-, and 37-bus distribution networks by employing the IDO. For stochastic problem-solving and modeling, the 2m + 1 PEM integrated with clustering was employed. Two deterministic and stochastic models without and with uncertainties, respectively, were applied to the problem. The findings of the investigation are as follows:

• The results cleared that the MORWTA improved all objectives by simultaneously reconfiguring the distribution networks and allocating wind turbines in comparison to the network's initial state. Consequently, the simultaneous approach of determining the network configuration optimally and the optimal injection of wind power into the network has enhanced the efficiency of the network and met all of the objectives.

• For the modified 33-bus network, in the deterministic model utilizing the IDO, the losses, VS, THD, VU, ENS, SAIFI, and SAIDI were decreased by 45.63%, 56.25%, 5.99%, 57.93%, 20.34%, 13.24%, 14.88%, and 48.71%, respectively, compared to the base network.

• The statistical analysis demonstrates that the IDO-solved deterministic-MORWTA had produced more effective results than the conventional DO, GWO, PSO, and AOA techniques by achieving superior statistical efficacy criteria for all networks. The comparison of deterministic- and stochastic MORWTA results confirms the superiority of the IDO by achieving a higher objective value and lower values for the Best, Mean, Worst, and standard criteria.

• For the modified 33-bus network, comparison of results revealed that the power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI were increased by 20.52%, 11.90%, 13.86%, 15.46%, 10.72%, 10.17%, 11.65% and 15.55%, respectively, when the stochastic model is used in place of the deterministic model without uncertainty consideration.

• For the unbalanced 25-bus network, the results demonstrated considering the WT generation and load uncertainties in the MORWTA problem in the form of stochastic-MORWTA, the value of each of the goals of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI is increased 18.35%, 9.07%, 10.43%, 12.46%, 11.90%, 9.28%, 12.16% and 14.36%, respectively in contrast to the deterministic scenario without uncertainty.

• For the unbalanced 37-bus network, the results demonstrated considering the WT generation and load uncertainties in the MORWTA problem in the form of stochastic-MORWTA, the value of each of the goals of power loss, VS, THD, VU, ENS, SAIFI, SAIDI, and MAIFI is increased 12.21%, 10.64%, 12.37%, 9.82%, 14.30%, 12.65%, 12.63% and 13.89%, respectively in contrast to the deterministic scenario without uncertainty.

• The results of the stochastic model demonstrated that the 2m + 1 PEM with clustering was an efficient method for modeling uncertainties and resolving the stochastic MORWTA problem. In addition, the results cleared that the uncertainties altered both the network configuration and the wind turbine capacity injected into the network, which had a significant impact on the value of each objective.

• In order for network operators to know the exact values of power losses, power quality, and reliability indices and make the correct decision, it is crucial to account for uncertainties in operation of the network via the MORWTA. In the absence of this, it is impossible to provide the network with reliable performance and optimal power quality in the presence of uncertainties.

• The robust unbalanced network reconfiguration with hybrid photovoltaic/wind energy system allocation utilizing the information gap decision theory are recommended for future research.