Abstract
The fourth industrial revolution witnessed significant advancements in automating numerous aircraft inspection tasks. Still, certain critical procedures continue to rely on manual execution, including the aero-engine blade weighing process. This task is of paramount importance for blade mass inspection and engine dynamic balancing. Yet, automation of aero-engine blade weighing remains a challenge due to the intricate geometry of engine blades, and the stringent requirements on precision. To address this gap, this paper introduces, for the first time, a vision-guided robotic system for autonomous aero-engine blade weighing. The proposed system presents a novel end-effector design incorporating a high-precision load cell for accurate and rapid weighing coupled with an imaging sensor for autonomous robotic perception capabilities. The system is tested in industrial settings, and the results show a high weighing precision and accuracy of 0.0404 g and of 0.0252 g, respectively. Our system offers the advantage of seamless integration into existing industrial setups without the need for facility reconfiguration. Video Link
Similar content being viewed by others
Introduction
Industrial automation emerged as a driving force for the Industry 4.0 concept, revolutionizing modern industries in recent decades. Robotic manipulators stand at the forefront of this transformation and significantly contribute to the mass production of high-value, specialized items1,2. For instance, industrial automation is becoming increasingly feasible due to the combination of low-cost computational power and the increasing availability of industrial robotic manipulators3,4. This led robotic automation in industrial facilities become a standard practice for various aerospace and automotive industrial applications including robotic machining1,5,6, dexterous manipulation4,7,8, and automated inspection9,10,11.
Automated inspection remains an essential operation in various industries. The generation of precise and accurate structural representations of mechanical components is of high importance, particularly in the aerospace sector for its stringent precision demands. Several initiatives have been proposed tackling automation for inspection of aircraft parts, including aircraft wings11,12,13 and fastener holes10,14,15. These works leverage advancements in computer vision and image processing to perform precision surface inspection and assessment of fastener holes. However, some applications, such as aero-engine blade weighing, require robotic manipulation where further complexity is introduced as robots need to physically interact with industrial components16,17.
Aero-engine blade weighing is of high importance for assessing blade weights to serve inspection and dynamic balancing tasks. Currently, aero-engine blade weighing is performed manually, where human operators are required to perform the mass measurement using conventional mass balances, prior to generating the sorting sequence of blades. Such manual operation tends to be time-consuming, labor-intensive, and prone to human error. This manual operation is because automating aero-engine blade weighing for dynamic balancing remains challenging, due to the complex and intricate geometries of the engine blades. To illustrate, an automated robotic system for aero-engine blade weighing needs to meet the following requirements: 1- accurate blade detection and 3D localization for high grasping success rates and 2- novel end-effector design encompassing a load cell to achieve the required weighing precision. This imposes a surging demand for an automated solution of aero-engine blade weighing, which is critical for aerospace maintenance production lines.
Motivated by the above, this paper introduces a novel, end-to-end vision-guided aero-engine blade weighing system with its corresponding intelligent algorithms for precision weighing. The proposed system introduces a novel end-effector design serving the dual purpose of automatic blade detection and precision weighing. The end-effector encompasses an imaging sensor for adaptability to diverse industrial environments and a load cell for direct, swift aero-engine blade mass measurements. On the other hand, a positioning refinement framework is proposed to enhance detection and grasping success rates. This work also presents a detailed testing and analysis of the full system along with its perception algorithms, with in-depth discussion on the practicality and applicability. This evaluation relies on two criteria: 1- Assessing the blade detection and position refinement framework for localization repeatability and 2- the sorting system’s weighing precision and accuracy, where a precision and accuracy of 0.0404 g and accuracy of 0.0252 g are achieved.
The rest of the paper is structured as follows: The Related Work section presents state-of-the-art methods for industrial inspection. The Results section presents the experimental setup and results regarding the detection success rates and weighing precision, while the Discussion section discusses the obtained results quantitatively and qualitatively. Finally, the Methods section presents the methodology behind the proposed system in terms of the robotic perception capabilities and end-effector designs, where both sufficed in the objective of precision inspection and weighing of aero-engine blades.
Related work
The drive for Industry 4.0 triggered significant advancements in automating inspection and manipulation tasks in various industries including aerospace18, automotive19, and agriculture17. Industrial inspection is critical in various production lines, where stringent safety and performance standards demands are present. Several initiatives have been proposed tackling automation for inspection of aircraft wings11,12,13 and fastener holes10,14,15. Kruglova et al.’s11 proposed a drone-embedded 3D scanner for inspecting aircraft wings. In addition, Salah et al.10 proposed high-speed inspection of countersinks in aerospace production lines with neuromorphic vision sensors. These works leverage advancements in computer vision and image processing to perform precision surface inspection and assessment of fastener holes. Such advancements motivate automated inspection in several crucial aerospace production lines9,20,21,22.
The aforementioned studies rely solely on computer vision and image processing techniques for inspection. Other inspection applications, such as aero-engine blade weighing, require pick-and-place scenarios that require robotic manipulation for assessing the structural integrity of industrial components23,24. Thus, Xia et al.25 introduced a multi-stage region of interest (ROI) extraction method for grasping detection and robotic manipulation in overlapping scenes using a single camera. Similarly, Huang et al.8 proposed a model-free grasping approach using neuromorphic cameras leveraging their high-speed nature and robustness to illumination conditions. Although these methods leverage images and events as perception modalities, approaches by Lin et al.26, Li et al.27, and Chen et al.28 employed point cloud data from depth cameras for absolute measurements in robot manipulation tasks.
Despite addressing manipulation in challenging scenarios, none of the previous methods specifically tackled the complexities of grasping and manipulating intricate objects, such as aero-engine blades. Therefore, several methods emerged leveraging tactile sensing technologies for object manipulation29,30,31,32,33,34. However, no end-to-end sorting system exists for aero-engine blade weighing and dynamic balancing while the precision requirements for engine dynamic balancing necessitate introducing a novel automated system that simultaneously and precisely inspects and weighs aero-engine blades. Thus, this paper introduces an automated aero-engine blade sorting system to achieve the dual objectives of inspection and dynamic balancing. To achieve this, the proposed system encompasses a novel end-effector encompassing a vision sensor and a load cell for adaptability and seamless integration into different industrial environments. In addition, the automated weighing system is presented along with its intelligent algorithms to ensure precision weighing of the aero-engine blades.
Results
Aero-engine blade weighing system setup
The setup of the proposed aero-engine blade weighing system is demonstrated in Fig. 1, where the proposed system setup mimics industrial settings and seamlessly replaces human operators without restructuring the industrial environment. An ABB-1600-10 industrial robot is utilized to maneuver the end-effector precisely to the target grasping poses. The end-effector encompasses an EGP 40-N-N-B schunk gripper to grasp the engine blades during the weighing process. In addition, S-Beam Load Cell DBBSMM-2kg-002 is strictly attached in line with the gripper for blade mass measurement. Twenty-two geometrically identical blades are randomly placed in 60 equally spaced slots in-plane with an ArUco fiducial marker, yet the blades vary in mass, ranging from 16 g to 17.3 g. Collectively, the blades and the fiducial marker are observed by the Intel RealSense D405 depth camera for blade detection and localization. We have validated our system through rigorous experiments throughout eight automated weighing trials for the Twenty-two aero-engine blades; refer to the supplementary video for the experiments. This rigorous testing protocol is essential for assessing the accuracy and repeatability of the system’s performance. Throughout each experimental trial, the system follows a sequential process, as depicted in Fig. 2: 1- Initial robot homing and blade detection utilizing the Yolov5s artificial neural network, 2- blade detection and localization refinement, 3- blade grasping and weighing, and 4- sorting for all blade mass measurements. The quantitative evaluation of sequences 1 and 2 is based on blade localization accuracy and repeatability, while sequences 3 and 4 assess aero-engine blade weighing precision. These validation metrics define the experimental validation protocol.
Setup of the proposed automated aero-engine blade inspection and weighing system. ABB 1600-10 controls the target poses of the end-effector upon feedback from the Intel D405 depth camera. Following blade detection and localization, each blade is picked by the Schunk gripper and undergoes precise weighing by means of a load cell.
System sequential blocks for robotic aero-engine blade inspection and weighing. (a) The blades are initially detected using Yolov5s. (b) Blade detection and localization refinement for blade localization robust against detection outliers. (c) Following detection, the end-effector moves towards the blade for grasping and undergoes precise weighing. (d) The process is repeated for all blades until a sorting scheme is generated for dynamic balancing.
Blade detection and localization repeatability
The proposed system’s performance is initially validated in terms of blade detection and localization precision. Given the importance of robust blade detection and localization, our approach refines YOLOv5s detections to increase robustness against potential outliers. Figure 3 illustrates the effectiveness of this refinement by comparing blade detection performance using YOLOv5s alone versus YOLOv5s with our proposed refinement method. With consistent detection and tracking of blade 2D image points, these 2D points are transformed into 3D positions, leveraging in-plane ArUco marker detection and alignment with the fiducial marker. Table 1 and Fig. 4 report the precision, \(\sigma _x\) and \(\sigma _y\), for the 3D blade localization in the x and y dimensions, respectively, where the precision is expressed as the standard deviation of each sub-sample of blade measurements. To determine the overall localization precision, an aggregate standard deviation of 0.42 mm is calculated using a pooled variance approach, accounting for differences in the mean positions of each blade. This validation highlights the system’s capability to achieve consistent and accurate 3D localization of detected blades, supporting precise weighing in aero-engine blade inspection, as demonstrated in the following section.
Aero-engine blade mass measurement precision
Following validation of blade detection and localization repeatability, the mass measurement precision is of the utmost importance to evaluate the proposed system, since the precision and accuracy of the system needs to be within the aerospace standards for deployment. In all experimental trials, we evaluate the standard deviation of the measurements to ensure repeatability. Figure 5 illustrates measurements across eight trials for 8 blades, highlighting the central tendencies and consistency of the proposed automated blade inspection and mass measurement throughout the experimental trials. Table 2 presents the mass measurements for 8 blades along with the mass measurement precision in terms of the standard deviation \(\sigma _{m}\), with the aggregate standard deviation being calculated using a pooled variance approach to accommodate for the varied mass of each blade. In addition to the weighing precision, we evaluate the weighing accuracy as the mean absolute error (MAE), \(\eta _{m}\), compared against the blade mass ground truth obtained from a calibrated PS 6100.X2.M mass balance. It is worth mentioning that the provided load cell measurements are generally accompanied with a bias. To eliminate load cell bias, the process flow in the proposed sorting system involves the robot moving the gripper to the proximity of the target blade and records the load-free measurement. The measured value represents the load cell bias which is then used to offset the measured blade mass accordingly. Consequently, the obtained bias-compensated measurements are compared to the ground truth of each blade, where the error falls between 0.002 g and 0.161 g.
While mass measurement precision is a primary evaluation metric for the proposed system, the accuracy of blade localization and grasping is critical for reliable weighing. To assess the system’s robustness under positional uncertainty, we introduced controlled offsets of 1, 3, and 5 mm to the grasping position in a series of tests. These offsets simulate potential uncertainties in blade positioning and enable us to evaluate the system’s ability to maintain weighing precision despite such variations. Figure 6 illustrates the mass measurements for the same blade grasped at each offset, demonstrating that the system’s precision remains consistent and comparable to the values reported in Table 2.
Sorting process time analysis
The proposed system streamlines the blade weighing and sorting process, achieving a processing time of approximately 25 seconds per blade. The breakdown of time for each sub-process is shown in Table 3.
This optimized workflow enables our system to operate significantly faster than manual processes, with time savings achieved through the following key design elements:
-
Integrated weighing mechanism: Unlike manual systems where each blade must be placed individually on a weighing balance, our system performs weighing immediately upon grasping each blade, thanks to the load cell embedded in the gripper.
-
Automated data logging: Data is logged electronically in real-time, eliminating the need for manual entry and reducing the likelihood of errors in recording measurements.
-
Automated sorting logic: Sorting is performed electronically within the software, allowing for immediate sorting order determination without manual intervention, as opposed to the manual sorting required after weighing and logging.
Discussion
The system’s two-fold evaluation criteria demonstrate two key factors. First, accurate detection for all observed engine blades is achieved critically and suffices the ultimate objective of dynamic balancing. Secondly, false detection is eliminated during the blade detection and localization stage. This is of essential importance so that no outliers are added to the balancing sequence when performing the blade operation on the aircraft engine. In addition, such robustness in detecting and localizing blades is significant for accurate grasping from desired end-effector poses, which impacts the precision of mass measurements during the grasping process. This precision is evident in the repeatability and accuracy observed across experimental trials. In addition, the presence of uncertainties in the gripping task is evaluated by adding offsets to the blade grasping position, where the obtained results are consistent with the reported system weighing precision. Ultimately, the system’s advantage lies in its adaptability for deployment in production lines. The proposed robotic perception capabilities enable seamless adaptation to diverse facilities. Moreover, the proposed automation framework for aero-engine blade weighing and sorting mitigates the drawbacks associated with human operation, addressing concerns related to human error and expediting the blade weighing and sorting processes achieving a processing time of 25 seconds per blade.
Methods
System overview
This section presents an overview of the novel robotic system designed for automating mass inspection and dynamic balancing of aero-engine blades as shown in Fig. 7. The proposed system comprises a robotic serial manipulator equipped with a customized end-effector that integrates three critical components: Intel RealSense D405 depth camera for scene observation, Schunk gripper EGP 40-N-N-B for secure grasping, and S-beam load cell DBBSMM-2kg-002 with a precision of 0.01 g for accurate mass measurements. The specifications and design of our customized end-effector are shown in Fig. 7 and Table 4, respectively. The gripper is attached directly to the load cell and is not in contact with other components of the end-effector, such that the load cell can sense the change in mass when the gripper holds the blade. The robot manipulator employed in this system is the ABB 1600-10/1.45, characterized by a payload capacity of 10 kg, a reach of 1.2 m, and a positional repeatability of 0.02 mm. The design selection for this robotic arm enhances the system’s capability to handle and maneuver aero-engine blades precisely during the mass measurement process.
An overview of the robotic aero-engine weighing and sorting system setup. The end-effector comprises a depth camera for blade detection and localization, observing the blade tray. Following detection, the robotic arm moves the end-effector, enclosing the load cell to inspect and weigh the engine blades.
Figure 8 shows our system’s electronic components and their connections. The command PC receives and processes measurements from different sensors, performs the needed computations to manipulate the robot, and reports the status and results to the operator using the Graphical User Interface (GUI). The two main sensing modules within the system are the depth camera for visual feedback and guidance, and the load cell for weight measurements. The load cell is connected to a digitizer for analog-to-digital (A/D) conversion, which is subsequently linked to an RS232 to USB converter, establishing a connection with a command computer. The feedback from the depth camera is used to localize the blades and the blade tray within the robot workspace in 3D. We utilize the camera in an eye-in-hand configuration to minimize the effect of calibration errors, enable a multi-stage blade localization process from different relative distances between the camera and the blade, and promote adaptation to different operation environments. Using the blades position, target trajectories for the robot manipulator are forwarded to the robot controller, which in turn controls the joints of the robot. This integrated system is based on the Robot Operating System (ROS), which provides efficient control and communication. The GUI, based on ROS JS, provides human operators with real-time process and measurement updates. The following features are available to the operator via the GUI:
-
User Controls: User Control over Robot: This includes robot home positioning, measurement initiation, and sorting.
-
Live Stream visual feedback and detection: Includes a live stream display that shows users how blades are detected within their tray.
-
Panel for Measurement Information: Provides the user with real-time updates on the blade’s current measurement. This panel shows information like the blade’s mass measurement and the sorting order of each blade.
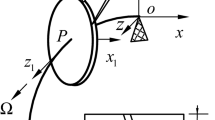
For robot guidance and control, we define the following frames of reference, see Fig. 7:
-
\(\mathcal {F}_{\mathcal {R}\mathcalligra {b}}:\) Robot base frame.
-
\(\mathcal {F}_{\mathcal {TCP}}:\) Tool center point frame.
-
\(\mathcal {F}_{\mathcal {C}}:\) RGB-D Camera frame.
-
\(\mathcal {F}_{\mathcal {G}}:\) Schunk Gripper frame.
-
\(\mathcal {F}_{\mathcal{A}\mathcal{r}}:\) Fiducial Marker frame.
-
\(\mathcal {F}_{\mathcalligra {b}^\mathcalligra {i}}:\) \(i^{th}\) Aero-engine blade frame.
-
\(\mathcal {F}_{\mathcal {S}^\mathcalligra {j}}:\) \(j^{th}\) Slot frame.
For robot kinematics and vision-based guidance computations, we utilize transformation matrices to articulate the relationship between a target frame \(\mathcal {F}_{\mathcal {T}}\) and a source frame \(\mathcal {F}_{\mathcal {S}}\). A transformation matrix comprises of two main components; a rotation matrix, defined as \({^\mathcal {T}\mathcal {R}}_{\mathcal {S}} \in \mathbb {R}^{3x3}\), and a position vector \({^\mathcal {T}\mathcal {P}}_{\mathcal {S}} \in \mathbb {R}^{3}\) the transformation matrix is defined \({^\mathcal {T}\mathcal {T}}_{\mathcal {S}} \in \mathbb {R}^{4x4}\) as follows:
The transformation matrix \({^{\mathcal {R}\mathcalligra {b}}}{\mathcal {T}}_{\mathcal {TCP}}\) between the robot’s base and its tool center point is computed by solving the robot’s forward kinematics as:
where \(\theta \in \mathbb {C}\) are the observed robot joint angles in the robot’s configuration space \(\mathbb {C}\), and \(g(\theta )\) is a nonlinear function representing the robot’s kinematics. Furthermore, the transformations \(^{\mathcal {TCP}}\mathcal {T}_{\mathcal {C}}\) and \(^{\mathcal {TCP}}\mathcal {T}_{\mathcal {G}}\) are constants that are obtained through the calibration procedure as explained in4,35.
The flow of the blade grasping and weighing process is illustrated in Fig. 9. Initially, the robot starts from the home position and localizes the blades tray using an ArUco marker to obtain an estimate of \({^{\mathcal {R}\mathcalligra {b}}\mathcal {T}_{\mathcal{A}\mathcal{r}}}\). Consequently, the pose of each slot within the contained \({^{\mathcal {R}\mathcalligra {b}}\mathcal {T}_{\mathcal {S}^\mathcalligra {j}}}\) is estimated its their pre-defined location in the tray. The camera feedback is then used to detect and localize all blades in the 3D workspace, matching each detected blade with its corresponding slot in the tray. The empty slots are, thereby, identified to ensure the system generalizes to arbitrary blade distributions and in cases where blades are missing, see Fig. 10. Following the successful localization of blades, the robot navigates to each blade and aligns the load cell axis with each blade, initiating the grasping process. Once grasped, the system records a measurement of the blade mass. After processing the mass measurement, the robot returns the grasped blade to its designated slot. This process is repeated for the entire blade set, ensuring each blade is accurately grasped, weighed, and placed in its respective slot. The system continuously updates the GUI to report the location and mass measurement of each blade and reports the sorting order in which the blades should be installed on the aero-engine to ensure dynamic balancing.
The sequence of operations our system performs to measure the mass of all blades within a single tray. The robot first localizes the tray and the slots within it using an ArUco marker. The robot then localizes the blades in the tray using a deep-learning model. Subsequently, the robot grips each blade and measures its mass using the load cell embedded in the gripper. Finally, the system updates the GUI and reports the correct order to install the blades in the aero-engine to the human operator.
(a) Detection of slots with target blades to be weighed in a configuration of empty slots. The empty slots are detected given their pre-defined location in the tray with respect to the ArUco marker. (b) The output of the system with blades weighed showing generalizibility of the proposed system to arbitrary number of blades placed in the tray.
Vision based control
Blade localization framework
Assume we are given a set [1, 2, 3, ... N] of blades, the blade localization and sorting process is summarized in Algorithm 1. A devised detector network, YOLOv5s, detects the blades within the tray and stores their pixel coordinates [u, v]. The coordinates are then transformed to world coordinates relative to the \(\mathcal {F}_{\mathcal {R}\mathcalligra {b}}\) using the pinhole camera model and depth value estimate. Concurrently, the slots the blades are in are located and associated with each blade by using the URDF of the tray, which contains the transformation of the tray to each slot \(\mathcal {F}_{\mathcal {S}}\). The association is based on finding the slot with the minimum Euclidean distance to the blade. A loop is initiated to move to each blade and center it in the image plane.
YOLOv5s architecture
In order to detect the blades and localize their position in the image plane, Ultralytics YOLOv5s36 was deployed, which is one of the mainstream algorithms in single-stage object detection. The algorithm has a relatively high reliability and stability in detecting objects at different scales and with high inference speed, which would allow for fast-paced automation of the process. YOLOv5s consists of three separate modules; the backbone, the neck, and the head. The backbone is based on the CSPDarknet5337 convolutional neural network. The backbone improves the model performance by relying on the cross stage part (CSP) blocks to extract feature maps of different sizes. The neck consists of the spatial pyramid pooling layer38, which realizes the fusion of feature maps from different receptive fields in order to fuse high-level and low-level feature maps for accurate regression of the position. Three main feature maps are generated to detect small, medium, and large objects. The feature maps are then combined with the preset anchors in the head to predict the final object bounding box coordinates along with, confidence scores, and object class. Non-maximum suppression (NMS) is also utilized to remove bounding boxes that do not encapsulate the whole object that is overlapping and redundant.
The variable \(l_{CIoU}\) represents the loss function for bounding box regression, which improves the accuracy of predicting bounding boxes for objects. The classification loss, denoted as \(l_{cls}\), quantifies the precision of the predicted class in relation to the bounding box. During the training process, the classification loss was 0 because only one category of items was available, specifically blades. The confidence loss, denoted as \(l_{obj}\), quantifies the precision of the objectness score, which predicts whether a given bounding box contains an object. The confidence score of the j’th projected box in the i’th grid is determined by dividing the grid into a grid of size \(S \times {S}\).
In the YOLOv5s model, the confidence loss function Eq.4, designated as \(l_{\text {obj}}\), is important for accurately recognizing the presence of objects within anchor boxes. This function runs on a grid with dimensions \(S \times S\), where each cell contains \(M\) specified anchor boxes. The binary cross-entropy loss, denoted as \(l_{\text {obj}}\), combines the contributions from two separate sums. The initial summation iterates through each grid cell and predicted anchor box. \(I_{ij}^{\text {obj}}\) indicates the presence of an identified object in the \(i\)-th grid cell and \(j\)-th anchor box. \(C_{j}\) and \(\hat{C}_{j}\) represent the actual and predicted confidence scores, respectively. The confidence score, \(\hat{C}_{j}\), is calculated using Equation 5. In this equation, \(P_{i,j}\) represents the probability of the bounding box \(\{i,j\}\) containing an object of a particular class, and \(IOU_{\text {pred}}^{\text {truth}}\) measures the Intersection over Union between the predicted and ground-truth bounding boxes. If there is no expected object in a given situation, the value assigned to \(\hat{C}_{j}\) is 0. The second component of the summation takes into consideration grid cells that do not contain objects. It includes a weighting coefficient \(\lambda _{\text {noobj}}\) to account for the detection of non-objects, and \(I_{ij}^{\text {noobj}}\) as an indicator for the absence of objects. In this context, \(M\) denotes the total quantity of anchor boxes assigned to each grid cell, while \(\hat{n}\) indicates the number of anchor boxes predicted by the model to contain an item.
The bounding box regression loss \(l_{CIoU}\) Eq. 6 in object identification models is essential for precisely determining the location of items within an image. YOLOv5s utilizes the complete intersection over union (CIoU) loss to enhance the regression work. The CIoU loss considers both the intersection over union (IoU) between the predicted and ground truth bounding boxes, as well as the Euclidean distance between the centers of the boxes and the consistency of their aspect ratios. \(\rho\) represents the Euclidean distance, \(c\) is the length of the diagonal of the smallest enclosing box, and \(v\) quantifies the degree of aspect ratio consistency with \(\alpha\) acting as a trade-off coefficient. The all-encompassing loss function directs the model towards making precise and accurate predictions for bounding boxes.
The fine-tuning of the model was conducted over a total of 117 epochs, where the values for \(l_{CIoU}\) and \(l_{obj}\) Fig. 11 were monitored to evaluate the quality of the training being performed.
Evaluation metrics
In order to evaluate the model performance, precision (P), recall (R) and F1 score are used. These parameters are meaningful indicators to be used when evaluating the classification performance of the model, and in this case, the ability of the model to detect the presence of all the blades in the scene to a high accuracy. The formulas to calculate each metric is as follows:
where TP refers to the samples predicted to be positive while being positive, FP refers to the false prediction of positive samples, and FN is the false prediction of negative samples.
where Eq. 11 refers to the average precision AP which is the area under the \(P-R\) curve with a higher value indicating good classifying performance. mAP refers to the mean average precision. The results of the training for precision, recall, and mAP are 0.83, 0.79 and 0.81, respectively, the F1 score was 0.81.
Transformation to world coordinates
After detecting the blades using YOLOv5 and knowing the pixel coordinates [u, v] of the blades, it is necessary to estimate their world coordinates to move the gripper accordingly to grasp and lift them. Since the camera is mounted on the end effector and follows the pinhole camera model, the pinhole projection of a 3D point \(P = [x,y,z]\) to a 2D point \(p=[u,v]\) can be utilized.
where K is the intrinsic camera property obtained through calibration of the camera, and \(\begin{bmatrix} R&t\end{bmatrix}\) is the extrinsic camera property. The availability of both of these matrices enables the estimation of the real world coordinates of the blades from the image plane. The coordinate systems available for 2D to 3D projection and their relationships are available in Fig. 12.
The orientation of each blade is calculated based on the orientation of the holder, which is determined from the ArUco fiducial. By obtaining the rotation of the ArUco fiducial, the system can infer the blade’s orientation as follows:
where \(^\mathcal{A}\mathcal{r}\mathcal {R}{_{\mathcalligra {b}_\mathcalligra {i}}}\) is the fixed rotation matrix between the ArUco marker and the blade. This calculation enables the system to align the gripper precisely with the blade for accurate handling.
It is important to note that the blade’s orientation relative to the holder is assumed to be fixed, as the slot confines the blade and limits any significant variations in orientation. This assumption holds across most blade weighing systems, where slot design constrains blade orientation. However, in cases where blade angles vary, orientation can be dynamically estimated from the camera feedback using methods such as YOLO with Oriented Bounding Box detection or semantic segmentation models.
Position-based visual servoing
In the robot control and guidance sequence of our system, either a desired camera pose \(^{\mathcal {R}\mathcalligra {b}}\mathcal {T}^{*}_{\mathcal {C}}\) or a desired gripper pose \(^{\mathcal {R}\mathcalligra {b}}\mathcal {T}^{*}_{\mathcal {G}}\) is defined based on a standoff pose \(^{\mathcalligra {b}^{\mathcalligra {i}}\mathcal {T}^{*}_{\mathcal {S}\mathcalligra {t}}}\) relative to the \(i^{th}\) blade, as follows:
or
Given that both the camera and the gripper are calibrated relative to the robot flange, both \(^{\mathcal {TCP}}\mathcal {T}_{\mathcal {C}}\) and \(^{\mathcal {TCP}}\mathcal {T}_{\mathcal {G}}\) are known. Accordingly, we compute a desired TCP pose \({^{\mathcal {R}\mathcalligra {b}}}\mathcal {T}^{*}_{\mathcal {TCP}}\) as:
or
Afterwards, a desired joint angles vector is defined \(\bar{\theta }\in \mathbb {C}\) such that:
We solve for \(\theta ^{*}\) using the Newton–Raphson inverse kinematic approach of the open-source Kinematic and Dynamics Library (KDL). We then generate a joint trajectory \(\theta ^{*}(t)\) between the current joint angles and the desired ones using the RRT-connect39 implementation of the Open Motion Planning Library40. A low-level PID controller then controls each joint to follow \(\theta ^{*}(t)\).
Weighing and sorting algorithm
Once the robot localizes the target blade, the process proceeds with the robot grasping the blade and measuring its mass. Generally, load cell measurements are accompanied with an additive bias, \(M_{initial}\). To circumvent this drawback, the robot moves the gripper to the blade proximity to record the \(M_{initial}\), which represents the load cell bias. Consequently, the robot then grasps the blade and obtains another measurement from the load cell denoted by \(\hat{M}^j_{final}\) . It must be noted that the grasped blade must be aligned with the gripper’s z-axis and the load cell’s measuring axis to minimize any moments from the weight of the blade. To account for noise, we pass the measurements through a low pass filter that averages multiple measurements as \(M_{final} = \Sigma _j \hat{M}^j_{final} / N, \hspace{0.2cm} j \in [1, N]\), where N denotes the total number of measurements. These measurements are then shifted by \(M_{initial}\) give the actual blade weight exerted on the load cell as:
Once the robot estimates the mass of a blade, it reports the measurement to the GUI in real-time, as shown in Fig. 13. This process is then repeated N times across the whole set of detected blades within the tray. The subsequent sorting procedure entails organizing the blades based on their mass measurements using a specialized technique. First, the blades are arranged in descending order according to their masses. The detected blades are then divided into two groups: S1 and S2. S1 initially includes the blades with the highest and lowest masses, while S2 contains the second highest and second lowest. Sequentially, S1 continues to add blades, ranked third highest and third lowest, while S2 accumulates blades in a similar manner. This alternating pattern continues until all blades are sorted. Following this, the S1 is stacked on top of S2, resulting in a balanced sorting order, as shown in Fig. 14. This method adheres to the requirements of jet engine rotors, ensuring a well-balanced distribution of measured blades.
It must be noted that the proposed system performs sorting numerically, outputting the optimal installation order for each blade based on its mass. While physical sorting is possible, our system does not implement it, as it would increase processing time by two to three times; this would require the robot to re-grasp each blade and place it in its designated slot after completing the numerical sorting. For applications where processing time is less critical, a physical sorting step could indeed be beneficial, as it may help reduce human error in downstream processes.
Data availibility
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Ji, W. & Wang, L. Industrial robotic machining: A review. Int. J. Adv. Manuf. Technol. 103, 1239–1255. https://doi.org/10.1007/s00170-019-03403-z (2019).
Ali, M.A., Irfan, M.S., Khan, T., Khalid, M.Y. & Umer, R. Graphene nanoparticles as data generating digital materials in industry 4.0. Sci. Rep.13, 4945, https://doi.org/10.1038/s41598-023-31672-y (2023).
Yan, X. & Melkote, S. Automated manufacturability analysis and machining process selection using deep generative model and siamese neural networks. J. Manuf. Syst. 67, 57–67. https://doi.org/10.1016/j.jmsy.2023.01.006 (2023).
Youssef, A., Bayoumy, A.M. & Atia, M.R. Investigation of using ann and stereovision in delta robot for pick and place applications. Math. Model. Eng. Problems (2021).
Ayyad, A. et al. Neuromorphic vision based control for the precise positioning of robotic drilling systems. Robotics Comput.-Integrated Manuf. 79, 102419 (2023).
Liu, Y. et al. A visual positioning and measurement system for robotic drilling. 461–466, https://doi.org/10.1109/AMC.2016.7496393 (2016).
Liang, W. et al. Visuo-tactile feedback-based robot manipulation for object packing. IEEE Robotics Autom. Lett. 8, 1151–1158. https://doi.org/10.1109/LRA.2023.3236884 (2023).
Huang, X. et al. Real-time grasping strategies using event camera. J. Intell. Manuf.33, https://doi.org/10.1007/s10845-021-01887-9 (2022).
Chen, S.-H. & Perng, D.-B. Automatic optical inspection system for ic molding surface. J. Intell. Manuf.27, https://doi.org/10.1007/s10845-014-0924-5 (2014).
Salah, M. et al. High speed neuromorphic vision-based inspection of countersinks in automated manufacturing processes. J. Intell. Manuf.[SPACE]https://doi.org/10.1007/s10845-023-02187-0 (2023).
Kruglova, T., Sayfeddine, D. & Vitaliy, K. Robotic laser inspection of airplane wings using quadrotor. Procedia Eng. 129, 245–251 (2015).
Burghardt, A., Kurc, K., Szybicki, D., Muszyńska, M. & Szczęch, T. Robot-operated inspection of aircraft engine turbine rotor guide vane segment geometry. Tech. Gazette 24, 345–348 (2017).
Smith, J. & Kochhar-Lindgren, D. Integrated hole and countersink inspection of aircraft components[SPACE]https://doi.org/10.4271/2013-01-2147 (2013).
Yu, L. et al. Vision based in-process inspection for countersink in automated drilling and riveting. Precis. Eng. 58, 35–46. https://doi.org/10.1016/j.precisioneng.2019.05.002 (2019).
Luker, Z. & Stansbury, E. In-process hole and fastener inspection using a high accuracy laser sensor[SPACE]https://doi.org/10.4271/2020-01-0015 (2020).
Borrell, J., Perez-Vidal, C. & Segura, J. V. Optimization of the pick-and-place sequence of a bimanual collaborative robot in an industrial production line. Int. J. Adv. Manuf. Technol. 130, 4221–4234. https://doi.org/10.1007/s00170-023-12922-9 (2024).
Navas, E., Shamshiri, R. R., Dworak, V., Weltzien, C. & FernÃindez, R. Soft gripper for small fruits harvesting and pick and place operations. Front. Robotics AI 10. https://doi.org/10.3389/frobt.2023.1330496 (2024).
Mehdizadeh Gavgani, B. et al. Soft switching multiple model predictive control with overlapping cross-over time strategy in an industrial high speed pick and place application. Control. Eng. Pract. 144, 105813. https://doi.org/10.1016/j.conengprac.2023.105813 (2024).
Polonara, M., Romagnoli, A., Biancini, G. & Carbonari, L. Introduction of collaborative robotics in the production of automotive parts: A case study. Machines12, https://doi.org/10.3390/machines12030196 (2024).
da Silva Santos, K. R., de Oliveira, W. R., Villani, E. & Dttmann, A. 3d scanning method for robotized inspection of industrial sealed parts. Comput. Ind. 147, 103850 (2023).
Shahid, L., Janabi-Sharifi, F. & Keenan, P. A hybrid vision-based surface coverage measurement method for robotic inspection. Robotics Comput.-Integrated Manuf. 57, 138–145. https://doi.org/10.1016/j.rcim.2018.11.009 (2019).
Abdulrahman, Y., Eltoum, M. A. M., Ayyad, A., Moyo, B. & Zweiri, Y. Aero-engine blade defect detection: A systematic review of deep learning models. IEEE Access 11, 53048–53061. https://doi.org/10.1109/ACCESS.2023.3280992 (2023).
Kleeberger, K., Bormann, R., Kraus, W. & Huber, M. F. A survey on learning-based robotic grasping. Curr. Robotics Rep. 1, 239–249. https://doi.org/10.1007/s43154-020-00021-6 (2020).
Morrison, D., Corke, P. & Leitner, J. Learning robust, real-time, reactive robotic grasping. Int. J. Robotics Res. 39, 183–201. https://doi.org/10.1177/0278364919859066 (2020).
Xia, J., Chi, J., Wu, C. & Zhao, F. Robot grasping detection in object overlapping scenes based on multi-stage roi extraction. In 2022 34th Chinese Control and Decision Conference (CCDC), 5066–5071, https://doi.org/10.1109/CCDC55256.2022.10034365 (2022).
Lin, H.-I. & Cong, M.N. Inference of 6-dof robot grasps using point cloud data. In 2019 19th International Conference on Control, Automation and Systems (ICCAS), 944–948, https://doi.org/10.23919/ICCAS47443.2019.8971464 (2019).
Li, S., Zhang, S., Fu, Y., Wang, H. & Liu, S. The grasping force control for force sensor-less robot through point clouds mask segmentation. In 2018 3rd International Conference on Robotics and Automation Engineering (ICRAE), 1–4, https://doi.org/10.1109/ICRAE.2018.8586712 (2018).
Chen, Z., Yuan, X., Gu, Q., Hu, C. & He, D. A digital twin system for 6dof robot grasping. In 2023 35th Chinese Control and Decision Conference (CCDC), 3292–3296, https://doi.org/10.1109/CCDC58219.2023.10327020 (2023).
Nguyen, P. V., Sunil, D. B. & Chow, T. W. Soft-stable interface in grasping multiple objects by wiring-tension. Sci. Rep. 13, 21537. https://doi.org/10.1038/s41598-023-47545-3 (2023).
Zhang, S. et al. Hardware technology of vision-based tactile sensor: A review. IEEE Sens. J. 22, 21410–21427. https://doi.org/10.1109/JSEN.2022.3210210 (2022).
Ward-Cherrier, B., Pestell, N. & Lepora, N. F. Neurotac: A neuromorphic optical tactile sensor applied to texture recognition. In 2020 IEEE International Conference on Robotics and Automation (ICRA), 2654–2660, https://doi.org/10.1109/ICRA40945.2020.9197046 (2020).
Welle, M. C. et al. Enabling robot manipulation of soft and rigid objects with vision-based tactile sensors. In 2023 IEEE 19th International Conference on Automation Science and Engineering (CASE), 1–7, https://doi.org/10.1109/CASE56687.2023.10260563 (2023).
Halwani, M. et al. A novel vision-based multi-functional sensor for normality and position measurements in precise robotic manufacturing. SSRN Electron. J.[SPACE]https://doi.org/10.2139/ssrn.4360666 (2023).
Sajwani, H. et al. Tactigraph: An asynchronous graph neural network for contact angle prediction using neuromorphic vision-based tactile sensing. Sensors23, https://doi.org/10.3390/s23146451 (2023).
Ayyad, A. et al. Neuromorphic vision based control for the precise positioning of robotic drilling systems. Robotics Comput.-Integrated Manuf. 79, 102419. https://doi.org/10.1016/j.rcim.2022.102419 (2023).
Jocher, G. et al. ultralytics/yolov5: v3.1 - Bug Fixes and Performance Improvements, https://doi.org/10.5281/zenodo.4154370 (2020).
Bochkovskiy, A., Wang, C.-Y. & Liao, H.-Y.M. Yolov4: Optimal speed and accuracy of object detection (2020). 2004.10934.
Lin, T.-Y. et al. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2117–2125 (2017).
Kuffner, J. & LaValle, S. Rrt-connect: An efficient approach to single-query path planning. In Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), 995–1001, https://doi.org/10.1109/ROBOT.2000.844730 (2000).
Sucan, I. A., Moll, M. & Kavraki, L. E. The open motion planning library. IEEE Robot. Autom. Mag. 19, 72–82. https://doi.org/10.1109/MRA.2012.2205651 (2012).
Acknowledgements
This work was supported by the Advanced Research and Innovation Center (ARIC), jointly funded by SANAD Aerotech (a Mubadala company) and Khalifa University of Science and Technology.
Author information
Authors and Affiliations
Contributions
M.R. Prepared the system setup and prepared the experiments. A.Y. Contributed to the manuscript writing and did the experiments. A.A. Provided technical supervision and contributed to the manuscript writing. L.A. Prepared experimental setups and the necessary hardware for the system. O.A. Prepared the perception algorithms and contributed to the manuscript writing. M.S. Provided technical supervision and contributed to the manuscript writing. B.M. Provided technical supervision. Y.Z. Project management and funding acquisition. Y.A. Provided technical supervision for experimental investigations and contributed to manuscript writing, project management, and funding acquisition.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ramadan, M., Youssef, A., Ayyad, A. et al. Vision-guided robotic system for aero-engine inspection and dynamic balancing. Sci Rep 14, 30742 (2024). https://doi.org/10.1038/s41598-024-80540-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-80540-w
This article is cited by
-
Automatic 3D contour localization for robotic glue spraying using deep learning and 3D point cloud processing technology
The International Journal of Advanced Manufacturing Technology (2025)
-
Research progress of intelligent thermal spraying system for aeroengine blades
The International Journal of Advanced Manufacturing Technology (2025)